Super-Accreting Active Galactic Nuclei as Neutrino Sources
Abstract
1. Introduction
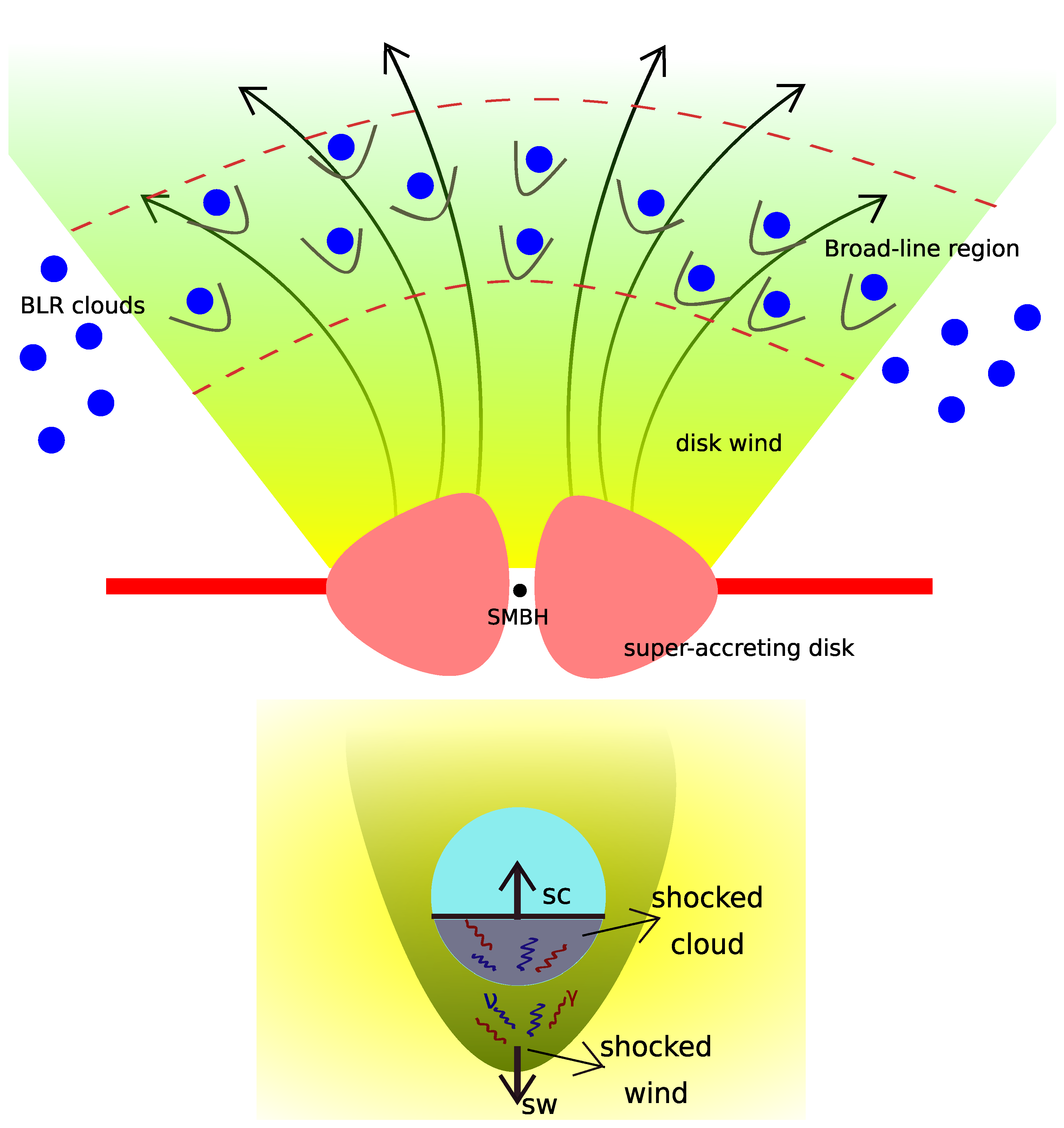
2. Wind-Cloud Interactions
2.1. General Parameters
2.2. Wind Photosphere
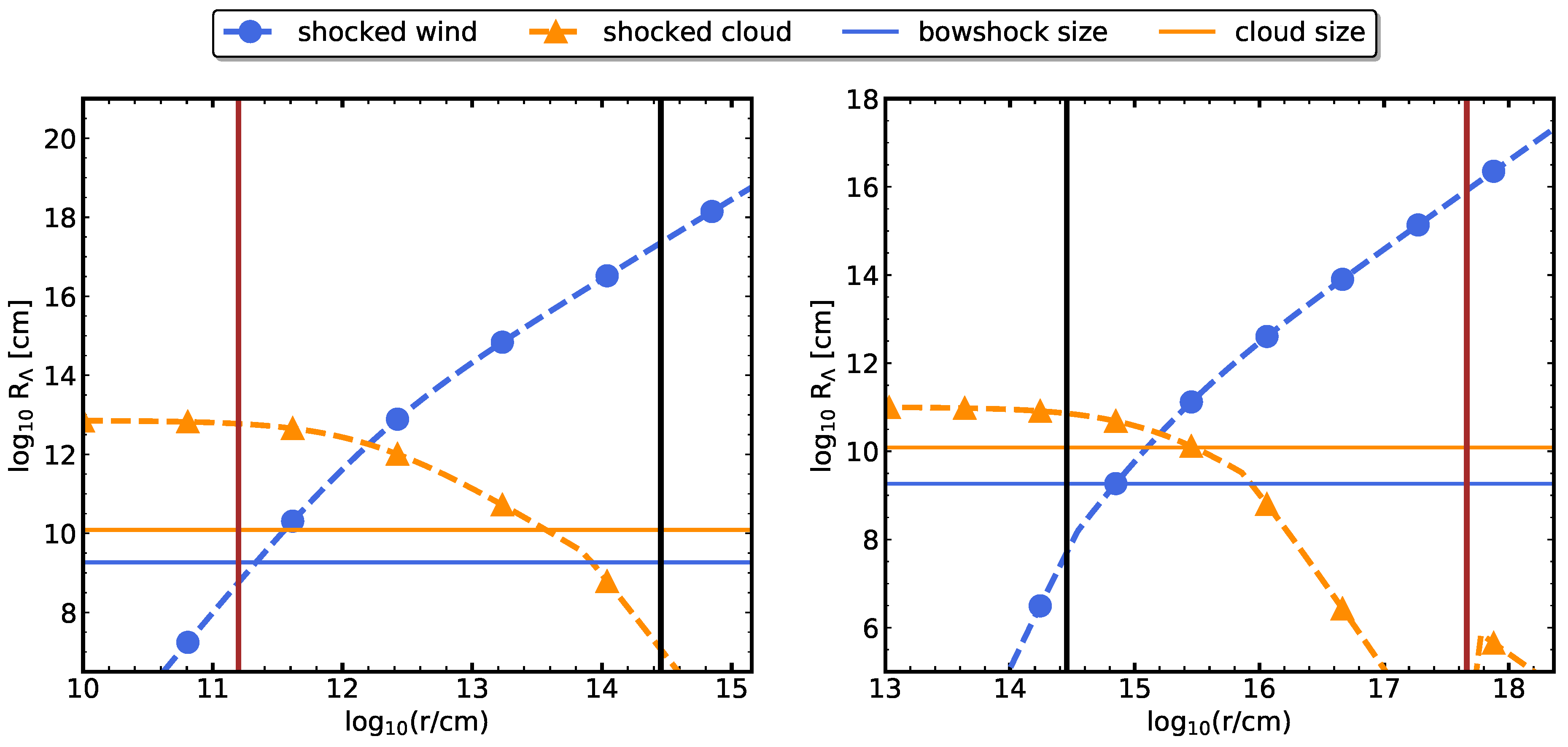
2.3. Shocks
2.4. Magnetic Field in the Clouds
3. Nonthermal Radiation
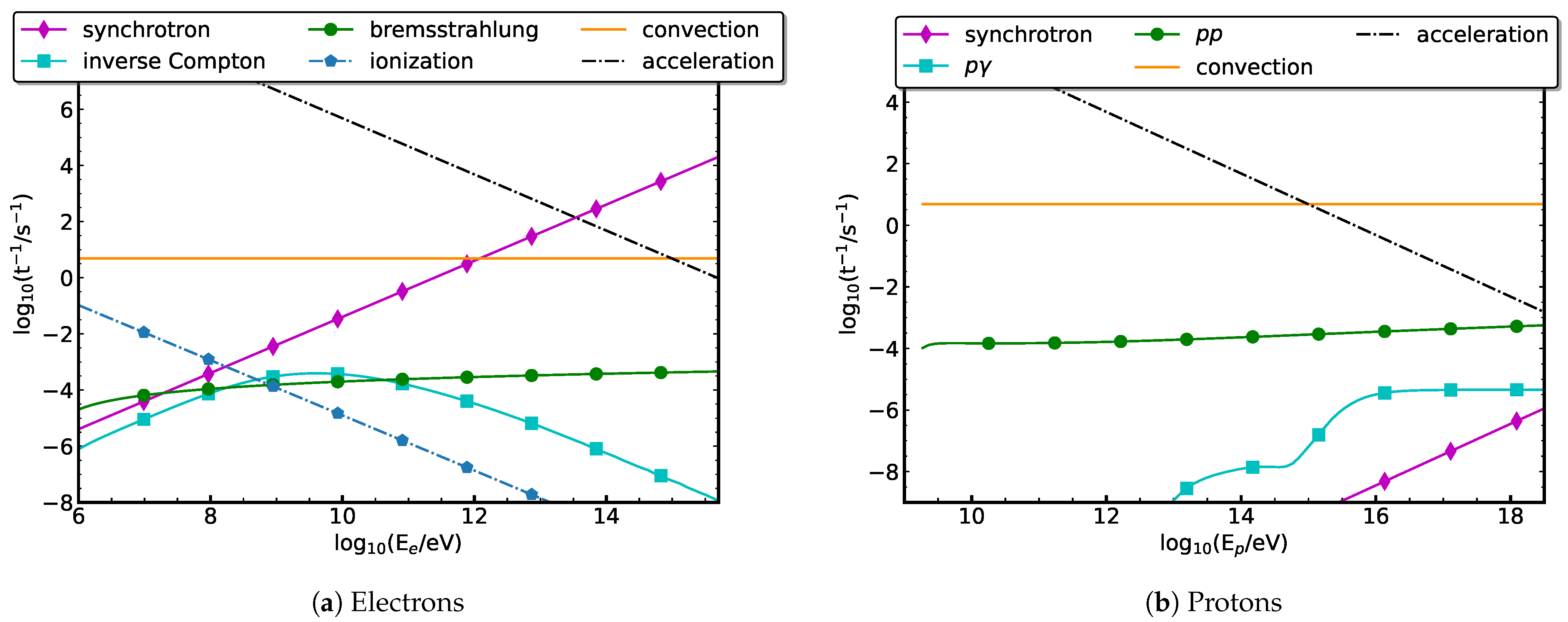
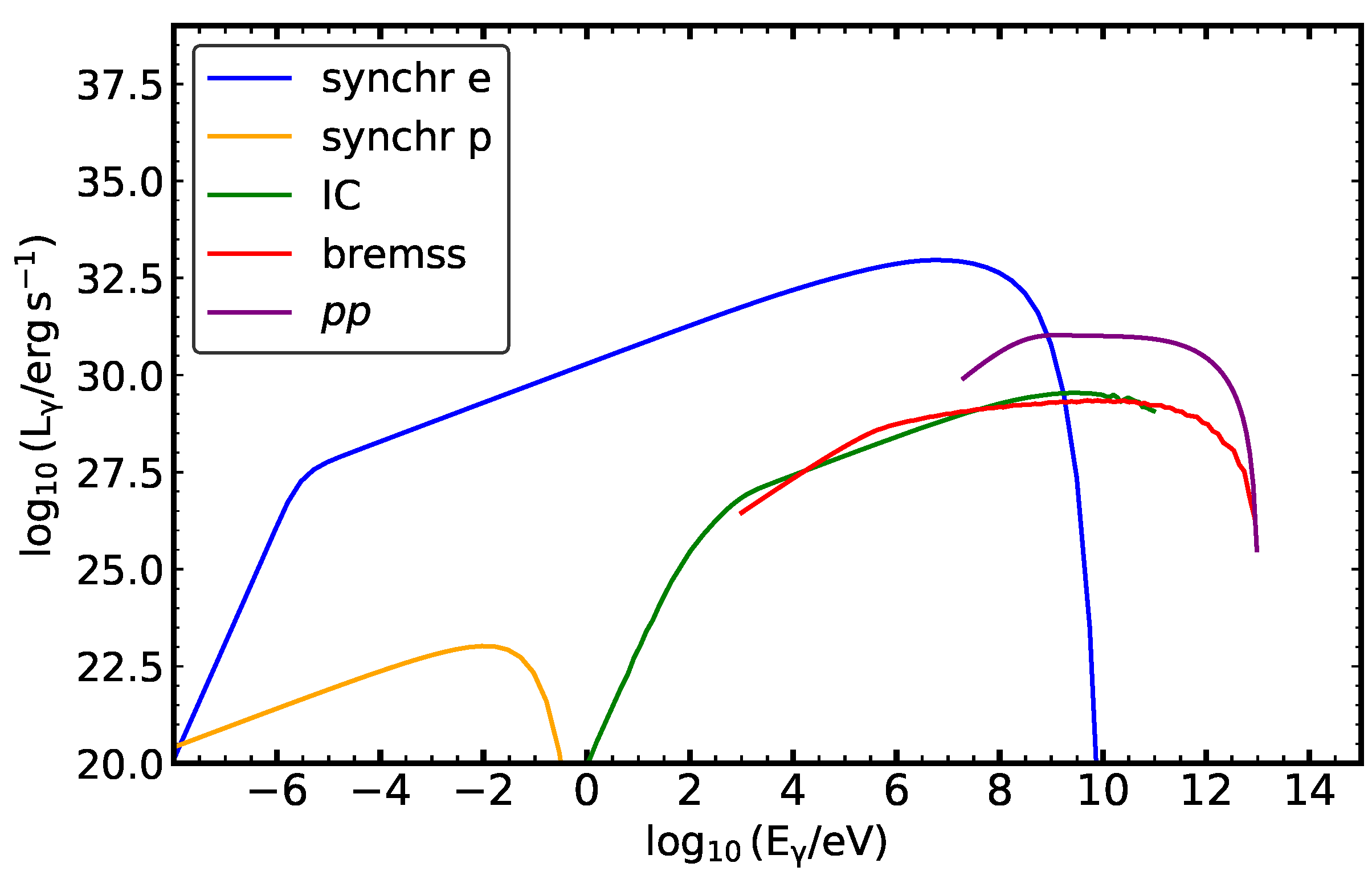
3.1. Model 1
3.2. Model 2
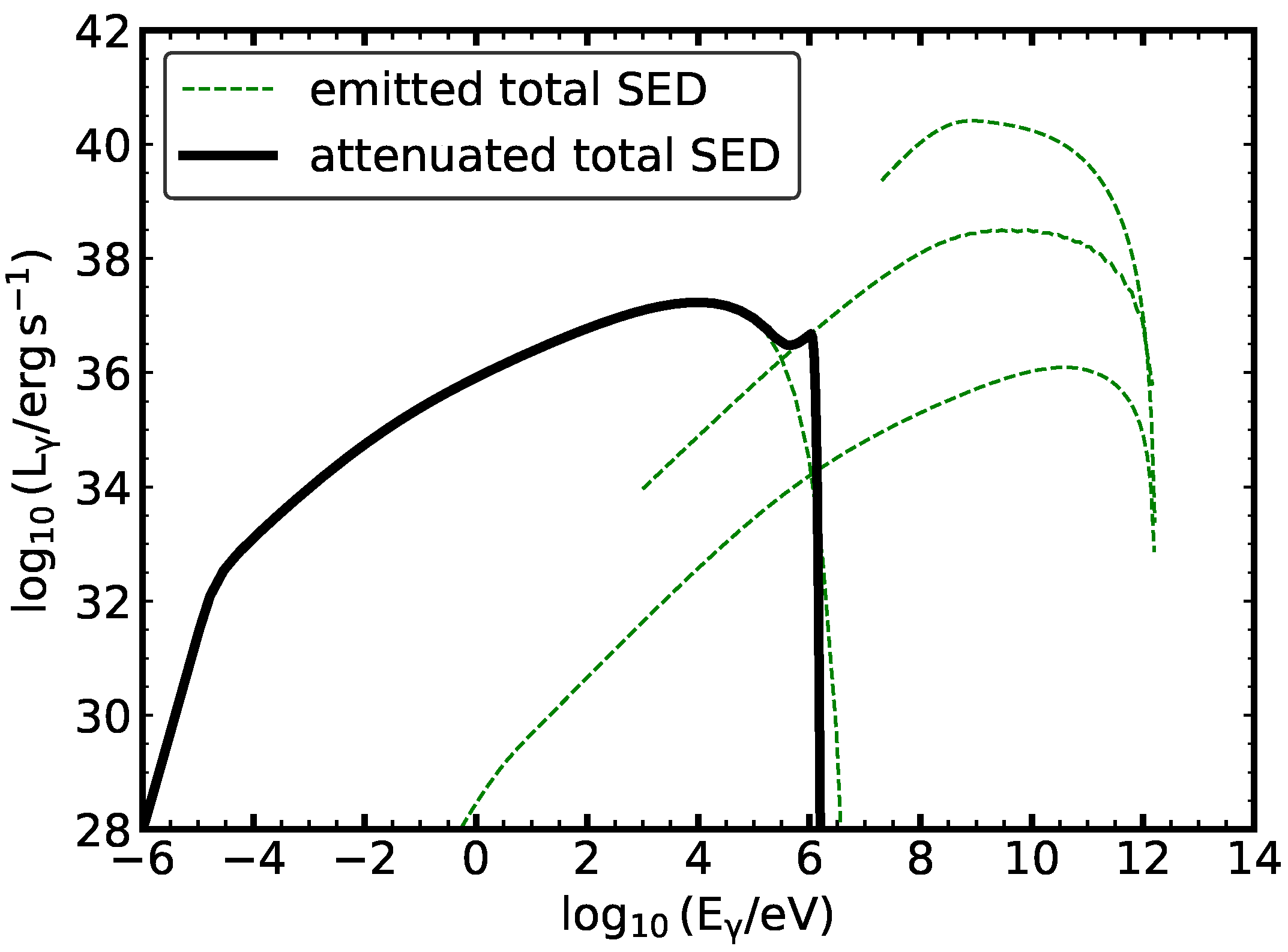
4. Gamma-Ray Absorption
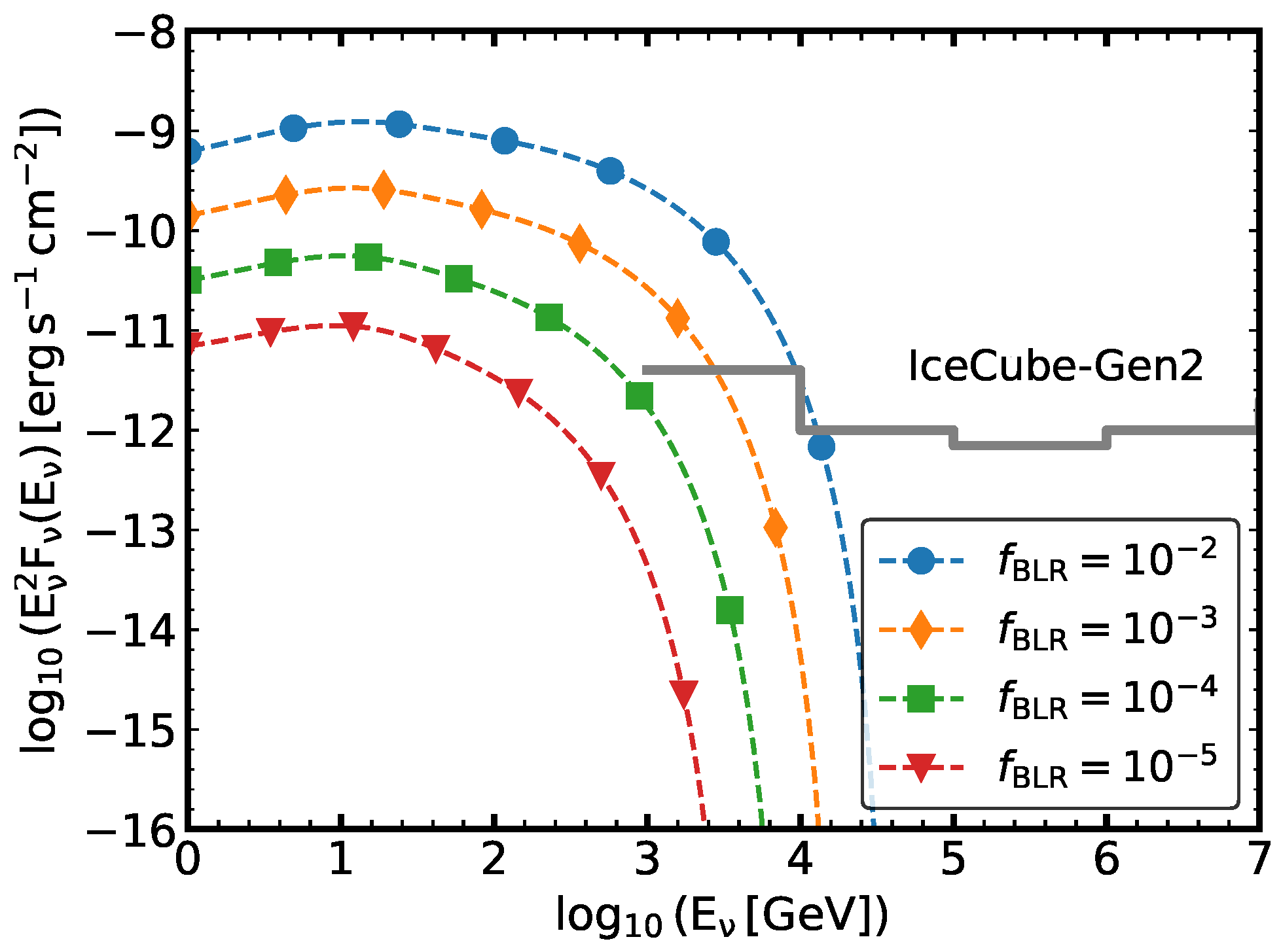
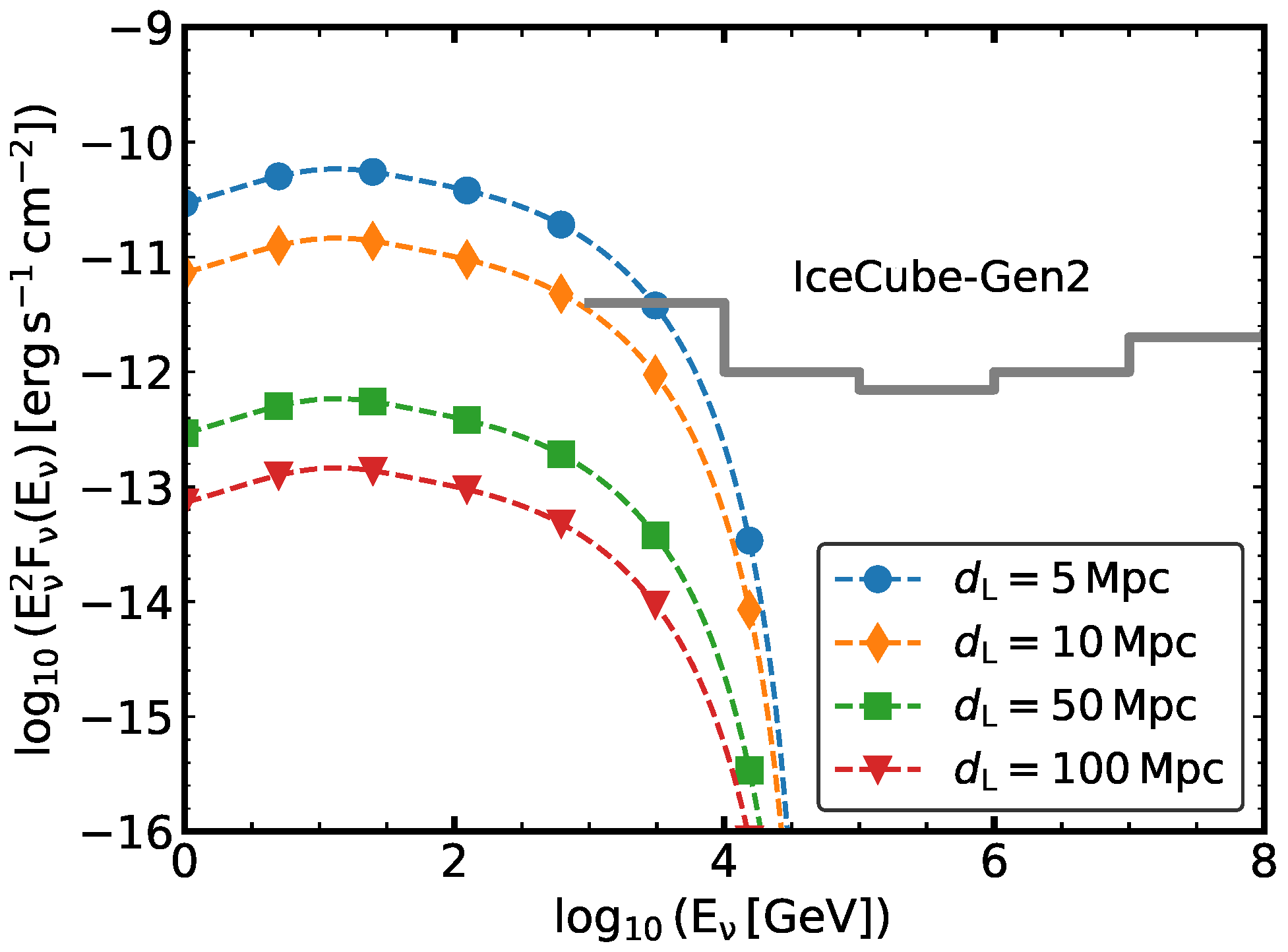
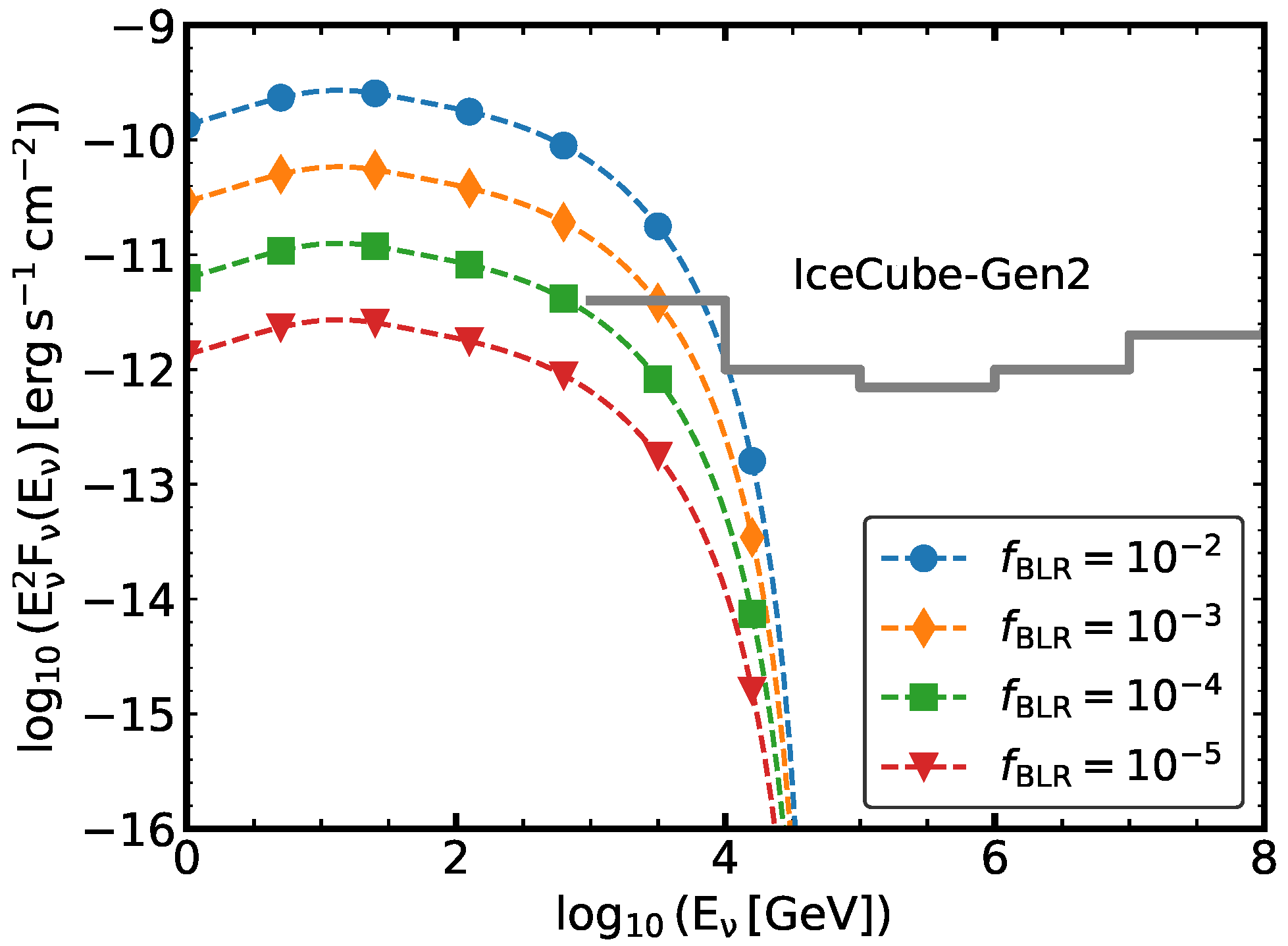
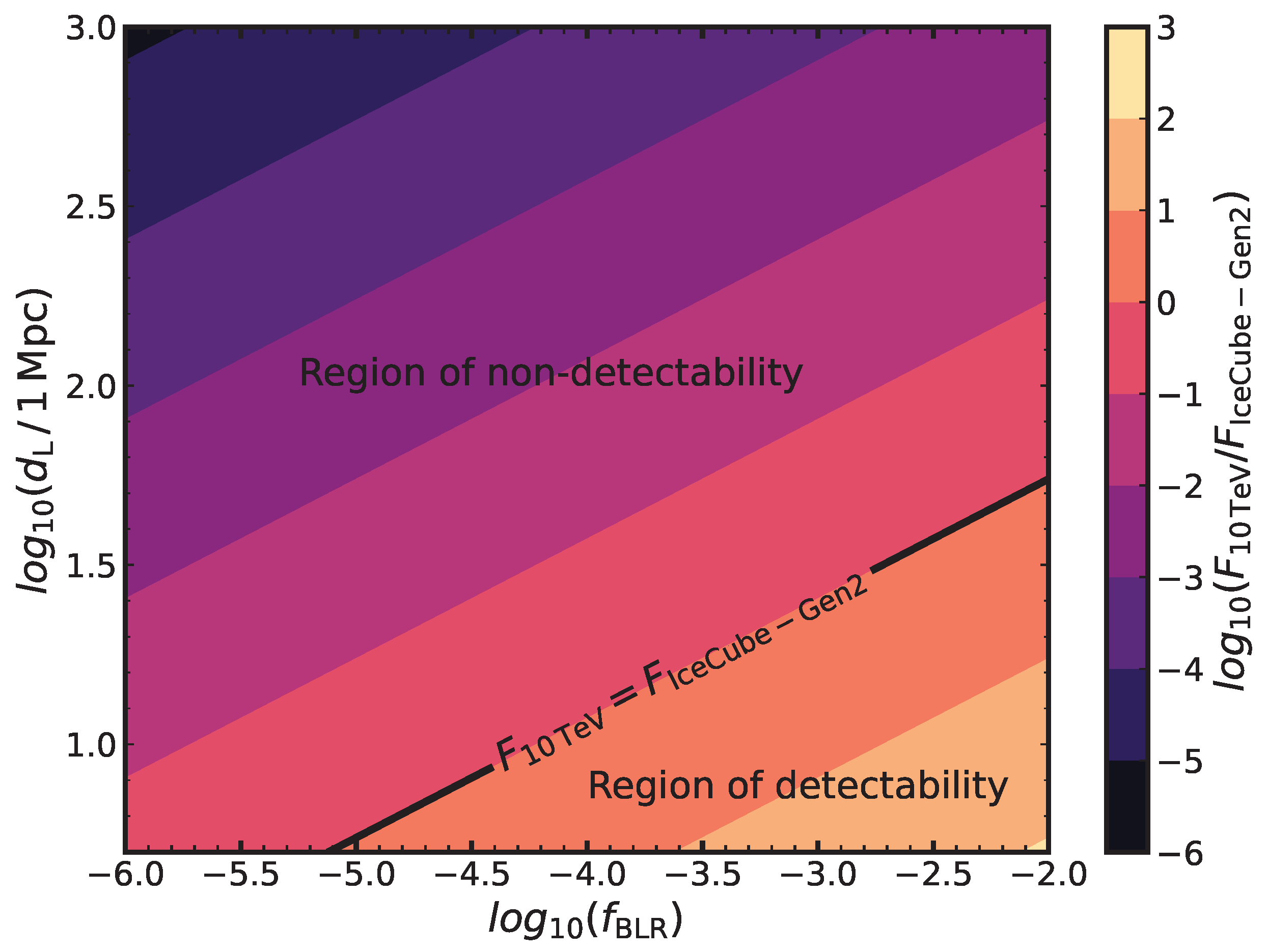
5. Neutrino Production
6. Final Remarks and Summary
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | After completing our work, we became aware of a paper by Huang et al. [29], which applied a similar approach to the case of NGC 1068. Our goal here is to develop a more general and detailed model. |
References
- Paczyńsky, B.; Wiita, P.J. Thick Accretion Disks and Supercritical Luminosities. Astron. Astrophys. 1980, 88, 23. [Google Scholar]
- Abramowicz, M.A.; Czerny, B.; Lasota, J.P.; Szuszkiewicz, E. Slim Accretion Disks. Astrophys. J. 1988, 332, 646. [Google Scholar] [CrossRef]
- Wiita, P.J. Thick supercritical accretion disks and active galactic nuclei. Comments Astrophys. 1982, 9, 251–260. [Google Scholar]
- Ohsuga, K.; Mori, M.; Nakamoto, T.; Mineshige, S. Supercritical Accretion Flows around Black Holes: Two-dimensional, Radiation Pressure-dominated Disks with Photon Trapping. Astrophys. J. 2005, 628, 368–381. [Google Scholar] [CrossRef]
- Fukue, J. Critical Accretion Disk. Publ. Astron. Soc. Jpn. 2004, 56, 569–580. [Google Scholar] [CrossRef]
- Ohsuga, K.; Mineshige, S. Why Is Supercritical Disk Accretion Feasible? Astrophys. J. 2007, 670, 1283–1290. [Google Scholar] [CrossRef]
- Jiang, Y.F.; Stone, J.M.; Davis, S.W. Super-Eddington Accretion Disks around Supermassive Black Holes. Astrophys. J. 2019, 880, 67. [Google Scholar] [CrossRef]
- Asahina, Y.; Ohsuga, K. General Relativistic Radiation Magnetohydrodynamics Simulations of Black Hole Accretion Disks: Comparison of Methods Based on Variable Eddington Tensor and Based on M1 Closure. Astrophys. J. 2022, 929, 93. [Google Scholar] [CrossRef]
- Ohsuga, K.; Mineshige, S. Global Structure of Three Distinct Accretion Flows and Outflows around Black Holes from Two-dimensional Radiation-magnetohydrodynamic Simulations. Astrophys. J. 2011, 736, 2. [Google Scholar] [CrossRef]
- McKinney, J.C.; Tchekhovskoy, A.; Sadowski, A.; Narayan, R. Three-dimensional general relativistic radiation magnetohydrodynamical simulation of super-Eddington accretion, using a new code HARMRAD with M1 closure. Mon. Not. R. Astron. Soc. 2014, 441, 3177–3208. [Google Scholar] [CrossRef]
- Sądowski, A.; Narayan, R.; McKinney, J.C.; Tchekhovskoy, A. Numerical simulations of super-critical black hole accretion flows in general relativity. Mon. Not. R. Astron. Soc. 2014, 439, 503–520. [Google Scholar] [CrossRef]
- Zhou, Y.; Feng, H.; Ho, L.C.; Yao, Y. Evidence for Optically Thick, Eddington-limited Winds Driven by Supercritical Accretion. Astrophys. J. 2019, 871, 115. [Google Scholar] [CrossRef]
- Liu, H.; Luo, B.; Brandt, W.N.; Brotherton, M.S.; Du, P.; Gallagher, S.C.; Hu, C.; Shemmer, O.; Wang, J.M. SDSS J075101.42+291419.1: A Super-Eddington Accreting Quasar with Extreme X-Ray Variability. Astrophys. J. 2019, 878, 79. [Google Scholar] [CrossRef]
- Berdina, L.A.; Tsvetkova, V.S.; Shulga, V.M. Super-Eddington accretion in the Q2237+0305 quasar? Astron. Astrophys. 2021, 645, A78. [Google Scholar] [CrossRef]
- Panessa, F.; Baldi, R.D.; Laor, A.; Padovani, P.; Behar, E.; McHardy, I. The origin of radio emission from radio-quiet active galactic nuclei. Nat. Astron. 2019, 3, 387–396. [Google Scholar] [CrossRef]
- Sotomayor, P.; Romero, G.E. Nonthermal radiation from the central region of super-accreting active galactic nuclei. Astron. Astrophys. 2022, 664, A178. [Google Scholar] [CrossRef]
- del Valle, M.V.; Müller, A.L.; Romero, G.E. High-energy radiation from collisions of high-velocity clouds and the Galactic disc. Mon. Not. R. Astron. Soc. 2018, 475, 4298–4308. [Google Scholar] [CrossRef]
- del Valle, M.V. Gamma-rays from reaccelerated cosmic rays in high-velocity clouds colliding with the Galactic disc. Mon. Not. R. Astron. Soc. 2022, 509, 4448–4456. [Google Scholar] [CrossRef]
- IceCube Collaboration; Abbasi, R.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Alameddine, J.M.; Alispach, C.; Alves, A.A., Jr.; et al. Evidence for neutrino emission from the nearby active galaxy NGC 1068. Science 2022, 378, 538–543. [Google Scholar] [CrossRef]
- Alvarez-Muñiz, J.; Mészáros, P. High energy neutrinos from radio-quiet active galactic nuclei. Phys. Rev. D 2004, 70, 123001. [Google Scholar] [CrossRef]
- Inoue, Y.; Khangulyan, D.; Doi, A. On the Origin of High-energy Neutrinos from NGC 1068: The Role of Nonthermal Coronal Activity. Astrophys. J. Lett. 2020, 891, L33. [Google Scholar] [CrossRef]
- Inoue, Y.; Khangulyan, D.; Doi, A. Gamma-ray and Neutrino Signals from Accretion Disk Coronae of Active Galactic Nuclei. Galaxies 2021, 9, 36. [Google Scholar] [CrossRef]
- Murase, K.; Kimura, S.S.; Mészáros, P. Hidden Cores of Active Galactic Nuclei as the Origin of Medium-Energy Neutrinos: Critical Tests with the MeV Gamma-Ray Connection. Phys. Rev. Lett. 2020, 125, 011101. [Google Scholar] [CrossRef] [PubMed]
- Murase, K. Hidden Hearts of Neutrino Active Galaxies. Astrophys. J. Lett. 2022, 941, L17. [Google Scholar] [CrossRef]
- Murase, K.; Stecker, F.W. High-Energy Neutrinos from Active Galactic Nuclei. arXiv 2022, arXiv:2202.03381. [Google Scholar] [CrossRef]
- Kheirandish, A.; Murase, K.; Kimura, S.S. High-energy Neutrinos from Magnetized Coronae of Active Galactic Nuclei and Prospects for Identification of Seyfert Galaxies and Quasars in Neutrino Telescopes. Astrophys. J. 2021, 922, 45. [Google Scholar] [CrossRef]
- Anchordoqui, L.A.; Krizmanic, J.; Stecker, F. High-Energy Neutrinos from NGC 1068. In Proceedings of the 37th International Cosmic Ray Conference, Berlin, Germany, 12–23 July 2021; p. 993. [Google Scholar] [CrossRef]
- Kurahashi, N.; Murase, K.; Santander, M. High-Energy Extragalactic Neutrino Astrophysics. Annu. Rev. Nucl. Part. Sci. 2022, 72, 365–387. [Google Scholar] [CrossRef]
- Huang, Y.H.; Wang, K.; Ma, Z.P. High-energy Neutrino Emission from NGC 1068 by Outflow-cloud Interactions. arXiv 2024, arXiv:2406.14001. [Google Scholar] [CrossRef]
- Mou, G.; Wang, W. Years delayed gamma-ray and radio afterglows originated from TDE wind-torus interactions. Mon. Not. R. Astron. Soc. 2021, 507, 1684–1698. [Google Scholar] [CrossRef]
- Kaspi, S.; Smith, P.S.; Netzer, H.; Maoz, D.; Jannuzi, B.T.; Giveon, U. Reverberation Measurements for 17 Quasars and the Size-Mass-Luminosity Relations in Active Galactic Nuclei. Astrophys. J. 2000, 533, 631–649. [Google Scholar] [CrossRef]
- Wevers, T.; van Velzen, S.; Jonker, P.G.; Stone, N.C.; Hung, T.; Onori, F.; Gezari, S.; Blagorodnova, N. Black hole masses of tidal disruption event host galaxies. Mon. Not. R. Astron. Soc. 2017, 471, 1694–1708. [Google Scholar] [CrossRef]
- Wevers, T.; Stone, N.C.; van Velzen, S.; Jonker, P.G.; Hung, T.; Auchettl, K.; Gezari, S.; Onori, F.; Mata Sánchez, D.; Kostrzewa-Rutkowska, Z.; et al. Black hole masses of tidal disruption event host galaxies II. Mon. Not. R. Astron. Soc. 2019, 487, 4136–4152. [Google Scholar] [CrossRef]
- Kesden, M. Tidal-disruption rate of stars by spinning supermassive black holes. Phys. Rev. D 2012, 85, 024037. [Google Scholar] [CrossRef]
- Yao, Y.; Ravi, V.; Gezari, S.; van Velzen, S.; Lu, W.; Schulze, S.; Somalwar, J.J.; Kulkarni, S.R.; Hammerstein, E.; Nicholl, M.; et al. Tidal Disruption Event Demographics with the Zwicky Transient Facility: Volumetric Rates, Luminosity Function, and Implications for the Local Black Hole Mass Function. Astrophys. J. Lett. 2023, 955, L6. [Google Scholar] [CrossRef]
- Müller, A.L.; Romero, G.E. Radiation from the impact of broad-line region clouds onto AGN accretion disks. Astron. Astrophys. 2020, 636, A92. [Google Scholar] [CrossRef]
- Bentz, M.C.; Peterson, B.M.; Pogge, R.W.; Vestergaard, M.; Onken, C.A. The Radius-Luminosity Relationship for Active Galactic Nuclei: The Effect of Host-Galaxy Starlight on Luminosity Measurements. Astrophys. J. 2006, 644, 133–142. [Google Scholar] [CrossRef]
- Blandford, R.D. Physical processes in active galactic nuclei. In Active Galactic Nuclei; Blandford, R.D., Netzer, H., Woltjer, L., Courvoisier, T.J.L., Mayor, M., Eds.; Springer: Berlin/Heidelberg, Germany, 1990; pp. 161–275. [Google Scholar]
- Antonucci, R. Unified models for active galactic nuclei and quasars. Annu. Rev. Astron. Astrophys. 1993, 31, 473–521. [Google Scholar] [CrossRef]
- Laor, A.; Barth, A.J.; Ho, L.C.; Filippenko, A.V. Is the Broad-Line Region Clumped or Smooth? Constraints from the Hα Profile in NGC 4395, the Least Luminous Seyfert 1 Galaxy. Astrophys. J. 2006, 636, 83–89. [Google Scholar] [CrossRef]
- Netzer, H. Revisiting the Unified Model of Active Galactic Nuclei. Annu. Rev. Astron. Astrophys. 2015, 53, 365–408. [Google Scholar] [CrossRef]
- Du, P.; Hu, C.; Lu, K.X.; Wang, F.; Qiu, J.; Li, Y.R.; Bai, J.M.; Kaspi, S.; Netzer, H.; Wang, J.M.; et al. Supermassive Black Holes with High Accretion Rates in Active Galactic Nuclei. I. First Results from a New Reverberation Mapping Campaign. Astrophys. J. 2014, 782, 45. [Google Scholar] [CrossRef]
- Du, P.; Lu, K.X.; Zhang, Z.X.; Huang, Y.K.; Wang, K.; Hu, C.; Qiu, J.; Li, Y.R.; Fan, X.L.; Fang, X.E.; et al. Supermassive Black Holes with High Accretion Rates in Active Galactic Nuclei. V. A New Size-Luminosity Scaling Relation for the Broad-line Region. Astrophys. J. 2016, 825, 126. [Google Scholar] [CrossRef]
- Holoien, T.W.S.; Huber, M.E.; Shappee, B.J.; Eracleous, M.; Auchettl, K.; Brown, J.S.; Tucker, M.A.; Chambers, K.C.; Kochanek, C.S.; Stanek, K.Z.; et al. PS18kh: A New Tidal Disruption Event with a Non-axisymmetric Accretion Disk. Astrophys. J. 2019, 880, 120. [Google Scholar] [CrossRef]
- Leloudas, G.; Dai, L.; Arcavi, I.; Vreeswijk, P.M.; Mockler, B.; Roy, R.; Malesani, D.B.; Schulze, S.; Wevers, T.; Fraser, M.; et al. The Spectral Evolution of AT 2018dyb and the Presence of Metal Lines in Tidal Disruption Events. Astrophys. J. 2019, 887, 218. [Google Scholar] [CrossRef]
- King, A.R.; Pounds, K.A. Black hole winds. Mon. Not. R. Astron. Soc. 2003, 345, 657–659. [Google Scholar] [CrossRef]
- King, A.R. Black hole outflows. Mon. Not. R. Astron. Soc. 2010, 402, 1516–1522. [Google Scholar] [CrossRef]
- Pounds, K.; Lobban, A.; Nixon, C. Exploring accretion disk physics and black hole growth with regular monitoring of ultrafast active galactic nucleus winds. Astron. Nachrichten 2017, 338, 249–255. [Google Scholar] [CrossRef]
- van Velzen, S.; Gezari, S.; Hammerstein, E.; Roth, N.; Frederick, S.; Ward, C.; Hung, T.; Cenko, S.B.; Stein, R.; Perley, D.A.; et al. Seventeen Tidal Disruption Events from the First Half of ZTF Survey Observations: Entering a New Era of Population Studies. Astrophys. J. 2021, 908, 4. [Google Scholar] [CrossRef]
- Kawaguchi, T. Comptonization in Super-Eddington Accretion Flow and Growth Timescale of Supermassive Black Holes. Astrophys. J. 2003, 593, 69–84. [Google Scholar] [CrossRef]
- Grupe, D.; Komossa, S.; Leighly, K.M.; Page, K.L. The Simultaneous Optical-to-X-Ray Spectral Energy Distribution of Soft X-Ray Selected Active Galactic Nuclei Observed by Swift. Astrophys. J. Suppl. Ser. 2010, 187, 64–106. [Google Scholar] [CrossRef]
- Coughlin, E.R.; Begelman, M.C. Hyperaccretion during Tidal Disruption Events: Weakly Bound Debris Envelopes and Jets. Astrophys. J. 2014, 781, 82. [Google Scholar] [CrossRef]
- Fukue, J.; Iino, E. Observational Appearance and Spectrum of Black-Hole Winds. Publ. Astron. Soc. Jpn. 2010, 62, 1399. [Google Scholar] [CrossRef]
- Sotomayor Checa, P.; Romero, G.E. Model for Population III microquasars. Astron. Astrophys. 2019, 629, A76. [Google Scholar] [CrossRef]
- Lee, H.M.; Kang, H.; Ryu, D. Supersonic Collisions between Two Gas Streams. Astrophys. J. 1996, 464, 131. [Google Scholar] [CrossRef][Green Version]
- Tenorio-Tagle, G. The collision of clouds with the galactic disk. Astron. Astrophys. 1981, 94, 338. [Google Scholar][Green Version]
- McCray, R.; Snow, T.P., Jr. The violent interstellar medium. Annu. Rev. Astron. Astrophys. 1979, 17, 213–240. [Google Scholar] [CrossRef]
- Wolfire, M.G.; McKee, C.F.; Hollenbach, D.; Tielens, A.G.G.M. Neutral Atomic Phases of the Interstellar Medium in the Galaxy. Astrophys. J. 2003, 587, 278–311. [Google Scholar] [CrossRef]
- Savić, Đ.; Popović, L.Č.; Shablovinskaya, E.; Afanasiev, V.L. Estimating supermassive black hole masses in active galactic nuclei using polarization of broad Mg II, H α, and H β lines. Mon. Not. R. Astron. Soc. 2020, 497, 3047–3054. [Google Scholar] [CrossRef]
- Araudo, A.T.; Bosch-Ramon, V.; Romero, G.E. Gamma rays from cloud penetration at the base of AGN jets. Astron. Astrophys. 2010, 522, A97. [Google Scholar] [CrossRef]
- Cooper, J.L.; Bicknell, G.V.; Sutherland, R.S.; Bland-Hawthorn, J. Starburst-Driven Galactic Winds: Filament Formation and Emission Processes. Astrophys. J. 2009, 703, 330–347. [Google Scholar] [CrossRef]
- Banda-Barragán, W.E.; Zertuche, F.J.; Federrath, C.; García Del Valle, J.; Brüggen, M.; Wagner, A.Y. On the dynamics and survival of fractal clouds in galactic winds. Mon. Not. R. Astron. Soc. 2019, 486, 4526–4544. [Google Scholar] [CrossRef]
- Czerny, B.; Hryniewicz, K. The origin of the broad line region in active galactic nuclei. Astron. Astrophys. 2011, 525, L8. [Google Scholar] [CrossRef]
- Müller, A.L.; Naddaf, M.H.; Zajaček, M.; Czerny, B.; Araudo, A.; Karas, V. Nonthermal Emission from Fall-back Clouds in the Broad-line Region of Active Galactic Nuclei. Astrophys. J. 2022, 931, 39. [Google Scholar] [CrossRef]
- Crutcher, R.M. Magnetic Fields in Molecular Clouds: Observations Confront Theory. Astrophys. J. 1999, 520, 706–713. [Google Scholar] [CrossRef]
- Crutcher, R.M.; Wandelt, B.; Heiles, C.; Falgarone, E.; Troland, T.H. Magnetic Fields in Interstellar Clouds from Zeeman Observations: Inference of Total Field Strengths by Bayesian Analysis. Astrophys. J. 2010, 725, 466–479. [Google Scholar] [CrossRef]
- Myers, P.C.; Basu, S. Magnetic Properties of Star-forming Dense Cores. Astrophys. J. 2021, 917, 35. [Google Scholar] [CrossRef]
- Crutcher, R.M. Magnetic Fields in Molecular Clouds. Annu. Rev. Astron. Astrophys. 2012, 50, 29–63. [Google Scholar] [CrossRef]
- Li, H.B.; Yuen, K.H.; Otto, F.; Leung, P.K.; Sridharan, T.K.; Zhang, Q.; Liu, H.; Tang, Y.W.; Qiu, K. Self-similar fragmentation regulated by magnetic fields in a region forming massive stars. Nature 2015, 520, 518–521. [Google Scholar] [CrossRef]
- Rees, M.J. Magnetic confinement of broad-line clouds in active galactic nuclei. Mon. Not. R. Astron. Soc. 1987, 228, 47P–50P. [Google Scholar] [CrossRef]
- Spruit, H.C. Theory of Magnetically Powered Jets; Lecture Notes in Physics; Belloni, T., Ed.; Springer: Berlin, Germany, 2010; Volume 794, p. 233. [Google Scholar] [CrossRef]
- del Palacio, S.; Bosch-Ramon, V.; Romero, G.E. Gamma rays from jets interacting with BLR clouds in blazars. Astron. Astrophys. 2019, 623, A101. [Google Scholar] [CrossRef]
- Silant’ev, N.A.; Gnedin, Y.N.; Buliga, S.D.; Piotrovich, M.Y.; Natsvlishvili, T.M. Magnetic fields of active galactic nuclei and quasars with regions of polarized broad H α lines. Astrophys. Bull. 2013, 68, 14–25. [Google Scholar] [CrossRef]
- Piotrovich, M.; Silant’ev, N.; Gnedin, Y.; Natsvlishvili, T.; Buliga, S. Determination of magnetic fields in broad line region of active galactic nuclei from polarimetric observations. New Astron. 2017, 51, 65–68. [Google Scholar] [CrossRef]
- Berezinskii, V.S.; Bulanov, S.V.; Dogiel, V.A.; Ptuskin, V.S. Astrophysics of Cosmic Rays; North-Holland: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Aharonian, F.A. Very High Energy Cosmic Gamma Radiation: A Crucial Window on the Extreme Universe; World Scientific: Singapore, 2004. [Google Scholar] [CrossRef]
- Hussein, M.; Shalchi, A. Detailed Numerical Investigation of the Bohm Limit in Cosmic Ray Diffusion Theory. Astrophys. J. 2014, 785, 31. [Google Scholar] [CrossRef]
- Drury, L.O. REVIEW ARTICLE: An introduction to the theory of diffusive shock acceleration of energetic particles in tenuous plasmas. Rep. Prog. Phys. 1983, 46, 973–1027. [Google Scholar] [CrossRef]
- Kelner, S.R.; Aharonian, F.A.; Bugayov, V.V. Energy spectra of gamma rays, electrons, and neutrinos produced at proton-proton interactions in the very high energy regime. Phys. Rev. D 2006, 74, 034018. [Google Scholar] [CrossRef]
- Grant, D.; Ackermann, M.; Karle, A.; Kowalski, M. Neutrino astronomy with the next generation IceCube Neutrino Observatory. Bull. Am. Astron. Soc. 2019, 51, 288. [Google Scholar]
- Osterbrock, D.E. Active galactic nuclei. Rep. Prog. Phys. 1991, 54, 579–633. [Google Scholar] [CrossRef]
- King, A.; Pounds, K. Powerful Outflows and Feedback from Active Galactic Nuclei. Annu. Rev. Astron. Astrophys. 2015, 53, 115–154. [Google Scholar] [CrossRef]
- Miller, J.M.; Kaastra, J.S.; Miller, M.C.; Reynolds, M.T.; Brown, G.; Cenko, S.B.; Drake, J.J.; Gezari, S.; Guillochon, J.; Gultekin, K.; et al. Flows of X-ray gas reveal the disruption of a star by a massive black hole. Nature 2015, 526, 542–545. [Google Scholar] [CrossRef]
- Alexander, K.D.; Berger, E.; Guillochon, J.; Zauderer, B.A.; Williams, P.K.G. Discovery of an Outflow from Radio Observations of the Tidal Disruption Event ASASSN-14li. Astrophys. J. Lett. 2016, 819, L25. [Google Scholar] [CrossRef]
- Hung, T.; Cenko, S.B.; Roth, N.; Gezari, S.; Veilleux, S.; van Velzen, S.; Gaskell, C.M.; Foley, R.J.; Blagorodnova, N.; Yan, L.; et al. Discovery of Highly Blueshifted Broad Balmer and Metastable Helium Absorption Lines in a Tidal Disruption Event. Astrophys. J. 2019, 879, 119. [Google Scholar] [CrossRef]
- Nicholl, M.; Wevers, T.; Oates, S.R.; Alexander, K.D.; Leloudas, G.; Onori, F.; Jerkstrand, A.; Gomez, S.; Campana, S.; Arcavi, I.; et al. An outflow powers the optical rise of the nearby, fast-evolving tidal disruption event AT2019qiz. Mon. Not. R. Astron. Soc. 2020, 499, 482–504. [Google Scholar] [CrossRef]
- Metzger, B.D.; Stone, N.C. A bright year for tidal disruptions. Mon. Not. R. Astron. Soc. 2016, 461, 948–966. [Google Scholar] [CrossRef]
- Lu, W.; Bonnerot, C. Self-intersection of the fallback stream in tidal disruption events. Mon. Not. R. Astron. Soc. 2020, 492, 686–707. [Google Scholar] [CrossRef]
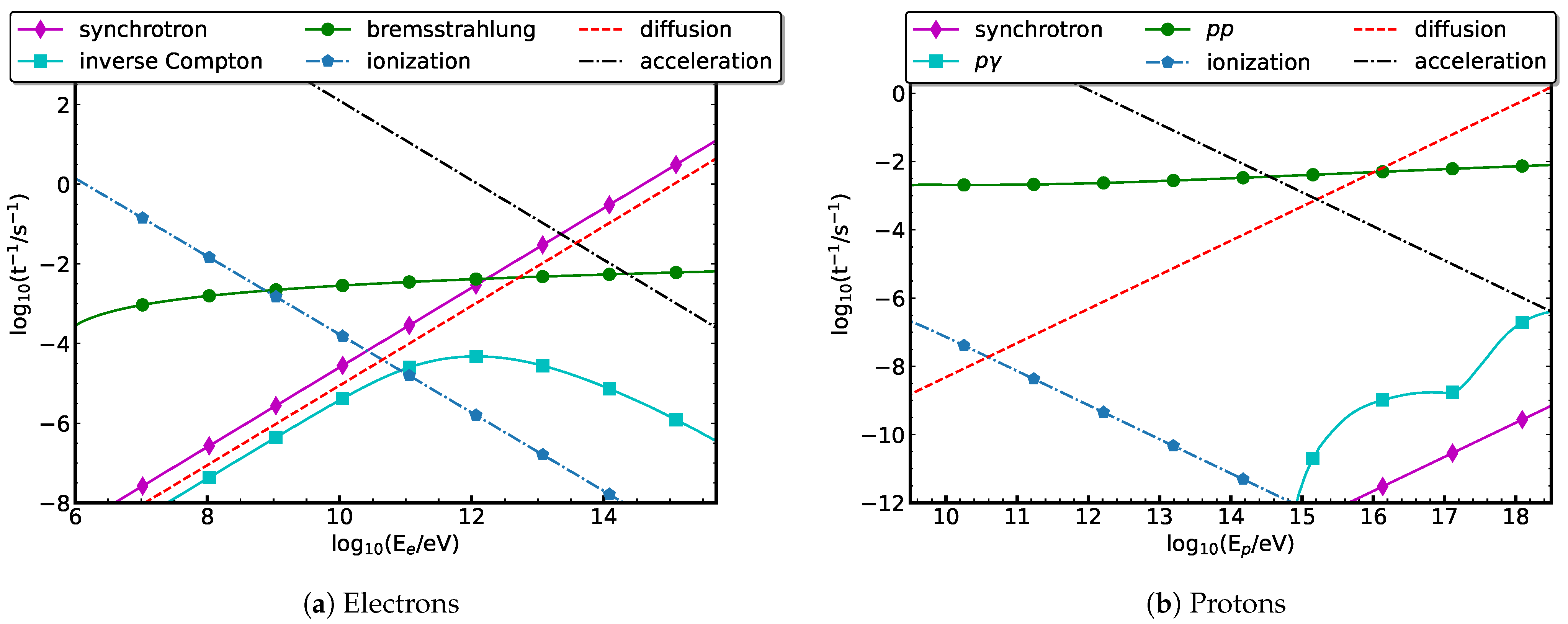
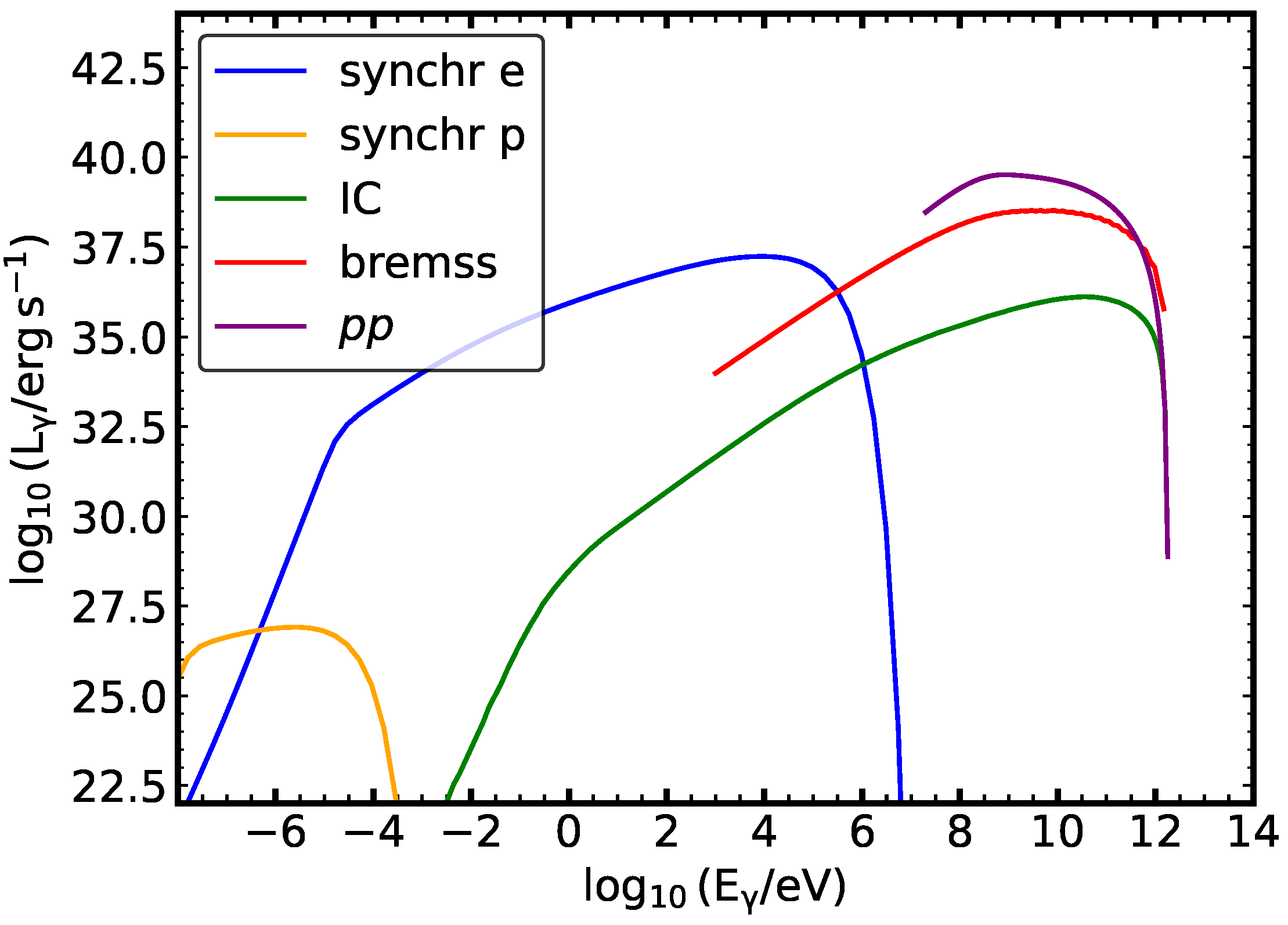
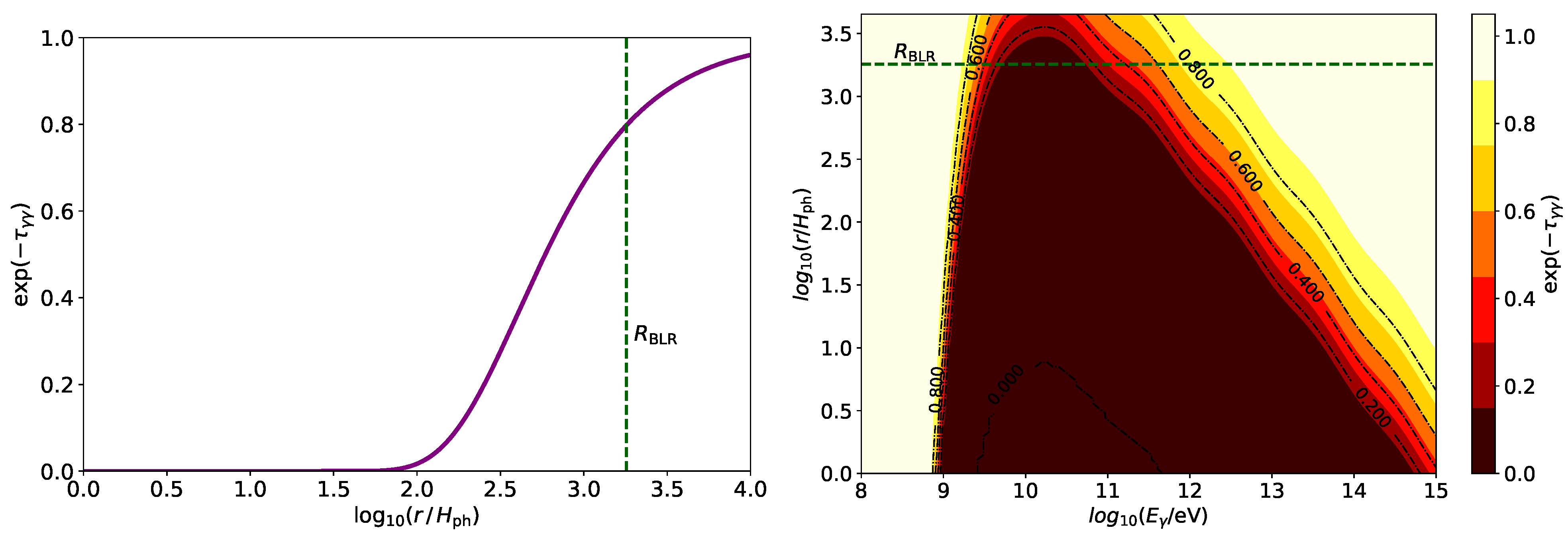
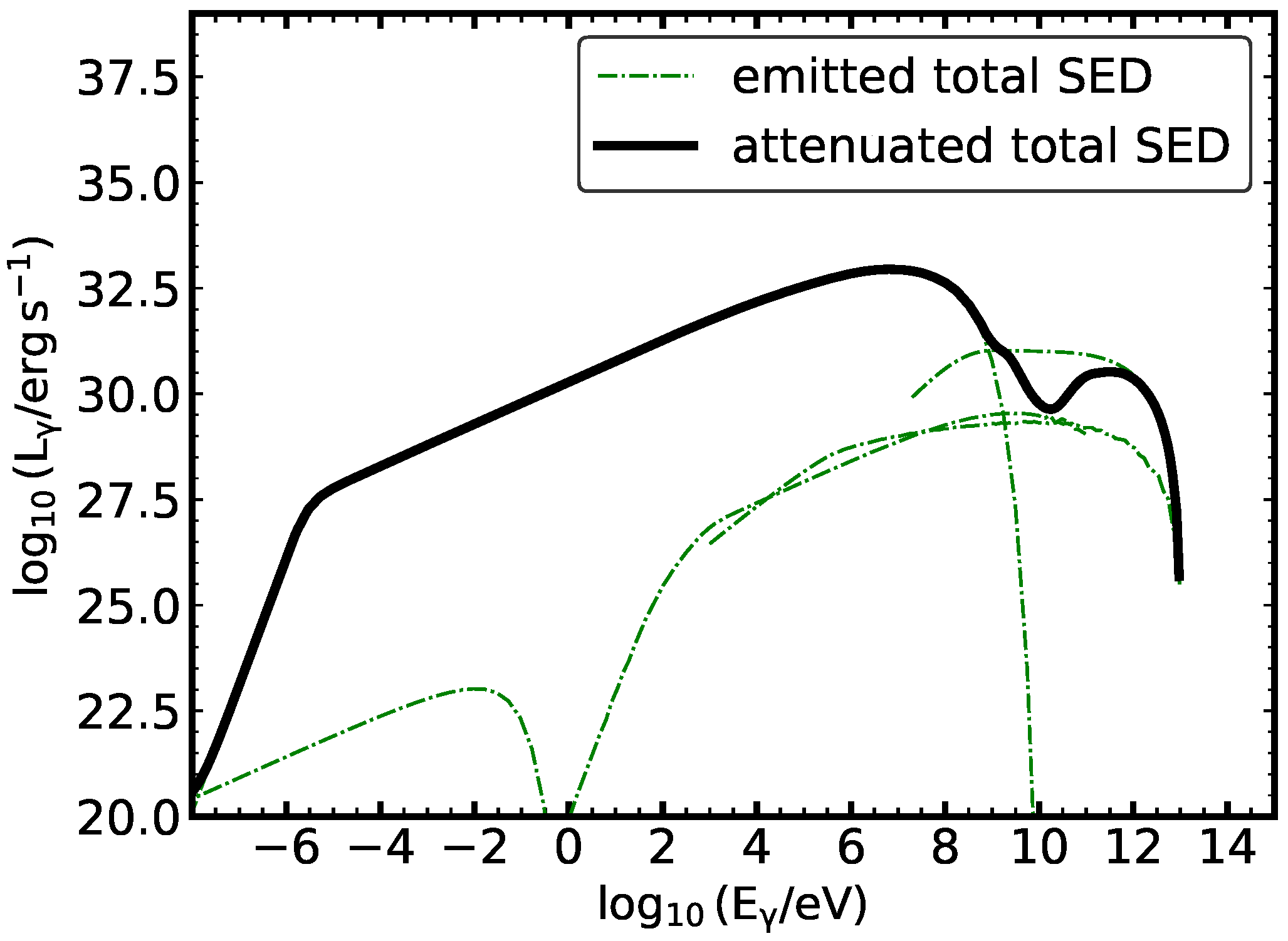
| Parameter | Value |
|---|---|
| Black hole mass | |
| Broad-line region size | |
| Broad-line region filling factor | |
| Cloud radius | |
| Cloud mass | |
| Cloud density | |
| Cloud velocity | |
| Number of clouds | |
| Wind solid angle | |
| Average interaction radius | |
| Bowshock size | |
| Model 1 | |
| Wind mass-loss rate | |
| Wind velocity | |
| Wind photosphere | |
| Model 2 | |
| Wind mass-loss rate | |
| Wind velocity | |
| Wind photosphere |
| Model 1 | >243.2 | >2506.5 | |||||
| Model 2 | >24.3 | >98.5 |
| Parameter | Value |
|---|---|
| Adopted parameters | |
| Minimum energy | |
| Relativistic particles fraction | |
| Hadron-to-lepton energy ratio | |
| Injection spectral index | |
| Diffusion coefficient | |
| Calculated parameters | |
| Model 1— shocked wind | |
| Electron maximum energy | |
| Proton maximum energy | |
| Magnetic field | |
| Gas number density | |
| Power in relativistic protons | |
| Power in relativistic electrons | |
| Model 2—shocked cloud | |
| Electron maximum energy | |
| Proton maximum energy | |
| Magnetic field | |
| Gas number density | |
| Power in relativistic protons | |
| Power in relativistic electrons |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Romero, G.E.; Sotomayor, P. Super-Accreting Active Galactic Nuclei as Neutrino Sources. Universe 2025, 11, 288. https://doi.org/10.3390/universe11090288
Romero GE, Sotomayor P. Super-Accreting Active Galactic Nuclei as Neutrino Sources. Universe. 2025; 11(9):288. https://doi.org/10.3390/universe11090288
Chicago/Turabian StyleRomero, Gustavo E., and Pablo Sotomayor. 2025. "Super-Accreting Active Galactic Nuclei as Neutrino Sources" Universe 11, no. 9: 288. https://doi.org/10.3390/universe11090288
APA StyleRomero, G. E., & Sotomayor, P. (2025). Super-Accreting Active Galactic Nuclei as Neutrino Sources. Universe, 11(9), 288. https://doi.org/10.3390/universe11090288






