Dynamical Systems Analysis of Timelike Geodesics in a Lorentz-Violating Black Hole Spacetime

Abstract

This paper investigates the global dynamics of timelike geodesics of a spherically symmetric black hole under Lorentz-violating effects governed by parameters $\lambda$ (scaling exponent) and ${\rm Y}$ (Lorentz violation strength). By employing dynamical system techniques, including Poincaré compactification and blow-up methods, we systematically explore finite and infinite equilibrium states of the system derived from a black hole solution with power-law corrections to the Schwarzschild metric. For varying $\lambda$ (ranging from −2 to 2) and fixed ${\rm Y}$ values, we classify the nature of equilibrium states (saddle, center, and node) and analyze their stability. Key findings reveal that the number of equilibrium states increases as $\lambda$ decreases: two states for $\lambda =2$, three for $\lambda =1$, four for $\lambda =2/3$, and additional configurations for $\lambda =-2$. The phase plane diagrams and global dynamics demonstrate distinct topological structures, including attractors at infinity and multi-horizon black hole solutions. Furthermore, degenerate equilibrium states at infinity are resolved through directional blow-ups, elucidating their non-hyperbolic behavior. This study highlights the critical role of Lorentz-violating parameters in shaping the stability and long-term evolution of timelike geodesics, offering new insights into modified black hole physics and spacetime dynamics.

1. Introduction

A black hole is a region of spacetime characterized by an extremely strong gravitational field, from which no particles or electromagnetic radiation, including light, can escape. In theoretical physics, the term “black hole with power-law hair” refers to a class of black hole solutions endowed with additional fields or structures—typically scalar fields—that exhibit power-law decay (as opposed to exponential decay) and persist outside the event horizon. Such solutions arise in theoretical frameworks extending beyond classical general relativity (GR). According to the classical no-hair theorem, an isolated black hole in GR is fully characterized by only three externally observable parameters: mass, electric charge, and angular momentum. This implies that all other information (often metaphorically termed “hair”) about the matter that formed the black hole is lost. However, in certain modified gravity theories and scalar-tensor extensions of GR, black hole solutions violating the no-hair theorem can exist. These solutions may support additional long-range fields (scalar or vector fields) outside the event horizon, a phenomenon referred to as “hair.” A notable example is found in Einstein–scalar field theories, where the scalar field couples minimally or non-minimally to gravity, yielding black hole solutions with power-law decaying hair [1,2,3].

Kalb–Ramond (KR) gravity was originally proposed in the context of string theory [4] and has since emerged as a promising theoretical framework for investigating deviations from conventional black hole physics [5,6,7,8,9,10,11,12,13,14]. In this theory, the KR field—represented by an antisymmetric tensor—couples non-minimally to gravity, offering a potential window into Lorentz symmetry violation in high-energy astrophysical environments. The additional degrees of freedom introduced through this interaction lead to profound modifications of black hole properties and spacetime geometry [15]. As an extension of general relativity, KR gravity incorporates not only the standard metric tensor $g_{\mu \nu }$ but also an antisymmetric rank-2 tensor field $B_{\mu \nu }$, known as the KR field. This field couples to string world-sheets in direct analogy to how the electromagnetic potential $A_{\mu }$ couples to point particles and arises naturally as a background field in string theory [16,17]. The antisymmetric nature of the KR field is expressed as

$$B_{\mu \nu }=-B_{\mu \nu },$$

(1)

with its field strength given by the following third-rank tensor:

$$H_{\mu \nu \rho }={\partial }_{\mu }{B}_{\nu \rho }+{\partial }_{\nu }{B}_{\rho \mu }+{\partial }_{\rho }{B}_{\mu \nu }.$$

(2)

The action for the self-interacting KR gravity is given by [18]

$$\begin{array}{cc}\hfill S=\int e{d}^{4}x[& {\displaystyle \frac{R}{2\kappa }}-{\displaystyle \frac{1}{12}}{H}_{\sigma \mu \nu }{H}^{\sigma \mu \nu }-V\left(B_{\mu \nu }{B}^{\mu \nu }\pm b_{\mu \nu }{b}^{\mu \nu }\right)\hfill \\ \hfill & +{\displaystyle \frac{1}{2\kappa }}\left({\xi }_2{B}^{\sigma \nu }{B^{\mu }}_{\nu }{R}_{\sigma \mu }+{\xi }_3{B}^{\mu \nu }{B}_{\mu \nu }R\right)],\hfill \end{array}$$

(3)

where

• e is the metric determinant;
• R is the “Ricci scalar curvature”;
• $H_{\sigma \mu \nu }$ denotes the “field strength” of the KR field (a fully antisymmetric 3-form);
• $\kappa =8\pi G$ is the gravitational coupling constant;
• $B_{\mu \nu }$ is the KR field;
• ${\xi }_2$ and ${\xi }_3$ are non-minimal coupling constants with dimensions of $\left[\xi \right]=L^2$.

The potential term $V\left(B_{\mu \nu }{B}^{\mu \nu }\pm b_{\mu \nu }{b}^{\mu \nu }\right)$ plays a crucial role in this framework. When the KR field $B_{\mu \nu }$ acquires a non-zero vacuum expectation value, $\langle B_{\mu \nu }\rangle =b_{\mu \nu }$, it defines a background tensor field configuration. This process results in the spontaneous breaking of Lorentz symmetry via the self-interaction mechanism of the KR field.

Studies on KR gravity have systematically explored multiple dimensions of this theoretical framework, with key focuses including (i) investigations of Lorentz symmetry breaking constraints in KR gravity, with a particular emphasis on timelike and lightlike geodesics in black hole spacetimes, (recent studies have established bounds on the Lorentz-violating parameters, determining parameter ranges compatible with Schwarzschild limits [19]); (ii) demonstrations that KR gravity can generate cosmological bounce solutions within the framework of generalized teleparallel gravity, thereby offering potential resolutions to the current observational absence of the KR field in modern cosmology [20]; and (iii) Exploration of strong gravitational lensing as a diagnostic tool for detecting extra dimensions and the KR field through comprehensive analyses of light deflection in diverse black hole geometries [21].

The present work aims to investigate the global dynamical system of circular geodesics, analyzing both finite phase planes near equilibrium states and large-scale dynamic configurations. From the perspective of dynamics, the equilibrium state can not only be understood as explaining where particles are about to start from or where they will eventually go but also allows for the study of the motion trajectories of surrounding particles. Building on the solutions and geodesics in KR gravity derived by Lessa et al. [22], we explore the implications of this theoretical framework, where the KR field describes a distinct class of gravitational interactions. In KR gravity, global dynamics govern cosmic evolution, including expansion and structure formation while also influencing black hole properties such as mass, charge, and spin [23]. Moreover, these dynamics may give rise to novel black hole solutions, such as hairy black holes or those with nontrivial topologies [24]. The geodesic motion of massive particles in black hole spacetimes provides critical insights into both the background spacetime geometry and modified gravitational dynamics. In the presence of fundamental fields like the Kalb–Ramond field, these trajectories exhibit modified orbital stability conditions, transitions between regular and chaotic dynamics, and distinctive observational signatures—offering a powerful framework for testing extended theories of gravity beyond general relativity, as demonstrated in [25].

To systematically analyze the behavior, we organize our study into several sections. Section 2.1 examines the dynamics at the scaling exponent $\lambda =2$, while Section 2.2, Section 2.3 and Section 2.4 explore how reducing $\lambda$ modifies the global dynamical behavior. Section 3 is the conclusion, which summarizes the results from the perspectives of mathematical consistency and practical physical significance.

2. Dynamical Systems Analysis

Considering a static and spherically symmetric vacuum spacetime solution for the action (Equation (3)) given by

$$d{s}^2=-A\left(r\right)d{t}^2+B\left(r\right)d{r}^2+r^{2}d{\theta }^2+r^2{\sin }^2\theta d{\varphi }^2.$$

we can obtain a power-law hairy black hole with the form [22,26]

$$d{s}^2=-\left[1-{\displaystyle \frac{R_s}{r}}+{\displaystyle \frac{{\rm Y}}{r^{\frac{2}{\lambda }}}}\right]d{t}^2+{\left[1-{\displaystyle \frac{R_s}{r}}+{\displaystyle \frac{{\rm Y}}{r^{\frac{2}{\lambda }}}}\right]}^{-1}d{r}^2+r^{2}d{\theta }^2+r^2{sin}^2\theta d{\varphi }^2,$$

(4)

where $R_s=2GM$ denotes the Schwarzschild radius, with $\lambda$ and ${\rm Y}$ serving as the Lorentz-violating parameters. The parameters $\lambda ={\left|b\right|}^2{\xi }_2$ and ${\rm Y}$ are Lorentz-violating parameters derived from the breaking of local Lorentz symmetry in a spherically symmetric black hole spacetime, which is driven by the vacuum expectation value of a Kalb–Ramond field (see reference [22] for more detail). The scaling exponent $\lambda$ regulates Lorentz violation scale dependence. While the mathematical framework permits Lorentz violation strength parameter ${\rm Y}\ge 0$ for theoretical consistency, as physical considerations impose stricter constraints. In realistic scenarios, ${\rm Y}$ must not only be non-negative but also sufficiently small, typically bounded above by $\mathcal{O}\left({10}^{-20}\right)$ (see [27]), to align with observable physical scales or phenomenological limits. Such parameters generally exhibit extremely small magnitudes, though their exact bounds may vary across different physical contexts (see [28]).

This black hole solution arises from Lorentz symmetry breaking induced by the non-zero vacuum expectation value of the KR field. The event horizon r is determined by solving

$$r^{{\displaystyle \frac{2}{\lambda }}}-R_s{r}^{{\displaystyle \frac{2}{\lambda }}-1}+{\rm Y}=0.$$

(5)

For a timelike particle, we introduce the substitution ${\displaystyle \frac{dr}{d\tau }}={\displaystyle \frac{dr}{d\varphi }}{\displaystyle \frac{L}{r^2}}$ and define $x={\displaystyle \frac{1}{r}}$. The equation of motion can then be expressed as

$${\displaystyle \frac{d^{2}x}{d{\varphi }^2}}+x={\displaystyle \frac{R_s}{2L^2}}+{\displaystyle \frac{3R_s}{2}}{x}^2-{\displaystyle \frac{{\rm Y}}{\lambda L^2}}{x}^{{\displaystyle \frac{2}{\lambda }}-1}-\left({\displaystyle \frac{1}{\lambda }}+1\right){\rm Y}{x}^{{\displaystyle \frac{2}{\lambda }}+1},$$

(6)

which can be transformed into an autonomous dynamical system

$$\begin{array}{cc}\hfill & \dot{x}=y,\hfill \\ \hfill & \dot{y}=-x+{\displaystyle \frac{R_s}{2L^2}}+{\displaystyle \frac{3R_s}{2}}{x}^2-{\displaystyle \frac{{\rm Y}}{\lambda L^2}}{x}^{{\displaystyle \frac{2}{\lambda }}-1}-\left({\displaystyle \frac{1}{\lambda }}+1\right){\rm Y}{x}^{{\displaystyle \frac{2}{\lambda }}+1},\hfill \end{array}$$

(7)

where the dot “·” denotes differentiation with respect to $\varphi$ and $L^2$ represents the dimension of the non-minimal coupling constants in the self-interacting KR field. The parameter ${\rm Y}$ governs the magnitude of Lorentz violation effects on the Schwarzschild solution.

For null particles, the equation of motion is

$${\displaystyle \frac{d^{2}x}{d{\varphi }^2}}+x={\displaystyle \frac{3R_s}{2}}{x}^2-\left({\displaystyle \frac{1}{\lambda }}+1\right){\rm Y}{x}^{{\displaystyle \frac{2}{\lambda }}+1},$$

(8)

and the corresponding autonomous dynamical system reads the following:

$$\begin{array}{cc}\hfill & \dot{x}=y,\hfill \\ \hfill & \dot{y}=-x+{\displaystyle \frac{3R_s}{2}}{x}^2-\left({\displaystyle \frac{1}{\lambda }}+1\right){\rm Y}{x}^{{\displaystyle \frac{2}{\lambda }}+1}.\hfill \end{array}$$

(9)

In the subsequent analysis, we set $G=M=1$ (which implies $R_s=2$) and $L=4$, and then investigate the global dynamics of System (7) by varying ${\rm Y}$ and considering four values of $\lambda$: 2, 1, 2/3, and −2. The relatively high angular momentum $L=4$ is chosen to prevent the particle from approaching the black hole too closely, where nonlinear terms dominate and the probability of chaos is high. As different values of $\lambda$ may correspond to distinct LV patterns or specific mathematical structures within the theory, we adopted the special values $\lambda =1$ and $\lambda =-2$, as used in [26]; to ensure generality, we further included $\lambda =2$ and $\lambda =2/3$, aiming to explore how variations in $\lambda$ affect the system’s dynamical behavior. The same analysis can be applied to the case of null particles, i.e., System (9).

2.1. Case I: $\lambda =2$

For the case where $\lambda =2$, we analyze the equilibrium states of System (7) by setting $\dot{x}=0$ and $\dot{y}=0$. This yields two finite equilibrium points:

$$\begin{array}{cc}\hfill & P_1=\left({\displaystyle \frac{-4+\sqrt{4+12{\rm Y}-3{{\rm Y}}^2}}{12({\rm Y}-2)}},0\right);\hfill \\ \hfill & P_2=\left({\displaystyle \frac{-4-\sqrt{4+12{\rm Y}-3{{\rm Y}}^2}}{12({\rm Y}-2)}},0\right).\hfill \end{array}$$

These equilibrium points are real and distinct when the parameter ${\rm Y}$ satisfies $0\le {\rm Y}<2$ or $2<{\rm Y}\le 2+4\sqrt{3}/3$. The local stability of these equilibrium points can be examined through the Jacobian matrix of System (7):

$$J={\left.\left(\begin{array}{cc}{\displaystyle \frac{\partial \dot{x}}{\partial x}}& {\displaystyle \frac{\partial \dot{x}}{\partial y}}\\ {\displaystyle \frac{\partial \dot{y}}{\partial x}}& {\displaystyle \frac{\partial \dot{y}}{\partial y}}\end{array}\right)\right|}_{x=x^{\ast }}={\left.\left(\begin{array}{cc}0& 1\\ 3(2-{\rm Y})x-1& 0\end{array}\right)\right|}_{x=x^{\ast }},$$

where $x^{\ast }$ is the equilibrium point of System (7).

By substituting the coordinates of the equilibrium points $P_1$ and $P_2$ into the Jacobian matrix J, we obtain their respective eigenvalues:

$$\begin{array}{cc}\hfill & P_1:\left\{\pm {\displaystyle \frac{\sqrt[4]{4+12{\rm Y}-3{{\rm Y}}^2}}{2}}\mathbf{i}\right\},\hfill \\ \hfill & P_2:\left\{\pm {\displaystyle \frac{\sqrt[4]{4+12{\rm Y}-3{{\rm Y}}^2}}{2}}\right\},\hfill \end{array}$$

where $\mathbf{i}$ denotes the imaginary unit. The eigenvalue analysis reveals that

• $P_1$ is a center (purely imaginary eigenvalues).
• $P_2$ is a saddle point (real eigenvalues of opposite signs).

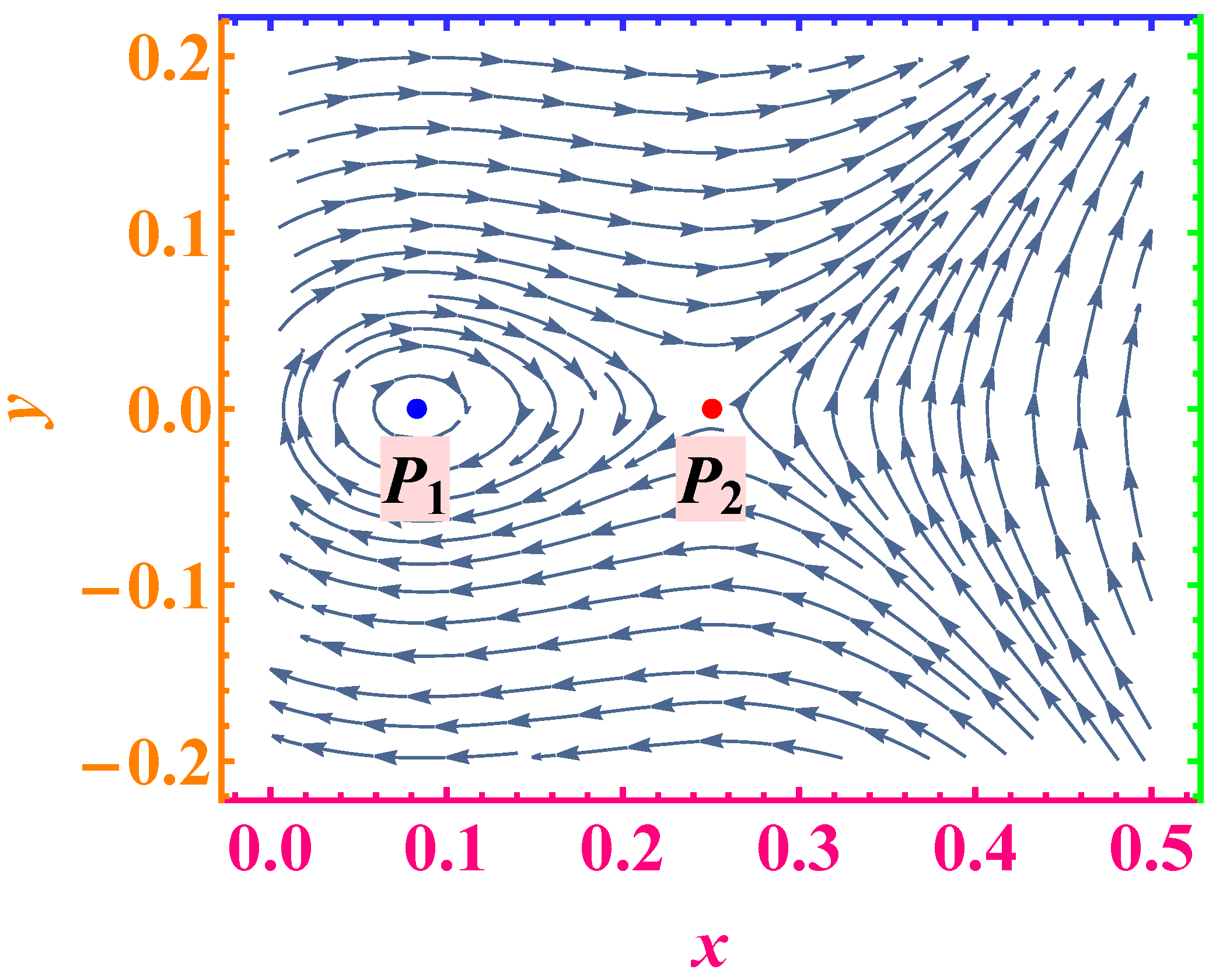
The equilibrium point $P_1$ corresponds to the outermost stable circular orbit (OSCO), which refers to the largest radial distance from a black hole at which a test particle can maintain a stable circular orbit under the influence of the black hole’s gravity. Beyond this radius, additional external forces (such as those from a surrounding matter distribution or a dark matter halo) may dominate over relativistic orbital stability. Point $P_2$ corresponds to the innermost stable circular orbit (ISCO) of the black hole, i.e., the smallest stable circular orbit that a test particle can maintain around a black hole without spiraling inward due to gravitational radiation or instability. Within the innermost stable circular orbit, the massive particles will quickly fall into the black hole. It marks the boundary between stable and unstable circular geodesics in the black hole’s spacetime. 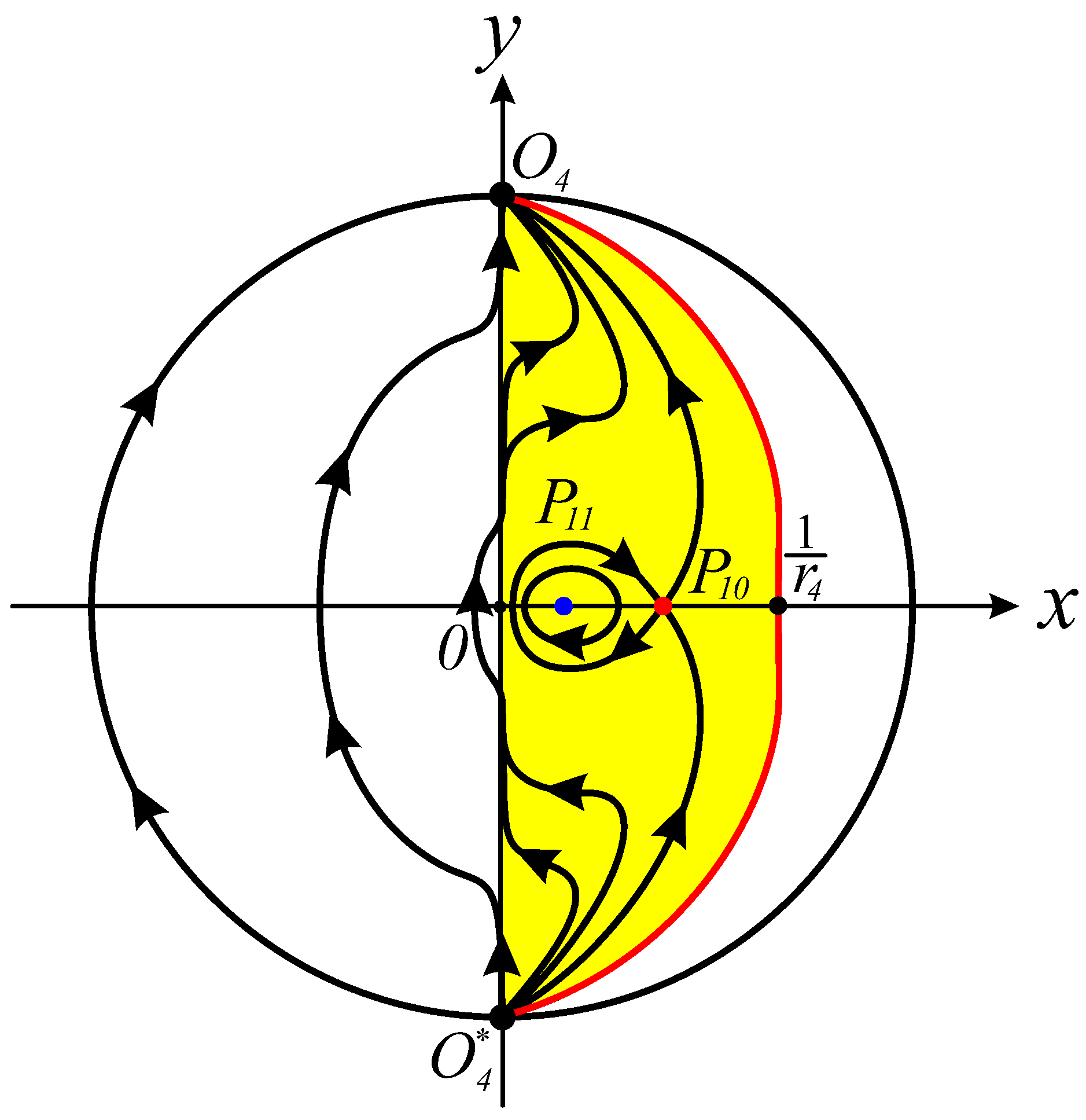Figure 1 illustrates the corresponding phase portrait of System (7) in the finite plane.

The behavior at infinity characterizes the limiting properties of physical systems and mathematical solutions as spatial coordinates approach infinity or temporal evolution tends to infinity. In dynamical systems, this asymptotic analysis determines solution behaviors through three fundamental scenarios: (i) convergence to attractors (stable equilibria), (ii) divergence with unbounded growth, or (iii) persistent oscillations manifesting as cycles. To analyze the behavior of System (7) at infinity, we employ Poincaré compactification [29,30], a powerful analytical method in dynamical systems theory that enables the study of polynomial vector fields at infinity by projecting the phase space onto a compact manifold, typically a sphere or a hemisphere, through stereographic projection. By employing local coordinate charts (e.g., $U_1$ and $U_2$) with transformations, this technique regularizes dynamics at infinity, allowing infinite trajectories to be analyzed as finite points. The method incorporates time rescaling and vector field normalization to preserve smoothness, thereby permitting standard tools like linearization and stability analysis to be applied to equilibria at infinity. Notably, Poincaré compactification provides a unified framework for characterizing both finite and infinite dynamics, revealing topological invariants and bifurcation structures essential for understanding a system’s global dynamic behavior while maintaining consistency with local flow properties near the boundary of the compactified space.

First, we consider the local chart $U_1$ through the following transformation:

$$x={\displaystyle \frac{1}{v_1}},y={\displaystyle \frac{u_1}{v_1}},$$

which converts System (7) to

$$\begin{array}{cc}\hfill {\dot{u}}_1& ={\displaystyle \frac{3}{2}}(2-{\rm Y})-v_1+{\displaystyle \frac{1}{32}}(2-{\rm Y})v_1^2-u_1^2{v}_1,\hfill \\ \hfill {\dot{v}}_1& =-u_1{v}_1^2.\hfill \end{array}$$

(10)

In this formulation, points with $v_1=0$ correspond to points at infinity in the original system (System (7)). However, System (10) possesses no equilibrium states satisfying $v_1=0$, prompting us to examine the local chart $U_2$ instead.

On the local chart $U_2$, we transform System (7) using the coordinates $x=u_2/v_2$, $y=1/v_2$ to obtain

$$\begin{array}{cc}\hfill {\dot{u}}_2& =v_2-{\displaystyle \frac{3}{2}}(2-{\rm Y})u_2^3+u_2^2{v}_2-{\displaystyle \frac{1}{32}}(2-{\rm Y})u_2{v}_2^2,\hfill \\ \hfill {\dot{v}}_2& =-{\displaystyle \frac{3}{2}}(2-{\rm Y})u_2^2{v}_2+u_2{v}_2^2-{\displaystyle \frac{1}{32}}(2-{\rm Y})v_2^3.\hfill \end{array}$$

(11)

The point $O_1=(0,0)$ in System (11) corresponds to the remaining infinite equilibrium points of the original system (System (7)) that were not captured by System (10). It indicates radial infinity of the black hole. Clearly, $O_1$ is an equilibrium state of System (11) and thus represents an infinite equilibrium state for the original system. However, $O_1$ is a degenerate point, as both eigenvalues of its Jacobian matrix vanish.

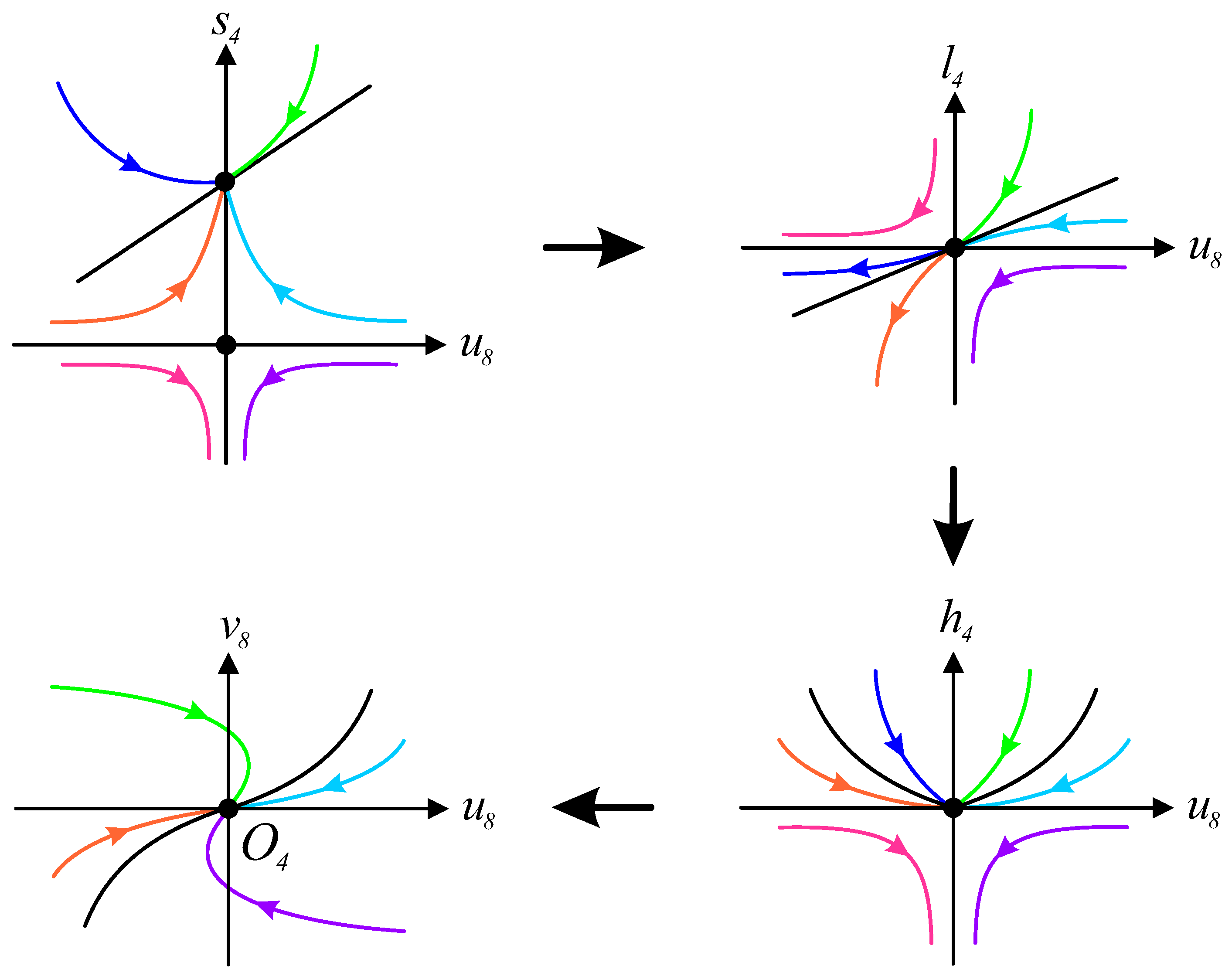
To analyze the local trajectory structure near $O_1$, we employ the blow-up technique [31]. This technique is a fundamental method in dynamical systems theory for analyzing degenerate singularities (e.g., higher-order singularities or nilpotent singularities). Its core concept involves using geometric transformations to “magnify” the singularity into a higher-dimensional manifold, thereby decomposing the system’s dynamics into tractable regular components. Here a singularity (alternatively termed an equilibrium point, fixed point, or critical point) corresponds to a state vector where the time derivatives of all system variables vanish identically. This condition implies that the system’s state remains invariant under temporal evolution. Specifically, the method first expands the singularity into a circle or curve on the manifold to eliminate degeneracy, then separates the trajectories into radial and angular dynamics for detailed analysis. Finally, by studying the dynamics on the blown-up manifold, the local phase portrait structure near the original singularity can be reconstructed. This technique is particularly powerful for studying non-hyperbolic singularities, nilpotent vector fields, and other challenging cases.

The characteristic polynomial of System (11) is given by

$${\mathcal{F}}_1(u_2,v_2)=u_2{Q}_m(u_2,v_2)-v_2{P}_m(u_2,v_2)=-v_2^2,$$

where $P_m(u_2,v_2)$ and $Q_m(u_2,v_2)$ represent the homogeneous polynomials of degree m (the minimal degree in System (11)) corresponding to the ${\dot{u}}_2$ and ${\dot{v}}_2$ components, respectively. For System (11), we specifically have $P_m(u_2,v_2)=v_2$ and $Q_m(u_2,v_2)=0$.

This analysis reveals that $v_2=0$ is the unique characteristic direction at the origin. To resolve the singularity, we perform a $u_2$-directional blow-up transformation, where

$$(u_2,v_2)\mapsto (u_2,u_2{h}_1),$$

which yields the following desingularized system:

$$\begin{array}{cc}\hfill & {\dot{u}}_2=u_2{h}_1-{\displaystyle \frac{3}{2}}\left(2-{\rm Y}\right)u_2^3+u_2^3{h}_1-{\displaystyle \frac{1}{32}}\left(2-{\rm Y}\right)u_2^3{h}_1^2,\hfill \\ \hfill & {\dot{h}}_1=-h_1^2.\hfill \end{array}$$

(12)

For the case when $u_2=0$, System (12) exhibits a single equilibrium $(0,0)$ with eigenvalues $\left\{0,0\right\}$, necessitating a secondary blow-up transformation. The characteristic polynomial ${\mathcal{F}}_{1a}=-2u_2{h}_1^2$ suggests the characteristic direction $h_1=0$, prompting the directional blow-up of $(u_2,h_1)$↦$(u_2,u_2{l}_1)$, where we factor out $u_2$ to obtain the following transformed system:

$$\begin{array}{cc}\hfill {\dot{u}}_2& =u_2\left[l_1-{\displaystyle \frac{3}{2}}(2-{\rm Y})u_2+u_2^2{l}_1\left(1-{\displaystyle \frac{1}{32}}(2-{\rm Y})u_2{l}_1\right)\right],\hfill \\ \hfill {\dot{l}}_1& =l_1\left[{\displaystyle \frac{3}{2}}(2-{\rm Y})u_2-2l_1+u_2^2{l}_1\left(-1+{\displaystyle \frac{1}{32}}(2-{\rm Y})u_2{l}_1\right)\right].\hfill \end{array}$$

(13)

The persistent degeneracy at $(0,0)$ with eigenvalues $\left\{0,0\right\}$ and characteristic polynomial ${\mathcal{F}}_{1b}=3u_2{l}_1((2-{\rm Y})u_2-l_1)$ motivates a third blow-up via $l_1=u_2{s}_1$, yielding

$$\begin{array}{cc}\hfill {\dot{u}}_2& =u_2\left[-{\displaystyle \frac{3}{2}}(2-{\rm Y})+s_1\left(1+u_2^2\left(1-{\displaystyle \frac{1}{32}}(2-{\rm Y})u_2^2{s}_1\right)\right)\right],\hfill \\ \hfill {\dot{s}}_1& =s_1\left[3(2-{\rm Y})-3s_1+u_2^2{s}_1\left(-2+{\displaystyle \frac{1}{16}}(2-{\rm Y})u_2^2{s}_1\right)\right].\hfill \end{array}$$

(14)

System (14) exhibits two non-degenerate equilibria with the following characteristics:

(1).

$e_{11}=(0,0)$: Eigenvalues $\left\{-3(2-{\rm Y})/2,3(2-{\rm Y})\right\}$, with

-

A saddle point for all ${\rm Y}\ne 2$.

(2).

$e_{12}=(0,2-{\rm Y})$: Eigenvalues $\left\{({\rm Y}-2)/2,2({\rm Y}-2)\right\}$, yielding

-

A stable node when ${\rm Y}<2$.

-

An unstable node when ${\rm Y}>2$.

Although in experimental implementations and physical applications, ${\rm Y}$ is typically constrained to a very small non-negative value ($0\le {\rm Y}\ll 1$) to reflect real-world physical conditions, in this theoretical framework, we allow ${\rm Y}$ to vary widely to ensure the system’s mathematical consistency.

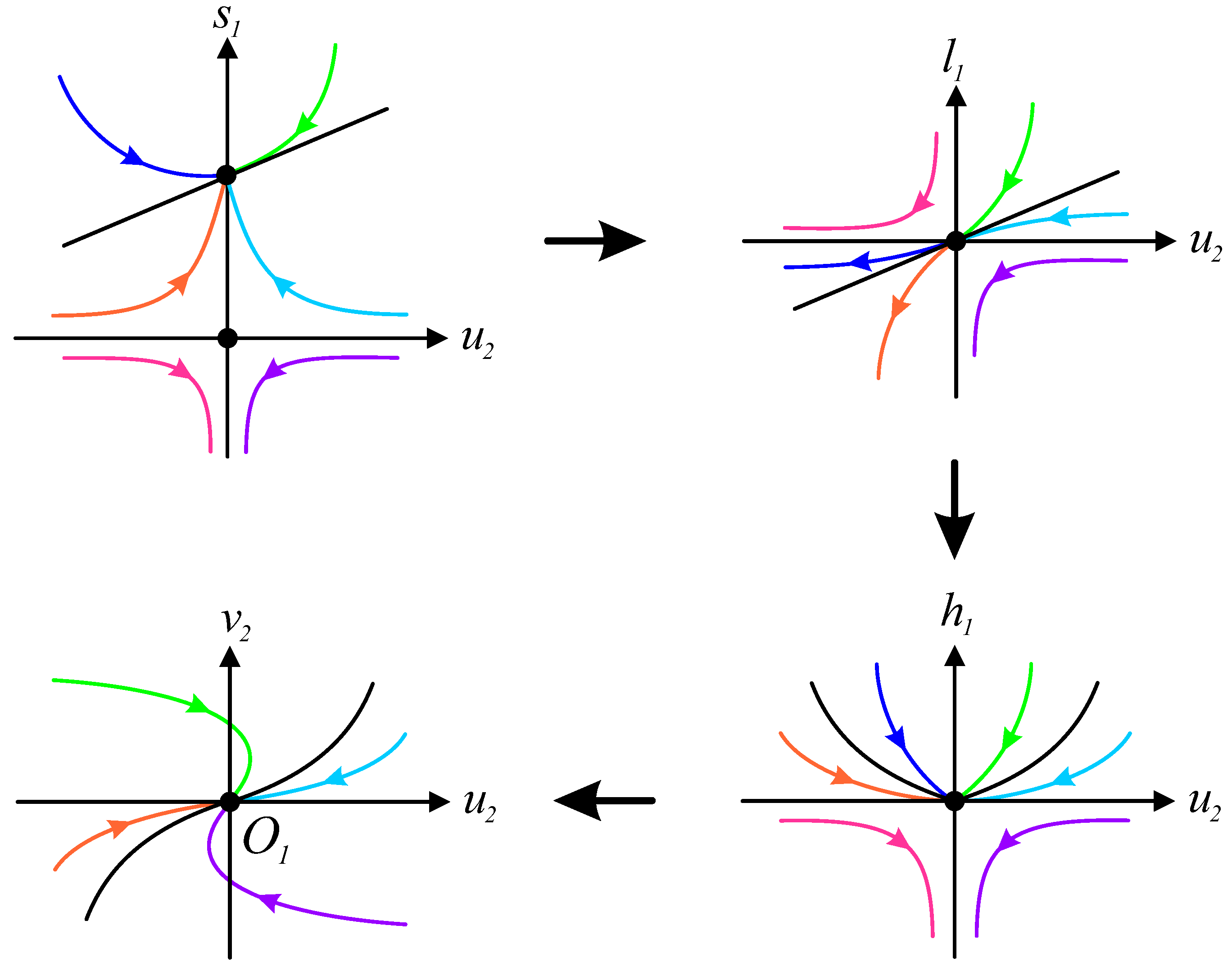
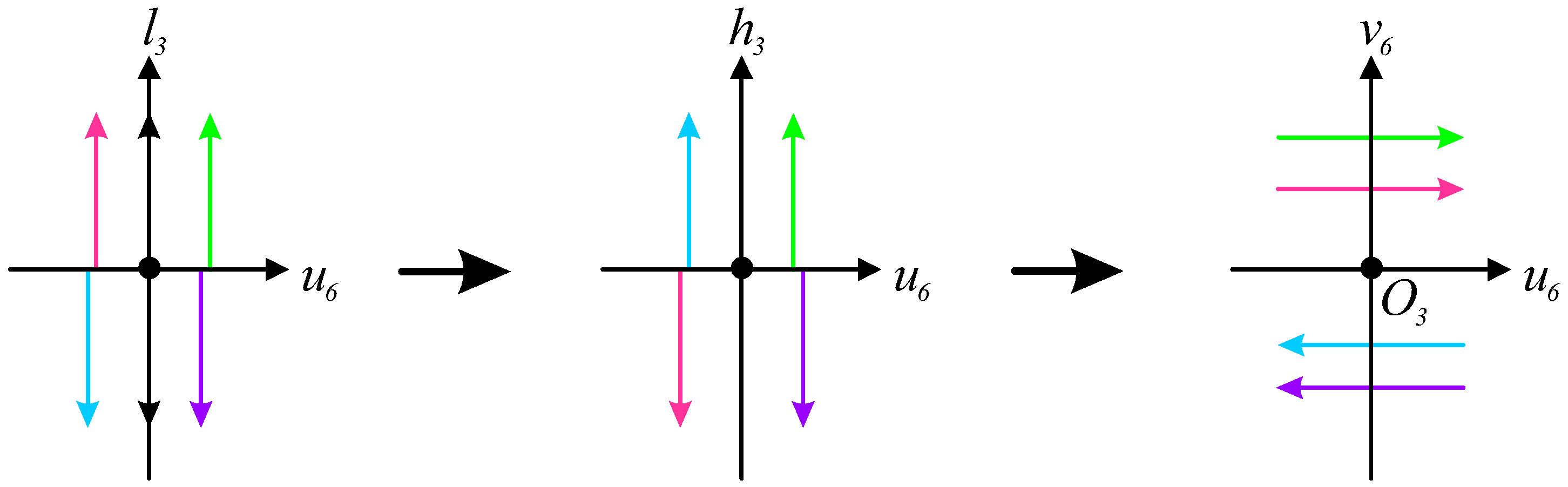
Through systematic reversal of the blow-up transformations (as illustrated in Figure 2), we reconstruct the original system’s phase portrait. Figure 2 specifically demonstrates this process for the parameter value ${\rm Y}=0.0025$, which has been previously investigated in [22]. The complete dynamical behavior of System (7), incorporating both finite and infinite analyses, is presented in Figure 3, and the corresponding equilibrium points are summarized in

Table 1. Equilibrium points of System (7) for $\lambda =2$.

Point	Existence	Eigenvalues	Stability	Location in Black Hole Spacetime
$P_1$	$0\le {\rm Y}<2$ or $2<{\rm Y}2+4\sqrt{3}/3$	$\pm {\displaystyle \frac{\sqrt[4]{4+12{\rm Y}-3{{\rm Y}}^2}}{2}}\mathbf{i}$	Center	Outermost stable circular orbit
$P_2$	$0\le {\rm Y}<2$ or $2<{\rm Y}2+4\sqrt{3}/3$	$\pm {\displaystyle \frac{\sqrt[4]{4+12{\rm Y}-3{{\rm Y}}^2}}{2}}$	Saddle	Innermost stable circular orbit
$O_1$	Always	$0,0$	Sink for ${\rm Y}=0.0025$	Radial infinity ($r\to \infty$)

. In this graphical representation, $r_1=1.9975$ signifies the black hole’s event horizon when $\lambda =2$ and ${\rm Y}=0.0025$, with the red curve establishing a bijective mapping from the physical domain $[r_1,+\infty )$ to the compactified coordinate $x\in (0,0.5006]$ through the inversion transformation $x=1/r_1$.

2.2. Case II: $\lambda =1$

For $\lambda =1$, System (7) possesses three finite equilibrium points:

$$P_3=(A_3,0),P_4=(A_4,0),P_5=(A_5,0),$$

where the algebraic expressions for $A_3$, $A_4$ and $A_5$ are provided in Appendix A. The existence conditions for these equilibria are as follows:

• $P_3$ exists for all parameter values.
• $P_4$ and $P_5$ are real when ${\rm Y}\in (0,1.15591]$.
• $P_4$ and $P_5$ coincide at ${\rm Y}=1.15591$ (bifurcation point).

The eigenvalues for each equilibrium $P_i$ ($i=3,4,5$) are given by

$${\lambda }_i^{\pm }=\pm {\displaystyle \frac{1}{4}}\sqrt{-16-{\rm Y}+96A_i-96A_i^2}.$$

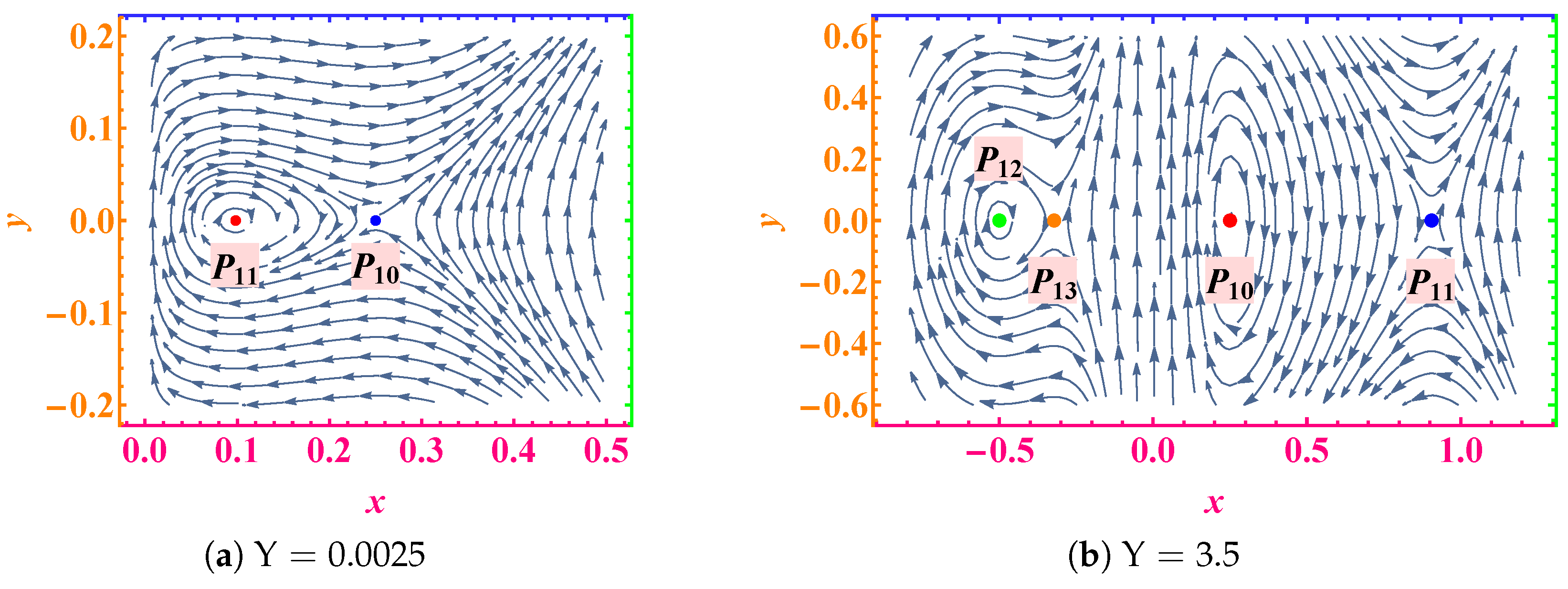
Stability analysis reveals that when it is hyperbolic, $P_3$ and $P_4$ are centers, and $P_5$ is a saddle point for ${\rm Y}\in (0,1.155914)$. The equilibrium point $P_3$ is located between the inner and outer event horizons of the black hole. Point $P_4$ corresponds to the outermost stable circular orbit of the black hole, while $P_5$ corresponds to the innermost stable circular orbit. Figure 4 illustrates the finite phase plane of System (7) for $\lambda =1$ and ${\rm Y}=0.0025$. Due to the significant spatial separation of $P_3$ from the other equilibria, the phase portrait is presented in two panels for clarity. Remarkably, the trajectories surrounding the point $P_3$ exhibit an exceptionally narrow closed configuration, characterized by opposing directional orientations on either side that ultimately converge at an extremely distance from $P_3$. This distinctive topological feature arises from the presence of either a distant equilibrium point or an asymptotic attractor.

To investigate System (7)’s dynamical behavior at infinity, we employ the Poincaré compactification method. On the local chart $U_1$, we introduce the following coordinate transformation:

$$x={\displaystyle \frac{1}{v_3}},y={\displaystyle \frac{u_3}{v_3}},$$

which transforms System (7) into

$$\begin{array}{cc}\hfill {\dot{u}}_3& =-2{\rm Y}+3v_3-{\displaystyle \frac{1}{16}}(16+{\rm Y})v_3^2+{\displaystyle \frac{1}{16}}{v}_3^3-u_3^2{v}_3^2,\hfill \\ \hfill {\dot{v}}_3& =-u_3{v}_3^3.\hfill \end{array}$$

(15)

The transformed system (System (15)) satisfies ${\dot{u}}_3\ne 0$ when $v_3=0$, since

$${\left.{\dot{u}}_3\right|}_{v_3=0}=-2{\rm Y}\ne 0(\mathrm{for}\mathrm{generic}\mathrm{parameter}\mathrm{values}).$$

This implies that System (15) admits no equilibrium points on the line $v_3=0$ in local chart $U_1$. Consequently, the original system (System (7)) possesses no equilibrium points at infinity in this local chart.

Similarly, on the local chart $U_2$, the coordinate transformations $x=u_4/v_4$ and $y=1/v_4$ transform System (7) into

$$\begin{array}{cc}\hfill {\dot{u}}_4& =v_4^2+2{\rm Y}{u}_4^4-3u_4^3{v}_4+{\displaystyle \frac{1}{16}}(16+{\rm Y})u_4^2{v}_4^2-{\displaystyle \frac{1}{16}}{u}_4{v}_4^3,\hfill \\ \hfill {\dot{v}}_4& =2{\rm Y}{u}_4^3{v}_4-3u_4^2{v}_4^2+{\displaystyle \frac{1}{16}}(16+{\rm Y})u_4{v}_4^3-{\displaystyle \frac{1}{16}}{v}_4^4.\hfill \end{array}$$

(16)

This system admits the equilibrium state $O_2=(0,0)$, which corresponds to the infinite equilibrium state of the original system. In black hole spacetime, it indicates radial infinity. However, $O_2$ is a degenerate point, as both eigenvalues of the Jacobian matrix vanish. To analyze the local dynamics near this singularity, we employ the blow-up technique.

The characteristic polynomial of System (16) is given by ${\mathcal{F}}_2=-v_4^3$, indicating that $v_4=0$ is the sole characteristic direction. Performing a $u_4$-directional blow-up via the transformation $(u_4,v_4)\mapsto (u_4,u_4{h}_2)$, we derive

$$\begin{array}{cc}\hfill {\dot{u}}_4& =2{\rm Y}{u}_4^3+u_4{h}_2^2-3u_4^3{h}_2+{\displaystyle \frac{1}{16}}(16+{\rm Y})u_4^3{h}_2^2-{\displaystyle \frac{1}{16}}{u}_4^3{h}_2^3,\hfill \\ \hfill {\dot{h}}_2& =-h_2^3.\hfill \end{array}$$

(17)

Since the system for $u_4=0$ admits only one equilibrium state, $(0,0)$, with eigenvalues $\{0,0\}$, a further blow-up transformation is required to resolve the degeneracy. The characteristic polynomial of the system is given by

$${\mathcal{F}}_{2a}=-2u_4{h}_2\left({\rm Y}{u}_4^2-h_2^2\right).$$

Although both $u_4=0$ and $h_2=0$ define characteristic directions, we simplify the analysis by performing a u-directional blow-up via the substitution $h_2=u_4{l}_2$. This yields the following transformed system:

$$\begin{array}{cc}\hfill {\dot{u}}_4& =2{\rm Y}{u}_4-3u_4^2{l}_2+u_4{l}_2^2+{\displaystyle \frac{1}{16}}(16+{\rm Y})u_4^3{l}_2^2-{\displaystyle \frac{1}{16}}{u}_4^3{l}_2^3,\hfill \\ \hfill {\dot{l}}_2& =2{\rm Y}{l}_2+3u_4{l}_2^2-2l_2^3-{\displaystyle \frac{1}{16}}(16+{\rm Y})u_4^2{l}_2^3+{\displaystyle \frac{1}{16}}{u}_4^3{l}_2^4.\hfill \end{array}$$

(18)

On the line $u_4=0$, this system exhibits three equilibrium states: (1) $e_{21}=(0,0)$ with eigenvalues $\{2{\rm Y},2{\rm Y}\}$, which indicates instability when ${\rm Y}>0$; (2) $e_{22}=\left(0,\sqrt{{\rm Y}}\right)$ with eigenvalues $\{2{\rm Y},-4{\rm Y}\}$; and (3) $e_{23}=\left(0,-\sqrt{{\rm Y}}\right)$ with eigenvalues $\{2{\rm Y},-4{\rm Y}\}$. Thus, for ${\rm Y}>0$, $e_{22}$ and $e_{23}$ are real saddle points, both of which are unstable. By systematically reverting the blow-up transformations, we reconstruct the local dynamics near the degenerate point $O_2$.

All the equilibrium points of System (7) for $\lambda =1$, incorporating both finite and infinite points, are summarized in

Table 2. Equilibrium points of System (7) for $\lambda =1$.

Point	Existence	Eigenvalues	Stability	Location in Black Hole Spacetime
$P_3$	Always	$\pm {\displaystyle \frac{1}{4}}\sqrt{-16-{\rm Y}+96A_3-96A_3^2}$	Center	Between the inner and outer event horizons
$P_4$	${\rm Y}\in (0,1.15591]$	$\pm {\displaystyle \frac{1}{4}}\sqrt{-16-{\rm Y}+96A_4-96A_4^2}$	Center	Outermost stable circular orbit
$P_5$	${\rm Y}\in (0,1.15591]$	$\pm {\displaystyle \frac{1}{4}}\sqrt{-16-{\rm Y}+96A_5-96A_5^2}$	Saddle	Innermost stable circular orbit
$O_2$	Always	$0,0$	Sink for ${\rm Y}=0.0025$	Radial infinity ($r\to \infty$)

See Appendix A for the algebraic expressions for $A_3$, $A_4$, and $A_5$.

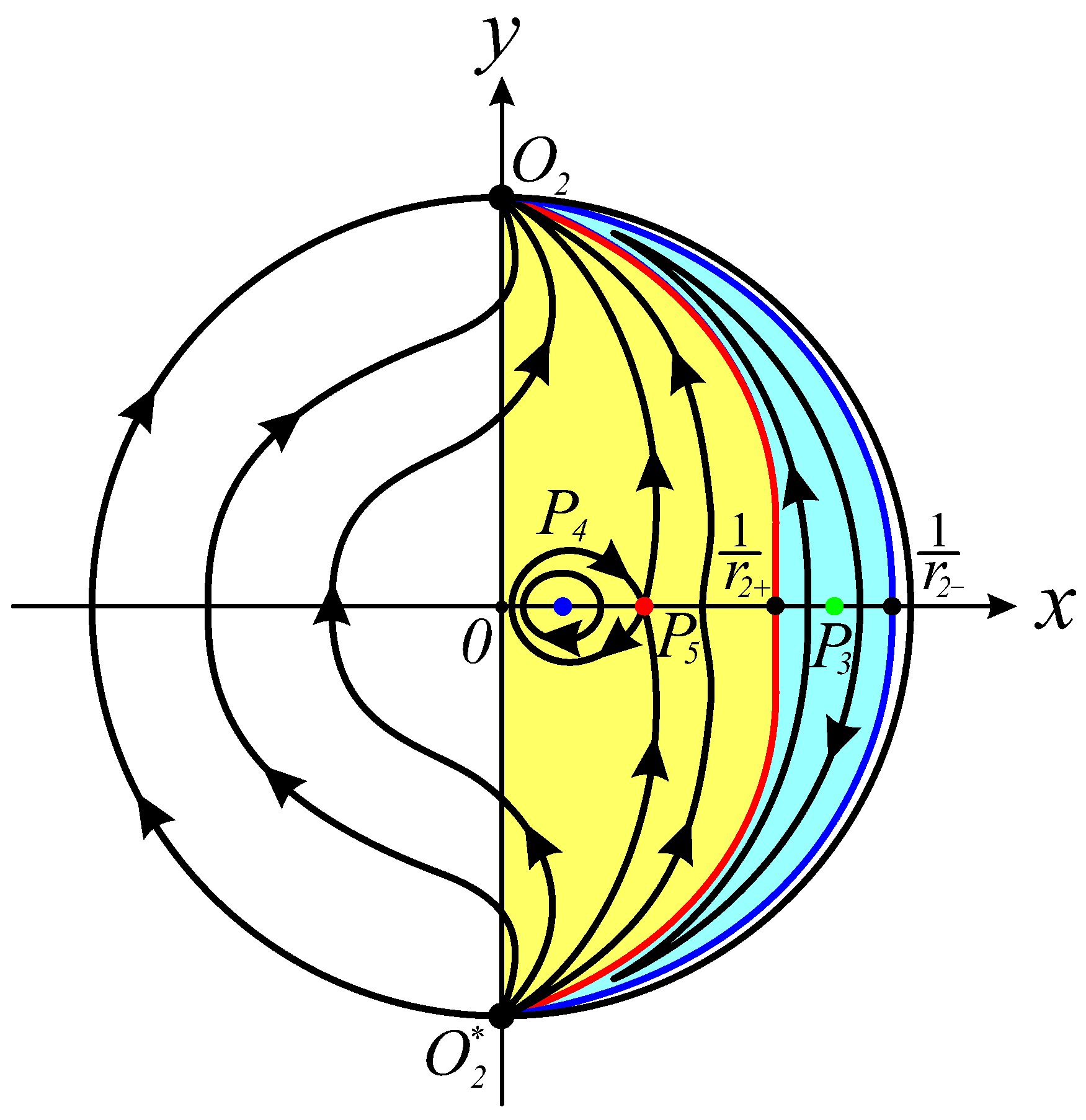
. Figure 5 and Figure 6 illustrate the blow-up sequence and the corresponding global dynamics, respectively. In Figure 6, for the parameter configuration $\lambda =1$ and ${\rm Y}=0.0025$, Equation (5) yields the inner and outer event horizons of the black hole at $r_{2-}=0.00125$ and $r_{2+}=1.9987$, respectively. The red curve (blue curve) establishes a bijective mapping from the physical domain $[r_{2+},+\infty )$ ($[r_{2-},+\infty )$) to the compactified coordinate $x\in (0,0.5003]$ ($x\in (0,800)$) via the inverse coordinate transformation $x=1/r$, where r is taken as $r_{2+}$ ($r_{2-}$).

2.3. Case III: $\lambda =2/3$

Consider System (7) with parameters $\lambda =2/3$, $L=4$ and $R_s=2$. By setting $\dot{x}=0$ and $\dot{y}=0$, we obtain four finite equilibrium points:

$$\begin{array}{cccc}\hfill & P_6=(A_6,0),\hfill & \hfill & P_7=(A_7,0),\hfill \\ \hfill & P_8=(A_8,0),\hfill & \hfill & P_9=(A_9,0).\hfill \end{array}$$

The explicit expressions for $A_6$, $A_7$, $A_8$, and $A_9$ are provided in Appendix B. The eigenvalues of the Jacobian matrix evaluated at each equilibrium point are given by

$${\lambda }_j^{\pm }=\pm {\displaystyle \frac{1}{4}}\sqrt{-16+96A_j-3{\rm Y}{A}_j-160{\rm Y}{A}_j^3},j=6,7,8,9.$$

Due to the complexity of the equilibrium coordinates, analytical determination of linear stability proves challenging. Therefore, we focus our analysis on the specific case where ${\rm Y}=0.0025$. For this parameter value, the coordinates of the equilibrium points become

$$\begin{array}{cccc}\hfill & P_6=(-22.073323,0),\hfill & \hfill & P_7=(0.081865,0),\hfill \\ \hfill & P_8=(0.250078,0),\hfill & \hfill & P_9=(21.739915,0),\hfill \end{array}$$

with corresponding eigenvalues, where

$$\begin{array}{cccc}\hfill & {\lambda }_6^{\pm }=\pm 11.637909,\hfill & \hfill & {\lambda }_7^{\pm }=\pm 0.707163\mathbf{i},\hfill \\ \hfill & {\lambda }_8^{\pm }=\pm 0.707078,\hfill & \hfill & {\lambda }_9^{\pm }=\pm 11.288968\mathbf{i}.\hfill \end{array}$$

From these eigenvalues, we conclude that $P_6$ and $P_8$ are saddle points, while $P_7$ and $P_9$ are centers. The equilibrium point $P_6$ is non-physical since its coordinate is $x<0$, indicating a negative radial distance. Point $P_7$ corresponds to the outermost stable circular orbit of the black hole, while $P_8$ corresponds to the innermost stable circular orbit. Point $P_9$ is located within the inner event horizons of the black hole. Figure 7 illustrates the finite phase plane of System (7) for $\lambda =2/3$ and ${\rm Y}=0.0025$, with the right panel showing a magnified view of the region indicated by the red rectangle in the left panel.

To investigate the behavior of System (7) at infinity, we employ Poincaré compactification. First, we consider the local chart $U_1$ by introducing the following transformation:

$$x={\displaystyle \frac{1}{v_5}},y={\displaystyle \frac{u_5}{v_5}}.$$

Under this coordinate change, System (7) transforms to

$$\begin{array}{cc}\hfill \dot{u_5}& =-{\displaystyle \frac{5}{2}}{\rm Y}-{\displaystyle \frac{3}{32}}(32-{\rm Y})v_5^2-v_5^3+{\displaystyle \frac{1}{16}}{v}_5^4-u_5^2{v}_5^3,\hfill \\ \hfill \dot{v_5}& =-u_5{v}_5^4.\hfill \end{array}$$

(19)

A straightforward analysis of the transformed system (System (19)) demonstrates the absence of equilibrium points satisfying $v_5=0$. Consequently, we proceed to examine the system’s behavior on the complementary local chart $U_2$.

Applying the coordinate transformations $x=u_6/v_6$ and $y=1/v_6$ to System (7) on the local chart $U_2$, we obtain the following transformed system:

$$\begin{array}{cc}\hfill {\dot{u}}_6& =v_6^3+{\displaystyle \frac{5}{2}}{\rm Y}{u}_6^5-{\displaystyle \frac{3}{32}}(32-{\rm Y})u_6^3{v}_6^2+u_6^2{v}_6^3-{\displaystyle \frac{1}{16}}{u}_6{v}_6^4,\hfill \\ \hfill {\dot{v}}_6& ={\displaystyle \frac{5}{2}}{\rm Y}{u}_6^4{v}_6-{\displaystyle \frac{3}{32}}(32-{\rm Y})u_6^2{v}_6^3+u_6{v}_6^4-{\displaystyle \frac{1}{16}}{v}_6^5.\hfill \end{array}$$

(20)

The origin $O_3=(0,0)$ represents an equilibrium state of System (20), corresponding to an infinite equilibrium of the original system. It represents radial infinity in the black hole spacetime. This equilibrium is degenerate, as evidenced by both eigenvalues being identically zero. To analyze this degenerate case, we employ the blow-up method.

The characteristic polynomial of System (20) is given by ${\mathcal{F}}_4=-v_6^4$, indicating $v_6=0$ as the sole characteristic direction. Performing the $u_6$-directional blow-up transformation $(u_6,v_6)\mapsto (u_6,u_6{h}_3)$ and eliminating the common factor $u_6^2$, we derive the following desingularized system:

$$\begin{array}{cc}\hfill {\dot{u}}_6& ={\displaystyle \frac{5}{2}}{\rm Y}{u}_6^3+u_6{h}_3^3-{\displaystyle \frac{3}{32}}(32-{\rm Y})u_6{h}_3^2+u_6^3{h}_3^3-{\displaystyle \frac{1}{16}}{u}_6^3{h}_3^4,\hfill \\ \hfill {\dot{h}}_3& ={\displaystyle \frac{5}{2}}(1-{\rm Y})u_6^2{h}_3-h_3^4.\hfill \end{array}$$

(21)

When $u_6=0$, the system (System (21)) reduces to a single equilibrium at the origin $(0,0)$ with double-zero eigenvalues $\{0,0\}$. To resolve this degeneracy, we perform a secondary blow-up transformation. The characteristic polynomial of the system is ${\mathcal{F}}_{4a}={\displaystyle \frac{5}{2}}(1-2{\rm Y})u_6^3{h}_3$, revealing two characteristic directions: $u_6=0$ and $h_3=0$. We implement a u-directional blow-up via the substitution $h_3=u_6{l}_3$ and eliminate the common factor $u_6^6$ to obtain

$$\begin{array}{cc}\hfill {\dot{u}}_6& ={\displaystyle \frac{5}{2}}{\rm Y}{u}_6+u_6^2{l}_3^3+u_6^4{l}_3^3-{\displaystyle \frac{3}{32}}(32-{\rm Y})u_6^3{l}_3^5-{\displaystyle \frac{1}{16}}{u}_6^5{l}_3^4,\hfill \\ \hfill {\dot{l}}_3& ={\displaystyle \frac{5}{2}}(1-2{\rm Y})l_3-2u_6{l}_3^4-2u_6^3{l}_3^4+{\displaystyle \frac{3}{32}}(32-{\rm Y})u_6^2{l}_3^6+{\displaystyle \frac{1}{16}}{u}_6^4{l}_3^5.\hfill \end{array}$$

(22)

The reduced system at $u_6=0$ possesses the unique equilibrium $e_{31}=(0,0)$ with eigenvalues $\left\{{\displaystyle \frac{5}{2}}(1-2{\rm Y}),{\displaystyle \frac{5}{2}}{\rm Y}\right\}$. This yields the following stability classification:

• A saddle point when ${\rm Y}>{\displaystyle \frac{1}{2}}$.
• An unstable node when $0<{\rm Y}<{\displaystyle \frac{1}{2}}$.

The local dynamical behavior near the origin of System (20) can be systematically reconstructed through inverse blow-up transformations. Figure 8 demonstrates this reconstruction procedure for the specific case of ${\rm Y}=0.0025$, while Figure 9 displays the complete global phase portrait of the original system (System (7)) with parameters $\lambda =2/3$ and ${\rm Y}=0.0025$. All the equilibrium points of System (7) for $\lambda =1$ and ${\rm Y}=0.0025$ are summarized in

Table 3. Equilibrium points of System (7) for $\lambda =2/3$ and ${\rm Y}=0.0025$.

Point	Eigenvalues	Stability	Location in Black Hole Spacetime
$P_6$	$\pm 11.637909$	Center	∖
$P_7$	$\pm 0.707163\mathbf{i}$	Center	Outermost stable circular orbit
$P_8$	$\pm 0.707078$	Saddle	Innermost stable circular orbit
$P_9$	$\pm 11.288968\mathbf{i}$	Center	Within the inner event horizons
$O_3$	$0,0$	Sink	Radial infinity ($r\to \infty$)

.

For the above parameter set $(\lambda ,{\rm Y})$. Equation (5) generates two distinct event horizons in an inner horizon at $r_{3-}=0.05006$ and an outer horizon at $r_{3+}=1.999375$. The coordinate mapping ($x=1/r$) reveals the following topological structure:

• The red curve bijectively maps the exterior spacetime region $[r_{3+},+\infty )$ to the compactified coordinate interval $x\in (0,0.5002]$.

• The blue curve similarly maps the interior domain $[r_{3-},+\infty )$ to $x\in (0,19.9750)$.

Note that both coordinate mappings are implemented through the conformal transformation $x=1/r$, with the radial coordinate r evaluated at the respective horizon positions ($r_{3+}$ for the exterior and $r_{3-}$ for the interior). As $P_9$ lies inside the inner horizon $r_{3-}$ (a classically forbidden region where qualitative theory fails), we will disregard $P_9$ in physical and experimental studies.

2.4. Case IV: $\lambda =-2$

For the special case when $\lambda =-2$, we apply the time transformation $d\varphi =x^{2}d\tau$ to System (7) to eliminate the $x^2$ terms in the denominators. This yields the following transformed system:

$$\begin{array}{cc}\hfill x^{\prime }& =x^{2}y,\hfill \\ \hfill y^{\prime }& ={\displaystyle \frac{{\rm Y}}{32}}+{\displaystyle \frac{1}{16}}(1-8{\rm Y})x^2-x^3+3x^4,\hfill \end{array}$$

(23)

where the prime notation ($\prime$) denotes differentiation with respect to the transformed time variable $\tau$.

The system (System (23)) admits four equilibrium points in the finite plane, where

$$\begin{array}{cccc}\hfill P_{10}& =\left({\displaystyle \frac{1}{4}},0\right),\hfill & \hfill P_{11}& =\left(A_{11},0\right),\hfill \\ \hfill P_{12}& =\left(A_{12},0\right),\hfill & \hfill P_{13}& =\left(A_{13},0\right).\hfill \end{array}$$

The explicit expressions for coefficients $A_{11}$, $A_{12}$, and $A_{13}$ are provided in Appendix C. Among these equilibrium points, $P_{10}$ and $P_{11}$ remain real for all parameter values, while $P_{12}$ and $P_{13}$ become real only when ${\rm Y}\in \left[{\displaystyle \frac{37+14\sqrt{7}}{24}},+\infty \right).$ Notably, these two points coincide when ${\rm Y}$ takes the critical value ${\displaystyle \frac{37+14\sqrt{7}}{24}}$.

The linear stability analysis yields the following eigenvalues:

$$\begin{array}{cc}\hfill & {\lambda }_{10}^{\pm }=\pm {\displaystyle \frac{\sqrt{1-8{\rm Y}}}{16\sqrt{2}}},\hfill \\ \hfill & {\lambda }_k^{\pm }=\pm {\displaystyle \frac{A_k\sqrt{A_k-8{\rm Y}{A}_k-24A_k^2+96A_k^3}}{2\sqrt{2}}},k=11,12,13.\hfill \end{array}$$

(24)

This leads to the following stability classification:

• For ${\rm Y}<1/8$,

  -

  $P_{10}$ is a saddle point.

  -

  $P_{11}$ is a center.

• For ${\rm Y}>1/8$,

  -

  $P_{10}$ becomes a center.

  -

  $P_{11}$ transforms into a saddle.

• At the critical value ${\rm Y}=1/8$, both points become non-hyperbolic with eigenvalues $\{0,0\}$.
• When $P_{12}$ and $P_{13}$ exist,

  -

  $P_{12}$ is always a center.

  -

  $P_{13}$ is always a saddle.

For ${\rm Y}<1/8$, point $P_{10}$ represents the innermost stable circular orbit of the black hole and $P_{11}$ corresponds to the outermost stable circular orbit, while for ${\rm Y}>1/8$ point, $P_{10}$ represents the outermost stable circular orbit and $P_{11}$ corresponds to the innermost stable circular orbit. Point $P_9$ is located within the inner event horizons of the black hole. Points $P_{12}$ and $P_{13}$ are non-physical because of their negative radial distance.

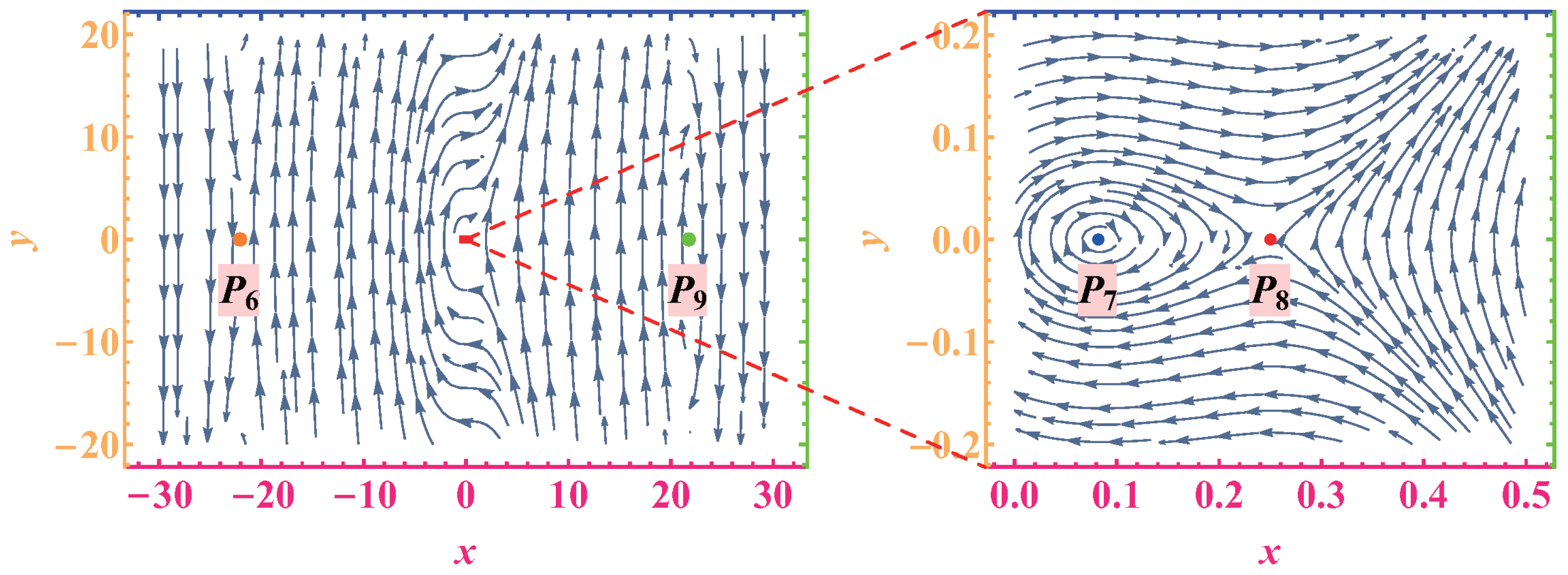
Figure 10 illustrates the system’s phase portraits for two representative cases: (a) ${\rm Y}=0.0025$ showing the typical configuration for small ${\rm Y}$ values and (b) ${\rm Y}=3.5$ demonstrating the system behavior beyond the second bifurcation point, chosen only for its mathematical significance in the parameter space. We should disregard it in physical and experimental studies.

On the local chart $U_1$, we perform the coordinate transformations $x=1/v_7$ and $y=u_7/v_7$, which transform System (23) into

$$\begin{array}{c}{u}_7^{\prime }=3-v_7+{\displaystyle \frac{1}{16}}(1-8{\rm Y})v_7^2-u_7{v}_7^2+{\displaystyle \frac{{\rm Y}}{32}}{v}_7^4,\hfill \\ v_7^{\prime }=-u_7{v}_7^2.\hfill \end{array}$$

Since this system admits no equilibrium states with $v_7=0$, the original system (System (23)) has no infinite equilibrium states on $U_1$. We therefore proceed to analyze the dynamics on the local chart $U_2$.

On $U_2$, we introduce the coordinates $x=u_8/v_8$ and $y=1/v_8$, under which System (23) becomes

$$\begin{array}{cc}\hfill & u_8^{\prime }=u_8^2{v}_8-3u_8^5+u_8^4{v}_8-{\displaystyle \frac{1}{16}}(1-8{\rm Y})u_8^3{v}_8^2-{\displaystyle \frac{{\rm Y}}{32}}{u}_8{v}_8^4,\hfill \\ \hfill & v_8^{\prime }=-3u_8^4{v}_8+u_8^3{v}_8^2-{\displaystyle \frac{1}{16}}(1-8{\rm Y})u_8^2{v}_8^3-{\displaystyle \frac{{\rm Y}}{32}}{v}_8^5.\hfill \end{array}$$

(25)

System (25) exhibits a degenerate equilibrium at $O_4=(0,0)$, with eigenvalues $\left\{0,0\right\}$ corresponding to the remaining infinite equilibrium points of System (23) outside $U_1$. In black hole spacetime, it indicates radial infinity. To resolve the degeneracy, we perform a blow-up analysis at $O_4$. The characteristic polynomial of System (25) is ${\mathcal{F}}_4=-u_8^2{v}_8^2$, indicating that $v_8=0$ is a characteristic direction. Applying the $u_8$-directional blow-up transformation $(u_8,v_8)\mapsto (u_8,u_8{h}_4)$ and canceling the common factor $u_8^2$, we obtain

$$\begin{array}{cc}\hfill & u_8^{\prime }=u_8{h}_4-3u_8^3+u_8^3{h}_4-{\displaystyle \frac{1}{16}}(1-8{\rm Y})u_8^3{h}_4^2-{\displaystyle \frac{{\rm Y}}{32}}{u}_8^3{h}_4^4,\hfill \\ \hfill & h_4^{\prime }=-h_4^2.\hfill \end{array}$$

(26)

For $u_8=0$, System (26) admits only the equilibrium $(0,0)$, again with eigenvalues $\left\{0,0\right\}$. A second blow-up is therefore necessary. The characteristic polynomial ${\mathcal{F}}_{4a}=-2u_8{h}_4^2$ reveals $h_4=0$ as a characteristic direction. Applying the u-directional blow-up $(u_8,h_4)\mapsto (u_8,u_8{l}_4)$ and simplifying by $u_8$, we derive

$$\begin{array}{cc}\hfill & u_8^{\prime }=u_8{l}_4-3u_8^2+u_8^3{l}_4-{\displaystyle \frac{1}{16}}(1-8{\rm Y})u_8^4{l}_4^2-{\displaystyle \frac{{\rm Y}}{32}}{u}_8^6{l}_4^4,\hfill \\ \hfill & l_4^{\prime }=3u_8{l}_4-2l_4^2-u_8^2{l}_4^2-{\displaystyle \frac{1}{16}}(1-8{\rm Y})u_8^3{l}_4^3+{\displaystyle \frac{{\rm Y}}{32}}{u}_8^5{l}_4^5.\hfill \end{array}$$

(27)

At $u_8=0$, this system again has a single equilibrium $(0,0)$ with eigenvalues $\left\{0,0\right\}$, necessitating a third blow-up. The characteristic polynomial ${\mathcal{F}}_{4b}=3u_8{l}_4(2u_8-l_4)$ identifies $l_4=0$ as a characteristic direction. Performing the $u_8$-directional blow-up $(u_8,l_4)\mapsto (u_8,u_8{s}_8)$ and simplifying by $u_8$, we obtain

$$\begin{array}{cc}\hfill & u_8^{\prime }=-3u_8+u_8{s}_4+u_8^3{s}_4-{\displaystyle \frac{1}{16}}(1-8{\rm Y})u_8^5{s}_4^2-{\displaystyle \frac{{\rm Y}}{32}}{u}_8^9{s}_4^4,\hfill \\ \hfill & s_4^{\prime }=6s_4-3s_4^2-2u_8^2{s}_4^2+{\displaystyle \frac{{\rm Y}}{16}}{u}_8^8{s}_4^5.\hfill \end{array}$$

(28)

For $u_8=0$, System (28) exhibits two equilibrium states:

• $e_{41}=(0,0)$, with eigenvalues $\{-3,6\}$ (a saddle point).

• $e_{42}=(0,2)$, with eigenvalues $\{-6,-1\}$ (a stable node).

By reversing the sequence of blow-up transformations, we reconstruct the phase portrait of the infinite equilibrium $O_4$, as illustrated in Figure 11.

All the equilibrium points of System (7) for $\lambda =-2$ and ${\rm Y}=0.0025$ are summarized in

Table 4. Equilibrium points of System (7) for $\lambda =-2$.

Point	Eigenvalues	Stability	Location in Black Hole Spacetime
$P_{10}$	$\pm {\displaystyle \frac{\sqrt{1-8{\rm Y}}}{16\sqrt{2}}}$	Saddle for ${\rm Y}<1/8$ and center for ${\rm Y}>1/8$	Innermost stable circular orbit for ${\rm Y}<1/8$ and outermost stable circular orbit for ${\rm Y}>1/8$
$P_{11}$	$\pm {\displaystyle \frac{A_{11}\sqrt{A_{11}-8{\rm Y}{A}_{11}-24A_{11}^2+96A_{11}^3}}{2\sqrt{2}}}$	Center for ${\rm Y}<1/8$ and saddle for ${\rm Y}>1/8$	Outermost stable circular orbit for ${\rm Y}<1/8$ and innermost stable circular orbit for ${\rm Y}>1/8$
$P_{12}$	$\pm {\displaystyle \frac{A_{12}\sqrt{A_{12}-8{\rm Y}{A}_{12}-24A_{12}^2+96A_{12}^3}}{2\sqrt{2}}}$	Saddle	∖
$P_{13}$	$\pm {\displaystyle \frac{A_{13}\sqrt{A_{13}-8{\rm Y}{A}_{13}-24A_{13}^2+96A_{13}^3}}{2\sqrt{2}}}$	Center	∖
$O_4$	$0,0$	Sink for ${\rm Y}=0.0025$	Radial infinity ($r\to \infty$)

See Appendix C for the algebraic expressions for $A_{11}$, $A_{12}$, and $A_{13}$.

. Employing the parameter configuration $(\lambda ,{\rm Y})=(-2,0.0025)$, the solution of Equation (5) determines a black hole event horizon located at $r_4=1.9901$. As illustrated by the red curve in Figure 12, a bijective correspondence is established between the unbounded domain $[r_4,+\infty )$ and the compactified coordinate range $x\in (0,0.5025]$ through the transformation $x=1/r_4$, where Figure 12 comprehensively demonstrates the global dynamical behavior of System (23).

3. Conclusions

In this work, we have systematically examined the influence of Lorentz-violating parameters ($\lambda$ and ${\rm Y}$) on the stability and structure of timelike geodesics in a spherically symmetric black hole spacetime incorporating power-law corrections to the Schwarzschild metric.

Through a comprehensive dynamical systems analysis—employing Poincaré compactification, blow-up methods, and numerical techniques—we explored the phase space structure for varying $\lambda$ values (ranging from −2 to 2) under a fixed and extremely small ${\rm Y}$. Our findings demonstrate a remarkable dependence of the equilibrium state topology on $\lambda$:

• At $\lambda =2$, the system exhibits two finite equilibrium states: $P_1$ (center) and $P_2$ (saddle), as illustrated in the phase portrait (Figure 1). The global dynamics further reveal an attractor at infinity (Figure 3).
• At $\lambda =1$, three equilibrium states emerge: $P_3$ (center), $P_4$ (center), and $P_5$ (saddle) (Figure 4). The spatial separation of $P_3$ necessitates a bifurcated phase-plane representation. Notably, the corresponding black hole solution possesses two horizons, with an attractor at infinity (Figure 6). Located between the inner and outer horizons, $P_3$ maintains partial applicability of differential equation qualitative theory, warranting its preservation as a mathematically and physically meaningful equilibrium state.
• At $\lambda =2/3$, four equilibrium states arise: $P_6$ (saddle), $P_7$ (center), $P_8$ (saddle), and $P_9$ (center) (Figure 7). Although $P_9$ is theoretically necessary to maintain mathematical consistency, its physical interpretation is precluded by its position within the inner horizon; thus, we exclude it from experimental considerations. The global dynamics reveals a $\lambda$-dependent enhancement in phase space complexity. Although mathematically excluded as an asymptotic attractor at infinity, this “attractor” re-emerges in the physically meaningful parameter region, exhibiting characteristic asymptotic convergence behavior (Figure 9).
• At $\lambda =-2$, four equilibrium states ($P_{10}$ and $P_{13}$: saddles; $P_{11}$ and $P_{12}$: centers) are observed, with their visibility strongly dependent on ${\rm Y}$ (Figure 10b). A degenerate equilibrium ($O_4$) acts as an attractor at infinity (Figure 12), and the horizon structure varies with parameter choices.

The parameter $\lambda$ governs the number of event horizons in the black hole spacetime: while the configuration features a single event horizon when $\lambda =2$ or $-2$, it develops two distinct horizons (an outer event horizon and an inner event horizon) for $\lambda =1$ or $2/3$. Notably, across all four values of $\lambda$, the black hole’s spacetime supports both an innermost stable circular orbit (ISCO) and an outermost stable circular orbit (OSCO). The locations of these orbits, however, are not universal but depend on the specific values of $\lambda$ and ${\rm Y}$, as both parameters collectively shape the black hole’s geometry.

A clear trend emerges: as $\lambda$ decreases, the number of equilibrium states increases, indicating a richer dynamical structure. Our results highlight the critical role of Lorentz-violating parameters in determining the black hole’s horizon structure and in governing both the stability and asymptotic behavior of circular geodesics. These findings provide a foundation for future investigations into modified black hole physics and the interplay between Lorentz violation and spacetime dynamics.