Phenomenological Charged Extensions of the Quantum Oppenheimer–Snyder Collapse Model
Abstract
1. Introduction
2. The Model
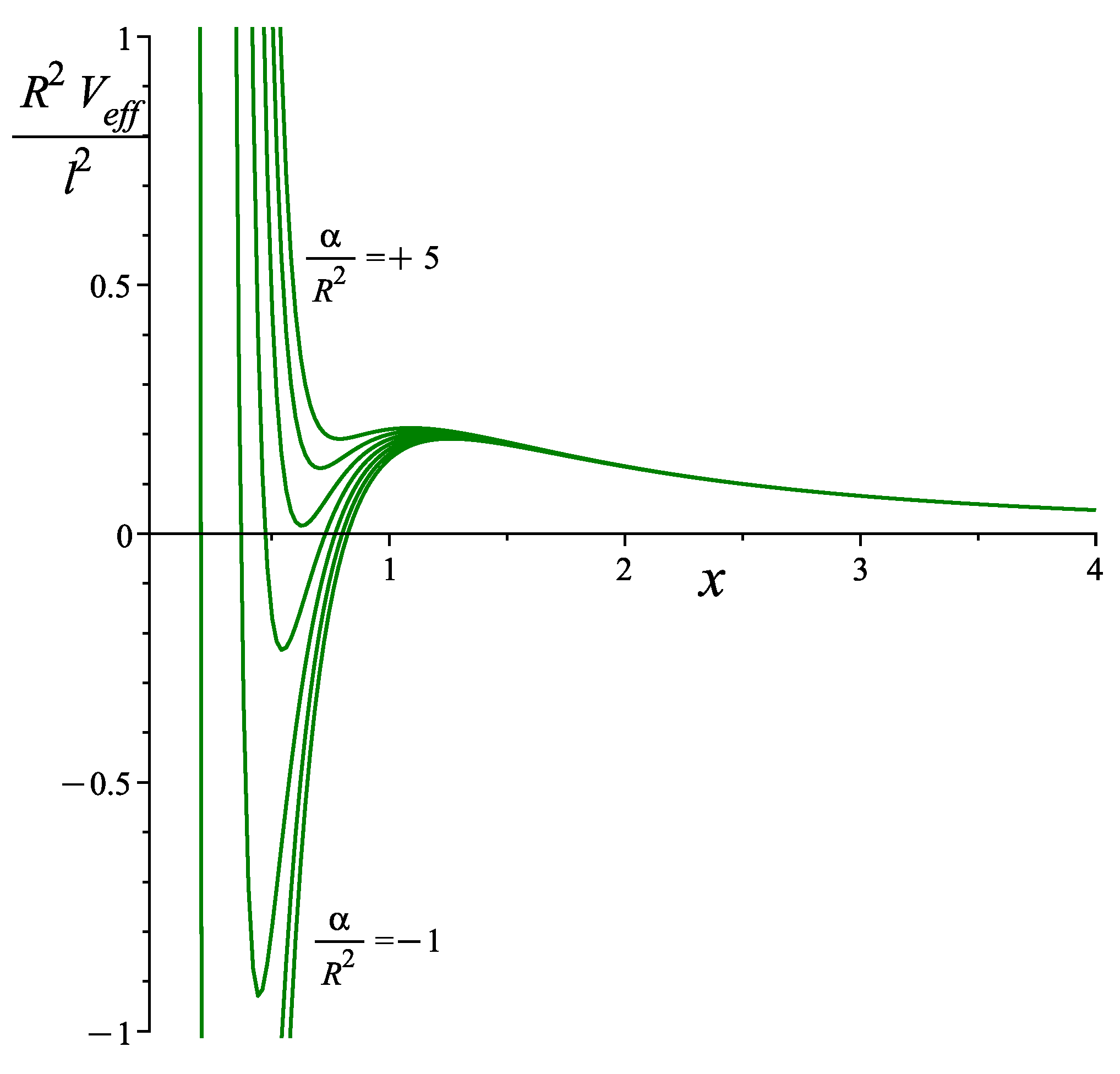
3. Null Circular Geodesics Around a Quantum-Corrected Charged Black Hole
4. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Oppenheimer, J.R.; Snyder, H. On Continued Gravitational Contraction. Phys. Rev. 1939, 56, 455. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Serber, R. On the Stability of Stellar Neutron Cores. Phys. Rev. 1938, 54, 540. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On Massive Neutron Cores. Phys. Rev. 1938, 55, 374. [Google Scholar] [CrossRef]
- Landau, L.D. Physik, On the Theory of Stars, Zeits. Sowjetunion 1932, 1, 285. [Google Scholar] [CrossRef]
- Tolman, R.C. Relativity, Thermodynamics and Cosmology; OXFORD University Press: Oxford, UK, 1934. [Google Scholar]
- Shapiro, S.L.; Teukolsky, S.A. Black Holes, White Dwarfs, and Neutron Stars; Wiley: Hoboken, NJ, USA, 1983. [Google Scholar]
- Thorne, K.S. Disk-Accretion onto a Black Hole. II. Evolution of the Hole. Astrophys. J. 1974, 191, 507. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Freeman: Dallas, TX, USA, 1973. [Google Scholar]
- Baumgarte, T.W.; Shapiro, S.L. Numerical Relativity: Solving Einstein’s Equations on the Computer; Cambridge University: Cambridge, UK, 2010. [Google Scholar]
- Bethe, H.A. Supernova Mechanisms. Rev. Mod. Phys. 1990, 62, 801. [Google Scholar] [CrossRef]
- Janka, H.T. Explosion Mechanisms of Core-Collapse Supernovae. Ann. Rev. Nuc. Part. Sci. USA 2012, 62, 407. [Google Scholar] [CrossRef]
- Ashtekar, A.; Bojowald, M. Quantum Geometry and the Schwarzschild Singularity. Class. Quan. Grav. 2005, 23, 391. [Google Scholar] [CrossRef]
- Hawking, S.W.; Ellis, G.F.R. The Large Scale Structure of Space-Time; Cambridge University Press: Cambridge, UK, 1973. [Google Scholar]
- Penrose, R. Gravitational Collapse: The Role of General Relativity. Riv. Del Nuo. Cim. 1969, 1, 252. [Google Scholar] [CrossRef]
- Wald, R.M. Gravitational Collapse and Cosmic Censorship; Springer: Dordrecht, The Netherlands, 1999. [Google Scholar] [CrossRef]
- Lewandowski, J.; Ma, Y.; Yang, J.; Zhang, C. Quantum Oppenheimer-Snyder and Swiss Cheese Models. Phys. Rev. Lett. 2023, 130, 101501. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A.; Pawlowski, T.; Singh, P. Quantum Nature of the Big Bang. Phys. Rev. Lett. 2006, 96, 141301. [Google Scholar] [CrossRef] [PubMed]
- Israel, W. Singular hypersurfaces and thin shells in general relativity. Nuovo C. B 1966, 44, 1. [Google Scholar] [CrossRef]
- Cruz, V.d.; Israel, W. Gravitational bounce. Nuovo C. A 1967, 51, 744. [Google Scholar] [CrossRef]
- Cao, L.-M.; Li, L.-Y.; Wu, L.-B.; Zhou, Y.-S. The instability of the inner horizon of the quantum-corrected black hole. Eur. Phys. J. C 2024, 84, 507. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, C.; Ma, Y. Shadow and stability of quantum-corrected black holes. Eur. Phys. J. C 2023, 83, 619. [Google Scholar] [CrossRef]
- Dong, S.-H.; Hosseinifar, F.; Studnička, F.; Hassanabadi, H. Some new properties of black holes in the quantum Oppenheimer-Snyder model. Phys. Lett. B 2025, 860, 139182. [Google Scholar] [CrossRef]
- Gong, H.; Li, S.; Zhang, D.; Fu, G.; Wu, J.-P. Quasinormal modes of quantum-corrected black holes. Phys. Rev. D 2024, 110, 044040. [Google Scholar] [CrossRef]
- Mazharimousavi, S.H. Quantum Oppenheimer-Snyder-Swiss Cheese model. Phys. Dark Univ. 2024, 45, 101532. [Google Scholar] [CrossRef]
- Hod, S. Cosmic censorship: Formation of a shielding horizon around a fragile horizon. Phys. Rev. D 2013, 87, 024037. [Google Scholar] [CrossRef]
- Hod, S. Charged Dyson shells supported in curved spacetimes of spherically symmetric central compact objects. Eur. Phys. J. C 2024, 84, 1148. [Google Scholar] [CrossRef]
- Mazharimousavi, S.H. Minimum asymptotic energy of a charged spherically symmetric thin-shell wormhole and its stability. Eur. Phys. J. C 2025, 85, 132. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mazharimousavi, S.H. Phenomenological Charged Extensions of the Quantum Oppenheimer–Snyder Collapse Model. Universe 2025, 11, 257. https://doi.org/10.3390/universe11080257
Mazharimousavi SH. Phenomenological Charged Extensions of the Quantum Oppenheimer–Snyder Collapse Model. Universe. 2025; 11(8):257. https://doi.org/10.3390/universe11080257
Chicago/Turabian StyleMazharimousavi, S. Habib. 2025. "Phenomenological Charged Extensions of the Quantum Oppenheimer–Snyder Collapse Model" Universe 11, no. 8: 257. https://doi.org/10.3390/universe11080257
APA StyleMazharimousavi, S. H. (2025). Phenomenological Charged Extensions of the Quantum Oppenheimer–Snyder Collapse Model. Universe, 11(8), 257. https://doi.org/10.3390/universe11080257





