INTEGRAL/ISGRI Post 2024-Periastron View of PSR B1259-63
Abstract
1. Introduction
2. Data Analysis
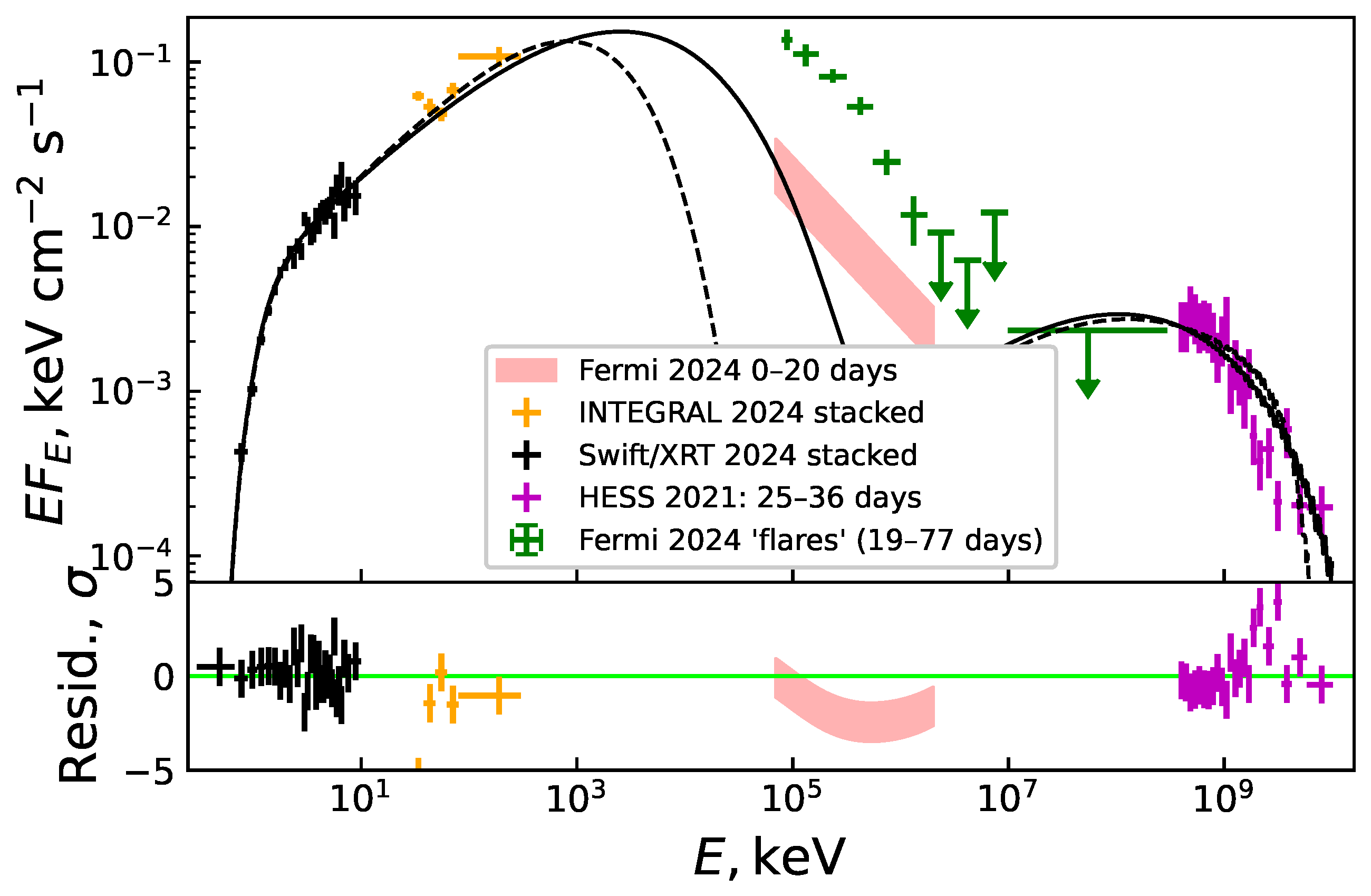
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | https://www.isdc.unige.ch/integral/analysis (accessed on 28 July 2025) |
References
- Johnston, S.; Manchester, R.N.; Lyne, A.G.; Bailes, M.; Kaspi, V.M.; Qiao, G.; D’Amico, N. PSR 1259-63: A Binary Radio Pulsar with a Be Star Companion. Astrophys. J. 1992, 387, L37. [Google Scholar] [CrossRef]
- Miller-Jones, J.C.A.; Deller, A.T.; Shannon, R.M.; Dodson, R.; Moldón, J.; Ribó, M.; Dubus, G.; Johnston, S.; Paredes, J.M.; Ransom, S.M.; et al. The geometric distance and binary orbit of PSR B1259-63. Mon. Not. R. Astron. Soc. 2018, 479, 4849–4860. [Google Scholar] [CrossRef]
- Chernyakova, M.; Malyshev, D. Gamma-ray binaries. In Proceedings of the Multifrequency Behaviour of High Energy Cosmic Sources–XIII, Palermo, Italy, 3–8 June 2019; Creative Commons: Mountain View, CA, USA, 2020; p. 45. [Google Scholar] [CrossRef]
- Melatos, A.; Johnston, S.; Melrose, D.B. Stellar wind and stellar disc models of dispersion and rotation measure variations in the PSR B1259—63/SS2883 binary system. Mon. Not. R. Astron. Soc. 1995, 275, 381–397. [Google Scholar] [CrossRef]
- Tavani, M.; Arons, J.; Kaspi, V.M. Regimes of High-Energy Shock Emission from the Be Star/Pulsar System PSR 1259-63. Astrophys. J. Lett. 1994, 433, L37. [Google Scholar] [CrossRef]
- Chernyakova, M.; Malyshev, D.; Mc Keague, S.; van Soelen, B.; Marais, J.P.; Martin-Carrillo, A.; Murphy, D. New insight into the origin of the GeV flare in the binary system PSR B1259-63/LS 2883 from the 2017 periastron passage. Mon. Not. R. Astron. Soc. 2020, 497, 648–655. [Google Scholar] [CrossRef]
- Chernyakova, M.; Malyshev, D.; van Soelen, B.; O’Sullivan, S.; Sobey, C.; Tsygankov, S.; Mc Keague, S.; Green, J.; Kirwan, M.; Santangelo, A.; et al. Multi-Wavelength Properties of the 2021 Periastron Passage of PSR B1259-63. Universe 2021, 7, 242. [Google Scholar] [CrossRef]
- Chernyakova, M.; Malyshev, D.; van Soelen, B.; Mc Keague, S.; O’Sullivan, S.P.; Buckley, D. The radio to GeV picture of PSR B1259-63 during the 2021 periastron passage. Mon. Not. R. Astron. Soc. 2024, 528, 5231–5241. [Google Scholar] [CrossRef]
- Chernyakova, M.; Malyshev, D.; van Soelen, B.; Finn Gallagher, A.; Matchett, N.; Russell, T.D.; van den Eijnden, J.; Lower, M.E.; Johnston, S.; Tsygankov, S.; et al. Multiwavelength coverage of the 2024 periastron passage of PSR B1259-63/LS 2883. Mon. Not. R. Astron. Soc. 2025, 536, 247–253. [Google Scholar] [CrossRef]
- Shaw, S.E.; Chernyakova, M.; Rodriguez, J.; Walter, R.; Kretschmar, P.; Mereghetti, S. INTEGRAL observations of the PSR B1259-63/SS2883 system after the 2004 periastron passage. Astron. Astrophys. 2004, 426, L33–L36. [Google Scholar] [CrossRef][Green Version]
- Chernyakova, M.; Neronov, A.; van Soelen, B.; Callanan, P.; O’Shaughnessy, L.; Babyk, I.; Tsygankov, S.; Vovk, I.; Krivonos, R.; Tomsick, J.A.; et al. Multi-wavelength observations of the binary system PSR B1259-63/LS 2883 around the 2014 periastron passage. Mon. Not. R. Astron. Soc. 2015, 454, 1358–1370. [Google Scholar] [CrossRef]
- Salganik, A.; Tsygankov, S.S.; Chernyakova, M.; Malyshev, D.; Poutanen, J. Discovery of a bimodal luminosity distribution in persistent Be/X-ray pulsar 2RXP J130159.6-635806. arXiv 2025, arXiv:2504.11263. [Google Scholar] [CrossRef]
- Burrows, D.N.; Hill, J.E.; Nousek, J.A.; Kennea, J.A.; Wells, A.; Osborne, J.P.; Abbey, A.F.; Beardmore, A.; Mukerjee, K.; Short, A.D.T.; et al. The Swift X-Ray Telescope. Space Sci. Rev. 2005, 120, 165–195. [Google Scholar] [CrossRef]
- Aharonian, F. et al. [H. E. S. S. Collaboration]; Ait Benkhali, F.; Aschersleben, J.; Ashkar, H.; Backes, M.; Barbosa Martins, V.; Batzofin, R.; Becherini, Y.; Berge, D.; Bernlöhr, K.; et al. H.E.S.S. observations of the 2021 periastron passage of PSR B1259-63/LS 2883. Astron. Astrophys. 2024, 687, A219. [Google Scholar] [CrossRef]
- Zabalza, V. Naima: A Python package for inference of particle distribution properties from nonthermal spectra. In Proceedings of the 34th International Cosmic Ray Conference (ICRC2015), The Hague, The Netherlands, 30 July–6 August 2015; Volume 34, p. 922. [Google Scholar] [CrossRef]
- Aharonian, F.A.; Kelner, S.R.; Prosekin, A.Y. Angular, spectral, and time distributions of highest energy protons and associated secondary gamma rays and neutrinos propagating through extragalactic magnetic and radiation fields. Phys. Rev. D 2010, 82, 043002. [Google Scholar] [CrossRef]
- Khangulyan, D.; Aharonian, F.A.; Kelner, S.R. Simple Analytical Approximations for Treatment of Inverse Compton Scattering of Relativistic Electrons in the Blackbody Radiation Field. Astrophys. J. 2014, 783, 100. [Google Scholar] [CrossRef]
- Khangulyan, D.; Aharonian, F.A.; Bogovalov, S.V.; Ribó, M. Gamma-Ray Signal from the Pulsar Wind in the Binary Pulsar System PSR B1259-63/LS 2883. Astrophys. J. 2011, 742, 98. [Google Scholar] [CrossRef]
- Negueruela, I.; Ribó, M.; Herrero, A.; Lorenzo, J.; Khangulyan, D.; Aharonian, F.A. Astrophysical Parameters of LS 2883 and Implications for the PSR B1259-63 Gamma-ray Binary. Astrophys. J. Lett. 2011, 732, L11. [Google Scholar] [CrossRef]
- Kennel, C.F.; Coroniti, F.V. Confinement of the Crab pulsar’s wind by its supernova remnant. Astrophys. J. 1984, 283, 694–709. [Google Scholar] [CrossRef]
- Tavani, M.; Arons, J. Theory of High-Energy Emission from the Pulsar/Be Star System PSR 1259-63. I. Radiation Mechanisms and Interaction Geometry. Astrophys. J. 1997, 477, 439–464. [Google Scholar] [CrossRef]
- Chen, A.M.; Takata, J.; Yi, S.X.; Yu, Y.W.; Cheng, K.S. Modelling multiwavelength emissions from PSR B1259-63/LS 2883: Effects of the stellar disc on shock radiations. Astron. Astrophys. 2019, 627, A87. [Google Scholar] [CrossRef]
- Usov, V.V.; Melrose, D.B. X-Ray Emission from Single Magnetic Early-Type Stars. Astrophys. J. 1992, 395, 575. [Google Scholar] [CrossRef]
- De Becker, M. Non-thermal emission processes in massive binaries. Astron. Astrophys. Rev. 2007, 14, 171–216. [Google Scholar] [CrossRef]
- Wade, G.A.; Petit, V.; Grunhut, J.; Neiner, C. Magnetic fields of Be stars: Preliminary results from a hybrid analysis of the MiMeS sample. arXiv 2014, arXiv:1411.6165. [Google Scholar] [CrossRef]
- ud-Doula, A.; Owocki, S.P.; Kee, N.D. Disruption of circumstellar discs by large-scale stellar magnetic fields. Mon. Not. R. Astron. Soc. 2018, 478, 3049–3055. [Google Scholar] [CrossRef]
- Zhang, S.; Torres, D.F.; Li, J.; Chen, Y.P.; Rea, N.; Wang, J.M. Long-term monitoring of LS I +61°303 with INTEGRAL. Mon. Not. R. Astron. Soc. 2010, 408, 642–646. [Google Scholar] [CrossRef]
- Li, J.; Torres, D.F.; Zhang, S. Spectral Analysis in Orbital/Superorbital Phase Space and Hints of Superorbital Variability in the Hard X-Rays of LS I +61°303. Astrophys. J. Lett. 2014, 785, L19. [Google Scholar] [CrossRef]
- Sullivan, A.G.; Romani, R.W. High-energy Emission from the Intrabinary Shocks in Redback Pulsars. Astrophys. J. 2025, 984, 146. [Google Scholar] [CrossRef]
- Kandel, D.; Romani, R.W.; An, H. The Synchrotron Emission Pattern of IntraBinary Shocks. Astrophys. J. 2019, 879, 73. [Google Scholar]
- Sim, M.; An, H.; Wadiasingh, Z. Modeling X-Ray and Gamma-Ray Emission from Redback Pulsar Binaries. Astrophys. J. 2024, 964, 109. [Google Scholar] [CrossRef]
- de Angelis, A.; Tatischeff, V.; Grenier, I.A.; McEnery, J.; Mallamaci, M.; Tavani, M.; Oberlack, U.; Hanlon, L.; Walter, R.; Argan, A.; et al. Science with e-ASTROGAM. A space mission for MeV-GeV gamma-ray astrophysics. J. High Energy Astrophys. 2018, 19, 1–106. [Google Scholar] [CrossRef]
- McEnery, J.; van der Horst, A.; Dominguez, A.; Moiseev, A.; Marcowith, A.; Harding, A.; Lien, A.; Giuliani, A.; Inglis, A.; Ansoldi, S.; et al. All-sky Medium Energy Gamma-ray Observatory: Exploring the Extreme Multimessenger Universe. Proc. Bull. Am. Astron. Soc. 2019, 51, 245. [Google Scholar] [CrossRef]
- Orlando, E.; Bottacini, E.; Moiseev, A.A.; Bodaghee, A.; Collmar, W.; Ensslin, T.; Moskalenko, I.V.; Negro, M.; Profumo, S.; Digel, S.W.; et al. Exploring the MeV sky with a combined coded mask and Compton telescope: The Galactic Explorer with a Coded aperture mask Compton telescope (GECCO). J. Cosmol. Astropart. Phys. 2022, 2022, 036. [Google Scholar] [CrossRef]
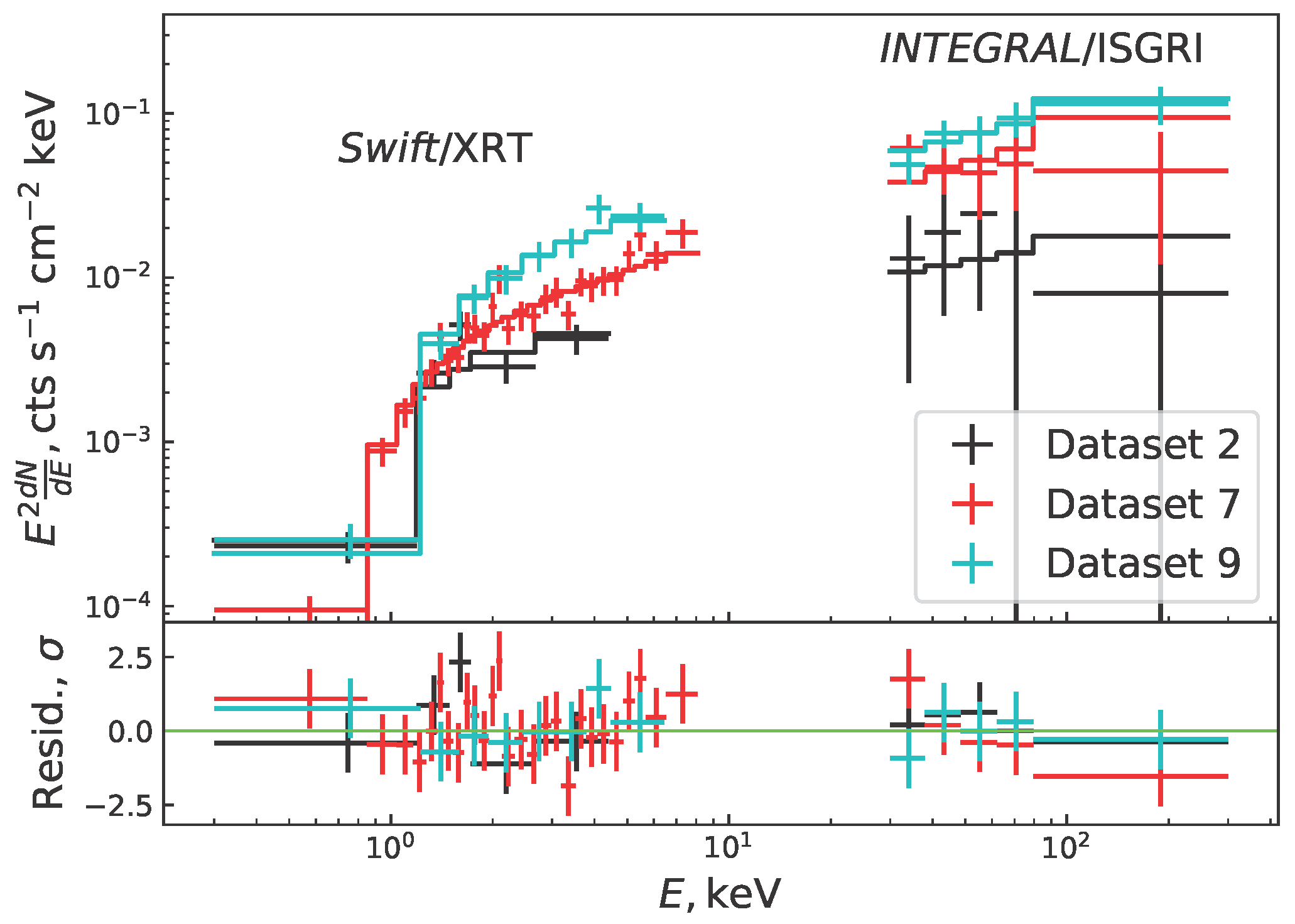
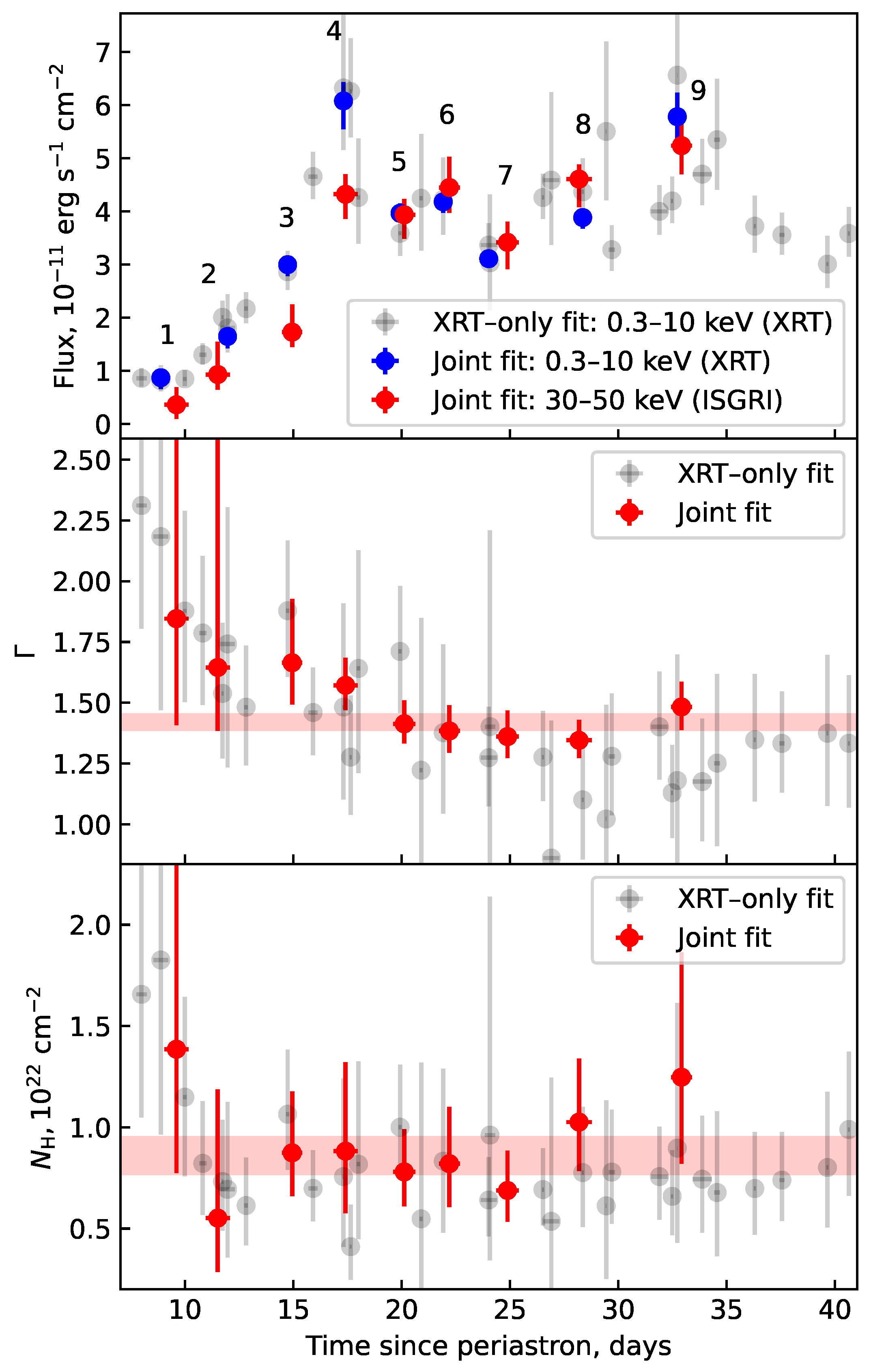
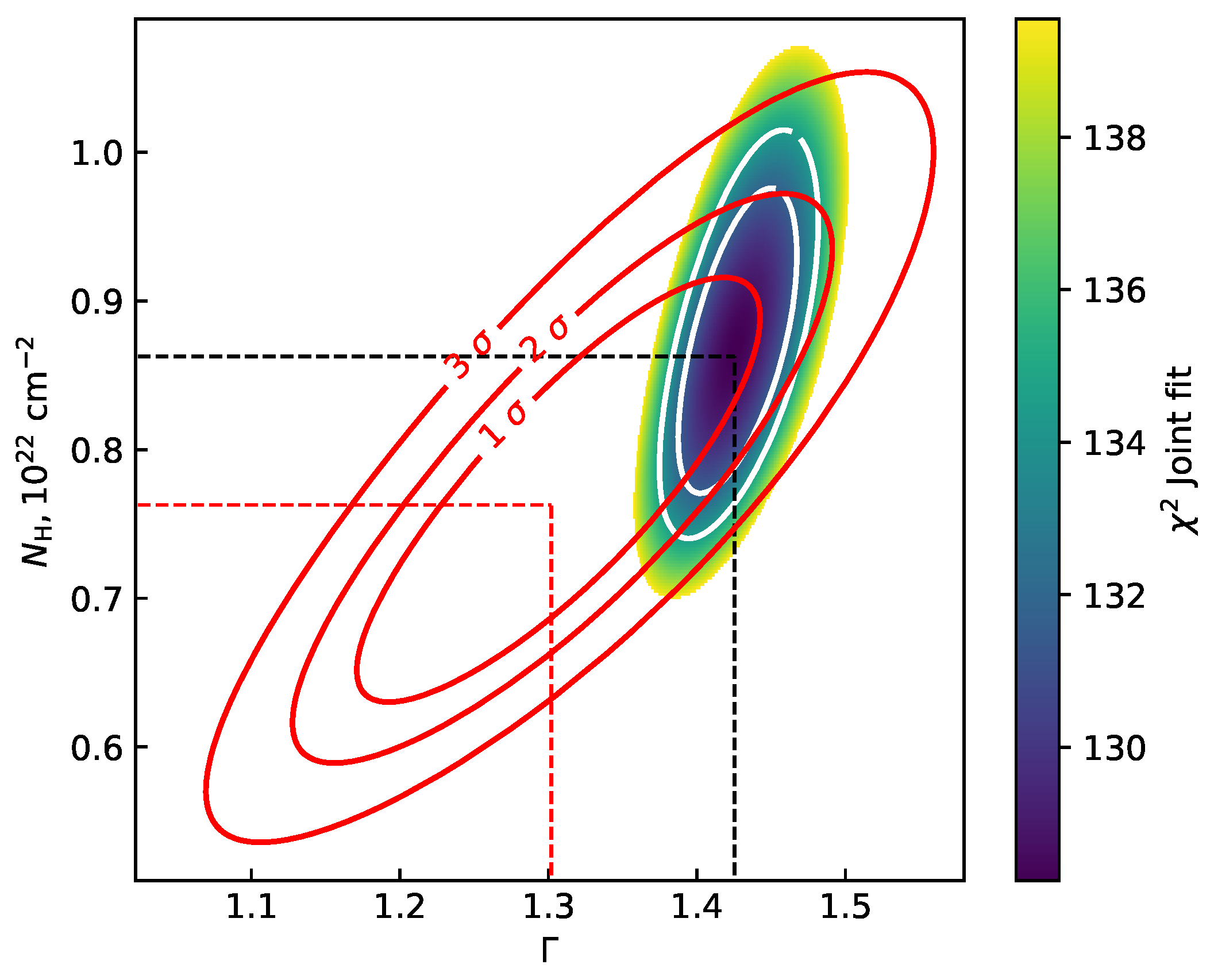
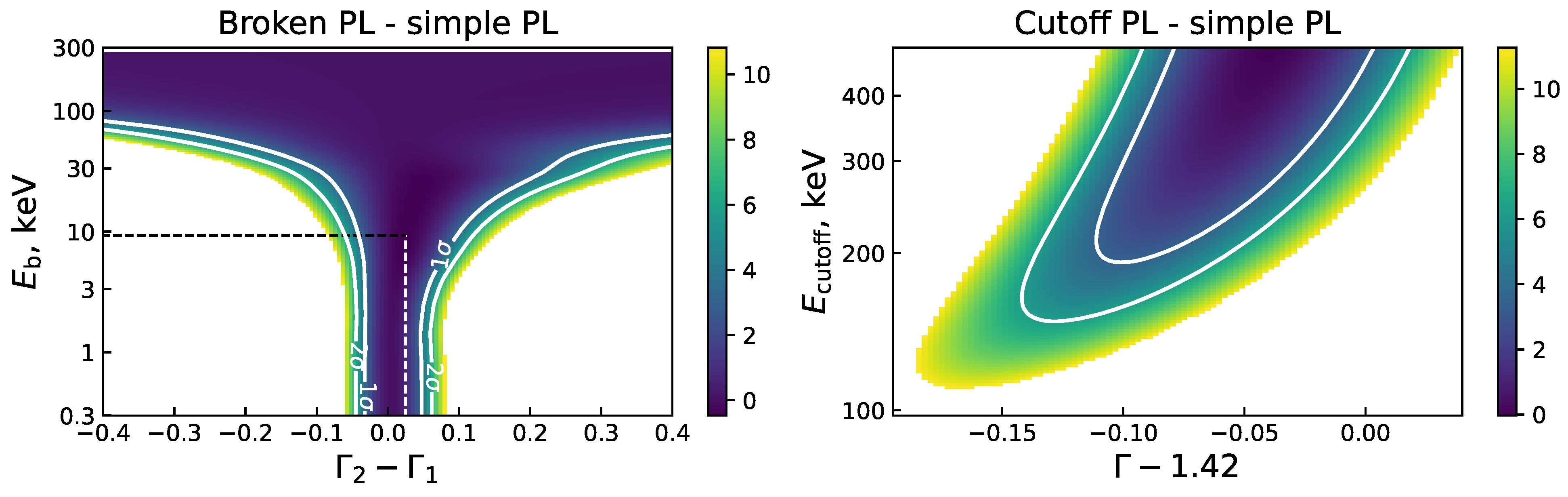
| Dataset No. | ScW Range | MJD | (0.3–10 keV) | (30–50 keV) | |||
|---|---|---|---|---|---|---|---|
| Days | |||||||
| 1 | 27980036–60 | 60501.2 | 9.6 | ||||
| 2 | 27990019–41 | 60503.1 | 11.5 | ||||
| 3 | 28000051–75 | 60506.5 | 14.9 | ||||
| 4 | 28010036–60 | 60509.0 | 17.4 | ||||
| 5 | 28020054–78 | 60511.7 | 20.1 | ||||
| 6 | 28030030–54 | 60513.8 | 22.2 | ||||
| 7 | 28040022–48 | 60516.5 | 24.9 | ||||
| 8 | 28050056–81 * | 60519.8 | 28.2 | ||||
| 9 | 28070023–47 | 60524.5 | 32.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuzin, A.; Malyshev, D.; Chernyakova, M.; van Soelen, B.; Santangelo, A. INTEGRAL/ISGRI Post 2024-Periastron View of PSR B1259-63. Universe 2025, 11, 254. https://doi.org/10.3390/universe11080254
Kuzin A, Malyshev D, Chernyakova M, van Soelen B, Santangelo A. INTEGRAL/ISGRI Post 2024-Periastron View of PSR B1259-63. Universe. 2025; 11(8):254. https://doi.org/10.3390/universe11080254
Chicago/Turabian StyleKuzin, Aleksei, Denys Malyshev, Maria Chernyakova, Brian van Soelen, and Andrea Santangelo. 2025. "INTEGRAL/ISGRI Post 2024-Periastron View of PSR B1259-63" Universe 11, no. 8: 254. https://doi.org/10.3390/universe11080254
APA StyleKuzin, A., Malyshev, D., Chernyakova, M., van Soelen, B., & Santangelo, A. (2025). INTEGRAL/ISGRI Post 2024-Periastron View of PSR B1259-63. Universe, 11(8), 254. https://doi.org/10.3390/universe11080254






