Toward the Alleviation of the H0 Tension in Myrzakulov f(R,T) Gravity
Abstract
1. Introduction
2. Myrzakulov Gravity
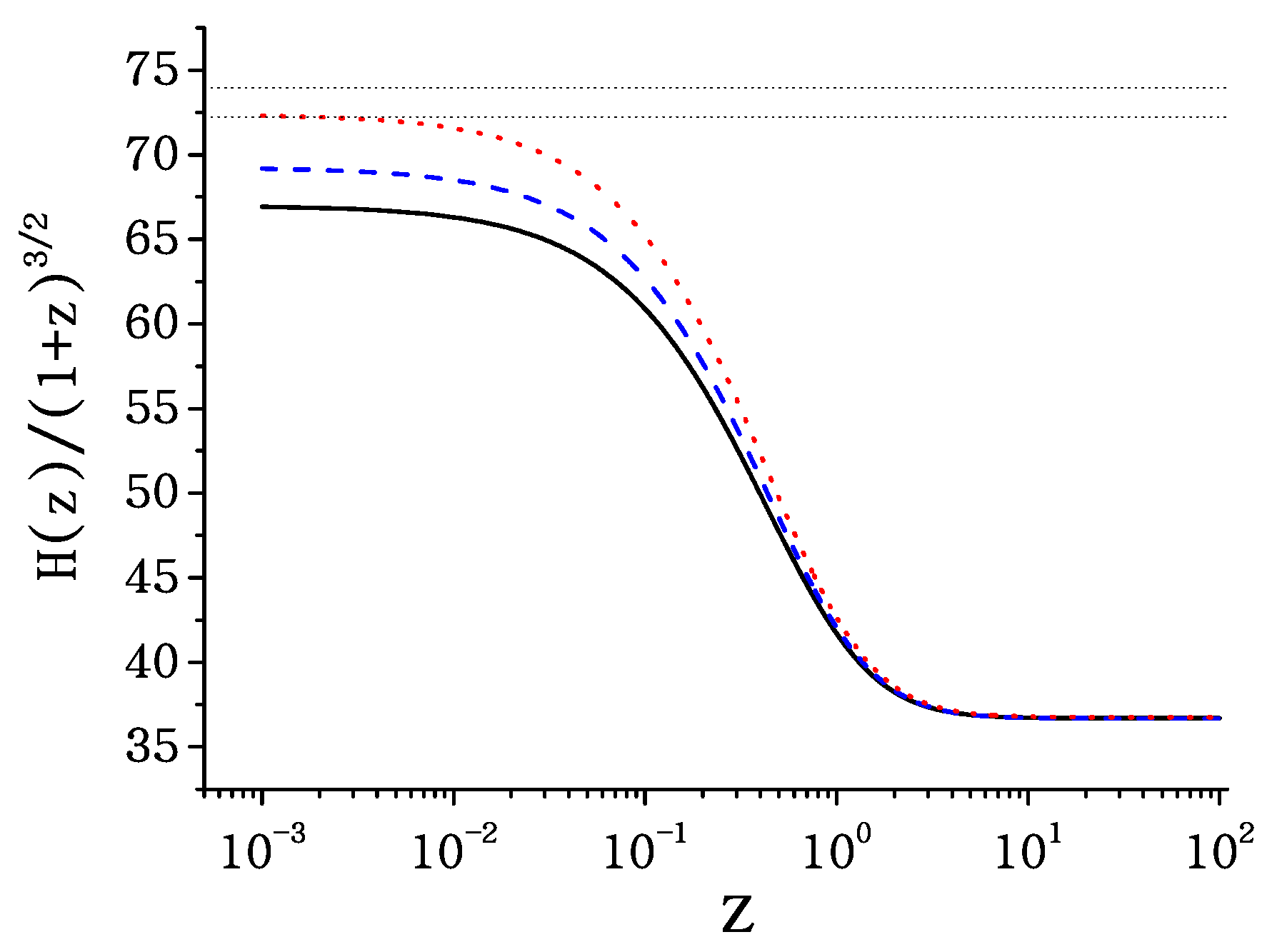
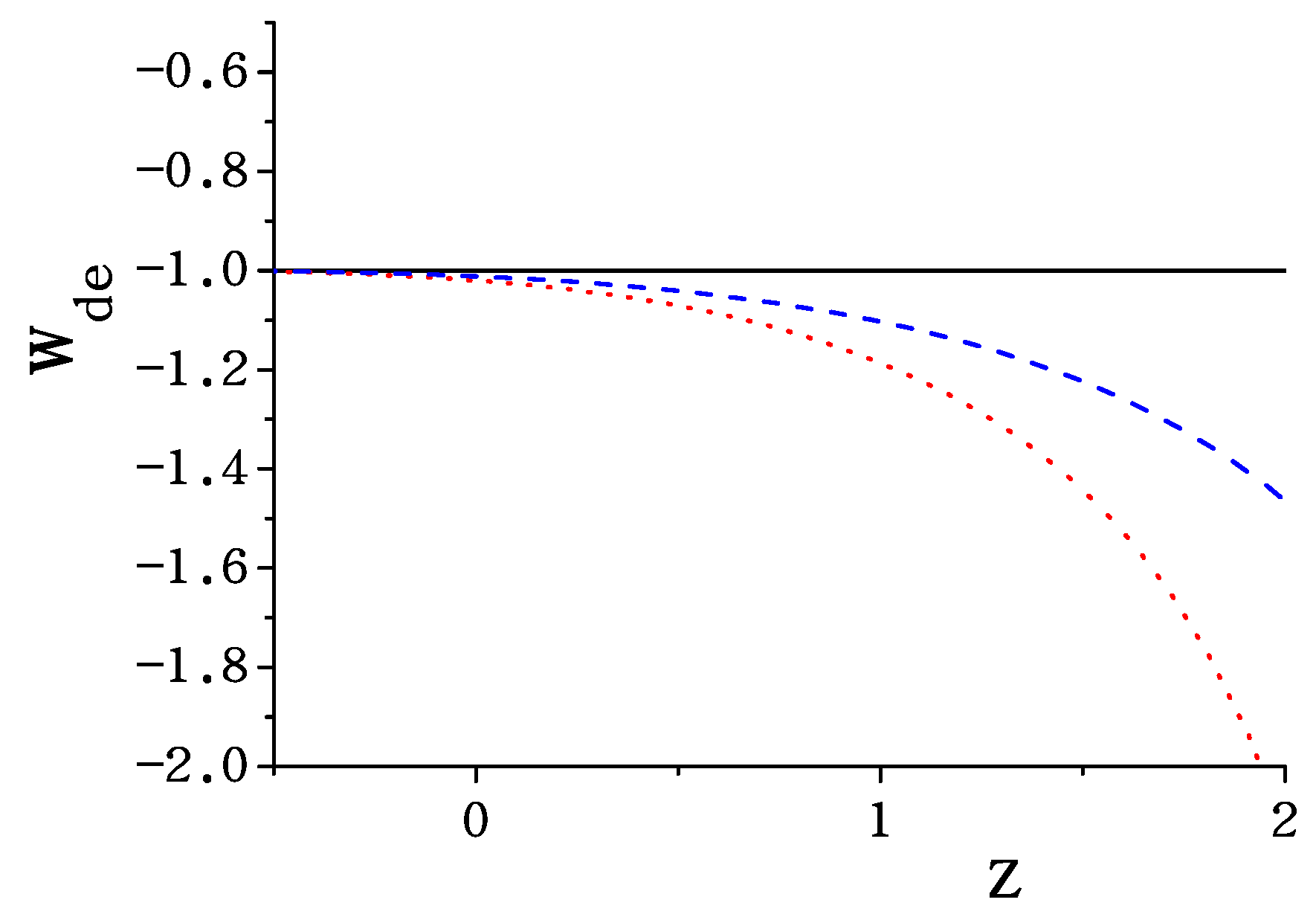
3. Toward the Alleviation of the Tension
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peebles, P.J.E.; Ratra, B. The Cosmological Constant and Dark Energy. Rev. Mod. Phys. 2003, 75, 559–606. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. New Astron. Rev. 2022, 95, 101659. [Google Scholar] [CrossRef]
- Capozziello, S.; Laurentis, M.D. Extended Theories of Gravity. Phys. Rept. 2011, 509, 167–321. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Lazkoz, R.; Salzano, V.; Moniz, P.V.; Capozziello, S.; Jiménez, J.B.; De Laurentis, M.; Olmo, G.J. Modified Gravity and Cosmology: An Update by the CANTATA Network; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Starobinsky, A. A new type of isotropic cosmological models without singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified f(R) gravity consistent with realistic cosmology: From matter dominated epoch to dark energy universe. Phys. Rev. D 2006, 74, 086005. [Google Scholar] [CrossRef]
- Song, Y.S.; Hu, W.; Sawicki, I. The Large Scale Structure of f(R) Gravity. Phys. Rev. D 2007, 75, 044004. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unifying inflation with LambdaCDM epoch in modified f(R) gravity consistent with Solar System tests. Phys. Lett. B 2007, 657, 238–245. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: From F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Olmo, G.J. Palatini Approach to Modified Gravity: f(R) Theories and Beyond. Int. J. Mod. Phys. D 2011, 20, 413–462. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified Gauss-Bonnet theory as gravitational alternative for dark energy. Phys. Lett. B 2005, 631, 1–6. [Google Scholar] [CrossRef]
- Felice, A.D.; Tsujikawa, S. Solar system constraints on f(G) gravity models. Phys. Rev. D 2009, 80, 063516. [Google Scholar] [CrossRef]
- Garcia, N.M.; Lobo, F.S.N.; Mimoso, J.P.; Harko, T. f(G) modified gravity and the energy conditions. J. Phys. Conf. Ser. 2011, 314, 012056. [Google Scholar] [CrossRef]
- Houndjo, M.J.S.; Rodrigues, M.E.; Momeni, D.; Myrzakulov, R. Exploring Cylindrical Solutions in Modified f(G) Gravity. Can. J. Phys. 2014, 92, 1528–1540. [Google Scholar] [CrossRef]
- Sharif, M.; Abbas, G. Dynamics of Shearfree Dissipative Collapse in f(G) Gravity. J. Phys. Soc. Jap. 2013, 82, 034006. [Google Scholar] [CrossRef]
- Bengochea, G.R.; Ferraro, R. Dark torsion as the cosmic speed-up. Phys. Rev. D 2009, 79, 124019. [Google Scholar] [CrossRef]
- Cai, Y.F.; Capozziello, S.; Laurentis, M.D.; Saridakis, E.N. f(T) teleparallel gravity and cosmology. Rept. Prog. Phys. 2016, 79, 106901. [Google Scholar] [CrossRef]
- Chen, S.H.; Dent, J.B.; Dutta, S.; Saridakis, E.N. Cosmological perturbations in f(T) gravity. Phys. Rev. D 2011, 83, 023508. [Google Scholar] [CrossRef]
- Myrzakulov, R. Accelerating universe from F(T) gravity. Eur. Phys. J. C 2011, 71, 1752. [Google Scholar] [CrossRef]
- Cai, Y.F.; Chen, S.H.; Dent, J.B.; Dutta, S.; Saridakis, E.N. Matter Bounce Cosmology with the f(T) Gravity. Class. Quant. Grav. 2011, 28, 215011. [Google Scholar] [CrossRef]
- Tamanini, N.; Boehmer, C.G. Good and bad tetrads in f(T) gravity. Phys. Rev. D 2012, 86, 044009. [Google Scholar] [CrossRef]
- Kofinas, G.; Saridakis, E.N. Teleparallel equivalent of Gauss-Bonnet gravity and its modifications. Phys. Rev. D 2014, 90, 084044. [Google Scholar] [CrossRef]
- Jiménez, J.B.; Heisenberg, L.; Koivisto, T. Coincident General Relativity. Phys. Rev. D 2018, 98, 044048. [Google Scholar] [CrossRef]
- Jiménez, J.B.; Heisenberg, L.; Koivisto, T. The Geometrical Trinity of Gravity. Universe 2019, 5, 173. [Google Scholar] [CrossRef]
- Lazkoz, R.; Lobo, F.S.N.; Ortiz-Banos, M.; Salzano, V. Observational constraints of f(Q) gravity. Phys. Rev. D 2019, 100, 104027. [Google Scholar] [CrossRef]
- Anagnostopoulos, F.K.; Basilakos, S.; Saridakis, E.N. First evidence that non-metricity f(Q) gravity could challenge ΛCDM. Phys. Lett. B 2021, 822, 136634. [Google Scholar] [CrossRef]
- Lu, J.; Zhao, X.; Chee, G. Cosmology in symmetric teleparallel gravity and its dynamical system. Eur. Phys. J. C 2019, 79, 530. [Google Scholar] [CrossRef]
- Mandal, S.; Sahoo, P.K.; Santos, J.R.L. Energy conditions in f(Q) gravity. Phys. Rev. D 2020, 102, 024057. [Google Scholar] [CrossRef]
- Ayuso, I.; Lazkoz, R.; Salzano, V. Observational constraints on cosmological solutions of f(Q) theories. Phys. Rev. D 2021, 103, 063505. [Google Scholar] [CrossRef]
- Myrzakulov, R. FRW Cosmology in F(R,T) gravity. Eur. Phys. J. C 2012, 72, 2203. [Google Scholar] [CrossRef]
- Saridakis, E.N.; Myrzakul, S.; Myrzakulov, K.; Yerzhanov, K. Cosmological applications of F(R,T) gravity with dynamical curvature and torsion. Phys. Rev. D 2020, 102, 023525. [Google Scholar] [CrossRef]
- Anagnostopoulos, F.K.; Basilakos, S.; Saridakis, E.N. Observational constraints on Myrzakulov gravity. Phys. Rev. D 2021, 103, 104013. [Google Scholar] [CrossRef]
- Myrzakul, T.; Yesmakhanova, K.; Myrzakulov, N.; Myrzakul, S.; Myrzakulov, K.; Yerzhanov, K.; Myrzakulov, R.; Nugmanova, G. Metric-affine Myrzakulov gravity theories with Gauss-Bonnet and boundary term scalars. arXiv 2021, arXiv:2101.05318. [Google Scholar]
- Iosifidis, D.; Myrzakulov, N.; Myrzakulov, R. Metric-Affine Version of Myrzakulov F(R,T,Q,T) Gravity and Cosmological Applications. Universe 2021, 7, 262. [Google Scholar] [CrossRef]
- Myrzakulov, N.; Myrzakulov, R.; Ravera, L. Metric-Affine Myrzakulov Gravity Theories. Symmetry 2021, 13, 1855. [Google Scholar] [CrossRef]
- Harko, T.; Myrzakulov, N.; Myrzakulov, R.; Shahidi, S. Non-minimal geometry–matter couplings in Weyl–Cartan space–times: f(R,T,Q,Tm)gravity. Phys. Dark Univ. 2021, 34, 100886. [Google Scholar] [CrossRef]
- Papagiannopoulos, G.; Basilakos, S.; Saridakis, E.N. Dynamical system analysis of Myrzakulov gravity. Phys. Rev. D 2022, 106, 103512. [Google Scholar] [CrossRef]
- Kazempour, S.; Akbarieh, A.R. Cosmological study in Myrzakulov F(R,T) quasi-dilaton massive gravity. Astropart. Phys. 2025, 165, 103060. [Google Scholar] [CrossRef]
- Zahran, E.H.M.; Bekir, A.; Ibrahim, R.A.; Myrzakulov, R. The new soliton solution types to the Myrzakulov-Lakshmanan-XXXII-equation. AIMS Math. 2024, 9, 6145–6160. [Google Scholar] [CrossRef]
- Maurya, D.C.; Myrzakulov, R. Transit cosmological models in F(R,) gravity theory. Eur. Phys. J. C 2024, 84, 534. [Google Scholar] [CrossRef]
- Maurya, D.C.; Myrzakulov, R. Exact cosmological models in metric-affine F(R, T) gravity. Eur. Phys. J. C 2024, 84, 625. [Google Scholar] [CrossRef]
- Maurya, D.C.; Yesmakhanova, K.; Myrzakulov, R.; Nugmanova, G. FLRW cosmology in metric-affine F(R,Q) gravity*. Chin. Phys. C 2024, 48, 125101. [Google Scholar] [CrossRef]
- Maurya, D.C.; Yesmakhanova, K.; Myrzakulov, R.; Nugmanova, G. Metric-Affine F(T,Q) gravity: Cosmological implications and constraints. Phys. Scripta 2024, 99, 105014. [Google Scholar] [CrossRef]
- Momeni, D.; Myrzakulov, R. Myrzakulov gravity in vielbein formalism: A study in Weitzenböck spacetime. Nucl. Phys. B 2025, 1015, 116903. [Google Scholar] [CrossRef]
- Lymperis, A.; Nugmanova, G.; Sergazina, A. Non-Singular Bounce Solutions in Myrzakulov f(R,T) Gravity. arXiv 2025, arXiv:2501.18524. [Google Scholar]
- Lymperis, A.; Nugmanova, G.; Sergazina, A. Correspondence Between Myrzakulov F(R,Q) Gravity and Tsallis Cosmology. arXiv 2025, arXiv:2502.04462. [Google Scholar]
- Eleonora, D.V.; Jackson, L.S.; Riess, A.; Pollo, A.; Poulin, V.; Gómez-Valent, A.; Weltman, A.; Palmese, A.; Huang, C.D.; van de Bruck, C.; et al. The Cosmo Verse White Paper: Addressing Observational Tensions in Cosmology with Systematics and Fundamental Physics. arXiv 2025, arXiv:2504.01669. [Google Scholar] [CrossRef]
- Aghanim, N. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Breuval, L.; Riess, A.G.; Casertano, S.; Yuan, W.; Macri, L.M.; Romaniello, M.; Murakami, Y.S.; Scolnic, D.; Anand, G.S.; Soszyński, I. Small Magellanic Cloud Cepheids Observed with the Hubble Space Telescope Provide a New Anchor for the SH0ES Distance Ladder. Astrophys. J. 2024, 973, 30. [Google Scholar] [CrossRef]
- Abdalla, E. Cosmology Intertwined II: The Hubble Constant Tension. JHEAp 2022, 34, 49–98. [Google Scholar]
- Valentino, E.D.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—A review of solutions. Class. Quant. Grav. 2021, 38, 153001. [Google Scholar] [CrossRef]
- Hu, J.P.; Wang, F.Y. Hubble Tension: The Evidence of New Physics. Universe 2023, 9, 94. [Google Scholar] [CrossRef]
- Hu, B.; Raveri, M. Can modified gravity models reconcile the tension between the CMB anisotropy and lensing maps in Planck-like observations? Phys. Rev. D 2015, 91, 123515. [Google Scholar] [CrossRef]
- Khosravi, N.; Baghram, S.; Afshordi, N.; Altamirano, N. H0 tension as a hint for a transition in gravitational theory. Phys. Rev. D 2019, 99, 103526. [Google Scholar] [CrossRef]
- Belgacem, E.; Dirian, Y.; Foffa, S.; Maggiore, M. Nonlocal gravity. Conceptual aspects and cosmological predictions. JCAP 2018, 3, 2. [Google Scholar] [CrossRef]
- El-Zant, A.; Hanafy, W.E.; Elgammal, S. H0 Tension and the Phantom Regime: A Case Study in Terms of an Infrared f(T) Gravity. Astrophys. J. 2019, 871, 210. [Google Scholar] [CrossRef]
- Basilakos, S.; Nesseris, S.; Anagnostopoulos, F.K.; Saridakis, E.N. Updated constraints on f(T) models using direct and indirect measurements of the Hubble parameter. JCAP 2018, 8, 8. [Google Scholar] [CrossRef]
- Adil, S.A.; Gangopadhyay, M.R.; Sami, M.; Sharma, M.K. Late-time acceleration due to a generic modification of gravity and the Hubble tension. Phys. Rev. D 2021, 104, 103534. [Google Scholar] [CrossRef]
- Nunes, R.C. Structure formation in f(T) gravity and a solution for H0 tension. JCAP 2018, 5, 52. [Google Scholar] [CrossRef]
- Lin, M.X.; Raveri, M.; Hu, W. Phenomenology of Modified Gravity at Recombination. Phys. Rev. D 2019, 99, 043514. [Google Scholar] [CrossRef]
- Yan, S.F.; Zhang, P.; Chen, J.W.; Zhang, X.Z.; Cai, Y.F.; Saridakis, E.N. Interpreting cosmological tensions from the effective field theory of torsional gravity. Phys. Rev. D 2020, 101, 121301. [Google Scholar] [CrossRef]
- D’Agostino, R.; Nunes, R.C. Measurements of H0 in modified gravity theories: The role of lensed quasars in the late-time Universe. Phys. Rev. D 2020, 101, 103505. [Google Scholar] [CrossRef]
- Capozziello, S.; Benetti, M.; Spallicci, A.D.A.M. Addressing the cosmological H0 tension by the Heisenberg uncertainty. Found. Phys. 2020, 50, 893–899. [Google Scholar] [CrossRef]
- Escamilla-Rivera, C.; Said, J.L. Cosmological viable models in f(T,B) theory as solutions to the H0 tension. Class. Quant. Grav. 2020, 37, 165002. [Google Scholar] [CrossRef]
- Valentino, E.D.; Melchiorri, A.; Mena, O.; Vagnozzi, S. Nonminimal dark sector physics and cosmological tensions. Phys. Rev. D 2020, 101, 063502. [Google Scholar] [CrossRef]
- Vagnozzi, S. New physics in light of the H0 tension: An alternative view. Phys. Rev. D 2020, 102, 023518. [Google Scholar] [CrossRef]
- da Silva, W.J.C.; Silva, R. Cosmological Perturbations in the Tsallis Holographic Dark Energy Scenarios. Eur. Phys. J. Plus 2021, 136, 543. [Google Scholar] [CrossRef]
- Anagnostopoulos, F.K.; Basilakos, S.; Saridakis, E.N. Bayesian analysis of f(T) gravity using fσ8 data. Phys. Rev. D 2019, 100, 083517. [Google Scholar] [CrossRef]
- Cai, Y.F.; Khurshudyan, M.; Saridakis, E.N. Model-independent reconstruction of f(T) gravity from Gaussian Processes. Astrophys. J. 2020, 888, 62. [Google Scholar] [CrossRef]
- Braglia, M.; Ballardini, M.; Finelli, F.; Koyama, K. Early modified gravity in light of the H0 tension and LSS data. Phys. Rev. D 2021, 103, 043528. [Google Scholar] [CrossRef]
- Adi, T.; Kovetz, E.D. Can conformally coupled modified gravity solve the Hubble tension? Phys. Rev. D 2021, 103, 023530. [Google Scholar] [CrossRef]
- WBarker, E.V.; Lasenby, A.N.; Hobson, M.P.; Handley, W.J. Systematic study of background cosmology in unitary Poincaré gauge theories with application to emergent dark radiation and H0 tension. Phys. Rev. D 2020, 102, 024048. [Google Scholar] [CrossRef]
- Wang, D.; Mota, D. Can f(T) gravity resolve the H0 tension? Phys. Rev. D 2020, 102, 063530. [Google Scholar] [CrossRef]
- Ballardini, M.; Braglia, M.; Finelli, F.; Paoletti, D.; Starobinsky, A.A.; Umiltà, C. Scalar-tensor theories of gravity, neutrino physics, and the H0 tension. JCAP 2020, 10, 44. [Google Scholar] [CrossRef]
- Cedeno, F.X.L.; Nucamendi, U. Revisiting cosmological diffusion models in Unimodular Gravity and the H0 tension. Phys. Dark Univ. 2021, 32, 100807. [Google Scholar]
- Odintsov, S.D.; Gómez, D.S.; Sharov, G.S. Analyzing the H0 tension in F(R) gravity models. Nucl. Phys. B 2021, 966, 115377. [Google Scholar] [CrossRef]
- Sivaram, C.; Arun, K.; Rebecca, L. The Hubble tension: Change in dark energy or a case for modified gravity? Indian J. Phys. 2022, 96, 1289–1292. [Google Scholar] [CrossRef]
- Mandal, S.; Sokoliuk, O.; Mishra, S.S.; Sahoo, P.K. H0 tension in torsion-based modified gravity. Nucl. Phys. B 2023, 993, 116285. [Google Scholar] [CrossRef]
- Escamilla, L.A.; Fiorucci, D.; Montani, G.; Valentino, E.D. Exploring the Hubble tension with a late time Modified Gravity scenario. Phys. Dark Univ. 2024, 46, 101652. [Google Scholar] [CrossRef]
- Tzerefos, C.; Saridakis, E. Alleviating the σ8 tension via Soft Cosmology and Modified Gravity. PoS 2023, CORFU2022, 210. [Google Scholar]
- Shimon, M. Possible resolution of the Hubble tension with Weyl invariant gravity. JCAP 2022, 4, 48. [Google Scholar] [CrossRef]
- Wang, D.; Mota, D. 4D Gauss–Bonnet gravity: Cosmological constraints, H0 tension and large scale structure. Phys. Dark Univ. 2021, 32, 100813. [Google Scholar] [CrossRef]
- Lazarides, G.; Maji, R.; Shafi, Q. Cosmic strings, inflation, and gravity waves. Phys. Rev. D 2021, 104, 095004. [Google Scholar] [CrossRef]
- de Araujo, J.C.N.; Felice, A.D.; Kumar, S.; Nunes, R.C. Minimal theory of massive gravity in the light of CMB data and the S8 tension. Phys. Rev. D 2021, 104, 104057. [Google Scholar] [CrossRef]
- Nilsson, N.A.; Park, M.I. Tests of standard cosmology in Hořava gravity, Bayesian evidence for a closed universe, and the Hubble tension. Eur. Phys. J. C 2022, 82, 873. [Google Scholar] [CrossRef]
- Petronikolou, M.; Basilakos, S.; Saridakis, E.N. Alleviating H0 tension in Horndeski gravity. Phys. Rev. D 2022, 106, 124051. [Google Scholar] [CrossRef]
- Banik, I.; Zhao, H. From Galactic Bars to the Hubble Tension: Weighing Up the Astrophysical Evidence for Milgromian Gravity. Symmetry 2022, 14, 1331. [Google Scholar] [CrossRef]
- Ren, X.; Yan, S.F.; Zhao, Y.; Cai, Y.F.; Saridakis, E.N. Gaussian processes and effective field theory of f(T) gravity under the H0 tension. Astrophys. J. 2022, 932, 131. [Google Scholar] [CrossRef]
- Rasouli, S.M.M.; Sakellariadou, M.; Moniz, P.V. Geodesic deviation in Sáez–Ballester theory. Phys. Dark Univ. 2022, 37, 101112. [Google Scholar] [CrossRef]
- Doroud, N.; Rasouli, S.M.M.; Jalalzadeh, S. A class of cosmological solutions in induced matter theory with conformally flat bulk space. Gen. Rel. Grav. 2009, 41, 2637–2656. [Google Scholar] [CrossRef]
- Aljaf, M.; Elizalde, E.; Khurshudyan, M.; Myrzakulov, K.; Zhadyranova, A. Solving the H0 tension in f(T) gravity through Bayesian machine learning. Eur. Phys. J. C 2022, 82, 1130. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Integral F(R) gravity and saddle point condition as a remedy for the H0-tension. Nucl. Phys. B 2022, 980, 115850. [Google Scholar] [CrossRef]
- Capozziello, S.; Lambiase, G. PeV IceCube signals and H0 tension in the framework of Non-Local Gravity. Eur. Phys. J. Plus 2022, 137, 735. [Google Scholar] [CrossRef]
- Gangopadhyay, M.R.; Pacif, S.K.J.; Sami, M.; Sharma, M.K. Generic Modification of Gravity, Late Time Acceleration and Hubble Tension. Universe 2023, 9, 83. [Google Scholar] [CrossRef]
- Schiavone, T.; Montani, G.; Bombacigno, F. f(R) gravity in the Jordan frame as a paradigm for the Hubble tension. Mon. Not. R. Astron. Soc. 2023, 522, L72–L77. [Google Scholar] [CrossRef]
- Tiwari, Y.; Ghosh, B.; Jain, R.K. Towards a possible solution to the Hubble tension with Horndeski gravity. Eur. Phys. J. C 2024, 84, 220. [Google Scholar] [CrossRef]
- Yang, K.; Gu, B.M.; Zhong, Y. Braneworld sum rules and positive tension branes in a massive gravity. Phys. Lett. B 2024, 850, 138545. [Google Scholar] [CrossRef]
- Montani, G.; Angelis, M.D.; Bombacigno, F.; Carlevaro, N. Metric f(R) gravity with dynamical dark energy as a scenario for the Hubble tension. Mon. Not. R. Astron. Soc. 2023, 527, L156–L161. [Google Scholar] [CrossRef]
- B, A.; Suresh, P.K. A possible solution to the Hubble tension from quantum gravity. Class. Quant. Grav. 2024, 41, 035002. [Google Scholar] [CrossRef]
- Silva, C. Quantum Complexity and the Hubble Tension: A Quantum Gravity Portrayal for the Large Scale Structure of the Cosmos. arXiv 2023, arXiv:2312.05267. [Google Scholar]
- Yarahmadi, M.; Salehi, A. Generalized Rastall Gravity coupled with neutrinos could solve the Hubble Tension. arXiv 2024, arXiv:2401.08871. [Google Scholar] [CrossRef]
- Desmond, H.; Hees, A.; Famaey, B. On the tension between the radial acceleration relation and Solar system quadrupole in modified gravity MOND. Mon. Not. R. Astron. Soc. 2024, 530, 1781–1795. [Google Scholar] [CrossRef]
- Romano, A.E. H0 Tension as a Manifestation of the Time Evolution of Matter-Gravity Coupling. arXiv 2024, arXiv:2402.11947. [Google Scholar]
- Bisabr, Y. Hubble Tension in Power-Law f(R) Gravity and Generalized Brans-Dicke Theory. arXiv 2024, arXiv:2403.13303. [Google Scholar] [CrossRef]
- Varela, M.B.; Bertolami, O. Hubble tension in a nonminimally coupled curvature-matter gravity model. JCAP 2024, 6, 25. [Google Scholar] [CrossRef]
- Duchaniya, L.K.; Mishra, B. The H_0 Tension and Late Time Phenomena in f(T,T) Gravity Framework: Role of H0 Priors. arXiv 2024, arXiv:2411.11923. [Google Scholar]
- Bisabr, Y. Brans-Dicke Theory and Hubble Tension: A Model for Early Dark Energy. arXiv 2024, arXiv:2409.08548. [Google Scholar] [CrossRef]
- Chaudhary, H.; Debnath, U.; Rahaman, F.; Mustafa, G.; Atamurotov, F. Early and late observational tension: Dark energy parametrizations in Horava-Lifshitz gravity via baryon acoustic oscillations. Phys. Scripta 2024, 99, 105037. [Google Scholar] [CrossRef]
- Banerjee, S.; Paul, A. Analysing Hubble Tension and Gravitational Waves for f(Q,T) Gravity Theories. arXiv 2024, arXiv:2408.14878. [Google Scholar]
- Montani, G.; Carlevaro, N.; Angelis, M.D. Modified Gravity in the Presence of Matter Creation: Scenario for the Late Universe. Entropy 2024, 26, 662. [Google Scholar] [CrossRef]
- Rebecca, L.; Sivaram, C.; Sebastian, D.; Arun, K. Can Hubble tension be eased by invoking a finite range for gravity? Mod. Phys. Lett. A 2024, 39, 2450073. [Google Scholar] [CrossRef]
- Haslbauer, M.; Banik, I.; Kroupa, P. The KBC void and Hubble tension contradict ΛCDM on a Gpc scale—Milgromian dynamics as a possible solution. Mon. Not. R. Astron. Soc. 2020, 499, 2845–2883. [Google Scholar] [CrossRef]
- Mazurenko, S.; Banik, I.; Kroupa, P. The redshift dependence of the inferred H0 in a local void solution to the Hubble tension. Mon. Not. R. Astron. Soc. 2025, 536, 3232–3241. [Google Scholar] [CrossRef]
- Banik, I.; Kalaitzidis, V. Testing the Local Void Hypothesis Using Baryon Acoustic Oscillation Measurements Over the Last Twenty Years. Mon. Not. R. Astron. Soc. 2025, 540, 545–561. [Google Scholar] [CrossRef]
- Hu, J.P.; Jia, X.D.; Hu, J.; Wang, F.Y. Hints of New Physics for the Hubble Tension: Violation of Cosmological Principle. Astrophys. J. Lett. 2024, 975, L36. [Google Scholar] [CrossRef]
- Yang, R.J. Conformal transformation in f(T) theories. EPL 2011, 93, 60001. [Google Scholar] [CrossRef]
- Gakis, V.; Kršxsxák, M.; Said, J.L.; Saridakis, E.N. Conformal gravity and transformations in the symmetric teleparallel framework. Phys. Rev. D 2020, 101, 064024. [Google Scholar] [CrossRef]
- Wright, M. Conformal transformations in modified teleparallel theories of gravity revisited. Phys. Rev. D 2016, 93, 103002. [Google Scholar] [CrossRef]
- Heisenberg, L.; Villarrubia-Rojo, H.; Zosso, J. Simultaneously solving the H0 and σ8 tensions with late dark energy. Phys. Dark Univ. 2023, 39, 101163. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Quantum de Sitter cosmology and phantom matter. Phys. Lett. B 2003, 562, 147–152. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Effective equation of state and energy conditions in phantom/tachyon inflationary cosmology perturbed by quantum effects. Phys. Lett. B 2003, 571, 1–10. [Google Scholar] [CrossRef]
- Vagnozzi, S. Seven Hints That Early-Time New Physics Alone Is Not Sufficient to Solve the Hubble Tension. Universe 2023, 9, 393. [Google Scholar] [CrossRef]
- Abdul-Karim, M.; Aguilar, J.; Ahlen, S.; Alam, S.; Allen, L.; Prieto, C.A.; Alves, O.; Anand, A.; Andrade, U.; Armengaud, E.; et al. DESI DR2 Results II: Measurements of Baryon Acoustic Oscillations and Cosmological Constraints. arXiv 2025, arXiv:2503.14738. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aljohani, M.A.; Mahmoud, E.E.; Yerzhanov, K.; Sergazina, A. Toward the Alleviation of the H0 Tension in Myrzakulov f(R,T) Gravity. Universe 2025, 11, 252. https://doi.org/10.3390/universe11080252
Aljohani MA, Mahmoud EE, Yerzhanov K, Sergazina A. Toward the Alleviation of the H0 Tension in Myrzakulov f(R,T) Gravity. Universe. 2025; 11(8):252. https://doi.org/10.3390/universe11080252
Chicago/Turabian StyleAljohani, Mashael A., Emad E. Mahmoud, Koblandy Yerzhanov, and Almira Sergazina. 2025. "Toward the Alleviation of the H0 Tension in Myrzakulov f(R,T) Gravity" Universe 11, no. 8: 252. https://doi.org/10.3390/universe11080252
APA StyleAljohani, M. A., Mahmoud, E. E., Yerzhanov, K., & Sergazina, A. (2025). Toward the Alleviation of the H0 Tension in Myrzakulov f(R,T) Gravity. Universe, 11(8), 252. https://doi.org/10.3390/universe11080252






