Evolving Wormholes in a Cosmological Background

Abstract

Wormholes are non-trivial topological structures that arise as exact solutions to Einstein’s field equations, theoretically connecting distinct regions of spacetime via a throat-like geometry. While static traversable wormholes necessarily require exotic matter that violates the classical energy conditions, subsequent studies have sought to minimize such violations by introducing time-dependent geometries embedded within cosmological backgrounds. This review provides a comprehensive survey of evolving wormhole solutions, emphasizing their formulation within both general relativity and alternative theories of gravity. We explore key developments in the construction of non-static wormhole spacetimes, including those conformally related to static solutions, as well as dynamically evolving geometries influenced by scalar fields. Particular attention is given to the wormholes embedded into Friedmann–Lemaître–Robertson–Walker (FLRW) universes and de Sitter backgrounds, where the interplay between the cosmic expansion and wormhole dynamics is analyzed. We also examine the role of modified gravity theories, especially in hybrid metric–Palatini gravity, which enable the realization of traversable wormholes supported by effective stress–energy tensors that do not violate the null or weak energy conditions. By systematically analyzing a wide range of time-dependent wormhole solutions, this review identifies the specific geometric and physical conditions under which wormholes can evolve consistently with null and weak energy conditions. These findings clarify how such configurations can be naturally integrated into cosmological models governed by general relativity or modified gravity, thereby contributing to a deeper theoretical understanding of localized spacetime structures in an expanding universe.

1. Introduction

Wormholes are hypothetical non-trivial topological structures that arise as exact solutions to Einstein’s field equations, characterized by two distinct regions of spacetime connected through a throat-like geometry. These structures have been studied within the framework of general relativity and alternative theories of gravity due to their implications for the causal structure of spacetime and energy condition violations. A foundational contribution to modern theoretical research on wormholes was made by Morris and Thorne [1], who formulated the concept of a static, spherically symmetric traversable wormhole. Their goal was to explore whether the Einstein field equations admitted geometries that permitted passage through the wormhole without encountering horizons or singularities. They demonstrated that keeping the wormhole throat open in a static configuration necessarily requires the violation of the null energy condition (NEC) by the matter threading the wormhole. More specifically, the stress–energy tensor $T_{\mu \nu }$ associated with these wormhole geometries must satisfy $T_{\mu \nu }{k}^{\mu }{k}^{\nu }<0$ for some null vector $k^{\mu }$, implying the presence of “exotic matter”. This conclusion sparked extensive research into the nature and theoretical viability of such exotic sources, such as the fundamental role of energy conditions, which are important in the classical singularity theorems and the causal structure of general relativity [2,3], highlighting the significance of their violation in the context of wormholes.

Subsequent investigations increasingly focused on reducing the dependence on exotic matter. In particular, one line of research has explored the possibility of dynamical or time-dependent spacetime geometries, wherein violations of energy conditions, such as the weak energy condition (WEC), may be restricted to localized regions or occur transiently. The development of evolving or non-static wormhole solutions has therefore emerged as a significant and productive avenue of the theoretical research [4,5,6]. Thus, motivated both by the requirements of embedding wormholes into cosmological backgrounds and by the hypothesis that time evolution could improve or confine the extent of energy condition violations, researchers have constructed a variety of dynamical wormhole models. Among the earliest contributions in this direction is the work of Kar [4], who investigated spacetimes that are conformally related to the static Morris–Thorne wormhole metric. In this framework, the introduction of a time-dependent conformal factor allows for the construction of non-static wormhole geometries that evolve over time while preserving the essential topological features of their static counterparts. It was shown that such evolving wormhole solutions can exist over finite, but potentially arbitrarily large, intervals of cosmic time. Under specific choices of the conformal factor and associated metric functions, the resulting stress–energy tensor can be arranged to satisfy the WEC throughout the duration of the wormhole’s existence. This represents a significant theoretical development, as static wormhole configurations invariably require stress–energy sources that violate at least the WEC.

Expanding upon this framework, Kar and Sahdev [5] developed a more general formalism for constructing spherically symmetric, time-dependent Lorentzian wormholes. Their analysis involved metrics characterized by time-dependent scale factors, allowing for the examination of evolving geometries under various cosmological expansion scenarios. The authors explored several specific cases, including exponential and power-law scale factors, as well as metrics incorporating additional compact extra dimensions. In scenarios involving exponentially decaying compact dimensions, analogous to those encountered in Kaluza–Klein-type models, distinct dynamical behaviors of the wormhole throat were observed, highlighting how the extra-dimensional dynamics can significantly influence the wormhole’s evolution and its compliance with energy conditions. Anchordoqui et al. [6] extended the study of dynamic wormhole geometries by constructing solutions in the context of an expanding universe driven by scalar fields. Their analysis demonstrated that scalar field configurations with minimal coupling to gravity can support cosmologically evolving wormhole structures, wherein the spacetime exhibits non-trivial temporal behavior. These results highlight the viability of scalar fields as sources of stress–energy capable of sustaining transient or evolving wormholes in a cosmological setting without the need for exotic matter violating energy conditions at all times.

The interplay between the local wormhole geometry and large-scale cosmological evolution was explored further by Roman [7], who examined Lorentzian wormholes embedded into a de Sitter spacetime. In this framework, driven by a positive cosmological constant, Roman presented a novel classical metric describing a wormhole whose geometry inflates in the de Sitter background. The study revealed that both the proper radial length and the throat radius of the wormhole experience exponential growth due to inflation. This mechanism suggests that early-universe inflation could potentially act as a natural enlargement process for Planck-scale wormholes, thereby rendering them macroscopic and possibly traversable at later times. In a related study, Kim [8] investigated wormhole solutions embedded within Friedmann–Lemaître–Robertson–Walker (FLRW) cosmologies, considering the full backreaction of the cosmological expansion on the wormhole geometry. The analysis demonstrated that the global scale factor dynamics significantly affect the wormhole’s throat properties and its stability conditions. Depending on the behavior of the cosmic expansion, the wormhole geometry may exhibit varying degrees of stability or transient behavior, suggesting non-trivial coupling between the local topological features and the universe’s large-scale structure. Much work has been conducted on time-dependent wormholes, and rather than summarizing the literature here, we refer the reader to Refs. [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31].

Moreover, alternative theories of gravity, such as $f\left(R\right)$ gravity [32,33,34,35,36,37,38,39,40,41,42,43]; hybrid metric–Palatini gravity [44,45]; teleparralel gravity [46,47]; linear curvature–matter couplings [48,49]; $f(R,T)$ gravity, where T is the trace of the energy momentum tensor [50,51,52,53,54,55,56,57,58]; energy-momentum squared gravity [59,60]; $f(R,L_m)$ gravity [61,62]; non-metricity $f\left(Q\right)$ gravity [63,64]; $f\left(\mathcal{T}\right)$ gravity, where $\mathcal{T}$ is the torsion scalar [65,66]; higher dimensions [67,68]; Finsler–Randers geometry [69]; Einstein–Cartan gravity [70]; modified Gauss–Bonnet gravity [71,72,73]; and conformal Weyl gravity [74,75], amongst many other approaches to gravity, have provided frameworks where the effective stress–energy tensor includes geometric contributions that can mimic the exotic matter’s behavior. These extensions allow for the realization of wormhole solutions without explicit violations of the classical energy conditions when interpreted in terms of effective fluid models. A particularly promising framework is hybrid metric–Palatini gravity [76,77], which combines the features of both metric and Palatini formalisms. This theory naturally introduces extra scalar degrees of freedom that can mimic the effects of exotic matter [78]. Several authors have explored wormhole [79,80], black hole [81,82], and cosmological [83,84] solutions in this context. These studies demonstrate that hybrid gravity can support traversable wormholes without explicit energy condition violations.

Hybrid metric–Palatini gravity exhibits a broad range of astrophysical applications. In particular, potential observational signatures of this theory at the Galactic Center have been investigated. In Ref. [85], the authors analyzed the orbital precession of the S2 star around the supermassive compact object at the Milky Way’s center, finding excellent agreement between simulated orbits in hybrid gravity and astronomical observations. This work was extended in Ref. [86], where the parameters of the hybrid metric–Palatini model were estimated using the Schwarzschild precession of S2, S38, and S55. Various values for the bulk mass density of extended matter were considered, with the results again being consistent with observational data. Ref. [87] further constrained hybrid gravity using the fundamental plane of elliptical galaxies in the weak-field regime. This study showed that hybrid gravity can reproduce the velocity dispersion and structural properties of elliptical galaxies without invoking dark matter. Additionally, alternative modifications to General GR have been proposed to explain specific astrophysical phenomena. For instance, a Yukawa-type modification of the Newtonian potential in the weak-field limit was investigated in Ref. [88]. Using the Parametrized Post-Newtonian (PPN) formalism, the authors simulated S-star orbits at the Galactic Center under both GR and Yukawa gravity, concluding that the latter offers a viable framework for constraining modified gravity parameters and testing alternative gravitational theories.

In Ref. [89], the authors investigated the dynamics of time-dependent traversable wormhole configurations embedded within a Friedmann–Lemaître–Robertson–Walker (FLRW) cosmological background, in the framework of the scalar–tensor representation of hybrid metric–Palatini gravity. Within this theoretical context, the authors derived the energy-momentum tensor components corresponding to the matter threading the wormhole geometry, expressing them in terms of the scalar field, the cosmological scale factor, the wormhole shape function, and other background cosmological quantities. To obtain explicit solutions, they considered a barotropic equation of the state for the background matter, characterized by a linear relationship between pressure and energy density. Under this assumption, this study demonstrates the existence of specific classes of wormhole solutions for which the matter content satisfies both the null energy condition (NEC) and the weak energy condition (WEC) at all times during the cosmological evolution.

In this work, we investigate evolving wormholes within cosmological backgrounds by considering both general relativity and extended gravity theories, with a particular focus on hybrid metric–Palatini gravity. Our aim is to determine the conditions under which wormholes can remain traversable and physically viable across cosmic epochs. By embedding dynamical wormhole metrics into FLRW backgrounds and analyzing their evolution under realistic matter sources and modified gravitational couplings, we explore new pathways for integrating localized topological structures into a consistent cosmological framework. Remarkably, we will see that several resulting spacetime geometries satisfy the NEC and WEC throughout the entire temporal evolution. These results represent important progress in identifying physically viable wormhole models that are compatible with generalized theories of gravity and are supported by non-exotic matter sources.

This paper is organised in the following manner: In Section 2, we present the spacetime metric and the gravitational field equations and analyze several specific solutions, including an evolving wormhole in a flat FRW universe. In Section 3, we present a wormhole in a time-dependent inflationary background and analyze the properties of the solutions and the NEC violation. In Section 4, we analyze evolving cosmological wormholes in hybrid metric–Palatini gravity. Finally, in Section 5, we summarize and discuss our resutls and conclude.

2. Evolving Wormholes in a Cosmological Background

2.1. The Spacetime Metric and the Stress–Energy Tensor

Consider the metric element of a wormhole in a cosmological background given by

$$d{s}^2={\Omega }^2\left(t\right)\left[-e^{2\Phi \left(r\right)}d{t}^2+{\displaystyle \frac{d{r}^2}{1-k{r}^2-\frac{b\left(r\right)}{r}}}+r^2\left(d{\theta }^2+{\sin }^2\theta d{\varphi }^2\right)\right]$$

(1)

where ${\Omega }^2\left(t\right)$ is the conformal factor, which is finite and positive definite throughout the domain of t. It is also possible to write the metric (1) using “physical time” instead of “conformal time”, by replacing t with $\tau =\int \Omega \left(t\right)dt$ and therefore $\Omega \left(t\right)$ with $R\left(\tau \right)$, where the latter is the functional form of the metric in the $\tau$ coordinate [4,5]. We shall use ‘conformal time’ in the present analysis, reserving $\tau$ for the specific cosmological models considered further ahead. When the form function and the redshift function vanish, $b\left(r\right)\to 0$ and $\Phi \left(r\right)\to 0$, respectively, the metric (1) becomes the FRW metric. As $\Omega \left(t\right)\to \mathrm{const}$ and $k\to 0$, it approaches the static wormhole metric.

To analyze the stress–energy tensor of the wormhole described by Equation (1), consider the orthonormal basis vectors defined by

$$\begin{array}{ccc}\hfill {\mathbf{e}}_{\widehat{t}}& =& {\Omega }^{-1}{e}^{-\Phi }{\mathbf{e}}_t,\hfill \\ \hfill {\mathbf{e}}_{\widehat{r}}& =& {\Omega }^{-1}{(1-b/r)}^{1/2}{\mathbf{e}}_r,\hfill \\ \hfill {\mathbf{e}}_{\widehat{\theta }}& =& {\Omega }^{-1}{r}^{-1}{\mathbf{e}}_{\theta },\hfill \\ \hfill {\mathbf{e}}_{\widehat{\varphi }}& =& {\Omega }^{-1}{\left(r\sin \theta \right)}^{-1}{\mathbf{e}}_{\varphi }.\hfill \end{array}$$

(2)

This basis represents the proper reference frame of a set of observers who always remain at rest at constant $r,\theta ,\varphi$. The Einstein field equation will be written as $G_{\widehat{\mu }\widehat{\nu }}=R_{\widehat{\mu }\widehat{\nu }}-{\displaystyle \frac{1}{2}}{g}_{\widehat{\mu }\widehat{\nu }}R=8\pi T_{\widehat{\mu }\widehat{\nu }},$ so that any cosmological constant terms will be incorporated as part of the stress–energy tensor $T_{\widehat{\mu }\widehat{\nu }}$. The components of the stress–energy tensor $T_{\widehat{\mu }\widehat{\nu }}$ are given by

$$T_{\widehat{t}\widehat{t}}=\rho (r,t),T_{\widehat{r}\widehat{r}}=-\tau (r,t),T_{\widehat{t}\widehat{r}}=-f(r,t),T_{\widehat{\varphi }\widehat{\varphi }}=T_{\widehat{\theta }\widehat{\theta }}=p(r,t),$$

(3)

with

$$\begin{array}{ccc}\hfill \rho (r,t)& =& {\displaystyle \frac{1}{8\pi }}{\displaystyle \frac{1}{{\Omega }^2}}\left[3e^{-2\Phi }{\left({\displaystyle \frac{\dot{\Omega }}{\Omega }}\right)}^2+\left(3k+{\displaystyle \frac{b^{\prime }}{r^2}}\right)\right],\hfill \end{array}$$

(4)

$$\begin{array}{ccc}\hfill \tau (r,t)& =& -{\displaystyle \frac{1}{8\pi }}{\displaystyle \frac{1}{{\Omega }^2}}\left\{e^{-2\Phi \left(r\right)}\left[{\left({\displaystyle \frac{\dot{\Omega }}{\Omega }}\right)}^2-2{\displaystyle \frac{\ddot{\Omega }}{\Omega }}\right]-\left[k+{\displaystyle \frac{b}{r^3}}-2{\displaystyle \frac{{\Phi }^{\prime }}{r}}\left(1-k{r}^2-{\displaystyle \frac{b}{r}}\right)\right]\right\},\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill f(r,t)& =& -{\displaystyle \frac{1}{8\pi }}\left[2{\displaystyle \frac{\dot{\Omega }}{{\Omega }^3}}{e}^{-\Phi }{\Phi }^{\prime }{\left(1-k{r}^2-{\displaystyle \frac{b}{r}}\right)}^{1/2}\right],\hfill \end{array}$$

(6)

$$\begin{array}{l}p(r,t)={\displaystyle \frac{1}{8\pi }}{\displaystyle \frac{1}{{\Omega }^2}}\{e^{-2\Phi \left(r\right)}\left[{\left({\displaystyle \frac{\dot{\Omega }}{\Omega }}\right)}^2-2{\displaystyle \frac{\ddot{\Omega }}{\Omega }}\right]+\left(1-k{r}^2-{\displaystyle \frac{b}{r}}\right)\\ \times \left[{\Phi }^{\prime \prime }+{(\Phi \prime )}^2-{\displaystyle \frac{2k{r}^3+b^{\prime }r-b}{2r(r-k{r}^3-b)}}{\Phi }^{\prime }-{\displaystyle \frac{2k{r}^3+b^{\prime }r-b}{2r^2(r-k{r}^3-b)}}+{\displaystyle \frac{{\Phi }^{\prime }}{r}}\right]\}.\hfill \end{array}$$

(7)

The overdot denotes a derivative with respect to t and the prime a derivative with respect to r. The physical interpretations of $\rho (r,t),\tau (r,t),f(r,t)$, and $p(r,t)$ are the following: the energy density, the radial tension per unit area, the energy flux in the (outward) radial direction, and lateral pressures as measured by observers stationed at constant $r,\theta ,\varphi$, respectively. The stress–energy tensor has a non-diagonal component due to the time dependence of $\Omega \left(t\right)$ and/or the dependence of the redshift function on the radial coordinate. The stress–energy tensor of an imperfect fluid was analyzed in [6].

To analyze the evolving wormhole, one chooses $\Phi \left(r\right)$ and $b\left(r\right)$ to give a reasonable wormhole at $t=0$, which is assumed to be the onset of the evolution. The radial proper length through the wormhole between any two points A and B at any $t=\mathrm{const}$ is given by

$$l\left(t\right)=\pm \Omega \left(t\right){\int }_{r_A}^{r_B}{\displaystyle \frac{dr}{{(1-k{r}^2-b/r)}^{1/2}}},$$

(8)

which is just $\Omega \left(t\right)$ times the initial radial proper separation.

To see that the “wormhole” form of the metric is preserved with time, consider an embedding of a $t=\mathrm{const}$ and $\theta =\pi /2$ slice (without a significant loss of generality) of the spacetime given by Equation (1) into a flat three-dimensional Euclidean space with the metric

$$d{s}^2=d{\overline{z}}^2+d{\overline{r}}^2+{\overline{r}}^2{d\varphi }^2.$$

(9)

The metric of the wormhole slice is

$$d{s}^2={\displaystyle \frac{{\Omega }^2\left(t\right)d{r}^2}{(1-k{r}^2-b\left(r\right)/r)}}+{\Omega }^2\left(t\right)r^{2}d{\varphi }^2.$$

(10)

Comparing the coefficients of ${d\varphi }^2$, one has

$$\begin{array}{ccc}\hfill \overline{r}& =& \Omega \left(t\right)r{|}_{t=\mathrm{const}},\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill {d\overline{r}}^2& =& \Omega {\left(t\right)}^2{dr}^2{|}_{t=\mathrm{const}}.\hfill \end{array}$$

(12)

Note that it is important to keep in mind, in particular when considering derivatives, that Equations (11) and (12) do not represent a “coordinate transformation” but rather a “rescaling” of the r coordinate on each $t=\mathrm{constant}$ slice.

With respect to the $\overline{z},\overline{r},\varphi$ coordinates, the “wormhole” form of the metric will be preserved if the metric on the embedded slice has the form

$$d{s}^2={\displaystyle \frac{d{\overline{r}}^2}{[1-\overline{b}\left(\overline{r}\right)/\overline{r}]}}+{\overline{r}}^2{d\varphi }^2,$$

(13)

where $\overline{b}\left(\overline{r}\right)$ has a minimum at some $\overline{b}\left({\overline{r}}_0\right)={\overline{r}}_0$. Equation (10) can be rewritten in the form of Equation (13) by using Equations (11) and (12) and

$$\overline{b}\left(\overline{r}\right)=\Omega \left(t\right)[k{r}^3+b\left(r\right)].$$

(14)

The evolving wormhole will have the same overall size and shape relative to the $\overline{z},\overline{r},\varphi$ coordinate system as the initial wormhole had relative to the initial $z,r,\varphi$ embedding space coordinate system. This due to the fact that the embedding space corresponds to $z,r$ coordinates which “scale” with time (each embedding space corresponds to a particular value of $t=\mathrm{constant}$). Following the embedding procedure outlined in [1], using Equations (9) and (13), one deduces that

$${\displaystyle \frac{d\overline{z}}{d\overline{r}}}=\pm {\left({\displaystyle \frac{\overline{r}}{\overline{b}\left(\overline{r}\right)}}-1\right)}^{-1/2}={\displaystyle \frac{dz}{dr}}.$$

(15)

Equation (15) implies

$$\overline{z}\left(\overline{r}\right)=\pm \int {\displaystyle \frac{d\overline{r}}{{(\overline{r}/\overline{b}\left(\overline{r}\right)-1)}^{1/2}}}=\pm \Omega \left(t\right)\int {\left({\displaystyle \frac{r-k{r}^3-b}{b+k{r}^3}}\right)}^{-1/2}dr=\pm \Omega \left(t\right)z\left(r\right).$$

(16)

Therefore, we see that the relation between the embedding space at any time t and the initial embedding space at $t=0$ is, from Equations (12) and (16),

$$d{s}^2=d{\overline{z}}^2+d{\overline{r}}^2+{\overline{r}}^2{d\varphi }^2={\Omega }^2\left(t\right)[d{z}^2+d{r}^2+r^2{d\varphi }^2].$$

(17)

Relative to the $\overline{z},\overline{r},\varphi$ coordinate system, the wormhole will always remain the same size, as the scaling of the embedding space compensates for the evolution of the wormhole. However, the wormhole will change size relative to the initial $t=0$ embedding space.

Writing the analog of the “flaring-out condition”for the evolving wormhole, we have

$${\displaystyle \frac{d^2\overline{r}\left(\overline{z}\right)}{d{\overline{z}}^2}}>0,$$

(18)

at or near the throat. From Equations (11), (12), (14), and (15), it follows that

$${\displaystyle \frac{d^2\overline{r}\left(\overline{z}\right)}{d{\overline{z}}^2}}={\displaystyle \frac{1}{\Omega \left(t\right)}}{\displaystyle \frac{b-b^{\prime 3}}{2{(b+k{r}^3)}^2}}={\displaystyle \frac{1}{\Omega \left(t\right)}}{\displaystyle \frac{d^{2}r\left(z\right)}{d{z}^2}}>0,$$

(19)

at or near the throat. Taking into account Equations (11) and (14), and

$${\overline{b}}^{\prime }\left(\overline{r}\right)={\displaystyle \frac{d\overline{b}}{d\overline{r}}}=b^{\prime }\left(r\right)={\displaystyle \frac{db}{dr}},$$

(20)

one may rewrite the right-hand side of Equation (19) relative to the barred coordinates as

$${\displaystyle \frac{d^2\overline{r}\left(\overline{z}\right)}{d{\overline{z}}^2}}=\left({\displaystyle \frac{\overline{b}-{\overline{b}}^{\prime }\overline{r}}{2{\overline{b}}^2}}\right)>0,$$

(21)

at or near the throat. One verifies that using the barred coordinates, the flaring-out condition, Equation (21), has the same form as that for the static wormhole.

2.1.1. $\Phi =0$ Wormholes

In particular, the analysis is simplified considerably considering a null redshift function, $\Phi \left(r\right)=0$. The stress–energy tensor components reduce to

$$\begin{array}{ccc}\hfill \rho (r,t)& =& {\displaystyle \frac{1}{8\pi }}{\displaystyle \frac{1}{{\Omega }^2}}\left[3{\left({\displaystyle \frac{\dot{\Omega }}{\Omega }}\right)}^2+3k+{\displaystyle \frac{b^{\prime }}{r^2}}\right],\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill \tau (r,t)& =& {\displaystyle \frac{1}{8\pi }}{\displaystyle \frac{1}{{\Omega }^2}}\left[-{\left({\displaystyle \frac{\dot{\Omega }}{\Omega }}\right)}^2+2{\displaystyle \frac{\ddot{\Omega }}{\Omega }}+k+{\displaystyle \frac{b}{r^3}}\right],\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill f(r,t)& =& 0,\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill p(r,t)& =& {\displaystyle \frac{1}{8\pi }}{\displaystyle \frac{1}{{\Omega }^2}}\left[{\left({\displaystyle \frac{\dot{\Omega }}{\Omega }}\right)}^2-2{\displaystyle \frac{\ddot{\Omega }}{\Omega }}-{\displaystyle \frac{2k{r}^3+b^{\prime }r-b}{2r^3}}\right].\hfill \end{array}$$

(25)

Considering the energy conditions, the WEC $(T_{\mu \nu }{U}^{\mu }{U}^{\nu }\ge 0$, ∀ timelike $U^{\mu })$ reduces to the following inequalities for the case of a diagonal energy-momentum tensor [4,5]:

$$\rho \ge 0,\rho -\tau \ge 0,\rho +p\ge 0\forall (r,t).$$

(26)

Taking into account Equations (22), (23), and (25), one can write down three inequalities which have to be satisfied if the WEC is not to be violated, given by

$$\begin{array}{ccc}\hfill {\displaystyle \frac{1}{{\Omega }^2}}\left[3{\left({\displaystyle \frac{\dot{\Omega }}{\Omega }}\right)}^2+3k+{\displaystyle \frac{b^{\prime }r}{r^3}}\right]& \ge & 0,\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{2}{{\Omega }^2}}\left[-{\displaystyle \frac{\ddot{\Omega }}{\Omega }}+2{\left({\displaystyle \frac{\dot{\Omega }}{\Omega }}\right)}^2+k-{\displaystyle \frac{b-b^{\prime }r}{2r^3}}\right]& \ge & 0,\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{2}{{\Omega }^2}}\left[-{\displaystyle \frac{\ddot{\Omega }}{\Omega }}+2{\left({\displaystyle \frac{\dot{\Omega }}{\Omega }}\right)}^2\right]+k+{\displaystyle \frac{b+b^{\prime }r}{2r^3{\Omega }^2}}& \ge & 0.\hfill \end{array}$$

(29)

However, we are essentially interested in the flat universe analysis, with $k=0$, in which Equations (27)–(29) reduce to

$$\begin{array}{ccc}\hfill {\displaystyle \frac{2}{{\Omega }^2}}\left[{\displaystyle \frac{3}{2}}{\left({\displaystyle \frac{\dot{\Omega }}{\Omega }}\right)}^2+{\displaystyle \frac{b^{\prime }r}{2r^3}}\right]& \ge & 0,\hfill \end{array}$$

(30)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{2}{{\Omega }^2}}\left[-{\displaystyle \frac{\ddot{\Omega }}{\Omega }}+2{\left({\displaystyle \frac{\dot{\Omega }}{\Omega }}\right)}^2-{\displaystyle \frac{b-b^{\prime }r}{2r^3}}\right]& \ge & 0,\hfill \end{array}$$

(31)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{2}{{\Omega }^2}}\left[-{\displaystyle \frac{\ddot{\Omega }}{\Omega }}+2{\left({\displaystyle \frac{\dot{\Omega }}{\Omega }}\right)}^2\right]+{\displaystyle \frac{b+b^{\prime }r}{2r^3{\Omega }^2}}& \ge & 0.\hfill \end{array}$$

(32)

Note that the inequality (30) is satisfied if $b^{\prime }\ge 0$ irrespective of the geometry being static or dynamic. However, if it is time-dependent, then the inequality (30) is satisfied even for a case where $b^{\prime }\le 0$, where one obtains the restriction

$${\displaystyle \frac{|b^{\prime }|}{r^2}}\le 3{\left({\displaystyle \frac{\dot{\Omega }}{\Omega }}\right)}^2.$$

(33)

For every $t=\mathrm{constant}$ slice, the inequality (33) has to hold, which means

$${\displaystyle \frac{|b^{\prime }|}{r^2}}\le \min \left[3{\left({\displaystyle \frac{\dot{\Omega }}{\Omega }}\right)}^2\right],$$

(34)

where $\min$ denotes the minimum value of the function in the given time interval.

The inequality (31) can never be satisfied for the static Morris–Thorne wormhole [1]. However, for the present evolving geometry with $b^{\prime }\ge 0$, it can be obeyed by imposing

$$F\left(t\right)\ge {\displaystyle \frac{b-b^{\prime }r}{2r^3}},$$

(35)

where for simplicity, the definition

$$F\left(t\right)=\left[2{\left({\displaystyle \frac{\dot{\Omega }}{\Omega }}\right)}^2-{\displaystyle \frac{\ddot{\Omega }}{\Omega }}\right]$$

(36)

is used. The inequality (35) implies that the value of $(b-b^{\prime }r)/r^3$ for all r must be less than or equal to the minimum value of the function $F\left(t\right)$, in the domain of t. Note that the imposition $F\left(t\right)>0$ is also necessary, as $(b-b^{\prime }r)/r^3>0$, due to the flaring-out condition. Therefore, one verifies from this analysis that dynamic spherically symmetric wormhole geometries can exist without violation of the WEC. However, these WEC-satisfying evolving wormholes may only exist for finite intervals of time due to the fact that $\Omega \left(t\right)$ is finite everywhere and satisfies the condition (35).

One can also use the Raychaudhuri equation to verify the non-violation of the WEC for dynamic wormholes [5]. Recall that the Raychaudhuri equation for a congruence of null rays [3] is given by

$${\displaystyle \frac{d\widehat{\theta }}{d\lambda }}=-{\displaystyle \frac{1}{2}}{\widehat{\theta }}^2-R_{\mu \nu }{k}^{\mu }{k}^{\nu }-2{\widehat{\sigma }}^2+2{\widehat{\omega }}^2,$$

(37)

where $\widehat{\theta }$ is the expansion of the congruence of null rays; $\widehat{\sigma }$ and $\widehat{\omega }$ are the shear force and vorticity of the geodesic bundle, respectively, which are zero for this case. From the Einstein field equation, we have $R_{\mu \nu }{k}^{\mu }{k}^{\nu }=T_{\mu \nu }{k}^{\mu }{k}^{\nu }$ for all null $k^{\mu }$. So, if $T_{\mu \nu }{k}^{\mu }{k}^{\nu }\ge 0$, we have ${\widehat{\theta }}^{-1}\ge {\widehat{\theta }}_0^{-1}+{\displaystyle \frac{\lambda }{2}}$ according to (37). Thus, if $\widehat{\theta }$ is negative anywhere, it has to go to $-\infty$ at a finite value of the affine parameter, $\lambda$; i.e., the bundle must necessarily come to a focus. Note that the physical meaning of $\widehat{\theta }$ being negative is simply that the volume of a small bundle of neighbouring geodesics is decreasing, namely that the geodesics are converging or focusing, which implies that gravity is attractive. In the case of a static wormhole, the expansion $\widehat{\theta }$ is given by

$$\widehat{\theta }={\displaystyle \frac{2\beta }{r}}{\displaystyle \frac{dr}{dl}},$$

(38)

where $\beta$ is a positive quantity. For $l<0$, $dr/dl$ is negative, so then is $\widehat{\theta }$ negative. However, $\widehat{\theta }\to -\infty$ only if $r\to 0$ since $dr/dl$ is always finite. Therefore, either the wormhole has a vanishing throat radius, which renders it non-traversable, or the WEC is violated.

For the evolving case, the expansion is given by

$$\widehat{\theta }={\displaystyle \frac{2\beta }{R\left(\tau \right)}}\left({\displaystyle \frac{dR\left(\tau \right)}{d\tau }}+{\displaystyle \frac{1}{r}}{\displaystyle \frac{dr}{dl}}\right).$$

(39)

Real time $\tau$ has now been used, and as long as $dR/d\tau >(1/r)|dr/dl|$, i.e., the wormhole is opening out fast enough, $\widehat{\theta }$ is never negative. Thus, the fact that the bundle does not focus no longer implies that the WEC is satisfied.

2.1.2. Specific Examples

For simplicity, in the examples that follow, the specific choice of the form function given by $b\left(r\right)=r_0$ is used (other choices of $b\left(r\right)$ may also be used) [4,5]. Thus, the WEC, condition (35), imposes the following restriction on $r_0$:

$$r_0^2\ge \max \left({\displaystyle \frac{1}{F\left(t\right)}}\right),$$

(40)

which restricts the minimum possible value of the throat radius of the wormhole.

• $\Omega \left(t\right)={(C-\omega t)}^{-1}$.
  Note that this is essentially the case of an inflationary wormhole universe, as discussed by Roman [7], which shall briefly be discussed further ahead. The fundamental idea was to obtain a macroscopic model of a wormhole which emerged from inflation. This choice of the scale factor leads to $F\left(t\right)=0$, implying that the WEC is violated for all times.
• $\Omega \left(t\right)=\sin \omega t$.
  This is essentially the scale factor used in closed FRW cosmological models. The expression for $F\left(t\right)$ is given by

  $$F\left(t\right)=2{\omega }^2(2{\cot }^2\omega t+1).$$

  (41)
  $F\left(t\right)$ has a minimum at $\omega t=\pi /2$; thus, the constraint on the allowed values of $r_0$ is $r_0^2{\omega }^2\ge 1/2$. The lifetime of this wormhole universe is $\pi /\omega$, and the time interval for which this universe can exist without collapsing into a singularity is $m\pi /\omega <t<(m+1)\pi /\omega$.
• $\Omega \left(t\right)={\left(\omega t\right)}^{\nu }$, $\nu$ integral or fractional.
  This is an important case, as the scale factors that arise in dust-filled or radiation-dominated FRW cosmologies with flat spacelike sections are obtained by considering specific values of $\nu$. For a generic $\nu$, the expression for $F\left(t\right)$ is given as

  $$F\left(t\right)={\displaystyle \frac{2\nu (\nu +1)}{t^2}},$$

  (42)

  and $F\left(t\right)\to 0$ as $t\to \pm \infty$. The constraint on $r_0$ is dependent on t, i.e,

  $$r_0^2\ge \max \left({\displaystyle \frac{t^2}{2\nu (\nu +1)}}\right).$$

  (43)
  This evolving wormhole can exist only for a finite interval of time. The lower bound on $r_0$ is decided by the maximum time t up to which we wish the wormhole to exist with the matter threading the geometry satisfying the WEC.

Consider now a special class of scale factors which exhibit “flashes” of WEC violation, where the matter threading the wormhole violates the energy conditions for small intervals of time. It is interesting to note that one can consider specific cases in which the intervals of WEC violation can be chosen to be very small. Consider the following examples:

• $\Omega \left(t\right)=\sin \omega t+a,$$a>1$.
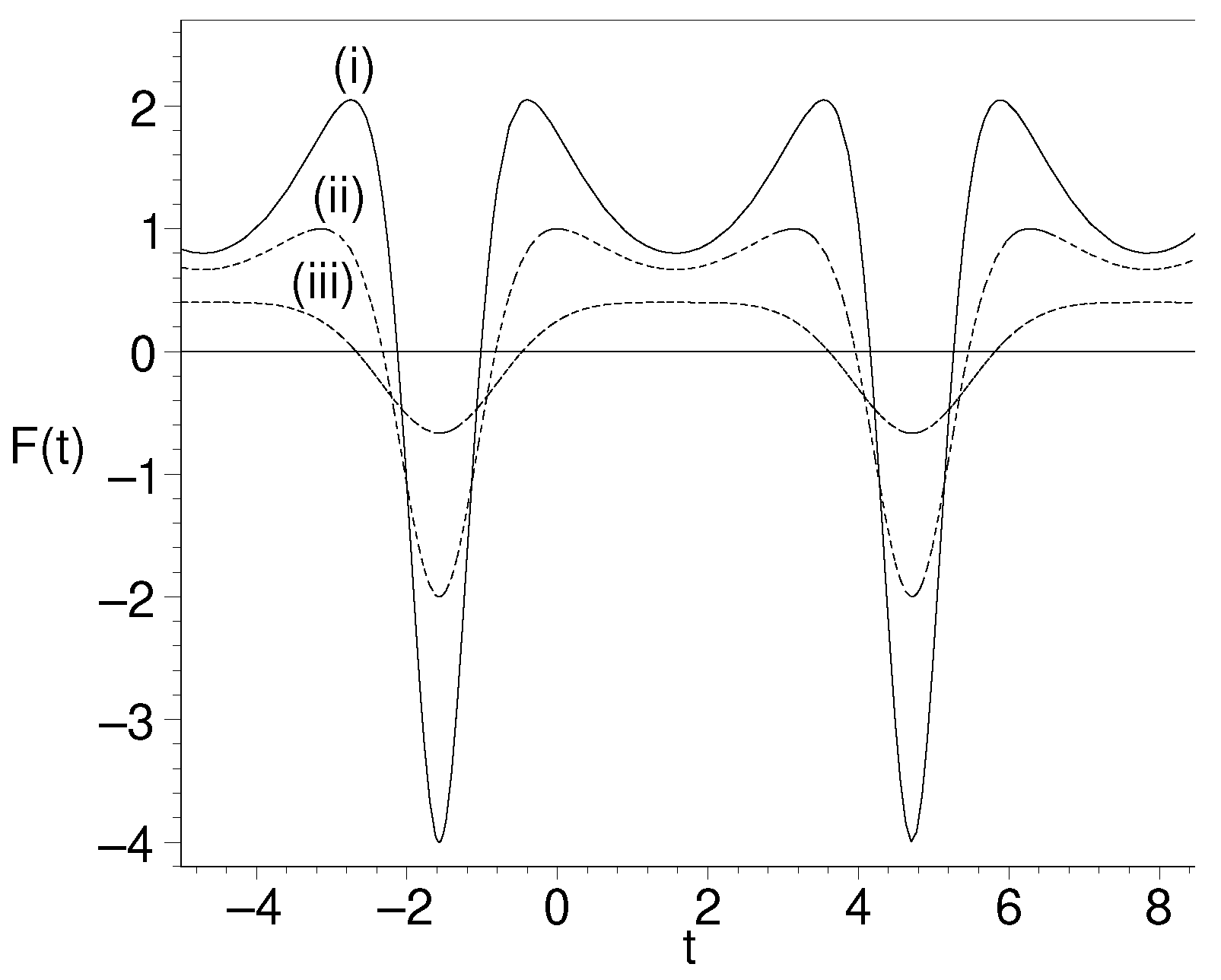
  This scale factor is reminiscent of the ‘bounce’-type solutions in cosmology which were constructed in order to avoid the Big Bang singularity. Thus, the function $F\left(t\right)$ is given by

  $$F\left(t\right)=2{\omega }^2\left[{\displaystyle \frac{2-{\sin }^2\omega t+a\sin \omega t}{{\left(\sin \omega t+a\right)}^2}}\right],$$

  (44)

  which is plotted in Figure 1 [5]. $F\left(t\right)$ takes negative values periodically, for the values of $\omega t$ given by $(2n+1)\pi /2$. This implies the violation of the WEC in the respective interval. Considering small values of the parameter a, one verifies that the interval for which $F\left(t\right)$ is negative becomes significantly shortened.

  Figure 1. A plot of $F\left(t\right)$ vs. t for $\Omega \left(t\right)=\sin \left(\omega t\right)+a$. Only the case of $\omega =1$ is considered, with respective values of (i) $a=1.5$, (ii) $a=2$, and (iii) $a=4$.

  Figure 1. A plot of $F\left(t\right)$ vs. t for $\Omega \left(t\right)=\sin \left(\omega t\right)+a$. Only the case of $\omega =1$ is considered, with respective values of (i) $a=1.5$, (ii) $a=2$, and (iii) $a=4$.
• $\Omega \left(t\right)=(t^2+a^2)/(t^2+b^2),$$b>a>0$.
  This choice of the scale factor implies that asymptotically, the geometry becomes a static wormhole. The function $F\left(t\right)$ is given by

  $$F\left(t\right)={\displaystyle \frac{4(b^2-a^2)(3t^2-a^2)}{(t^2+b^2){\left(t^2+a^2\right)}^2}}.$$

  (45)

  which is plotted in Figure 2 [5]. At $t=\pm a/\sqrt{3}$, we have $F\left(t\right)=0$. For $-a/\sqrt{3}<t<a/\sqrt{3}$, $F\left(t\right)$ is negative, implying the violation of the WEC.

2.2. A Wormhole in a Flat FRW Universe

Consider now a wormhole evolution in a flat $k=0$ FRW universe [4,5]. One chooses the scale factor to be identical to that in either the matter- or radiation-dominated FRW model [8]. Thus, the metric is given by

$$d{s}^2=-d{\tau }^2+{\tau }^n\left[{\displaystyle \frac{d{r}^2}{1-b\left(r\right)/r}}+r^2(d{\theta }^2+{\sin }^2\theta d{\varphi }^2)\right].$$

(46)

where real time is now used. n takes the values $1/2$ and $2/3$ for the radiation- and matter-dominated cases of the flat FRW universes, respectively. The stress–energy scenario for the metric (46) is the following:

$$\begin{array}{ccc}\hfill \rho (r,\tau )& =& {\displaystyle \frac{b^{\prime }}{{\tau }^{2n}{r}^2}}+{\displaystyle \frac{3n^2}{{\tau }^2}},\hfill \end{array}$$

(47)

$$\begin{array}{ccc}\hfill p_1\left(r,\tau \right)& =& -{\displaystyle \frac{b}{{\tau }^{2n}{r}^3}}-{\displaystyle \frac{n(3n-2)}{{\tau }^2}},\hfill \end{array}$$

(48)

$$\begin{array}{ccc}\hfill p_2(r,\tau )& =& {\displaystyle \frac{b-b^{\prime }r}{2r^3{\tau }^{2n}}}-{\displaystyle \frac{n(3n-2)}{{\tau }^2}}.\hfill \end{array}$$

(49)

For $r\to \infty$, one obtains $\rho ={\rho }_{FRW}=4/\left(3{\tau }^2\right)$, $p_1=p_2=0$ for dust and $\rho /3=p_1=p_2=1/\left(4{\tau }^2\right)$ for pure radiation.

The WEC inequality $\rho +p_1\ge 0$ reduces to the following:

$${\displaystyle \frac{b^{\prime }r-b}{2r^3{\left(\tau \right)}^{2n}}}+{\displaystyle \frac{2n}{{\left(c\tau \right)}^2}}\ge 0.$$

(50)

One may now consider several cases for the form function $b\left(r\right)$ and analyze the conditions that sprout therefrom. However, we shall not attempt this endeavor here. The particular case for $b\left(r\right)=r_0$ is analyzed in [4,5].

3. Wormholes in an Inflationary Background

3.1. The Metric and the Stress–Energy Tensor

A particularly interesting case of metric (1) is that of a wormhole in a time-dependent inflationary background considered by Thomas Roman [7]. We shall consider real time $\tau$ defined by $\tau =\int \Omega \left(t\right)dt$ and replace $\Omega \left(t\right)$ with $R\left(\tau \right)$. However, for notational convenience, we shall use the t coordinate (which below is interpreted as real time). Thus, the metric is given by

$$d{s}^2=-e^{2\Phi \left(r\right)}d{t}^2+e^{2\chi t}\left[{\displaystyle \frac{d{r}^2}{(1-b(r)/r)}}+r^2({d\theta }^2+si{n}^2\theta {d\varphi }^2)\right],$$

(51)

where the spatial part of the metric is multiplied by a de Sitter scale factor $R\left(t\right)=e^{2\chi t}$, with $\chi =\sqrt{\Lambda /3}$; $\Lambda$ is the cosmological constant [29]. The coordinates $r,\theta ,\varphi$ have the same geometrical interpretation as that in the Morris–Thorne case. For $\chi =0$, it becomes the static wormhole metric [1], while for $\Phi \left(r\right)=b\left(r\right)=0$, the metric (51) reduces to a flat de Sitter metric. By imposing $\Phi \left(r\right)\to 0,b/r\to 0$ as $r\to \infty$, the spacetime becomes asymptotically de Sitter. As in the static Morris–Thorne solution, $\Phi \left(r\right)$ is everywhere finite so that the only horizons present are cosmological. Note that the spacetime described by Equation (51), unlike the usual flat de Sitter spacetime, is inhomogeneous due to the presence of the wormhole.

The primary goal in the Roman analysis was to use inflation to enlarge an initially small [7], possibly submicroscopic, wormhole. $\Phi \left(r\right)$ and $b\left(r\right)$ are chosen to give a reasonable wormhole at $t=0$, which is assumed to be the onset of inflation. One can verify that the wormhole expands in size by considering the proper circumference C of the wormhole throat, $r=r_0,$ for $\theta =\pi /2$, at any time $t=\mathrm{const}$

$$C={\int }_0^{2\pi }{e}^{\chi t}{r}_{0}d\varphi =e^{\chi t}\left(2\pi r_0\right),$$

(52)

which is simply $e^{\chi t}$ times the initial circumference. The radial proper length between two points A and B, at any $t=\mathrm{const}$, is similarly given by Equation (8), which reduces to

$$l\left(t\right)=\pm e^{\chi t}{\int }_{r_A}^{r_B}{\displaystyle \frac{dr}{{[1-b\left(r\right)/r]}^{1/2}}},$$

(53)

which is $e^{\chi t}$ times the initial radial proper separation. Thus, both the size of the throat and the radial proper distance between the wormhole mouths increase exponentially with time. It is fairly straightforward to verify that the “wormhole form” of metric (51) is preserved with time by using the analysis following Equation (9) and by replacing the conformal factor with the scale factor, $R\left(t\right)=e^{2\chi t}$.

To determine the stress–energy tensor necessary to sustain the wormhole described by Equation (51), it is useful to consider the set of orthonormal basis vectors defined by

$$\begin{array}{ccc}\hfill {\mathbf{e}}_{\widehat{t}}& =& e^{-\Phi }{\mathbf{e}}_t,\hfill \\ \hfill {\mathbf{e}}_{\widehat{r}}& =& e^{-\chi t}{(1-b/r)}^{1/2}{\mathbf{e}}_r,\hfill \\ \hfill {\mathbf{e}}_{\widehat{\theta }}& =& e^{-\chi t}{r}^{-1}{\mathbf{e}}_{\theta },\hfill \\ \hfill {\mathbf{e}}_{\widehat{\varphi }}& =& e^{-\chi t}{\left(r\sin \theta \right)}^{-1}{\mathbf{e}}_{\varphi }.\hfill \end{array}$$

(54)

Thus, the stress–energy tensor components, $T_{\widehat{\mu }\widehat{\nu }}$, obtained from Equations (4)–(7) are given by

$$\begin{array}{ccc}\hfill T_{\widehat{t}\widehat{t}}& =& \rho (r,t)={\displaystyle \frac{1}{8\pi }}\left(3{\chi }^2{e}^{-2\Phi }+e^{-2\chi t}{\displaystyle \frac{b^{\prime }}{r^2}}\right),\hfill \end{array}$$

(55)

$$\begin{array}{ccc}\hfill T_{\widehat{r}\widehat{r}}& =& -\tau (r,t)={\displaystyle \frac{1}{8\pi }}\left\{-3{\chi }^2{e}^{-2\Phi }-e^{-2\chi t}\left[{\displaystyle \frac{b}{r^3}}-{\displaystyle \frac{2{\Phi }^{\prime }}{r}}\left(1-{\displaystyle \frac{b}{r}}\right)\right]\right\},\hfill \end{array}$$

(56)

$$\begin{array}{ccc}\hfill T_{\widehat{t}\widehat{r}}& =& -f(r,t)={\displaystyle \frac{1}{8\pi }}\left[2e^{-\Phi -\chi t}{\left(1-{\displaystyle \frac{b}{r}}\right)}^{1/2}\chi {\Phi }^{\prime }\right],\hfill \end{array}$$

(57)

$$\begin{array}{ccc}\hfill T_{\widehat{\theta }\widehat{\theta }}& =& T_{\widehat{\varphi }\widehat{\varphi }}=p(r,t)\hfill \\ & =& {\displaystyle \frac{1}{8\pi }}\{-3{\chi }^2{e}^{-2\Phi }+e^{-2\chi t}[{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{b}{r^3}}-{\displaystyle \frac{b^{\prime }}{r^2}}\right)+{\displaystyle \frac{{\Phi }^{\prime }}{r}}\left(1-{\displaystyle \frac{b}{2r}}-{\displaystyle \frac{b^{\prime }}{2}}\right)\hfill \\ & & +\left(1-{\displaystyle \frac{b}{r}}\right)\left({\Phi }^{\prime \prime }+({\Phi }^{\prime 2}\right)\left]\right\},\hfill \end{array}$$

(58)

where the quantities $\rho ,\tau ,f$, and p are defined as before, and are finite for all t and r. Note from Equation (57) that the flux vanishes at the wormhole throat. If $\Phi \left(r\right)\to 0,b/r\to 0$ as $r\to \infty$, the stress–energy tensor components asymptotically assume their de Sitter forms, i.e., $T_{\widehat{t}\widehat{t}}=-T_{\widehat{r}\widehat{r}}=-T_{\widehat{\theta }\widehat{\theta }}=-T_{\widehat{\varphi }\widehat{\varphi }}=3{\chi }^2$.

A particularly simple example of an inflating wormhole is obtained by setting a null redshift function $\Phi \left(r\right)=0$ [7] so that the stress–energy tensor components in an orthonormal frame reduce to

$$\begin{array}{ccc}\hfill T_{\widehat{t}\widehat{t}}& =& \rho (r,t)={\displaystyle \frac{1}{8\pi }}\left[3{\chi }^2+e^{-2\chi t}{\displaystyle \frac{b^{\prime }}{r^2}}\right]\hfill \end{array}$$

(59)

$$\begin{array}{ccc}\hfill T_{\widehat{r}\widehat{r}}& =& -\tau (r,t)={\displaystyle \frac{1}{8\pi }}\left[-3{\chi }^2-e^{-2\chi t}\left({\displaystyle \frac{b}{r^3}}\right)\right]\hfill \end{array}$$

(60)

$$\begin{array}{ccc}\hfill T_{\widehat{t}\widehat{r}}& =& -f(r,t)=0\hfill \end{array}$$

(61)

$$\begin{array}{ccc}\hfill T_{\widehat{\theta }\widehat{\theta }}& =& T_{\widehat{\varphi }\widehat{\varphi }}=p(r,t)={\displaystyle \frac{1}{8\pi }}\left[-3{\chi }^2+{\displaystyle \frac{e^{-2\chi t}}{2}}\left({\displaystyle \frac{b}{r^3}}-{\displaystyle \frac{b^{\prime }}{r^2}}\right)\right].\hfill \end{array}$$

(62)

Note that the stress–energy tensor components all approach their de Sitter space values for a large value of t. When $\chi =0$, the solution reduces to that of a static “zero-tidal-force” wormhole [1].

3.2. The Properties of the Solutions and NEC Violation

Analyzing the stress–energy components of an evolving wormhole, in particular those of an inflating wormhole, one verifies that a noticeable difference between the properties of a generic redshift function with $\Phi \left(r\right)\ne 0$ and that of $\Phi =0$ wormholes is the presence of a flux term, given by Equation (57). Following the Roman analysis [7], to clarify this difference, consider two coordinate systems associated with the wormhole. The first can be thought of as the rest frame of the wormhole geometry, i.e., an observer at rest in this frame is at constant $r,\theta ,\varphi$. The second can be associated with the rest frame of the wormhole material. One can define the rest frame of the wormhole material as that in which an observer co-moving with the material sees zero energy flux, and from Equation (57), one verifies that for $\Phi \left(r\right)\ne 0$, the wormhole material is not at rest in the $r,\theta ,\varphi$ coordinate system. For the $\Phi \left(r\right)=0$ metrics, the two coordinate systems coincide.

To analyze certain interesting properties of these wormholes, consider the four-velocity of an observer who remains at rest with respect to the $r,\theta ,\varphi$ coordinate system, given by $U^{\mu }=d{x}^{\mu }/d\tau =(e^{-\Phi \left(r\right)},0,0,0)$. The observer’s four-acceleration, $a^{\mu }={U^{\mu }}_{;\nu }{U}^{\nu }$, provides the following relations:

$$\begin{array}{ccc}\hfill a^t& =& 0\hfill \\ \hfill a^r& =& {\Gamma }_{tt}^r{\left({\displaystyle \frac{dt}{d\tau }}\right)}^2=e^{-2\chi t}{\Phi }^{\prime }(1-b/r).\hfill \end{array}$$

(63)

From the geodesic equation, a radially moving test particle which is initially at rest has the equation of motion

$${\displaystyle \frac{d^{2}r}{d{\tau }^2}}=-{\Gamma }_{tt}^r{\left({\displaystyle \frac{dt}{d\tau }}\right)}^2=-a^r.$$

(64)

Therefore, $a^r$ is the radial component of proper acceleration that an observer must maintain in order to remain at rest at constant $r,\theta ,\varphi$. Thus, from Equation (64), one deduces that for $\Phi \left(r\right)\ne 0$ wormholes, static or inflating, such observers do not move along geodesics (except at the throat), contrary to $\Phi \left(r\right)=0$ wormholes.

The analysis of the “attractive” or“repulsive” nature of the wormhole geometry is analogous to that in the Morris–Thorne case. Additionally, the sign of the energy flux depends on the sign of ${\Phi }^{\prime }$, or equivalently on the sign of $a^r$. From the flux term $f=-T_{\widehat{t}\widehat{r}}$, i.e., Equation (57), one verifies that if the wormhole is attractive, there is a negative energy flow out of it; if it is repulsive, there is a negative energy flow into it.

To analyze the NEC, one may follow the Roman analysis and consider the exoticity function. However, it is simpler to use the definition of the NEC for a radial null vector. Consider $k^{\widehat{\mu }}=(1,\pm 1,0,0)$, a radial outgoing (ingoing) null vector, so that from Equations (55)–(58), one has

$$T_{\widehat{\mu }\widehat{\nu }}{k}^{\widehat{\mu }}{k}^{\widehat{\nu }}={\displaystyle \frac{e^{-2\chi t}}{8\pi }}\left[\left({\displaystyle \frac{b^{\prime }}{r^2}}-{\displaystyle \frac{b}{r^3}}\right)-{\displaystyle \frac{2{\Phi }^{\prime }}{r}}\left(1-{\displaystyle \frac{b}{r}}\right)\right]\pm {\displaystyle \frac{e^{-\chi t}}{4\pi }}\left[{\left(1-{\displaystyle \frac{b}{r}}\right)}^{1/2}\chi {\Phi }^{\prime -\Phi }\right].$$

(65)

For $\Phi \left(r\right)=0$, Equation (65) reduces to

$$T_{\widehat{\mu }\widehat{\nu }}{k}^{\widehat{\mu }}{k}^{\widehat{\nu }}={\displaystyle \frac{e^{-2\chi t}}{8\pi }}\left({\displaystyle \frac{b^{\prime }}{r^2}}-{\displaystyle \frac{b}{r^3}}\right).$$

(66)

From Equation (65), one verifies that $(1-b/r)\to 0$ at the throat, considering the finite character of ${\Phi }^{\prime }$, and taking into account the flaring-out condition [1], the NEC is violated at or near the throat $r=b=r_0$. If $\rho$ is non-zero and finite for all t, then the NEC at the throat decays exponentially with time.

Roman [7] went on to explore interesting properties of inflating wormholes, in particular by analyzing the constraints placed on the initial size of the wormhole if the mouths were to remain in causal contact throughout the inflationary period and the maintenance of the wormhole during and after the decay of the false vacuum. It is also possible that the wormhole will continue to be enlarged by the subsequent FRW phase of expansion. One could perform a similar analysis to ours by replacing the de Sitter scale factor in Equation (51) with an FRW scale factor $a\left(t\right)$, which will be applied in the next section.

4. Evolving Cosmological Wormholes in Hybrid Metric–Palatini Gravity

The most natural extension of general relativity is considering curvature invariants in a gravitational Lagrangian. $f\left(R\right)$ gravity is one of the most famous examples of these kinds of theories. Considering the metric as a fundamental field and varying the action with respect to it, one receives metric $f\left(R\right)$ gravity [90,91,92,93,94]. This theory introduces additional scalar degrees of freedom, which should have a low mass in order to suitably explain the dynamics of the cosmos at a large scale. However, the effects of this low-mass scalar field should be detectable at small scales, such as in the Solar system, whereas there is no evidence for this [95,96]. From the viewpoint of the Palatin formalism and by varying the $f\left(R\right)$ action with respect to the metric and an independent connection [97], there is no longer an additional degree of freedom since the scalar field is an algebraic function of the trace of the energy-momentum tensor. This also, in itself, brings a problem because it resorts to an infinite tidal force on the surface of massive astrophysical-type objects [97].

The problems pointed out provide enough motivation to introduce a more compatible new framework. One idea is to introduce a hybrid metric–Palatini formalism [76]. On the one hand, this formalism introduces a long-range force into its scalar–tensor representation and therefore automatically passes local measurements such as those at the level of the Solar system. On the other hand, studies show that this hybrid theory explains cosmological epochs properly [77,83,84]. Thus, this hybrid metric–Palatini theory is a promising context for astrophysical [78,98,99] and cosmological [83,84,100,101,102,103] studies and also for perusing compact objects, such as black holes [79,80,81,82] and wormholes [44,45].

4.1. Action and Field Equations of Hybrid Metric–Palatini Gravity

The action of hybrid metric–Palatini gravity is given by

$$S={\displaystyle \frac{1}{16\pi G}}\int d^{4}x\sqrt{-g}\left[R+f\left(\mathcal{R}\right)\right]+S_m,$$

(67)

where R is the metric Ricci scalar, and $S_m$ is the matter action. $\mathcal{R}\equiv g^{\mu \nu }{\mathcal{R}}_{\mu \nu }$ is the Palatini curvature in which the Palatini Ricci tensor ${\mathcal{R}}_{\mu \nu }$ is given by

$${\mathcal{R}}_{\mu \nu }\equiv {\widehat{\Gamma }}_{\mu \nu ,\alpha }^{\alpha }-{\widehat{\Gamma }}_{\mu \alpha ,\nu }^{\alpha }+{\widehat{\Gamma }}_{\alpha \lambda }^{\alpha }{\widehat{\Gamma }}_{\mu \nu }^{\lambda }-{\widehat{\Gamma }}_{\mu \lambda }^{\alpha }{\widehat{\Gamma }}_{\alpha \nu }^{\lambda },$$

(68)

where ${\widehat{\Gamma }}_{\mu \nu }^{\alpha }$ is an independent connection. The scalar–tensor representation of this gravity is [76]

$$S={\displaystyle \frac{1}{16\pi G}}\int d^{4}x\sqrt{-g}\left[(1+\varphi )R+{\displaystyle \frac{3}{2\varphi }}{\partial }_{\mu }\varphi {\partial }^{\mu }\varphi -V\left(\varphi \right)\right]+S_m.$$

(69)

From a computational point of view, the above representation is clearly easier to handle. The field equations can be obtained by varying the action (69) with respect to the metric and the scalar field, as

$$\begin{array}{c}{G}_{\mu \nu }={\kappa }^2\left({\displaystyle \frac{1}{1+\varphi }}{T}_{\mu \nu }+T_{\mu \nu }^{\left(\varphi \right)}\right),\\ \end{array}$$

(70)

$$\begin{array}{c}\square \varphi +{\displaystyle \frac{1}{2\varphi }}{\partial }_{\mu }\varphi {\partial }^{\mu }\varphi +{\displaystyle \frac{\varphi [2V-(1+\varphi )V_{\varphi }]}{3}}={\displaystyle \frac{\varphi {\kappa }^2}{3}}T,\end{array}$$

(71)

where $T_{\mu \nu }$ and $T_{\mu \nu }^{\left(\varphi \right)}$ are the energy-momentum tensors of matter and the scalar field, respectively, and

$$T_{\mu \nu }^{\left(\varphi \right)}={\displaystyle \frac{1}{{\kappa }^2}}{\displaystyle \frac{1}{1+\varphi }}\left[{\nabla }_{\mu }{\nabla }_{\nu }\varphi -{\displaystyle \frac{3}{2\varphi }}{\nabla }_{\mu }\varphi {\nabla }_{\nu }\varphi +\left({\displaystyle \frac{3}{4\varphi }}{\nabla }_{\lambda }\varphi {\nabla }^{\lambda }\varphi -\square \varphi -{\displaystyle \frac{1}{2}}V\right)g_{\mu \nu }\right].$$

(72)

4.2. Traversable Cosmological Wormhole Solutions and Energy Conditions

In the framework of hybrid metric–Palatini gravity, four-dimensional traversable cosmological wormholes have been studied [89]. Traversable cosmological wormholes are shortcuts in spacetime that allow for human travel and expand with the universe according to the same scale factor. The exoticity of matter which supports wormhole spacetime has always provided grounds for doubt about whether it is possible to have such structures in nature. The results of [89] show that in the context of hybrid metric–Palatini gravity, there are four-dimensional wormhole structures supported completely with normal matter. Such matter distributions satisfy both the null and weak energy conditions throughout space and at all times. From one point of view, these results show that hybrid metric–Palatini gravity can be considered a rather more hopeful model and, from the other point of view, strengthens varying dark energy models because hybrid metric–Palatini gravity is one of them. In what follows, we review this kind of study.

The metric of a traversable cosmological wormhole can be written as

$$d{s}^2=-d{t}^2+a^2\left(t\right)\left[{\displaystyle \frac{d{r}^2}{1-\frac{b\left(r\right)}{r}}}+r^2\left(d{\theta }^2+{\sin }^2\theta d{\phi }^2\right)\right],$$

(73)

where $b\left(r\right)$ is the shape function, and $a\left(t\right)$ is the scale factor. The wormhole structure has a throat $r_0$ which corresponds to a minimum radial coordinate. In order to have a traversable wormhole, the shape function should satisfy the following conditions: (i) $b\left(r_0\right)=r_0$, (ii) $b\left(r\right)\le r$ and (iii) $r{b}^{\prime }\left(r\right)-b\left(r\right)<0$ (flaring-out condition) [1]. Here, we consider an anisotropic matter energy-momentum tensor $T_{\nu }^{\mu }=\mathrm{diag}(-\rho ,-\tau ,p,p)$, where $\rho$ is the energy density, $\tau$ is the radial tension, and p is the tangential pressure. Then, we take into account the metric (73) and the gravitational field equations (70), to obtain the following field equations:

$$\rho (t,r)=\left(3H^2+{\displaystyle \frac{b^{\prime }}{r^2{a}^2}}\right)\left(1+\varphi \right)+3\dot{\varphi }H+{\displaystyle \frac{3{\dot{\varphi }}^2}{4\varphi }}-{\displaystyle \frac{1}{2}}V\left(\varphi \right),$$

(74)

$$\tau \left(t,r\right)=\left(H^2+2{\displaystyle \frac{\ddot{a}}{a}}+{\displaystyle \frac{b}{r^3{a}^2}}\right)\left(1+\varphi \right)+2\dot{\varphi }H-{\displaystyle \frac{3{\dot{\varphi }}^2}{4\varphi }}+\ddot{\varphi }-{\displaystyle \frac{1}{2}}V\left(\varphi \right),$$

(75)

and

$$p\left(t,r\right)=\left(-H^2-2{\displaystyle \frac{\ddot{a}}{a}}-{\displaystyle \frac{r{b}^{\prime }-b}{2r^3{a}^2}}\right)\left(1+\varphi \right)-2\dot{\varphi }H+{\displaystyle \frac{3{\dot{\varphi }}^2}{4\varphi }}-\ddot{\varphi }+{\displaystyle \frac{1}{2}}V\left(\varphi \right),$$

(76)

where $H=\dot{a}/a$ and $\varphi =\varphi \left(t\right)$. Note that the overdot denotes the derivative with respect to the time coordinate, while the prime denotes the derivative with respect to r. In addition, we set $16\pi G=1$ for notational simplicity.

In order to find the behavior of energy-momentum tensor components, we have to solve the equation of motion corresponding to a time-dependent scalar field (71) given by

$$\ddot{\varphi }+3\dot{\varphi }H-{\displaystyle \frac{{\dot{\varphi }}^2}{2\varphi }}-{\displaystyle \frac{1}{3}}\varphi \left[T+\left(1+\varphi \right){\displaystyle \frac{dV}{d\varphi }}-2V\left(\varphi \right)\right]=0,$$

(77)

where T is the trace of the energy-momentum tensor given by

$$T\left(t,r\right)=T_{\mu }^{\mu }=-\rho -\tau +2p=-2\left({\displaystyle \frac{b^{\prime }}{a^2{r}^2}}+3H^2+3{\displaystyle \frac{\ddot{a}}{a}}\right)(1+\varphi )-3\ddot{\varphi }+{\displaystyle \frac{3{\dot{\varphi }}^2}{2\varphi }}-9\dot{\varphi }H+2V\left(\varphi \right).$$

(78)

Since the scalar field $\varphi$ depends only on time, the differential Equation (77) should be independent of r. To this end, the trace $T\left(t,r\right)$ in this equation has to be r-independent. According to (78), this leads to $b^{\prime }/r^2=C{H}_0^2$, where C is an arbitrary dimensionless constant and $H_0$ is the present value of the Hubble parameter. Consequently, the shape function can be obtained as $b\left(r\right)=r_0+C{H}_0^2(r^3-r_0^3)/3$, which clearly satisfies $b\left(r_0\right)=r_0$. The flaring-out condition at the throat yields $C{H}_0^2{r}_0^2<1$. In what follows, we set $C=0$ which satisfies the flaring-out condition and simplifies the solution.

Now, we can solve the differential Equation (77) numerically for $\varphi$. However, it is useful to re-express the equation in terms of dimensionless functions of the scale factor a. Considering the following definitions

$$\ddot{\varphi }=\ddot{a}{\varphi }^{\prime }\left(a\right)+{\dot{a}}^2{\varphi }^{\prime \prime }\left(a\right),\dot{\varphi }=\dot{a}{\varphi }^{\prime }\left(a\right),\ddot{a}=H\dot{a}+\dot{H}a,\dot{H}=\dot{a}{H}^{\prime }\left(a\right),\dot{a}=Ha,$$

(79)

where the prime denotes the derivative with respect to the scale factor, $U=V/3H_0^2$, and $E=H/H_0$, the differential Equation (77) acquires the final form below:

$${\varphi }^{\prime \prime }\left(a\right)-{\displaystyle \frac{{\varphi }^{\prime 2}}{2\varphi \left(a\right)}}+{\displaystyle \frac{4(a{\varphi }^{\prime }\left(a\right)+\varphi \left(a\right))}{a^2}}+{\displaystyle \frac{E^{\prime }\left(a\right){\varphi }^{\prime }\left(a\right)}{E\left(a\right)}}+{\displaystyle \frac{2\varphi \left(a\right)E^{\prime }\left(a\right)}{aE\left(a\right)}}-{\displaystyle \frac{\varphi \left(a\right)}{a^{2}E{\left(a\right)}^2}}{\displaystyle \frac{dU}{d\varphi }}=0.$$

(80)

In the above differential equation, we have three unknown functions, namely $\varphi \left(a\right)$, $E\left(a\right)$, and $U\left(\varphi \right)$. Since we intend to solve Equation (80) for $\varphi \left(a\right)$, we have to determine E and U. In order to deduce E, we consider background quantities, ${\rho }_b\left(t\right)=3H^2$ and ${\tau }_b\left(t\right)=H^2+2\ddot{a}/a$ and a barotropic equation of the state ${\tau }_b=-{\omega }_b{\rho }_b$, which leads to $E=a^{-3\left({\omega }_b+1\right)/2}$ or, equivalently, $a\left(t\right)\propto t^{2/3(1+{\omega }_b)}$. Then, by using dimensionless definitions, Equations (74)–(76) take the forms

$${\displaystyle \frac{\rho }{3H_0^2}}={\displaystyle \frac{1+\varphi \left(a\right)}{a^{3\left({\omega }_b+1\right)}}}+{\displaystyle \frac{{\varphi }^{\prime }\left(a\right)}{a^{3{\omega }_b+2}}}+{\displaystyle \frac{{\varphi }^{\prime 2}\left(a\right)}{4a^{3{\omega }_b+1}\varphi \left(a\right)}}-{\displaystyle \frac{1}{2}}U\left(\varphi \right),$$

(81)

$${\displaystyle \frac{\rho -\tau }{3H_0^2}}=\left({\displaystyle \frac{{\omega }_b+1}{a^{3\left({\omega }_b+1\right)}}}-{\displaystyle \frac{r_0}{3a^2{H}_0^2{r}^3}}\right)\left(1+\varphi \left(a\right)\right)+{\displaystyle \frac{\left({\omega }_b+1\right){\varphi }^{\prime }\left(a\right)}{2a^{3{\omega }_b+2}}}+{\displaystyle \frac{{\varphi }^{\prime 2}\left(a\right)}{2a^{3{\omega }_b+1}\varphi \left(a\right)}}-{\displaystyle \frac{{\varphi }^{\prime \prime }\left(a\right)}{3a^{3{\omega }_b+1}}},$$

(82)

and

$${\displaystyle \frac{\rho +p}{3H_0^2}}=\left({\displaystyle \frac{{\omega }_b+1}{a^{3\left({\omega }_b+1\right)}}}+{\displaystyle \frac{r_0}{6a^2{H}_0^2{r}^3}}\right)\left(1+\varphi \left(a\right)\right)+{\displaystyle \frac{\left({\omega }_b+1\right){\varphi }^{\prime }\left(a\right)}{2a^{3{\omega }_b+2}}}+{\displaystyle \frac{{\varphi }^{\prime 2}\left(a\right)}{2a^{3{\omega }_b+1}\varphi \left(a\right)}}-{\displaystyle \frac{{\varphi }^{\prime \prime }\left(a\right)}{3a^{3{\omega }_b+1}}}.$$

(83)

Here, we consider $r_0=A{H}_0^{-1}$ for the wormhole throat so that the terms are dimensionless. We set the dimensionless constant A to unity. Regarding the potential for the scalar field $U\left(\varphi \right)$, we consider a quartic potential ${\varphi }^4$.

To construct wormhole structures, we follow a reverse procedure; namely, we first build the geometry with the required conditions and then find the energy-momentum profile. So, checking the energy conditions plays a fundamental role. We expect that normal matter should satisfy the energy conditions. The weak energy condition (WEC) is defined as $T_{\mu \nu }{u}^{\mu }{u}^{\nu }\ge 0$, where $u^{\mu }$ is a timelike vector. In terms of the components of the energy-momentum tensor, it is expressed as $\rho \ge 0$, $\rho -\tau \ge 0$, and $\rho +p\ge 0$. The null energy condition (NEC) is given by $T_{\mu \nu }{k}^{\mu }{k}^{\nu }\ge 0$, where $k^{\mu }$ is any null vector. One could express this condition in terms of the energy-momentum tensor components as $\rho -\tau \ge 0$ and $\rho +p\ge 0$, which are last two inequalities in the WEC.

In the following, we will review the satisfaction of the energy conditions for specific solutions with ${\omega }_b=1/3$ and ${\omega }_b=0$ where, respectively, $E=a^{-2}$ ($a\left(t\right)\propto t^{1/2}$) and $E=a^{-3/2}$ ($a\left(t\right)\propto t^{2/3}$). These choices correspond tentatively to the radiation and matter epochs.

4.3. Specific Cases of ${\omega }_b=1/3$ and ${\omega }_b=0$

In Figure 3, the behaviors of $\rho$, $\rho -\tau$, and $\rho +p$ with respect to the redshift z are displayed for ${\omega }_b=1/3$. These behaviors have been depicted for different values of r. Here, we have set the initial conditions for solving Equation (80) numerically to $\varphi \left(\delta \right)={\varphi }^{\prime }\left(\delta \right)={10}^{-4}$, where $\delta$ is very close to $a=0$. This figure exhibits that these quantities are decreasing functions of time (or equivalently increasing functions of redshift), while they are always positive. Consequently, the NEC and the WEC remain satisfied at all times.

Regarding the case ${\omega }_b=0$ and by setting the initial conditions to $\varphi \left(\delta \right)={10}^{-4}$ and ${\varphi }^{\prime }\left(\delta \right)=-{\displaystyle \frac{1}{2}}$, the energy conditions are depicted in Figure 4. For this case, the NEC and the WEC are satisfied at all times and for any radial coordinates r as well. $\rho$, $\rho -\tau$, and $\rho +p$ also decrease (increase) with time (redshift).

5. Conclusions

In this work, we have investigated the theoretical construction and physical viability of evolving wormhole solutions embedded within cosmological backgrounds, focusing on both general relativity and modified gravity frameworks, with particular emphasis on hybrid metric–Palatini gravity. Motivated by the foundational insight that static traversable wormholes necessitate exotic matter that violates the classical energy conditions, we have explored time-dependent geometries as a means to minimize these violations and embed wormholes consistently within dynamically evolving and physically realistic cosmological models. We reviewed and extended several classes of evolving wormhole solutions, including those conformally related to static metrics, wormholes sustained by minimally coupled scalar fields, and configurations embedded into Friedmann–Lemaître–Robertson–Walker (FLRW) and de Sitter spacetimes. Our analysis confirmed that the dynamical character of the spacetime—particularly when influenced by cosmic expansion, scalar field evolution, or modified gravity couplings—can play a crucial role in localizing or even eliminating violations of the null and weak energy conditions. In particular, within the framework of hybrid metric–Palatini gravity, we demonstrated that the additional scalar degrees of freedom introduced by the theory contribute effective geometric modifications to the stress–energy tensor, which can successfully mimic the role of exotic matter. This permits the construction of traversable wormholes that are supported entirely by matter fields obeying the NEC and the WEC across the full temporal evolution of the universe.

These results represent a meaningful advancement toward identifying wormhole geometries that are not only mathematically consistent but also physically viable within the broader context of gravitational theory and cosmological modeling. By embedding localized topological structures within an expanding universe and incorporating generalized gravitational couplings, we have established new avenues for reconciling the theoretical existence of traversable wormholes with the constraints imposed by classical and semiclassical energy conditions. This line of inquiry significantly enhances our understanding of how non-trivial spacetime features can be naturally accommodated in cosmological scenarios. Despite the progress achieved, several open questions and challenges remain. The dynamical stability of these evolving wormhole solutions—especially under scalar, tensor, and mixed-mode perturbations—remains an important topic of investigation, particularly in anisotropic or inhomogeneous cosmological settings. Furthermore, the interplay between wormhole geometries and phenomena such as early-universe inflation, quantum gravitational effects, and late-time cosmic acceleration deserves further attention. Understanding whether inflationary mechanisms can amplify microscopic wormholes to macroscopic sizes, or whether quantum corrections might stabilize or destabilize such geometries, could provide key insights into the viability of wormholes as physical objects.

Future work will aim to extend the classification of evolving wormhole solutions across a broader spectrum of alternative gravity theories, including $f\left(R\right)$, scalar–tensor, and Gauss–Bonnet frameworks, as well as higher-dimensional and compactified scenarios. The inclusion of non-minimal couplings, anisotropic matter sources, and rotating geometries will also be explored to capture the richness of the possible configurations better. Finally, investigations into the thermodynamic and quantum properties of these wormhole solutions—such as their entropy content, particle creation rates, and semiclassical backreaction—may illuminate deeper aspects of gravitational dynamics and spacetime topology. Ultimately, a more complete understanding of how such non-trivial spacetime structures interact with the evolving fabric of the universe has the potential to shed light on profound and unresolved questions concerning the nature of gravity, the topology of spacetime, and the fundamental architecture of the cosmos.