Abstract
As neutrino experiments enter the precision era, it is desirable to identify any deviation between data and theoretical predictions and to provide possible models as explanation. Particularly useful is the description in terms of non-standard interactions (NSIs), which can be related to neutral (NC-NSI) or charged (CC-NSI) currents. Previously, we have developed the code eft-neutrino that connects NSI with generic ultraviolet (UV) models at tree-level matching. In this work, we integrate our code with other tools, increasing the matching between the UV and infrared (IR) theories to a one-loop level. As a working example, we consider the pion and kaon decay, the main production mechanisms in accelerator neutrino experiments. We provide up-to-date allowed regions on a set of Wilson coefficients related to pion and kaon decay. We also illustrate how our chain of codes can be applied to particular UV models, showing that a seemingly large allowed CC-NSI value can be significantly reduced when considering a specific UV model.
1. Introduction
Neutrino physics is approaching the precision era. A new generation of accelerator, atmospheric, and astrophysical neutrino facilities is under development to measure neutrino properties with unprecedented accuracy. The deep underground neutrino experiment (DUNE) is now under construction and is projected to deliver the sub-percent measurements of oscillation parameters and lepton–universality tests [1,2]. In Japan, Hyper-Kamiokande will bring an eight-fold mass increase over Super-K and will start data-taking in 2027, providing complementary sensitivity to proton decay, supernova neutrinos, and CP violation in the lepton sector [3]. At the energy frontier, forward detectors such as FASER and SND@LHC have already observed the first TeV-scale neutrino interactions and aim to measure charged current (CC) events by the end of LHC Run-3, opening a qualitatively new window on neutrino interactions and forward meson production [4,5,6].
All of these beamlines overwhelmingly depend on leptonic meson decays for their neutrino fluxes. The channels and alone supply more than 90% of the flux at DUNE and Hyper-K, while forward decays generate the bulk of the large Hadron collider (LHC) neutrino spectrum. Thanks to the precise experimental control of decay rates and lattice QCD calculations of hadronic matrix elements, these processes are among the cleanest electroweak observables. The latest NA62 charged-kaon branching ratio measurement [7], when interpreted within the low energy effective field theory (LEFT) framework, already forces the dominant vector-type Wilson coefficient to satisfy as shown by EFT analyses in Refs. [8,9]. Comparable (or even stronger) bounds apply to scalar and tensor structures [10]. Given such precision, any deviation observed by upcoming neutrino detectors could plausibly originate in the production stage and would point to charged-current non-standard interactions (CC-NSI) or other beyond-the-standard-model (BSM) effects occurring in meson decay.
Non-standard neutrino interactions were first introduced by Wolfenstein in 1978 to describe coherent forward scattering in matter [11]. Comprehensive reviews by Ohlsson [12] and by Farzan & Tortola [13] summarized three decades of phenomenology, while more recent global fits highlight the parameter degeneracies that next-generation beams must resolve [14]. Non-standard interactions (NSIs) parametrize new sources for charged (neutral) currents apart from the usual W (Z) mediated processes, (see also [15,16] for recent reviews). Such NSIs can modify the standard predictions for neutrino production, detection, and/or propagation through matter [11,17]. Model builders have explored many ultraviolet (UV) complete scenarios that give rise to NSI, including extended scalar doublets, vector leptoquarks, and new gauge bosons. Notably, several of these scenarios generate sizable CC-NSI effects only at the one-loop level, thereby evading tree-level constraints (see, for instance, [18,19,20,21,22,23,24,25,26,27,28,29]).
The natural framework to connect such UV completions with experimental observables is effective field theory (EFT). Below the electroweak scale, the LEFT describes meson decays through five four-fermion operators whose Wilson coefficients are denoted by . These coefficients match onto the standard model effective field theory (SMEFT) at GeV and can then be evolved up to high mass scales. The complete tree-level LEFT↔SMEFT operator dictionary was provided in [30], while the one-loop extension was presented in [31]. Loop effects are crucial. For instance, they can enforce correlations with flavor-changing processes that would be invisible in a purely low-energy fit.
A set of public codes now renders this multi-scale program computationally feasible. Among these, flavio provides predictions and likelihoods for hundreds of flavor observables [32]; wilson performs renormalization-group running and threshold matching across SMEFT, LEFT, and QED/QCD EFTs [33]; and smelli wraps these ingredients into a global likelihood engine [34]. From a top–down perspective, codes such as matchmakereft [35] and Matchete [36] aim to provide the one-loop matching from given UV models to the SMEFT or LEFT. Focusing exclusively on SMEFT as the target EFT, SOLD [37,38] is particularly useful. It not only provides a user-friendly implementation of the tree-level matching results presented in [39], but also extends those to one-loop matching (at present restricted to UV models containing new fermions or scalars). Focusing on neutrino experiments, in [40], we developed the code eft-neutrinos, which automatically provides the UV matching to Wilson coefficients in the LEFT at the tree level.
In this work, we extend our previous analysis to the one-loop matching level, relying on the recent developments of SOLD. In particular, we aim to map the UV models that could be responsible for possible anomalies detected in future neutrino experiments such as DUNE, Hyper-K, and FASER. For pion decay, we have already mapped all UV realizations at tree level in our previous work [40]. We will go beyond these findings by extending the matching to one-loop order. We also generalize the analysis to include kaon decays. By doing so, we provide a more complete framework to interpret potential neutrino anomalies in terms of underlying new physics, ensuring that loop-induced scenarios are properly accounted for.
This work is organized as follows: in Section 2, we present the methodology employed in our work and set up the notation. In Section 3, we then present our results, in particular, the bounds on the CC-NSI parameters as well as on the relevant SMEFT Wilson coefficients for pion and kaon decays. In Section 4, we put our findings into perspective and conclude.
2. Methodology
Given the non-observation of unexpected resonances at the LHC, the influence of new heavy states can only be detected indirectly. This task is generally accomplished by resorting to an effective field theory approach, where the impact of BSM states is encapsulated into the Wilson coefficients (WCs) of higher dimensional operators. To determine the current constraints on dimension-six SMEFT Wilson coefficients, we make use of a chain of public tools, summarized in Figure 1, that connect low-energy observables to possible high-energy physics.

Figure 1.
Chain of codes employed in our analysis.
In practice, our analysis proceeds as follows. First, we used our code eft-neutrinos [40] to compute the set of dimension-six SMEFT Wilson coefficients relevant for pion and kaon decays (for a given choice of NSI parameters). Next, we fed those coefficients into the combination of flavio, wilson, and smelli [32,33,34], which together provide a global fit to flavor and other precision observables; this allowed us to determine the current experimental bounds on the chosen SMEFT coefficients. Then, using SOLD [37,38], we identified which UV models (at one-loop matching order) could generate those effective coefficients. Finally, for representative UV models, we considered all the SMEFT coefficients they induce (beyond just the ones directly related to pion and kaon decay) and fed those back into the global fit via flavio, wilson, and smelli. This iterative procedure ultimately yielded the allowed values for the CC-NSI parameters after consistently incorporating loop effects and complementary constraints. Figure 1 illustrates this workflow.
In the next section, we present the UV models relevant for meson decays, as well as the current constraints on the SMEFT WCs related to these observables. In the remainder of this section, we briefly discuss our notation.
In accelerator-based neutrino experiments, neutrinos are mainly produced via charged-current processes (in meson decays). In this context, it is natural to employ an EFT where the and Z bosons have been integrated out; we denote this low-energy effective theory as the weak effective field theory (WEFT). In neutrino phenomenology, the Wilson coefficients in the WEFT are commonly expressed in terms of NSI parameters. For our purposes, the relevant part of the WEFT Lagrangian is given by (see [30,41])
We assume that all charged fermions are in the mass eigenstate basis. Here, V is the Cabibbo–Kobayashi–Maskawa (CKM) quark mixing matrix, GeV is the Higgs vacuum expectation value, and are the left- and right-handed chirality projection operators (), and (as appears in the tensor term above). We can relate this Lagrangian to the more commonly used LEFT basis, yielding the following correspondence (in the notation of [30]):
where and we use an asterisk to denote complex conjugation. One can perform the tree-level matching to the SMEFT, which was performed in [30]. For completeness, we reproduce it below
where
We are adopting the so-called up basis where the up quark and charged lepton Yukawa matrices are diagonal.
In order to connect the CC-NSI parameters to measurable neutrino observables, we employ a quantum field theory (QFT) framework for neutrino oscillations and interactions [42,43,44,45]. For accelerator neutrino experiments, where neutrinos are produced through pion decay, one finds that the differential event rate for neutrinos produced with flavor , detected with flavor , and energy at a detector at a distance L from the source S is given by [46]
where is the number of target particles in the detector, is the standard model neutrino flux of flavor , and is the standard model charged-current cross section for producing a charged lepton of flavor at neutrino energy . The exponential oscillation term involves (the neutrino mass-squared differences), the baseline L, and the leptonic mixing matrix U (the Pontecorvo–Maki–Nakagawa–Sakata, PMNS matrix). The matrix encodes the NSI effects in the neutrino production process; it is defined as
In Equation (9) and above, , , , and denote the charged-pion, charged-lepton (of flavor ), up-quark, and down-quark masses, respectively.
It is clear from the equation above that accelerator neutrino experiments are sensitive only to the particular combination . It is straightforward to express these effective CC-NSI parameters in terms of the SMEFT WCs. We reproduce here the relevant expression for completeness (taken from [40]):
Here, we define , where the index refers to the flavor of the charged lepton produced.
3. Results
Given the analysis chain introduced in Figure 1, we obtained the current constraints on all SMEFT WCs relevant to pion and kaon decays. The results are shown in Figure 2, Figure 3 and Figure 4.

Figure 2.
Bounds on the CC-NSI that affect pion decay: (a) Bound on due to SMEFT WCs and . (b) Bound on due to SMEFT WC , and on due to . (c) Bound on due to SMEFT WCs and . In black, we show the bounds coming directly from pion or tau decays [47].

Figure 3.
Bounds on the SMEFT WCs that affect pion decay: (a) Bound on . (b) Bounds on and (recall that indices 11 (12) correspond to coefficients entering pion (kaon) decays). (c) Bound on . (d) Bound on . In red we show the bounds coming directly from pion or tau decays [47]. (e) Bound on . In red, we show the bounds coming directly from pion or tau decays [47].

Figure 4.
Bounds on the SMEFT WCs that affect kaon decay: (a) Bound on . (b) Bound on . In red, we show the bounds coming directly from kaon or tau decays [47]. (c) Bound on . In red, we show the bounds coming directly from kaon or tau decays [47]. (d) Bound on . In red, we show the bounds coming directly from kaon or tau decays [47].
In Figure 2, we show the bounds on the CC-NSI parameters relevant for pion decay, namely , , and . By considering only one SMEFT WC nonzero at a time, we obtain the red/blue bands. We also include as black lines the current limits extracted directly from pion or tau decay experiments [47]. In Figure 3, we show the bounds on each SMEFT WC that enters into the prediction of the pion decay rate (again turning on one coefficient at a time). In red, we show the present limits coming directly from pion or tau decays [47]. A similar analysis can be made for the SMEFT WCs that impact the kaon decay. Figure 4 shows the corresponding bounds for kaon decay, where the direct limits from kaon or tau decays [47] are shown in red.
Regarding the SMEFT WCs related to pion decay, as the plots clearly show, the coefficients are among the least constrained by flavio. However, one must also include the bound that comes directly from pion decay, which significantly reduces the maximum allowed values for and . Therefore, we focus on models that can generate the coefficients and .
The complete list of UV models (up to one-loop matching) relevant for pion and kaon decays is provided in the eft-neutrinos (https://gitlab.com/alcherchiglia/eft-neutrinos, accessed on 11 May 2025) repository. As an illustrative example, we consider a UV model containing a leptoquark . Its quantum numbers under the gauge group are . Performing the one-loop matching with SOLD, we obtain
This model also generates other WCs at one-loop matching (such as a contribution to ). In fact, there is already a tree-level contribution to in this model. To suppress such tree-level effects, we restrict the Yukawa couplings to involve only third-generation quarks in the loop. In other words, we only consider the case where . With this choice, the one-loop contribution to vanishes. Therefore, we consider a UV model containing where only the couplings , , , and (and their hermitian conjugate) are nonzero. We also consider that they are real for simplicity. Under these assumptions, we find the allowed region in the plane of vs. . The result is shown in Figure 5.
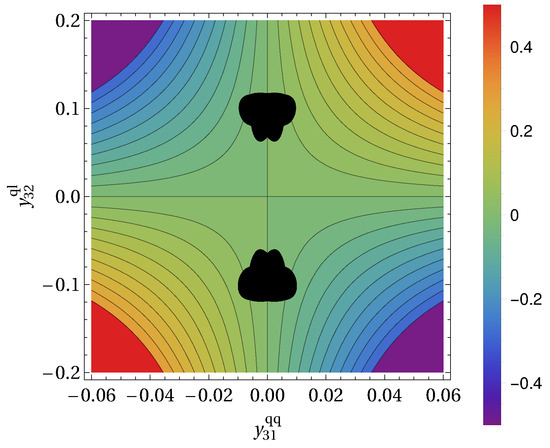
Figure 5.
Allowed region in the parameter plane at 90% C.L. in black. Contour lines (in units of ) indicate the values of , considering and .
In Figure 5, we show in black the 90% C.L. allowed region on the parameters . We checked that the black regions do not appreciably depend on . Thus, it is possible to choose them at the edge of perturbativity (), maximizing the value of . For the UV model under consideration, the mass of the leptoquark can be interpreted as the high scale. We choose it to be . With these values, we also display contour lines corresponding to different values of (the numbers are in units of ). After including the bounds coming from the other WCs, we find that can reach at most TeV−2. Therefore, the maximum allowed in this UV model is much lower than our initial analysis suggested. The main constraint coming from B-decays into Kaons are induced at tree-level.
A similar reasoning applies to the coefficient that affects kaon decay. We verified that an analogous pattern emerges in that case, with the only difference being that is taken to be nonzero (set to 1) instead of .
Another illustrative UV scenario is one in which we add a scalar doublet with quantum numbers . We assume that this new scalar does not mix with the standard Higgs doublet and does not develop a vacuum expectation value. We further assume that only a specific pair of its Yukawa couplings are nonzero, namely and . Under these conditions, there is a tree-level contribution to the operator
We have performed the one-loop matching of this model to the SMEFT, again taking only and to be nonzero. As expected, many other SMEFT operators are induced at one loop. However, the most stringent bound still comes from the pion decay process, setting
Thus, assuming Yukawa couplings, this translates to a lower bound on the new scalar’s mass of order 3.5 TeV.
For the analogous coefficient (entering the kaon decay prediction), one would instead take as the only nonzero d-type Yukawa (in place of ). We performed this analysis and found that the strongest constraint in this case still comes directly from kaon decay, namely
Thus, for couplings, the new scalar’s mass must be of order 7.6 TeV or above.
Other models can be devised and analyzed as well, using the results available in the eft-neutrinos framework. A thorough exploration of all possibilities is beyond the scope of this work, since our primary aim was to demonstrate and exemplify the multi-tool analysis chain depicted in Figure 1.
4. Discussion
Neutrino experiments are now delving into the precision regime. In this scenario, the constraints on possible new phenomena will either become more stringent (if no new effects are observed) or else a clear sign of new physics will emerge. In the latter case, the use of an EFT approach is particularly promising, as it provides a consistent way to connect low-energy observables (such as those measured at neutrino experiments) with possible underlying UV models.
In this work, we have focused on potential new physics effects in accelerator neutrino experiments arising from the modifications of the standard pion or kaon decay processes that produce neutrino beams. The imprints of such new phenomena can be conveniently expressed as effective CC-NSI parameters. Using an EFT approach, we mapped out all UV models containing new fermions or scalars at the one-loop matching level that could affect pion or kaon decay rates. Once a specific model was chosen, we then illustrated how bounds from other measurements (mainly precision flavor experiments) further constrain the maximum allowed CC-NSI values in that scenario. For example, in the leptoquark model discussed in the last section, an NSI coupling that initially appeared to be sizable was shown to be bounded at the level once the full set of constraints was applied. This demonstrates that a seemingly large CC-NSI signal at low energy can be significantly reduced when embedded in a complete UV theory due to the correlated constraints from other observables.
Our findings highlight the importance of an integrated multi-scale analysis for the neutrino sector. By combining state-of-the-art EFT tools and computational codes, we provide a blueprint for interpreting future neutrino experimental results within a broad landscape of new physics models. If upcoming facilities such as DUNE or Hyper-Kamiokande observe anomalies in neutrino oscillation data, our EFT-based framework can be immediately applied to pinpoint which classes of UV models could explain the observations. Conversely, if no deviations from the Standard Model are seen, the same framework will translate the improved experimental sensitivities into tighter bounds on NSI parameters and, in turn, on the allowed scale of new physics.
Looking ahead, there are several directions in which this work can be extended. While we restricted our attention to UV completions with new scalars or fermions (for which automated one-loop matching is currently available), future studies could incorporate other types of mediators (such as new gauge bosons) or consider higher-order matching effects. The methodology presented here for meson decays can also be adapted to investigate NSIs in neutrino detection or propagation. Ultimately, as neutrino experiments push the frontiers of precision, maintaining a strong interplay between theoretical EFT techniques and experimental efforts will be crucial for uncovering any subtle hints of new physics.
Funding
A.C. acknowledges support from the National Council for Scientific and Technological Development (CNPq), Brazil.
Data Availability Statement
The code and data supporting this work are available in the GitLab repository eft-neutrinos (https://gitlab.com/alcherchiglia/eft-neutrinos, accessed on 11 May 2025).
Conflicts of Interest
The author declares no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| BSM | Beyond standard model |
| CC-NSI | Charged current non-standard interactions |
| DUNE | Deep underground neutrino experiment |
| EFT | Effective field theory |
| Hyper-K | Hyper-Kamiokande |
| IR | Infrared |
| LHC | Large Hadron collider |
| LEFT | Low energy effective field theory |
| NC-NSI | Neutral current non-standard interactions |
| NSI | Non-standard interactions |
| SMEFT | Standard model effective field theory |
| UV | Ultra-violet |
| WEFT | Weak effective field theory |
| WC | Wilson coefficient |
References
- Abi, B.; Acciarri, R.; Acero, M.A.; Adamowski, M.; Albright, C.H.; Andrieu, J.; Andrews, M.; Anjos, R.; Aoki, M.; Asaadi, J.; et al. Deep Underground Neutrino Experiment (DUNE), Far Detector Technical Design Report, Volume II: DUNE Physics. arXiv 2020, arXiv:2002.03005. [Google Scholar]
- Abi, B.; Acciarri, R.; Acero, M.A.; Adamowski, M.; Albright, C.H.; Andrieu, J.; Andrews, M.; Anjos, R.; Aoki, M.; Asaadi, J.; et al. Prospects for beyond the Standard Model physics searches at the Deep Underground Neutrino Experiment. Eur. Phys. J. C 2021, 81, 322. [Google Scholar] [CrossRef]
- Abe, K.; Bronner, C.; Haga, Y.; Hayato, Y.; Ikeda, M.; Iyogi, K.; Kameda, J.; Kanemura, Y.; Kato, Y.; Mine, S.; et al. Hyper-Kamiokande Design Report. arXiv 2018, arXiv:1805.04163. [Google Scholar]
- Mammen Abraham, R.; Ahdida, C.; Ariga, A.; Ariga, T.; Bai, Y.; Boyd, J.; Cheng, C.; Chou, J.P.; De Vries, J.; Dobson, M.; et al. First Measurement of νe and νμ Interaction Cross Sections at the LHC with FASER’s Emulsion Detector. Phys. Rev. Lett. 2024, 133, 021802. [Google Scholar] [CrossRef]
- Abreu, H.; Ahdida, C.; Ariga, A.; Ariga, T.; Bai, Y.; Boyd, J.; Cheng, C.; Chou, J.P.; De Vries, J.; Dobson, M.; et al. First Direct Observation of Collider Neutrinos with FASER at the LHC. Phys. Rev. Lett. 2023, 131, 031801. [Google Scholar] [CrossRef]
- Albanese, R.; Ahdida, C.; Aleksandrov, A.; An, F.; Andreazza, A.; Andrieu, B.; Arduini, G.; Ariga, A.; Ariga, T.; Bai, Y.; et al. Observation of Collider Muon Neutrinos with the SND@LHC Experiment. Phys. Rev. Lett. 2023, 131, 031802. [Google Scholar] [CrossRef]
- Cortina Gil, E.; Romano, A.; Fantechi, R.; Hahn, F.; Lamanna, M.; Sozzi, M.; Ceccucci, A.; Cenci, P.; Ruggiero, G.; Lurkin, N.; et al. Measurement of the very rare K+→π+ν decay. J. High Energy Phys. 2021, 6, 93. [Google Scholar] [CrossRef]
- Li, T.; Ma, X.D.; Schmidt, M.A. Implication of K→πν for generic neutrino interactions in effective field theories. Phys. Rev. D 2020, 101, 055019. [Google Scholar] [CrossRef]
- Gorbahn, M.; Moldanazarova, U.; Sieja, K.H.; Stamou, E.; Tabet, M. The anatomy of K+→π+ν distributions. Eur. Phys. J. C 2024, 84, 680. [Google Scholar] [CrossRef]
- Deppisch, F.F.; Fridell, K.; Harz, J. Constraining lepton number violating interactions in rare kaon decays. J. High Energy Phys. 2020, 12, 186. [Google Scholar] [CrossRef]
- Wolfenstein, L. Neutrino Oscillations in Matter. Phys. Rev. D 1978, 17, 2369–2374. [Google Scholar] [CrossRef]
- Ohlsson, T. Status of non-standard neutrino interactions. Rept. Prog. Phys. 2013, 76, 044201. [Google Scholar] [CrossRef]
- Farzan, Y.; Tortola, M. Neutrino oscillations and Non-Standard Interactions. Front. Phys. 2018, 6, 10. [Google Scholar] [CrossRef]
- Coloma, P.; Gonzalez-Garcia, M.C.; Maltoni, M.; Pinheiro, J.a.P.; Urrea, S. Global constraints on non-standard neutrino interactions with quarks and electrons. J. High Energy Phys. 2023, 8, 32. [Google Scholar] [CrossRef]
- Bhupal Dev, P.S.; Babu, K.S.; Brdar, V.; Dutta, B.; Fernandez-Martinez, E.; Gonzalez-Garcia, M.C.; Han, T.; Lindner, M.; Machado, P.A.N.; Maltoni, M.; et al. Neutrino Non-Standard Interactions: A Status Report. SciPost Phys. Proc. 2019, 2, 001. [Google Scholar] [CrossRef]
- Arguelles, C.A.; Brdar, V.; Coloma, P.; Denton, P.B.; de Gouvêa, A.; Kelly, K.J.; Machado, P.A.N.; Maltoni, M.; Parke, S.; Peñaranda, S.; et al. Snowmass white paper: Beyond the standard model effects on neutrino flavor: Submitted to the proceedings of the US community study on the future of particle physics (Snowmass 2021). Eur. Phys. J. C 2023, 83, 15. [Google Scholar] [CrossRef]
- Mikheyev, S.P.; Smirnov, A.Y. Resonance Amplification of Oscillations in Matter and Spectroscopy of Solar Neutrinos. Sov. J. Nucl. Phys. 1985, 42, 913–917. [Google Scholar]
- Bergmann, S.; Grossman, Y.; Pierce, D.M. Can lepton flavor violating interactions explain the atmospheric neutrino problem? Phys. Rev. D 2000, 61, 053005. [Google Scholar] [CrossRef]
- Antusch, S.; Baumann, J.P.; Fernandez-Martinez, E. Non-Standard Neutrino Interactions with Matter from Physics Beyond the Standard Model. Nucl. Phys. B 2009, 810, 369–388. [Google Scholar] [CrossRef]
- Gavela, M.B.; Hernandez, D.; Ota, T.; Winter, W. Large gauge invariant non-standard neutrino interactions. Phys. Rev. D 2009, 79, 013007. [Google Scholar] [CrossRef]
- Meloni, D.; Ohlsson, T.; Winter, W.; Zhang, H. Non-standard interactions versus non-unitary lepton flavor mixing at a neutrino factory. J. High Energy Phys. 2010, 4, 41. [Google Scholar] [CrossRef]
- Altmannshofer, W.; Tammaro, M.; Zupan, J. Non-standard neutrino interactions and low energy experiments. J. High Energy Phys. 2019, 9, 83, Erratum in J. High Energy Phys. 2021, 11, 113. [Google Scholar] [CrossRef]
- Babu, K.S.; Dev, P.S.B.; Jana, S.; Thapa, A. Non-Standard Interactions in Radiative Neutrino Mass Models. J. High Energy Phys. 2020, 3, 6. [Google Scholar] [CrossRef]
- Bischer, I.; Rodejohann, W. General neutrino interactions from an effective field theory perspective. Nucl. Phys. B 2019, 947, 114746. [Google Scholar] [CrossRef]
- Davidson, S.; Gorbahn, M. Charged lepton flavor change and nonstandard neutrino interactions. Phys. Rev. D 2020, 101, 015010. [Google Scholar] [CrossRef]
- Terol-Calvo, J.; Tórtola, M.; Vicente, A. High-energy constraints from low-energy neutrino nonstandard interactions. Phys. Rev. D 2020, 101, 095010. [Google Scholar] [CrossRef]
- Babu, K.S.; Gonçalves, D.; Jana, S.; Machado, P.A.N. Neutrino Non-Standard Interactions: Complementarity Between LHC and Oscillation Experiments. Phys. Lett. B 2021, 815, 136131. [Google Scholar] [CrossRef]
- Du, Y.; Li, H.L.; Tang, J.; Vihonen, S.; Yu, J.H. Non-standard interactions in SMEFT confronted with terrestrial neutrino experiments. J. High Energy Phys. 2021, 3, 19. [Google Scholar] [CrossRef]
- Du, Y.; Li, H.L.; Tang, J.; Vihonen, S.; Yu, J.H. Exploring SMEFT induced nonstandard interactions: From COHERENT to neutrino oscillations. Phys. Rev. D 2022, 105, 075022. [Google Scholar] [CrossRef]
- Jenkins, E.E.; Manohar, A.V.; Stoffer, P. Low-Energy Effective Field Theory below the Electroweak Scale: Operators and Matching. J. High Energy Phys. 2018, 3, 16, Erratum in J. High Energy Phys. 2023, 12, 43. [Google Scholar] [CrossRef]
- Dekens, W.; Stoffer, P. Low-energy effective field theory below the electroweak scale: Matching at one loop. J. High Energy Phys. 2019, 10, 197, Erratum in J. High Energy Phys. 2022, 11, 148. [Google Scholar] [CrossRef]
- Straub, D.M. Flavio: A Python package for flavour and precision phenomenology in the Standard Model and beyond. arXiv 2018, arXiv:1810.08132. [Google Scholar]
- Aebischer, J.; Kumar, J.; Straub, D.M. Wilson: A Python package for the running and matching of Wilson coefficients above and below the electroweak scale. Eur. Phys. J. C 2018, 78, 1026. [Google Scholar] [CrossRef]
- Aebischer, J.; Kumar, J.; Stangl, P.; Straub, D.M. A Global Likelihood for Precision Constraints and Flavour Anomalies. Eur. Phys. J. C 2019, 79, 509. [Google Scholar] [CrossRef]
- Carmona, A.; Lazopoulos, A.; Olgoso, P.; Santiago, J. Matchmakereft: Automated tree-level and one-loop matching. SciPost Phys. 2022, 12, 198. [Google Scholar] [CrossRef]
- Fuentes-Martín, J.; König, M.; Pagès, J.; Thomsen, A.E.; Wilsch, F. A proof of concept for matchete: An automated tool for matching effective theories. Eur. Phys. J. C 2023, 83, 662. [Google Scholar] [CrossRef]
- Guedes, G.; Olgoso, P.; Santiago, J. Towards the one loop IR/UV dictionary in the SMEFT: One loop generated operators from new scalars and fermions. SciPost Phys. 2023, 15, 143. [Google Scholar] [CrossRef]
- Guedes, G.; Olgoso, P. From the EFT to the UV: The complete SMEFT one-loop dictionary. arXiv 2024, arXiv:2412.14253. [Google Scholar]
- de Blas, J.; Criado, J.C.; Perez-Victoria, M.; Santiago, J. Effective description of general extensions of the Standard Model: The complete tree-level dictionary. J. High Energy Phys. 2018, 3, 109. [Google Scholar] [CrossRef]
- Cherchiglia, A.; Santiago, J. DUNE potential as a new physics probe. J. High Energy Phys. 2024, 3, 18. [Google Scholar] [CrossRef]
- Cirigliano, V.; Jenkins, J.; Gonzalez-Alonso, M. Semileptonic decays of light quarks beyond the Standard Model. Nucl. Phys. B 2010, 830, 95–115. [Google Scholar] [CrossRef]
- Giunti, C.; Kim, C.W.; Lee, J.A.; Lee, U.W. On the treatment of neutrino oscillations without resort to weak eigenstates. Phys. Rev. D 1993, 48, 4310–4317. [Google Scholar] [CrossRef]
- Akhmedov, E.K.; Kopp, J. Neutrino Oscillations: Quantum Mechanics vs. Quantum Field Theory. J. High Energy Phys. 2010, 4, 8, Erratum in J. High Energy Phys. 2013, 10, 52. [Google Scholar] [CrossRef]
- Kobach, A.; Manohar, A.V.; McGreevy, J. Neutrino Oscillation Measurements Computed in Quantum Field Theory. Phys. Lett. B 2018, 783, 59–75. [Google Scholar] [CrossRef]
- Falkowski, A.; González-Alonso, M.; Tabrizi, Z. Consistent QFT description of non-standard neutrino interactions. J. High Energy Phys. 2020, 11, 48. [Google Scholar] [CrossRef]
- Bresó-Pla, V.; Falkowski, A.; González-Alonso, M.; Monsálvez-Pozo, K. EFT analysis of New Physics at COHERENT. J. High Energy Phys. 2023, 5, 74. [Google Scholar] [CrossRef]
- Falkowski, A.; González-Alonso, M.; Kopp, J.; Soreq, Y.; Tabrizi, Z. EFT at FASERν. J. High Energy Phys. 2021, 10, 86. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).