Properties of the Object HESS J1731-347 as a Twin Compact Star
Abstract
1. Introduction
2. Equations of State for Compact Star Twins Describing HESS J1731-347
2.1. Hadronic EoS
2.2. Quark Matter EoS
2.2.1. CSS Model
2.2.2. Non-Local NJL Model
2.2.3. Maxwell Construction and Seidov Criterion for Stellar Stability
2.2.4. QCD Conformality and Trace Anomaly Inside Twin Compact Stars
3. Results
3.1. Compact Star Structure
Moment of Inertia and Tidal Deformabilities
3.2. Energy Release at the Onset of Deconfinement Leading to the Compact Star Twins Transition
3.3. Rotating Compact Stars
3.4. f-Modes and Damping Times
3.5. The Crust of Twin Compact Stars
4. Discussion
5. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QM | Quark Matter |
| RHIC | Relativistic Heavy Ion Collisions |
| EoS | Equation of State |
| GW | Gravitational Waves |
| NICER | Neutron Star Composition Explorer |
| QCD | Quantum Chromodynamics |
| RMF | Relativistic Mean Field |
| OGE | One Gluon Exchange |
| MFA | Mean Field Approximation |
| TOV | Tolman–Oppenheimer–Volkoff |
| MoI | Moment of Inertia |
| TD | Tidal deformability |
| MSP | Millisecond Pulsar |
| LMXB | Low-Mass X-ray Binary |
Appendix A
- central energy density;
- M gravitational mass;
- rest mass;
- radius at the equator (circumferential, i.e., is the proper circumference);
- angular velocity;
- angular velocity of a particle in circular orbit at the equator;
- rotational/gravitational energy;
- angular momentum;
- I moment of inertia;
- height from surface of last stable co-rotating circular orbit in equatorial plane (circumferential);
- height from surface of last stable counter-rotating circular orbit in equatorial plane (circumferential);
- polar redshift;
- backward equatorial redshift;
- forward equatorial redshift;
- ratio of central value of potential ω to Ω;
- coordinate equatorial radius;
- axes ratio (polar to equatorial).
| M | I | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [ g cm−3] | [] | [] | [km] | [ s−1] | [ s−1] | [ g cm2] | [km] | [km] | [km] | |||||||
| 2.6 | 0.2466 | 0.2486 | 23.33 | 0.1608 | 0.1608 | 0.0179 | 0.02959 | 0.1617 | 8.927 | 0 | 0 | 0.02428 | 0.1545 | −0.1059 | 0.09017 | 0.6256 |
| 2.716 | 0.2998 | 0.3034 | 21.57 | 0.1996 | 0.1996 | 0.02524 | 0.04851 | 0.2136 | 15.83 | 0 | 0 | 0.03232 | 0.1838 | −0.119 | 0.1063 | 0.5757 |
| 2.838 | 0.371 | 0.3772 | 20.44 | 0.2411 | 0.2411 | 0.03431 | 0.08086 | 0.2947 | 27.73 | 0 | 0 | 0.04289 | 0.2193 | −0.1332 | 0.1263 | 0.542 |
| 2.965 | 0.5681 | 0.5837 | 20.05 | 0.3088 | 0.3088 | 0.05714 | 0.2192 | 0.624 | 83.72 | 0 | 0 | 0.06974 | 0.3012 | −0.1606 | 0.1654 | 0.523 |
| 3.098 | 0.5975 | 0.6147 | 20.09 | 0.3161 | 0.3161 | 0.06022 | 0.2456 | 0.683 | 94.45 | 0 | 0 | 0.07363 | 0.3125 | −0.1639 | 0.1743 | 0.5228 |
| 3.237 | 0.5596 | 0.5747 | 19.95 | 0.3086 | 0.3087 | 0.05594 | 0.2103 | 0.5987 | 78.91 | 0 | 0 | 0.06893 | 0.2989 | −0.1599 | 0.1711 | 0.5207 |
| 3.382 | 0.54 | 0.554 | 19.86 | 0.3052 | 0.3052 | 0.05359 | 0.1927 | 0.5551 | 71.03 | 0 | 0 | 0.0666 | 0.292 | −0.1578 | 0.1701 | 0.519 |
| 3.533 | 0.532 | 0.5455 | 19.8 | 0.3041 | 0.3041 | 0.05256 | 0.1855 | 0.5361 | 67.64 | 0 | 0 | 0.0657 | 0.2894 | −0.157 | 0.1701 | 0.5177 |
| 3.692 | 0.5277 | 0.541 | 19.77 | 0.3035 | 0.3035 | 0.052 | 0.1818 | 0.5263 | 65.91 | 0 | 0 | 0.06521 | 0.2879 | −0.1565 | 0.17 | 0.5171 |
| 3.857 | 0.5285 | 0.5419 | 19.78 | 0.3036 | 0.3036 | 0.05211 | 0.1825 | 0.5283 | 66.25 | 0 | 0 | 0.06531 | 0.2882 | −0.1566 | 0.17 | 0.5173 |
| 4.03 | 0.5337 | 0.5473 | 19.81 | 0.3043 | 0.3044 | 0.05277 | 0.187 | 0.54 | 68.32 | 0 | 0 | 0.06589 | 0.2899 | −0.1572 | 0.1701 | 0.518 |
| 4.21 | 0.5395 | 0.5534 | 19.86 | 0.3051 | 0.3051 | 0.05352 | 0.1922 | 0.5538 | 70.8 | 0 | 0 | 0.06653 | 0.2918 | −0.1578 | 0.1701 | 0.5189 |
| 4.399 | 0.5503 | 0.5648 | 19.91 | 0.3069 | 0.3069 | 0.05483 | 0.2018 | 0.5779 | 75.13 | 0 | 0 | 0.06781 | 0.2956 | −0.1589 | 0.1706 | 0.52 |
| 4.596 | 0.5629 | 0.5782 | 19.97 | 0.3093 | 0.3093 | 0.05633 | 0.2133 | 0.606 | 80.24 | 0 | 0 | 0.06934 | 0.3001 | −0.1602 | 0.1714 | 0.5209 |
| 4.802 | 0.578 | 0.5941 | 20.02 | 0.3122 | 0.3122 | 0.05805 | 0.2271 | 0.6394 | 86.37 | 0 | 0 | 0.07119 | 0.3054 | −0.1618 | 0.1726 | 0.5218 |
| 5.017 | 0.5927 | 0.6096 | 20.07 | 0.3151 | 0.3151 | 0.05969 | 0.241 | 0.6722 | 92.44 | 0 | 0 | 0.07302 | 0.3108 | −0.1634 | 0.1739 | 0.5226 |
| 5.242 | 0.6021 | 0.6196 | 20.1 | 0.317 | 0.317 | 0.06073 | 0.2501 | 0.6934 | 96.39 | 0 | 0 | 0.07421 | 0.3142 | −0.1644 | 0.1746 | 0.523 |
| 5.477 | 0.6081 | 0.626 | 20.12 | 0.3182 | 0.3182 | 0.06138 | 0.256 | 0.7071 | 98.97 | 0 | 0 | 0.07496 | 0.3163 | −0.165 | 0.1749 | 0.5232 |
| 5.722 | 0.6093 | 0.6272 | 20.13 | 0.3184 | 0.3184 | 0.0615 | 0.2571 | 0.7097 | 99.47 | 0 | 0 | 0.0751 | 0.3167 | −0.1651 | 0.175 | 0.5233 |
| 5.978 | 0.5725 | 0.5882 | 20.0 | 0.3111 | 0.3111 | 0.05743 | 0.222 | 0.6272 | 84.11 | 0 | 0 | 0.07051 | 0.3035 | −0.1613 | 0.1721 | 0.5215 |
| 6.246 | 0.507 | 0.5191 | 18.89 | 0.318 | 0.318 | 0.04736 | 0.1572 | 0.4344 | 50.18 | 0 | 0 | 0.06551 | 0.2886 | −0.1567 | 0.1817 | 0.4941 |
| 6.526 | 0.5734 | 0.5896 | 17.67 | 0.3739 | 0.3739 | 0.05098 | 0.1943 | 0.4568 | 52.78 | 0 | 0 | 0.08079 | 0.3321 | −0.169 | 0.2132 | 0.4578 |
| 6.818 | 0.6852 | 0.71 | 16.8 | 0.4411 | 0.4411 | 0.05863 | 0.2782 | 0.5543 | 68.0 | 0 | 0 | 0.1047 | 0.3974 | −0.1853 | 0.2534 | 0.4294 |
| 7.124 | 0.82 | 0.8575 | 16.35 | 0.5028 | 0.5028 | 0.06766 | 0.4044 | 0.7069 | 89.71 | 0 | 0 | 0.1332 | 0.4727 | −0.2012 | 0.2953 | 0.4113 |
| 7.443 | 0.9643 | 1.018 | 16.11 | 0.5568 | 0.5569 | 0.07659 | 0.5688 | 0.8978 | 115.8 | 0 | 0 | 0.1648 | 0.5538 | −0.2159 | 0.337 | 0.3987 |
| 7.776 | 1.112 | 1.186 | 15.99 | 0.6045 | 0.6045 | 0.0851 | 0.7707 | 1.121 | 147.0 | 0 | 0 | 0.1986 | 0.6398 | −0.2293 | 0.3782 | 0.3888 |
| 8.124 | 1.257 | 1.354 | 15.91 | 0.6469 | 0.6469 | 0.0926 | 1.001 | 1.36 | 179.5 | 0 | 1.107 | 0.2339 | 0.7292 | −0.2414 | 0.4174 | 0.3801 |
| 8.488 | 1.396 | 1.518 | 15.86 | 0.6845 | 0.6845 | 0.09938 | 1.256 | 1.612 | 213.9 | 0 | 2.716 | 0.2702 | 0.8213 | −0.2523 | 0.4544 | 0.3722 |
| 8.869 | 1.519 | 1.665 | 15.81 | 0.7155 | 0.7156 | 0.1047 | 1.498 | 1.839 | 239.3 | 0 | 4.067 | 0.3042 | 0.9078 | −0.2614 | 0.4863 | 0.3653 |
| 9.266 | 1.646 | 1.821 | 15.76 | 0.7478 | 0.7478 | 0.11 | 1.786 | 2.099 | 273.6 | 0 | 5.581 | 0.3423 | 1.007 | −0.2709 | 0.5193 | 0.3578 |
| 9.681 | 1.753 | 1.954 | 15.7 | 0.7746 | 0.7747 | 0.1139 | 2.036 | 2.31 | 294.9 | 0 | 6.788 | 0.3769 | 1.097 | −0.2784 | 0.5471 | 0.351 |
| 10.11 | 1.862 | 2.092 | 15.63 | 0.8019 | 0.802 | 0.1182 | 2.326 | 2.549 | 325.8 | 0 | 8.121 | 0.4149 | 1.198 | −0.2864 | 0.5755 | 0.3439 |
| 10.57 | 1.954 | 2.21 | 15.55 | 0.8261 | 0.8261 | 0.1212 | 2.576 | 2.74 | 345.0 | 0 | 9.21 | 0.4499 | 1.292 | −0.293 | 0.6 | 0.3372 |
| 11.04 | 2.038 | 2.319 | 15.46 | 0.8494 | 0.8495 | 0.1237 | 2.814 | 2.912 | 360.9 | 0 | 10.22 | 0.4847 | 1.388 | −0.2992 | 0.6226 | 0.3304 |
| 11.54 | 2.11 | 2.411 | 15.36 | 0.8705 | 0.8705 | 0.1257 | 3.017 | 3.046 | 370.4 | 0 | 11.07 | 0.517 | 1.477 | −0.3045 | 0.6428 | 0.3241 |
| 12.05 | 2.174 | 2.497 | 15.26 | 0.891 | 0.891 | 0.1273 | 3.21 | 3.167 | 378.9 | 0 | 11.87 | 0.549 | 1.567 | −0.3095 | 0.6616 | 0.3179 |
| 12.59 | 2.246 | 2.595 | 15.15 | 0.9137 | 0.9138 | 0.1297 | 3.461 | 3.329 | 400.0 | 0 | 12.84 | 0.5865 | 1.678 | −0.3155 | 0.6819 | 0.3112 |
| 13.16 | 2.299 | 2.668 | 15.03 | 0.9337 | 0.9338 | 0.1309 | 3.635 | 3.421 | 406.0 | 0 | 13.54 | 0.6186 | 1.772 | −0.32 | 0.6987 | 0.305 |
| 13.75 | 2.347 | 2.733 | 14.91 | 0.9533 | 0.9533 | 0.132 | 3.793 | 3.497 | 410.5 | 0.1641 | 14.18 | 0.6501 | 1.866 | −0.3244 | 0.7145 | 0.2991 |
| 14.36 | 2.39 | 2.793 | 14.79 | 0.9726 | 0.9726 | 0.133 | 3.945 | 3.565 | 415.6 | 0.3427 | 14.78 | 0.6814 | 1.963 | −0.3285 | 0.7295 | 0.2932 |
| 15.0 | 2.429 | 2.85 | 14.65 | 0.9922 | 0.9922 | 0.1338 | 4.089 | 3.622 | 419.7 | 0.5065 | 15.36 | 0.7132 | 2.062 | −0.3326 | 0.7439 | 0.2874 |
| 15.68 | 2.46 | 2.893 | 14.52 | 1.011 | 1.011 | 0.1342 | 4.194 | 3.646 | 418.1 | 0.6379 | 15.8 | 0.7422 | 2.154 | −0.3361 | 0.7568 | 0.2818 |
| 16.38 | 2.486 | 2.93 | 14.38 | 1.029 | 1.029 | 0.1345 | 4.283 | 3.658 | 415.4 | 0.7613 | 16.21 | 0.7706 | 2.245 | −0.3395 | 0.7689 | 0.2765 |
| 17.11 | 2.507 | 2.961 | 14.24 | 1.047 | 1.047 | 0.1346 | 4.359 | 3.658 | 411.6 | 0.8775 | 16.56 | 0.7982 | 2.335 | −0.3427 | 0.7805 | 0.2712 |
| 17.88 | 2.526 | 2.989 | 14.09 | 1.066 | 1.066 | 0.1348 | 4.429 | 3.652 | 408.3 | 0.9884 | 16.9 | 0.8259 | 2.427 | −0.3458 | 0.7916 | 0.2661 |
| 18.68 | 2.544 | 3.014 | 13.95 | 1.085 | 1.085 | 0.1349 | 4.498 | 3.645 | 405.9 | 1.099 | 17.23 | 0.8542 | 2.523 | −0.349 | 0.8026 | 0.261 |
| 19.52 | 2.564 | 3.045 | 13.81 | 1.105 | 1.105 | 0.1355 | 4.596 | 3.656 | 409.4 | 1.227 | 17.64 | 0.8862 | 2.638 | −0.3526 | 0.8139 | 0.2557 |
| 20.39 | 2.575 | 3.062 | 13.66 | 1.124 | 1.124 | 0.1355 | 4.641 | 3.63 | 405.2 | 1.32 | 17.89 | 0.9133 | 2.735 | −0.3555 | 0.8236 | 0.2508 |
| 21.31 | 2.582 | 3.073 | 13.52 | 1.141 | 1.141 | 0.1353 | 4.671 | 3.596 | 399.8 | 1.398 | 18.1 | 0.9384 | 2.825 | −0.3581 | 0.8324 | 0.2463 |
| 22.26 | 2.586 | 3.077 | 13.39 | 1.158 | 1.158 | 0.1351 | 4.684 | 3.555 | 394.0 | 1.464 | 18.25 | 0.9605 | 2.905 | −0.3604 | 0.8404 | 0.2423 |
| 23.26 | 2.588 | 3.082 | 13.25 | 1.175 | 1.175 | 0.1347 | 4.696 | 3.512 | 387.4 | 1.523 | 18.4 | 0.9832 | 2.989 | −0.3626 | 0.8478 | 0.2382 |
| 24.3 | 2.587 | 3.08 | 13.13 | 1.19 | 1.19 | 0.1343 | 4.691 | 3.464 | 381.1 | 1.573 | 18.48 | 1.002 | 3.058 | −0.3644 | 0.8545 | 0.2348 |
| 25.39 | 2.584 | 3.075 | 13.02 | 1.205 | 1.205 | 0.1339 | 4.679 | 3.414 | 374.2 | 1.616 | 18.54 | 1.019 | 3.123 | −0.3661 | 0.8606 | 0.2315 |
| 26.52 | 2.58 | 3.07 | 12.9 | 1.219 | 1.219 | 0.1334 | 4.667 | 3.365 | 367.9 | 1.656 | 18.6 | 1.036 | 3.187 | −0.3678 | 0.8665 | 0.2284 |
| 27.71 | 2.575 | 3.06 | 12.8 | 1.232 | 1.232 | 0.1329 | 4.644 | 3.313 | 361.4 | 1.69 | 18.62 | 1.05 | 3.24 | −0.3691 | 0.8718 | 0.2256 |
| 28.95 | 2.567 | 3.048 | 12.69 | 1.245 | 1.245 | 0.1323 | 4.614 | 3.258 | 354.1 | 1.719 | 18.62 | 1.063 | 3.288 | −0.3703 | 0.8767 | 0.2229 |
| 30.25 | 2.56 | 3.037 | 12.59 | 1.257 | 1.258 | 0.1317 | 4.585 | 3.205 | 347.3 | 1.745 | 18.62 | 1.075 | 3.336 | −0.3715 | 0.8814 | 0.2204 |
| M | I | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [ g cm−3] | [] | [] | [km] | [ s−1] | [ s−1] | [ g cm2] | [km] | [km] | [km] | |||||||
| 2.6 | 0.2466 | 0.2486 | 23.33 | 0.1608 | 0.1608 | 0.0179 | 0.02959 | 0.1617 | 8.927 | 0 | 0 | 0.02428 | 0.1545 | −0.1059 | 0.09017 | 0.6256 |
| 2.673 | 0.2778 | 0.2807 | 22.16 | 0.1844 | 0.1845 | 0.02224 | 0.0401 | 0.1911 | 12.67 | 0 | 0 | 0.029 | 0.172 | −0.1139 | 0.09978 | 0.5925 |
| 2.748 | 0.3159 | 0.32 | 21.24 | 0.2098 | 0.2098 | 0.02735 | 0.05507 | 0.2306 | 18.15 | 0 | 0 | 0.03471 | 0.1921 | −0.1225 | 0.111 | 0.5659 |
| 2.825 | 0.3609 | 0.3666 | 20.56 | 0.2358 | 0.2358 | 0.03304 | 0.07568 | 0.2821 | 25.71 | 0 | 0 | 0.04139 | 0.2144 | −0.1314 | 0.1236 | 0.5455 |
| 2.904 | 0.4141 | 0.4221 | 20.07 | 0.2622 | 0.2622 | 0.03935 | 0.1043 | 0.3496 | 36.2 | 0 | 0 | 0.04924 | 0.2395 | −0.1406 | 0.138 | 0.53 |
| 2.985 | 0.4767 | 0.4877 | 19.74 | 0.2887 | 0.2887 | 0.04621 | 0.1438 | 0.4376 | 50.75 | 0 | 0 | 0.05841 | 0.2677 | −0.1501 | 0.1543 | 0.5185 |
| 3.068 | 0.5495 | 0.5646 | 19.56 | 0.315 | 0.315 | 0.05349 | 0.1975 | 0.551 | 70.15 | 0 | 0 | 0.06902 | 0.299 | −0.1599 | 0.1725 | 0.5103 |
| 3.154 | 0.634 | 0.6545 | 19.48 | 0.3409 | 0.3409 | 0.06116 | 0.2705 | 0.6974 | 96.06 | 0 | 0 | 0.08135 | 0.3343 | −0.1699 | 0.1928 | 0.5047 |
| 3.243 | 0.7292 | 0.7566 | 19.49 | 0.3658 | 0.3658 | 0.06889 | 0.3661 | 0.8796 | 128.6 | 0 | 0 | 0.09527 | 0.373 | −0.1799 | 0.2148 | 0.501 |
| 3.333 | 0.8694 | 0.9086 | 19.66 | 0.3951 | 0.3951 | 0.07933 | 0.5351 | 1.19 | 185.6 | 0 | 0 | 0.1156 | 0.4281 | −0.1927 | 0.2432 | 0.4995 |
| 3.427 | 1.137 | 1.202 | 20.34 | 0.4308 | 0.4308 | 0.09799 | 0.9616 | 1.962 | 332.0 | 0 | 0 | 0.1531 | 0.5271 | −0.2123 | 0.2866 | 0.5064 |
| 3.523 | 1.452 | 1.553 | 21.31 | 0.4555 | 0.4555 | 0.1178 | 1.643 | 3.171 | 567.6 | 0 | 1.277 | 0.1962 | 0.6395 | −0.2308 | 0.3313 | 0.5187 |
| 3.621 | 1.66 | 1.787 | 21.95 | 0.4667 | 0.4667 | 0.1296 | 2.195 | 4.133 | 754.4 | 0 | 3.341 | 0.2245 | 0.7133 | −0.2412 | 0.3597 | 0.5265 |
| 3.723 | 1.717 | 1.851 | 22.1 | 0.47 | 0.47 | 0.1326 | 2.356 | 4.405 | 805.6 | 0 | 3.901 | 0.2326 | 0.7343 | −0.2439 | 0.3702 | 0.5279 |
| 3.827 | 1.709 | 1.842 | 22.06 | 0.4701 | 0.4701 | 0.1321 | 2.329 | 4.354 | 794.6 | 0 | 3.817 | 0.2317 | 0.7318 | −0.2436 | 0.3712 | 0.5272 |
| 3.934 | 1.703 | 1.835 | 22.03 | 0.47 | 0.47 | 0.1317 | 2.31 | 4.319 | 787.4 | 0 | 3.753 | 0.2309 | 0.7298 | −0.2433 | 0.3712 | 0.5268 |
| 4.044 | 1.702 | 1.835 | 22.03 | 0.47 | 0.47 | 0.1318 | 2.309 | 4.319 | 787.3 | 0 | 3.753 | 0.2309 | 0.7297 | −0.2433 | 0.3712 | 0.5268 |
| 4.157 | 1.706 | 1.839 | 22.05 | 0.47 | 0.47 | 0.132 | 2.321 | 4.34 | 791.6 | 0 | 3.79 | 0.2313 | 0.731 | −0.2435 | 0.3712 | 0.527 |
| 4.274 | 1.711 | 1.845 | 22.07 | 0.4701 | 0.4701 | 0.1323 | 2.337 | 4.368 | 797.5 | 0 | 3.841 | 0.232 | 0.7327 | −0.2437 | 0.3712 | 0.5274 |
| 4.393 | 1.71 | 1.844 | 22.06 | 0.4701 | 0.4701 | 0.1322 | 2.334 | 4.363 | 796.3 | 0 | 3.832 | 0.2318 | 0.7323 | −0.2436 | 0.3712 | 0.5273 |
| 4.516 | 1.709 | 1.842 | 22.06 | 0.4701 | 0.4701 | 0.1321 | 2.329 | 4.354 | 794.5 | 0 | 3.816 | 0.2316 | 0.7318 | −0.2436 | 0.3712 | 0.5272 |
| 4.643 | 1.707 | 1.84 | 22.05 | 0.47 | 0.47 | 0.132 | 2.323 | 4.343 | 792.2 | 0 | 3.796 | 0.2314 | 0.7312 | −0.2435 | 0.3712 | 0.5271 |
| 4.773 | 1.705 | 1.837 | 22.04 | 0.47 | 0.47 | 0.1319 | 2.317 | 4.332 | 790.0 | 0 | 3.776 | 0.2311 | 0.7305 | −0.2434 | 0.3712 | 0.5269 |
| 4.906 | 1.703 | 1.835 | 22.03 | 0.47 | 0.47 | 0.1318 | 2.309 | 4.319 | 787.4 | 0 | 3.754 | 0.2309 | 0.7297 | −0.2433 | 0.3712 | 0.5268 |
| 5.044 | 1.7 | 1.832 | 22.02 | 0.4699 | 0.4699 | 0.1316 | 2.302 | 4.305 | 784.4 | 0 | 3.727 | 0.2305 | 0.7289 | −0.2432 | 0.3712 | 0.5266 |
| 5.185 | 1.697 | 1.829 | 22.01 | 0.4698 | 0.4699 | 0.1314 | 2.293 | 4.29 | 781.4 | 0 | 3.699 | 0.2302 | 0.728 | −0.2431 | 0.3711 | 0.5265 |
| 5.33 | 1.694 | 1.825 | 22.0 | 0.4698 | 0.4698 | 0.1313 | 2.284 | 4.274 | 778.2 | 0 | 3.671 | 0.2298 | 0.727 | −0.2429 | 0.371 | 0.5263 |
| 5.479 | 1.691 | 1.822 | 21.99 | 0.4697 | 0.4697 | 0.1311 | 2.275 | 4.256 | 774.6 | 0 | 3.638 | 0.2294 | 0.7259 | −0.2428 | 0.3709 | 0.5261 |
| 5.633 | 1.688 | 1.818 | 21.98 | 0.4696 | 0.4696 | 0.1309 | 2.264 | 4.238 | 770.8 | 0 | 3.603 | 0.229 | 0.7247 | −0.2426 | 0.3708 | 0.526 |
| 5.79 | 1.684 | 1.814 | 21.96 | 0.4695 | 0.4695 | 0.1307 | 2.253 | 4.218 | 766.9 | 0 | 3.567 | 0.2285 | 0.7235 | −0.2425 | 0.3707 | 0.5258 |
| 5.952 | 1.68 | 1.809 | 21.95 | 0.4694 | 0.4694 | 0.1305 | 2.242 | 4.197 | 762.8 | 0 | 3.528 | 0.228 | 0.7222 | −0.2423 | 0.3705 | 0.5256 |
| 6.119 | 1.676 | 1.805 | 21.94 | 0.4693 | 0.4693 | 0.1302 | 2.23 | 4.175 | 758.3 | 0 | 3.487 | 0.2275 | 0.7208 | −0.2421 | 0.3704 | 0.5254 |
| 6.29 | 1.672 | 1.8 | 21.92 | 0.4691 | 0.4692 | 0.13 | 2.216 | 4.152 | 753.5 | 0 | 3.442 | 0.2269 | 0.7193 | −0.2419 | 0.3701 | 0.5251 |
| 6.466 | 1.667 | 1.795 | 21.9 | 0.469 | 0.469 | 0.1297 | 2.202 | 4.127 | 748.5 | 0 | 3.396 | 0.2263 | 0.7177 | −0.2417 | 0.3699 | 0.5249 |
| 6.648 | 1.662 | 1.789 | 21.88 | 0.4689 | 0.4689 | 0.1294 | 2.188 | 4.1 | 743.2 | 0 | 3.345 | 0.2256 | 0.716 | −0.2415 | 0.3697 | 0.5246 |
| 6.834 | 1.657 | 1.783 | 21.87 | 0.4687 | 0.4687 | 0.1291 | 2.173 | 4.073 | 737.8 | 0 | 3.294 | 0.225 | 0.7143 | −0.2412 | 0.3694 | 0.5244 |
| 7.025 | 1.652 | 1.777 | 21.85 | 0.4686 | 0.4686 | 0.1288 | 2.158 | 4.048 | 732.6 | 0 | 3.245 | 0.2243 | 0.7126 | −0.241 | 0.3692 | 0.5241 |
| 7.222 | 1.648 | 1.773 | 21.83 | 0.4684 | 0.4685 | 0.1286 | 2.145 | 4.025 | 728.0 | 0 | 3.201 | 0.2238 | 0.7111 | −0.2408 | 0.369 | 0.5239 |
| 7.424 | 1.639 | 1.762 | 21.8 | 0.4682 | 0.4682 | 0.128 | 2.119 | 3.978 | 718.7 | 0 | 3.11 | 0.2226 | 0.708 | −0.2404 | 0.3685 | 0.5234 |
| 7.632 | 1.625 | 1.747 | 21.75 | 0.4677 | 0.4678 | 0.1272 | 2.081 | 3.91 | 704.8 | 0 | 2.975 | 0.2209 | 0.7035 | −0.2398 | 0.3677 | 0.5227 |
| 7.845 | 1.612 | 1.732 | 21.7 | 0.4673 | 0.4673 | 0.1264 | 2.041 | 3.839 | 690.7 | 0 | 2.836 | 0.2191 | 0.6988 | −0.2391 | 0.3669 | 0.522 |
| 8.065 | 1.597 | 1.715 | 21.65 | 0.4668 | 0.4669 | 0.1255 | 2.0 | 3.765 | 676.0 | 0 | 2.69 | 0.2172 | 0.6938 | −0.2384 | 0.366 | 0.5212 |
| 8.291 | 1.584 | 1.7 | 21.6 | 0.4664 | 0.4664 | 0.1248 | 1.963 | 3.699 | 662.7 | 0 | 2.557 | 0.2155 | 0.6894 | −0.2378 | 0.3652 | 0.5204 |
| 8.523 | 1.59 | 1.707 | 21.62 | 0.4666 | 0.4666 | 0.1251 | 1.979 | 3.728 | 668.5 | 0 | 2.616 | 0.2162 | 0.6913 | −0.2381 | 0.3656 | 0.5208 |
| 8.761 | 1.31 | 1.392 | 20.35 | 0.4618 | 0.4618 | 0.1054 | 1.255 | 2.388 | 396.4 | 0 | 0 | 0.1819 | 0.6012 | −0.2245 | 0.3505 | 0.4988 |
| 9.007 | 1.202 | 1.271 | 19.27 | 0.478 | 0.478 | 0.09317 | 0.9847 | 1.811 | 275.5 | 0 | 0 | 0.1742 | 0.5799 | −0.2207 | 0.3573 | 0.4744 |
| 9.259 | 1.195 | 1.264 | 18.4 | 0.5092 | 0.5092 | 0.08745 | 0.922 | 1.591 | 225.8 | 0 | 0 | 0.1827 | 0.6006 | −0.2237 | 0.377 | 0.4511 |
| 9.518 | 1.239 | 1.314 | 17.71 | 0.5479 | 0.5479 | 0.08575 | 0.9566 | 1.535 | 206.7 | 0 | 0 | 0.2004 | 0.6445 | −0.2301 | 0.4032 | 0.4303 |
| 9.784 | 1.309 | 1.395 | 17.19 | 0.5878 | 0.5878 | 0.08644 | 1.045 | 1.563 | 202.0 | 0 | 0.5569 | 0.2231 | 0.7013 | −0.2378 | 0.4314 | 0.4129 |
| 10.06 | 1.39 | 1.489 | 16.79 | 0.6262 | 0.6263 | 0.0884 | 1.167 | 1.637 | 204.9 | 0 | 1.588 | 0.2486 | 0.765 | −0.2457 | 0.4596 | 0.3983 |
| 10.34 | 1.475 | 1.59 | 16.46 | 0.6629 | 0.6629 | 0.09098 | 1.311 | 1.738 | 212.0 | 0 | 2.665 | 0.2762 | 0.834 | −0.2536 | 0.4874 | 0.3856 |
| 10.63 | 1.56 | 1.693 | 16.21 | 0.6967 | 0.6967 | 0.09394 | 1.471 | 1.856 | 221.8 | 0 | 3.741 | 0.3047 | 0.906 | −0.2611 | 0.5139 | 0.3747 |
| 10.93 | 1.643 | 1.794 | 16.0 | 0.7275 | 0.7275 | 0.09688 | 1.637 | 1.978 | 231.3 | 0 | 4.766 | 0.3335 | 0.9789 | −0.2681 | 0.5384 | 0.3651 |
| 11.23 | 1.723 | 1.894 | 15.81 | 0.7573 | 0.7574 | 0.09981 | 1.815 | 2.106 | 243.2 | 0 | 5.797 | 0.3634 | 1.056 | −0.2749 | 0.5624 | 0.356 |
| 11.55 | 1.796 | 1.985 | 15.65 | 0.7832 | 0.7832 | 0.1025 | 1.982 | 2.224 | 252.5 | 0 | 6.708 | 0.3917 | 1.129 | −0.2809 | 0.5836 | 0.3483 |
| 11.87 | 1.867 | 2.075 | 15.51 | 0.8086 | 0.8086 | 0.1052 | 2.159 | 2.347 | 264.4 | 0 | 7.631 | 0.4209 | 1.206 | −0.2868 | 0.6042 | 0.3408 |
| 12.2 | 1.931 | 2.156 | 15.37 | 0.8316 | 0.8316 | 0.1075 | 2.324 | 2.457 | 273.7 | 0 | 8.455 | 0.4489 | 1.28 | −0.2922 | 0.6227 | 0.3339 |
| 12.54 | 1.987 | 2.229 | 15.25 | 0.852 | 0.852 | 0.1095 | 2.474 | 2.552 | 280.6 | 0 | 9.176 | 0.4751 | 1.35 | −0.2968 | 0.639 | 0.3279 |
| 12.9 | 2.04 | 2.298 | 15.14 | 0.8716 | 0.8716 | 0.1115 | 2.625 | 2.647 | 289.2 | 0 | 9.887 | 0.5013 | 1.422 | −0.3014 | 0.6548 | 0.3221 |
| 13.26 | 2.092 | 2.367 | 15.03 | 0.8911 | 0.8912 | 0.1134 | 2.781 | 2.742 | 298.7 | 0 | 10.59 | 0.5283 | 1.497 | −0.3059 | 0.6701 | 0.3164 |
| 13.63 | 2.138 | 2.428 | 14.92 | 0.9091 | 0.9091 | 0.1151 | 2.921 | 2.823 | 306.0 | 0 | 11.22 | 0.5537 | 1.568 | −0.31 | 0.684 | 0.3111 |
| 14.01 | 2.178 | 2.482 | 14.82 | 0.9256 | 0.9257 | 0.1166 | 3.046 | 2.893 | 311.5 | 0 | 11.77 | 0.5777 | 1.636 | −0.3136 | 0.6965 | 0.3062 |
| 14.4 | 2.214 | 2.531 | 14.73 | 0.9412 | 0.9413 | 0.1178 | 3.16 | 2.951 | 315.6 | 0 | 12.27 | 0.6006 | 1.702 | −0.3169 | 0.708 | 0.3016 |
| 14.8 | 2.248 | 2.576 | 14.63 | 0.9562 | 0.9562 | 0.1189 | 3.267 | 3.003 | 319.2 | 0 | 12.73 | 0.6229 | 1.767 | −0.3202 | 0.7188 | 0.2973 |
| 15.22 | 2.279 | 2.619 | 14.54 | 0.9709 | 0.971 | 0.12 | 3.374 | 3.054 | 323.8 | 0.08803 | 13.19 | 0.6451 | 1.833 | −0.3233 | 0.7293 | 0.293 |
| 15.64 | 2.308 | 2.661 | 14.45 | 0.9853 | 0.9854 | 0.1211 | 3.48 | 3.104 | 329.1 | 0.2284 | 13.63 | 0.6674 | 1.9 | −0.3264 | 0.7394 | 0.2889 |
| 16.08 | 2.334 | 2.696 | 14.36 | 0.9989 | 0.9989 | 0.122 | 3.572 | 3.143 | 332.8 | 0.3501 | 14.02 | 0.6882 | 1.964 | −0.3291 | 0.7486 | 0.285 |
| 16.53 | 2.356 | 2.728 | 14.28 | 1.012 | 1.012 | 0.1228 | 3.653 | 3.173 | 335.4 | 0.456 | 14.37 | 0.7078 | 2.024 | −0.3317 | 0.7571 | 0.2814 |
| 17.0 | 2.376 | 2.755 | 14.19 | 1.024 | 1.024 | 0.1234 | 3.724 | 3.197 | 337.0 | 0.5515 | 14.68 | 0.7264 | 2.082 | −0.3341 | 0.765 | 0.278 |
| 17.47 | 2.394 | 2.78 | 14.11 | 1.036 | 1.036 | 0.124 | 3.789 | 3.215 | 338.1 | 0.641 | 14.96 | 0.7443 | 2.138 | −0.3363 | 0.7725 | 0.2747 |
| 17.96 | 2.409 | 2.802 | 14.03 | 1.047 | 1.047 | 0.1245 | 3.848 | 3.23 | 338.9 | 0.7252 | 15.22 | 0.7615 | 2.193 | −0.3383 | 0.7795 | 0.2715 |
| 18.46 | 2.423 | 2.822 | 13.95 | 1.058 | 1.058 | 0.1249 | 3.9 | 3.239 | 339.4 | 0.8033 | 15.46 | 0.7782 | 2.246 | −0.3403 | 0.7862 | 0.2685 |
| 18.98 | 2.435 | 2.839 | 13.87 | 1.069 | 1.069 | 0.1253 | 3.947 | 3.246 | 339.3 | 0.8741 | 15.67 | 0.794 | 2.297 | −0.3422 | 0.7925 | 0.2656 |
| 19.51 | 2.446 | 2.854 | 13.8 | 1.079 | 1.079 | 0.1256 | 3.987 | 3.247 | 338.9 | 0.9389 | 15.87 | 0.809 | 2.346 | −0.344 | 0.7985 | 0.2628 |
| 20.06 | 2.454 | 2.866 | 13.72 | 1.089 | 1.089 | 0.1258 | 4.021 | 3.244 | 337.9 | 0.9984 | 16.04 | 0.8233 | 2.394 | −0.3456 | 0.8041 | 0.2602 |
| 20.62 | 2.462 | 2.877 | 13.65 | 1.099 | 1.099 | 0.126 | 4.05 | 3.239 | 336.7 | 1.052 | 16.19 | 0.837 | 2.439 | −0.3472 | 0.8094 | 0.2576 |
| 21.2 | 2.468 | 2.886 | 13.58 | 1.109 | 1.109 | 0.1261 | 4.077 | 3.232 | 335.6 | 1.104 | 16.33 | 0.8502 | 2.483 | −0.3487 | 0.8145 | 0.2552 |
| 21.79 | 2.474 | 2.895 | 13.5 | 1.118 | 1.118 | 0.1262 | 4.101 | 3.223 | 334.3 | 1.153 | 16.47 | 0.863 | 2.526 | −0.3501 | 0.8194 | 0.2528 |
| 22.4 | 2.478 | 2.902 | 13.43 | 1.127 | 1.127 | 0.1262 | 4.121 | 3.213 | 332.9 | 1.199 | 16.59 | 0.8753 | 2.568 | −0.3515 | 0.8241 | 0.2505 |
| 23.03 | 2.482 | 2.907 | 13.36 | 1.136 | 1.136 | 0.1262 | 4.138 | 3.2 | 331.4 | 1.242 | 16.7 | 0.8871 | 2.609 | −0.3527 | 0.8286 | 0.2483 |
| 23.67 | 2.484 | 2.91 | 13.3 | 1.145 | 1.145 | 0.1262 | 4.15 | 3.185 | 329.7 | 1.282 | 16.79 | 0.8983 | 2.648 | −0.354 | 0.8329 | 0.2462 |
| 24.33 | 2.486 | 2.913 | 13.23 | 1.154 | 1.154 | 0.1262 | 4.16 | 3.169 | 327.8 | 1.319 | 16.88 | 0.909 | 2.685 | −0.3551 | 0.8371 | 0.2441 |
| 25.02 | 2.487 | 2.914 | 13.16 | 1.162 | 1.162 | 0.126 | 4.165 | 3.149 | 325.4 | 1.352 | 16.95 | 0.919 | 2.72 | −0.3562 | 0.8409 | 0.2421 |
| 25.72 | 2.486 | 2.914 | 13.1 | 1.17 | 1.17 | 0.1259 | 4.167 | 3.129 | 322.9 | 1.382 | 17.0 | 0.9283 | 2.753 | −0.3572 | 0.8447 | 0.2403 |
| 26.44 | 2.486 | 2.913 | 13.03 | 1.178 | 1.179 | 0.1257 | 4.165 | 3.106 | 320.2 | 1.41 | 17.05 | 0.9372 | 2.784 | −0.3581 | 0.8482 | 0.2384 |
| 27.18 | 2.484 | 2.911 | 12.97 | 1.186 | 1.186 | 0.1255 | 4.161 | 3.083 | 317.4 | 1.435 | 17.09 | 0.9455 | 2.813 | −0.359 | 0.8516 | 0.2367 |
| 27.94 | 2.482 | 2.907 | 12.91 | 1.194 | 1.194 | 0.1252 | 4.154 | 3.059 | 314.4 | 1.457 | 17.12 | 0.9532 | 2.84 | −0.3598 | 0.8549 | 0.2351 |
| 28.72 | 2.479 | 2.902 | 12.85 | 1.201 | 1.201 | 0.125 | 4.144 | 3.032 | 311.2 | 1.478 | 17.13 | 0.9603 | 2.865 | −0.3606 | 0.858 | 0.2335 |
| 29.52 | 2.476 | 2.897 | 12.79 | 1.208 | 1.208 | 0.1247 | 4.132 | 3.006 | 307.9 | 1.496 | 17.15 | 0.967 | 2.889 | −0.3612 | 0.861 | 0.2319 |
| 30.35 | 2.471 | 2.891 | 12.73 | 1.215 | 1.215 | 0.1244 | 4.117 | 2.978 | 304.6 | 1.513 | 17.15 | 0.9732 | 2.91 | −0.3619 | 0.8639 | 0.2305 |
| 31.2 | 2.467 | 2.885 | 12.67 | 1.222 | 1.222 | 0.124 | 4.102 | 2.951 | 301.2 | 1.528 | 17.14 | 0.9789 | 2.93 | −0.3625 | 0.8667 | 0.2291 |
| 32.07 | 2.462 | 2.877 | 12.62 | 1.228 | 1.229 | 0.1237 | 4.084 | 2.921 | 297.7 | 1.542 | 17.13 | 0.9842 | 2.949 | −0.363 | 0.8694 | 0.2277 |
| 32.97 | 2.457 | 2.869 | 12.56 | 1.235 | 1.235 | 0.1233 | 4.065 | 2.893 | 294.2 | 1.554 | 17.12 | 0.9891 | 2.966 | −0.3636 | 0.8719 | 0.2264 |
| 33.89 | 2.452 | 2.861 | 12.51 | 1.241 | 1.241 | 0.1229 | 4.044 | 2.864 | 290.6 | 1.565 | 17.1 | 0.9935 | 2.981 | −0.364 | 0.8744 | 0.2252 |
| 34.84 | 2.445 | 2.851 | 12.45 | 1.247 | 1.248 | 0.1225 | 4.021 | 2.833 | 287.0 | 1.575 | 17.07 | 0.9976 | 2.995 | −0.3644 | 0.8768 | 0.2239 |
| 35.82 | 2.438 | 2.84 | 12.4 | 1.254 | 1.254 | 0.1221 | 3.996 | 2.801 | 283.3 | 1.584 | 17.03 | 1.001 | 3.008 | −0.3648 | 0.879 | 0.2227 |
| 36.82 | 2.433 | 2.832 | 12.35 | 1.26 | 1.26 | 0.1215 | 3.973 | 2.772 | 279.5 | 1.592 | 17.0 | 1.005 | 3.02 | −0.3652 | 0.8815 | 0.2216 |
| 37.85 | 2.425 | 2.82 | 12.29 | 1.266 | 1.266 | 0.1211 | 3.945 | 2.739 | 275.6 | 1.599 | 16.95 | 1.008 | 3.03 | −0.3655 | 0.8837 | 0.2204 |
| 38.91 | 2.419 | 2.811 | 12.24 | 1.272 | 1.272 | 0.1204 | 3.92 | 2.708 | 271.6 | 1.608 | 16.91 | 1.011 | 3.041 | −0.3658 | 0.8862 | 0.2193 |
| M | I | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| [ g cm−3] | [] | [] | [km] | [ s−1] | [ s−1] | [ g cm2] | [km] | [km] | [km] | |||||||
| 2.636 | 0.263 | 0.2646 | 22.55 | 0.1748 | 0.1748 | 0.02052 | 0.03515 | 0.1768 | 11.05 | 0 | 0 | 0.02689 | 0.1643 | −0.1105 | 0.09535 | 0.6039 |
| 2.709 | 0.3007 | 0.3033 | 21.48 | 0.2012 | 0.2013 | 0.02569 | 0.0491 | 0.2144 | 16.05 | 0 | 0 | 0.03257 | 0.1847 | −0.1194 | 0.1066 | 0.5731 |
| 2.785 | 0.3455 | 0.3494 | 20.7 | 0.2283 | 0.2283 | 0.0315 | 0.06857 | 0.264 | 23.18 | 0 | 0 | 0.03923 | 0.2073 | −0.1286 | 0.1193 | 0.5499 |
| 2.862 | 0.3988 | 0.4047 | 20.14 | 0.2558 | 0.2558 | 0.03799 | 0.09601 | 0.3299 | 33.33 | 0 | 0 | 0.04709 | 0.2328 | −0.1382 | 0.1338 | 0.5326 |
| 2.942 | 0.4625 | 0.4712 | 19.78 | 0.2836 | 0.2836 | 0.04515 | 0.1348 | 0.4177 | 47.68 | 0 | 0 | 0.05641 | 0.2616 | −0.1482 | 0.1505 | 0.52 |
| 3.024 | 0.5798 | 0.5947 | 19.57 | 0.3235 | 0.3235 | 0.05702 | 0.2242 | 0.609 | 80.76 | 0 | 0 | 0.07323 | 0.3112 | −0.1635 | 0.1773 | 0.5094 |
| 3.108 | 0.7982 | 0.8279 | 19.97 | 0.3699 | 0.3699 | 0.07636 | 0.4584 | 1.089 | 170.9 | 0 | 0 | 0.103 | 0.3943 | −0.1851 | 0.2184 | 0.511 |
| 3.195 | 1.032 | 1.082 | 20.72 | 0.3998 | 0.3998 | 0.09382 | 0.8093 | 1.779 | 307.1 | 0 | 0 | 0.1336 | 0.4765 | −0.203 | 0.2574 | 0.5212 |
| 3.284 | 1.166 | 1.229 | 21.15 | 0.4125 | 0.4126 | 0.1024 | 1.055 | 2.247 | 400.6 | 0 | 0 | 0.151 | 0.5224 | −0.2117 | 0.2799 | 0.5272 |
| 3.375 | 1.193 | 1.259 | 21.22 | 0.4155 | 0.4155 | 0.1039 | 1.107 | 2.341 | 418.7 | 0 | 0 | 0.1548 | 0.5323 | −0.2135 | 0.2865 | 0.5277 |
| 3.469 | 1.193 | 1.258 | 21.21 | 0.4158 | 0.4158 | 0.1037 | 1.104 | 2.335 | 416.9 | 0 | 0 | 0.1548 | 0.5322 | −0.2135 | 0.2875 | 0.5274 |
| 3.566 | 1.192 | 1.257 | 21.2 | 0.4158 | 0.4158 | 0.1036 | 1.102 | 2.33 | 415.8 | 0 | 0 | 0.1547 | 0.532 | −0.2134 | 0.2877 | 0.5273 |
| 3.665 | 1.192 | 1.258 | 21.2 | 0.4158 | 0.4158 | 0.1037 | 1.103 | 2.332 | 416.4 | 0 | 0 | 0.1547 | 0.5321 | −0.2135 | 0.2876 | 0.5273 |
| 3.767 | 1.193 | 1.259 | 21.21 | 0.4157 | 0.4157 | 0.1038 | 1.106 | 2.338 | 417.7 | 0 | 0 | 0.1548 | 0.5324 | −0.2135 | 0.2873 | 0.5275 |
| 3.872 | 1.194 | 1.259 | 21.22 | 0.4156 | 0.4157 | 0.1038 | 1.107 | 2.34 | 418.3 | 0 | 0 | 0.1548 | 0.5324 | −0.2135 | 0.287 | 0.5276 |
| 3.98 | 1.193 | 1.259 | 21.21 | 0.4157 | 0.4157 | 0.1038 | 1.106 | 2.339 | 417.9 | 0 | 0 | 0.1548 | 0.5324 | −0.2135 | 0.2872 | 0.5275 |
| 4.091 | 1.193 | 1.259 | 21.21 | 0.4158 | 0.4158 | 0.1037 | 1.105 | 2.337 | 417.4 | 0 | 0 | 0.1548 | 0.5323 | −0.2135 | 0.2874 | 0.5274 |
| 4.205 | 1.192 | 1.258 | 21.2 | 0.4158 | 0.4158 | 0.1037 | 1.104 | 2.333 | 416.7 | 0 | 0 | 0.1547 | 0.5322 | −0.2135 | 0.2876 | 0.5273 |
| 4.322 | 1.192 | 1.257 | 21.2 | 0.4158 | 0.4158 | 0.1036 | 1.102 | 2.329 | 415.7 | 0 | 0 | 0.1546 | 0.5319 | −0.2134 | 0.2877 | 0.5273 |
| 4.442 | 1.191 | 1.256 | 21.19 | 0.4158 | 0.4158 | 0.1035 | 1.1 | 2.325 | 414.7 | 0 | 0 | 0.1546 | 0.5317 | −0.2134 | 0.2879 | 0.5271 |
| 4.566 | 1.19 | 1.255 | 21.19 | 0.4158 | 0.4158 | 0.1034 | 1.097 | 2.319 | 413.5 | 0 | 0 | 0.1544 | 0.5313 | −0.2133 | 0.288 | 0.527 |
| 4.693 | 1.188 | 1.253 | 21.18 | 0.4158 | 0.4158 | 0.1033 | 1.094 | 2.313 | 412.2 | 0 | 0 | 0.1543 | 0.531 | −0.2133 | 0.2881 | 0.5268 |
| 4.824 | 1.187 | 1.252 | 21.17 | 0.4157 | 0.4157 | 0.1032 | 1.091 | 2.306 | 410.6 | 0 | 0 | 0.1541 | 0.5305 | −0.2132 | 0.2882 | 0.5267 |
| 4.958 | 1.185 | 1.25 | 21.16 | 0.4157 | 0.4157 | 0.103 | 1.088 | 2.3 | 409.2 | 0 | 0 | 0.1539 | 0.53 | −0.2131 | 0.2882 | 0.5265 |
| 5.096 | 1.184 | 1.248 | 21.15 | 0.4156 | 0.4156 | 0.1029 | 1.084 | 2.292 | 407.7 | 0 | 0 | 0.1537 | 0.5295 | −0.213 | 0.2883 | 0.5264 |
| 5.238 | 1.181 | 1.246 | 21.14 | 0.4155 | 0.4156 | 0.1027 | 1.08 | 2.283 | 405.7 | 0 | 0 | 0.1535 | 0.5289 | −0.2129 | 0.2883 | 0.5262 |
| 5.384 | 1.179 | 1.243 | 21.13 | 0.4155 | 0.4155 | 0.1025 | 1.074 | 2.273 | 403.5 | 0 | 0 | 0.1532 | 0.5282 | −0.2127 | 0.2883 | 0.5259 |
| 5.534 | 1.176 | 1.241 | 21.12 | 0.4154 | 0.4154 | 0.1023 | 1.069 | 2.261 | 401.1 | 0 | 0 | 0.1529 | 0.5274 | −0.2126 | 0.2883 | 0.5257 |
| 5.688 | 1.174 | 1.237 | 21.1 | 0.4152 | 0.4153 | 0.1021 | 1.063 | 2.249 | 398.5 | 0 | 0 | 0.1526 | 0.5265 | −0.2124 | 0.2883 | 0.5254 |
| 5.847 | 1.171 | 1.234 | 21.09 | 0.4151 | 0.4151 | 0.1019 | 1.056 | 2.236 | 395.8 | 0 | 0 | 0.1522 | 0.5255 | −0.2123 | 0.2883 | 0.5252 |
| 6.01 | 1.167 | 1.23 | 21.07 | 0.415 | 0.415 | 0.1016 | 1.05 | 2.223 | 392.9 | 0 | 0 | 0.1518 | 0.5245 | −0.2121 | 0.2882 | 0.5249 |
| 6.177 | 1.164 | 1.227 | 21.06 | 0.4148 | 0.4149 | 0.1014 | 1.042 | 2.208 | 389.8 | 0 | 0 | 0.1514 | 0.5234 | −0.2119 | 0.2881 | 0.5246 |
| 6.349 | 1.16 | 1.223 | 21.04 | 0.4147 | 0.4147 | 0.1011 | 1.035 | 2.193 | 386.6 | 0 | 0 | 0.151 | 0.5223 | −0.2117 | 0.288 | 0.5243 |
| 6.526 | 1.156 | 1.218 | 21.02 | 0.4145 | 0.4145 | 0.1008 | 1.027 | 2.177 | 383.2 | 0 | 0 | 0.1505 | 0.521 | −0.2114 | 0.2879 | 0.5239 |
| 6.708 | 1.152 | 1.214 | 21.0 | 0.4143 | 0.4143 | 0.1004 | 1.018 | 2.16 | 379.7 | 0 | 0 | 0.15 | 0.5197 | −0.2112 | 0.2878 | 0.5236 |
| 6.895 | 1.148 | 1.209 | 20.98 | 0.4141 | 0.4141 | 0.1001 | 1.009 | 2.142 | 375.9 | 0 | 0 | 0.1495 | 0.5184 | −0.2109 | 0.2876 | 0.5232 |
| 7.087 | 1.143 | 1.204 | 20.96 | 0.4139 | 0.4139 | 0.09976 | 0.9999 | 2.123 | 372.1 | 0 | 0 | 0.149 | 0.5169 | −0.2107 | 0.2875 | 0.5228 |
| 7.284 | 1.138 | 1.199 | 20.93 | 0.4136 | 0.4137 | 0.09938 | 0.9903 | 2.104 | 368.0 | 0 | 0 | 0.1484 | 0.5154 | −0.2104 | 0.2873 | 0.5224 |
| 7.487 | 1.133 | 1.193 | 20.91 | 0.4134 | 0.4134 | 0.09898 | 0.9802 | 2.084 | 363.8 | 0 | 0 | 0.1478 | 0.5138 | −0.2101 | 0.2871 | 0.522 |
| 7.695 | 1.152 | 1.214 | 21.0 | 0.4143 | 0.4143 | 0.1005 | 1.018 | 2.16 | 379.8 | 0 | 0 | 0.1501 | 0.5198 | −0.2112 | 0.2878 | 0.5236 |
| 7.91 | 1.154 | 1.216 | 21.01 | 0.4144 | 0.4144 | 0.1006 | 1.023 | 2.169 | 381.7 | 0 | 0 | 0.1503 | 0.5205 | −0.2113 | 0.2879 | 0.5238 |
| 8.13 | 1.063 | 1.116 | 20.57 | 0.4099 | 0.4099 | 0.09335 | 0.8447 | 1.811 | 307.4 | 0 | 0 | 0.1395 | 0.4917 | −0.2058 | 0.2837 | 0.5157 |
| 8.356 | 0.8885 | 0.9258 | 19.21 | 0.4127 | 0.4128 | 0.07483 | 0.5352 | 1.14 | 169.3 | 0 | 0 | 0.1216 | 0.4436 | −0.1958 | 0.28 | 0.4865 |
| 8.589 | 0.8933 | 0.9322 | 17.78 | 0.4633 | 0.4633 | 0.06748 | 0.4941 | 0.9373 | 125.2 | 0 | 0 | 0.1337 | 0.4742 | −0.2017 | 0.3095 | 0.4473 |
| 8.828 | 0.9929 | 1.044 | 16.88 | 0.5271 | 0.5272 | 0.06968 | 0.5896 | 0.983 | 125.6 | 0 | 0 | 0.1614 | 0.545 | −0.2144 | 0.3506 | 0.4183 |
| 9.074 | 1.124 | 1.193 | 16.33 | 0.5883 | 0.5883 | 0.07514 | 0.7518 | 1.123 | 140.3 | 0 | 0 | 0.196 | 0.6323 | −0.2281 | 0.3937 | 0.3976 |
| 9.327 | 1.263 | 1.354 | 15.99 | 0.6425 | 0.6425 | 0.08153 | 0.9571 | 1.309 | 161.1 | 0 | 0.7999 | 0.2337 | 0.7273 | −0.241 | 0.4353 | 0.382 |
| 9.587 | 1.399 | 1.516 | 15.76 | 0.6895 | 0.6895 | 0.08786 | 1.19 | 1.517 | 184.3 | 0 | 2.432 | 0.2728 | 0.8257 | −0.2526 | 0.4738 | 0.3696 |
| 9.854 | 1.529 | 1.672 | 15.61 | 0.7302 | 0.7302 | 0.09385 | 1.442 | 1.736 | 208.9 | 0 | 3.984 | 0.3123 | 0.926 | −0.2631 | 0.509 | 0.3593 |
| 10.13 | 1.649 | 1.819 | 15.48 | 0.766 | 0.766 | 0.09922 | 1.702 | 1.952 | 232.5 | 0 | 5.425 | 0.3515 | 1.027 | −0.2725 | 0.5408 | 0.3502 |
| 10.41 | 1.758 | 1.955 | 15.38 | 0.7971 | 0.7971 | 0.1039 | 1.958 | 2.159 | 253.9 | 0 | 6.732 | 0.3896 | 1.126 | −0.2807 | 0.5691 | 0.3421 |
| 10.7 | 1.859 | 2.083 | 15.29 | 0.8255 | 0.8255 | 0.1083 | 2.218 | 2.361 | 276.2 | 0 | 7.975 | 0.4276 | 1.227 | −0.2883 | 0.5952 | 0.3347 |
| 11.0 | 1.948 | 2.197 | 15.2 | 0.8501 | 0.8502 | 0.1119 | 2.457 | 2.54 | 293.9 | 0 | 9.056 | 0.4632 | 1.323 | −0.2949 | 0.6179 | 0.328 |
| 11.3 | 2.03 | 2.302 | 15.12 | 0.8729 | 0.8729 | 0.1152 | 2.691 | 2.709 | 311.2 | 0 | 10.07 | 0.4981 | 1.418 | −0.301 | 0.6386 | 0.3217 |
| 11.62 | 2.105 | 2.402 | 15.04 | 0.8945 | 0.8946 | 0.1182 | 2.923 | 2.871 | 328.7 | 0 | 11.03 | 0.5328 | 1.516 | −0.3068 | 0.6579 | 0.3156 |
| 11.94 | 2.173 | 2.492 | 14.96 | 0.9144 | 0.9144 | 0.1208 | 3.141 | 3.019 | 344.6 | 0 | 11.9 | 0.5662 | 1.612 | −0.3121 | 0.6754 | 0.31 |
| 12.28 | 2.231 | 2.57 | 14.89 | 0.932 | 0.9321 | 0.123 | 3.329 | 3.139 | 356.0 | 0 | 12.64 | 0.5969 | 1.701 | −0.3166 | 0.6907 | 0.3048 |
| 12.62 | 2.283 | 2.64 | 14.81 | 0.9483 | 0.9483 | 0.1249 | 3.502 | 3.246 | 365.8 | 0 | 13.31 | 0.626 | 1.787 | −0.3207 | 0.7046 | 0.3 |
| 12.97 | 2.331 | 2.705 | 14.74 | 0.9641 | 0.9641 | 0.1267 | 3.672 | 3.347 | 376.4 | 0.1583 | 13.95 | 0.6549 | 1.874 | −0.3247 | 0.7177 | 0.2954 |
| 13.33 | 2.375 | 2.767 | 14.67 | 0.9792 | 0.9792 | 0.1284 | 3.835 | 3.442 | 386.9 | 0.3244 | 14.55 | 0.6831 | 1.961 | −0.3286 | 0.7299 | 0.291 |
| 13.7 | 2.415 | 2.823 | 14.6 | 0.9937 | 0.9938 | 0.1299 | 3.986 | 3.525 | 396.3 | 0.4739 | 15.1 | 0.7104 | 2.047 | −0.3321 | 0.7413 | 0.2867 |
| 14.08 | 2.451 | 2.873 | 14.52 | 1.007 | 1.007 | 0.1311 | 4.123 | 3.597 | 404.1 | 0.6053 | 15.6 | 0.7364 | 2.13 | −0.3353 | 0.7517 | 0.2827 |
| 14.48 | 2.481 | 2.916 | 14.45 | 1.02 | 1.02 | 0.1322 | 4.244 | 3.656 | 410.5 | 0.7246 | 16.04 | 0.761 | 2.211 | −0.3383 | 0.7612 | 0.2788 |
| 14.88 | 2.51 | 2.956 | 14.38 | 1.033 | 1.033 | 0.1331 | 4.354 | 3.706 | 415.3 | 0.8299 | 16.44 | 0.7844 | 2.288 | −0.3411 | 0.77 | 0.2753 |
| 15.29 | 2.533 | 2.99 | 14.31 | 1.044 | 1.044 | 0.1339 | 4.448 | 3.743 | 418.8 | 0.9236 | 16.79 | 0.8062 | 2.361 | −0.3436 | 0.7781 | 0.2719 |
| 15.72 | 2.554 | 3.02 | 14.24 | 1.055 | 1.055 | 0.1346 | 4.531 | 3.774 | 421.3 | 1.007 | 17.1 | 0.827 | 2.431 | −0.3459 | 0.7856 | 0.2687 |
| 16.16 | 2.572 | 3.045 | 14.17 | 1.066 | 1.066 | 0.1351 | 4.605 | 3.796 | 423.1 | 1.083 | 17.38 | 0.8467 | 2.499 | −0.3482 | 0.7926 | 0.2656 |
| 16.61 | 2.588 | 3.069 | 14.1 | 1.076 | 1.077 | 0.1356 | 4.67 | 3.813 | 424.2 | 1.153 | 17.64 | 0.8655 | 2.564 | −0.3502 | 0.7991 | 0.2627 |
| 17.07 | 2.602 | 3.089 | 14.03 | 1.086 | 1.087 | 0.136 | 4.727 | 3.824 | 424.9 | 1.218 | 17.87 | 0.8834 | 2.627 | −0.3521 | 0.8053 | 0.2599 |
| 17.54 | 2.615 | 3.108 | 13.96 | 1.096 | 1.096 | 0.1363 | 4.783 | 3.835 | 425.6 | 1.279 | 18.08 | 0.9008 | 2.689 | −0.3539 | 0.8112 | 0.2573 |
| 18.03 | 2.626 | 3.124 | 13.89 | 1.106 | 1.106 | 0.1366 | 4.831 | 3.84 | 426.1 | 1.336 | 18.28 | 0.9175 | 2.749 | −0.3557 | 0.8168 | 0.2547 |
| 18.54 | 2.635 | 3.137 | 13.83 | 1.115 | 1.115 | 0.1369 | 4.873 | 3.841 | 426.2 | 1.389 | 18.46 | 0.9334 | 2.808 | −0.3573 | 0.8221 | 0.2522 |
| 19.05 | 2.644 | 3.15 | 13.76 | 1.124 | 1.124 | 0.1371 | 4.911 | 3.84 | 426.1 | 1.438 | 18.62 | 0.9486 | 2.864 | −0.3589 | 0.8271 | 0.2499 |
| 19.58 | 2.65 | 3.159 | 13.7 | 1.133 | 1.133 | 0.1372 | 4.941 | 3.834 | 425.5 | 1.482 | 18.76 | 0.9629 | 2.917 | −0.3603 | 0.8318 | 0.2476 |
| 20.13 | 2.656 | 3.168 | 13.64 | 1.141 | 1.141 | 0.1373 | 4.967 | 3.826 | 424.4 | 1.521 | 18.88 | 0.9765 | 2.969 | −0.3617 | 0.8363 | 0.2455 |
| 20.69 | 2.66 | 3.174 | 13.58 | 1.149 | 1.149 | 0.1374 | 4.987 | 3.814 | 423.1 | 1.558 | 18.99 | 0.9893 | 3.017 | −0.3629 | 0.8406 | 0.2434 |
| 21.26 | 2.663 | 3.178 | 13.52 | 1.157 | 1.157 | 0.1374 | 5.003 | 3.8 | 421.5 | 1.591 | 19.09 | 1.001 | 3.064 | −0.3642 | 0.8447 | 0.2414 |
| 21.86 | 2.666 | 3.181 | 13.46 | 1.165 | 1.165 | 0.1373 | 5.015 | 3.784 | 419.5 | 1.622 | 19.17 | 1.013 | 3.109 | −0.3653 | 0.8485 | 0.2395 |
| 22.47 | 2.666 | 3.183 | 13.39 | 1.173 | 1.173 | 0.1373 | 5.022 | 3.764 | 417.2 | 1.651 | 19.24 | 1.024 | 3.151 | −0.3664 | 0.8522 | 0.2377 |
| 23.09 | 2.667 | 3.183 | 13.34 | 1.18 | 1.18 | 0.1371 | 5.025 | 3.743 | 414.6 | 1.677 | 19.3 | 1.034 | 3.191 | −0.3673 | 0.8557 | 0.2359 |
| 23.73 | 2.666 | 3.182 | 13.28 | 1.187 | 1.187 | 0.137 | 5.025 | 3.72 | 411.8 | 1.701 | 19.35 | 1.044 | 3.228 | −0.3683 | 0.8591 | 0.2342 |
| 24.4 | 2.665 | 3.18 | 13.22 | 1.194 | 1.194 | 0.1368 | 5.021 | 3.695 | 408.7 | 1.723 | 19.38 | 1.053 | 3.264 | −0.3691 | 0.8623 | 0.2326 |
| 25.08 | 2.663 | 3.177 | 13.16 | 1.201 | 1.201 | 0.1365 | 5.014 | 3.668 | 405.4 | 1.743 | 19.41 | 1.061 | 3.297 | −0.37 | 0.8653 | 0.231 |
| 25.77 | 2.66 | 3.173 | 13.11 | 1.208 | 1.208 | 0.1363 | 5.004 | 3.64 | 401.9 | 1.761 | 19.42 | 1.069 | 3.327 | −0.3707 | 0.8682 | 0.2295 |
| 26.49 | 2.657 | 3.168 | 13.05 | 1.215 | 1.215 | 0.1359 | 4.991 | 3.611 | 398.1 | 1.777 | 19.43 | 1.076 | 3.356 | −0.3714 | 0.8711 | 0.2281 |
| 27.23 | 2.653 | 3.162 | 13.0 | 1.221 | 1.221 | 0.1356 | 4.975 | 3.581 | 394.2 | 1.791 | 19.43 | 1.083 | 3.382 | −0.372 | 0.8737 | 0.2267 |
| 27.99 | 2.648 | 3.154 | 12.94 | 1.227 | 1.227 | 0.1353 | 4.956 | 3.549 | 390.3 | 1.805 | 19.43 | 1.089 | 3.407 | −0.3726 | 0.8763 | 0.2254 |
References
- Lattimer, J.M. Constraints on Nuclear Symmetry Energy Parameters. Particles 2023, 6, 30–56. [Google Scholar] [CrossRef]
- Carlson, B.V.; Dutra, M.; Lourenço, O.; Margueron, J. Low-energy nuclear physics and global neutron star properties. Phys. Rev. C 2023, 107, 035805. [Google Scholar] [CrossRef]
- Reed, B.T.; Fattoyev, F.J.; Horowitz, C.J.; Piekarewicz, J. Implications of PREX-2 on the Equation of State of Neutron-Rich Matter. Phys. Rev. Lett. 2021, 126, 172503. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Abbott, R.; Abbott, T.D.; Abraham, S.; Acernese, F.; Ackley, K.; Adams, C.; Adhikari, R.X.; Adya, V.B.; Affeldt, C.; Agathos, M.; et al. GW190814: Gravitational Waves from the Coalescence of a 23 Solar Mass Black Hole with a 2.6 Solar Mass Compact Object. Astrophys. J. Lett. 2020, 896, L44. [Google Scholar] [CrossRef]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; DeCesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2019, 4, 72–76. [Google Scholar] [CrossRef]
- Fan, Y.Z.; Han, M.Z.; Jiang, J.L.; Shao, D.S.; Tang, S.P. Maximum gravitational mass MTOV=2.25-0.07+0.08M⊙ inferred at about 3% precision with multimessenger data of neutron stars. Phys. Rev. D 2024, 109, 043052. [Google Scholar] [CrossRef]
- Ascenzi, S.; Graber, V.; Rea, N. Neutron-star measurements in the multi-messenger Era. Astropart. Phys. 2024, 158, 102935. [Google Scholar] [CrossRef]
- Abac, A.; Abramo, R.; Albanesi, S.; Albertini, A.; Agapito, A.; Agathos, M.; Albertus, C.; Andersson, N.; Andrade, T.; Andreoni, I.; et al. The Science of the Einstein Telescope. arXiv 2025, arXiv:2503.12263. [Google Scholar]
- Gerlach, U.H. Equation of State at Supranuclear Densities and the Existence of a Third Family of Superdense Stars. Phys. Rev. 1968, 172, 1325–1330. [Google Scholar] [CrossRef]
- Kampfer, B. On the Possibility of Stable Quark and Pion Condensed Stars. J. Phys. A 1981, 14, L471–L475. [Google Scholar] [CrossRef]
- Glendenning, N.K.; Kettner, C. Nonidentical neutron star twins. Astron. Astrophys. 2000, 353, L9. [Google Scholar]
- Schertler, K.; Greiner, C.; Thoma, M.H. Medium effects and the structure of neutron stars in the effective mass bag model. In Proceedings of the 26th International Workshop on Gross Properties of Nuclei and Nuclear Excitation: Nuclear Astrophysics (Hirschegg 98), Hirschegg, Austria, 11–17 January 1998; pp. 148–152. [Google Scholar]
- Alvarez-Castillo, D.E.; Blaschke, D. Proving the CEP with compact stars? In Proceedings of the 17th Conference of Young Scientists and Specialists, Dubna, Russia, 8–12 April 2013.
- Benic, S.; Blaschke, D.; Alvarez-Castillo, D.E.; Fischer, T.; Typel, S. A new quark-hadron hybrid equation of state for astrophysics - I. High-mass twin compact stars. Astron. Astrophys. 2015, 577, A40. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.E.; Blaschke, D.B. High-mass twin stars with a multipolytrope equation of state. Phys. Rev. C 2017, 96, 045809. [Google Scholar] [CrossRef]
- Montana, G.; Tolos, L.; Hanauske, M.; Rezzolla, L. Constraining twin stars with GW170817. Phys. Rev. D 2019, 99, 103009. [Google Scholar] [CrossRef]
- Blaschke, D.; Alvarez-Castillo, D.E.; Ayriyan, A.; Grigorian, H.; Largani, N.K.; Weber, F. Astrophysical aspects of general relativistic mass twin stars. In Topics on Strong Gravity: A Modern View on Theories and Experiments; World Scientific Europe: London, UK, 2020; pp. 207–256. [Google Scholar] [CrossRef]
- Zacchi, A.; Tolos, L.; Schaffner-Bielich, J. Twin Stars within the SU(3) Chiral Quark-Meson Model. Phys. Rev. D 2017, 95, 103008. [Google Scholar] [CrossRef]
- Espino, P.L.; Paschalidis, V. Fate of twin stars on the unstable branch: Implications for the formation of twin stars. Phys. Rev. D 2022, 105, 043014. [Google Scholar] [CrossRef]
- Carlomagno, J.P.; Contrera, G.A.; Grunfeld, A.G.; Blaschke, D. Hybrid Isentropic Twin Stars. Universe 2024, 10, 336. [Google Scholar] [CrossRef]
- Vinciguerra, S.; Salmi, T.; Watts, A.L.; Choudhury, D.; Riley, T.E.; Ray, P.S.; Bogdanov, S.; Kini, Y.; Guillot, S.; Chakrabarty, D.; et al. An Updated Mass–Radius Analysis of the 2017–2018 NICER Data Set of PSR J0030+0451. Astrophys. J. 2024, 961, 62. [Google Scholar] [CrossRef]
- Salmi, T.; Choudhury, D.; Kini, Y.; Riley, T.E.; Vinciguerra, S.; Watts, A.L.; Wolff, M.T.; Arzoumanian, Z.; Bogdanov, S.; Chakrabarty, D.; et al. The Radius of the High-mass Pulsar PSR J0740+6620 with 3.6 yr of NICER Data. Astrophys. J. 2024, 974, 294. [Google Scholar] [CrossRef]
- Salmi, T.; Deneva, J.S.; Ray, P.S.; Watts, A.L.; Choudhury, D.; Kini, Y.; Vinciguerra, S.; Cromartie, H.T.; Wolff, M.T.; Arzoumanian, Z.; et al. A NICER View of PSR J1231-1411: A Complex Case. Astrophys. J. 2024, 976, 58. [Google Scholar] [CrossRef]
- Choudhury, D.; Salmi, T.; Vinciguerra, S.; Riley, T.E.; Kini, Y.; Watts, A.L.; Dorsman, B.; Bogdanov, S.; Guillot, S.; Ray, P.S.; et al. A NICER View of the Nearest and Brightest Millisecond Pulsar: PSR J0437–4715. Astrophys. J. Lett. 2024, 971, L20. [Google Scholar] [CrossRef]
- Li, J.J.; Sedrakian, A.; Alford, M. Confronting new NICER mass-radius measurements with phase transition in dense matter and twin compact stars. J. Cosmol. Astropart. Phys. 2025, 2, 002. [Google Scholar] [CrossRef]
- Doroshenko, V.; Suleimanov, V.; Pühlhofer, G.; Santangelo, A. A strangely light neutron star within a supernova remnant. Nat. Astron. 2022, 6, 1444–1451. [Google Scholar] [CrossRef]
- Kubis, S.; Wójcik, W.; Castillo, D.A.; Zabari, N. Relativistic mean-field model for the ultracompact low-mass neutron star HESS J1731-347. Phys. Rev. C 2023, 108, 045803. [Google Scholar] [CrossRef]
- Li, J.J.; Sedrakian, A. Baryonic models of ultra-low-mass compact stars for the central compact object in HESS J1731-347. Phys. Lett. B 2023, 844, 138062. [Google Scholar] [CrossRef]
- Brodie, L.; Haber, A. Nuclear and hybrid equations of state in light of the low-mass compact star in HESS J1731-347. Phys. Rev. C 2023, 108, 025806. [Google Scholar] [CrossRef]
- Veselsky, M.; Koliogiannis, P.S.; Petousis, V.; Leja, J.; Moustakidis, C.C. How the HESS J1731-347 object could be explained using K-condensation. Phys. Lett. B 2025, 860, 139185. [Google Scholar] [CrossRef]
- Horvath, J.E.; Rocha, L.S.; de Sá, L.M.; Moraes, P.H.R.S.; Barão, L.G.; de Avellar, M.G.B.; Bernardo, A.; Bachega, R.R.A. A light strange star in the remnant HESS J1731-347: Minimal consistency checks. Astron. Astrophys. 2023, 672, L11. [Google Scholar] [CrossRef]
- Di Clemente, F.; Drago, A.; Pagliara, G. Is the Compact Object Associated with HESS J1731-347 a Strange Quark Star? A Possible Astrophysical Scenario for Its Formation. Astrophys. J. 2024, 967, 159. [Google Scholar] [CrossRef]
- Ju, M.; Chu, P.; Wu, X.; Liu, H. Hess J1731-347 is likely a quark star based on the density-dependent vMIT bag model. Eur. Phys. J. C 2025, 85, 40. [Google Scholar] [CrossRef]
- Rather, I.A.; Panotopoulos, G.; Lopes, I. Quark models and radial oscillations: Decoding the HESS J1731-347 compact object’s equation of state. Eur. Phys. J. C 2023, 83, 1065. [Google Scholar] [CrossRef]
- Oikonomou, P.T.; Moustakidis, C.C. Color-flavor locked quark stars in light of the compact object in the HESS J1731-347 and the GW190814 event. Phys. Rev. D 2023, 108, 063010. [Google Scholar] [CrossRef]
- Yuan, Y.J.; Zhou, X. Thermal Evolution of the Central Compact Object in HESS J1731-347 as Evidence for a Color-flavor-locked Strange Star. Res. Astron. Astrophys. 2025, 25, 055016. [Google Scholar] [CrossRef]
- Li, J.J.; Sedrakian, A.; Alford, M. Hybrid Star Models in the Light of New Multimessenger Data. Astrophys. J. 2024, 967, 116. [Google Scholar] [CrossRef]
- Gao, B.; Yan, Y.; Harada, M. Reconciling constraints from the supernova remnant HESS J1731-347 with the parity doublet model. Phys. Rev. C 2024, 109, 065807. [Google Scholar] [CrossRef]
- Laskos-Patkos, P.; Koliogiannis, P.; Moustakidis, C. Hybrid stars and the stiffness of the nuclear equation of state in light of the HESS J1731-347 remnant. EPJ Web Conf. 2024, 304, 02007. [Google Scholar] [CrossRef]
- Laskos-Patkos, P.; Koliogiannis, P.S.; Moustakidis, C.C. Hybrid stars in light of the HESS J1731-347 remnant and the PREX-II experiment. Phys. Rev. D 2024, 109, 063017. [Google Scholar] [CrossRef]
- Mariani, M.; Ranea-Sandoval, I.F.; Lugones, G.; Orsaria, M.G. Could a slow stable hybrid star explain the central compact object in HESS J1731-347? Phys. Rev. D 2024, 110, 043026. [Google Scholar] [CrossRef]
- Sagun, V.; Giangrandi, E.; Dietrich, T.; Ivanytskyi, O.; Negreiros, R.; Providência, C. What Is the Nature of the HESS J1731-347 Compact Object? Astrophys. J. 2023, 958, 49. [Google Scholar] [CrossRef]
- Hong, B.; Ren, Z. Mixed dark matter models for the peculiar compact object in remnant HESS J1731-347 and their implications for gravitational wave properties. Phys. Rev. D 2024, 109, 023002. [Google Scholar] [CrossRef]
- El Hanafy, W. Quadratic Rastall gravity: From low-mass HESS J1731-347 to high-mass PSR J0952-0607 pulsars. Eur. Phys. J. C 2024, 84, 355. [Google Scholar] [CrossRef]
- Tewari, S.; Chatterjee, S.; Kumar, D.; Mallick, R. Analyzing the dense matter equation of states in the light of the compact object HESS J1731-347. Phys. Rev. D 2025, 111, 103009. [Google Scholar] [CrossRef]
- Danielewicz, P.; Lacey, R.; Lynch, W.G. Determination of the equation of state of dense matter. Science 2002, 298, 1592–1596. [Google Scholar] [CrossRef] [PubMed]
- Typel, S. Variations on the excluded-volume mechanism. Eur. Phys. J. A 2016, 52, 16. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.; Ayriyan, A.; Benic, S.; Blaschke, D.; Grigorian, H.; Typel, S. New class of hybrid EoS and Bayesian M-R data analysis. Eur. Phys. J. A 2016, 52, 69. [Google Scholar] [CrossRef]
- Kaltenborn, M.A.R.; Bastian, N.U.F.; Blaschke, D.B. Quark-nuclear hybrid star equation of state with excluded volume effects. Phys. Rev. D 2017, 96, 056024. [Google Scholar] [CrossRef]
- Zdunik, J.L.; Bejger, M.; Haensel, P.; Gourgoulhon, E. Phase transitions in rotating neutron stars cores: Back bending, stability, corequakes and pulsar timing. Astron. Astrophys. 2006, 450, 747–758. [Google Scholar] [CrossRef]
- Alford, M.G.; Han, S.; Prakash, M. Generic conditions for stable hybrid stars. Phys. Rev. D 2013, 88, 083013. [Google Scholar] [CrossRef]
- Pal, S.; Podder, S.; Chaudhuri, G. Is the central compact object in HESS J1731-347 a hybrid star with a quark core? An analysis with the constant speed of sound parametrization. Astrophys. J. 2025, 983, 24. [Google Scholar] [CrossRef]
- Blaschke, D.B.; Gomez Dumm, D.; Grunfeld, A.G.; Klahn, T.; Scoccola, N.N. Hybrid stars within a covariant, nonlocal chiral quark model. Phys. Rev. C 2007, 75, 065804. [Google Scholar] [CrossRef]
- Ivanytskyi, O. Asymptotically conformal color-flavor-locked quark matter within a nonlocal chiral quark model. Phys. Rev. D 2025, 111, 034004. [Google Scholar] [CrossRef]
- Zdunik, J.L.; Haensel, P. Maximum mass of neutron stars and strange neutron-star cores. Astron. Astrophys. 2013, 551, A61. [Google Scholar] [CrossRef]
- Shahrbaf, M.; Antić, S.; Ayriyan, A.; Blaschke, D.; Grunfeld, A.G. Constraining free parameters of a color superconducting nonlocal Nambu–Jona-Lasinio model using Bayesian analysis of neutron stars mass and radius measurements. Phys. Rev. D 2023, 107, 054011. [Google Scholar] [CrossRef]
- Gomez Dumm, D.; Blaschke, D.B.; Grunfeld, A.G.; Scoccola, N.N. Phase diagram of neutral quark matter in nonlocal chiral quark models. Phys. Rev. D 2006, 73, 114019. [Google Scholar] [CrossRef]
- Blaschke, D.; Alvarez Castillo, D.E.; Benic, S.; Contrera, G.; Lastowiecki, R. Nonlocal PNJL models and heavy hybrid stars. PoS 2012, Confinement X, 249. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.E.; Blaschke, D.B.; Grunfeld, A.G.; Pagura, V.P. Third family of compact stars within a nonlocal chiral quark model equation of state. Phys. Rev. D 2019, 99, 063010. [Google Scholar] [CrossRef]
- Blaschke, D.; Ayriyan, A.; Alvarez-Castillo, D.E.; Grigorian, H. Was GW170817 a Canonical Neutron Star Merger? Bayesian Analysis with a Third Family of Compact Stars. Universe 2020, 6, 81. [Google Scholar] [CrossRef]
- Seidov, Z.F. The stability of a star with a phase change in general relativity theory. Sov. Astron. 1971, 15, 347. [Google Scholar]
- Krüger, T.; Tews, I.; Hebeler, K.; Schwenk, A. Neutron matter from chiral effective field theory interactions. Phys. Rev. C 2013, 88, 025802. [Google Scholar] [CrossRef]
- Drischler, C.; Holt, J.W.; Wellenhofer, C. Chiral Effective Field Theory and the High-Density Nuclear Equation of State. Ann. Rev. Nucl. Part. Sci. 2021, 71, 403–432. [Google Scholar] [CrossRef]
- Hebeler, K.; Lattimer, J.M.; Pethick, C.J.; Schwenk, A. Equation of state and neutron star properties constrained by nuclear physics and observation. Astrophys. J. 2013, 773, 11. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Ho, W.C.G.; Lattimer, J.M.; Loewenstein, M.; et al. The Radius of PSR J0740+6620 from NICER and XMM-Newton Data. Astrophys. J. Lett. 2021, 918, L28. [Google Scholar] [CrossRef]
- Fraga, E.S.; Kurkela, A.; Vuorinen, A. Interacting quark matter equation of state for compact stars. Astrophys. J. Lett. 2014, 781, L25. [Google Scholar] [CrossRef]
- Fujimoto, Y.; Fukushima, K.; McLerran, L.D.; Praszalowicz, M. Trace Anomaly as Signature of Conformality in Neutron Stars. Phys. Rev. Lett. 2022, 129, 252702. [Google Scholar] [CrossRef]
- Marczenko, M. Average speed of sound in neutron stars. Phys. Rev. C 2024, 110, 045811. [Google Scholar] [CrossRef]
- Marczenko, M.; McLerran, L.; Redlich, K.; Sasaki, C. Reaching percolation and conformal limits in neutron stars. Phys. Rev. C 2023, 107, 025802. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Hirvonen, J.; Komoltsev, O.; Kurkela, A.; Nättilä, J.; Vuorinen, A. Strongly interacting matter exhibits deconfined behavior in massive neutron stars. Nat. Commun. 2023, 14, 8451. [Google Scholar] [CrossRef]
- Marczenko, M.; Redlich, K.; Sasaki, C. Curvature of the energy per particle in neutron stars. Phys. Rev. D 2024, 109, L041302. [Google Scholar] [CrossRef]
- Marczenko, M. Conformality thresholds in neutron stars. J. Subatomic Part. Cosmol. 2025, 3, 100043. [Google Scholar] [CrossRef]
- Ivanytskyi, O.; Blaschke, D.B. Recovering the Conformal Limit of Color Superconducting Quark Matter within a Confining Density Functional Approach. Particles 2022, 5, 514–534. [Google Scholar] [CrossRef]
- Jiménez, J.C.; Lazzari, L.; Gonçalves, V.P. How the QCD trace anomaly behaves at the core of twin stars? Phys. Rev. D 2024, 110, 114014. [Google Scholar] [CrossRef]
- Christian, J.E.; Zacchi, A.; Schaffner-Bielich, J. Classifications of Twin Star Solutions for a Constant Speed of Sound Parameterized Equation of State. Eur. Phys. J. A 2018, 54, 28. [Google Scholar] [CrossRef]
- Laskos-Patkos, P.; Lalazissis, G.A.; Wang, S.; Meng, J.; Ring, P.; Moustakidis, C.C. Speed of sound bounds and first-order phase transitions in compact stars. Phys. Rev. C 2025, 111, 025801. [Google Scholar] [CrossRef]
- Tolman, R.C. Static solutions of Einstein’s field equations for spheres of fluid. Phys. Rev. 1939, 55, 364–373. [Google Scholar] [CrossRef]
- Oppenheimer, J.R.; Volkoff, G.M. On massive neutron cores. Phys. Rev. 1939, 55, 374–381. [Google Scholar] [CrossRef]
- Harrison, B.K.; Thorne, K.S.; Wakano, M.; Wheeler, J.A. Gravitation Theory and Gravitational Collapse; University of Chicago Press: Chicago, IL, USA, 1965. [Google Scholar]
- Bassa, C.G.; Pleunis, Z.; Hessels, J.W.T.; Ferrara, E.C.; Breton, R.P.; Gusinskaia, N.V.; Kondratiev, V.I.; Sanidas, S.; Nieder, L.; Clark, C.J.; et al. LOFAR discovery of the fastest-spinning millisecond pulsar in the Galactic field. Astrophys. J. Lett. 2017, 846, L20. [Google Scholar] [CrossRef]
- Most, E.R.; Papenfort, L.J.; Weih, L.R.; Rezzolla, L. A lower bound on the maximum mass if the secondary in GW190814 was once a rapidly spinning neutron star. Mon. Not. Roy. Astron. Soc. 2020, 499, L82–L86. [Google Scholar] [CrossRef]
- Miller, M.C.; Lamb, F.K.; Dittmann, A.J.; Bogdanov, S.; Arzoumanian, Z.; Gendreau, K.C.; Guillot, S.; Harding, A.K.; Ho, W.C.G.; Lattimer, J.M.; et al. PSR J0030+0451 Mass and Radius from NICER Data and Implications for the Properties of Neutron Star Matter. Astrophys. J. Lett. 2019, 887, L24. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Bogdanov, S.; Ray, P.S.; Ludlam, R.M.; Guillot, S.; Arzoumanian, Z.; Baker, C.L.; Bilous, A.V.; Chakrabarty, D.; et al. A NICER View of PSR J0030+0451: Millisecond Pulsar Parameter Estimation. Astrophys. J. Lett. 2019, 887, L21. [Google Scholar] [CrossRef]
- Riley, T.E.; Watts, A.L.; Ray, P.S.; Bogdanov, S.; Guillot, S.; Morsink, S.M.; Bilous, A.V.; Arzoumanian, Z.; Choudhury, D.; Deneva, J.S.; et al. A NICER View of the Massive Pulsar PSR J0740+6620 Informed by Radio Timing and XMM-Newton Spectroscopy. Astrophys. J. Lett. 2021, 918, L27. [Google Scholar] [CrossRef]
- Mauviard, L.; Guillot, S.; Salmi, T.; Choudhury, D.; Dorsman, B.; González-Caniulef, D.; Hoogkamer, M.; Huppenkothen, D.; Kazantsev, C.; Kini, Y.; et al. A NICER view of the 1.4 solar-mass edge-on pulsar PSR J0614–3329. arXiv 2025, arXiv:2506.14883. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. GW170817: Measurements of neutron star radii and equation of state. Phys. Rev. Lett. 2018, 121, 161101. [Google Scholar] [CrossRef] [PubMed]
- Bauswein, A.; Just, O.; Janka, H.T.; Stergioulas, N. Neutron-star radius constraints from GW170817 and future detections. Astrophys. J. Lett. 2017, 850, L34. [Google Scholar] [CrossRef]
- Annala, E.; Gorda, T.; Kurkela, A.; Vuorinen, A. Gravitational-wave constraints on the neutron-star-matter Equation of State. Phys. Rev. Lett. 2018, 120, 172703. [Google Scholar] [CrossRef]
- Sneppen, A.; Just, O.; Bauswein, A.; Damgaard, R.; Watson, D.; Shingles, L.J.; Collins, C.E.; Sim, S.A.; Xiong, Z.; Martinez-Pinedo, G.; et al. Helium as an Indicator of the Neutron-Star Merger Remnant Lifetime and its Potential for Equation of State Constraints. arXiv 2024, arXiv:2411.03427. [Google Scholar]
- Kramer, M.; Stairs, I.H.; Manchester, R.N.; Wex, N.; Deller, A.T.; Coles, W.A.; Ali1, M.; Burgay, M.; Camilo, F.; Cognard, I.; et al. Strong-Field Gravity Tests with the Double Pulsar. Phys. Rev. X 2021, 11, 041050. [Google Scholar] [CrossRef]
- Landry, P.; Kumar, B. Constraints on the moment of inertia of PSR J0737-3039A from GW170817. Astrophys. J. Lett. 2018, 868, L22. [Google Scholar] [CrossRef]
- Miao, Z.; Li, A.; Dai, Z.G. On the moment of inertia of PSR J0737-3039 A from LIGO/Virgo and NICER. Mon. Not. Roy. Astron. Soc. 2022, 515, 5071–5080. [Google Scholar] [CrossRef]
- Silva, H.O.; Holgado, A.M.; Cárdenas-Avendaño, A.; Yunes, N. Astrophysical and theoretical physics implications from multimessenger neutron star observations. Phys. Rev. Lett. 2021, 126, 181101. [Google Scholar] [CrossRef]
- Ravenhall, D.G.; Pethick, C.J. Neutron Star Moments of Inertia. Astrophys. J. 1994, 424, 846. [Google Scholar] [CrossRef]
- Chubarian, E.; Grigorian, H.; Poghosyan, G.S.; Blaschke, D. Deconfinement phase transition in rotating nonspherical compact stars. Astron. Astrophys. 2000, 357, 968–976. [Google Scholar]
- Bejger, M.; Blaschke, D.; Haensel, P.; Zdunik, J.L.; Fortin, M. Consequences of a strong phase transition in the dense matter equation of state for the rotational evolution of neutron stars. Astron. Astrophys. 2017, 600, A39. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Prakash, M. Neutron Star Observations: Prognosis for Equation of State Constraints. Phys. Rept. 2007, 442, 109–165. [Google Scholar] [CrossRef]
- Kramer, M.; Wex, N. The double pulsar system: A unique laboratory for gravity. Class. Quant. Grav. 2009, 26, 073001. [Google Scholar] [CrossRef]
- Hinderer, T. Tidal Love numbers of neutron stars. Astrophys. J. 2008, 677, 1216–1220, Erratum in Astrophys. J. 2009, 697, 964. https://doi.org/10.1088/0004-637X/697/1/964. [Google Scholar] [CrossRef]
- Damour, T.; Nagar, A. Relativistic tidal properties of neutron stars. Phys. Rev. D 2009, 80, 084035. [Google Scholar] [CrossRef]
- Binnington, T.; Poisson, E. Relativistic theory of tidal Love numbers. Phys. Rev. D 2009, 80, 084018. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. I-Love-Q Relations in Neutron Stars and their Applications to Astrophysics, Gravitational Waves and Fundamental Physics. Phys. Rev. D 2013, 88, 023009. [Google Scholar] [CrossRef]
- Hinderer, T.; Lackey, B.D.; Lang, R.N.; Read, J.S. Tidal deformability of neutron stars with realistic equations of state and their gravitational wave signatures in binary inspiral. Phys. Rev. D 2010, 81, 123016. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.E. The energy budget of the transition of a neutron star into the third family branch. Astron. Nachr. 2021, 342, 234–239. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.E.; Antoniadis, J.; Ayriyan, A.; Blaschke, D.; Danchev, V.; Grigorian, H.; Largani, N.K.; Weber, F. Accretion-induced collapse to third family compact stars as trigger for eccentric orbits of millisecond pulsars in binaries. Astron. Nachr. 2019, 340, 878–884. [Google Scholar] [CrossRef]
- Chanlaridis, S.; Ohse, D.; Alvarez-Castillo, D.E.; Antoniadis, J.; Blaschke, D.; Danchev, V.; Langer, N.; Misra, D. Formation of twin compact stars in low-mass X-ray binaries: Implications on eccentric and isolated millisecond pulsar populations. Astron. Astrophys. 2025, 695, A16. [Google Scholar] [CrossRef]
- Romani, R.W.; Kandel, D.; Filippenko, A.V.; Brink, T.G.; Zheng, W. PSR J0952-0607: The Fastest and Heaviest Known Galactic Neutron Star. Astrophys. J. Lett. 2022, 934, L17. [Google Scholar] [CrossRef]
- Hessels, J.W.T.; Ransom, S.M.; Stairs, I.H.; Freire, P.C.C.; Kaspi, V.M.; Camilo, F. A radio pulsar spinning at 716-hz. Science 2006, 311, 1901–1904. [Google Scholar] [CrossRef] [PubMed]
- Nozawa, T.; Stergioulas, N.; Gourgoulhon, E.; Eriguchi, Y. Construction of highly accurate models of rotating neutron stars: Comparison of three different numerical schemes. Astron. Astrophys. Suppl. Ser. 1998, 132, 431. [Google Scholar] [CrossRef]
- Komatsu, H.; Eriguchi, Y.; Hachisu, I. Rapidly rotating general relativistic stars. I - Numerical method and its application to uniformly rotating polytropes. Mon. Not. Roy. Astron. Soc. 1989, 237, 355–379. [Google Scholar] [CrossRef]
- Cook, G.B.; Shapiro, S.L.; Teukolsky, S.A. Rapidly rotating polytropes in general relativity. Astrophys. J. 1994, 422, 227–242. [Google Scholar] [CrossRef]
- Stergioulas, N.; Friedman, J.L. Comparing models of rapidly rotating relativistic stars constructed by two numerical methods. Astrophys. J. 1995, 444, 306. [Google Scholar] [CrossRef]
- Breu, C.; Rezzolla, L. Maximum mass, moment of inertia and compactness of relativistic stars. Mon. Not. Roy. Astron. Soc. 2016, 459, 646–656. [Google Scholar] [CrossRef]
- Gärtlein, C.; Sagun, V.; Ivanytskyi, O.; Blaschke, D.; Lopes, I. Fastest spinning millisecond pulsars: Indicators for quark matter in neutron stars? arXiv 2024, arXiv:2412.07758. [Google Scholar]
- Jyothilakshmi, O.P.; Krishnan, P.E.S.; Sreekanth, V.; Chandrakar, H.; Jha, T.K. Fundamental Oscillation Modes in Neutron Stars with Hyperons and Delta Baryons. Symmetry 2025, 17, 230. [Google Scholar] [CrossRef]
- Kokkotas, K.D.; Apostolatos, T.A.; Andersson, N. The Inverse problem for pulsating neutron stars: A ’Fingerprint analysis’ for the supranuclear equation of state. Mon. Not. Roy. Astron. Soc. 2001, 320, 307–315. [Google Scholar] [CrossRef]
- Ho, W.C.G.; Jones, D.I.; Andersson, N.; Espinoza, C.M. Gravitational waves from transient neutron star f-mode oscillations. Phys. Rev. D 2020, 101, 103009. [Google Scholar] [CrossRef]
- Detweiler, S.L.; Lindblom, L. On the nonradial pulsations of general relativistic stellar models. Astrophys. J. 1985, 292, 12–15. [Google Scholar] [CrossRef]
- Sotani, H.; Tominaga, K.; Maeda, K.i. Density discontinuity of a neutron star and gravitational waves. Phys. Rev. D 2002, 65, 024010. [Google Scholar] [CrossRef]
- Pradhan, B.K.; Chatterjee, D.; Lanoye, M.; Jaikumar, P. General relativistic treatment of f-mode oscillations of hyperonic stars. Phys. Rev. C 2022, 106, 015805. [Google Scholar] [CrossRef]
- Zerilli, F.J. Effective potential for even parity Regge-Wheeler gravitational perturbation equations. Phys. Rev. Lett. 1970, 24, 737–738. [Google Scholar] [CrossRef]
- Pradhan, B.K.; Chatterjee, D.; Alvarez-Castillo, D.E. Probing hadron–quark phase transition in twin stars using f-modes. Mon. Not. Roy. Astron. Soc. 2024, 531, 4640–4655. [Google Scholar] [CrossRef]
- Kubis, S. The nuclear symmetry energy and stability of matter in neutron star. Phys. Rev. C 2007, 76, 025801. [Google Scholar] [CrossRef]
- Baym, G.; Bethe, H.A.; Pethick, C. Neutron star matter. Nucl. Phys. A 1971, 175, 225–271. [Google Scholar] [CrossRef]
- Fortin, M.; Providencia, C.; Raduta, A.R.; Gulminelli, F.; Zdunik, J.L.; Haensel, P.; Bejger, M. Neutron star radii and crusts: Uncertainties and unified equations of state. Phys. Rev. C 2016, 94, 035804. [Google Scholar] [CrossRef]
- Canullan-Pascual, M.O.; Mariani, M.; Ranea-Sandoval, I.F.; Orsaria, M.G.; Weber, F. Consistent crust-core interpolation and its effect on non-radial neutron star oscillations. In Proceedings of the 11th International Workshop on Astronomy and Relativistic Astrophysics: From Quarks to Cosmos, Aguas Calientes, Peru, 2–6 September 2024. Astron.Nachr. 2025, 346, 3–4. [Google Scholar] [CrossRef]
- Neill, D.; Newton, W.G.; Tsang, D. Resonant Shattering Flares as Multimessenger Probes of the Nuclear Symmetry Energy. Mon. Not. Roy. Astron. Soc. 2021, 504, 1129–1143, Erratum in Mon. Not. Roy. Astron. Soc. 2022, 513, 310. https://doi.org/10.1093/mnras/stac1033. [Google Scholar] [CrossRef]
- Antonelli, M.; Montoli, A.; Pizzochero, P. Insights into the physics of neutron star interiors from pulsar glitches. In Astrophysics in the XXI Century with Compact Stars; World Scientific: Singapore, 2022; pp. 219–281. [Google Scholar] [CrossRef]
- Link, B.; Epstein, R.I.; Lattimer, J.M. Pulsar constraints on neutron star structure and equation of state. Phys. Rev. Lett. 1999, 83, 3362–3365. [Google Scholar] [CrossRef]
- Andersson, N.; Glampedakis, K.; Ho, W.C.G.; Espinoza, C.M. Pulsar glitches: The crust is not enough. Phys. Rev. Lett. 2012, 109, 241103. [Google Scholar] [CrossRef] [PubMed]
- Chamel, N. Neutron conduction in the inner crust of a neutron star in the framework of the band theory of solids. Phys. Rev. C 2012, 85, 035801. [Google Scholar] [CrossRef]
- Zhang, N.B.; Li, B.A. Imprints of high-density nuclear symmetry energy on the crustal fraction of neutron star moment of inertia. Particles 2025, 8, 12. [Google Scholar] [CrossRef]
- Dong, Z.Z.; Lau, S.Y.; Yagi, K. New modeling for hybrid stars with an elastic quark core. arXiv 2024, arXiv:2412.16636. [Google Scholar]
- Drischler, C.; Melendez, J.A.; Furnstahl, R.J.; Garcia, A.J.; Zhang, X. BUQEYE guide to projection-based emulators in nuclear physics. Front. Phys. 2022, 10, 1092931. [Google Scholar] [CrossRef]
- Dietrich, T.; Coughlin, M.W.; Pang, P.T.H.; Bulla, M.; Heinzel, J.; Issa, L.; Tews, I.; Antier, S. Multimessenger constraints on the neutron-star equation of state and the Hubble constant. Science 2020, 370, 1450–1453. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Steiner, A.W. Neutron Star Masses and Radii from Quiescent Low-Mass X-ray Binaries. Astrophys. J. 2014, 784, 123. [Google Scholar] [CrossRef]
- Chatziioannou, K.; Yagi, K.; Klein, A.; Cornish, N.; Yunes, N. Probing the Internal Composition of Neutron Stars with Gravitational Waves. Phys. Rev. D 2015, 92, 104008. [Google Scholar] [CrossRef]
- Lackey, B.D.; Wade, L. Reconstructing the neutron-star equation of state with gravitational-wave detectors from a realistic population of inspiralling binary neutron stars. Phys. Rev. D 2015, 91, 043002. [Google Scholar] [CrossRef]
- Raithel, C.A.; Özel, F.; Psaltis, D. From Neutron Star Observables to the Equation of State. II. Bayesian Inference of Equation of State Pressures. Astrophys. J. 2017, 844, 156. [Google Scholar] [CrossRef]
- Ayriyan, A.; Blaschke, D.; Grunfeld, A.G.; Alvarez-Castillo, D.; Grigorian, H.; Abgaryan, V. Bayesian analysis of multimessenger M-R data with interpolated hybrid EoS. Eur. Phys. J. A 2021, 57, 318. [Google Scholar] [CrossRef]
- Ayriyan, A.; Alvarez-Castillo, D.; Blaschke, D.; Grigorian, H. Bayesian Analysis for Extracting Properties of the Nuclear Equation of State from Observational Data including Tidal Deformability from GW170817. Universe 2019, 5, 61. [Google Scholar] [CrossRef]
- Ayriyan, A.; Alvarez-Castillo, D.E.; Benic, S.; Blaschke, D.; Grigorian, H.; Typel, S. Bayesian analysis for a new class of hybrid EoS models using mass and radius data of compact stars. Acta Phys. Polon. Supp. B 2017, 10, 799–804. [Google Scholar] [CrossRef]
- Ayriyan, A.; Alvarez-Castillo, D.E.; Blaschke, D.; Grigorian, H.; Sokolowski, M. New Bayesian analysis of hybrid EoS constraints with mass-radius data for compact stars. Phys. Part. Nucl. 2015, 46, 854–857. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.; Ayriyan, A.; Barnaföldi, G.G.; Pósfay, P. Studying the Landau Mass Parameter of the Extended σ-ω Model for Neutron Star Matter. Phys. Part. Nucl. 2020, 51, 725–729. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.; Ayriyan, A.; Barnaföldi, G.G.; Grigorian, H.; Pósfay, P. Studying the parameters of the extended σ-ω model for neutron star matter. Eur. Phys. J. ST 2020, 229, 3615–3628. [Google Scholar] [CrossRef]
- Ayriyan, A.; Blaschke, D.; Carlomagno, J.P.; Contrera, G.A.; Grunfeld, A.G. Bayesian analysis of hybrid neutron star EOS constraints within an instantaneous nonlocal chiral quark matter model. Universe 2025, 11, 141. [Google Scholar] [CrossRef]
- Li, J.J.; Tian, Y.; Sedrakian, A. Bayesian inferences on covariant density functionals from multimessenger astrophysical data: Nucleonic models. Phys. Rev. C 2025, 111, 055804. [Google Scholar] [CrossRef]
- Li, J.J.; Tian, Y.; Sedrakian, A. Bayesian Constraints on Covariant Density Functional Equations of State of Compact Stars with New NICER Mass-Radius Measurements. arXiv 2024, arXiv:2412.16513. [Google Scholar]
- Güven, H.; Bozkurt, K.; Khan, E.; Margueron, J. Multimessenger and multiphysics Bayesian inference for the GW170817 binary neutron star merger. Phys. Rev. C 2020, 102, 015805. [Google Scholar] [CrossRef]
- Prakash, A.; Gupta, I.; Breschi, M.; Kashyap, R.; Radice, D.; Bernuzzi, S.; Logoteta, D.; Sathyaprakash, B.S. Detectability of QCD phase transitions in binary neutron star mergers: Bayesian inference with the next generation gravitational wave detectors. Phys. Rev. D 2024, 109, 103008. [Google Scholar] [CrossRef]
- Jiang, J.L.; Ecker, C.; Rezzolla, L. Bayesian Analysis of Neutron-star Properties with Parameterized Equations of State: The Role of the Likelihood Functions. Astrophys. J. 2023, 949, 11. [Google Scholar] [CrossRef]
- Grundler, X.; Li, B.A. Bayesian Quantification of Observability and Equation of State of Twin Stars. arXiv 2025, arXiv:2506.13677. [Google Scholar]
- Morawski, F.; Bejger, M. Neural network reconstruction of the dense matter equation of state derived from the parameters of neutron stars. Astron. Astrophys. 2020, 642, A78. [Google Scholar] [CrossRef]
- Fujimoto, Y.; Fukushima, K.; Murase, K. Methodology study of machine learning for the neutron star equation of state. Phys. Rev. D 2018, 98, 023019. [Google Scholar] [CrossRef]
- Farrell, D.; Baldi, P.; Ott, J.; Ghosh, A.; Steiner, A.W.; Kavitkar, A.; Lindblom, L.; Whiteson, D.; Weber, F. Deducing neutron star equation of state from telescope spectra with machine-learning-derived likelihoods. J. Cosmol. Astropart. Phys. 2023, 12, 022. [Google Scholar] [CrossRef]
- Li, B.A.; Grundler, X.; Xie, W.J.; Zhang, N.B. Bayesian Inference of Core Properties of Hybrid Stars from Future High-Precision Measurements of Their Radii. arXiv 2025, arXiv:2505.00194. [Google Scholar]
- Li, J.J.; Sedrakian, A. Bayesian inferences on covariant density functionals from multimessenger astrophysical data: The impacts of likelihood functions of low density matter constraints. arXiv 2025, arXiv:2505.00911. [Google Scholar]
- Magnall, S.J.; Ecker, C.; Rezzolla, L.; Lasky, P.D.; Goode, S.R. Physics-Informed Priors Improve Gravitational-Wave Constraints on Neutron-Star Matter. arXiv 2025, arXiv:2504.21526. [Google Scholar]
- Finch, E.; Legred, I.; Chatziioannou, K.; Essick, R.; Han, S.; Landry, P. Unified nonparametric equation-of-state inference from the neutron-star crust to perturbative-QCD densities. arXiv 2025, arXiv:2505.13691. [Google Scholar]
- Fujimoto, Y.; Fukushima, K.; Murase, K. Extensive Studies of the Neutron Star Equation of State from the Deep Learning Inference with the Observational Data Augmentation. JHEP 2021, 03, 273. [Google Scholar] [CrossRef]
- Ventagli, G.; Saltas, I.D. Deep learning inference of the neutron star equation of state. J. Cosmol. Astropart. Phys. 2025, 01, 073. [Google Scholar] [CrossRef]
- Sun, B.; Lattimer, J.M. Correlations Between the Neutron Star Mass-Radius Relation and the Equation of State of Dense Matter. arXiv 2024, arXiv:2412.14645. [Google Scholar]
- Lindblom, L.; Zhou, T. Uncertainty quantification for the relativistic inverse stellar structure problem. Phys. Rev. D 2025, 111, 063024. [Google Scholar] [CrossRef]
- Reed, B.T.; Somasundaram, R.; De, S.; Armstrong, C.L.; Giuliani, P.; Capano, C.; Brown, D.A.; Tews, I. Toward Accelerated Nuclear-physics Parameter Estimation from Binary Neutron Star Mergers: Emulators for the Tolman–Oppenheimer–Volkoff Equations. Astrophys. J. 2024, 974, 285. [Google Scholar] [CrossRef]
- Pelicer, M.R.; Cruz-Camacho, N.; Conde, C.; Friedenberg, D.; Roy, S.; Zhang, Z.; Manning, T.A.; Alford, M.G.; Clevinger, A.; Grefa, J.; et al. Building Neutron Stars with the MUSES Calculation Engine. arXiv 2025, arXiv:2502.07902. [Google Scholar]
- Pelicer, M.; Dexheimer, V.; Grefa, J. An Overview of the MUSES Calculation Engine and How It Can Be Used to Describe Neutron Stars. arXiv 2025, arXiv:2505.14921. [Google Scholar]
- Sharifi, Z.; Bigdeli, M.; Alvarez-Castillo, D. Studying VLOCV twin compact stars with binary mergers. Phys. Rev. D 2021, 103, 103011. [Google Scholar] [CrossRef]
- Shahrbaf, M.; Blaschke, D.; Typel, S.; Farrar, G.R.; Alvarez-Castillo, D.E. Sexaquark dilemma in neutron stars and its solution by quark deconfinement. Phys. Rev. D 2022, 105, 103005. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.; Marczenko, M. Compact Star Twins with a Dark Matter Core. Acta Phys. Polon. Supp. 2022, 15, 28. [Google Scholar] [CrossRef]
- Lyra, F.; Moreira, L.; Negreiros, R.; Gomes, R.O.; Dexheimer, V. Compactness in the thermal evolution of twin stars. Phys. Rev. C 2023, 107, 025806. [Google Scholar] [CrossRef]
- Lindblom, L. Parametric representations of neutron-star equations of state with phase transitions. Phys. Rev. D 2024, 110, 043018. [Google Scholar] [CrossRef]
- Carlomagno, J.P.; Contrera, G.A.; Grunfeld, A.G.; Blaschke, D. Thermal twin stars within a hybrid equation of state based on a nonlocal chiral quark model compatible with modern astrophysical observations. Phys. Rev. D 2024, 109, 043050. [Google Scholar] [CrossRef]
- Christian, J.E.; Schaffner-Bielich, J.; Rosswog, S. Which first order phase transitions to quark matter are possible in neutron stars? Phys. Rev. D 2024, 109, 063035. [Google Scholar] [CrossRef]
- Zhang, N.B.; Li, B.A. Impact of the nuclear equation of state on the formation of twin stars. Eur. Phys. J. A 2025, 61, 31. [Google Scholar] [CrossRef]
- Naseri, M.; Bozzola, G.; Paschalidis, V. Exploring pathways to forming twin stars. Phys. Rev. D 2024, 110, 044037. [Google Scholar] [CrossRef]
- Laskos-Patkos, P.; Moustakidis, C. Signatures of hadron-quark phase transition through the r-mode instability in twin stars. HNPS Adv. Nucl. Phys. 2024, 30, 104–109. [Google Scholar] [CrossRef]
- Christian, J.E.; Schaffner-Bielich, J. Confirming the Existence of Twin Stars in a NICER Way. Astrophys. J. 2022, 935, 122. [Google Scholar] [CrossRef]
- Mendes, M.; Christian, J.E.; Fattoyev, F.J.; Schaffner-Bielich, J. Constraining twin stars with cold neutron star cooling data. Phys. Rev. D 2025, 111, 063007. [Google Scholar] [CrossRef]
- Chen, J.; Ji, Z. Observational and Theoretical Constraints on First-Order Phase Transitions in Neutron Stars. arXiv 2025, arXiv:2502.05519. [Google Scholar]
- Christian, J.E.; Rather, I.A.; Gholami, H.; Hofmann, M. Comprehensive Analysis of Constructing Hybrid Stars with an RG-consistent NJL Model. arXiv 2025, arXiv:2503.13626. [Google Scholar]
- Sagert, I.; Fischer, T.; Hempel, M.; Pagliara, G.; Schaffner-Bielich, J.; Mezzacappa, A.; Thielemann, F.K.; Liebendorfer, M. Signals of the QCD phase transition in core-collapse supernovae. Phys. Rev. Lett. 2009, 102, 081101. [Google Scholar] [CrossRef] [PubMed]
- Sagert, I.; Pagliara, G.; Hempel, M.; Schaffner-Bielich, J. Is there Quark Matter in (Low-Mass) Pulsars? J. Phys. G 2008, 35, 104079. [Google Scholar] [CrossRef]
- Fischer, T.; Bastian, N.U.F.; Wu, M.R.; Baklanov, P.; Sorokina, E.; Blinnikov, S.; Typel, S.; Klähn, T.; Blaschke, D.B. Quark deconfinement as a supernova explosion engine for massive blue supergiant stars. Nat. Astron. 2018, 2, 980–986. [Google Scholar] [CrossRef]
- Kubis, S.; Wójcik, W.; Zabari, N. Multilayer neutron stars with scalar mesons crossing term. Phys. Rev. C 2020, 102, 065803. [Google Scholar] [CrossRef]
- Ivanytskyi, O. Quarkyonic picture of isospin QCD. arXiv 2025, arXiv:2505.07076. [Google Scholar]
- Kojo, T.; Suenaga, D.; Chiba, R. Isospin QCD as a Laboratory for Dense QCD. Universe 2024, 10, 293. [Google Scholar] [CrossRef]
- Yao, N.; Sorensen, A.; Dexheimer, V.; Noronha-Hostler, J. Structure in the speed of sound: From neutron stars to heavy-ion collisions. Phys. Rev. C 2024, 109, 065803. [Google Scholar] [CrossRef]
- Ayriyan, A.; Grigorian, H. Model of the Phase Transition Mimicking the Pasta Phase in Cold and Dense Quark-Hadron Matter. EPJ Web Conf. 2018, 173, 03003. [Google Scholar] [CrossRef]
- Ayriyan, A.; Bastian, N.U.; Blaschke, D.; Grigorian, H.; Maslov, K.; Voskresensky, D.N. Robustness of third family solutions for hybrid stars against mixed phase effects. Phys. Rev. C 2018, 97, 045802. [Google Scholar] [CrossRef]
- Alvarez-Castillo, D.; Blaschke, D.; Typel, S. Mixed phase within the multi-polytrope approach to high-mass twins. Astron. Nachr. 2017, 338, 1048–1051. [Google Scholar] [CrossRef]
- Blaschke, D.; Alvarez-Castillo, D. A mixing interpolation method to mimic pasta phases in compact star matter. Eur. Phys. J. A 2020, 56, 124. [Google Scholar] [CrossRef]
- Maslov, K.; Yasutake, N.; Ayriyan, A.; Blaschke, D.; Grigorian, H.; Maruyama, T.; Tatsumi, T.; Voskresensky, D.N. Hybrid equation of state with pasta phases and third family of compact stars. Phys. Rev. C 2019, 100, 025802. [Google Scholar] [CrossRef]
- Lope-Oter, E.; Wojnar, A. Twin stars in General Relativity and Extended Theories of Gravity. J. Cosmol. Astropart. Phys. 2025, 1, 054. [Google Scholar] [CrossRef]
- Pereira, J.P.; Flores, C.V.; Lugones, G. Phase transition effects on the dynamical stability of hybrid neutron stars. Astrophys. J. 2018, 860, 12. [Google Scholar] [CrossRef]
- Rau, P.B.; Sedrakian, A. Unstable modes of hypermassive compact stars driven by viscosity and gravitational radiation. Mon. Not. Roy. Astron. Soc. 2021, 509, 1854–1870. [Google Scholar] [CrossRef]
- Lugones, G.; Mariani, M.; Ranea-Sandoval, I.F. A model-agnostic analysis of hybrid stars with reactive interfaces. J. Cosmol. Astropart. Phys. 2023, 3, 028. [Google Scholar] [CrossRef]
- Kini, Y.; Salmi, T.; Vinciguerra, S.; Watts, A.L.; Bilous, A.; Galloway, D.K.; Wateren, E.v.d.; Khalsa, G.P.; Bogdanov, S.; Buchner, J.; et al. Constraining the properties of the thermonuclear burst oscillation source XTE J1814-338 through pulse profile modelling. Mon. Not. Roy. Astron. Soc. 2024, 535, 1507–1525. [Google Scholar] [CrossRef]
- Laskos-Patkos, P.; Moustakidis, C.C. XTE J1814-338: A potential hybrid star candidate. Phys. Rev. D 2025, 111, 063058. [Google Scholar] [CrossRef]
- Yagi, K.; Yunes, N. Approximate Universal Relations for Neutron Stars and Quark Stars. Phys. Rept. 2017, 681, 1–72. [Google Scholar] [CrossRef]
- Largani, N.K.; Fischer, T.; Sedrakian, A.; Cierniak, M.; Alvarez-Castillo, D.E.; Blaschke, D.B. Universal relations for rapidly rotating cold and hot hybrid stars. Mon. Not. Roy. Astron. Soc. 2022, 515, 3539–3554. [Google Scholar] [CrossRef]
- Wu, Z.; Wen, D. Precisely constraining the properties of neutron stars using new universal relations and astronomical observations*. Chin. Phys. C 2025, 49, 045109. [Google Scholar] [CrossRef]
- Landry, P.; Chakravarti, K. Prospects for constraining twin stars with next-generation gravitational-wave detectors. arXiv 2022, arXiv:2212.09733. [Google Scholar]
- Counsell, A.R.; Gittins, F.; Andersson, N.; Tews, I. Interface modes in inspiralling neutron stars: A gravitational-wave probe of first-order phase transitions. arXiv 2025, arXiv:2504.06181. [Google Scholar]
- Glendenning, N.K.; Pei, S.; Weber, F. Signal of quark deconfinement in the timing structure of pulsar spindown. Phys. Rev. Lett. 1997, 79, 1603–1606. [Google Scholar] [CrossRef]
- Largani, N.K.; Fischer, T.; Shibagaki, S.; Cerdá-Durán, P.; Torres-Forné, A. Neutron stars in accreting systems—Signatures of the QCD phase transition. Astron. Astrophys. 2024, 687, A245. [Google Scholar] [CrossRef]
- Tsaloukidis, L.; Koliogiannis, P.S.; Kanakis-Pegios, A.; Moustakidis, C.C. Twin stars as probes of the nuclear equation of state: Effects of rotation through the PSR J0952-0607 pulsar and constraints via the tidal deformability from the GW170817 event. Phys. Rev. D 2023, 107, 023012. [Google Scholar] [CrossRef]
- Gittins, F.; Andersson, N.; Jones, D.I. Modelling neutron star mountains. Mon. Not. Roy. Astron. Soc. 2020, 500, 5570–5582. [Google Scholar] [CrossRef]
- Morales, J.A.; Horowitz, C.J. Anisotropic neutron star crust, solar system mountains, and gravitational waves. Phys. Rev. D 2024, 110, 044016. [Google Scholar] [CrossRef]

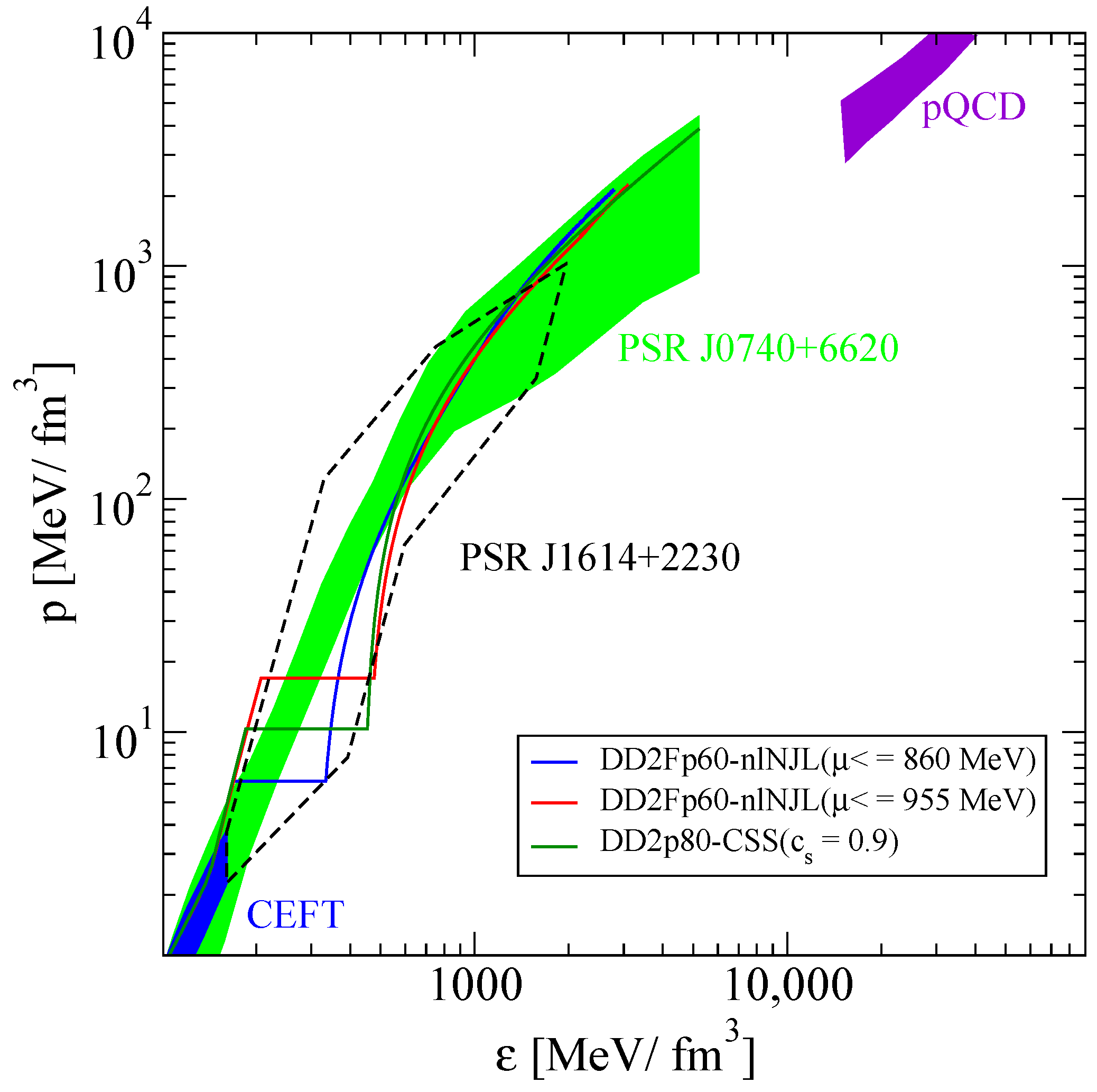
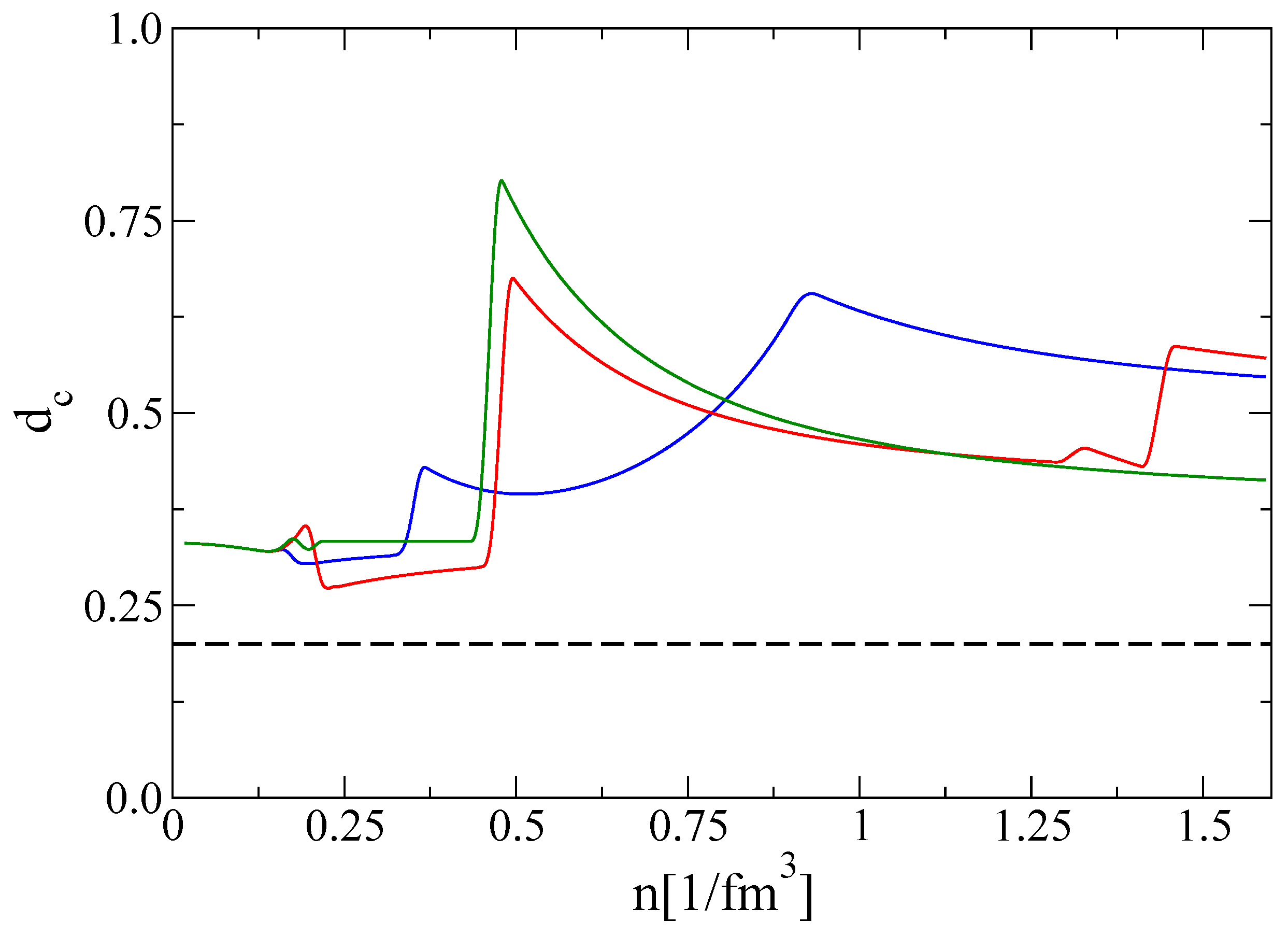
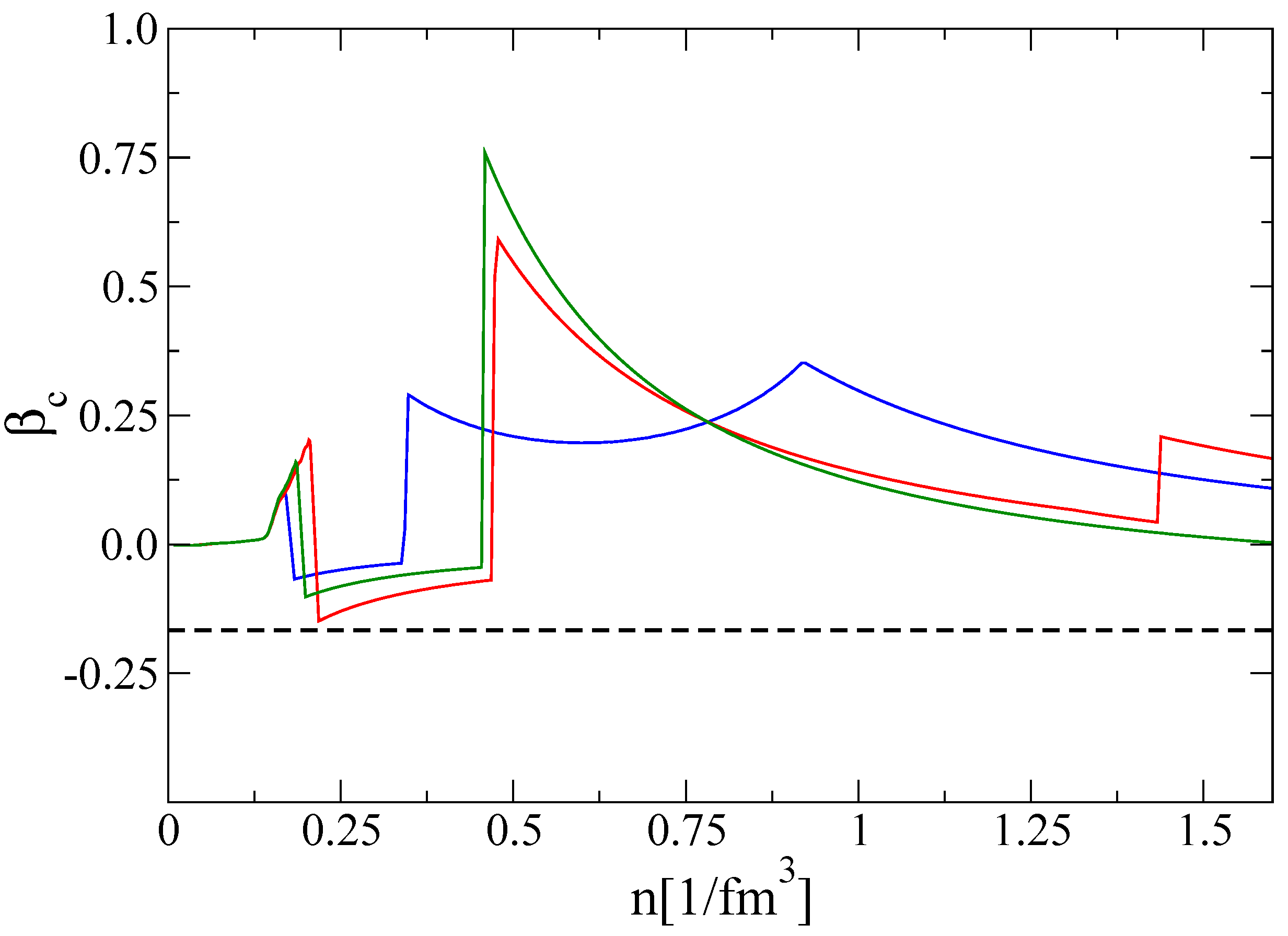

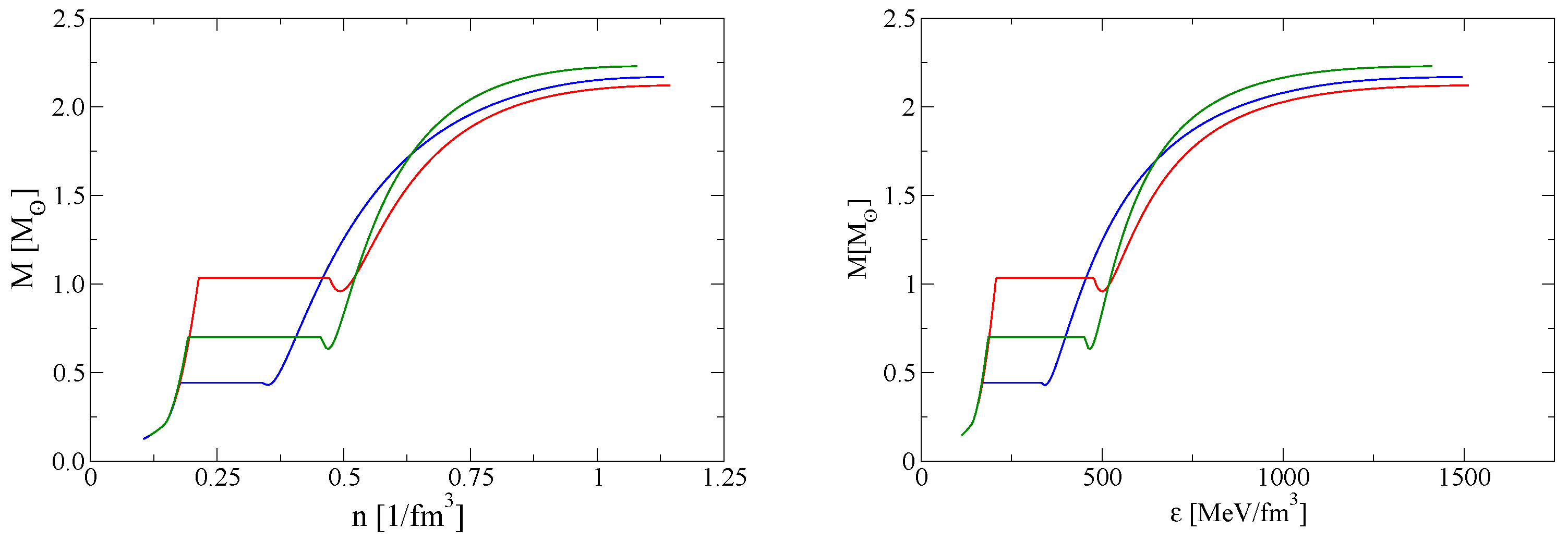
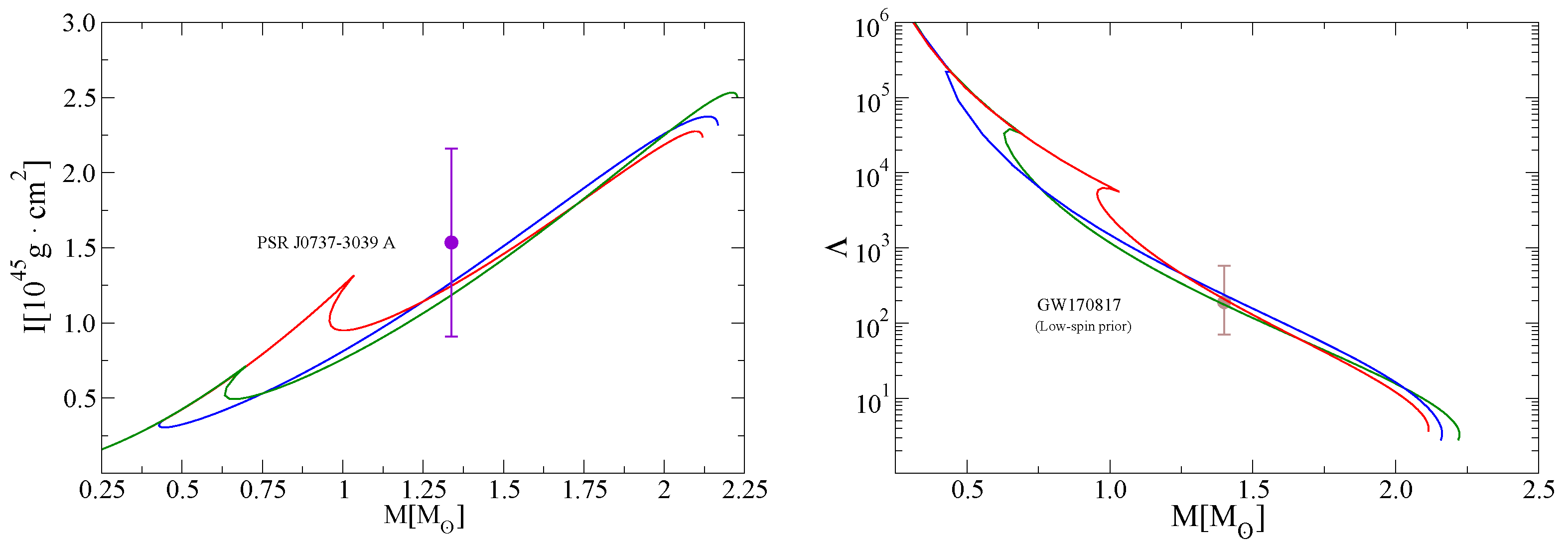


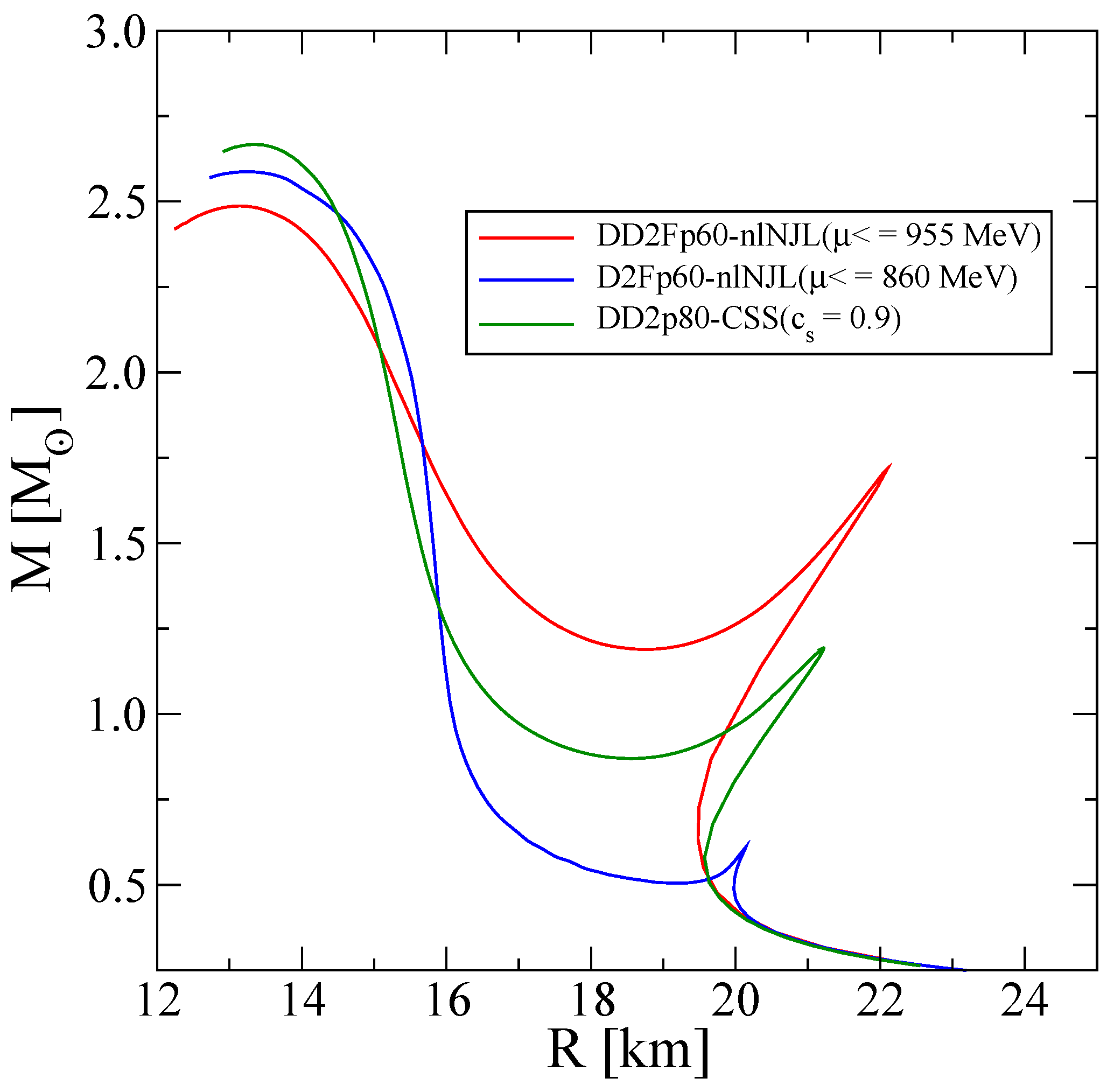
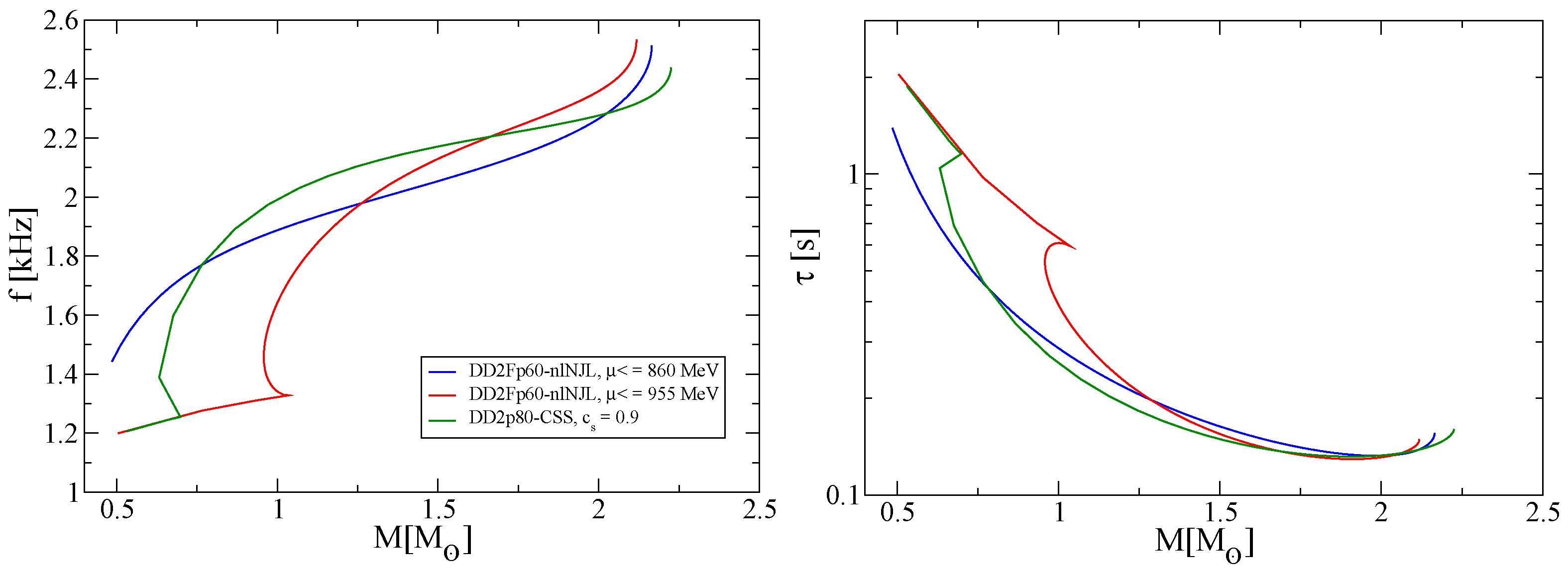
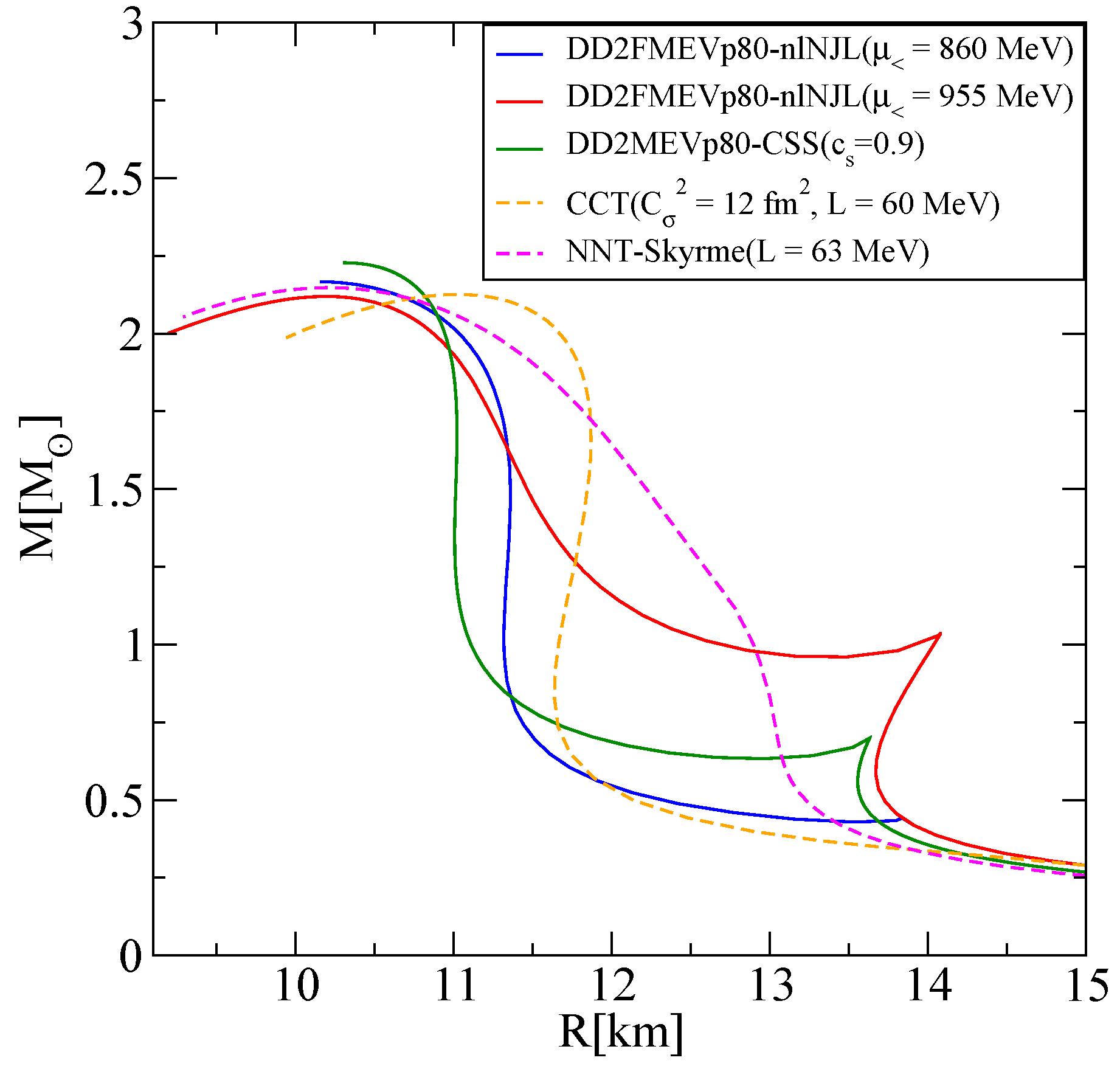
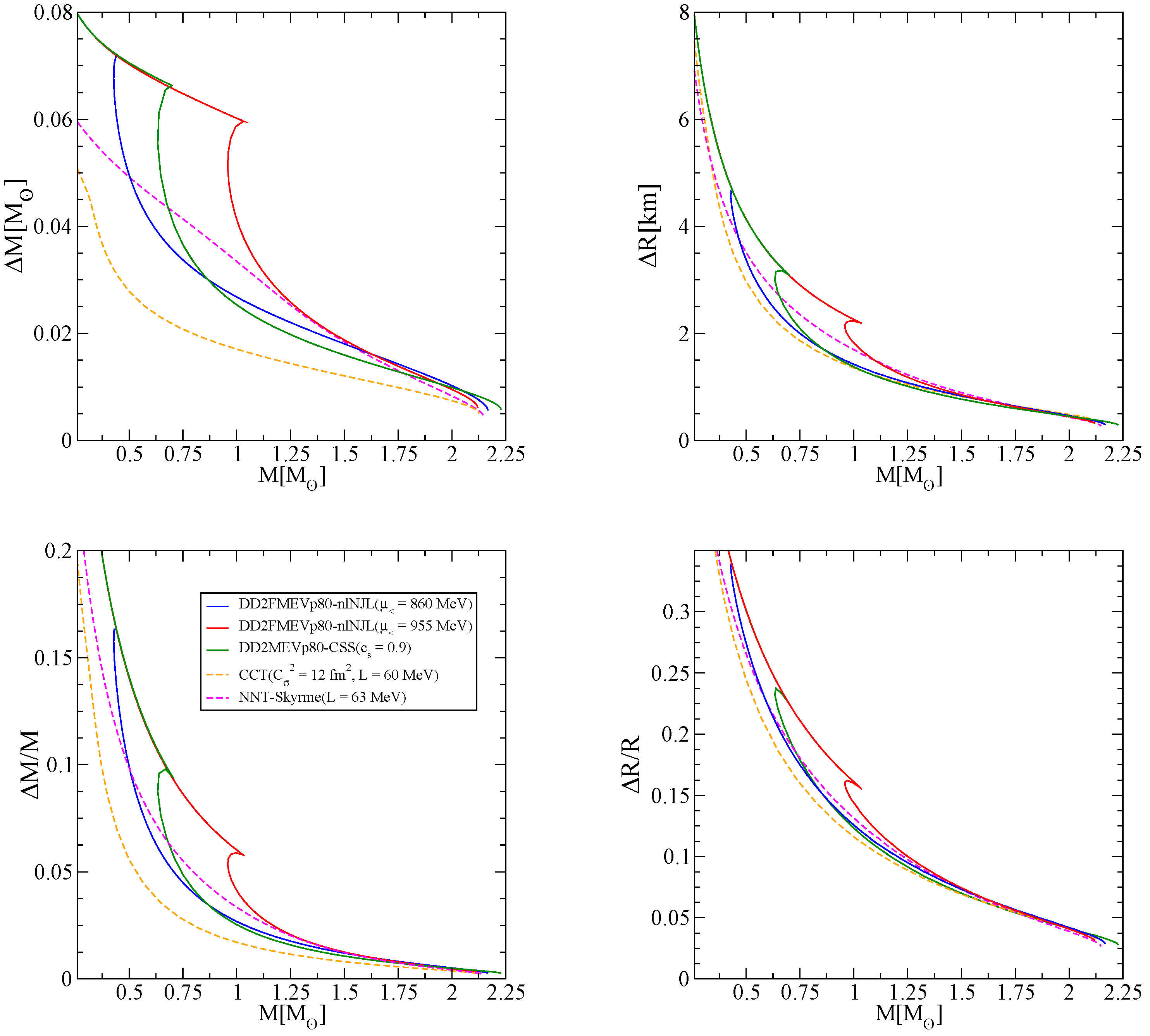
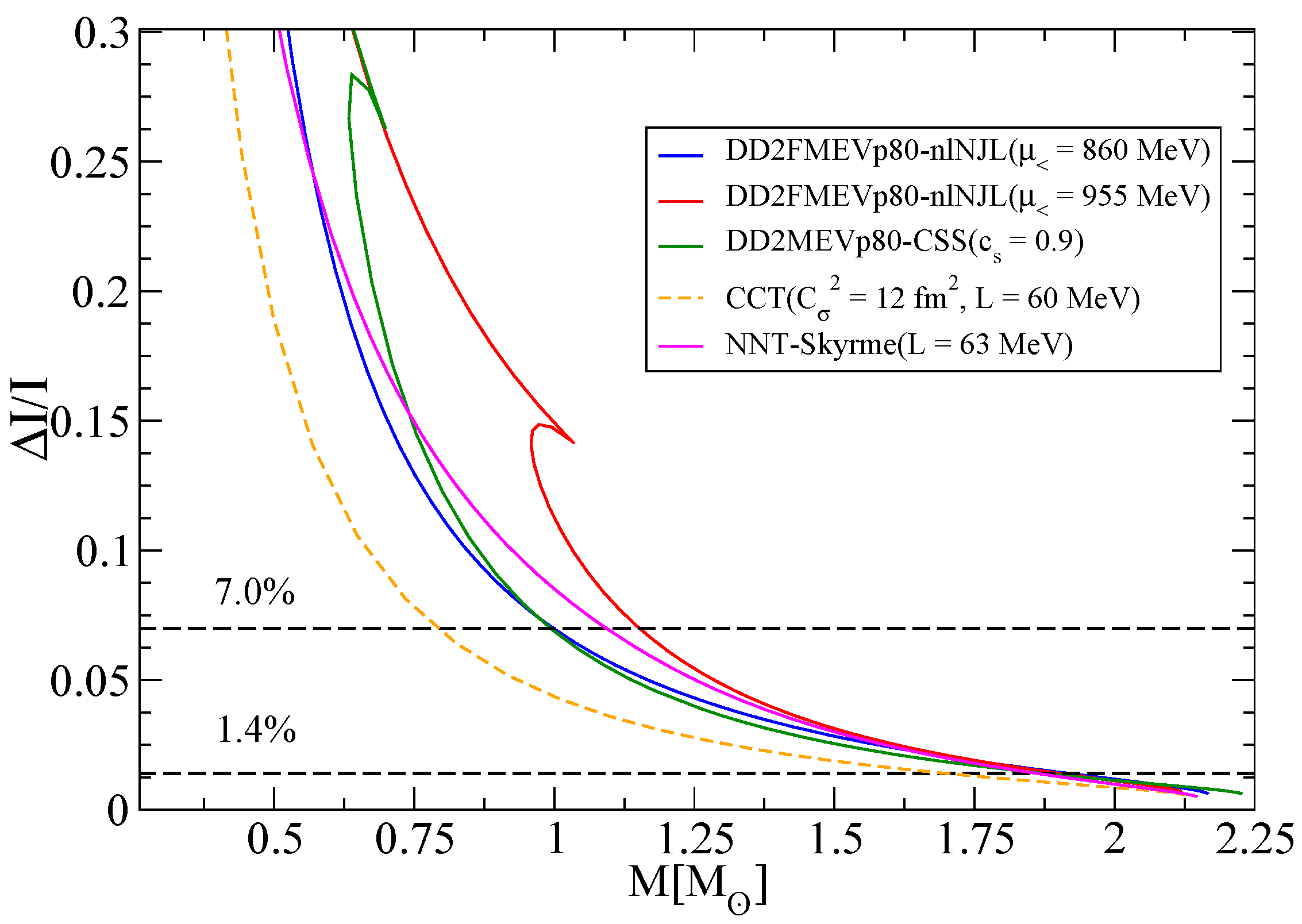
| Model | Mon set [M⊙] | ntrans [1/fm3] | εtrans [MeV/fm3] | ptrans [MeV/fm3] | Δε [MeV/fm3] |
|---|---|---|---|---|---|
| DD2MEVp80-CSS (cs = 0.9) | 0.7 | 0.193 | 185.220 | 10.313 | 268.573 |
| DD2FMEVp80-nlNJL | Set 1 | Set 2 |
|---|---|---|
| [MeV] | 860 | 955 |
| [MeV] | 150 | 150 |
| [MeV] | 1700 | 1700 |
| [MeV] | 350 | 350 |
| B [MeV/fm3] | 65 | 65 |
| 0.05 | 0.05 | |
| 0.12 | 0.12 | |
| [MeV] | 993.030 | 1048.010 |
| [MeV/fm3] | 6.151 | 17.019 |
| [MeV/fmfm3] | 169.274 | 207.269 |
| [fm−3] | 0.177 | 0.214 |
| [] | 0.45 | 1.00 |
| Model | M [M⊙] | M [ergs] | R [km] |
|---|---|---|---|
| DD2MEVp80-CSS ( = 0.9) | 0.00057 | 1.72 | |
| DD2FMEVp80-nlNJL ( 860 MeV) | 0.00003 | 0.75 | |
| DD2FMEVp80-nlNJL ( 955 MeV) | 0.00114 | 1.61 |
| Hadronic Model | S [MeV] | L [MeV] | [1/fm3] |
|---|---|---|---|
| DD2MEVp80/DD2FMEVp80 | 34.74 | 63.87 | 0.078 |
| CCT-C2σ12-L60 | 30.00 | 60.00 | 0.0644 |
| NNT-SKyrme-L63 | 30.60 | 63.12 | 0.081 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alvarez-Castillo, D.E. Properties of the Object HESS J1731-347 as a Twin Compact Star. Universe 2025, 11, 224. https://doi.org/10.3390/universe11070224
Alvarez-Castillo DE. Properties of the Object HESS J1731-347 as a Twin Compact Star. Universe. 2025; 11(7):224. https://doi.org/10.3390/universe11070224
Chicago/Turabian StyleAlvarez-Castillo, David E. 2025. "Properties of the Object HESS J1731-347 as a Twin Compact Star" Universe 11, no. 7: 224. https://doi.org/10.3390/universe11070224
APA StyleAlvarez-Castillo, D. E. (2025). Properties of the Object HESS J1731-347 as a Twin Compact Star. Universe, 11(7), 224. https://doi.org/10.3390/universe11070224






