Abstract
The central singularity present in black hole (BH) spacetimes arising in the general theory of relativity (GR) can be avoided by using various methods. In the present work we have investigated the gravitational effect of one of such spacetime known as a black-bounce-Reissner–Nordström spacetime. We revisited its horizon structure along with first integrals of its geodesic equations. We derived the expressions for Newtonian radial acceleration for freely infalling neutral test particles. For the description of tidal effects, the geodesic deviation equations are derived and solved analytically as well as numerically. To be specific, in the numerical approach, we have opted for two initial conditions to elaborate on the evolution of geodesic deviation vectors in radial and angular directions. The corresponding nature of geodesic deviation vectors in radial and angular directions is then compared with the standard results such as Schwarzschild and Reissner–Nordström BHs in order to figure out the differences.
1. Introduction
Gravity itself seems to be one of the greatest puzzles of all time and Einstein’s GR [1,2,3] is still believed to give its most precise description to date. A few theoretical solutions of the fundamental field equations of GR have been identified as some mysterious astrophysical objects such as BHs. However, these BH spacetimes themselves pose some practical limits on the underlying theory itself. Many attempts have been made in order to avoid the naturally occurring central singularities in the recent past. The notion of ‘singularity’ is complicated as far as GR is concerned [4,5] since the solution of Einstein’s Field Equations (EFEs) is not just the spacetime metric, describing the gravitational field and the spacetime geometry, but also the spacetime manifold on which the metric is defined. Hence, a point of spacetime cannot be defined as a singularity in GR, as, by definition, the spacetime structure would not be defined there. A better way is to look for the geodesics [3,6]. Thus, a given spacetime arising as a solution of the EFE is considered to be singular if it is geodesically incomplete. Again, in GR one is free to use any coordinate system; hence, one has to use the curvature invariants [7]. A breakthrough in the understanding of spacetime singularities was the singularity theorem of Penrose, which identified general conditions under which a spacetime must be geodesically incomplete [8].
One important fact is that although the solutions of EFE, established as BHs, are accompanied with singularities, it is still not the singularity which fundamentally characterizes the BH [1,2,8]. It is the presence of the BH’s event horizon which does so [1,2,3]. That is why it is theoretically possible to construct a BH solution free from singularities, known as regular BHs.
A metric which is singular at the center (i.e., the Riemannian curvature there is infinite) can be converted to a regular metric by removing the singularity along with its close neighborhood from spacetime and then smoothly joining its remaining part to one more copy of this part. In this way, the Schwarzschild metric can be converted into a wormhole throat or BH depending on the region in which it resides. In a similar line of action, some models have been proposed which modify and regularize the Riemannian metric behavior near singularity while almost preserving the geometry in the regions of weak or moderate curvature. One of the pioneering works in this field was by J. Bardeen [9], who probably used for the first time a regular BH metric rather than the Schwarzschild metric.
A more recent development came from Simpson and Visser, who proposed another regular solution [10,11]. The black bounce proposal by Simpson and Visser is actually based on Elli’s proposal for wormholes, via the radial function later recovered by them [8,12,13] and from references therein. Simpson and Visser applied the coordinate transformation r to to modify the Schwarzschild metric to avoid central singularity. The modified metric is known as the Simpson–Visser (SV) spacetime or the Schwarzschild spacetime with black bounce [10]. Like the Bardeen solution, their model includes a parameter without an immediate physical interpretation. Depending on the value of this parameter, the solution may describe a BH, a regular BH, or a wormhole [10,11]. The presence of a throat inside the event horizon and the ability of the solution to interpolate between a regular BH and a wormhole define the class of objects known as black bounces. Afterwards, the electrically charged counterpart of this SV spacetime was also derived in a similar manner [14,15,16] followed by the rotating extension presented in [17].
The presence of tidal forces prevail from our solar system to the most mysterious extreme gravity events such as BH mergers. Studies related to tidal forces have become more relevant in view of recent advancements in observation facilities in the form of missions like LIGO [18,19]. The significance of the study of tidal forces has also been discussed in view of their interrelation with gravitational waves [20]. Tidal forces around various interesting non-rotating spacetime backgrounds have been studied recently [21,22,23,24,25,26].
Motivated by the above studies, we study the tidal forces and their effect in the background of a black-bounce-Reissner–Nordström BH (black-bounce-RNBH) spacetime in this article. Generalized geodesic deviation equations are derived and solved to observe the possible difference due to the presence of length scale parameters a and charge parameter Q involved here. The article is arranged as follows, in Section 2 the horizon structure of black-bounce-RNBH spacetime is reviewed. In Section 3, we discuss the first integrals of geodesic equations and the effective potential for neutral massive test particles. In Section 4, the Newtonian acceleration for a radially infalling neutral test particle is discussed in detail along with the tidal forces. Generalized geodesic deviation equations and their generalized and specific solutions are discussed in Section 5. Conclusions and future directions are discussed in Section 6.
2. Black-Bounce-Reissner–Nordström Spacetime
A black-bounce-RNBH spacetime is considered a black-bounce extension of general Reissner–Nordström spacetime [1]. The metric for black-bounce-RNBH spacetime is given as,
where
where M and Q, respectively, represent the mass and charge of the black-bounce-RNBH. Here a is known as a length-scale parameter which is related to the Planck length; it is also known as the bounce parameter. The presence of a non-zero bounce parameter is the foremost requirement for the regularization procedure chosen to make the classical black hole spacetimes regular at the center. It does not have any immediate physical interpretation so far.
The RNBH metric describes a charged, non-rotating BH and is derived from the Einstein–Maxwell field equations [1]. The black-bounce-RNBH spacetime arises when the standard Maxwell electromagnetism is coupled with an anisotropic fluid. It is a theoretical construct in GR that modifies the traditional RNBH solution to eliminate its singularity, resulting in a globally regular and traversable spacetime [16,27,28,29]. The black-bounce-RN spacetime reduces to the RN spacetime in absence of length-scale parameter, the black-bounce-Schwarzschild spacetime in the absence of the charge parameter, and to the Schwarzschild BH in the absence of both the length-scale and charge parameter, i.e., and simultaneously [2]. Further, it reduces to the Ellis wormhole [12] with and .
Event Horizon of Black-Bounce-RNBH Spacetime
Horizons of the spacetime given in Equation (1) are represented as,
where corresponds to our universe and a copy of it, respectively. On fixing , Equation (4) gives the distances of the outer and inner horizons, respectively [1]. The presence of the bounce parameter changes the horizon structure and there are constraints on all three parameters for Equation (1) to correspond different geometries as in [28], shown in Table 1.

Table 1.
Table listing the possible theoretical conditions on various parameters involved in black-bounce RN spacetime to represent the respective enlisted physical object.
As the presence of the length-scale or bounce parameter removes the singularity present at the center in the RN BH arising in GR and replaces it with a bounce [16,27,28,29], the horizon structure is also modified accordingly. In order to visualize this modification, and specifically the characteristics of the event horizon, we have plotted the event horizon radius of the BH with the length-scale parameter a and BH charge Q, depicted in Figure 1.
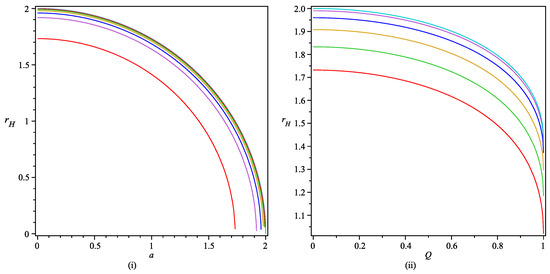
Figure 1.
The event horizon radius vs. length-scale parameter a and BH charge Q at . Left panel (i): curves from bottom to top represent possible horizon radius for to . Right panel (ii): curves from bottom to top represent possible horizon radius for to .
It can be inferred from Figure 1 that as , the event horizon also tends to zero as a approaches its limiting value, i.e., 2. Physically, it can be described as the transformation of the BH spacetime into a wormhole spacetime [27,28]. On the other hand, as Q approaches its upper limit, i.e., , this limiting value for a reduces to 1. Similarly, as the parameter a increases, the maximum allowed value of Q correspondingly decreases.
3. First Integrals of Geodesic Equations
The generalized set up of geodesic equations and their constraint equations [1,2,3,24,30] are given by,
where represents the spacetime coordinates and represents the differentiation of with respect to the affine parameter . Constant e in Equation (6) takes values 0 and for null and timelike geodesics, respectively. For neutral timelike geodesics (i.e., with ), Equation (5) reduces to the following set of equations for a given spacetime metric,
with time-like constraint,
This set of equations from Equation (7) to Equation (11) is the basic initial requisite for the study of various phenomena related to timelike geodesics around black-bounce-RNBH spacetime.
Effective Potential for Black-Bounce-RNBH Spacetime
Now we restrict ourselves to the study of neutral test particles moving in the equatorial plane only. For this, one has to fix . Thus, the integration of Equations (7) and (10) results in,
where the integrating constant corresponds to the conserved total energy E and corresponds to the conserved angular momentum L of the neutral test particle [1,2,3,24,30]. Using Equations (12) and (13) with in the constraint Equation (11), the energy conservation equation for the time-like geodesics [1,2,3,24,30] takes the following form,
where is defined as an effective potential and can be expressed as,
The effective potential of black-bounce-RNBH spacetime is modified as compared to SBH [1,2] due to the presence of bounce and charge parameters in this case. If one compares termwise, the first term arises due to the Newtonian gravitational potential, the second term shows the presence of a repulsive centrifugal potential, and the third term represents the relativistic correction of GR which is proportional to [21,24]. The extra term in Equation (15) is due to the presence of both bounce and charge parameters.
4. Newtonian Radial Acceleration
On substituting for radial geodesics, i.e., where , the Equation (14) reduces to,
A test particle which is initially at rest and starts falling freely from a fixed position b will have initial energy [21,22,24,31]. Newtonian acceleration for test particles falling freely along such radial geodesics is known as ‘Newtonian radial acceleration’. For radial geodesics, where a particle has zero angular momentum, the particle is falling radially towards or away from the center. Hence, this acceleration quantifies the stretch or compression exerted on the particle and in this way it gives some hint as to the tidal force present there due to the central object. It is defined as [21,22,24,31,32],
For black-bounce-RNBH spacetime, using Equation (16), the Newtonian radial acceleration takes the following form,
The analysis of this radial force plays an important role in understanding the possible difference in the effect of the gravitational field compared with that of an SBH and RNBH qualitatively. Figure 2i shows a clear comparison of these three cases where radial acceleration for an SBH (shown in the dashed blue curve) diverges near the center; for an RNBH (shown in the dotted black curve), this divergence occurs before that of an SBH. For a regular BH (shown in the solid red curve), radial acceleration drops to a minimum near the center and again increases and remains finite. Figure 2ii shows that as the value of bounce parameter a increases from zero to 2, the qualitative nature of radial acceleration changes as the minima disappear for higher values of a and acceleration becomes negligible. It hints as to the qualitative nature of the radial tidal force present near the center for such BHs.
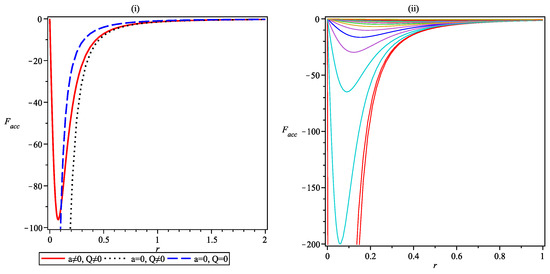
Figure 2.
(i) Newtonian radial acceleration for SBH, RNBH, and regular BH, (ii) variation in Newtonian radial acceleration with r where curves from bottom to top depict corresponding acceleration function for to .
To study the effect of the gravitational field of the black-bounce-RNBH spacetime on the orbiting neutral test particle, one may be interested in looking for the possible distance from where a neutral test particle bounces back, as happened in a standard RNBH [21]. To derive the expression for this distance, one will have to look for the real root of equation . After solving such a relation for black-bounce-RNBH, the expression for such a distance comes out as,
Analysis of Tidal Forces Acting in Black-Bounce-RNBH Spacetime
For any arbitrary object or test particles moving in a strong gravitational field, the study of geodesic deviation explains the effect of spacetime curvature on their relative motion [1,2,3,33]. It gives a quantitative analysis of the divergence or convergence present for neighboring geodesics as an effect of the underlying gravitational field. In the present work, the methodology used in [21,22,24,30,33] is adopted to derive the corresponding geodesic deviation equation or Jacobi field equation,
where represent the connection normal vectors to infinitesimally close geodesics, while represents the tangent vector to the geodesics.
The tetrad basis for radial free-fall reference frames in a given spacetime background is,
where the normalization condition is satisfied by . being a Minkowski metric. Hence, the geodesic deviation vector can be devised as,
The expressions for radial and angular tidal forces can be obtained by substituting Equation (22) into Equation (20) as,
where correspond to and directions, respectively. Equation (20) for the time coordinate gives , giving zero tidal force corresponding to t-coordinate. To study the geodesic deviation is to find out the relative acceleration between neighboring geodesics, if any. does not give any physical information in this respect. Explicit expressions for tidal forces along radial and angular directions are given in Equations (23) and (24). As coordinate r depicts the distance from the center, one can treat it as a radial parameter and observe the variation in radial and angular tidal forces with r while fixing other parameters , and a to different possible values. One can infer from Equation (23) that the tidal force in the radial direction becomes zero at,
where
Figure 3i represents the comparative plots of the radial tidal force around an SBH, RNBH spacetime, and a black-bounce-RNBH with different possible values of the BH parameters involved therein. As seen in the figure, the radial tidal force for an SBH is always positive and diverges near singularity, which represents the infinite radial stretching [21,24,31] as the object reaches near the center. As charge parameter Q comes into play, the tidal force curve now has a maximum and diverges in the opposite direction to that of an SBH, while for a black-bounce-RNBH, the radial tidal force is finite everywhere; hence, no infinite radial stretching is present. Figure 3ii depicts the tidal force in the radial direction, for a fixed value of the charge parameter, i.e., , and for different values of bounce parameter a, as shown in the figure. As the value of a is increased, the curve for becomes flatter and the maximum of the curve shifts towards a larger value of r. Now Figure 3iii represents , for a fixed value of the bounce parameter, i.e., and different values of charge parameter Q, as shown in the figure. Again, curves for become flatter with increasing Q values, but interestingly, they flip on the limiting value of Q, i.e., 1.
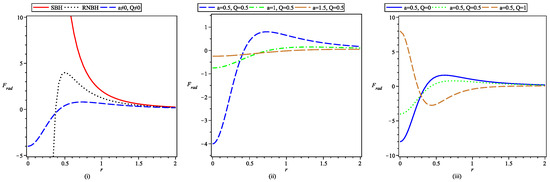
Figure 3.
Plot of radial tidal force of a black-bounce-RNBH as a function of radial parameter r, with and fixed values of the parameters shown in legends of the figures.
Figure 4 depicts the variation in the radial tidal force with radial parameter r for an SBH, RNBH, regular BH, and wormhole. It is clearly visible that despite being finite, the tidal force in the case of a regular BH is substantially strong in comparison to the wormhole, where the traveler/particle feels almost a negligible force near the center. In addition to it, in the case of a regular BH, there exists a non-zero value of distance where the particle bounces back, although the tidal force is finite but the particle does not approach the singularity after a certain distance.
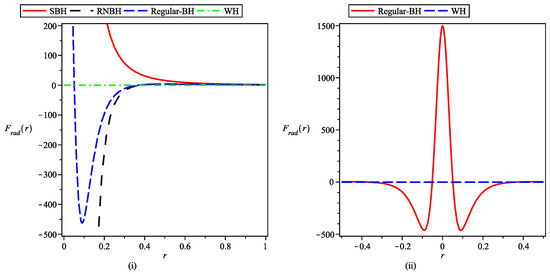
Figure 4.
Plot of radial tidal force as a function of r for different parameter settings as shown in legend.
Figure 5i represents the comparative plots of the angular tidal force around an SBH, RNBH spacetime, and a black-bounce-RNBH with different possible values of the BH parameters involved therein. The curve corresponding to an SBH diverges to negative infinity as one approaches to singularity, representing the infinite angular compressing present there [21,24,31], while this divergence is absent in the case of a black-bounce-RNBH, again assuring the finite value tidal force is present everywhere.
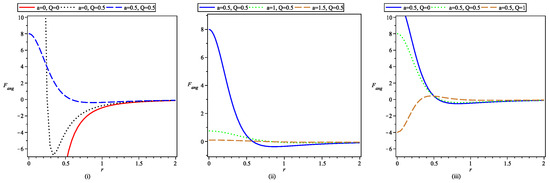
Figure 5.
Plot of radial angular tidal force of a black-bounce-RNBH as a function of radial parameter r, with and fixed values of the parameters shown in the legends of the figures.
Figure 5ii depicts the tidal force in an angular direction, for a fixed value of the charge parameter, i.e., , and for different values of bounce parameter a, as shown in the figure. As the value of a is increased, the curve for also becomes flatter. Now Figure 5iii represents , for a fixed value of the bounce parameter, i.e., , and for different values of charge parameter Q, as shown in the figure. It is noticed that as the value of charge Q reaches near its upper limiting value, i.e., 1, the qualitative nature of the radial as well as the angular tidal force changes near the center as depicted in Figure 3iii and Figure 5iii.
Figure 6 depicts the variation in the angular tidal force with radial parameter r for an SBH, RNBH, regular BH, and wormhole. The angular tidal force is quantitatively strong in the case of a regular BH in comparison to a wormhole, similar to the radial direction.
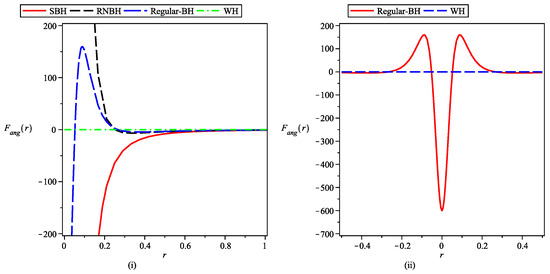
Figure 6.
Plot of angular tidal force as a function of r for different parameter settings as shown in the legend.
In the next section the geodesic deviation equations for black-bounce-RNBH spacetime are solved in order know more about the relative acceleration of freely falling particles in this geometry.
5. Revisiting the Geodesic Deviation Equations and Their Solutions
To devise the geodesic deviation equations, we have assumed massive neutral particles in the form of charge neutral dust infalling radially in a charged black bounce spacetime due to the presence of tidal force.
The boundary conditions chosen are as follows: ICI corresponds to release from rest, at the radial coordinate , a body constituted of dust with no internal motion, while ICII corresponds to a body constituted of dust to ‘explode’ at , where . The effect of different initial conditions is visible in the result and is discussed in detail with the help of plots. Using Equation (14) for particles falling freely along radial geodesics, i.e., having , the radial coordinate r can be written as,
Now let us re-frame the set of geodesics deviation equations given in Equations (23) and (24) as the function of the radial coordinate itself,
The analytic solutions [21] of Equations (27) and (28) can be written in standard form using elliptical integrals as,
where , , , and are constants of integration.
For the numerical solutions of Equations (27) and (28), we have opted for the boundary conditions used in [21,24,32,33]. A particle falling from its initial position outside the event horizon is considered in the above boundary conditions. Specifically, the first initial condition ICI is,
According to this condition the 4-velocity component of an infalling particle is taken as zero, i.e., , which further fixes the energy of the particles . Similarly, the second initial condition IC-II mathematically reads as,
which physically corresponds to the particle ‘exploding’ at . Now,
and thus, the energy E of the infalling test particle is not a fixed parameter. One can say that the energy of the particle also affects the kinematical evolution of the geodesic deviation vectors in this condition.
It can be observed from Figure 7, Figure 8, Figure 9 and Figure 10 that for large values of r, the variation in the geodesic deviation vector with radial distance is similar, while near singularity, the relative compression or stretching becomes weaker as both a and Q become non-zero. A further increment in both of these parameters shows a further decrement in the corresponding geodesic deviation vector magnitude, showing the presence of a comparatively weak gravitational field.
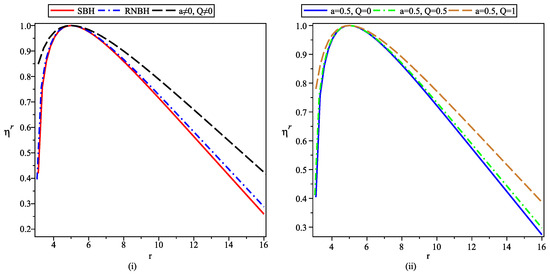
Figure 7.
Variation in radial geodesic vector with radial parameter r under ICI, where and other parameters have different mentioned values in the figure.
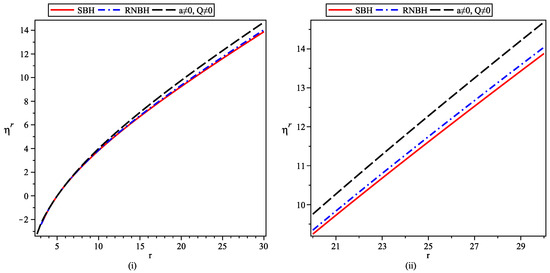
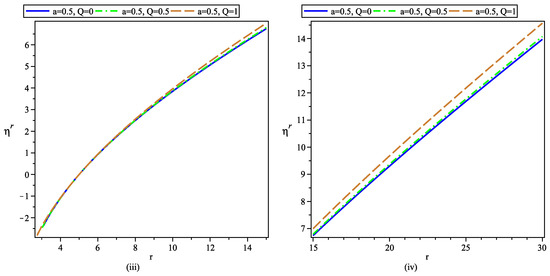
Figure 8.
Variation in radial geodesic vector with radial parameter r under ICII, where and other parameters have different mentioned values in the figure.
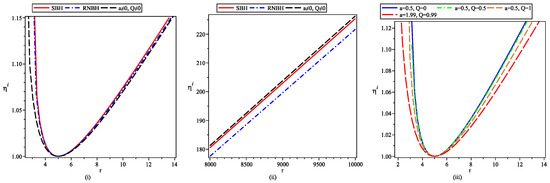
Figure 9.
Variation in angular geodesic vector with radial parameter r under ICI, where and other parameters have different mentioned values in the figure.
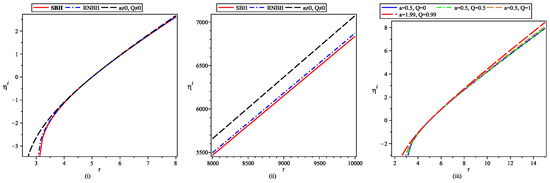
Figure 10.
Variation in angular geodesic vector with radial parameter r under ICII, where and other parameters have different mentioned values in the figure.
As the radial parameter varies beyond the event horizon radius, the relative separation between geodesics increases first, reaches a maximum value, and then decreases. Although the qualitative behavior shown in Figure 7i,ii is similar, one can observe the difference due to the presence of scale and charge parameters a and Q. As a and Q have non-zero values and either of the parameters increase, the steepness of the curves obtained on both sides of the maxima decrease. It is worth noting that the position of the maxima is unaffected due to the change in the values of a and Q.
Under IC-II the initially diverging geodesics keep on diverging and divergence is stronger in the presence of a and Q as depicted in Figure 8.
In contrast to the radial geodesic deviation vector, the corresponding vector in the angular direction decreases up to a certain distance and then increases further under IC-I. The qualitative behavior is similar but the magnitude of the vector becomes smaller with increasing values of either a or Q. It again depicts a correspondingly weaker gravitational field around the given BH.
6. Conclusions
In the present work, we focused on black-bounce-RNBH spacetime and discussed the evolution of tidal forces in its vicinity. The discussion was carried forward with the help of equations of motion for tidal forces in radial and angular directions. For a better understanding of the gravitational field and its effect, the geodesic deviation equations were derived and solved analytically as well as numerically. A few key results of this study are outlined as below:
- (i)
- The presence or absence of horizons defines whether it is a black bounce (with event horizon) or a wormhole-like structure (without horizon). Different conditions for the possible horizon structure are tabulated in Table 1.
- (ii)
- The expression for Newtonian radial acceleration is obtained for black-bounce-RNBH spacetime, and further, the tidal forces in radial and angular directions are analyzed in detail. Newtonian radial acceleration is plotted as a function of radial parameter r, in order to identify the quantitative difference to those of classical BHs (SBH, RNBH).
- (iii)
- Comparative plots for tidal forces show the absence of infinite radial stretching and infinite angular compression in the case of black-bounce-RNBH spacetime for any object approaching central singularity. As the particle reaches near the central region, now it is not turned apart by infinite forces as in the case of an SBH, but the magnitude of the tidal forces reaches their respective maximum and decreases afterwards.
- (iv)
- The tidal force in the case of a regular BH is substantially strong in comparison to a wormhole, where the traveler/particle feels an almost negligible force near the center. In addition to it, in the case of a regular BH, there exists a non-zero value of distance where the particle bounces back, although the tidal force is finite but the particle does not approach the singularity after a certain distance.
- (v)
- The generalized set up of geodesic deviation equations around black-bounce-RNBH spacetime are derived and solved analytically in terms of elliptical integrals.
- (vi)
- The geodesic deviation equations are also solved numerically using two initial conditions, the first corresponding to the particle starting from rest and having fixed energy, while the second corresponds to an exploding particle with a varying energy value along its path. The numerical plots are shown in Figure 7, Figure 8, Figure 9 and Figure 10. If one observes that under IC-I radial divergence between neighboring geodesics starts at a fixed r and it increases for far distances from THE center, in the near central region, the behavior is the opposite. The strength of relative separation reduces for black-bounce-RNBH spacetime in comparison to an SBH and RNBH. In contrast, the initially diverging geodesics keep on diverging in radial as well as angular directions under IC-II.
- (vii)
- In the angular direction, the initially converging geodesics for an SBH diverge under IC-I. Now if one observes the far field behavior, the non-zero and increasing values of both Q and a result in a larger magnitude of the separation vector, thus helping the relative divergence of geodesics. A similar pattern is seen under IC-II in the angular direction.
- (viii)
- To visualize any observational signature arising due to distinct tidal behaviors, one needs to carry out the study of phenomena such as the formation and properties of the accretion disk around the rotating counterpart of such BHs or study the kinematics of geodesic flows in general. Further, the study of these phenomena will be helpful to look for the physical implications of the bounce parameter, especially in the bounce or throat region where the parameter shows its significant presence.
The work presented in this article is important so as to have a better understanding of the gravitational field of black-bounce-RNBH spacetime. It can be extended further to discuss the tidal force transition through the bounce, which can be studied in order to understand the gravitating effects of a wormhole-like or bounce passage to another region. We intend to report these issues with possible analytic solutions in the near future.
Funding
This research received no external funding.
Data Availability Statement
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
Acknowledgments
The author is indebted to the anonymous referees for their valuable comments which helped in improving the quality and presentation of this article substantially. The author is also thankful to P. Semwal, Dept. of Mathematics, R. S. R. Govt. Degree College Barkot (Uttarkashi) for their useful discussions. The author also acknowledges the support from Inter University Center for Astronomy & Astrophysics (IUCAA), Pune under its Visiting Associateship Programme, where part of this work was completed.
Conflicts of Interest
The author declares no conflict of interest.
References
- Hartle, J.B. Gravity: An Introduction to Einstein’s General Relativity; Pearson Education Inc.: Singapore, 2003. [Google Scholar]
- Wald, R.M. General Relativity; University of Chicago Press: Chicago, IL, USA, 1984. [Google Scholar]
- Poisson, E. A Relativist’s Toolkit: The Mathematics of Black-Hole Mechanics; Cambridge University Press: London, UK, 2009. [Google Scholar] [CrossRef]
- Stoica, O.C. The Geometry of Black Hole singularities. Adv. High Energy Phys. 2014, 2014, 907518. [Google Scholar] [CrossRef]
- Tipler, F.J. Energy conditions and spacetime singularities. Phys. Rev. D 1978, 17, 2521–2528. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Rubin, S.G. Black Holes, Cosmology and Extra Dimensions; World Scientific: Singapore, 2013. [Google Scholar]
- Lobo, F.S.N.; Rodrigues, M.E.; de Sousa Silva, M.V.; Simpson, A.; Visser, M. Novel black-bounce spacetimes: Wormholes, regularity, energy conditions, and causal structure. Phys. Rev. D 2021, 103, 084052. [Google Scholar] [CrossRef]
- Rodrigues, M.E.; Silva, M.V.d.S. Black-bounces with multiple throats and anti-throats. Class. Quant. Grav. 2023, 40, 225011. [Google Scholar] [CrossRef]
- Bardeen, J. Non-singular general-relativistic gravitational collapse. In Proceedings of the GR5, Tbilisi, USSR, 9–16 September 1968; Volume 42, p. 174. [Google Scholar]
- Simpson, A.; Visser, M. Black-bounce to traversable wormhole. J. Cosmol. Astropart. Phys. 2019, 2, 042. [Google Scholar] [CrossRef]
- Simpson, A. Traversable Wormholes, Regular Black Holes, and Black-Bounces. Master’s Thesis, Victoria University of Wellington, Wellington, New Zealand, 2019. [Google Scholar]
- Ellis, H. Ether flow through a drainhole: A particle model in general relativity. J. Math. Phys. 1973, 14, 104. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Walia, R.K. Field sources for Simpson-Visser spacetimes. Phys. Rev. D 2022, 105, 044039. [Google Scholar] [CrossRef]
- Cañate, P. Black bounces as magnetically charged phantom regular black holes in Einstein-nonlinear electrodynamics gravity coupled to a self-interacting scalar field. Phys. Rev. D 2022, 106, 024031. [Google Scholar] [CrossRef]
- Bokulić, A.; Smolić, I.; Jurić, T. Constraints on singularity resolution by nonlinear electrodynamics. Phys. Rev. D 2022, 106, 064020. [Google Scholar] [CrossRef]
- Franzin, E.; Liberati, S.; Mazza, J.; Simpson, A.; Visser, M. Charged black-bounce spacetimes. J. Cosmol. Astropart. Phys. 2021, 7, 036. [Google Scholar] [CrossRef]
- Mazza, J.; Franzin, E.; Liberati, S. A novel family of rotating black hole mimickers. J. Cosmol. Astropart. Phys. 2021, 2021, 082. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, D.; Abernathy, R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101, Erratum in Phys. Rev. Lett. 2018, 121, 129901. [Google Scholar] [CrossRef]
- Goswami, R.; Ellis, G.F.R. Tidal forces are gravitational waves. Class. Quant. Grav. 2021, 38, 085023. [Google Scholar] [CrossRef]
- Crispino, L.C.B.; Higuchi, A.; Oliveira, L.A.; de Oliveira, E.S. Tidal forces in Reissner–Nordström spacetimes. Eur. Phys. J. C 2016, 76, 168. [Google Scholar] [CrossRef]
- Vandeev, V.P.; Semenova, A.N. Tidal forces in Kottler spacetimes. Eur. Phys. J. C 2021, 81, 610. [Google Scholar] [CrossRef]
- Lima, H.C.D.; Crispino, L.C.B. Tidal forces in the charged Hayward black hole spacetime. Int. J. Mod. Phys. D 2020, 29, 2041014. [Google Scholar] [CrossRef]
- Uniyal, R. Tidal forces around Schwarzschild black hole in cloud of strings and quintessence. Eur. Phys. J. C 2022, 82, 567. [Google Scholar] [CrossRef]
- Arora, D.; Bambhaniya, P.; Dey, D.; Joshi, P.S. Tidal forces in the Simpson–Visser black-bounce and wormhole spacetimes. Phys. Dark Univ. 2024, 44, 101487. [Google Scholar] [CrossRef]
- Albacete, E.; Richartz, M. Tidal Forces in Majumdar-Papapetrou Spacetimes. Universe 2024, 10, 62. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, Y. Gravitational lensing by a black-bounce-Reissner–Nordström spacetime. Eur. Phys. J. C 2022, 82, 471. [Google Scholar] [CrossRef]
- Guo, Y.; Miao, Y.G. Charged black-bounce spacetimes: Photon rings, shadows and observational appearances. Nucl. Phys. B 2022, 983, 115938. [Google Scholar] [CrossRef]
- Murodov, S.; Badalov, K.; Rayimbaev, J.; Ahmedov, B.; Stuchlík, Z. Charged Particles Orbiting Charged Black-Bounce Black Holes. Symmetry 2024, 16, 109. [Google Scholar] [CrossRef]
- Uniyal, R.; Chandrachani Devi, N.; Nandan, H.; Purohit, K.D. Geodesic Motion in Schwarzschild Spacetime Surrounded by Quintessence. Gen. Rel. Grav. 2015, 47, 16. [Google Scholar] [CrossRef]
- Martel, K.; Poisson, E. A One parameter family of time symmetric initial data for the radial infall of a particle into a Schwarzschild black hole. Phys. Rev. D 2002, 66, 084001. [Google Scholar] [CrossRef]
- Liu, J.; Chen, S.; Jing, J. Tidal effects of a dark matter halo around a galactic black hole. Chin. Phys. C 2022, 46, 105104. [Google Scholar] [CrossRef]
- Gad, R.M. Geodesics and Geodesic Deviation in a Stringy Charged Black Hole. Astrophys. Space Sci. 2010, 330, 107–114. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).