A Novel Logarithmic Approach to General Relativistic Hydrodynamics in Dynamical Spacetimes
Abstract
1. Introduction
2. The “3 + 1” Logarithmic Approach to GRHD
3. Preliminary Numerical Applications
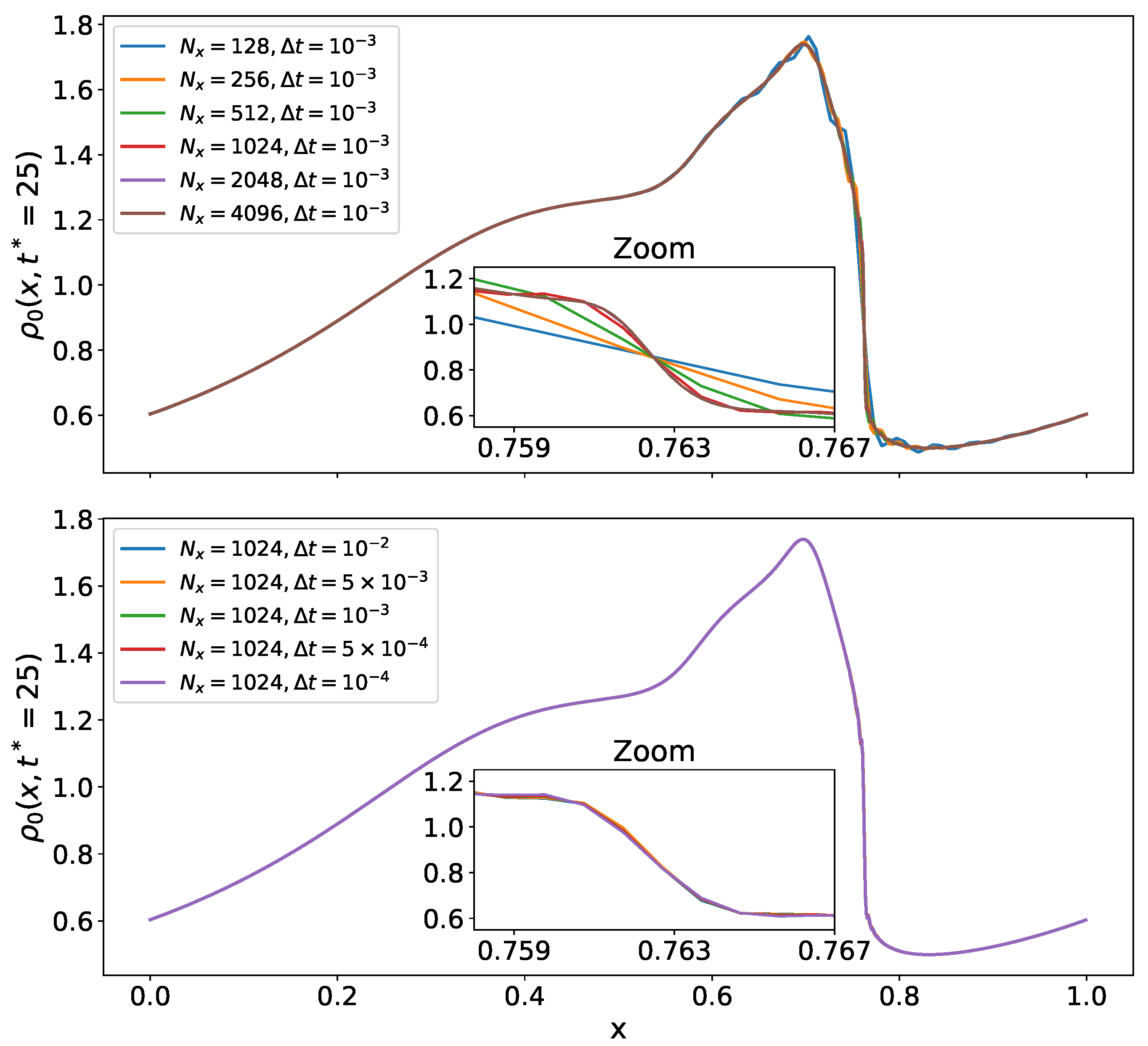
3.1. Propagation of Classical Sound Wave in Nonlinear Regime
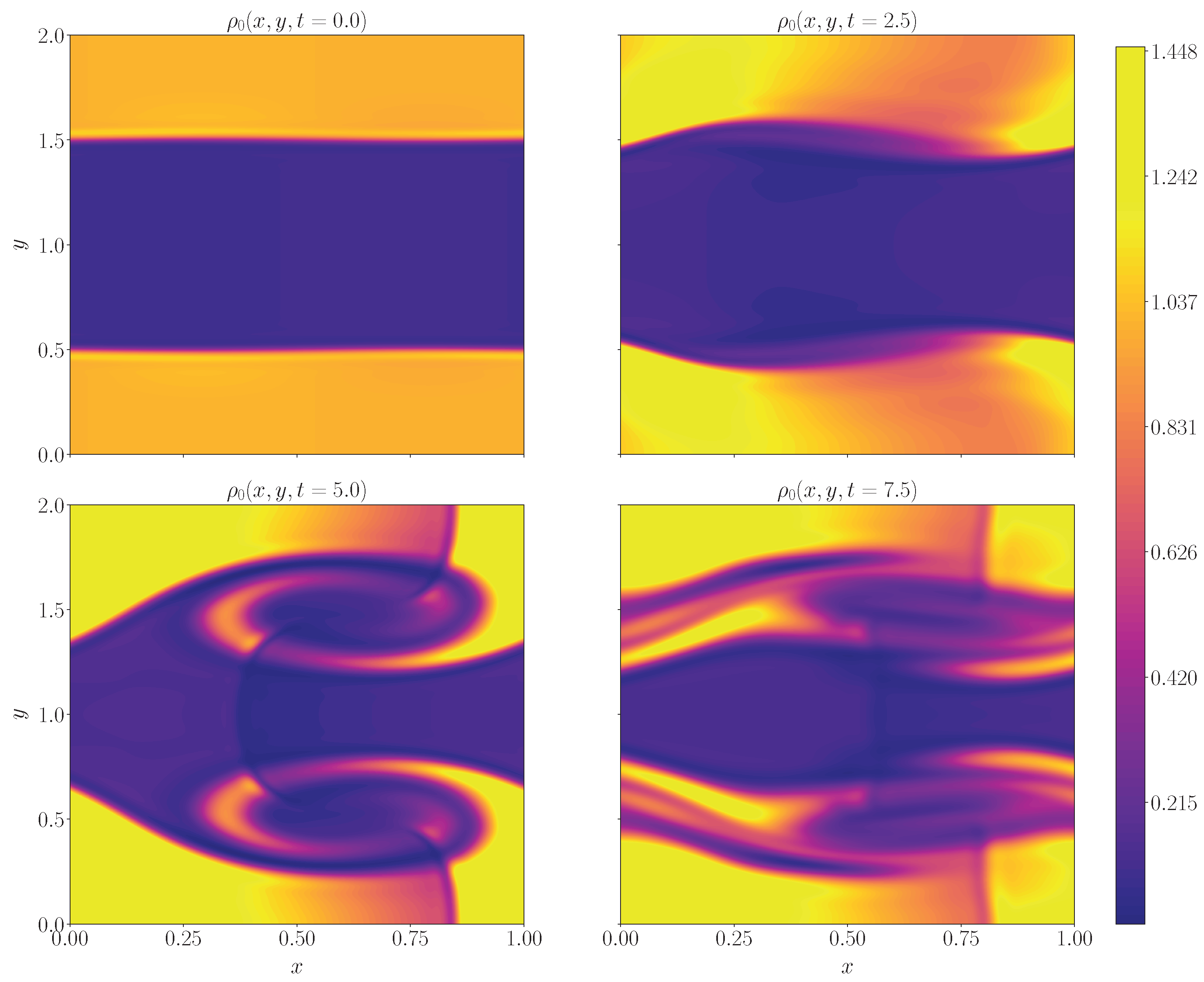
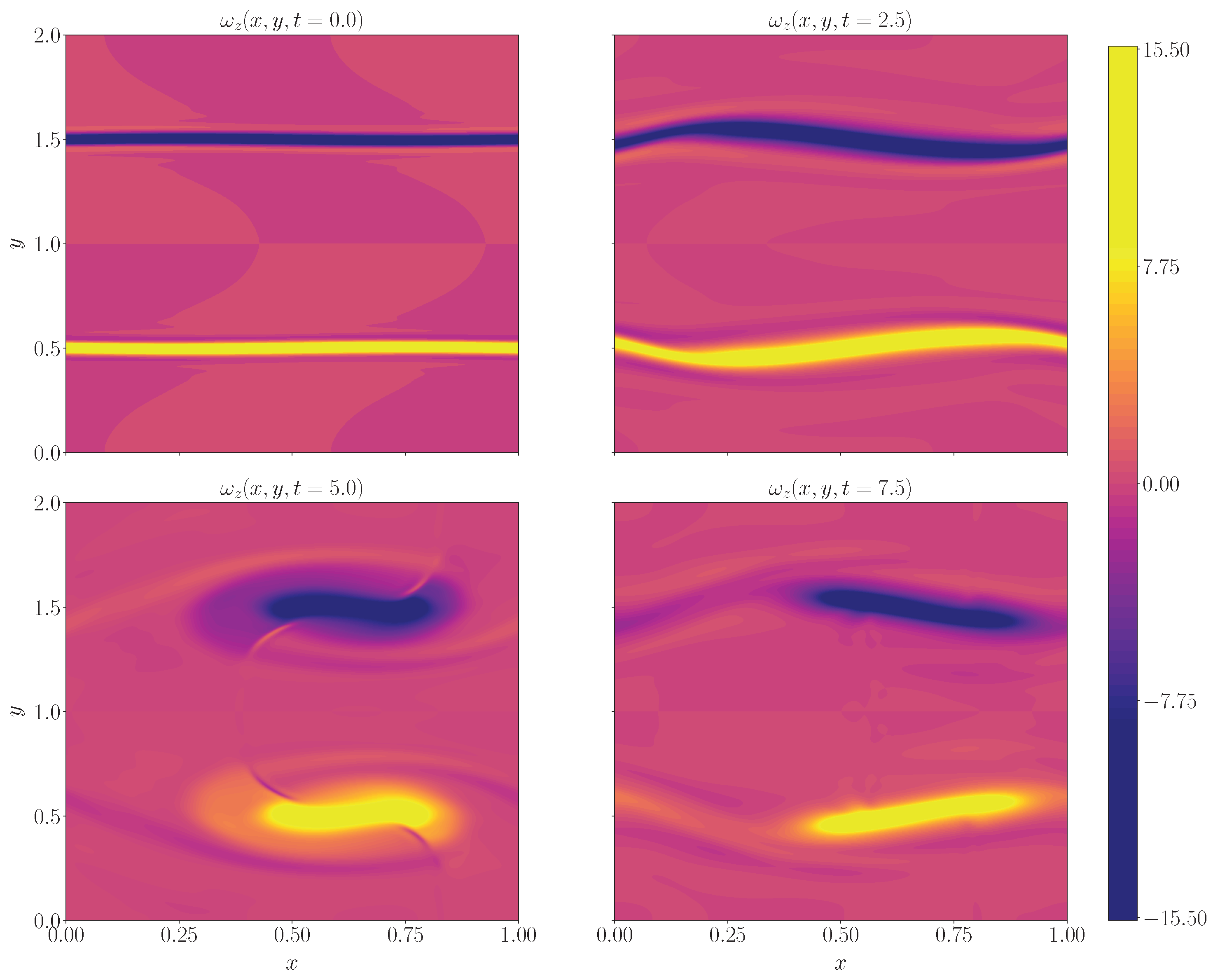
3.2. Kelvin–Helmholtz Instability
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
| 1 | Pressure normalization should involve , which is the reference mass–energy density adopted for the normalization of the stress–energy tensor; yet this coincides with under the chosen units. |
References
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Blandford, R.D.; Payne, D.G. Hydromagnetic flows from accretion discs and the production of radio jets. Mon. Not. R. Astron. Soc. 1982, 199, 883–903. [Google Scholar] [CrossRef]
- De Villiers, J.P.; Hawley, J.F.; Krolik, J.H.; Hirose, S. Magnetically driven accretion in the Kerr metric. III. Unbound outflows. Astrophys. J. 2005, 620, 878. [Google Scholar] [CrossRef]
- Radice, D.; Perego, A.; Zappa, F.; Bernuzzi, S. GW170817: Joint constraint on the neutron star equation of state from multimessenger observations. Astrophys. J. Lett. 2018, 852, L29. [Google Scholar] [CrossRef]
- Baiotti, L.; Rezzolla, L. Binary neutron star mergers: A review of Einstein’s richest laboratory. Rep. Prog. Phys. 2017, 80, 096901. [Google Scholar] [CrossRef]
- Giacomazzo, B.; Perna, R. Formation of stable magnetars from binary neutron star mergers. Astrophys. J. Lett. 2013, 771, L26. [Google Scholar] [CrossRef]
- Fernández, R.; Tchekhovskoy, A.; Quataert, E.; Foucart, F.; Kasen, D. Long-term GRMHD simulations of neutron star merger accretion discs: Implications for electromagnetic counterparts. Mon. Not. R. Astron. Soc. 2019, 482, 3373–3393. [Google Scholar] [CrossRef]
- Ciolfi, R. Binary neutron star mergers after GW170817. Front. Astron. Space Sci. 2020, 7, 27. [Google Scholar] [CrossRef]
- Durrer, R.; Neronov, A. Cosmological magnetic fields: Their generation, evolution and observation. Astron. Astrophys. Rev. 2013, 21, 1–109. [Google Scholar] [CrossRef]
- Subramanian, K. The origin, evolution and signatures of primordial magnetic fields. Rep. Prog. Phys. 2016, 79, 076901. [Google Scholar] [CrossRef]
- Wilson, J.R. Numerical Study of Fluid Flow in a Curved Spacetime. Astrophys. J. 1972, 173, 431–444. [Google Scholar] [CrossRef]
- Font, J.A. Hydrodynamics in full general relativity: Formulations, implementations, and tests. Phys. Rev. D 2000, 62, 084017. [Google Scholar] [CrossRef]
- Shibata, M.; Sekiguchi, Y.I. Three-dimensional simulations of stellar core collapse in full general relativity: Nonaxisymmetric dynamical instabilities. Phys. Rev. D 2005, 71, 024014. [Google Scholar] [CrossRef]
- Arnowitt, R.; Deser, S.; Misner, C.W. Republication of: The dynamics of general relativity. Gen. Relativ. Gravit. 2008, 40, 1997–2027. [Google Scholar] [CrossRef]
- Shibata, M.; Nakamura, T. Evolution of three-dimensional gravitational waves: Harmonic slicing case. Phys. Rev. D 1995, 52, 5428–5444. [Google Scholar] [CrossRef]
- Baumgarte, T.W.; Shapiro, S.L. On the numerical integration of Einstein’s field equations. Phys. Rev. D 1999, 59, 024007. [Google Scholar] [CrossRef]
- Alcubierre, M.; Allen, G.; Brügmann, B.; Seidel, E.; Suen, W.-M. Towards a stable numerical evolution of strongly gravitating systems in general relativity: The Conformal Transverse-Traceless Decomposition. Phys. Rev. D 2000, 62, 124011. [Google Scholar] [CrossRef]
- Zlochower, Y.; Baker, J.G.; Campanelli, M.; Lousto, C.O. Accurate black hole evolutions by fourth-order numerical relativity. Phys. Rev. D—Part. Fields Gravit. Cosmol. 2005, 72, 024021. [Google Scholar] [CrossRef]
- Campanelli, M.; Lousto, C.O.; Marronetti, P.; Zlochower, Y. Accurate Evolutions of Orbiting Black-Hole Binaries Without Excision. Phys. Rev. Lett. 2006, 96, 111101. [Google Scholar] [CrossRef]
- Bardeen, J.M. Gauge-invariant cosmological perturbations. Phys. Rev. D 1980, 22, 1882. [Google Scholar] [CrossRef]
- Kodama, H.; Sasaki, M. Cosmological perturbation theory. Prog. Theor. Phys. Suppl. 1984, 78, 1–166. [Google Scholar] [CrossRef]
- Oliynyk, T.A. Cosmological Newtonian limit. Phys. Rev. D 2014, 89, 124002. [Google Scholar] [CrossRef]
- Räsänen, S. Applicability of the linearly perturbed FRW metric and Newtonian cosmology. Phys. Rev. D—Part. Fields Gravit. Cosmol. 2010, 81, 103512. [Google Scholar] [CrossRef]
- Adamek, J.; Daverio, D.; Durrer, R.; Kunz, M. gevolution: A cosmological N-body code based on General Relativity. J. Cosmol. Astropart. Phys. 2016, 2016, 053. [Google Scholar] [CrossRef]
- Tauber, J. et al. [ESA; The Planck Scientific Collaboration] The planck mission. Adv. Space Res. 2004, 34, 491–496. [Google Scholar] [CrossRef]
- Abbott, T.M.; Aguena, M.; Alarcon, A.; Allam, S.; Alves, O.; Amon, A.; Andrade-Oliveira, F.; Annis, J.; Avila, S.; Bacon, D.; et al. Dark Energy Survey Year 3 results: Cosmological constraints from galaxy clustering and weak lensing. Phys. Rev. D 2022, 105, 023520. [Google Scholar] [CrossRef]
- Laureijs, R.; Gondoin, P.; Duvet, L.; Criado, G.S.; Hoar, J.; Amiaux, J.; Auguères, J.L.; Cole, R.; Cropper, M.; Ealet, A.; et al. Euclid: ESA’s mission to map the geometry of the dark universe. In Proceedings of the Space Telescopes and Instrumentation 2012: Optical, Infrared, and Millimeter Wave, Amsterdam, The Netherlands, 1–6 July 2012; SPIE: Bellingham, DC, USA, 2012; Volume 8442, pp. 329–336. [Google Scholar]
- Palenzuela, C.; Lehner, L.; Ponce, M.; Liebling, S.L.; Anderson, M.; Neilsen, D.; Motl, P. Electromagnetic and gravitational outputs from binary-neutron-star coalescence. Phys. Rev. Lett. 2013, 111, 061105. [Google Scholar] [CrossRef] [PubMed]
- Dionysopoulou, K.; Alic, D.; Palenzuela, C.; Rezzolla, L.; Giacomazzo, B. General-relativistic resistive magnetohydrodynamics in three dimensions: Formulation and tests. Phys. Rev. D—Part. Fields Gravit. Cosmol. 2013, 88, 044020. [Google Scholar] [CrossRef]
- Ripperda, B.; Bacchini, F.; Porth, O.; Most, E.R.; Olivares, H.; Nathanail, A.; Rezzolla, L.; Teunissen, J.; Keppens, R. General-relativistic resistive magnetohydrodynamics with robust primitive-variable recovery for accretion disk simulations. Astrophys. J. Suppl. Ser. 2019, 244, 10. [Google Scholar] [CrossRef]
- Martí, J.M.; Müller, E. Numerical hydrodynamics in special relativity. Living Rev. Relativ. 1999, 2, 3. [Google Scholar] [CrossRef]
- Del Zanna, L.; Bucciantini, N. An efficient shock-capturing central-type scheme for multidimensional relativistic flows. Astron. Astrophys. 2002, 390, 1177–1186. [Google Scholar] [CrossRef]
- Imbrogno, M.; Meringolo, C.; Servidio, S. Extreme gravitational interactions in the problem of three black holes in general relativity. Class. Quantum Gravity 2023, 40, 075008. [Google Scholar] [CrossRef]
- Bona, C.; Massó, J. Einstein’s evolution equations as a system of balance laws. Phys. Rev. D 1989, 40, 1022. [Google Scholar] [CrossRef] [PubMed]
- Bona, C.; Masso, J.; Seidel, E.; Stela, J. New formalism for numerical relativity. Phys. Rev. Lett. 1995, 75, 600. [Google Scholar] [CrossRef] [PubMed]
- Alcubierre, M.; Allen, G.; Bona, C.; Fiske, D.; Goodale, T.; Guzmán, F.S.; Hawke, I.; Hawley, S.H.; Husa, S.; Koppitz, M.; et al. Towards standard testbeds for numerical relativity. Class. Quantum Gravity 2003, 21, 589. [Google Scholar] [CrossRef]
- Alcubierre, M. Introduction to 3 + 1 Numerical Relativity; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Akbarian, A.; Choptuik, M.W. Black hole critical behavior with the generalized BSSN formulation. Phys. Rev. D 2015, 92, 084037. [Google Scholar] [CrossRef]
- Alekseenko, A.M. Constraint preserving boundary conditions for the linearized BSSN formulation. arXiv 2004, arXiv:gr-qc/0405080. [Google Scholar]
- Gundlach, C.; Martin-Garcia, J.M. Well-posedness of formulations of the Einstein equations with dynamical lapse and shift conditions. Phys. Rev. D—Part. Fields Gravitat. Cosmol. 2006, 74, 024016. [Google Scholar] [CrossRef]
- Brown, J.D. Covariant formulations of Baumgarte, Shapiro, Shibata, and Nakamura and the standard gauge. Phys. Rev. D—Part. Fields Gravitat. Cosmol. 2009, 79, 104029. [Google Scholar] [CrossRef]
- Mignone, A.; Bodo, G.; Massaglia, S.; Matsakos, T.; Tesileanu, O.; Zanni, C.; Ferrari, A. PLUTO: A Numerical Code for Computational Astrophysics. Astrophys. J. Suppl. Ser. 2007, 170, 228–242. [Google Scholar] [CrossRef]
- Baiotti, L.; Giacomazzo, B.; Rezzolla, L. Accurate evolutions of inspiralling and magnetized neutron stars: Equal-mass binaries. Phys. Rev. D 2008, 78, 084033. [Google Scholar] [CrossRef]
- Galeazzi, F.; Kastaun, W.; Rezzolla, L.; Font, J.A. Implementation of a simplified approach to radiative transfer in general relativity. Phys. Rev. D—Part. Fields Gravitat. Cosmol. 2013, 88, 064009. [Google Scholar] [CrossRef]
- Baiotti, L.; Pietri, R.D.; Manca, G.M.; Rezzolla, L. Accurate simulations of the dynamical bar-mode instability in full general relativity. Phys. Rev. D—Part. Fields Gravitat. Cosmol. 2007, 75, 044023. [Google Scholar] [CrossRef]
- Meringolo, C.; Servidio, S.; Veltri, P. A spectral method algorithm for numerical simulations of gravitational fields. Class. Quantum Gravity 2021, 38, 075027. [Google Scholar] [CrossRef]
- Meringolo, C.; Servidio, S. Aliasing Instabilities in the Numerical Evolution of the Einstein Field Equations. Gen. Relativ. Gravit. 2021, 53, 95. [Google Scholar] [CrossRef]
- Beckwith, K.; Stone, J.M. A second-order Godunov method for multi-dimensional relativistic magnetohydrodynamics. Astrophys. J. Suppl. Ser. 2011, 193, 6. [Google Scholar] [CrossRef]
- Radice, D.; Rezzolla, L. THC: A new high-order finite-difference high-resolution shock-capturing code for special-relativistic hydrodynamics. Astron. Astrophys. 2012, 547, A26. [Google Scholar] [CrossRef]
- Bertschinger, E. Simulations of structure formation in the universe. Annu. Rev. Astron. Astrophys. 1998, 36, 599–654. [Google Scholar] [CrossRef]
- Hahn, O.; Paranjape, A. General relativistic screening in cosmological simulations. Phys. Rev. D 2016, 94, 083511. [Google Scholar] [CrossRef]
- Zou, J.; Zhu, Z.; Zhao, Z.; Bian, L. Numerical simulations of density perturbation and gravitational wave production from cosmological first-order phase transition. arXiv 2025, arXiv:2502.20166. [Google Scholar]
- Adamek, J.; Daverio, D.; Durrer, R.; Kunz, M. General Relativistic N-body simulations in the weak field limit. Phys. Rev. D—Part. Fields Gravitat. Cosmol. 2013, 88, 103527. [Google Scholar] [CrossRef]
- Mertens, J.B.; Giblin, J.T., Jr.; Starkman, G.D. Integration of inhomogeneous cosmological spacetimes in the BSSN formalism. Phys. Rev. D 2016, 93, 124059. [Google Scholar] [CrossRef]
- Stein, R.F.; Nordlund, Å. Realistic solar convection simulations. Sol. Phys. 2000, 192, 91–108. [Google Scholar] [CrossRef]
- Macpherson, H.J.; Lasky, P.D.; Price, D.J. Inhomogeneous cosmology with numerical relativity. Phys. Rev. D 2017, 95, 064028. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Imbrogno, M.; Megale, R.; Del Zanna, L.; Servidio, S. A Novel Logarithmic Approach to General Relativistic Hydrodynamics in Dynamical Spacetimes. Universe 2025, 11, 194. https://doi.org/10.3390/universe11060194
Imbrogno M, Megale R, Del Zanna L, Servidio S. A Novel Logarithmic Approach to General Relativistic Hydrodynamics in Dynamical Spacetimes. Universe. 2025; 11(6):194. https://doi.org/10.3390/universe11060194
Chicago/Turabian StyleImbrogno, Mario, Rita Megale, Luca Del Zanna, and Sergio Servidio. 2025. "A Novel Logarithmic Approach to General Relativistic Hydrodynamics in Dynamical Spacetimes" Universe 11, no. 6: 194. https://doi.org/10.3390/universe11060194
APA StyleImbrogno, M., Megale, R., Del Zanna, L., & Servidio, S. (2025). A Novel Logarithmic Approach to General Relativistic Hydrodynamics in Dynamical Spacetimes. Universe, 11(6), 194. https://doi.org/10.3390/universe11060194






