A Novel Search Technique for Low-Frequency Periodic Gravitational Waves
Abstract
1. Introduction
2. The Paradigm
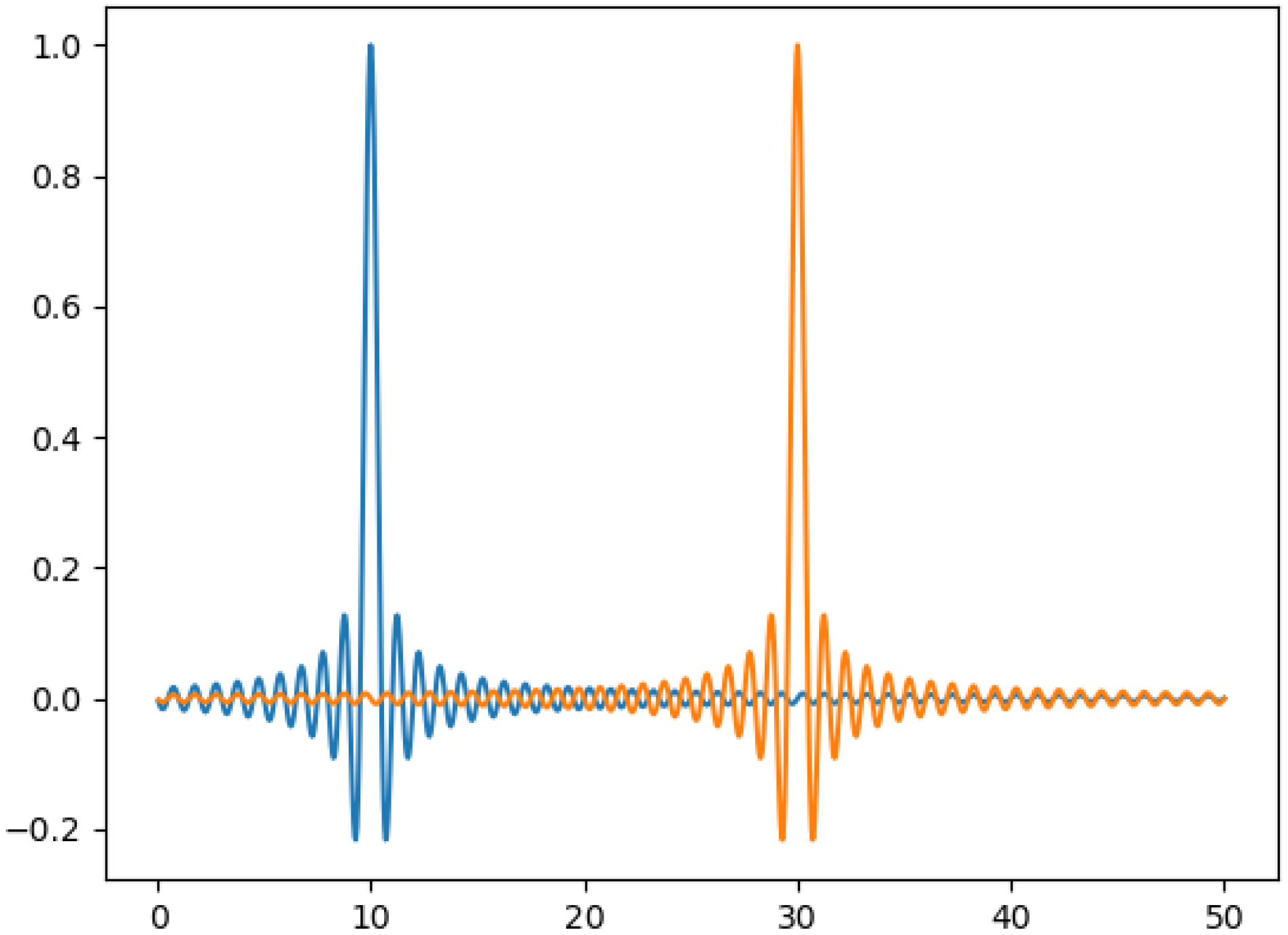
3. The Product Signal
- Case I: We assume that the orbital period is an odd integer multiple, namely 365, of the rotational period of Earth, or, . Also, we assume that the neutron star does not spin down, i.e., its frequency remains constant throughout the observation period in the source frame, that is, we take .
- Case II: We relax the first condition and assume actual periods for orbital and rotational motion. They are not related by an integer multiple. Specifically, we assume (note that the relevant period here is a sidereal day, not the mean solar day). However, here we also assume the spin-down to be zero, or .
- Case III: We relax the above two conditions; orbital and rotational periods not related by an integer and also one spin-down are assumed. Thus, and .
3.1. Case I
3.2. Case II
3.2.1. The Choice of and the Phase
3.2.2. The Phase Metric and the Number of Sky Patches
3.3. Case III
3.3.1. The Phase and Its Approximate Form
3.3.2. The Phase Metric and the Number of Sky Patches
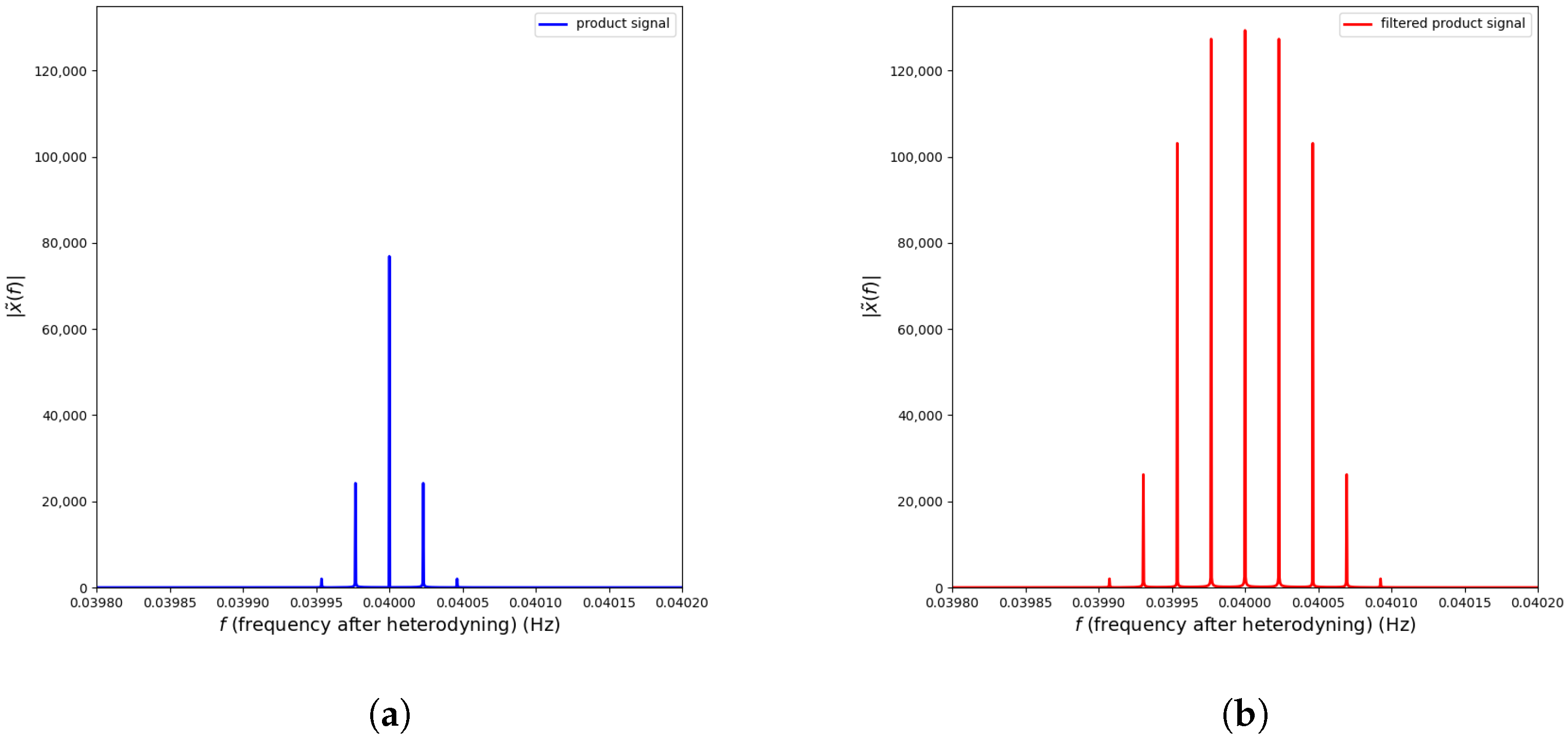
4. The Product Noise
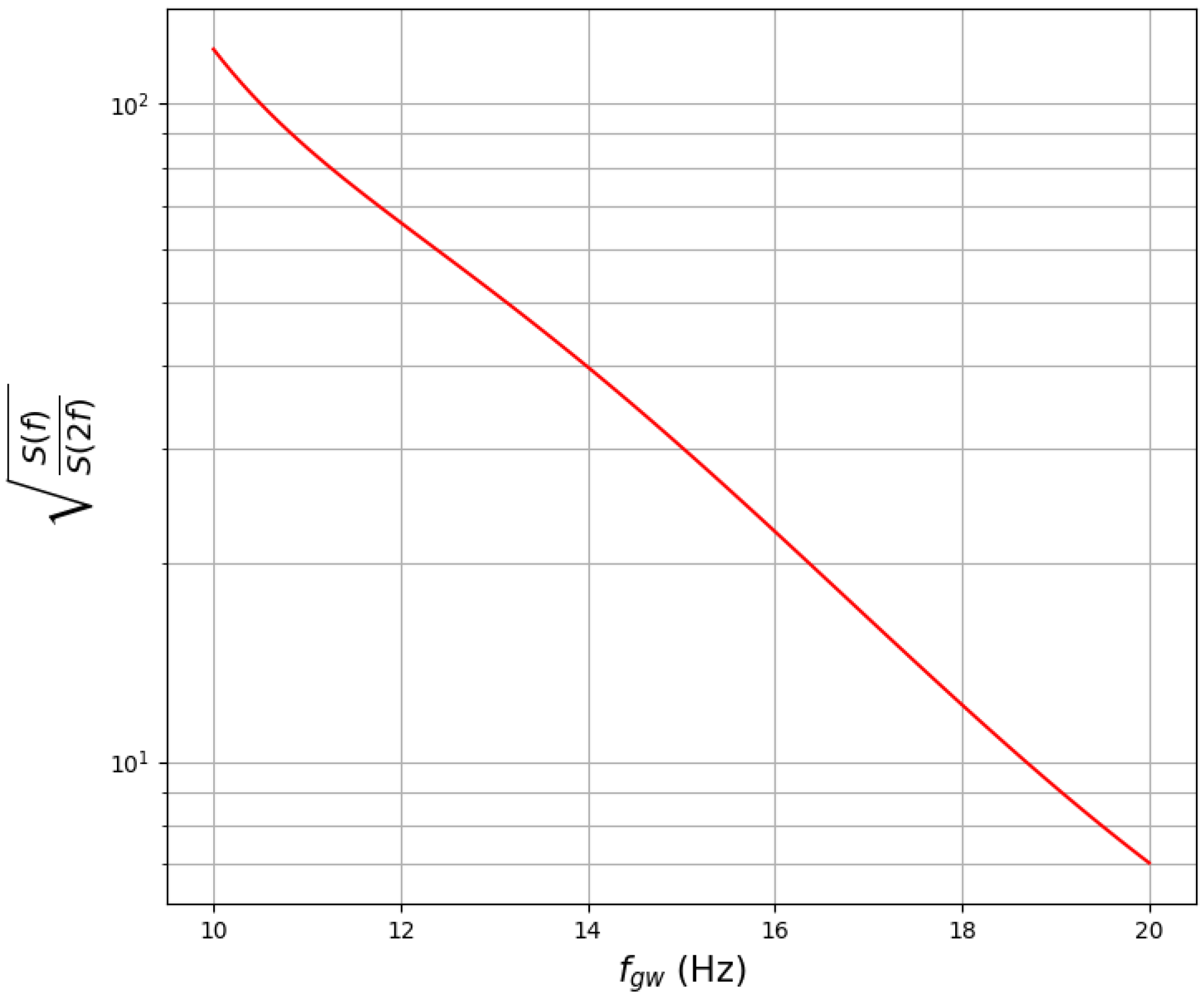
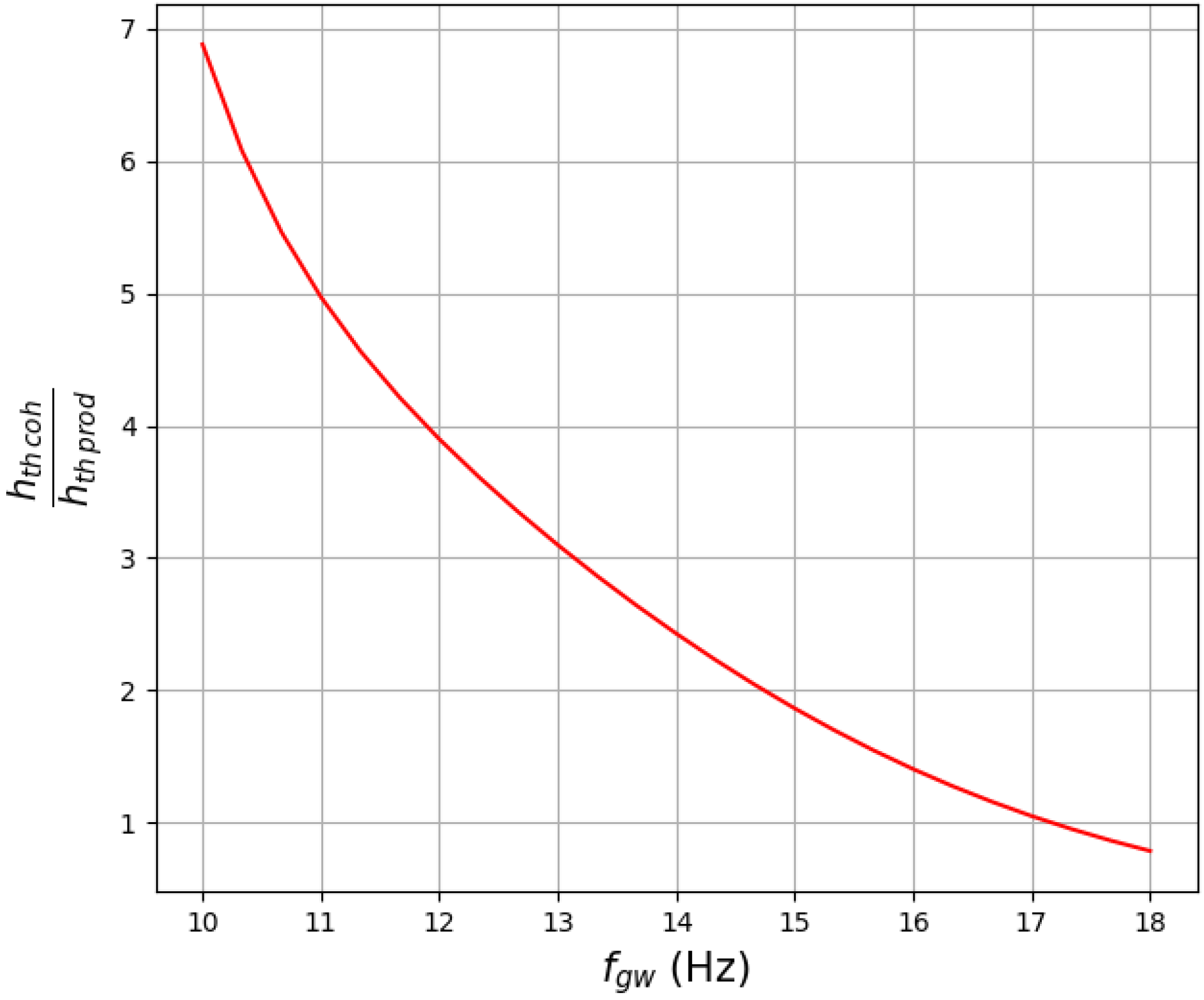
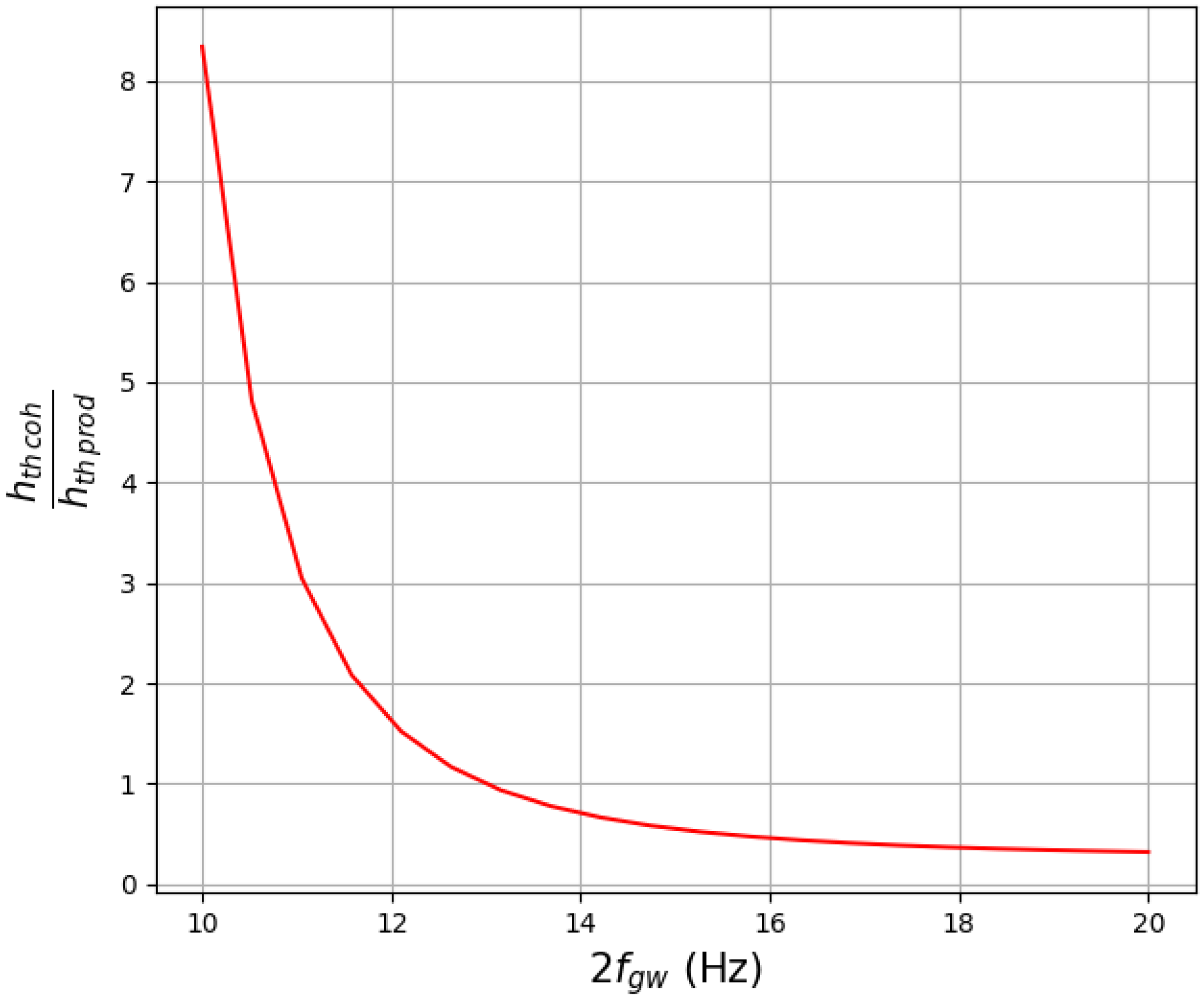
5. Sensitivities and Thresholds
GW Signal at 10 Hz
6. From Circular to Elliptical
7. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GW | Gravitational Wave |
| SSB | Solar System Barycenter |
| FFT | Fast Fourier Transform |
Appendix A. The Amplitudes Describing the Product Signal in Case I
Appendix B. The Finite-Time Delta Function
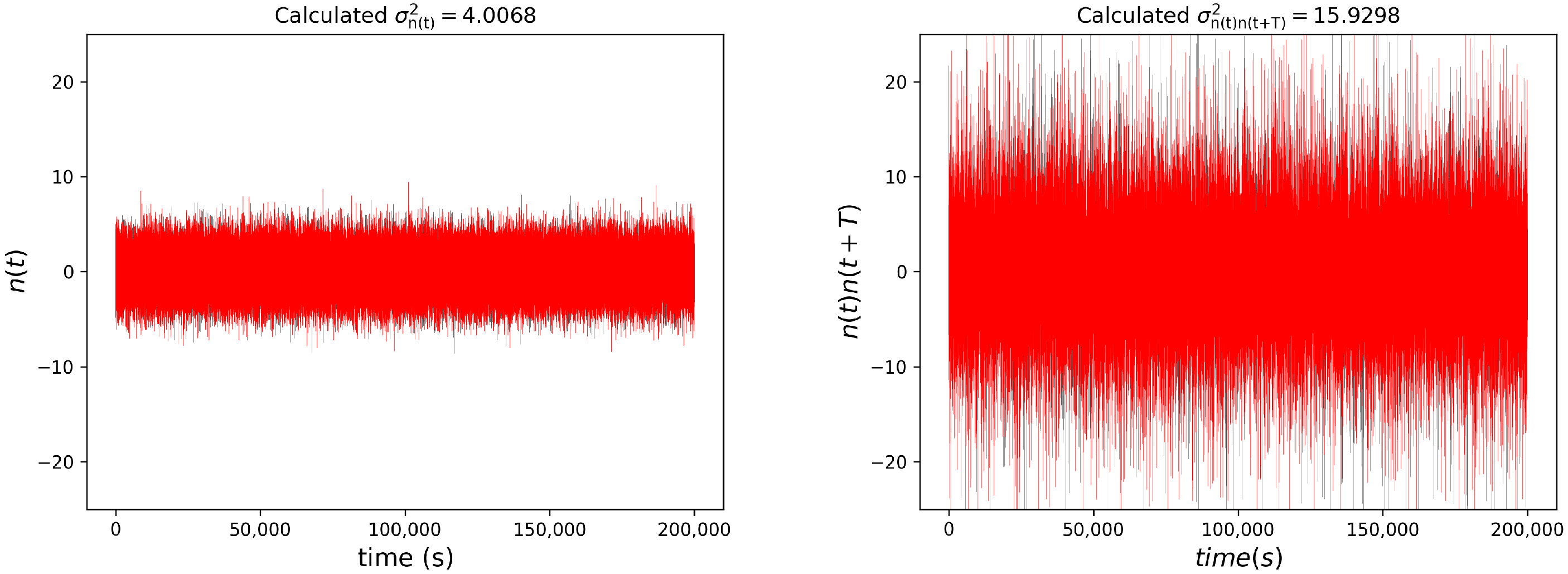
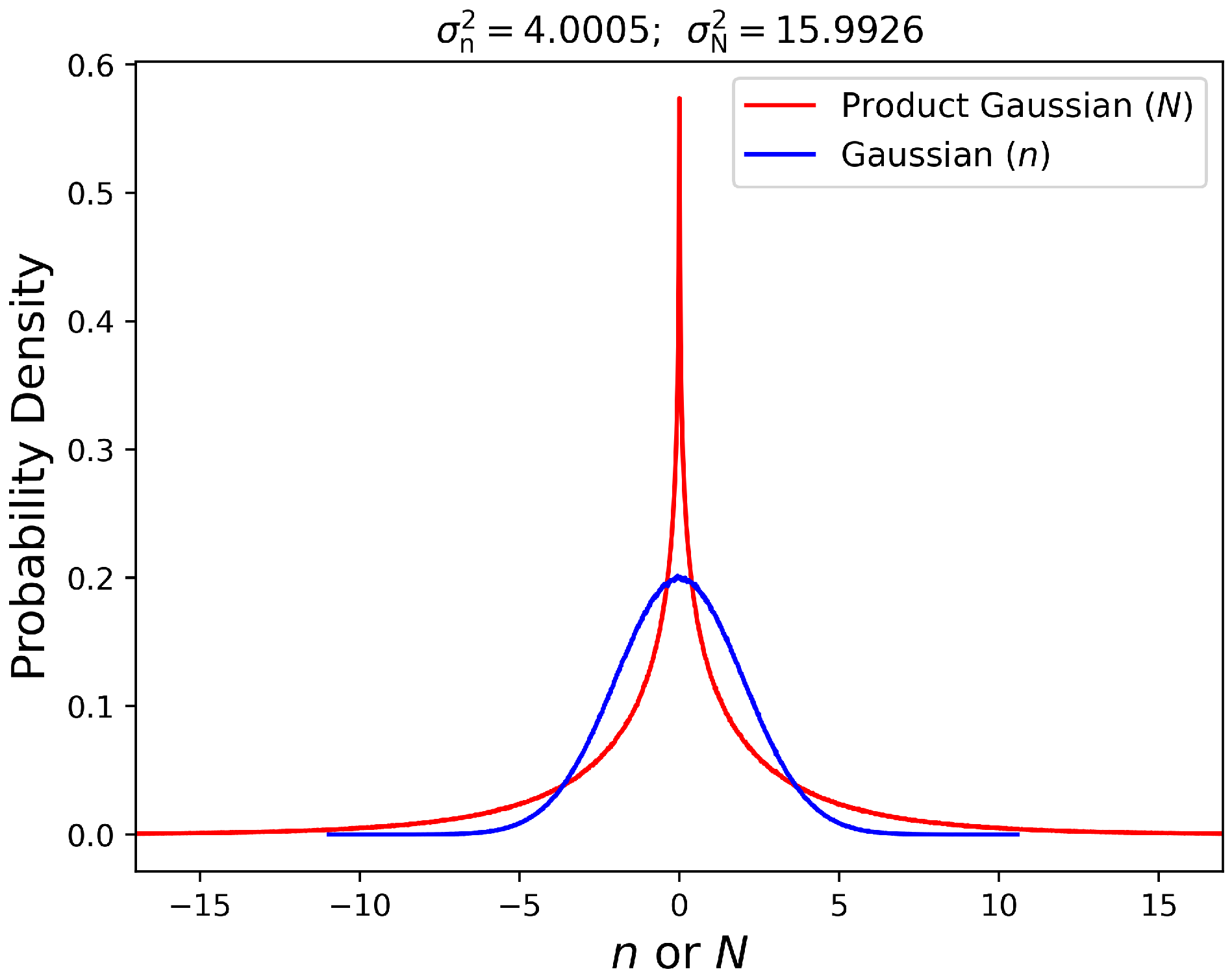
Appendix C. The Statistics of the Product Noise
| 1 | The uncertainties quoted are at the 90 percent confidence level. |
| 2 | Our analysis will only include the first derivative of the variation in the pulsar’s angular velocity. |
References
- Aasi, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Advanced LIGO. Class. Quantum Grav. 2015, 32, 074001. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Abernathy, M.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Thorne, K.S. Gravitational Radiation. In 300 Years of Gravitation; Hawking, S., Israel, W., Eds.; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Accadia, T.; Acernese, F.; Alshourbagy, M.; Amico, P.; Antonucci, F.; Aoudia, S.; Arnaud, N.; Arnault, C.; Arun, K.G.; Astone, P.; et al. Virgo: A laser interferometer to detect gravitational waves. J. Instrum. 2012, 7, P03012. [Google Scholar] [CrossRef]
- Schutz, B.F.; Tinto, M. Antenna patterns of interferometric detectors of gravitational waves—I. Linearly polarized waves. Mon. Not. R. Astron. Soc. 1987, 224, 131–154. [Google Scholar] [CrossRef]
- Gürsel, Y.; Tinto, M. Near optimal solution to the inverse problem for gravitational-wave bursts. Phys. Rev. D 1989, 40, 3884–3938. [Google Scholar] [CrossRef]
- Sathyaprakash, B.S.; Dhurandhar, S.V. Choice of filters for the detection of gravitational waves from coalescing binaries. Phys. Rev. D 1991, 44, 3819–3834. [Google Scholar] [CrossRef]
- Jaranowski, P.; Krolak, A. Optimal solution to the inverse problem for the gravitational wave signal of a coalescing compact binary. Phys. Rev. D 1994, 49, 1723–1739. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Abernathy, M.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; et al. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2. Phys. Rev. Lett. 2017, 118, 221101. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. GW170814: A Three-Detector Observation of Gravitational Waves from a Binary Black Hole Coalescence. Phys. Rev. Lett. 2017, 119, 141101. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. GWTC-1: A Gravitational-Wave Transient Catalog of Compact Binary Mergers Observed by LIGO and Virgo during the First and Second Observing Runs. Phys. Rev. X 2019, 9, 031040. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; Adya, V.; et al. Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Aso, Y.; Michimura, Y.; Somiya, K.; Ando, M.; Miyakawa, O.; Sekiguchi, T.; Tatsumi, D.; Yamamoto, H. Interferometer design of the KAGRA gravitational wave detector. Phys. Rev. D 2013, 88, 043007. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Abernathy, M.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; et al. All-sky search for periodic gravitational waves in the O1 LIGO data. Phys. Rev. D 2017, 96, 062002. [Google Scholar] [CrossRef]
- Abbott, B.; Abbott, R.; Abbott, T.; Abernathy, M.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.; et al. First low-frequency Einstein@Home all-sky search for continuous gravitational waves in Advanced LIGO data. arXiv 2017, arXiv:1707.02669. [Google Scholar] [CrossRef]
- Prix, R. Search for continuous gravitational waves: Metric of the multidetector F-statistic. Phys. Rev. D 2007, 75, 023004. [Google Scholar] [CrossRef]
- Sathyaprakash, B.S.; Schutz, B.F. Physics, Astrophysics and Cosmology with Gravitational Waves. Living Rev. Relativ. 2009, 12, 2. [Google Scholar] [CrossRef]
- Owen, B.J. Maximum Elastic Deformations of Compact Stars with Exotic Equations of State. Phys. Rev. Lett. 2005, 95, 211101. [Google Scholar] [CrossRef]
- Johnson-McDaniel, N.K.; Owen, B.J. Maximum elastic deformations of relativistic stars. Phys. Rev. D 2013, 88, 044004. [Google Scholar] [CrossRef]
- Tinto, M. A Fast Data Processing Technique for Continuous Gravitational Wave Searches. Universe 2021, 7, 486. [Google Scholar] [CrossRef]
- Brady, P.R.; Creighton, T. Searching for periodic sources with LIGO. II. Hierarchical searches. Phys. Rev. D 2000, 61, 082001. [Google Scholar] [CrossRef]
- Jaranowski, P.; Królak, A.; Schutz, B.F. Data analysis of gravitational-wave signals from spinning neutron stars: The signal and its detection. Phys. Rev. D 1998, 58, 063001. [Google Scholar] [CrossRef]
- Cutler, C.; Schutz, B.F. Generalized F-statistic: Multiple detectors and multiple gravitational wave pulsars. Phys. Rev. D 2005, 72, 063006. [Google Scholar] [CrossRef]
- Brady, P.R.; Creighton, T.; Cutler, C.; Schutz, B.F. Searching for periodic sources with LIGO. Phys. Rev. D 1998, 57, 2101–2116. [Google Scholar] [CrossRef]
- Dhurandhar, S.; Krishnan, B.; Mukhopadhyay, H.; Whelan, J.T. Cross-correlation search for periodic gravitational waves. Phys. Rev. D 2008, 77, 082001. [Google Scholar] [CrossRef]
- Dhurandhar, S.V.; Vecchio, A. Searching for continuous gravitational wave sources in binary systems. Phys. Rev. D 2001, 63, 122001. [Google Scholar] [CrossRef]
- Jaranowski, P.; Krolak, A. Data analysis of gravitational-wave signals from spinning neutron stars. III. Detection statistics and computational requirements. Phys. Rev. D 2000, 61, 062001. [Google Scholar] [CrossRef]
- Feller, W. An Introduction to Probability Theory and Its Applications, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1968; Volume 1. [Google Scholar]
- Dhurandhar, S. Understanding Mathematical Concepts in Physics: Insights from Geometrical and Numerical Approaches; Lecture Notes in Physics; Springer: Cham, Swizterland, 2024; Volume 1030. [Google Scholar] [CrossRef]
- Wette, K. Estimating the sensitivity of wide-parameter-space searches for gravitational-wave pulsars. Phys. Rev. D 2012, 85, 042003. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Mechanics, Third Edition: Volume 1 (Course of Theoretical Physics), 3rd ed.; Butterworth-Heinemann: New York, NY, USA, 1976. [Google Scholar]
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D.; et al. Laser Interferometer Space Antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar]
- Hu, W.R.; Wu, Y.L. The Taiji Program in Space for gravitational wave physics and the nature of gravity. Natl. Sci. Rev. 2017, 4, 685–686. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th ed.; Dover Publications: New York, NY, USA, 1964. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raj, H.; Dhurandhar, S.; Tinto, M. A Novel Search Technique for Low-Frequency Periodic Gravitational Waves. Universe 2025, 11, 168. https://doi.org/10.3390/universe11060168
Raj H, Dhurandhar S, Tinto M. A Novel Search Technique for Low-Frequency Periodic Gravitational Waves. Universe. 2025; 11(6):168. https://doi.org/10.3390/universe11060168
Chicago/Turabian StyleRaj, Harshit, Sanjeev Dhurandhar, and Massimo Tinto. 2025. "A Novel Search Technique for Low-Frequency Periodic Gravitational Waves" Universe 11, no. 6: 168. https://doi.org/10.3390/universe11060168
APA StyleRaj, H., Dhurandhar, S., & Tinto, M. (2025). A Novel Search Technique for Low-Frequency Periodic Gravitational Waves. Universe, 11(6), 168. https://doi.org/10.3390/universe11060168






