Abstract
The interaction between particles and their surrounding medium can induce a squeezed back-to-back correlation between particles and antiparticles. In this paper, the squeezed fermion back-to-back correlation (fBBC) for expanding sources is studied. The formulas of the fBBC correlation function of fermion–antifermion pairs for expanding sources are given. The expanding flow leads to a decrease in the fBBC of proton–antiproton pairs and - pairs in the high-momentum region, an increase in the fBBC in the low-momentum region, and a narrowing width of the fBBC varies with in-medium mass in the low-momentum region. Even though the expanding flow influences fBBC, the fBBC of proton–antiproton pairs and - pairs can still offer possible observation signals as the collision energy varies from a few GeV to 200 GeV.
PACS:
25.75.-q; 25.75.Gz
1. Introduction
In relativistic heavy-ion collisions, it is anticipated that a hot and dense medium will be generated. This medium’s interaction with particles can lead to a squeezed back-to-back correlation between particles and antiparticles [1,2,3,4,5,6,7,8,9]. The relationship between the squeezed back-to-back correlation and the in-medium mass modification of fermions (bosons) is established via the Bogoliubov–Valatin (Bogoliubov) transformation. This transformation links the creation (annihilation) operators of particles within the medium to those of their equivalent free particles in the vacuum [1,2,3,4,5,6,7,8,9]. Investigating squeezed back-to-back correlations could offer a novel perspective for probing the dynamical and thermal properties of the particle emission source in relativistic heavy-ion collisions.
The fermion back-to-back correlations (fBBCs) were studied based a homogeneous particle-emitting source [8]. The fBBC of protons and antiprotons was expected to be experimentally observed in relativistic heavy-ion collisions, similarly to the Andreev reflection of electrons off the boundary of a superconductor [8,9]. The fBBC may show notable magnitudes for protons and antiprotons with high momenta and low mass shifts, but vanishes when there is no in-medium mass modification. As the net baryonic density rises, the fBBC becomes markedly suppressed [8]. The earlier findings were drawn from a homogeneous particle-emitting source. However, the sources of particle emission formed during relativistic heavy-ion collisions are expanding and inhomogeneous. To enhance the model’s realism, the previous research extended to the use of a Gaussian source with radial flow to describe the particle emission.
The impacts of the expanding flow on the fBBC of proton–antiproton pairs and - pairs are analysed in this paper. Due to the expanding flow, the fBBC is enhanced in regions with small momentum but weakened in areas with large momentum. The results indicate that the fBBC of proton–antiproton and - provides observable signals as the collision energy varies from a few GeV to 200 GeV. For a small in-medium mass modification, the fBBC of - provides a stronger signal compared to that of proton–antiproton. Unfortunately, currently, no experimental data exist on fBBC. And the existing experimental data cannot provide a conclusion on whether fBBC exists. The results of this paper are exclusively obtained through theoretical modeling.
The rest of this paper will proceed as follows. Section 2 extends the formulas of the fBBC correlation function of fermion–antifermion pairs for expanding sources, building upon Refs. [1,2,8,9]. Section 3 demonstrates the effects of expanding flow on the fBBC of proton–antiproton pairs and - pairs. Finally, Section 4 provides a summary and discussion.
2. Formulas
For a homogeneous source, the fBBC correlation function for fermion–antifermion pairs with back-to-back momenta and is defined as [8,9]
3. Results
In this section, the impacts of the expanding flow on the fBBC of proton–antiproton pairs and - pairs are discussed. The mass of proton in vacuum, denoted by , is taken as 938.27 MeV [10], and the of is taken as 1115.68 MeV [10]. It is assumed that the in-medium mass shift of the fermion and antifermion is the same, represented by the parameter = . The freeze-out temperature T for both the proton and antiproton is taken as 140 MeV [8]. The freeze-out temperature of and is also set as 140 MeV. In the calculations, the spatial width parameter of the source R is assumed to be 7 fm [2,6]. The radial velocity parameter is taken as 0, 0.3, and 0.5 [2,6], respectively. When is set to 0, it represents a static source. The parameter in Equation (7) is set as 2 fm/c [2,6,8].
3.1. fBBC of Proton–Antiproton Pairs
In Figure 1, the fBBC results of proton–antiproton as a function of at 500 and 1000 MeV are shown. The proton’s chemical potential ranges from around 0 to 400 MeV as the collision energy varies from a few GeV to 200 GeV [11]. Thus, in the left, (a) and (d), center, (b) and (e), and right, (c) and (f), panels of Figure 1, Figure 2 and Figure 3, the proton’s chemical potential is taken as 0, 100 MeV, and 400 MeV, respectively. As the proton’s chemical potential increases, the peak value of the fBBC of proton–antiproton decreases. When the proton’s in-medium mass is below around 1100 MeV, the expanding flow enhances the fBBC of proton–antiproton at 500 MeV and suppresses it at 1000 MeV. Conversely, when exceeds 1100 MeV, the expanding flow suppresses the fBBC of proton–antiproton at 500 MeV while slightly improving it at 1000 MeV. This phenomenon becomes more pronounced as the radial velocity increases.
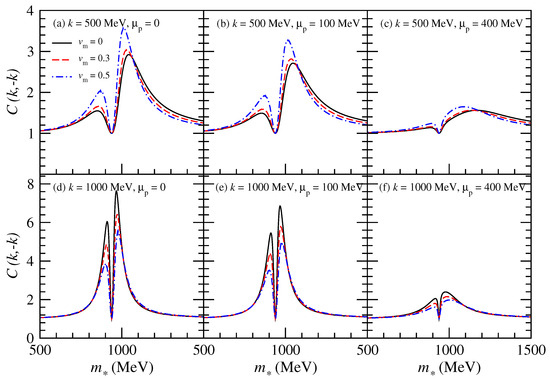
Figure 1.
(Color online) The fBBC results of proton–antiproton as a function of at 500 and 1000 MeV. Here, is the chemical potential of the proton, and is taken as 0, 100 MeV and 400 MeV, respectively.
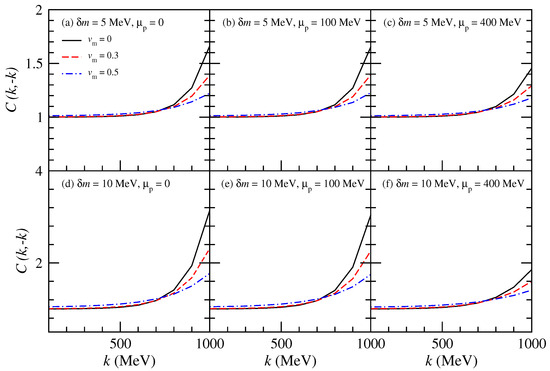
Figure 2.
(Color online) The fBBC results of proton–antiproton as a function of k at 5 and 10 MeV. Here, is taken as 0, 100 MeV, and 400 MeV, respectively.
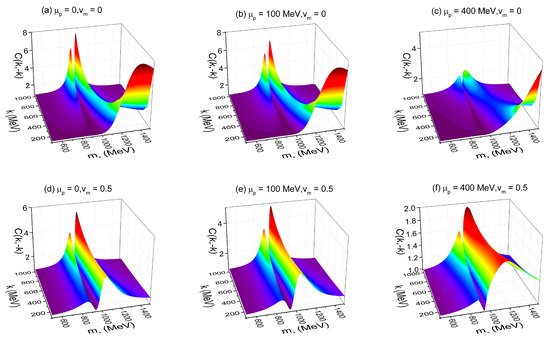
Figure 3.
(Color online) The fBBC results of proton–antiproton in the -k plane. Here, is taken as 0, 100 MeV, and 400 MeV, respectively.
In Figure 2, the fBBC results of proton–antiproton as a function of k at 5 and 10 MeV are shown. The proton’s mass was expected to be reduced in the medium [12,13,14]. Therefore, here, is treated as positive, and this means . The fBBC of proton–antiproton increases as the momentum k increases. The expanding flow enhances the fBBC in the low-momentum region but suppresses it in the high-momentum region. Consequently, the expanding flow induces a reduction in the slope of fBBC as k varies, with this effect becoming more noticeable as the radial velocity rises.
In Figure 3, the fBBC results of proton–antiproton in the -k plane are shown. Plots (a)–(c) present the results for the static source, while plots (d)–(f) present the results for the expanding source with a radial velocity parameter of 0.5. The expanding flow’s impact on fBBC varies across different k regions: it suppresses fBBC in the large k region, strengthens it in the small k region, and narrows the distribution width of fBBC with in the small k region. This effect may lead to the detection of fBBC in the small-momentum region even when there is little change in mass in the medium. As the proton’s chemical potential increases, the value of the fBBC of proton–antiproton decreases. For 400 MeV, the fBBC of proton–antiproton for the expanding source may be observed even when there is little change in mass in the medium, both in regions with high and low momenta. Thus, the fBBC of proton–antiproton provides observable signals as the collision energy varies from a few GeV to 200 GeV. It is worth mentioning that the conclusion is based a finite time suppression factor used to model a more gradual freeze-out. As the in Equation (7) increases, decreases, leading to a decline in the strength of fBBC. In Ref. [3], the Lévy-type time suppression factor is used to study the back-to-back correlations (BBCs) of . For fixed , the Lévy-type time suppression factor exhibits stronger dampening of BBC relative to the time suppression factor used in this paper. The impacts of the time suppression factor on fBBC and BBC are similar [1,2,3,4,6,8,9]. The experimental observability of fBBC is therefore critically dependent on the emission source’s temporal distributions, where a narrow temporal distribution substantially increases both the strength and observation probability. However, the fBBC signal may be completely suppressed for a wide emission source’s temporal distribution.
3.2. fBBC of - Pairs
In Figure 4, the fBBC results of - as a function of at 500 and 1000 MeV are shown. Here, is the chemical potential of , and is taken as 0, 100 MeV, and 400 MeV, respectively. The value of is simply taken in the same way as for the proton. The impacts of the expanding flow on the fBBC results of - are similar to the impacts of the expanding flow on the fBBC results of proton–antiproton. For identical values of chemical potential and k, the peak value of fBBC for - is greater than that for proton–antiproton. This is due to the larger mass of in vacuum compared to proton in vacuum. A similar phenomenon also appears in the BBC of bosons–antibosons [1,2,3,4,6].
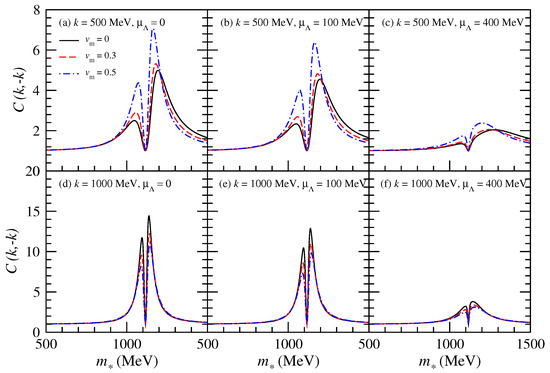
Figure 4.
(Color online) The fBBC results of - as a function of at 500 and 1000 MeV. Here, is the chemical potential of , and is taken as 0, 100 MeV, and 400 MeV, respectively.
In Figure 5, the fBBC results of - as a function of k at 5 and 10 MeV are shown. The fBBC of - increases as the momentum k increases. The expanding flow leads to a reduction in the slope of fBBC as k varies, which becomes more pronounced as the radial velocity increases. This phenomenon is similar to the effects of the expanding flow on the fBBC results of proton–antiproton.
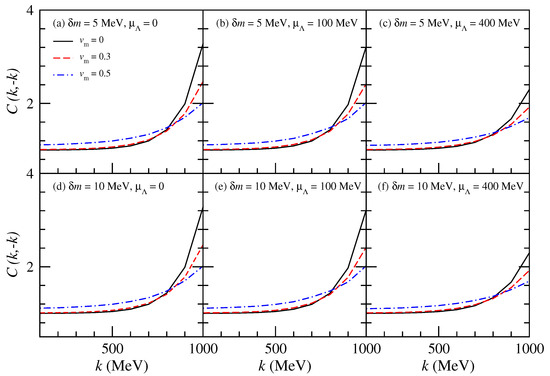
Figure 5.
(Color online) The fBBC results of - as a function of k at 5 and 10 MeV.
In Figure 6, the fBBC results of - in the -k plane are presented. Plots (a)–(c) present the results for the static source, while plots (d)–(f) present the results for the expanding source with a radial velocity parameter of 0.5. The expanding flow causes a reduction in fBBC of - in the high-momentum region, an increase in fBBC in the low-momentum region, and a decrease in the distribution width of fBBC with in the low-momentum region. For a little in-medium mass modification, the fBBC of - provides a stronger signal compared to that of proton–antiproton. This arises from the higher vacuum rest mass of the compared to that of the proton.
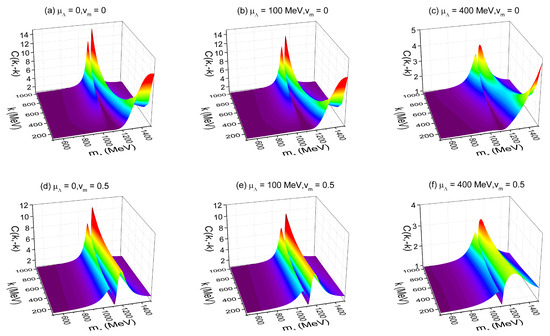
Figure 6.
(Color online) The fBBC results of - in the -k plane.
The fBBC of proton–antiproton pairs and - manifests a dichotomous peak structure as a function of the in-medium mass , with two distinct peaks flanking the vacuum mass value. This indicates that the fBBC exhibits a non-monotonic dependence on the in-medium mass modification , regardless of whether the in-medium mass lies above or below the vacuum mass; the fBBC initially rises, peaks, and subsequently diminishes as increases. The fBBC exhibits detectable signatures when resides within a small range; beyond this threshold, the signal becomes small and experimentally unobservable. This phenomenon of the fBBC is similar to the BBC of bosons–antibosons [1,2,3,4,5,6].
4. Summary and Discussion
In relativistic heavy-ion collisions, the interactions between particles and their surrounding medium can lead to a squeezed back-to-back correlation between particles and antiparticles. In this paper, the fBBC of fermions and antifermions is studied based on a Gaussian source with radial flow. The formulas of the fBBC correlation functions for local equilibrium expanding sources are given based on the work in Refs. [1,2,6,8].
The impacts of the expanding flow on the fBBC of proton–antiproton pairs and - pairs are analyzed. The expanding flow leads to a decrease in fBBC for proton–antiproton and - pairs in the high-momentum region, an increase in fBBC in the low-momentum region, and a narrowing width of the fBBC varies with in the low-momentum region. The fBBC of - exhibits a stronger signal than that of proton–antiproton when there is a slight in-medium mass modification, with identical values of chemical potential and momentum.
The current analysis shows that the fBBC of proton–antiproton and - may provide observable signals as the collision energy varies from a few GeV to 200 GeV. As demonstrated in Ref. [9], Coulomb and phonon interactions exert negligible influence on fBBC. The study advocates single-event analysis in high-momentum regimes to search for the fBBC [9]. However, currently, no experimental data exist on fBBC. And the existing experimental data cannot provide a conclusion on whether fBBC exists. The momentum distribution of fermions may be affected by the in-medium mass modification [8,9], and experimental data on the momentum spectra of fermions are available. It is necessary to study the impacts of the in-medium mass modification on the momentum spectra of fermions, further optimize parameter settings based on experimental data, and study the observability of fBBC.
In this paper, a Gaussian source with radial flow is used. However, the sources formed in relativistic heavy-ion collisions may deviate from spherically symmetric. Studying the fBBC further based on more reasonable sources offers an interesting direction for additional investigation.
Funding
This research was supported by the National Natural Science Foundation of China under Grant No. 11905085.
Data Availability Statement
The dataset is available on request from the author.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Asakawa, M.; Csörgő, T.; Gyulassy, M. Squeezed Correlations and Spectra for Mass-Shifted Bosons. Phys. Rev. Lett. 1999, 83, 4013. [Google Scholar] [CrossRef]
- Padula, S.S.; Krein, G.; Csörgő, T.; Hama, Y.; Panda, P.K. Back-to-back correlations for finite expanding fireballs. Phys. Rev. C 2006, 73, 044906. [Google Scholar] [CrossRef]
- Dudek, D.M.; Padula, S.S. Squeezed K+K− correlations in high energy heavy ion collisions. Phys. Rev. C 2010, 82, 034905. [Google Scholar] [CrossRef]
- Padula, S.S.; Socolowski, O., Jr. Searching for squeezed particle-antiparticle correlations in high-energy heavy-ion collisions. Phys. Rev. C 2010, 82, 034908. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, J.; Zhang, W.N. Squeezed correlations of ϕ meson pairs for hydrodynamic sources in high-energy heavy-ion collisions. Phys. Rev. C 2015, 92, 024906. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, J.; Zhang, W.N. Relativistic effects on the back-to-back correlation functions of boson-antiboson pairs in high energy heavy ion collisions. Chin. Phys. C 2015, 39, 034103. [Google Scholar] [CrossRef][Green Version]
- Xu, P.Z.; Zhang, W.N.; Zhang, Y. Squeezed back-to-back correlation between bosons and antibosons with different in-medium masses in high-energy heavy-ion collisions. Phys. Rev. C 2019, 99, 011902. [Google Scholar] [CrossRef]
- Panda, P.K.; Csörgő, T.; Hama, Y.; Krein, G.; Padula, S.S. Squeezed fermions at relativistic heavy ion colliders. Phys. Lett. B 2001, 512, 49. [Google Scholar] [CrossRef]
- Soller, H. Where to look for hadronic squeezed correlations at RHIC. Nucl. Phys. A 2020, 1000, 121813. [Google Scholar] [CrossRef]
- Navas, S. et al. [Particle Data Group]. Review of Particle Physics. Phys. Rev. D 2024, 110, 030001. [Google Scholar] [CrossRef]
- Adamczyk, L. et al. [STAR Collaboration]. Bulk properties of the medium produced in relativistic heavy-ion collisions from the beam energy scan program. Phys. Rev. C 2017, 96, 044904. [Google Scholar] [CrossRef]
- Fiolhais, M.; Christov, C.; Neuber, T.; Bergmann, M.; Goeke, K. Neutron-proton mass difference in a baryonic medium and the Nolen-Schiffer anomaly. Phys. Lett. B 1991, 269, 43. [Google Scholar] [CrossRef]
- Meißner, U.-G.; Rakhimov, A.M.; Wirzba, A.; Yakhshiev, U.T. Neutron-proton mass difference in nuclear matter. Eur. Phys. J. A 2007, 31, 357–364. [Google Scholar] [CrossRef]
- Meißner, U.-G.; Rakhimov, A.M.; Wirzba, A.; Yakhshiev, U.T. Neutron-proton mass difference in isospin-asymmetric nuclear matter. Eur. Phys. J. A 2007, 32, 299–309. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).