Galaxy Superclusters and Their Complexes in the Cosmic Web

Abstract

The richest and largest structures in the cosmic web are galaxy superclusters, their complexes (associations of several almost connected very rich superclusters), and planes. Superclusters represent a special environment where the evolution of galaxies and galaxy groups and clusters differs from the evolution of these systems in a low-density environment. The richest galaxy clusters reside in superclusters. The richest superclusters in the nearby Universe form a quasiregular pattern with the characteristic distance between superclusters 120–140 h⁻¹ Mpc. Moreover, superclusters in the nearby Universe lie in two huge perpendicular planes with the extent of several hundreds of megaparsecs, the Local Supercluster plane and the Dominant supercluster plane. The origin of these patterns in the supercluster distribution is not yet clear, and it is an open question whether the presence of such structures can be explained within the ΛCDM cosmological model. This review presents a brief story of superclusters, their discovery, definitions, main properties, and large-scale distribution.

1. Introduction

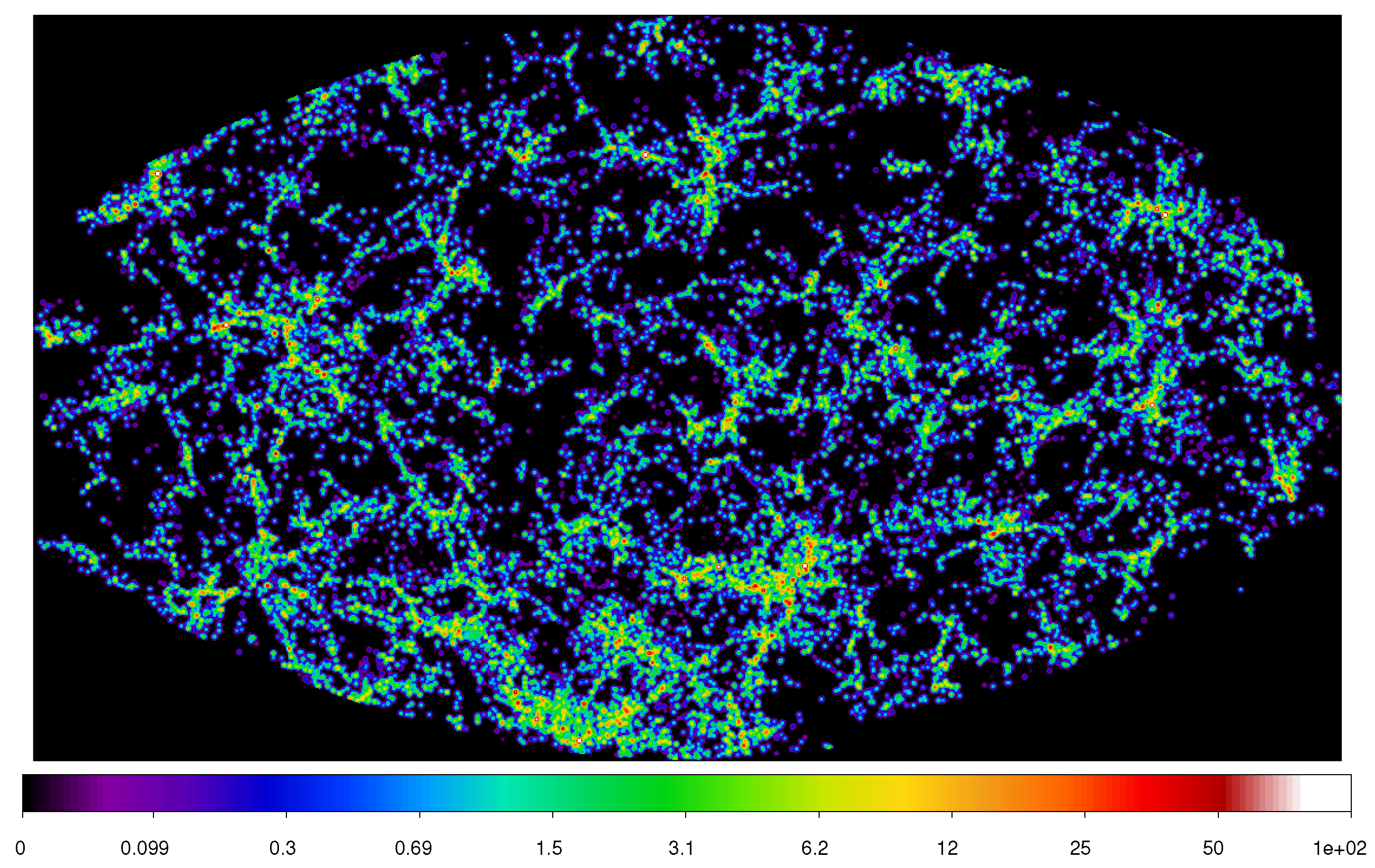
One of the major achievements of the modern observational cosmology in the last century is the discovery that galaxies and their systems form a web-like pattern now called the cosmic web, shown in Figure 1 [1,2,3]. The web-like distribution of matter presents a huge variety of galaxy systems from the galaxy clusters as nodes of the cosmic web, connected by elongated filaments of groups and single galaxies, and separated by huge underdense regions with almost no visible matter. The Cold Dark Matter cosmological model was accepted as a standard model in the 1990 (see, for example, Critical Dialogues in Cosmology [4]). According to the standard Cold Dark Matter cosmological model with cosmological constant (ΛCDM) model, dark matter is the main matter component in the cosmic web, alongside dark energy, and the formation and evolution of galaxies, galaxy groups, and clusters is governed by the dark side—dark matter and dark energy. Many methods have been developed to quantify the cosmic web and to study its properties. One of the first and most common methods among them is the two-point correlation function and its counterpart—power spectrum [5,6]. To describe the morphology of the cosmic web, higher-order statistics are used, as N-point correlation functions, the wavelet analysis, clustering and percolation analysis, various morphological methods, Minkowski functionals, Genus, Betti numbers, and shapefinders among them, Nth nearest neighbours, graph-based methods, fractal analysis, spherical collapse, Gaussian mixture modelling, and others. A review of these methods can be found in [5,6,7,8,9,10,11,12,13,14,15,16,17].

To detect and classify various cosmic web elements, many special methods have been developed, such as clustering analysis, various methods to determine cosmic filaments, and so on [18]. Based on these methods, cosmic web elements can be divided into dense nodes, elongated filaments, flattened sheets, and voids between them [18,19]. Among these methods, the percolation and clustering methods stand up as the first statistical methods to determine superclusters.

High-density regions of the cosmic web, which embed galaxies, groups, and clusters connected by filaments, are called galaxy superclusters. With their rich inner structure, superclusters as hosts of all cosmic web elements can be considered miniature Universes [20,21,22]. The richest superclusters may embed several tens of rich (Abell) clusters and their sizes may reach 200 $h^{-1}$ Mpc, while poor superclusters like our own, Local or Virgo supercluster, consist of only one rich cluster surrounded by filaments of poorer groups, including the Local Group of galaxies, and having an extent of approximately 20 $h^{-1}$ Mpc. Superclusters host the richest galaxy clusters and the brightest galaxies (which are the brightest galaxies of rich clusters). Opposite regions to superclusters are underdense regions between superclusters, called cosmic voids. Among well-known voids and supervoids, for example, are the Local void, the Bootes void, the Eridanus supervoid, and others, with sizes exceeding 100 $h^{-1}$ Mpc [23,24,25,26]. Superclusters host approximately 15% of all galaxies, and they occupy 1% of the total volume of the Universe, while voids fill 70–90% of the total volume of the Universe [19]. In overdense regions (superclusters), the growth of structures and the evolution of galaxies and galaxy systems are different from those in cosmic underdense regions (voids) [27,28,29,30]. Superclusters, as deep potential wells, act as attractors toward which matter flows from their surrounding low-density regions [9,31,32,33,34,35,36].

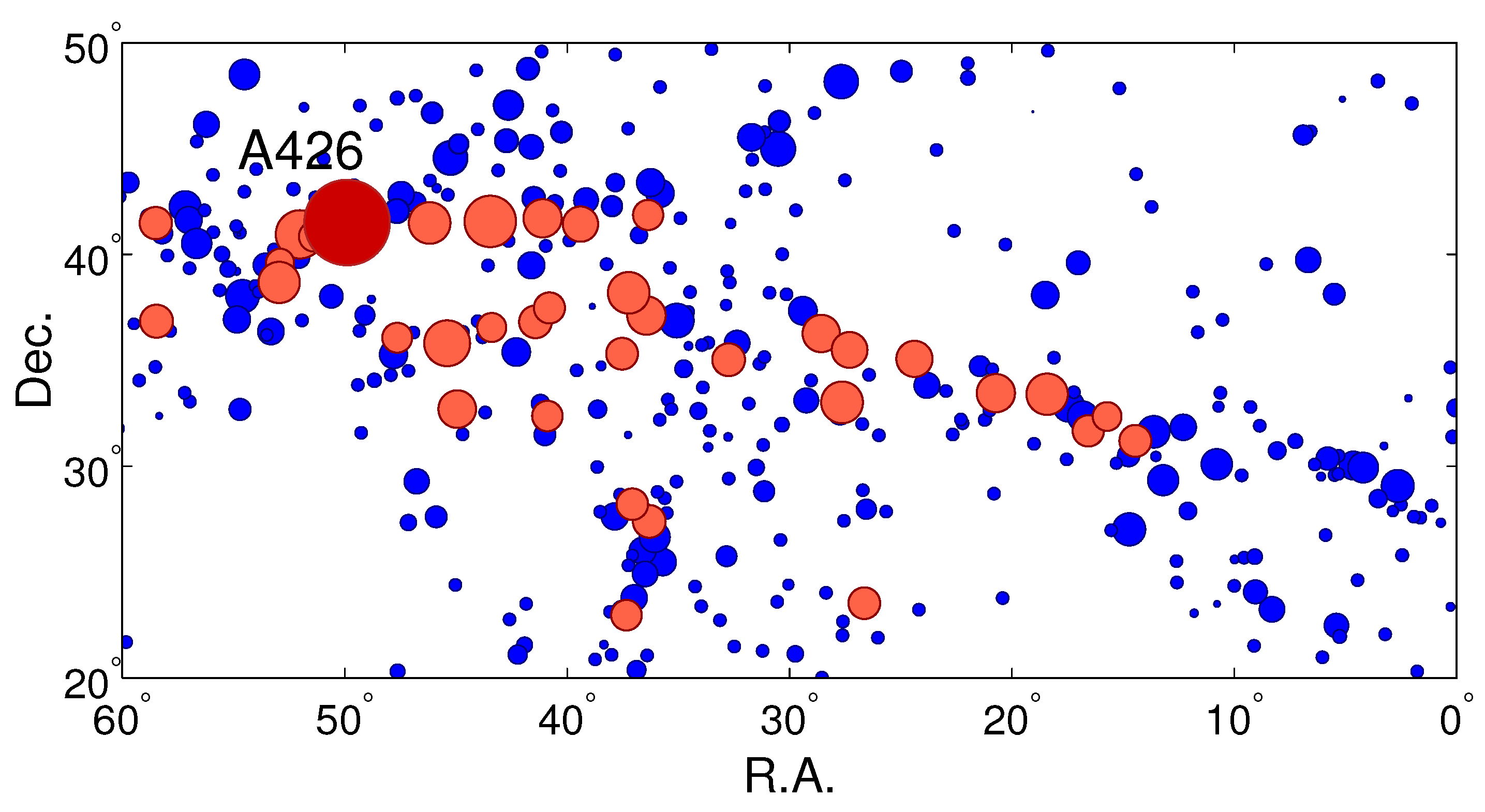
The presence of superclusters or clusters of clusters (second-order clusters) in the distribution of galaxy clusters was noticed already by Harlow Shapley in 1930 [37]. This structure is now known as the Shapley supercluster, and it is the richest supercluster in the nearby Universe [22]. Our own Local Group of galaxies is located on the outskirts of the Local or Virgo supercluster [38,39].

The discovery of the cosmic web initiated the question on the co-evolution of various elements of this pattern. One of the first superclusters studied in detail is the Perseus-Pisces supercluster, which is an elongated structure with the Perseus cluster as the richest galaxy cluster in it (Abell cluster A 426), and with other clusters and groups [1,40]. These studies revealed correlated alignments of the brightest cluster galaxies and galaxy groups and clusters along the supercluster axis, as well as the morphological segregation of galaxies in the supercluster. Early-type galaxies are located mostly in rich clusters and along the main body of the supercluster, while late-type galaxies lie in the outskirt regions—filaments and poor groups. These findings suggest that galaxies, groups, and superclusters evolve together [40].

This review provides a brief overview of the studies of galaxy superclusters. First, I present various definitions of superclusters, and supercluster catalogues determined based on different definitions and traced by different objects: galaxies, optical and X-ray clusters, and other objects. Next, I discuss supercluster morphology, mass determination, and structure, biasing problems (relative distribution of visible and dark matter in superclusters), fractal properties of superclusters, as well as the evolution of superclusters in the cosmic web. Then, I describe superclusters as a special environment in which galaxies and galaxy systems form and evolve. An important part of this review is dedicated to the largest systems in the cosmic web, supercluster complexes and planes, and to the almost regular pattern detected in the supercluster distribution, with the 120–140 $h^{-1}$ Mpc scale between rich superclusters. It has been suggested in the literature (e.g., [41]) that its origin is related to the Baryon Acoustic Oscillations. I will provide arguments against this interpretation and in support of the idea that the origin of this pattern is related to the dark matter perturbations in the very early Universe.

The extreme cases of observed objects usually provide the most stringent tests for theories; this motivates the need for a detailed understanding of various properties of the richest superclusters, their complexes, and planes. The properties of the high-density cores of superclusters have been proposed as a cosmological probe to test the standard Cold Dark Matter cosmological model with cosmological constant (ΛCDM) model [20,42]. Therefore, I discuss whether the presence of such planes and the regular pattern in the supercluster distribution is compatible with the standard ΛCDM model.

The early reviews of the first studies of superclusters were by Jan Oort [3] and by Neta Bahcall [43]. The story of the discovery and present studies of the dark matter, cosmic web, and superclusters can be found in the book “Dark matter and cosmic web story” by Jaan Einasto [44]. In this book, several chapters are dedicated to the study of superclusters in the cosmic web based on both simulations and observations. In my review, I focus on observational studies. In the further text, I use the term the nearby Universe for the redshift up to approximately $z\approx 0.1$. The local Universe refers to our close cosmic neighbourhood (mostly the Local, Virgo supercluster) with redshifts $z<0.02$.

2. Supercluster Definitions and Catalogues

Superclusters as the connected overdensity regions in the cosmic web have been defined on the basis of individual objects (typically optical or X-ray groups and/or clusters of galaxies) or luminosity-density or velocity fields, calculated using galaxy data [21,35,45,46,47,48,49,50]. One of the most common methods to detect superclusters in the distribution of groups and clusters of galaxies is the cluster analysis or the Friend-of-Friend (FoF; percolation) method [51,52]. In this method, systems (in our case—superclusters) are determined using a certain neighbourhood radius or linking length which is used to link galaxies, groups, or clusters together into systems. The neighbourhood of each galaxy group and/or cluster up to a certain neighbourhood radius or linking length is searched for neighbouring groups/clusters. Every group/cluster closer than the linking length to any other group or cluster in the system is considered a member of the system. If the linking length is small, then all clusters are isolated. With the increase in the linking length at first systems of clusters form at cluster pairs and triplets. With the further increase in linking length the number of systems and their richness (number of members) increases. At a certain linking length, individual systems start to join into huge systems, which may penetrate the whole volume under study, and a percolation occurs. Therefore, it is important to find a linking length which separates individual superclusters before percolation.

When using the luminosity-density field, the first step is to choose a proper smoothing length to calculate the luminosity-density field in order to detect superclusters. Next step is to choose the density level (usually in the units of the mean luminosity-density of the sample) to define superclusters. For example, ref. [53] determined the luminosity-density field using the Sloan Digital Sky Survey MAIN galaxy data and smoothing kernel based on the $B_3$ spline function with 8 $h^{-1}$ Mpc smoothing length to determine superclusters in the galaxy data (see also [54] for kernel definitions). In this review, the global luminosity-density determined in this way is denoted as $D8$.

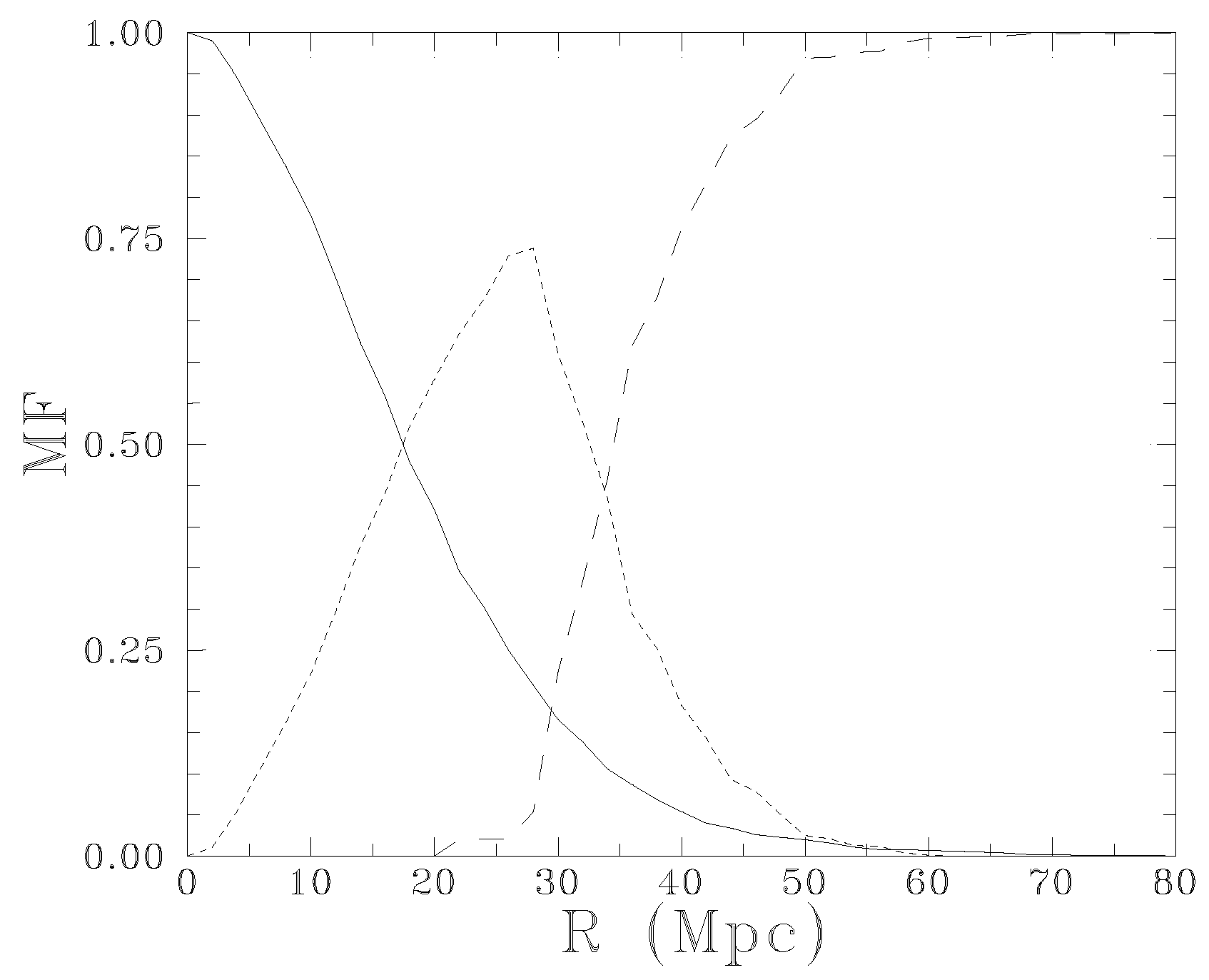
In the determination of superclusters, several criteria have been used to select the linking length or density level. Widely, these can be divided into three classes. First, superclusters have been defined as connected systems with linking length or density threshold before percolation, having, for example, the maximum number of superclusters in the sample. I illustrate this in Figure 2, which shows fractions of clusters in superclusters of different richness (multiplicity function $MF$) versus the neighbourhood radius (linking length) R for rich Abell clusters [55]. This figure shows that at small linking lengths all clusters are isolated. With increasing neighbourhood radius, clusters are gathered at first into systems of intermediate richness (with the number of clusters in superclusters or supercluster richness $2\le N_{CL}\le 31$), and the fraction of single (isolated) clusters decreases. At larger radii, extremely large superclusters with multiplicity (number of clusters) $N_{CL}\ge 32$ start to form. By further increasing the neighbourhood radius, superclusters begin to merge into huge structures, and finally, all clusters percolate and form a single system penetrating the whole volume under study. Each linking length value divides objects under study into high-density populations (connected systems), and low-density populations (isolated objects).

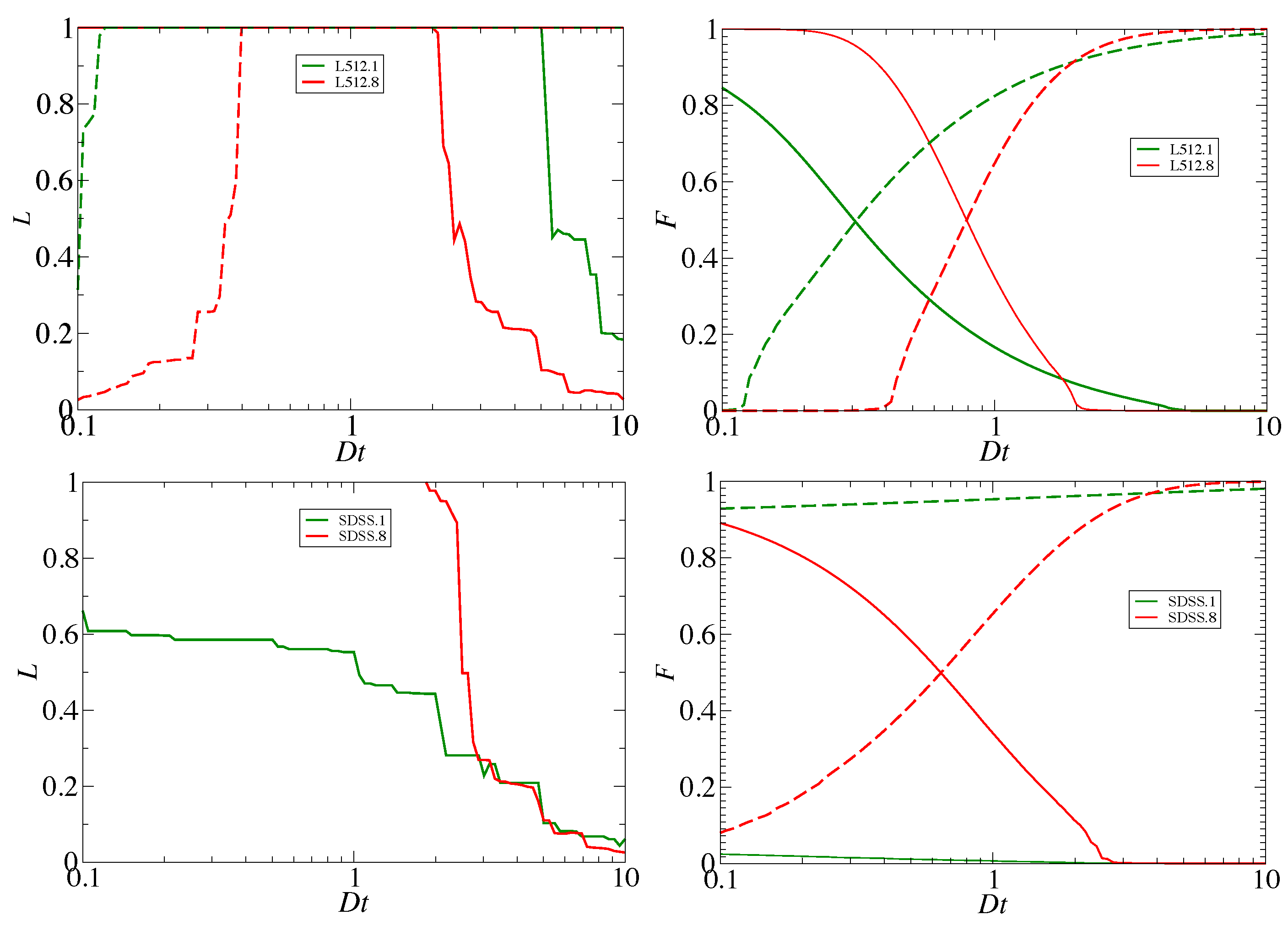
With percolation methods, it is possible to follow systems in over- and underdense regions, and to study their properties in detail, both from simulations and observations. Figure 3 shows the lengths L and filling factors F of systems as a function of threshold density $D_t$. The upper panels of Figure 3 show these properties for ΛCDM simulation with resolution $N_{\mathrm{grid}}=512$ and $N_{\mathrm{part}}=N_{\mathrm{grid}}^3$ particles, and with the cube size $L_0=512$ $h^{-1}$ Mpc. The lower panels show distributions for galaxy groups from the SDSS DR8. For superclusters (connected cosmic web elements determined with the smoothing length 8 $h^{-1}$ Mpc) the filling factor $F_{scl}=V_{scl}/V_{tot}$, where $V_{scl}$ denotes the volume occupied by superclusters, and $V_{tot}$ denotes the total volume of the sample. Filling factors of other cosmic web elements are defined in the same way. Cluster sizes are expressed in units of the sample size, $L_0$ (the effective side length in the case of the SDSS sample). Figure 3 shows the lengths and volumes of the largest clusters and voids (percolation functions) as functions of the threshold density, $D_t$.

As seen in this figure, with the increase in the threshold density $D_t$, the volume occupied by voids increases, and the volume covered by large systems decreases. At the threshold density $D_t\approx 5$ superclusters occupy approximately 1% of the total volume, as shown also by Cautun et al. [19]. At a very high threshold density, there exist only a few high-density regions—peaks of the density field as ordinary clusters of galaxies. These peaks are isolated from each other and cover a small volume (filling factor) in space. The percolation functions of superclusters for ΛCDM model and SDSS samples are rather similar.

One can also note that the percolation functions of voids for the ΛCDM model and SDSS samples are very different. At a very low threshold density, void sizes of the ΛCDM model are small; they form isolated bubbles inside the large over-density cluster, and the filling factor of the largest void is very small. Void bubbles are separated from each other by dark matter sheets. Some sheets have tunnels that permit the formation of some larger connected voids. With increasing threshold density, the role of tunnels rapidly increases, and tunnels join neighbouring voids. At a certain threshold density, the largest void is percolating, but still not filling a large fraction of the volume. The major difference between models and observations is the absence in SDSS samples of the fine structure of voids. At all smoothing lengths, SDSS voids are percolating, and the percolation threshold density is not defined. For small smoothing lengths, the percolating SDSS void is the only void.

In order to obtain superclusters as the largest still relatively isolated systems a neighbourhood radius should be smaller than the percolation radius. In [55], who used data on rich (Abell) clusters of galaxies to detect high-density regions—superclusters in the cluster distribution, the linking length 24 $h^{-1}$ Mpc was selected to define superclusters. This value is close to the Poisson radius of Abell clusters (radius of the sphere that contains one cluster, $R_P=3V/{\left(4\pi N\right)}^{1/3}$; where V is the volume of the sample, and N is the number of clusters in the sample. $R_{P\left(Abell\right)}=26$ $h^{-1}$ Mpc). At this linking length, the size of the largest supercluster is approximately 100–150 $h^{-1}$ Mpc. The first catalogues of superclusters of rich (Abell) clusters were compiled in this way [45,55,56,57,58]. Ref. [59] presented supercluster catalogues based on Abell clusters for several linking lengths. 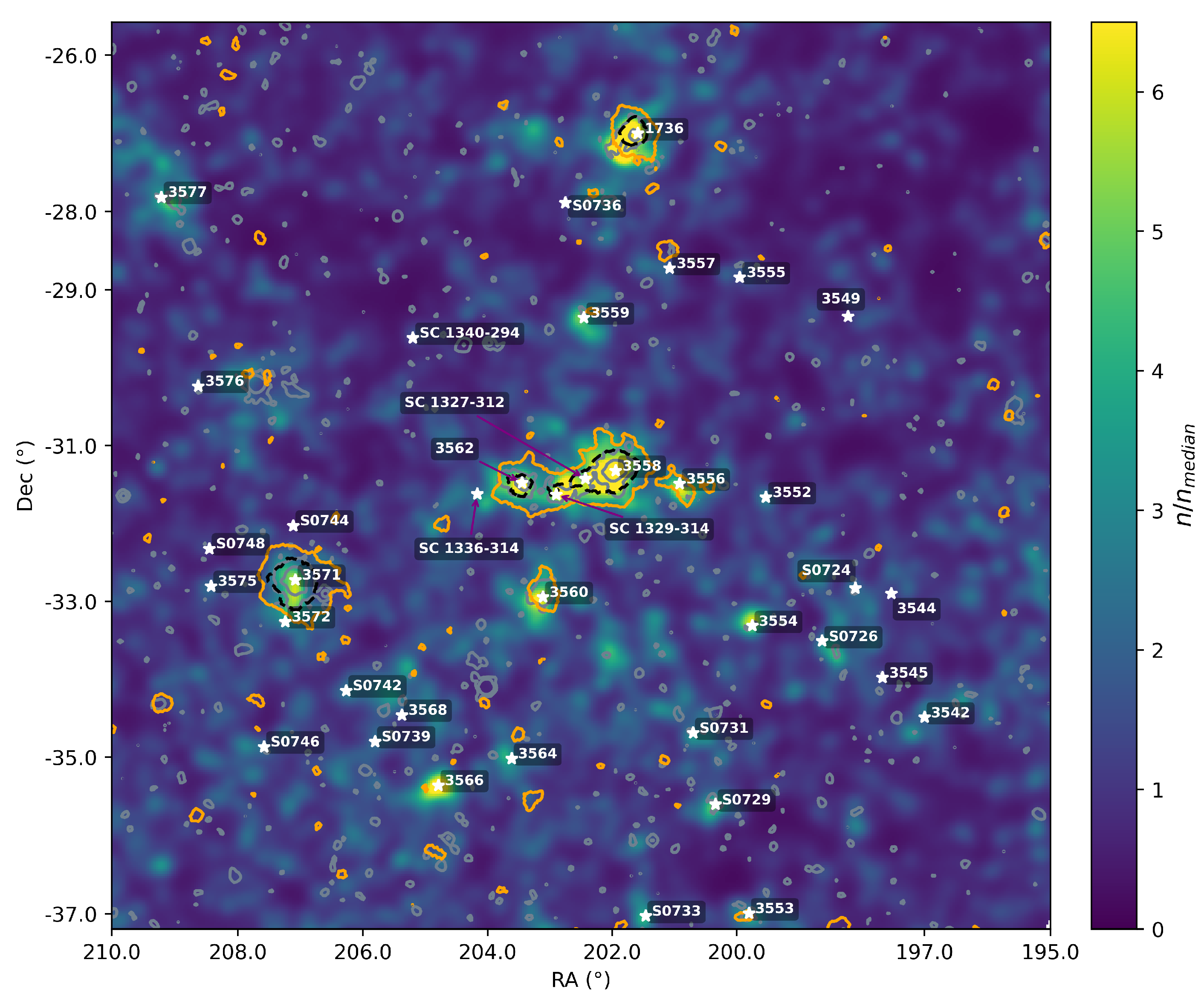Figure 4 shows the 3D distribution of Abell clusters and X-ray clusters in superclusters, based on data from [55]. This criterion was adopted in a recent catalogue of superclusters in redshift interval $0.05<z<0.42$ by [21].

Recently, a huge structure was detected, using data on X-ray clusters, and nicknamed the Quipu superstructure [60]. Cluster distribution in this structure is rather sparse, and these were linked together applying the Friend-of-Friend method with a large linking length. Therefore, the authors call it a “superstructure”, not a supercluster. The Quipu superstructure embeds several poor superclusters of Abell clusters, determined in the supercluster catalogue by [55], and a long filament that connects these superclusters. This is owing to the use of a larger linking length than in [55] to link clusters together into a system.

In the case of the luminosity-density field, the largest superclusters have approximately the same size, 100–150 $h^{-1}$ Mpc, when applying the threshold density level $D=5$ (in units of mean luminosity density) for the SDSS MAIN galaxy sample (see [53], and also [61] in the case of the Sloan Great Wall superclusters). Ref. [53] applied two different criteria for the density level to determine superclusters in the galaxy distribution, fixed and adaptive density levels. In catalogues with a fixed density level, the criteria for the density level can be searched for in the same way as in the case of linking length, i.e., the threshold density for the selection of superclusters should be selected so that it separates individual superclusters before percolation [53,62]. In addition, ref. [53] searched for each supercluster its individual characteristic density level at which a given supercluster is separated from the neighbouring superclusters. The resulting catalogue of superclusters is called adaptive catalogue. The choice of superclusters with fixed and adaptive density levels is illustrated in Figure 5 [53,63]. Typically, superclusters determined using these criteria are not gravitationally bound.

Another criterion is to search for the largest structures that will survive the cosmic expansion in an acceleratingly expanding Universe, and will remain bound also in the future (future collapsing superclusters or superstes–clusters) [48,50,64,65]. The first catalogue of superclusters, in which superclusters, determined using the luminosity-density field, which was applied to the SDSS MAIN galaxy data, were defined as structures that evolve into isolated, virialised structures in the future, was by [48]. Using this criterion, ref. [50] compiled a catalogue of superclusters in the redshift interval z = 0.5–0.9, based on the CAMIRA cluster sample constructed using the Subaru Hyper Suprime-Cam survey data. Although individual superclusters have also been detected at higher redshifts, this is at present the highest redshift interval at which supercluster catalogues have been determined.

Third, using the velocity field of galaxies, large-scale structures in the cosmic web—superclusters and voids—can be defined as regions in space where galaxy velocities are directed inward or outward under gravity. Galaxy superclusters are then defined as converging peculiar velocity field regions—regions, where, on average, peculiar velocities of galaxies are pointing towards the central high-density regions (basins of attraction or BoA) [35,49,66,67]. Superclusters as BoAs are volumes in space in which the velocities of galaxies and galaxy groups are, on average, pointing toward a central attractor. The central attractor of a supercluster may be the richest cluster in it. In the case of BoAs with large, typically elongated, central high-density regions that embed several rich clusters, the central attractor may lie on the axis or filament between clusters [35]. In the case of large BoAs, such as the Laniakea supercluster [49], only the central, highest-density parts may collapse in the future [65], while smaller BoA superclusters, such as, for example, the Arrowhead supercluster [66], may fully collapse during future evolution. As an example, Figure 6 presents the BoAs of superclusters in the nearby Universe from [35].

Opposite to BoAs, basins of repulsions (BoRs) are defined as regions in which peculiar velocities of galaxies are directed outwards [35]. Simulations show that the whole space can be divided between BoAs [68]. The borders of BoAs (watershed regions) are regions where the values of velocities are the lowest, or, in other words, these are surfaces where velocity flows (streamlines) diverge, pointing at one side to the one BoA central attractor, and pointing on the other side to the central attractor of another BoA. Conventional superclusters form central high-density regions of BoAs. In order to keep the traditional definition of superclusters as the high-density regions of the cosmic web, ref. [69] proposed to call low-density regions around superclusters in the BoAs supercluster cocoons. Simulations show velocity change at supercluster borders within BoAs [70].

Supercluster catalogues have also been generated using a different approach. For example, catalogues of cosmic voids have been generated using the watershed transform algorithm, and using the inversion of this algorithm, catalogues of overdensities or “superclusters” have been generated and made available [71].

As already mentioned, first supercluster catalogues were compiled using data on rich optical (Abell) clusters of galaxies. Refs. [45,55] also included X-ray clusters into their supercluster catalogues. They noted that X-ray clusters tend to be more strongly clustered than optical clusters. First catalogues based on X-ray clusters only based on ROSAT data were compiled by [64,72]. Ref. [73] compiled a catalogue of superclusters of X-ray-selected superclusters identified in the first SRG/eROSITA survey in the western Galactic hemisphere up to the redshift $z=0.8$. We also mention that the Friend-of-Friend method was applied to compile quasar system catalogues [74,75]. The web links of some supercluster catalogues mentioned in the text and available online are given in the Note [21,50,53,55,58,72,73,76]1.

3. Supercluster Morphology

Superclusters can be characterised using several properties, including their shapes, sizes, masses, and others. I start the description of superclusters from the analysis of their shapes and sizes. The overall shape of superclusters was analysed, approximating their shapes with triaxial ellipsoids [56,77]. These studies show that superclusters are elongated; even the most round superclusters have the ratio of their shortest and longest axis $a/c<0.5$. One interesting result of these studies is the finding that the most elongated, thin superclusters were also the most perpendicular to the line-of-sight [77]. The richest supercluster in the Sloan Great Wall complex, supercluster SCl 126, is among them [57]. The authors interpreted this as a signature of the large-scale peculiar motions toward the supercluster central axis, which makes the supercluster appear thinner than it actually is; an evidence of the so-called “Kaiser effect” [78].

A more detailed analysis of the shapes and inner structure of superclusters is provided by the application of Minkowski functionals (MFs) and so-called shapefinders calculated on the basis of MFs [54,79,80]. Four MFs characterise morphology and topology of isodensity contours, which embed superclusters. For a given surface, MFs are as follows:

• The first Minkowski functional $V_0$ is the enclosed volume V;
• The second Minkowski functional $V_1$ is proportional to the area of the surface S, namely,

  $$V_1={\displaystyle \frac{1}{6}}S;$$

  (1)
• The third Minkowski functional $V_2$ is proportional to the integrated mean curvature C,

  $$V_2={\displaystyle \frac{1}{3\pi }}C,C={\displaystyle \frac{1}{2}}{\int }_S\left({\displaystyle \frac{1}{R_1}}+{\displaystyle \frac{1}{R_2}}\right)dS,$$

  (2)

  where $R_1$ and $R_2$ are the two local principal radii of curvature.
• The fourth Minkowski functional $V_3$ is proportional to the integrated Gaussian curvature (or Euler characteristic) $\chi$,

  $$V_3={\displaystyle \frac{1}{2}}\chi ,\chi ={\displaystyle \frac{1}{2\pi }}{\int }_S\left({\displaystyle \frac{1}{R_1{R}_2}}\right)dS.$$

  (3)

The Euler characteristic is related to the genus, G

$$\begin{array}{ccc}\hfill G& =& 1-V_3.\hfill \end{array}$$

(4)

It gives the number of isolated clumps and voids in the enclosed volume:

$$V_3=N_{\mathrm{clumps}}+N_{\mathrm{bubbles}}-N_{\mathrm{tunnels}}.$$

(5)

On the basis of MFs, one can define the so-called shapefinders, which characterise the thickness, breadth, and length of an object: $H_1=3V/S$ (thickness), $H_2=S/C$ (breadth), and $H_3=C/4\pi$ (length). These quantities have dimensions of length, and these are normalised to give $H_i=R$ for a sphere of radius R. For a convex surface, the shapefinders $H_i$ follow the inequalities $H_1\le H_2\le H_3$. Prolate ellipsoids (pancakes) are characterised by $H_1<<H_2\approx H_3$, while oblate ellipsoids (filaments) are described by $H_1\approx H_2<<H_3$. Additionally, Sahni et al. [10] defined two dimensionless shapefinders $K_1$ (planarity) and $K_2$ (filamentarity): $K_1=(H_2-H_1)/(H_2+H_1)$ and $K_2=(H_3-H_2)/(H_3+H_2)$ [10,11]. The overall morphology of a supercluster can be described by the shapefinders $K1$ and $K2$, and their ratio, $K1/K2$ (the shape parameter).

MFs and Genus have been applied to study the topology of the whole cosmic web, and to compare it with the Gaussian random fields, as well as to study the properties of the Cosmic Microwave Background [7,81,82,83]. MFs and shapefinders have been used to study the integrated shapes of a set of superclusters from mock catalogues, simulating data from the Sloan Digital Sky Survey (SDSS), and also to analyse morphological properties of the cosmic web, from different cosmologies [84,85]. These studies showed that superclusters are elongated, dominantly with filament morphology, with length up to approximately 100 $h^{-1}$ Mpc. These studies also suggested that geometrical properties of the cosmic web are somewhat different in different cosmological models.

Ref. [54] applied MFs and shapefinders to characterise a small sample of individual richest superclusters in detail, defined using the 2degree Field (2dF) galaxy data and data from the Millennium simulations. As a next step in the studies of supercluster morphology, ref. [62] analysed the morphological properties of 36 individual rich superclusters determined by applying the SDSS galaxy data. Further, refs. [63,86] applied the same methodology to study the morphology of a large sample of superclusters from SDSS.

The studies of supercluster morphology showed that poor and very poor superclusters are mostly spherical. The richest superclusters are elongated; the limit between rich and poor superclusters is approximately at supercluster sizes $D_{scl}\approx 20$ $h^{-1}$ Mpc, luminosities $L_{scl}=4\times {10}^{12}{h}^{-2}{L}_{\odot }$, and masses approximately $M\approx 5\times {10}^{15}{M}_{\odot }$ [21,86,87]. 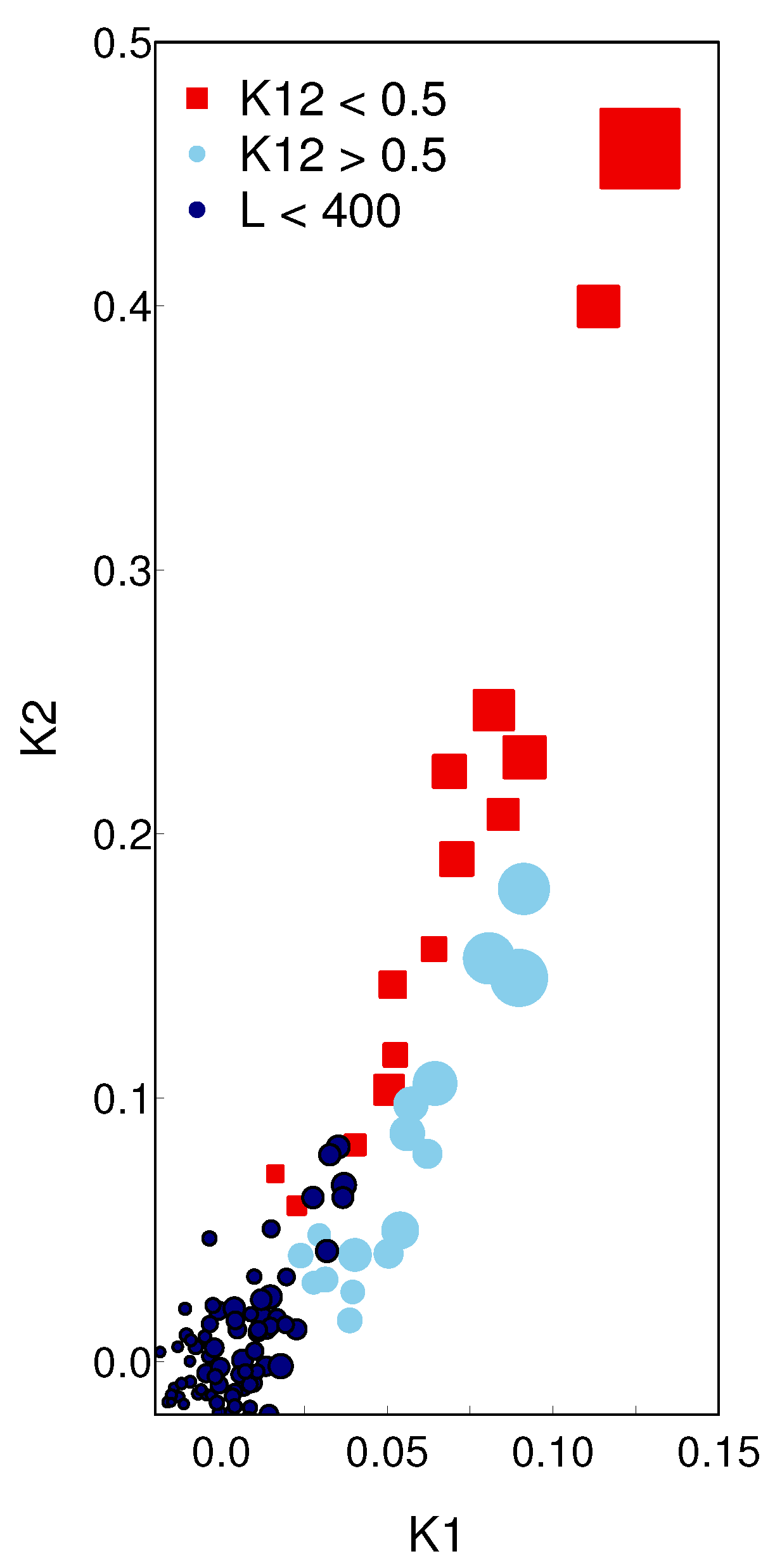According to their shape parameter $K12=K1/K2$, rich superclusters can be divided into less elongated and more elongated superclusters. This is shown in Figure 7, which presents the shapefinders $K1$-$K2$ plane for superclusters of different luminosity [87]. Rich, more elongated superclusters with $K12<0.5$ are richer and bigger than less elongated superclusters with $K12>0.5$. The sizes of the largest superclusters may exceed 150 $h^{-1}$ Mpc [21]. There are only a few rich superclusters with a quasi-spherical shape [88]. The fourth MF characterises the inner structure of superclusters (their clumpiness). Poor superclusters have typically small clumpiness, while rich superclusters with complicated inner structure have high clumpiness values [86,87].

The physical and morphological properties of superclusters are correlated: richer superclusters are more elongated, and they have higher clumpiness values than poor superclusters. This enables us to apply the Principal Component Analysis (PCA) to derive the scaling relations for superclusters and to determine the fundamental plane of superclusters [87]. This analysis showed that superclusters can be characterised with a small number of parameters, as their luminosity, which is strongly correlated with supercluster mass and size, and shape parameters (shapefinders and clumpiness). Correlation between physical and morphological parameters has been used to estimate supercluster masses (see Section 4 and [87,89]).

In the shapefinder’s space, superclusters form a curve called the morphological signature, characteristic to multibranching, elongated objects [54,62]. At high densities within superclusters, the morphological signature of superclusters changes rapidly [54,62]. This property, together with the analysis of the density distribution in superclusters have been used to define high-density cores of superclusters—high-density regions which may embed several rich galaxy clusters (Section 6 and [90]). If superclusters have been defined as future collapsing systems, then such superclusters may correspond to high-density cores of superclusters defined using linking length or density level near percolation [91].

One interesting result of the studies of supercluster morphology is that, according to their inner structure, superclusters can be divided into filament-type and spider-type superclusters [54,62]. Filament- and multibranching filament-type superclusters have rather simple inner structure with only a few galaxy filaments connecting galaxy clusters in the supercluster. The richest supercluster in the Sloan Great Wall is an example of this type of supercluster. In spider- and multispider-type superclusters, clusters are connected by many filaments. The second richest supercluster in the Sloan Great Wall is of the multispider type [62]. Superclusters with a similar overall shape may have different fine structure [87].

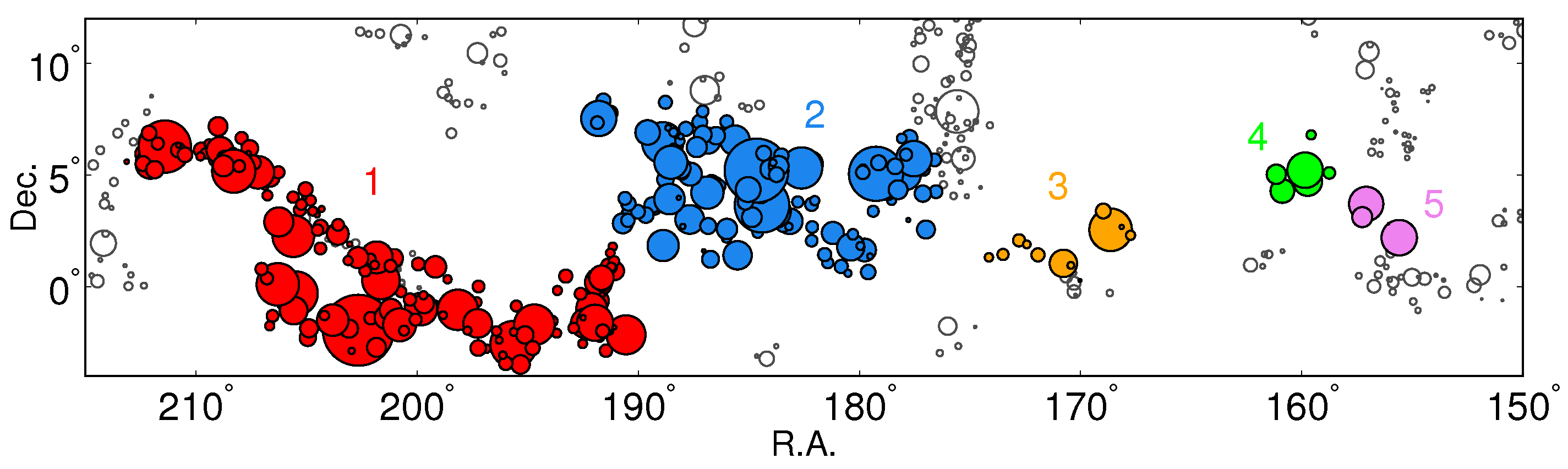
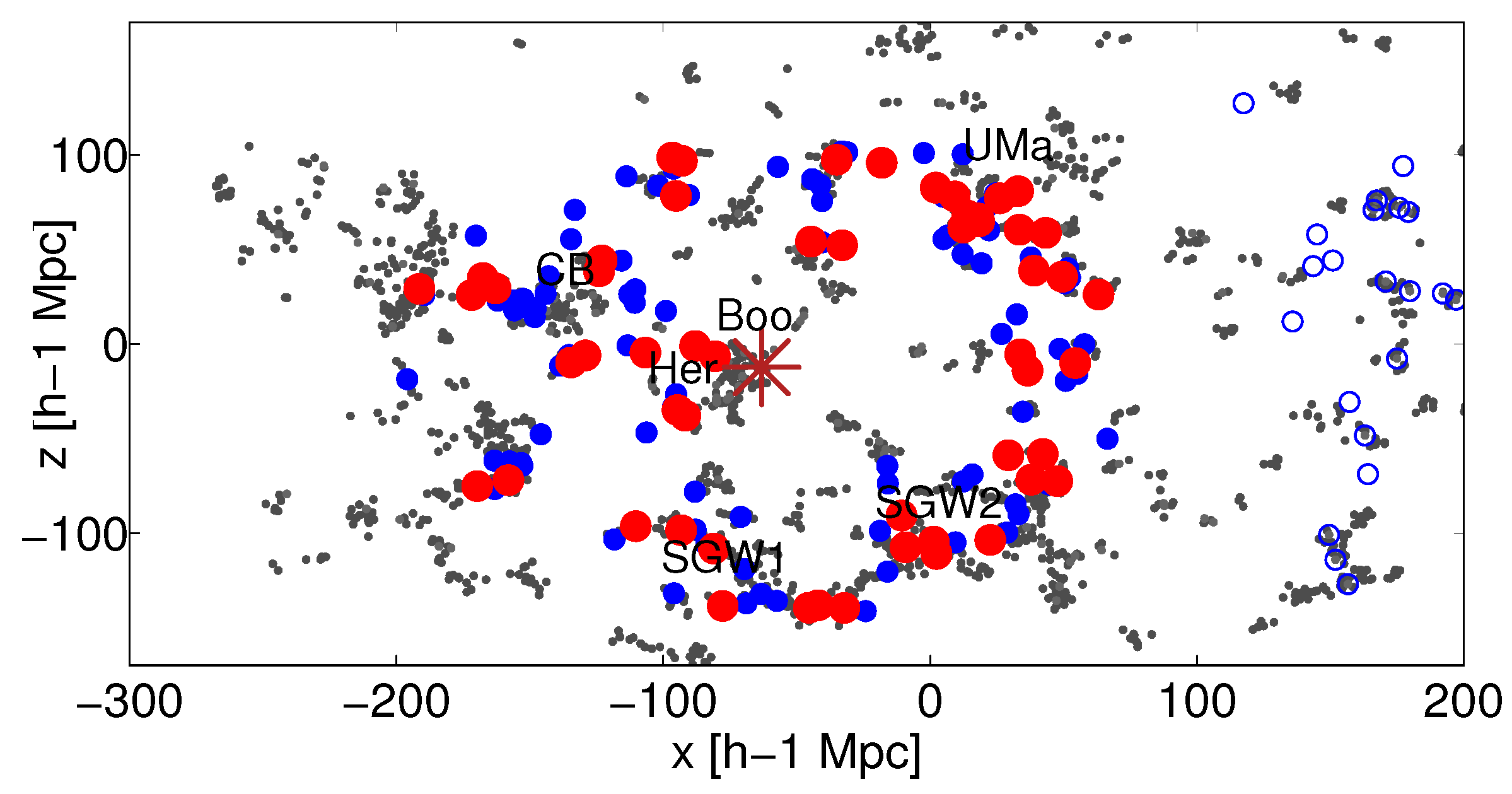
We can ask the question whether the supercluster morphology and its large-scale environment (location in the cosmic web) are related. This question was addressed in [62]. They analysed the location of superclusters, for which they determined inner morphology, in the cosmic web. Most interestingly, this analysis showed that rich superclusters at redshifts approximately z = 0.07–0.08 form three chains of rich superclusters, separated by voids. At the intersection of these chains lies the Corona Borealis supercluster, which is of multispider type. One chain is formed by superclusters in the Sloan Great Wall, which are of multibranching filament type and multispider type. Superclusters in other chains are not as rich as the Sloan Great Wall superclusters. These are the multispider-type Bootes supercluster and the filament-type Ursa Major supercluster, among others. Ref. [62] concluded that, as the number of superclusters in their analysis was relatively small, their study did not give a definite answer to the question whether there is a connection between the morphology of superclusters and their large-scale distribution.

The supercluster morphology can be used as a test for cosmological models [54,79]. Ref. [92] demonstrated that during the future evolution, the structures in the cosmic web will sharpen. This affects the shape of superclusters, which will become more compact and round [93]. Ref. [54] showed that the morphology of observed superclusters is not yet fully recovered among simulated superclusters.

4. Supercluster Masses

One of the most important characteristics of superclusters is their mass. Superclusters represent overdensity regions of the cosmic web, where most of the mass comes from the dark matter. Observationally, this mass is traced by visible structures such as galaxies, groups, and clusters, connected by filaments, and intercluster gas. This introduces a bias in supercluster masses and the estimation of supercluster masses may be challenging. Therefore, this section presents the estimations of supercluster masses based on observations, and the next section (Section 5) is dedicated to the discussion of biases in the supercluster masses due to the dark matter content of superclusters, and how well this is traced by visible structures in superclusters.

Superclusters are high-density regions in the cosmic web, which embed galaxy groups and clusters, as well as single galaxies, which do not belong to any detectable group (within observational limitations of a particular observational data used to determine superclusters), and gas. Galaxy clusters in superclusters are connected by filaments of poor groups, single galaxies, and gas, and the mass in filaments is taken into account when considering masses of these structures. Therefore, the mass of superclusters is the sum of the masses of these elements:

$$M_{scl}=\sum M_{\mathrm{g}\mathrm{r},\mathrm{c}\mathrm{l}}+\sum M_{\mathrm{single}}+M_{\mathrm{gas}}+M_{\mathrm{D}\mathrm{M}\left(\mathrm{additional}\right)},$$

(6)

where $\sum M_{\mathrm{g}\mathrm{r},\mathrm{c}\mathrm{l}}$ denotes the total mass in groups and clusters in a supercluster, $\sum M_{\mathrm{single}}$ is the sum of masses of single galaxies, and $M_{\mathrm{gas}}$ represents the total mass of gas in a supercluster. With $M_{\mathrm{DM}\left(\mathrm{additional}\right)}$, we denote possible additional dark matter in superclusters, which is not traced by visible structures in a supercluster—galaxies, groups, clusters, and gas. This will be discussed in the next section.

In these studies, which define superclusters on the basis of group and cluster data, one common method to find supercluster masses is the calculation of the sum of the masses of their member groups and clusters. The catalogues of superclusters by [21,73] provide masses of superclusters found in this way.

The supercluster catalogue by [21] is based on galaxy groups from [94]. This catalogue presents masses of groups as found in [95], $M_{500}$, which by [21] are converted to virial mass $M_{200}$ as follows: $M_{200}=\frac{200}{500}{\left(\frac{R_{200}}{R_{500}}\right)}^3{M}_{500}$ (here mass $M_{500}$ and radius $R_{500}$, and mass $M_{200}$ and radius $R_{200}$ denote mass and radius, within which the mean density is 500 and 200 times the critical density of the universe). For an NFW profile with a concentration parameter of about 4–8, $R_{500}\approx 0.65\times R_{200}$ [96]. To obtain the bound halo mass for groups (including dark matter in groups), this mass is scaled: $M_{bound}~2.2\times M_{200}$. The sum of the bound masses of a group in a supercluster gives the mass of a supercluster. Therefore, in these calculations, the mass of groups takes into account both masses of galaxies and masses of dark matter haloes. These masses may still be underestimated as the mass in very poor groups and single galaxies, and the gas mass is not taken into account.

The masses of superclusters in [73], based on eROSITA clusters, are determined as a sum of virial masses of clusters, $M_{200}$, which are calculated using masses $M_{500}$ of its member clusters, $M_{200}\approx 1.46\times M_{500}$ as described in detail in [73]. To calculate total supercluster masses, the authors use a relation based on simulations by [97], $M_{\mathrm{cl}}=0.39\times M_{scl}$, where $M_{cl}$ is the sum of virial masses ($M_{200}$) of clusters within a supercluster.

The masses of groups have been used to calculate the supercluster masses in several studies [50,88,91,98]. When calculating the mass of superclusters using group and cluster masses, one source of uncertainty is related to how precisely the masses of groups and clusters have been found. Ref. [98] used several mass estimations for galaxy groups. Namely, they used virial masses of groups calculated by [99] ($M_{200}$), and for poor groups for which virial masses are poorly defined, they used the relation between the stellar mass of the brightest group galaxies and the halo mass [100]. Another possibility is to use for poor groups the median mass of these groups, multiplied by the number of these groups in a supercluster. Ref. [98] compared these two methods and found a good agreement in mass estimation. The mass of single galaxies has been taken into account using several different approaches. Single galaxies may be the brightest galaxies of faint groups, for which other group members are too faint to be included in flux-limited redshift surveys. The mass of such groups can be calculated using the galaxy mass–halo mass relation [100] or by using the median mass of very poor groups as a proxy of their mass. These mass estimated agree well [91,98].

Approximately 10% of supercluster mass comes from intercluster gas [101,102]. Therefore, supercluster masses can be calculated by summing the masses of groups and clusters, and adding the estimated gas mass in superclusters [20,91,102]. In total, ref. [20] estimated that the contribution of rich groups and clusters to the total mass of superclusters is approximately 75% of the total mass, and 10% and 5% of the mass comes from poor groups and single galaxies, correspondingly. The remaining mass comes from the gas in the supercluster. These studies have shown that while the masses of poor superclusters may be of the order of a rich galaxy cluster, $M\approx 1\times {10}^{14}{M}_{\odot }$, the masses of the richest superclusters may be of the order of $M\approx 1\times {10}^{16}{M}_{\odot }$ or even higher.

From observations, one can determine the luminosity of groups and clusters in a supercluster. Also, for superclusters determined using the luminosity-density field, the total luminosity of superclusters can be calculated. Therefore, the mass of a supercluster can be calculated using the luminosity of a supercluster, and the mass-to-light ratio $M/L$. In this way the mass in dark matter is also taken into account. However, at first, we should know the characteristic mass-to-light ratio for superclusters, its possible dependence on supercluster richness, and perhaps on other properties of superclusters. These problems were discussed in [91,98]. Ref. [103] showed that the mass-to-light ratio of galaxy groups is $M/L\approx 400$, and this ratio is higher for poorer groups. They also found that $M/L$ of groups does not depend on the global environment of groups. However, ref. [98] showed that $M/L$ of groups is higher in supercluster outskirt regions. They attributed this to the fact that these regions are mostly populated by poor groups while rich clusters with lower $M/L$ values preferentially lie in the high-density cores of superclusters. Therefore, while poor superclusters have mass-to-light ratio $M/L\approx 400$, rich superclusters have lower $M/L$ values, $M/L\approx$ 250–300 [88,91,98]. Ref. [88] speculated that perhaps poor superclusters embed a higher fraction of dark matter than rich superclusters. Comparison of the masses of superclusters calculated from the masses of member groups, and using the total luminosity of groups and these $M/L$ values showed a good agreement [89,91,98].

As described in Section 3, using PCA, one can derive the scaling relations for superclusters that combine morphological and physical parameters of superclusters to obtain supercluster luminosities. This provides an independent method to calculate supercluster masses using the luminosity found with scaling relations, and $M/L$ ratios obtained in previous studies. Ref. [89] applied this method to estimate the masses of the BOSS Great Wall superclusters. Masses, calculated in this way, agreed well with the masses of these superclusters found using luminosities and stellar masses of galaxies.

Supercluster masses have also been estimated using data on supercluster volumes and their overdensity. In this method, the mass of superclusters is found using data on the volume of a supercluster, and its overdensity compared to the mean cosmic density [72,104]. Under the assumption that the mass density correlates with luminosity density, ref. [104] divided the volume of superclusters into cells, and calculated the mass of superclusters as the sum of the mass of each grid cell as $M={\rho }_{c}DV$, where D is the luminosity density in a cell in the units of the mean densities, $V=$ is the volume of the cell, and ${\rho }_c$ is the critical density of the Universe.

One source of the difference in supercluster masses from different studies can be attributed to the difference in the supercluster definition. For example, while [50] define superclusters as future collapsing systems, ref. [21] define superclusters as relatively isolated high-density regions (superclusters with high-density cores surrounded by lower-density outskirts regions). As a consequence, the highest-mass superclusters in these studies have masses of the order of $M\approx 1\times {10}^{15}{h}^{-1}{M}_{\odot }$ in [50] and $M\approx 2.5\times {10}^{16}{M}_{\odot }$ in [21].

5. Superclusters as Biased Traces of the Mass in the Cosmic Web

Biases in mass estimations related to the differences between observed mass and total mass are related to the more general problem of how well the visible matter traces the distribution of dark matter in the Universe. The problem of the relative distribution of visible and dark matter is usually referred to as a biasing problem, introduced by [78]. Namely, galaxy clusters, especially clusters in superclusters represent high-density peaks in the cosmic density field, thus being biased tracers of this field [43,105]. However, the emphasis in studies of the biasing problem is mostly on the study of the distribution of matter in low-density regions of the cosmic web—voids [106]. For example, using N-body simulations, the hierarchical nature of the cosmic web was discussed by [107]. The authors defined cosmic web elements as nodes (galaxy groups and clusters), filaments, walls, and voids, and studied the properties of galaxies in various environments. This study showed, among other results, that in high-density environments (in our context—in superclusters, although this was not specifically addressed in this study) the distribution of low-mass haloes follows the distribution of high-mass haloes.

Next, I focus on the relative distribution of visible and dark matter in superclusters. First of all, the total mass of superclusters can be estimated using simulations. For example, if the mass of superclusters is determined using masses of galaxy groups and clusters embedded in superclusters, then the total mass of superclusters, obtained in this way, may be underestimated if the mass in poor groups and single galaxies, as well as the mass of gas in superclusters is not taken into account [97]. They estimated that depending on the mass (richness) limit of groups and clusters used to determine superclusters, the bias factor introduced in mass estimation may be of the order of 1.6–1.8.

The comparison of the mass of SCl A2142 based on group masses with these predictions from simulations showed that the bias value was slightly lower—1.5 [98]. In this study, the mass in poor groups and single galaxies, as well as the mass of gas in the supercluster, were taken into account, and this may be the reason for the lower bias value.

Review paper [43] provides extensive discussion on the masses and mass-to-light ratios of galaxy clusters. In particular, the author addresses the question of possible extra dark matter in clusters, in addition to the dark matter related to dark matter haloes of galaxies in clusters. Based on masses and luminosity of clusters, it is shown that typical mass-to-light ratios of galaxy clusters are $M/L\approx$ 200–300, and there is no additional dark matter. The same conclusion is made for superclusters.

Observational proof of the presence of possible additional dark matter in superclusters may come from the studies of supercluster masses from lensing surveys. One example is the analysis of the distribution of mass and light in the Abell 901/902 supercluster at redshift $z=0.165$ [108]. This supercluster embeds two galaxy clusters connected by a filament of galaxy groups. The distribution of dark matter in the A901/902 supercluster was analysed using a weak lensing analysis. This analysis showed that visible galaxies and clusters in the supercluster trace well the distribution of dark matter, with no need for extra dark matter.

Also, in the study of the King Ghidorah supercluster, the question of relative distribution of stellar mass and dark matter was addressed [109]. The distribution of dark matter was determined using weak lensing signals. The distribution of stellar mass was found using the stellar mass in massive galaxies in the supercluster. The comparison of these two maps revealed strong correlation between these two. The authors concluded that visible mass follows the distribution of dark matter. This conclusion was supported by the analysis of mock catalogues.

These examples lead to the same conclusion: up until now, there is no strong evidence of the presence of extra dark matter in superclusters, which may strongly bias the estimation of supercluster masses.

6. Supercluster Structure—High-Density Cores and Outskirts

When analysing the density distribution in superclusters of various richness, determined using the luminosity-density field of galaxies, refs. [47,90] noticed important differences between rich and poor superclusters. While rich superclusters had high-density central parts or cores, in poor superclusters, even maximal densities were lower, typical of the outskirt regions of rich superclusters. The division between rich and poor superclusters was approximately the same, as later found using PCA, as described in Section 3. At the border of high-density cores (hereafter HDCs), the morphology of superclusters changes [54,62]. The analysis of the structure of superclusters in the Sloan Great Wall with normal mixture modelling also showed that these superclusters have several high-density cores [91]. Ref. [42] called such regions nucleation regions in superclusters, and they presented a list of such regions in nearby superclusters. Cores in their study were defined as large gravitationally bound regions in superclusters, which may host two or more clusters and groups, and where the density of matter is high enough to survive cosmic expansion and collapse in the future.

Typically, HDCs of superclusters embed one or several rich clusters, connected by filaments of poor groups and galaxies. The overall masses of HDCs are of the order of $M\approx$ 0.5–$5\times {10}^{15}{M}_{\odot }$, i.e., of the same order as the masses of superclusters determined using the future collapse criterion [42,110]. Ref. [88] noted that the most spherical superclusters from the adaptive supercluster catalogue by [53] correspond to the high-density cores of superclusters from the catalogue, in which superclusters were defined using fixed density threshold.

The detailed analysis of the mass distribution in the HDCs of superclusters reveals a small density minimum around the central clusters of HDCs. Refs. [20,111] showed that this minimum marks the borders of the region of influence around clusters. Within the regions of influence, all galaxies, groups, and filaments are falling into clusters. The radius of the spheres of influence has been called depletion radius in [112]. The density contrast at the borders of the regions of influence is of the order $\Delta {\rho }_{inf}$ = 30–40. Using the spherical collapse model, ref. [20] showed that the regions of influence were at turnaround and started to collapse at redshifts $z\approx$ 0.3–0.4.

Another characteristic density contrast in the matter distribution around clusters is the turnaround density contrast. In the ΛCDM Universe with non-zero cosmological constant $\Delta {\rho }_{turn}=13.1$ [65,113] (and references therein). Typical radii of turnaround regions in the HDCs of superclusters are of the order of $R_{turn}\approx$ 5–10 $h^{-1}$ Mpc. However, in the richest superclusters in the nearby Universe, the Shapley and the Corona Borealis superclusters, the radius of the turnaround region is even larger, $R_{turn}\approx$ 12–13 $h^{-1}$ Mpc.

7. Fractal Properties of Superclusters

The cosmic web can be described as a multifractal pattern, with different fractal dimensions at different scales [6,8,114,115,116]. One method to find the fractal dimension of the cosmic web is provided by the correlation analysis [6]. Many studies have shown that the slope of the correlation function changes at a certain scale, which shows the crossover from correlations in galaxy groups and clusters to the correlations between galaxies in the filamentary pattern connecting clusters; in other words, from one fractal regime to another, with a different fractal dimension which also means a crossover from a non-linear dynamical regime at small scales to linear dynamical regime at large scales [6,43,116,117]. Fractal dimensions can be calculated from the slope of the correlation function $\xi \left(r\right)$, which give us the so-called structure function, $g\left(r\right)=1+\xi \left(r\right)$, and the fractal dimension $D\left(r\right)=3+dlogg\left(r\right)/dlogr$, where r denotes distance between galaxy pairs.

At scales up to $r\approx$ 3–10 $h^{-1}$ Mpc (depending on the sample under study) $D\approx$ 1–1.5, telling that the structures are more one-dimensional. At larger scales $D\approx$ 2–3, showing the crossover to more two-dimensional structures [6,117]. Ref. [57] showed that fractal dimension of clusters in very rich superclusters has a value $D\approx 1.4$, and fractal dimension determined using all clusters is $D\approx 2$. Among individual superclusters, the fractal properties of the Saraswati supercluster were analysed by [118]. This study applied the so-called box-counting method to estimate the fractal dimension of the supercluster. They found that $D\approx$ 1.7–2, showing that the Saraswati supercluster is essentially a planar structure.

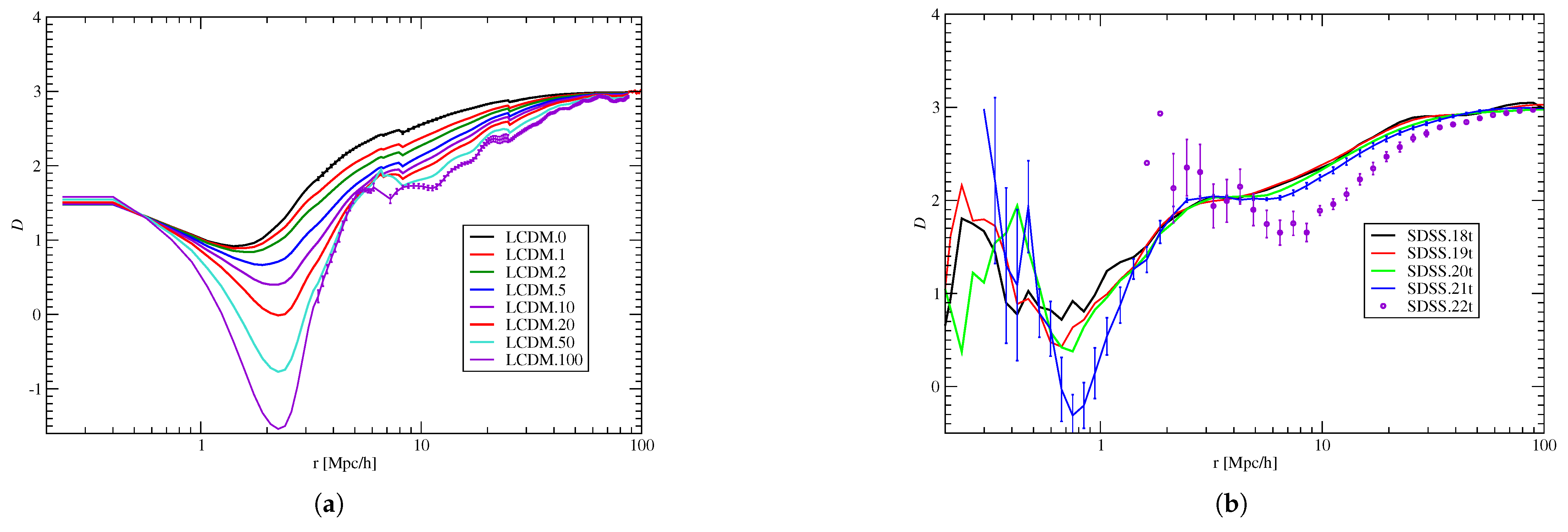
The fractal dimension at different scales is shown in Figure 8, which presents the fractal dimensions on the left panel, calculated using particle data in the $\Lambda$$CDM$ model, calculated in a box with size 512 $h^{-1}$ Mpc with various particle density limits, as shown in the figure. The right panel of Figure 8 shows the fractal dimension of SDSS galaxy samples with various luminosity limits.

At separations $r\le 3$ $h^{-1}$ Mpc, correlation and fractal functions of galaxies reflect the galaxy or dark matter distribution in groups and clusters within halos. The fractal dimension changes within limits $-1\le D\le 1.5$. At larger distances, the fractal dimension gradually increases from 1 to 3 at the largest distance studied, 100 $h^{-1}$ Mpc. Therefore, the fractal dimension is not constant, as in simple fractal models.

In the small separation region, the spatial correlation function of the LCDM model samples is proportional to the density of matter, and measures the density profile inside the DM halos. The fractal dimension function of the LCDM samples depends on the particle density limit ${\rho }_0$, but still, the crossover from one fractal regime to another occurs approximately at distances r = 5–6 $h^{-1}$ Mpc. The fractal dimension of the SDSS sample behaves similarly, but note that the change in fractal dimension of the brightest galaxies with $M<-22$ occurs at larger distances than in the case of lower luminosity galaxies. The brightest galaxies in the sample are mostly the brightest galaxies in clusters in superclusters, and the change in the fractal dimension is related to the crossover from clusters in the supercluster core regions to outskirts. As shown above, at high-density cores of rich superclusters, the morphological signature of superclusters also changes. The possible connection of these two changes may be one direction in the future studies of superclusters.

At still larger scales, up to over 100 $h^{-1}$ Mpc the correlation function of all galaxies is featureless, except, of course, the famous Baryon Acoustic Oscillation (BAO) feature [119]. Therefore, at large scales, even in samples with very large structures, the fractal dimension does not change [120]. This is often interpreted as a signature of the homogeneity of the galaxy distribution at scales larger than this limit, 100 $h^{-1}$ Mpc. However, this interpretation has been questioned [121], and it is not in agreement with the presence of very large underdense regions (voids) and superclusters, with sizes over 100 $h^{-1}$ Mpc, as, for example, superclusters in the Sloan Great Wall and in the BOSS Great Wall, the Bootes void, the Eridanus supervoid, associated with the CMB Cold Spot, and other voids [23,24,25,26,53,122]. Very large voids detected in the distribution of luminous galaxies or galaxy groups/clusters are not empty, but filled with the hierarchical, filamentary web of fainter galaxies, in which the sizes of smaller voids between these structures depend on the luminosity limit of galaxies used to determine these voids [107,123,124,125,126].

The correlation function may be similar for samples of very different geometry, as it does not contain phase information, as shown in detail in [127]. As discussed in [116,117,120,121], the two-point correlation function is self-averaging up to approximately 30 $h^{-1}$ Mpc, and at these scales and higher, it is characterised by a fractal dimension $D\approx$ 2–3, and this cannot be interpreted as a crossover to homogeneity [121]. This conclusion agrees with observational evidence on the lack of homogeneity in the distribution of superclusters and voids at scales at least up to 300 $h^{-1}$ Mpc in the nearby universe [24,36,75,120,128].

As mentioned, underdense regions (voids) in the cosmic web are of a hierarchical nature. Voids determined using luminous galaxies may be divided into smaller voids by filaments of fainter galaxies, but this does not change the fractal dimension of the samples under study. For example, in Figure 8 (right panel), the fractal dimension of SDSS galaxy samples is the same for galaxy samples with a wide range of magnitude limits, M = −18–−21, while the mean diameters of voids delineated by galaxies with $M<-20$ are almost twice as large as mean diameters of voids delineated by fainter galaxies, $M<-18.8$, 23 versus 13 $h^{-1}$ Mpc [124] (see also [107]). These void size values agree well with the determinations of void sizes based on SDSS data and galaxy magnitude limit $M_r<-20$ [129], who found that median effective void sizes are in the range of 15–19 $h^{-1}$ Mpc, based on different void finding algorithms. The sizes of voids depend also on the sample size [71].

8. Supercluster Evolution in the Cosmic Web

The formation and evolution of the cosmic web under the gravity of dark matter and the acceleration from dark energy can only be followed using simulations [130]. Simulations show that the formation of the present-day structures in the cosmic web began with the growth of tiny density perturbations in the very early Universe under gravity [2,131,132]. During evolution, positive dark matter density perturbations grow by merging and infall of surrounding proto-structures, and as a result, the present-day cosmic web consists of structures of various properties and characteristic scales, from dwarf galaxies to rich clusters, filaments, and voids between them. Superclusters, which host rich galaxy clusters, connected by filaments of poor groups and single galaxies, form where positive sections of medium- and large-scale dark matter density perturbations combine. Dark matter perturbations of a scale of about 100 $h^{-1}$ Mpc give rise to the largest superclusters. An analysis of the simulations of the future evolution of the cosmic web and various structures in it in the $\Lambda$$CDM$ Universe with a non-zero cosmological constant shows that in the distant future, structures in the cosmic web will be of higher contrast, superclusters will become more spherical and compact, and voids will become emptier [92,93].

The whole cosmic web can be divided between the BoAs (superclusters with cocoons) (see Section 2). Superclusters fill only a small fraction of BoA space, about 1% at the present epoch. To understand the evolution of various populations in the cosmic web, their evolution should be analysed simultaneously. Various populations in the dark matter density field can be defined, using different smoothing lengths. The evolution of cluster-size and supercluster-size populations in the density field in a redshift interval z = 30–0 was followed by [69]. Figure 9 shows four snapshots from the simulations, which were performed in the box size 256 $h^{-1}$ Mpc with ${512}^3$ particles using the GADGET code. Figure 9 presents snapshots at redshifts $z=30$, $z=10$, $z=3,$ and $z=0$, in the upper panel without smoothing, and in the lower panel, with a smoothing length 8 $h^{-1}$ Mpc, which has also been used to determine observed superclusters using the density field method (Section 2). High-density regions in the lower panel represent superclusters, and low-density regions represent voids or supercluster cocoons between superclusters. The figure shows that the supercluster locations and the BoA borders do not change much during the evolution of the cosmic web, and an essential evolution of various populations in BoAs occurs at smaller scales within superclusters and their cocoons. Volumes in comoving coordinates and masses of BoAs remain approximately constant during evolution, whereas masses of superclusters increase during evolution by a factor of about 3 by the infall of surrounding matter inside BoAs to superclusters. The most massive ΛCDM superclusters have, at the present epoch, masses $M_{scl}\approx {10}^{16}M\odot$, and the most massive supercluster basins have at all epochs masses $M_{basin}\approx 2\times {10}^{17}{M}_{\odot }$. The exchange of matter between neighbouring BoAs is minimal, because the velocity flows within BoAs is directed inwards.

Using observational data, the future evolution of individual high-density cores of superclusters, and/or the evolution of full superclusters, as well as the dynamical state of superclusters, are most commonly analysed using the spherical collapse model [5]. This model follows the evolution of a spherical shells, determined by the dark matter mass in its interior. The evolution of spherical shells can be characterised by several important epochs. To analyse the evolution of superclusters, important epochs are the turnaround and the future collapse [65]. The spherical overdensity within a radius R can be described as $\Delta \rho \equiv \rho /{\rho }_m$, where $\rho$ is the matter density in the volume, and ${\rho }_m$ is the mean matter density. This overdensity expands together with the Universe, but because of its internal gravitation, it expands more slowly than the surrounding background.

At a certain epoch, this (slower) expansion may stop, and the region starts to contract. This epoch is called a turnaround. Depending on the value of the density contrast $\Delta \rho$, the turnaround may occur in the past, at present, or in the future, or may not occur at all. In an expanding $\Lambda$$CDM$ universe, the turnaround density contrast at the present (at redshift $z=0$) is $\Delta {\rho }_{turn}=13.1$. If a spherical density perturbation is not high enough to collapse at present, it may still collapse in the future, if its density contrast (future collapse density contrast) now (at redshift $z=0$) is $\Delta {\rho }_{FC}=8.73$. The density contrast $\Delta {\rho }_{ZG}=5.41$ corresponds to so-called zero gravity (ZG), at which the radial peculiar velocity component of test particle velocity equals the Hubble expansion and the gravitational attraction of the system and its expansion are equal. The density contrast $\Delta \rho =\rho /{\rho }_{\mathrm{m}}=1$ corresponds to the linear mass scale or the Einstein–Straus radius at which the radial velocity around a system reaches the Hubble velocity, $u=HR$ and peculiar velocities $v_{\mathrm{pec}}=0$ [113,134]. This scale approximately corresponds to the cocoon boundaries [65,113,134]. The mass M of a density perturbation within a sphere with radius R can be calculated as

$$\left(R\right)=1.45·{10}^{14}{\Omega }_{\mathrm{m}}0\Delta \rho {\left(R/5 h^{-1}\mathrm{Mpc}\right)}^3·{(1+z)}^3{h}^{-1}{M}_{\odot },$$

(7)

where ${\Omega }_{\mathrm{m}}0$ is the matter density and $\Delta \rho$ denotes density contrast.

The density contrast at turnaround depends on cosmological parameters. For example, for ${\Omega }_{\mathrm{m}}=1$, the density perturbation at the turnaround is $\Delta {\rho }_{\mathrm{T}}={(3\pi /4)}^2=5.55$ (the density contrast ${\delta }_{\mathrm{T}}=\Delta {\rho }_{\mathrm{T}}-1=4.55)$ [6].

Superclusters, which have been defined as future collapsing systems, will collapse by definition. In superclusters with high-density cores surrounded by lower-density outskirts regions, the high-density cores may reach turnaround at present, and start to collapse during future evolution, if the density contrast in their cores is as high as $\Delta \rho \ge \Delta {\rho }_{FC}$.

To apply the spherical collapse model, at first, one must calculate the distribution of mass in the supercluster, centred at its centre of mass (most massive cluster; in superclusters with several high-density cores, this distribution is calculated for each core). Based on the mass distribution, one can find the density contrast around the central cluster, and this can be directly compared with the characteristic density contrasts from the spherical collapse model. This approach has been used to analyse the evolution of superclusters, as the Shapley, the Laniakea, the Corona Borealis, the Sloan Great Wall, the BOSS Great Wall, the Perseus-Pisces, the Hercules, the Coma, the Saraswati, and others ([20,42,65,91,98,134,135,136,137,138,139,140] and references therein). Ref. [42] provides a list of 105 cores in 53 rich superclusters in the nearby Universe. They emphasise that these cores are the most massive structures that may be collapsing now or in the future.

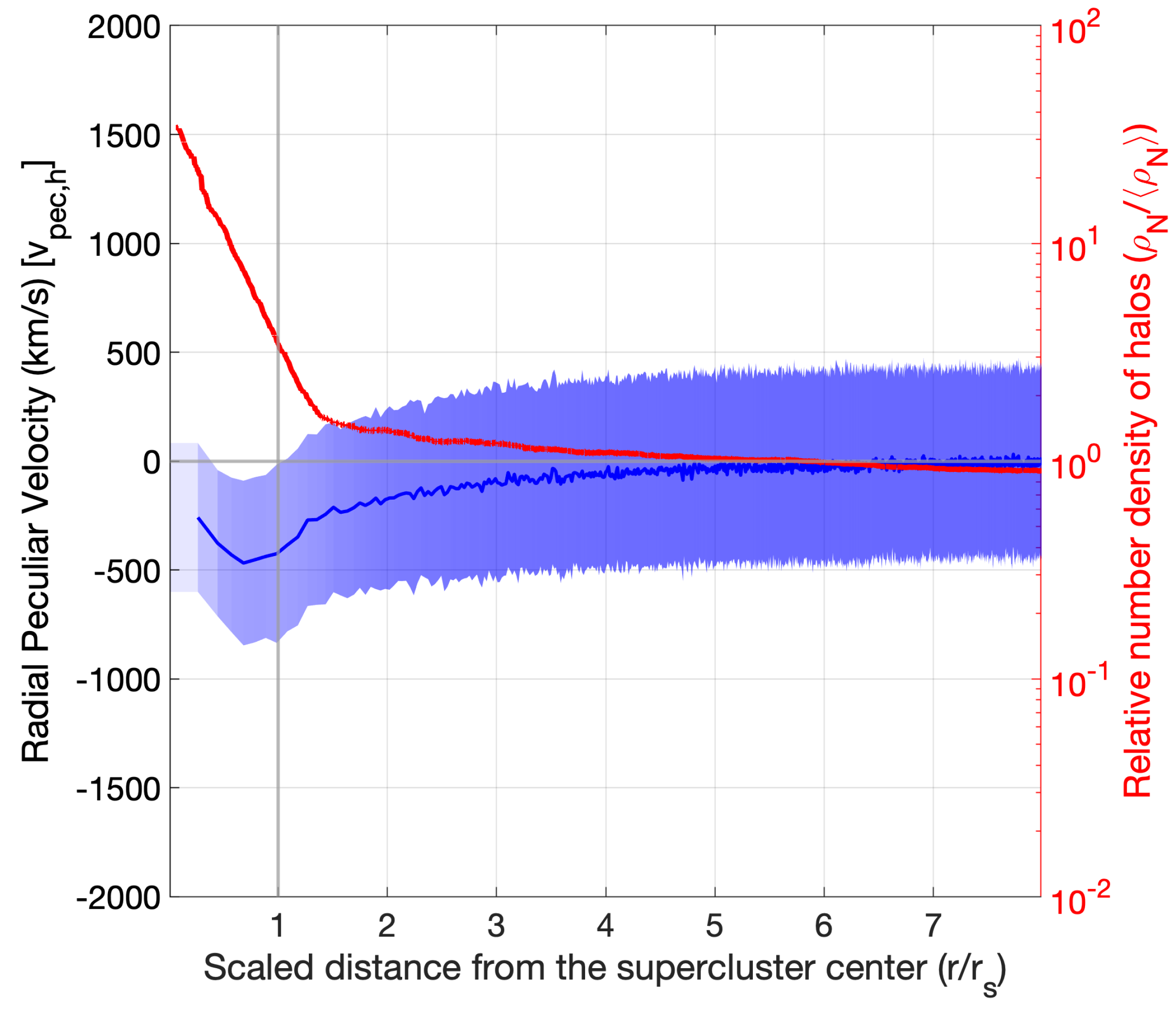
The detailed analysis of the dynamics of groups and clusters in superclusters and in their high-density cores requires data on the peculiar velocities of galaxy groups and clusters (dark matter haloes) in superclusters. These data are available for simulated superclusters. Therefore, Figure 10 shows radial peculiar velocities of dark matter haloes in superclusters versus the scaled distance from the supercluster centre (in units of $r_s$, half the size of a supercluster) (phase space diagram) by [21]. In this figure, more than 90% of supercluster member halos have a negative supercluster-centric peculiar velocity component. This means that their movements are influenced by the gravitational potential of their host supercluster. This influence is weak in supercluster outskirts, at large scaled distances, and negligible on the halos outside the supercluster region. The velocities of dark matter haloes at scaled distances half the size of superclusters (the core regions) are directed toward supercluster centres, and this may lead to the collapse of these centres in the future.

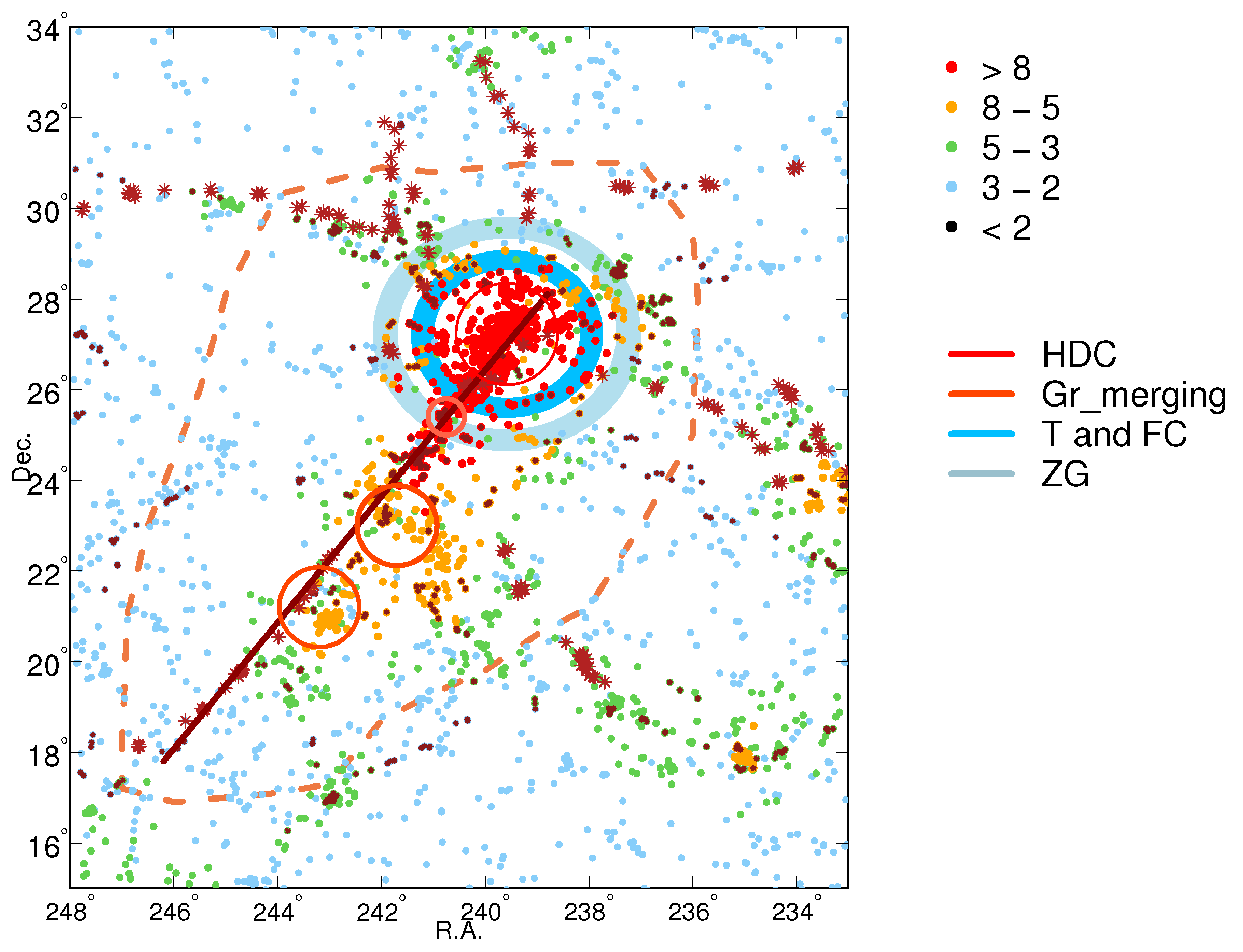
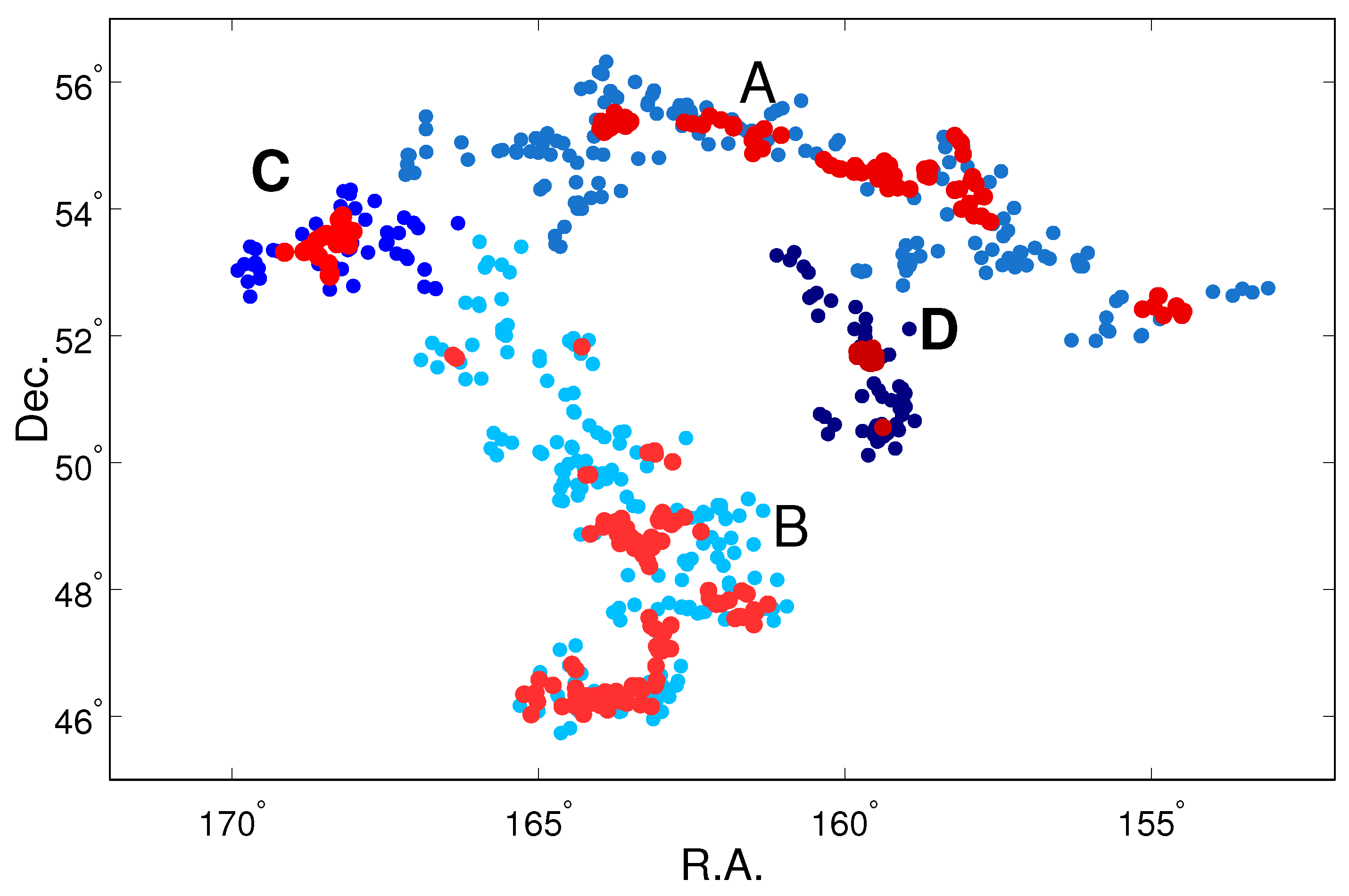
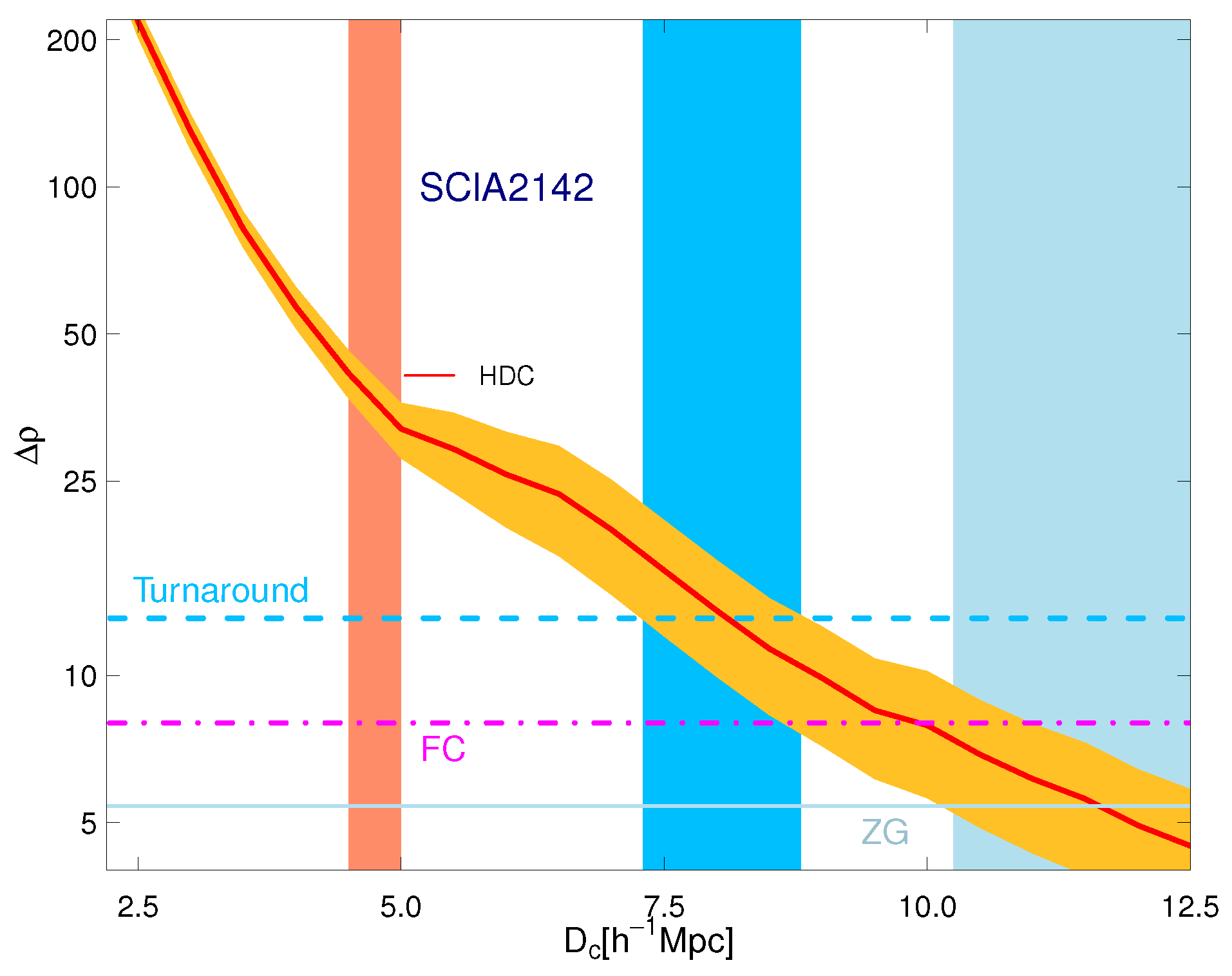
From the observational side, the supercluster A 2142 is an example of a collapsing supercluster with one high-density core [98,111]. As an example, we show in Figure 11 the sky distribution of galaxies, groups and filaments in this supercluster and in the cocoon around it, where we mark the turnaround, future collapse (FC), and zero gravity (ZG) regions of the supercluster. Figure 12 presents the density contrast versus supercluster-centric distance for this supercluster, calculated using the distribution of mass in SCl A2142 [111]. The sizes of turnaround, future collapse, and zero gravity regions are calculated based on the density contrast (mass distribution) in the supercluster and the spherical collapse model. For the Corona Borealis superclusters these regions have been found by [20].

If a supercluster has several HDCs which are far apart from each other, then each core may collapse separately in the distant future, and the supercluster may split and form several smaller superclusters. Such scenario has been predicted for the superclusters in the Sloan Great Wall and in the BOSS Great Wall (BGW) [20,91]. 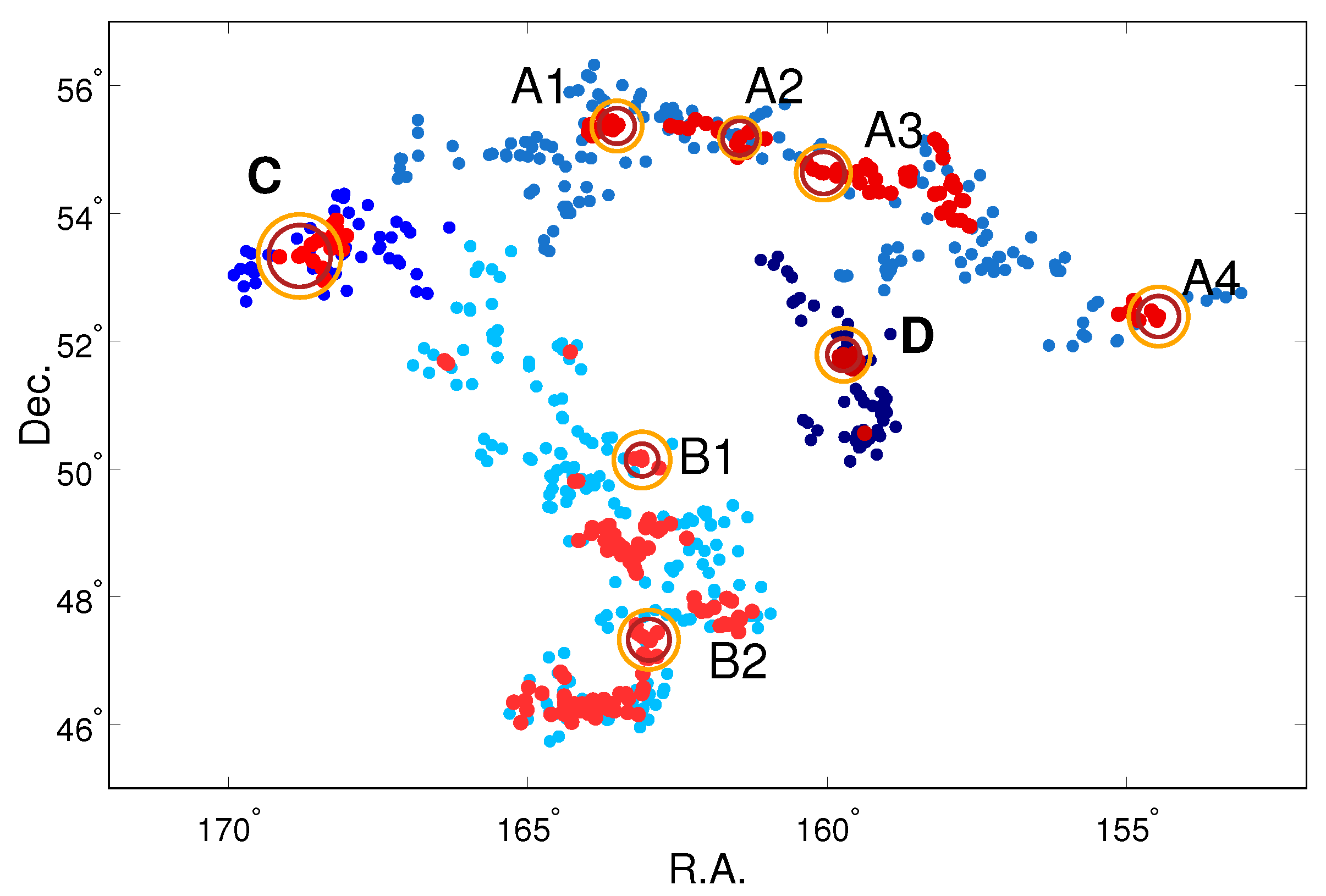We show high-density cores of superclusters in the BGW with their turnaround and future collapse regions in Figure 13. The sizes of these regions are calculated using the mass distribution around the most massive cluster in each core. In the BGW the distances between cores are so large that they will collapse separately in the future and form smaller superclusters.

If the distance between rich clusters in the HDCs of superclusters is smaller than the future collapse radius, then during the future evolution of a supercluster, such HDCs may merge and form a massive HDC. This evolution scenario was predicted, for example, for the Corona Borealis supercluster and for the Shapley supercluster in the nearby Universe [20,65]. A detailed comparison of the radii and masses of superclusters in the nearby Universe and at redshift $z=0.5$ was presented in [20], and we show this comparison also in Figure 14. In this figure, the masses and sizes of nearby superclusters (redshift $z=0$) are taken from [20,91,111], and extrapolated to higher redshifts based on the predictions of the spherical collapse model. 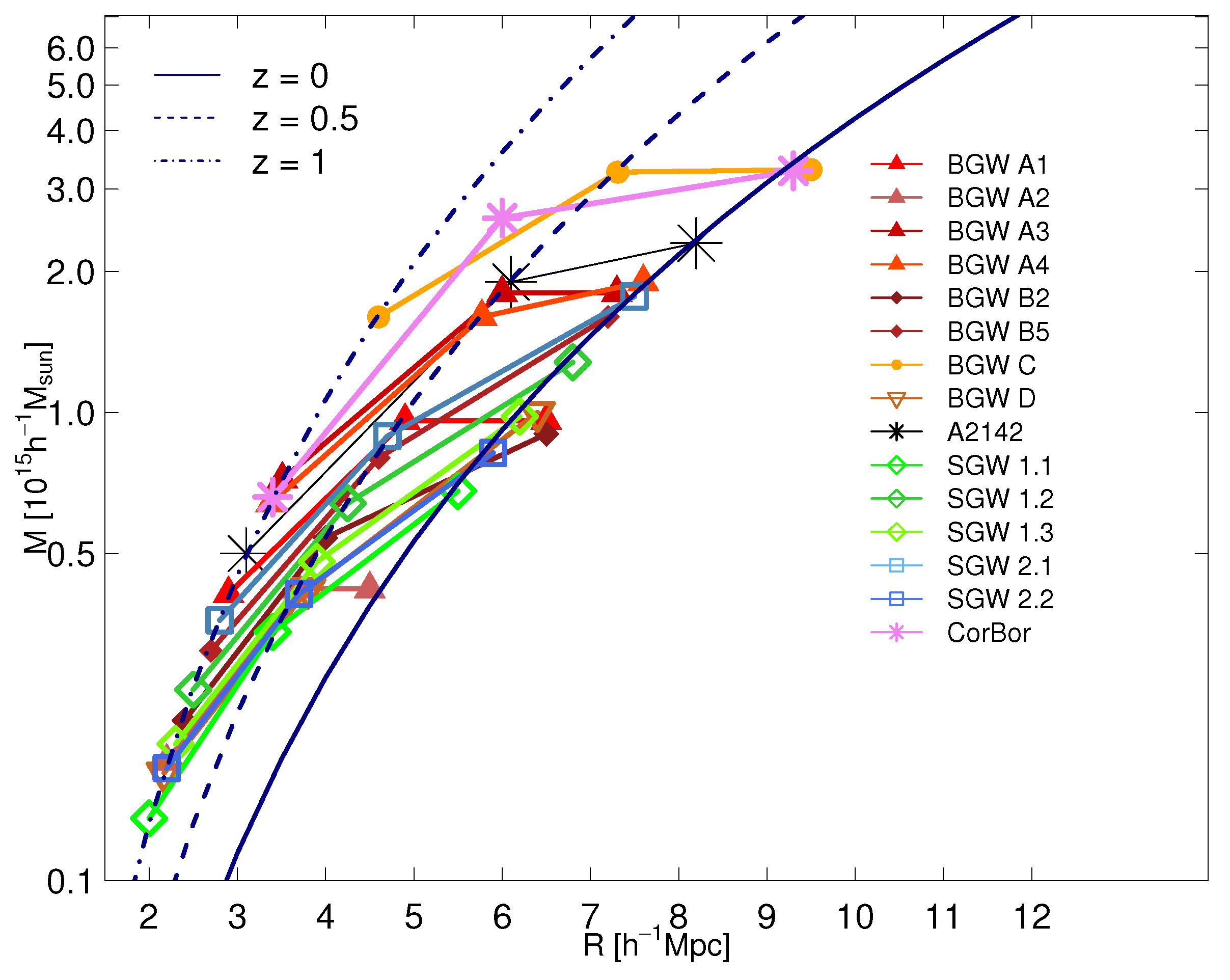In the case of the BOSS Great Wall (BGW), superclusters at redshifts $z=0.46$, and the masses and sizes of collapsing regions are based on these values at the BGW redshift, $z\approx 0.5$, and extrapolated to lower and higher redshifts using the spherical collapse model and the distribution of mass in the BGW superclusters. This figure shows that the most massive high-density core among the BGW superclusters, BGW C, has a mass and size similar to the core of the Corona Borealis supercluster in the nearby Universe, of the order of $M\approx$ 3–$4\times {10}^{15}{M}_{\odot }$ and 10 $h^{-1}$ Mpc at redshift $z=0$. The masses and sizes of the collapsing cores of other superclusters lie in the range of $M\approx$ 0.2–$2\times {10}^{15}{M}_{\odot }$ and 2–8 $h^{-1}$ Mpc. We also refer to [42], which provides an analysis of HDCs (nucleation regions of superclusters) and their future evolution. Ref. [20] proposed that the number and properties of collapsing cores of superclusters may serve as a cosmological test.

The reliability of the predictions made for observed superclusters, depends, of course, on how well the masses of turnaround regions of HDCs are estimated. For example, ref. [20] estimated that in order to merge in the distant future, the masses of different HDCs in the BGW should be ten times higher than estimated in their study, which leads to the mass-to-light ratios $M/L\approx 3000$. This value is unrealistic. Therefore, ref. [20] concluded that the cores of the BGW superclusters will separate in the distant future.

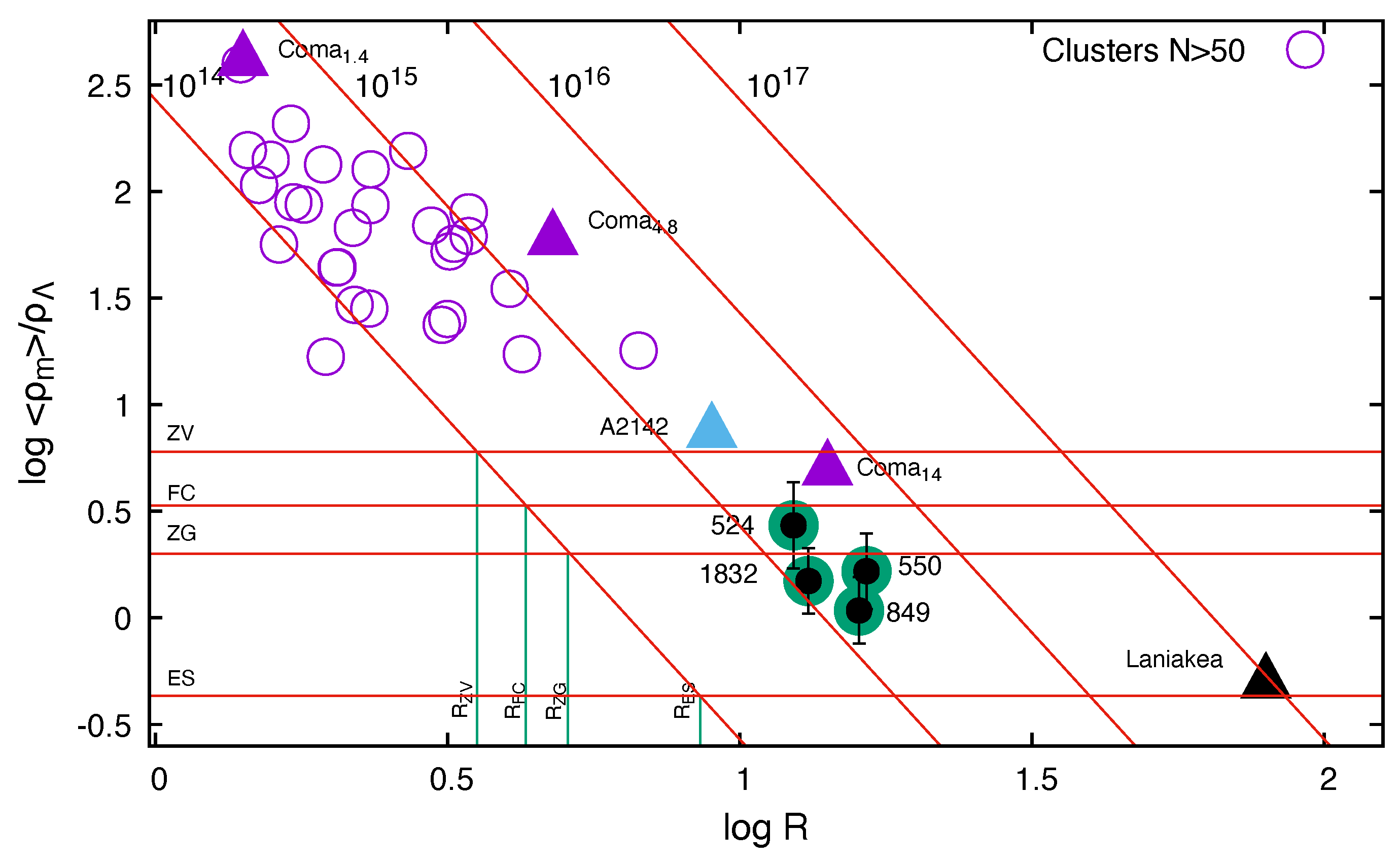
Finally, we present Figure 15, which shows the dynamical state of galaxy clusters and superclusters from the dark energy (DE) (and dark matter) perspective, the so-called $\Lambda$ significance diagram [88,134]. The energy density ratio $\langle {\rho }_{\mathrm{M}}\rangle /{\rho }_{\Lambda }$, as calculated for the system under study, measures the influence of DE. The $\Lambda$ significance diagram is a $log(\langle {\rho }_{\mathrm{M}}\rangle /{\rho }_{\Lambda })$ versus $logR$ graph, where R is the radius of a system, $\langle {\rho }_{\mathrm{M}}\rangle$ is its average mass density, and ${\rho }_{\Lambda }$ is the DE density equal to the global value ${\rho }_{\Lambda }\approx 6\times {10}^{-30}$ g cm⁻³.

The location of a galaxy system in the $\Lambda$ significance diagram indicates whether its overall dynamics is dominated by gravity or by the outward ‘antigravity’ expulsion of DE. The lines in the figure are as follows. The ratio $\langle {\rho }_{\mathrm{M}}\rangle /{\rho }_{\Lambda }$ can be expressed as $log(\langle {\rho }_{\mathrm{M}}\rangle /{\rho }_{\Lambda })=0.43+log(M/{10}^{12}{M}_{\odot })-3\times log(R/\mathrm{Mpc})$, where M is the mass within the radius R of a system. The intersections of the lines with horizontal lines of constant $log(\langle {\rho }_{\mathrm{M}}\rangle /{\rho }_{\Lambda })$ give the following scales or radii for the mass M:

• The zero-velocity radius $R_{\mathrm{ZV}}$ (at this distance, a test particle system-centric radial velocity $u=Hr-v_{pec}$ is $v_{pec}=Hr$ and $u=0$). This corresponds to the turnaround radius in the spherical collapse model.
• The zero-gravity radius $R_{\mathrm{ZG}}$ (gravity force equal to Einstein’s antigravity force). Thus, acceleration is zero, $du/dt=0$, which indicates the maximum radius of a gravitationally bound system at the present epoch.
• The Einstein–Straus radius $R_{\mathrm{ES}}$ (the radial velocity reaches the Hubble velocity, $u=Hr$). This last, longest distance corresponds to the spherical volume where the mass M produces an average density that is equal to the cosmic global density.

In Figure 15, these three different radii are shown for the systems of mass ${10}^{14}{M}_{\odot }$. For spherical and homogenous systems, the horizontal lines $\mathrm{ZV}$, $\mathrm{ZG},$ and $\mathrm{ES}$ correspond to the constant ratios of $\langle {\rho }_{\mathrm{M}}\rangle /{\rho }_{\Lambda }$ = 6, 2, and 3/7.

In Figure 15, clusters of galaxies (from the SDSS survey) are shown with purple circles; they all lie in the region of structures that have pass turnaround and are collapsing, as one could expect for clusters. Based on the density distribution, the locations of several clusters and superclusters in this figure is shown. The supercluster A2142 core region is shown as a blue triangle near the ZG line. For the Coma cluster, regions of several radii are presented. At small radius ($Com{a}_{1.4}$), the figure shows the location of the Coma cluster itself, larger radius ($Com{a}_{4.8}$) corresponds to the Coma cluster with its region of influence, in a good agreement with recent estimates using Cosmicflows-4 data [141]. The largest radius ($Com{a}_{14}$) shows the FC region around the Coma cluster. The Laniakea supercluster BoA borders are located near the $\langle {\rho }_{\mathrm{M}}\rangle /{\rho }_{\Lambda }$ = 3/7 ($\mathrm{ES}$) line. Only the central part of Laniakea may collapse in the future [65]. Almost spherical superclusters (objects 524, 550, 849, and 1832 in the figure [88]) lie between the core of SCl A2142 and the Laniakea, showing that their outskirts are not collapsing yet.

9. Superclusters as an Environment for Galaxies, Groups, and Clusters

Already early studies of superclusters provided evidence of the coevolution of superclusters, galaxies, and galaxy systems embedded in them [40]. Galaxies can be divided into two major classes according to their star formation and morphological properties: quiescent galaxies, which are typically red and of early-type, and actively star-forming galaxies having blue colours and late types [142,143,144,145]. The analysis of galaxy populations in the Perseus-Pisces supercluster demonstrated that the central parts of this supercluster are mostly populated by early-type galaxies, while the percentage of late-type galaxies increases in the supercluster outskirts [1,40,146]. This is now known as the morphological segregation or the morphology–density relation, in which ‘morphology’ denotes various properties of galaxies: their morphological type, star formation activity, colour, and so on. This relation tells that rich galaxy clusters and especially their central parts are mostly populated by early-type galaxies, and late-type galaxies are preferentially located on the outskirts of clusters or in poor groups [147]. In fact, the morphology–density relation extends from central parts of galaxy clusters up to the lowest global-density environment, populated by very poor galaxy groups and single galaxies [28,148]. Early-type galaxies are located in the central part of rich clusters or in central parts of poor groups in filaments between clusters [149].

Recent studies have shown that the global environment strongly affects the richness of galaxy groups and clusters. X-ray clusters are more frequent in superclusters [55]. Also, clusters in superclusters have a higher probability to have substructure than isolated clusters [150]. In the Ursa Major supercluster, relaxed groups lie in high-density regions, while non-relaxed clusters with substructure can preferentially be found in the outskirts of the supercluster [151]. 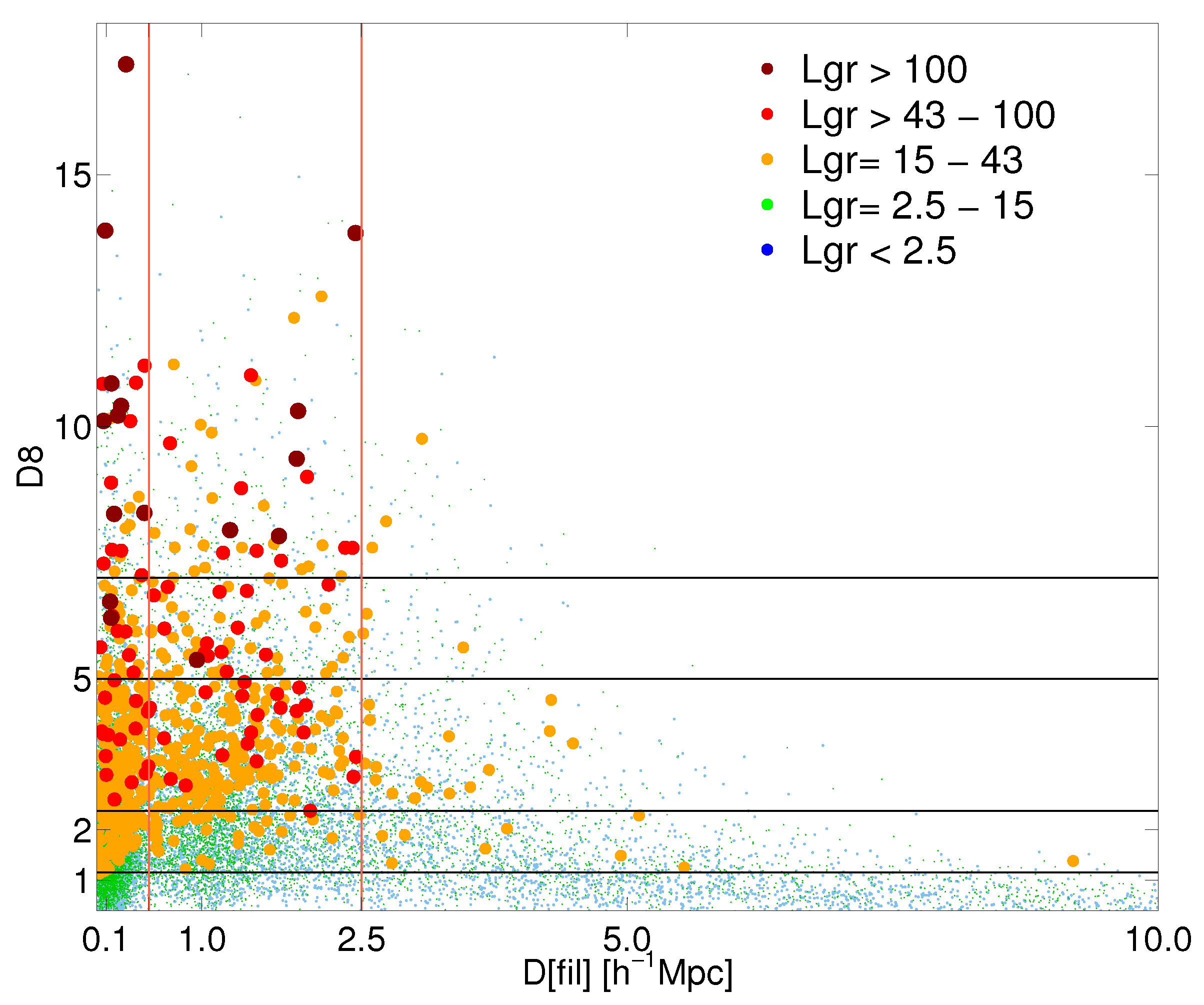Figure 16 shows the effect of the environment on the richness (luminosity) of groups in the global luminosity-density $D8$–distance to the nearest filament axis $D_{fil}$ plane [29]. The luminosity–density values in this figure ($D8$, calculated using smoothing length 8 $h^{-1}$ Mpc) are expressed in units of mean luminosity density, ${\mathit{\ell }}_{\mathrm{mean}}$ = 1.65 $\times {10}^{-2}$$\frac{{10}^{10} h^{-2}{L}_{\odot }}{{\left(h^{-1}\mathrm{Mpc}\right)}^3}$ [28,53]. In Figure 16, galaxy groups and clusters can be considered as being located in filaments or in filament outskirts if the distance to the nearest filament axis $D_{fil}\le 2.5$ $h^{-1}$ Mpc ($D_{fil}\le 0.5$ $h^{-1}$ Mpc for filament members). In the global luminosity-density field, the density threshold $D8=5$ marks superclusters, and $D8=7$ corresponds to the HDCs of superclusters.

There are several important aspects to notice in this figure. It shows that the richest and most luminous clusters with luminosity $L_{gr}\ge 100\times {10}^{10} h^{-2}{L}_{\odot }$ all lie in superclusters or in the HDCs of superclusters with $D8\ge 5$ in filaments or filament outskirts, with $D_{fil}\le 2.5$ $h^{-1}$ Mpc. Clusters grow by infall of groups and galaxies along filaments, and a dense environment of superclusters is especially suited for that. Refs. [152,153] called this an environmental enhancement of galaxy groups near rich clusters. One can also notice that intermediate luminosity groups with $43\le L_{gr}\le 100\times {10}^{10} h^{-2}{L}_{\odot }$ and $15\le L_{gr}\le 43\times {10}^{10} h^{-2}{L}_{\odot }$ are in abundance at the outskirts of superclusters ($1<D8<5$). Such groups avoid the lowest global density regions (watersheds) between superclusters, with $D8<1$. However, very poor groups (mainly galaxy pairs and triplets with luminosity $L_{gr}\le 2.5\times {10}^{10} h^{-2}{L}_{\odot }$) and galaxies which do not belong to any group (single galaxies) can be found everywhere in the cosmic web, from superclusters to the lowest global density environments (voids or watershed regions) [28,29]. We note that single galaxies and very poor groups with $D_{fil}>2.5$ $h^{-1}$ Mpc are, most probably, members of faint filaments which were not detected based on data from the SDSS MAIN spectroscopic survey, used in [29]. The change in group and cluster properties at threshold densities $D8=5$ which have been used to define superclusters, means that when looking for the physical definition of superclusters, the analysis of the dependence of the properties of galaxy groups and clusters on the global density may provide additional information. Rich clusters are located in superclusters, and this is related to the high value of their correlation amplitude [43].

A possible connection between the location of galaxy groups and clusters and their properties is known as a halo assembly bias, which addresses the question whether other factors are important in shaping the properties of groups and clusters apart from their masses [154]. This problem has been addressed in many studies. These studies have shown that clusters in high-density regions (cosmic web nodes) tend to more often be X-ray sources, and to have higher X-ray luminosities and temperatures than groups and clusters in lower-density environments, such as filaments [155,156,157]. This may mean that clusters in denser environments, such as superclusters, have experienced more mergers than isolated clusters in their assembling history [157,158].

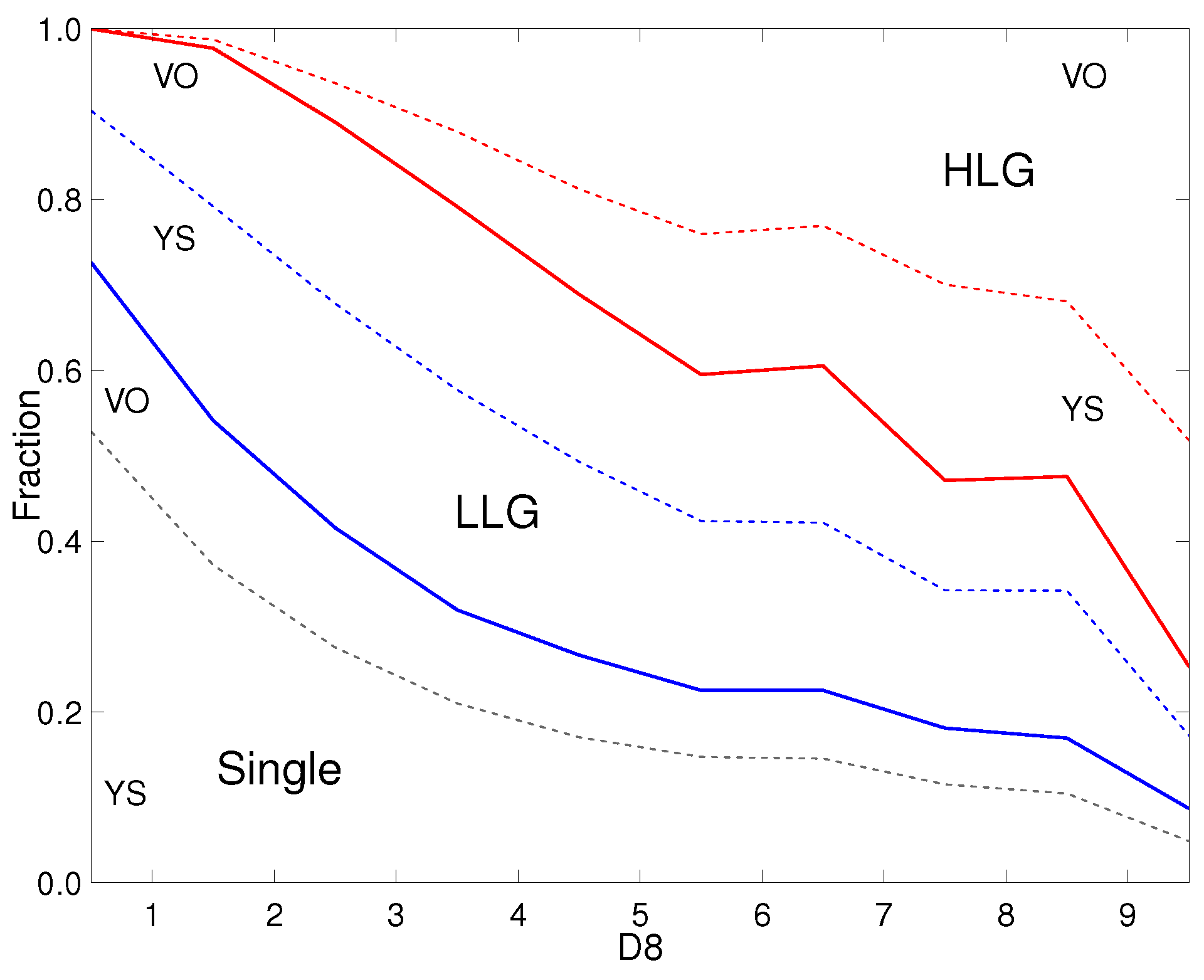
The star formation properties of galaxies are less affected by the global environment. We show this in Figure 17, which presents the group and galaxy content of various global luminosity-density regions based on the Sloan Digital Sky survey data. As in Figure 16, one can see that in the supercluster environment, the abundance of luminous groups and clusters increases. Poor groups and single galaxies lie preferentially in the low global density environment. The galaxy and group populations of superclusters differ from those in a low-density environment between superclusters. The percentage of red, quiescent galaxies in superclusters is higher than in low-density environments, up to 60% [90,159]. In the lowest global density environment populated by single galaxies and very poor groups, up to one-third of all galaxies are quiescent [28].

Groups of the same richness in superclusters are more luminous than those in the low-density regions. This phenomenon is especially strong for poor groups. Moreover, groups in superclusters embed higher percentages of red, early-type galaxies in comparison with groups of the same richness in low-density regions [28,29,159,160]. Even single galaxies, from the volume-limited samples of the same absolute magnitude limit in superclusters, have, on average, higher luminosities than single galaxies elsewhere [29]. Also, in superclusters of filament morphology, galaxy groups of the same richness host galaxies with larger stellar masses, and a higher fraction of early-type and red galaxies in comparison with groups in superclusters of spider morphology [160].

Group richness varies strongly with the global environment. In superclusters quiescent galaxies lie preferentially in rich groups and clusters. In other regions of the cosmic web, quiescent galaxies are hosted by poor groups, or they do not belong to any group [28]. Considering that superclusters host approximately 15% of all galaxies, one can see that quiescent galaxies in low-density regions outnumber, by far, such galaxies in rich groups in superclusters. Even among dwarf galaxies in low-density environments, there are quiescent galaxies [149,161]. These results demonstrate that in quenching the star formation in galaxies, processes, which are effective within and in the neighbourhood of galaxies and their dark matter haloes, play an important role, and the effect of larger-scale environments is less important [28,161].

The largest difference in galaxy properties within superclusters and elsewhere in the cosmic web is related to the properties of the brightest galaxies in groups and clusters. The brightest galaxies of the richest clusters (BCGs), which lie in superclusters, with luminosities $L_{gr}\ge 15\times {10}^{10} h^{-2}{L}_{\odot }$, are mostly quiescent, with stellar populations older than at least 4 Gyrs. The BCGs have stellar masses $log{M}^{*}>11.0$, red colours, and stellar velocity dispersions ${\sigma }^{*}>300$ $km/s$ [28,29,162,163,164,165]. These properties suggest that the formation and growth of the present-day BCGs began at early stages of their host cluster’s evolution. The poor groups, which can be found everywhere in the cosmic web, may also have star-forming brightest galaxies ([28,29,166] and references therein).

We may assume that individual rich superclusters, with thousands of galaxies (in volume-limited samples, which include brighter galaxies only) have, on average, similar galaxy populations. Still, surprisingly, the galaxy populations of individual rich superclusters are different [61]. The comparison of galaxy populations in elongated and flattened superclusters shows that superclusters of different overall shape have similar stellar populations [167]. Therefore, these differences are related to the inner structure of superclusters. Filament-type superclusters, with a small number of filaments between clusters, embed, on average, a higher percentage of red, quiescent galaxies than spider-type superclusters, in which clusters are connected by a large number of filaments [160,168]. In spider-type superclusters, galaxy clusters have larger amount of substructure, and this affects the star-formation properties of galaxies in them [168]. At redshifts around $z\le 0.9$, more connected clusters tend to have a higher number of star-forming member galaxies (web-feeding model) [169,170]. This result is in agreement with the earlier result that superclusters with dynamically active clusters have a higher percentage of star-forming galaxies.

The properties of filaments in superclusters have been analysed in several studies. The studies of the Local supercluster have revealed the filamentary pattern around the Virgo cluster [39,171]. Early analysis of the filamentary patterns in and around superclusters was performed mainly using percolation (clustering) analysis. At present, several filament finders are available, as the Discrete Persistent Structure Extractor (DisPerSE), Nexus (an algorithm for the identification of cosmic web environments: clusters, filaments, walls, and voids), a graph-based filament detection method T-Rex, a marked point process (Bisous model) based filaments, and others [19,76,172,173,174,175,176].

The number of filaments connected to a cluster defines the cluster’s connectivity C. Three filaments connected to the Coma cluster were found with the DisPerSE filament finder by [175]. Applying Bisous filaments, the connectivity of the richest clusters in the A 2142 and in the Corona Borealis superclusters have been found to be C = 2–6 [20,111]. First detections of the connectivity of superclusters have shown that the connectivity of the A 2142, the Corona Borealis and the Shapley superclusters is in the range of C = 6–7 [20,22,111]. The connectivity of poor groups outside superclusters is lower, usually in the range of C = 1–2.

Typically, filaments within superclusters are short, with a length less than 5 $h^{-1}$ Mpc, but long filaments in superclusters may have lengths larger than 15 $h^{-1}$ Mpc, and such filaments may extend farther away from superclusters, to low-density regions around them [20,76,111]. Galaxies closer to the filament axis are more massive than those farther away from filaments [76].

Usually, filaments have been traced by galaxies. In the study of the Shapley supercluster filaments, determined with the T-REX filament finder, were analysed also using data on gas [22]. Gas content in filaments between clusters in superclusters is one factor that affects the star-formation properties of galaxies. This has been demonstrated for the richest supercluster in the nearby Universe, the Shapley supercluster [22].

High-redshift protoclusters are candidates of the present-day rich clusters that lie in superclusters. Thus, the study of protoclusters and their galaxy content provides information on the galaxy evolution in superclusters. For example, quenched galaxies have been detected in a protocluster at redshift $z=3.37$ [177]. Quenched galaxies with stellar populations older than 10 Gyrs (galaxies which have stopped forming stars at least 10 Gyrs ago) have been found among both the brightest cluster galaxies and satellites in rich clusters in superclusters in the nearby Universe [28].

The important and fast-developing field, which provides information on the coevolution of galaxies and structures in which these are embedded, is the study of alignments between galaxies, clusters, and their host systems, including superclusters [40,56,178,179,180] (and references therein). Refs. [1,40] showed that in the Perseus-Pisces supercluster, the brightest galaxies in groups and clusters, as well as groups and clusters themselves, are aligned along the supercluster axis, which is a signature of their coevolution in the cosmic web. Correlated alignments between neighbouring groups and clusters in superclusters and in the cosmic web up to scales 100 $h^{-1}$ Mpc were detected by [56,178,179,181,182]. In the supercluster SCl A2142, the brightest galaxies in the main cluster of the supercluster, A2142, are aligned with the cluster A2142. Also, the radio and X-ray haloes of this cluster are elongated and aligned along the cluster and supercluster axis, as are groups infalling into the cluster. This suggests that structures in the supercluster have grown through merging and accretion along the supercluster axis. Moreover, SCl A2142 hosts an FRII radio galaxy with giant lobes, which are also aligned with the supercluster axis [183].

One interesting problem is the effect of the supercluster environment on the properties of radio galaxies, especially to radio galaxies with giant $\ge 3$ Mpc radio lobes. Studies of giant radio galaxies (GRGs) in various environments show that radio galaxies with radio lobes $\ge 3$ Mpc preferentially lie in low-density environments [184]. Moreover, identifying GRGs with polarised emissions behind superclusters can be used to estimate the magnetic field strength of sub-micro Gauss within the supercluster environment [184].

10. Superclusters and the Cosmic Microwave Background (CMB)

High-precision measurements of the CMB with the WMAP and especially Planck satellites opened a new window into the many branches of cosmology, including supercluster studies. First of all, I mention the discovery of a new supercluster at redshift $z=0.45$ in the distribution of galaxy clusters detected by analysing the XMM-Newton follow-up observations for the confirmation of Planck cluster catalogue [185]. The hot intercluster gas in superclusters can be detected from the thermal Sunyaev–Zeldovich (tSZ) signal using the full-sky Compton parameter maps (y-maps) reconstructed from the Planck multi-frequency channel maps [186,187]. This approach has been applied, for example, by [22,88]. In particular, in this way, ref. [22] investigated the relation between the star-formation rate in galaxies and the Compton y parameter, and its dependence on the environment defined by intercluster filaments in the Shapley supercluster. Figure 18 shows the galaxy density maps of the central part of the Shapley supercluster, in which optical clusters from [188] are plotted with stars, and contours of different colour correspond to Compton y parameter values and X-ray contours from the ROSAT all-sky survey map, as described in the figure caption.

The largest structures in the cosmic web—superclusters and supervoids affect CMB photons, very slightly heating or cooling them, correspondingly. This effect is known as the integrated Sachs–Wolfe (ISW) effect (see [189] for details and references). This effect has been detected in the studies of superclusters and supervoids using various datasets, including Dark Energy Survey data, and represents one interesting direction for the future studies [122,128,189,190]. Ref. [60] described several superstructures of X-ray clusters in the nearby Universe and mention that these superstructures should produce a modification on the CMB background.

11. The Rich and Important Superclusters

For us in the Milky Way galaxy, the most important supercluster is, of course, our cosmic home, the Virgo supercluster. Enhanced density of nebulae in the direction of the Virgo constellation was noticed already by William and John Herscel [63,191]. Gerard de Vaucouleur noticed a concentration of galaxy systems in Virgo, and described this as a “supergalaxy” or “supercluster” [38,192]. The Virgo supercluster consists of the main cluster—the Virgo cluster, and a filamentary patterns around it, with the extent approximately 20 $h^{-1}$ Mpc [39,54,149,171,193]. Our Local Group of galaxies is located in the galaxy filament which connects the Virgo and the Fornax superclusters [194]. The studies of the Local supercluster are important, as in this region it is possible to study much fainter galaxies than in studies of more distant superclusters. One interesting result of such studies is the discovery of relatively isolated, early-type dwarf galaxies [149,161]. These studies extend the quenching of star formation in galaxies to much lower luminosities than in more distant samples.

The very elongated Perseus-Pisces supercluster or the Perseus-Pisces chain, plotted in Figure 19, is one of those structures which led to the discovery of the cosmic web [1,40]. The Perseus-Pisces supercluster is also the first supercluster for which it was found that galaxy clusters in it are elongated along the supercluster axis. The brightest cluster galaxies are aligned with the supercluster axis as well. In addition, these first studies already demonstrated the presence of the large-scale morphological segregation of galaxies along the Perseus-Pisces filaments [1,40,146]. These properties are signatures of the common origin and evolution of galaxies, galaxy clusters, and the whole supercluster [1,40].

The nearby Coma supercluster is another supercluster that led to the discovery of the cosmic web [196,197]. The concentration of nebulae in the direction of the Coma constellation was first noticed by William Herschel in 1802 [63]. The Coma supercluster with rich Coma (Abell A1656) and A1367 clusters is one of the best-studied superclusters [197]. However, there is no consensus whether in the distant future its two richest galaxy clusters, A1656 and A1367, will merge, or if they are not massive enough to merge, and instead they will move away from each other as the Universe expands [42]. The Coma supercluster lies in a filament that connects our Local supercluster, the Coma, and the Hercules supercluster.

The Hercules supercluster, at redshift $z\approx 0.04$, embeds 12 Abell clusters in [55] supercluster catalogue. This supercluster is very clumpy, and these clumps are often considered separate, collapsing in the future superclusters. One of them, centred at the cluster A2052, is one of the most spherical superclusters [88]. The central cluster of another component of the Hercules supercluster, A2199, is rotating [198]. Kinematics of the Hercules supercluster determined by Abell clusters A2147, A2151, and A2152 were studied by [199], who found that the Hercules supercluster, traced by these clusters, may be gravitationally bound, with a mass of approximately $M\approx 7.6\pm 2.0\times {10}^{15} h^{-1}{M}_{\odot }$. Ref. [200] analysed in detail the kinematics of the Hercules supercluster, traced by Abell clusters A2151, A2152, and A2147 in their study. They estimated that the total mass of the supercluster is $M\approx 2.1\times {10}^{15}{M}_{\odot }$; this is the lower mass limit for the full supercluster.

The richest supercluster in the nearby Universe is the Shapley supercluster (Figure 18; see [22] for detailed description and references). In the core region of the Shapley, multiple filaments of galaxies and gas connect galaxy clusters. The role of filaments in quenching galaxies in them was recently discussed in detail by [22]. The mass of the Shapley supercluster is $M\approx 5\times {10}^{16}{h}^{-1}{M}_{\odot }$ [188]. The core region of the Shapley supercluster with several merging rich clusters, X-ray clusters among them, is collapsing, and according to the mass and size estimations, it will form the most massive collapsing structure in the nearby Universe detected so far, with a mass and radius of the order of $M\approx 1.3\times {10}^{16}{h}^{-1}{M}_{\odot }$ and $R\approx 12.4$ $h^{-1}$ Mpc [65,135].

The Coma, Hercules, and Perseus-Pisces superclusters are well seen in the velocity field of galaxies, traced by CosmisFlows data. Among other structures, the Shapley supercluster stands out also in the velocity field of the nearby Universe using the newest CosmicFlows data [35,36].

The Vela supercluster in the direction of the zone of avoidance at redshift $z\approx 0.06$ is a massive supercluster, discovered by [201]. They showed that this supercluster consists of two structures with rich clusters, observed by [202].

The Horologium-Reticulum supercluster in the Southern sky at a redshift approximately $z\approx 0.08$ with its 27 rich (Abell) clusters in the [45] catalogue has been studied in detail by [203]. They showed that galaxy clusters in this supercluster form two components in redshift space. With a length over 100 $h^{-1}$ Mpc the Horologium-Reticulum supercluster is one of the largest superclusters in the Southern sky. The authors of [203,204] estimate that the lower limit of the mass of the Horologium-Reticulum supercluster is $M\approx 5\times {10}^{16}{h}^{-1}{M}_{\odot }$, comparable to that of the Shapley supercluster.

One of the richest superclusters in the Northern sky in the nearby Universe is the Corona Borealis supercluster, at redshift $z=0.07$ with a mass of $M\approx 1.3\times {10}^{16}{M}_{\odot }$ [20] (and references therein). The core region with three very rich galaxy clusters (A2065, A2061/A2067, and A2089) is at turnaround, and these clusters will form the second most massive collapsing structure in the nearby Universe in the distant future, with the mass and radius approximately $M\approx 4.7\times {10}^{15}{M}_{\odot }$ and $R\approx 12.5$ $h^{-1}$ Mpc [20,42,137,205,206].

The Aquarius supercluster at redshift $z=0.086-0.112$ actually consists of two superclusters, one with five galaxy clusters at redshift $z=0.086$, and another, containing 14 galaxy clusters, at redshift $z=0.112$. The second supercluster may by connected with a galaxy filament extending up to redshift $z\approx 0.14$ [207,208,209].

Another interesting supercluster in the nearby Universe within the redshift range $z<0.1$ is the supercluster SCl A2142 at redshift $z=0.09$ [98]. In comparison with the Shapley and the Corona Borealis superclusters, SCl A2142 is poorer, containing one very rich galaxy cluster only. The central region of the cluster A2142 is mostly populated with galaxies with very old stellar populations. Such galaxies are also abundant in the low-density region surrounding this supercluster [111]. The overall structure of this supercluster is interesting, as it contains an almost spherical, collapsing main body with the elongated central cluster A2142 aligned along the supercluster axis, and a long, almost straight filament-like tail which extends farther away from the supercluster and forms the longest straight structure in the cosmic web detected so far, with a length of approximately 75 $h^{-1}$ Mpc [111]. In total, the supercluster SCl A2142 has 6–7 filaments connected to it. This is similar to the connectivity of the Corona Borealis and the Shapley superclusters [20,22].

On ancient maps, the distant, unknown regions were sometimes marked as “here live the dragons”. In the cosmic web, we can indicate where the “dragons” actually live. Namely, ref. [57] determined a rich supercluster at redshift $z\approx 0.1$ in the direction of the Draco constellation, which they named the Draco supercluster. In their list, the Draco supercluster embeds 16 rich clusters. We may say that the Draco supercluster guards the borders of the nearby Universe, as the redshift $z\approx 0.1$ is often considered an approximate limit for the nearby Universe.

A rich supercluster at slightly higher redshift in the Southern sky is the Sculptor supercluster at redshift $z\approx 0.113$ with 22 Abell clusters in it [55]. It has an approximate length of 150 $h^{-1}$ Mpc, and the lower limit of its mass is $M\approx 2\times {10}^{16}{h}^{-1}{M}_{\odot }$ [77,210].

Moving to higher redshifts, the Abell 901/902 supercluster at redshift $z=0.165$ is another example of a supercluster consisting of two galaxy clusters connected by a filament with galaxy groups [108]. It stands out among other superclusters because of the studies of the dark matter distribution in it using a weak lensing analysis of the structures within this supercluster [108]. In this paper, the authors detected four main structures in the supercluster, which followed the distribution of matter in clusters and between them. Most importantly, they concluded that visible galaxies and clusters in the supercluster trace the distribution of dark matter well, with no need for the extra dark matter which does not follow the distribution of visible matter.

Several very rich superclusters were described for the first time by [21] in their supercluster catalogue, which covers the redshift range $0.05\le z\le 0.42$. The richest among them is the supercluster at redshift $z=0.25$, centred at the rich cluster A1835. The authors of the catalogue named this supercluster as the Einasto supercluster in honour of Prof. Jaan Einasto, who is one of the discoverers of the cosmic web. Jaan Einasto has studied galaxy superclusters for decades, and is actively contributing to the field now [44]. Ref. [21] estimate that the mass and extent of the Einasto supercluster are $M\approx 2.6\times {10}^{16}{M}_{\odot }$ and 110 $h^{-1}$ Mpc.

Another remarkable supercluster in the [21] catalogue is the Saraswati supercluster at redshift $z=0.28$, discovered by [139]. In total, this supercluster embeds 51 galaxy groups and clusters, the most massive among them being cluster A2631. The total mass of the Saraswati supercluster is of the order of $M\approx 2.6\times {10}^{16}{M}_{\odot }$, and the length of it is approximately 200 $h^{-1}$ Mpc [21,139]. The Saraswati supercluster has a collapsing core, which is comparable to the collapsing cores of superclusters in the nearby Universe, with the mass and radius of the order of $M\approx 4\times {10}^{15}{M}_{\odot }$ and $R\approx 20$ Mpc.

The richest supercluster detected so far at redshifts $z\approx 0.5-0.6$ is the King Ghidorah supercluster, discovered by [109]. The King Ghidorah supercluster embeds several density enhancements with more than ten galaxy clusters, connected by filaments. Ref. [109] estimated that its mass is approximately $M\approx 1.1\times {10}^{16}{M}_{\odot }$.

At redshifts $z\approx 0.9$, several superclusters have been discovered [211,212,213,214]. The most massive among them is the supercluster at redshift $z=0.9$, with a mass of the order of M = 0.1–$5\times {10}^{15}{M}_{\odot }$ and size $\approx 15$ Mpc [213]. At still higher redshifts, the richest proto-supercluster discovered so far is the Hyperion proto-supercluster at redshift $z=2.45$ [140]. The authors estimated that its mass is of the order of M = 0.1–$2.7\times {10}^{14}{M}_{\odot }$ and its maximal extent of the order of $\approx 150$ Mpc. At redshift $z\approx 3.3$, a proto-supercluster, nicknamed Elentári, was discovered in the COSMOS field [215].

12. Great Walls as Complexes of Rich Superclusters

At the largest overdensities of the cosmic web, very rich superclusters form complexes in which several rich (and poor) superclusters are almost connected. In the nearby Universe, the richest supercluster complex is the Sloan Great Wall (SGW) [24,61,216]. Its richest superclusters were mapped already in early supercluster catalogues [45,57]. Ref. [77] noticed that the richest supercluster among them is one of the flattest, interpreting this as an effect of peculiar motions of galaxies and galaxy groups toward the supercluster axis, perpendicular to the line-of-sight. The definitions of the Sloan Great Wall differ in various studies. Ref. [24] consider this agglomeration of galaxy clusters as one huge, approximately 200 Mpc long structure. In [21,53] supercluster catalogues, the Sloan Great Wall consists of several rich and poor superclusters. In Figure 20, we show the sky distribution of galaxy groups and clusters in the SGW region.

In the extensive study of the morphology and galaxy content of the two richest superclusters of the Sloan Great Wall, ref. [61] showed that these superclusters have different morphology and galaxy content. The richest supercluster in the SGW is of multibranching filament morphology, while the second richest supercluster has multispider morphology; on average, the richest supercluster in the SGW contains a higher percentage of red, quiescent galaxies than the second richest supercluster. Considering these differences, ref. [61] concluded that the formation history and evolution of individual superclusters in the SGW have been different, and the SGW is not a genuine physical structure but rather an assembly of very rich galaxy systems. The total length of the SGW is approximately ≈ 200 Mpc, and its mass is $M\approx 2\times {10}^{16}{h}^{-1}{M}_{\odot }$. The richest superclusters in the SGW contain several high-density cores that will collapse in the distant future, and the SGW may split into several superclusters [91].

The studies that analysed whether the presence of such a rich complex of superclusters in the nearby Universe is in agreement with the standard cosmological model still leave this as an open question. While some studies found that the presence of both the Shapley supercluster and the SGW in our cosmic neighbourhood is hardly compatible with the standard ΛCDM model, other studies showed that such systems are present in very large simulations [24,217]. Moreover, ref. [24] even predicted that there might be another, even bigger and more massive supercluster system within redshift $z<0.8$.

In 2016, a huge supercluster complex at redshift $z=0.47$, consisting of four rich and very rich superclusters, was discovered [104]. This supercluster complex obtained a nickname the BOSS Great Wall (BGW). The sky distribution of galaxies in the HDCs and outskirts of the four BGW superclusters is plotted in Figure 21.

The richest supercluster in the BGW alone, BGW A, has a length approximately equal to the total length of the SGW. The total mass of the BGW superclusters exceeds the mass of the SGW at least twice [91]. In comparison with the nearby rich superclusters, the BGW superclusters are more elongated, and the reason why there are no such elongated superclusters in our cosmic neighbourhood is not yet clear [91,104]. The Perseus-Pisces supercluster is also very elongated but not as rich, massive, and large as the BGW superclusters.

An analysis of the structure and mass distribution of the BGW superclusters showed that these superclusters contain altogether eight high-density cores [110]. These HDCs may form separate superclusters in the distant future, as discussed in Section 8. The most massive of these HDCs has a mass similar to that of the collapsing core in the Corona Borealis supercluster in the nearby Universe, $M\approx 3.3\times {10}^{15}{h}^{-1}{M}_{\odot }$. This may weaken, but does not remove the tension with the ΛCDM model, which does not predict a large number of very rich and large superclusters in our nearby cosmic neighbourhood. It is also an open question whether the BGW fits the prediction by [24], as superclusters in this study and in [104] have been defined in a different way.

Recently, a huge structure was detected, using data on X-ray clusters, and nicknamed as the Quipu superstructure [60]. Cluster distribution in this structure is rather sparse, and these were linked together applying the Friend-of-Friend method with a large linking length. Therefore, the authors call it a “superstructure”, not a supercluster. The Quipu superstructure embeds several poor superclusters of Abell clusters, determined in the supercluster catalogue by [55], and a long filament of X-ray clusters which connect these superclusters. This is a good example of how data on different wavelengths complement each other to obtain a better view of the Universe.

13. Supercluster Planes

Clusters of galaxies surrounding the Local supercluster plane (Supergalactic plane), described by de Vaucouleur [38,192], are located along this plane, extending it up to the distances of several hundred megaparsecs [51,218,219,220]. Radio galaxies up to large distances also follow the Local supercluster plane, as well as X-ray luminous galaxy clusters in our cosmic neighbourhood (see also Figure 4) [221,222]. The richest superclusters that form this plane are the Local Supercluster, the Coma supercluster, the Pisces-Cetus supercluster, the Perseus-Pisces supercluster, and the Hydra-Centaurus supercluster [57,222]. The Local supercluster plane separates two local voids, the Northern and the Southern Local supervoids, both having diameter approximately 100 $h^{-1}$ Mpc [45,124,218,223,224].

Moreover, the most luminous early-type galaxies in the nearby Universe are also concentrated on this plane, while similarly luminous spiral galaxies are located farther away from this plane [219]. Very luminous early-type galaxies are the brightest galaxies in rich galaxy groups and clusters, which preferentially lie in superclusters or in filaments in supercluster neighbourhood [28,29]. In the local Universe, their distribution follows superclusters in the Local supercluster plane.

Perpendicular to the Local supercluster plane, ref. [57] discovered another plane, the Dominant supercluster plane, with an extent of at least 600 $h^{-1}$ Mpc. They listed superclusers which are arranged along the Dominant supercluster plane. In the Southern sky, the superclusters that form the Dominant Supercluster Plane are the Aquarius-Cetus (9), the Aquarius (19), the Aquarius B (8), the Pisces-Cetus (17), the Horologium-Reticulum (26), the Sculptor (22), the Fornax-Eridanus (12), and the Caelum (11) superclusters. Here, the number in parentheses is the number of rich (Abell) clusters in these superclusters in the [57] supercluster catalogue. In the Northern sky, the Corona Borealis (8), the Bootes (12), the Hercules (12), the Virgo-Coma (16), the Vela (9), the Leo (9), the Leo A (10), the Leo-Virgo (8), and the Bootes A (10) superclusters are arranged along this plane. As the Dominant supercluster plane crosses the Local supercluster plane, some superclusters belong to both. Superclusters in these planes are assembled in a number of intertwined chains of rich superclusters [57].

It is not yet clear whether the presence of such planes is in agreement with our standard cosmological model. For example, using constrained simulations of the nearby Universe in the 500 $h^{-1}$ Mpc box [225] found that a plane with the extent of approximately 100 $h^{-1}$ Mpc can be recovered in simulations. However, 0.28% of random realisations of simulations only matched both underdense and overdense regions of the nearby Universe, and their simulation box was not large enough to test the presence of a supercluster plane hundreds of megaparsecs in size. Also, they did not analyse the probability of finding two perpendicular supercluster planes. Refs. [220,226,227,228] speculate that such planes may be a signature of long, nearly straight strings.

14. Regularity in the Distribution of Rich Superclusters

In Section 3, the possible relation between the location of superclusters in the cosmic web and their morphology was discussed. Now, we describe the quasiregular pattern discovered in the large-scale distribution of rich superclusters. The first step in this direction was the study by [34], who discovered that in the narrow pencil-beam survey of galaxies in the direction of the North and South Galactic poles, the distribution of galaxies had regularly located peaks, which corresponded to the clusters of galaxies. Next, the study of the 3D distribution of rich galaxy clusters and superclusters unveiled an almost regular pattern with the same characteristic distance between superclusters, 120–140 $h^{-1}$ Mpc [45,229]. This pattern is best seen in the 3D distribution of very rich superclusters of Abell clusters of galaxies across huge underdense regions with diameters over 100 $h^{-1}$ Mpc. In [45], the authors applied several methods in their study of the large-scale distribution of rich superclusters. They started with the plots that showed the presence of a quasiregular pattern of rich superclusters and underdense regions between them. Various methods, such as the analysis of the sizes of underdense regions between the rich (Abell) clusters and superclusters, where underdense regions were defined using two different methods, pencil-beams, and the 3D empty sphere method, confirmed the presence of quasiregular patterns in the distribution of rich superclusters. The authors also analysed the distribution of the nearest neighbour distances between rich superclusters. All these tests suggested that the distribution of rich superclusters resembles an almost regular lattice with the sizes of “lattice cells” in the range of 120–140 $h^{-1}$ Mpc [45]. Underdense regions between very rich superclusters in this lattice are not completely empty but contain hierarchical, filamentary structures of faint galaxies and poor groups (Section 7). A quasi-periodic structure in the distribution of the SDSS’s LOWZ galaxy dataset was detected by [230].

The analysis of the correlation function and power spectrum of rich clusters in superclusters demonstrated that the correlation function has a series of maxima with an interval of the same scale, 120–140 $h^{-1}$ Mpc, and the power spectrum has a maxima at this scale [229,231]. These maxima are not seen in the correlation function of all galaxies, and also not in the correlation function of all groups and clusters. The reason for that is simple—single galaxies and very poor groups can be found everywhere in the cosmic web, and the distances between them average out when calculating the correlation function. If the distribution of rich superclusters in the cosmic web were random, then there were also no such maxima in the correlation function of clusters in superclusters. The maxima in the correlation function appear when rich galaxy clusters, as density enhancements, form a quasiregular 3D pattern [231]. The presence of the regular patterns in the distribution of rich clusters was further confirmed by applying the regularity periodogram [226].

Intriguingly, a hint of the quasiregular pattern in the distribution of quasar systems at redshifts $z>1$ was also found [74]. The scale of this possible pattern, 400 $h^{-1}$ Mpc, differs from the scale found in the distribution of nearby rich superclusters. The question of whether this patterns is real, or just a visual appearance, is still open.

The MAIN galaxy sample of the Sloan Digital Sky Survey covers a part of the pattern of superclusters. Three chains of rich superclusters in this region were described in Section 3 [62]. Rich superclusters in this sky region from the supercluster catalogue by [53], based on the SDSS galaxy data, form three chains in an almost round, “doughnut-shaped” structure with a scale of 120–140 $h^{-1}$ Mpc, centred at the cluster A 1795 in the Bootes supercluster, and marked by rich galaxy clusters in superclusters of the Sloan Great Wall, the Corona Borealis supercluster, the Ursa Major supercluster, and others [62,232]. Figure 22 shows the distribution of galaxy groups and clusters from [99] group catalogue, based on the SDSS MAIN galaxy sample, in superclusters centred at cluster A 1795 in the Bootes supercluster. In this figure, Cartesian coordinates are defined as in Liivamägi et al. [53]: $x=-dsin\lambda$, $y=dcos\lambda cos\eta$, and $z=dcos\lambda sin\eta$, where d is the comoving distance, and $\lambda$ and $\eta$ are the SDSS survey coordinates. In the SDSS, the survey coordinates form a spherical coordinate system, where $(\eta ,\lambda )=(0,90.)$ corresponds to $(R.A.,Dec.)=(275.,0.)$, $(\eta ,\lambda )=(57.5,0.)$ corresponds to $(R.A.,Dec.)=(0.,90.)$, and at $(\eta ,\lambda )=(0.,0.)$, $(R.A.,Dec.)=(185.,32.5)$. In Figure 22, one can see rich clusters with at least 50 member galaxies in superclusters forming an almost spherical structure with the characteristic size of approximately 120–140 $h^{-1}$ Mpc around cluster A 1795 in the Bootes supercluster. Clusters in the Hercules supercluster, almost projected to the Bootes supercluster, are located at the closest to us edge of the structure [232]. At the farthest edge, this structure is bordered by a giant underdense region, described earlier by [24,62], and noted also in [232].

The structure centred at A 1795 is also seen in the CosmicFlows 4 data, named “Ho’oleilana” (“Sent murmurs of awakening” from the Hawaiian Kumulipo creation chant) [233]. Therefore, this structure, as a part of the quasiregular patterns in the distribution of rich galaxy clusters and superclusters, was determined by different datasets (namely, Abell clusters and superclusters, SDSS galaxies, groups, superclusters, and CosmicFlows 4 data on peculiar velocities of galaxies and galaxy groups) and different methods, but all these show the presence of this pattern, with the characteristic distance between centres of rich superclusters being approximately 120–140 $h^{-1}$ Mpc.

The structure in Figure 22 around cluster A 1795 is formed by rich clusters (red circles in the figure) in the richest superclusters of the Sloan Great Wall (SGW1 and SGW2), in the Corona Borealis supercluster (CB), in the Ursa Major supercluster (UMa), and in other superclusters. In

Table 1. Data of superclusters.

(1)	(2)	(3)	(4)	(5)	(6)	(7)
ID (Long)	${\displaystyle Dist.}$	${\mathit{L}}_{\mathbf{tot}}$	${\mathit{D}}_{\mathbf{peak}}$	${\mathit{M}}_{\mathit{M}\mathbf{/}\mathit{L}}$	${\mathit{M}}_{\mathit{gr}}$	ID
239+027+0091	264	1809	22.2	0.65	0.74	A2142
184+003+0077	231	2919	15.0	1.01	1.06	SGW2
167+040+0078	225	751	14.6	0.32	0.43	95 *
202−001+0084	256	5163	14.0	1.72	2.44	SGW1
230+027+0070	215	2874	11.5	1.29	0.96	Corona Borealis
272+054+0071	207	1618	9.2	0.72	0.19	Ursa Major
227+007+0045	135	379	8.7	0.16	0.27	154 *
151+054+0047	139	465	6.8	0.20
230+008+0030	106	436		0.14	0.57	Hercules1
247+040+0020	92	527		0.23	0.51	Hercules2
216+016+0051	159	284	8.5	0.12	0.27	Bootes

The columns are as follows: 1: Long ID of a supercluster AAA+BBB+ZZZZ, where AAA is R.A., +/− BBB is Dec. (in degrees), and ZZZZ is 1000z (see [53] for details); 2: the distance of a supercluster, in $h^{-1}$ Mpc; 3: the total weighted luminosity of galaxies in the supercluster, $L_{\mathrm{tot}}$, in ${10}^{10}{h}^{-2}{L}_{\odot }$; 4: the luminosity density value at the density maximum (density contrast), $D_{\mathrm{peak}}$, in units of the mean luminosity density [53]; 5: mass of a supercluster calculated using $M/L=300$, in units of ${10}^{16}{M}_{\odot }$; 6: mass of a supercluster calculated using the sum of supercluster member groups in the adaptive supercluster catalogue ([53], in units of ${10}^{16}{M}_{\odot }$); 7: ID of the supercluster; (*) denotes the supercluster ID in the catalogue by Einasto et al. [55]. SGW1 and SGW2 refer to the two richest superclusters in the Sloan Great Wall, A2142 is the supercluster SCl A2142 [98], Hercules1 and Hercules2—the Hercules supercluster, the Corona Borealis supercluster ([20] and references therein), the Bootes supercluster, the Ursa Major supercluster.

, we present data on these superclusters, including supercluster masses. As for all these superclusters, luminosities are available from [232], and the supercluster masses have been calculated using supercluster luminosities and mass-to-light ratios $M/L=300$, as described in Section 4. For comparison, we also provide supercluster masses, calculated using the sum of supercluster member group masses.

The mass of the central cluster in the Bootes supercluster A 1795 is $M\approx$ 6.6–$11.2\times {10}^{14}{M}_{\odot }$ [99,234]. The mass of the Bootes supercluster itself is the lowest among superclusters in this shell, $M_{Boo}\approx 0.1\times {10}^{16}{M}_{\odot }$. Masses of superclusters in the walls of this structure are more than one hundred times higher than the mass of the central cluster, A1795, of the order of $M_{scl}\approx$ 0.2–$3.5\times {10}^{16}{M}_{\odot }$. The total mass in superclusters in the shell walls is at least $M_{tot}\approx 25\times {10}^{16}{M}_{\odot }$.

The huge sizes of these structures tell us that the origin of these structures, and quasiregular patterns in the supercluster distribution should come from the very early Universe. Ref. [232] concluded that the process behind these structures is still unknown. Ref. [233] interpreted the structure that they named Ho’oleilana as a Baryon Acoustic Oscillation (BAO) shell. However, in the BAO shells, the central mass is always much higher than the mass in the shell walls [235]. The analysis of the masses of superclusters contradicts the interpretation of Ho’oleilana as BAO shell, as proposed in [233]. Ref. [232] already provided arguments against BAO interpretation. Namely, its radius is larger than $\approx 109$ $h^{-1}$ Mpc, the BAO scale, and structures are wide, being in the interval of 120–140 $h^{-1}$ Mpc. In addition, the quasiregular pattern in the supercluster distribution is traced by the rich and massive superclusters, and this suggests that its origin is related to the dark matter distribution, and not to baryon oscillations, as these are much weaker. The distribution of galaxy clusters and superclusters is given by the initial density perturbation field, generated during or after the inflation period of the evolution of the dark matter-dominated Universe. In contrast, baryonic acoustic oscillations are generated by sound waves in the baryonic matter before recombination. It is an open question whether the presence of such a quasiregular pattern of rich superclusters can be explained within the ΛCDM cosmological model, as also discussed in [226].

15. Summary and Outlook

Summarising the studies of superclusters since the discovery of the cosmic web, traced by superclusters connected by filaments and separated by voids [2,3,40], we can see a tremendous change. First of all, superclusters played a crucial role in the discovery of the cosmic web: the understanding that superclusters are connected by filaments and separated by voids, forming a pattern now called the cosmic web, was introduced for the first time by the Tartu group of astronomers in their studies of nearby superclusters [1,40]. This discovery is also described in [3]. In the first review of superclusters, ref. [3] mentioned that approximately 20 superclusters were known, with a more detailed description of four nearby superclusters, namely, the Virgo, Coma, Perseus, and Hercules superclusters. In contrast, the latest supercluster catalogues of optical groups and clusters contain data on 662 superclusters in the redshift range $0.05\le z\le 0.42$ [21], and on 633 superclusters in the redshift range $0.5\le z\le 1.0$ [50]. The newest catalogues of superclusters of X-ray clusters include data on eight superclusters in the very local Universe within redshift $z<0.03$ [72], and 1338 superclusters in the Western hemisphere up to redshifts $z=0.8$, 520 of them embed at least three member clusters [73]. Superclusters in the nearby Universe are also traced using the velocity field of galaxies up to redshift $z\approx 0.1$ [9,35,36].

The most massive supercluster in the nearby Universe is one of the first superclusters discovered, the Shapley supercluster, with a mass of approximately $M\approx 5\times {10}^{16}{h}^{-1}{M}_{\odot }$. At higher redshifts, several massive superclusters have been discovered, as the Saraswati, the Einasto, and the King Ghidorah superclusters, with masses of the same order as the Shapley superclusters. The extent of the richest superclusters may reach up to 200 $h^{-1}$ Mpc.

Superclusters represent a special environment for the formation and evolution of galaxies, groups, and clusters. They embed the richest galaxy clusters and the most massive galaxies—the brightest galaxies of rich clusters. On average, superclusters host a higher percentage of red, quiescent galaxies than surrounding low-density regions. X-ray clusters are more frequent in superclusters. They also affect the radio lobes of giant radio galaxies. The preferred alignment of galaxies, groups, and clusters along the supercluster axis, discovered already in the first supercluster studies, has been confirmed by several later studies. It is interesting to note that in his review on superclusters in 1983, Jan Oort had already emphasised the importance of the studies of the coevolution of superclusters and galaxies and galaxy systems within them [3]. This is one of the important future directions in supercluster studies also now. Another direction in the future studies of superclusters is a more detailed analysis of their dynamical properties, as well as of the fractal properties of superclusters.

Superclusters serve as a cosmological test in many ways. The number, density, masses, shapes, and other properties of superclusters and their high-density cores can be compared with cosmological simulations with various cosmologies. The further studies of superclusters will, hopefully, uncover which are the processes in the early Universe behind the regularity of superclusters in the nearby Universe, and whether this regularity can also be detected at higher redshifts. They will clarify the origin of supercluster planes, now speculated as being signatures of long strings in the early Universe.

All this has been made possible thanks to the multiwavelength surveys of galaxies, and from the simulation side, thanks to the simulations in increasingly larger simulation boxes. In this respect, cosmology is now facing a new breakthrough epoch in the next 5–10 years. This will be possible thanks to ongoing and new (full-sky) multiwavelength galaxy surveys, such as 4MOST, J-PAS, DESI, Euclid, JWST (early galaxies at cosmic dawn), CMB surveys, SPHEREx, and others, which enable tracing the density and velocity fields of galaxies up to high redshifts. The combination of various types of data and methods may lead to a better definition of superclusters. The study of superclusters may help to understand the origin of Hubble tension.

In summary, future deep and wide galaxy surveys will provide the opportunity to compare the abundance and properties of superclusters at higher redshifts with the ones in simulations. Therefore, it will be possible to identify and characterise superclusters up to high redshift so as to understand supercluster evolution together with the evolution of the cosmic web and galaxies within. Future studies will hopefully provide us with a better definition of superclusters that take into account the properties of galaxies and groups in superclusters, and velocity data with higher precision than is possible at present. This enables us to compare the properties of galaxies in large, high-density regions like superclusters and in underdense regions like voids to understand the factors affecting their growth and evolution. The current era of deep multiwavelength large sky surveys provides us with the perfect opportunity.