Dark Universe from QFT Mechanisms and Possible Experimental Probes
Abstract
1. Introduction
2. Mixing in QFT and Dark Components of the Universe
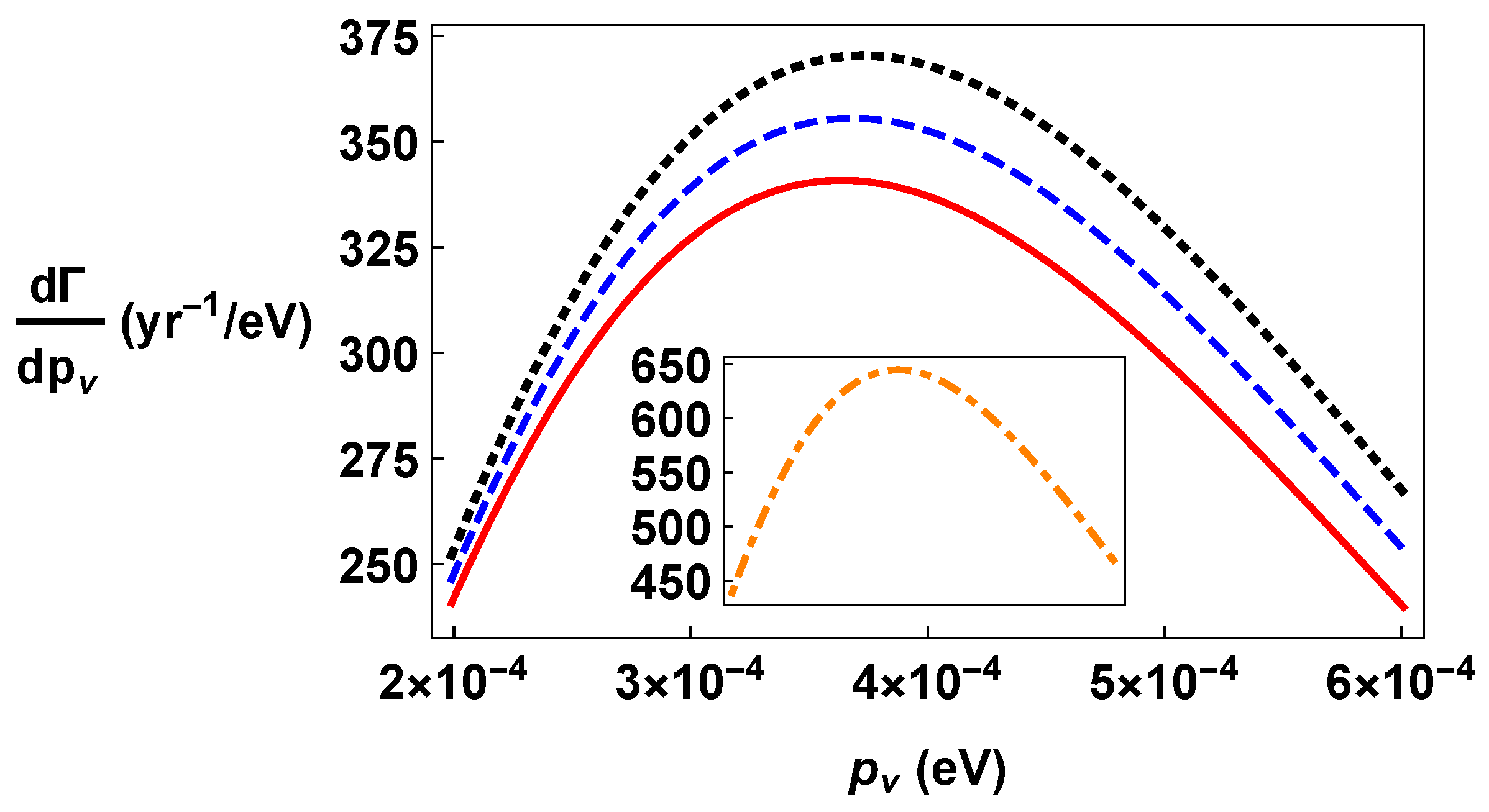
3. Neutrino Capture on Tritium
4. Rydberg Atoms
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ade, P.A.R. et al. [Planck Collaboration] Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys 2016, 594, A13. [Google Scholar] [CrossRef]
- De Bernardis, P.; Ade, P.A.; Bock, J.J.; Bond, J.R.; Borrill, J.; Boscaleri, A.; Cobleet, K.; Crill, B.P.; De Gasperis, G.; Farese, P.C.; et al. A flat Universe from high-resolution maps of the cosmic microwave background radiation. Nature 2000, 404, 955. [Google Scholar] [CrossRef] [PubMed]
- Spergel, D.N.; Verde, L.; Peiris, H.V.; Komatsu, E.; Nolta, M.R.; Bennett, C.L.; Halpern, M.; Hinshaw, G.; Jarosik, N.; Kogut, A.; et al. First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters. Astrophys. J. Suppl. Ser. 2003, 148, 175. [Google Scholar] [CrossRef]
- Dodelson, S.; Narayanan, V.K.; Tegmark, M.; Scranton, R.; Budavari, T.; Connolly, A.; Csabai, I.; Eisenstein, D.; Frieman, J.A.; Gunn, J.E.; et al. The Three-dimensional Power Spectrum from Angular Clustering of Galaxies in Early Sloan Digital Sky Survey Data. Astrophys. J. 2002, 572, 140. [Google Scholar] [CrossRef]
- Szalay, A.S.; Jain, B.; Matsubara, T.; Scranton, R.; Vogeley, M.S.; Connolly, A.; Dodelson, S.; Eisenstein, D.; Frieman, J.A.; Gunn, J.E.; et al. Karhunen-Loève Estimation of the Power Spectrum Parameters from the Angular Distribution of Galaxies in Early Sloan Digital Sky Survey Data. Astrophys. J. 2003, 591, 1. [Google Scholar] [CrossRef]
- Peebles, P.J.E.; Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys. 2003, 75, 559. [Google Scholar] [CrossRef]
- Riess, A.G.; Strolger, L.; Tonry, J.; Casertano, S.; Ferguson, H.C.; Mobasher, B.; Challis, P.; Filippenko, A.V.; Jha, S.; Li, W.; et al. Type Ia Supernova Discoveries at z>1 from the Hubble Space Telescope: Evidence for Past Deceleration and Constraints on Dark Energy Evolution. Astrophys. J. 2004, 607, 665. [Google Scholar] [CrossRef]
- Trimble, V. Exotic dark matter in the universe. Annu. Rev. Astron. Astrophys. 1987, 25, 425–472. [Google Scholar] [CrossRef]
- Hinshaw, G.; Larson, D.; Komatsu, E.; Spergel, D.N.; Bennett, C.L.; Dunkley, J.; Nolta, M.R.; Halpern, M.; Hill, R.S.; Odegard, N.; et al. Nine-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Parameter Results. Astrophys. J. Suppl. Ser. 2013, 208, 19. [Google Scholar] [CrossRef]
- Hin, T.; Gupta, V. The Dark Matter: A Review of Current Understanding. Phys. Rep. 2020, 843, 1–54. [Google Scholar]
- Bertone, G.; Hooper, D.; Silk, J. Particle dark matter: Evidence, candidates and constraints. Phys. Rep. 2005, 405, 279. [Google Scholar] [CrossRef]
- D’amico, G.; Kamionkowski, M.; Sigurdson, K. Dark matter astrophysics. arXiv 2012, arXiv:0907.1912(2012). [Google Scholar]
- Bertone, G. Particle Dark Matter: Observation, Models and Searches; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Bottino, A.; Fornengo, N. Dark matter and its particle candidates. lectures published in Trieste 1998, non-accelerator particle physics. arXiv 1988, arXiv:hep-ph/9904469. [Google Scholar]
- Feng, J.L. Dark Matter Candidates from Particle Physics and Methods of Detection. Ann. Rev. Nuc. Part. Sci. 2010, 48, 495–545. [Google Scholar] [CrossRef]
- Chang, J.; Ambrosi, G.; An, Q.; Asfandiyarov, R.; Azzarello, P.; Bernardini, P.; Bertucci, B.; Cai, M.S.; Caragiulo, M.; Chen, D.Y.; et al. The DArk Matter Particle Explorer mission. Astrop. Phys. 2017, 95, 6–24. [Google Scholar] [CrossRef]
- Profumo, S.; Giani, L.; Piattella, O.F. An Introduction to Particle Dark Matter. Universe 2019, 5, 213. [Google Scholar] [CrossRef]
- Bertone, G.; Tait, T.M.P. A new era in the search for dark matter. Nature 2018, 562, 51–56. [Google Scholar] [CrossRef]
- Hooper, D. Particle Dark Matter; The Dawn of the LHC Era: Boulder, CO, USA, 2010; pp. 709–764. [Google Scholar]
- Boehm, C.; Fayet, P.; Silk, J. Light and heavy dark matter particles. Phys. Rev. D 2004, 69, 101302. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Finkbeiner, D.P.; Slatyer, T.R.; Weiner, N. A theory of dark matter. Phys. Rev. D 2009, 79, 015014. [Google Scholar] [CrossRef]
- Khoury, J. Alternative to particle dark matter. Phys. Rev. D 2015, 91, 024022. [Google Scholar] [CrossRef]
- Comelli, D.; Pietroni, M.; Riotto, A. Dark energy and dark matter. Phys. Lett. B 2003, 571, 115–120. [Google Scholar] [CrossRef]
- Farrar, G.R.; Peebles, P.J.E. Interacting Dark Matter and Dark Energy. Astroph. J. 2004, 604, 1. [Google Scholar] [CrossRef]
- Baudis, L. Dark matter detection. J. Phys. G Nucl. Part Phys. 2016, 43, 044001. [Google Scholar] [CrossRef]
- Hui, L. Wave dark matter. Ann. Rev. Astr. Astroph. 2021, 59, 247–289. [Google Scholar] [CrossRef]
- Gaskins, J.M. A review of indirect searches for particle dark matter. Contemp. Phys. 2016, 57, 496–525. [Google Scholar] [CrossRef]
- Capolupo, A.; Pisacane, G.; Quaranta, A.; Romeo, F. Probing mirror neutrons and dark matter through cold neutron interferometry. Phys. Dark Universe 2024, 46, 101688. [Google Scholar] [CrossRef]
- Capolupo, A.; Quaranta, A.; Serao, R. The impact of the X17 boson on particle physics anomalies: Muon anomalous magnetic moment, Lamb shift and W mass. Phys. Dark Universe 2025, 47, 101748. [Google Scholar] [CrossRef]
- Iwamoto, S.; Seller, K.; Trócsányi, Z. Sterile neutrino dark matter in a U(1) extension of the standard model. J. Cosmol. Astropart. Phys. 2022, 1, 35. [Google Scholar] [CrossRef]
- Ilten, P.; Soreq, Y.; Williams, M.; Xue, W. Serendipity in dark photon searches. J. High Energy Phys. 2018, 6, 4. [Google Scholar] [CrossRef]
- Huang, P.; Wagner, C.E.M. Blind spots for neutralino dark matter in the MSSM with an intermediate mA. Phys. Rev. D 2014, 90, 015018. [Google Scholar] [CrossRef]
- Low, M.; Wang, L.T. Neutralino dark matter at 14 TeV and 100 TeV. J. High Energy Phys. 2014, 2014, 161. [Google Scholar] [CrossRef]
- Enqvist, K.; Mazumdar, A. Cosmological consequences of MSSM flat directions. Phys. Rep. 2003, 380, 99–234. [Google Scholar] [CrossRef]
- Roszkowski, L.; Sessolo, E.M.; Trojanowski, S. WIMP dark matter candidates and searches- current status and future prospects. Rep. Prog. Phys. 2018, 81, 066201. [Google Scholar] [CrossRef] [PubMed]
- Carroll, S.M. The cosmological constant. Liv. Rev. Relativ. 2001, 4, 1. [Google Scholar] [CrossRef]
- Dolan, M.J.; Kahlhoefer, F.; McCabe, C.; Schmidt-Hoberg, K. A taste of dark matter: Flavour constraints on pseudoscalar mediators. J. High Energ. Phys. 2015, 2015, 171. [Google Scholar] [CrossRef]
- Martin, S.P. A supersymmetry primer. Adv. Ser. Direct. J. High Energy Phys. 1998, 18, 1. [Google Scholar]
- Beekveld, M.V.; Caron, S.; Austri, R.R.D. The current status of fine-tuning in supersymmetry. J. High Energ. Phys. 2020, 2020, 147. [Google Scholar] [CrossRef]
- Baer, H.; Barger, V.; Huang, P.; Tata, X. Natural supersymmetry: LHC, dark matter and ILC searches. J. High Energ. Phys. 2012, 2012, 109. [Google Scholar] [CrossRef]
- Munoz, C. Model of supersymmetry for dark matter. EPJ Web Conf. 2017, 36, 01002. [Google Scholar] [CrossRef]
- Gomez, M.E.; Lazarides, G.; Pallis, C. yukawa quasi-unification. Nucl. Phys. B 2002, 638, 165–185. [Google Scholar] [CrossRef]
- Lopez, J.L.; Yuan, K.; Nanopoulos, D.V. SUSY guts dark matter. Nucl. Phys. B 1991, 267, 2. [Google Scholar] [CrossRef]
- Feng, J.L.; Matcvhev, K.T.; Wilczek, F. Neutralino dark matter in focus point supersymmetry. Phys. Lett. B 2000, 482, 4. [Google Scholar] [CrossRef]
- Nath, P.; Arnowitt, R. Nonuniversal soft supersymmetry breaking and dark matter. Phys. Rev. D 1997, 56, 5. [Google Scholar] [CrossRef]
- Cohen, T.; Lisanti, M.; Pierce, A.; Slatyer, T.R. Wino dark matter under siege. J. Cosmol. Astropart. Phys. 2013, 2013, 061. [Google Scholar] [CrossRef]
- Fan, J.; Reece, M. In wino veritas? Indirect searches shed light on neutralino dark matter. J. High Energ. Phys. 2013, 2013, 124. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. New Astron. Rev. 2022, 95, 101659. [Google Scholar] [CrossRef]
- Misiaszek, M.; Rossi, N. Direct detection of dark matter: A critical review. Symmetry 2024, 16, 201. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Effects of the axion through the Higgs portal on primordial gravitational waves during the electroweak breaking. Phys. Rev. D 2023, 107, 064071. [Google Scholar] [CrossRef]
- Pandey, S.; Hall, E.D.; Evans, M. First results from the axion dark-matter birefringent cavity (ADBC) experiment. Phys. Rev. Lett. 2024, 133, 111003. [Google Scholar] [CrossRef]
- Oswald, R.; Nevsky, A.; Vogt, V.; Schiller, S.; Figueroa, N.; Zhang, K.; Tretiak, O.; Antypas, D.; Budker, D.; Banerjee, A.; et al. Search for dark matter induced oscillations of fundamental constant using molecular spectroscopy. Phys. Rev. Lett. 2022, 129, 031302. [Google Scholar] [CrossRef]
- Dror, J.A.; Gori, S.; Munbodh, P. QCD axion-mediated dark matter. J. High Energy Phys. 2023, 2023, 128. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H. CP conservation in the presence of pseudoparticles. Phys. Rev. Lett. 1977, 38, 1440. [Google Scholar] [CrossRef]
- Peccei, R.D.; Quinn, H. Constraints imposed by CP conservation in the presence of pseudoparticles. Phys. Rev. D 1977, 16, 1791. [Google Scholar] [CrossRef]
- Weinberg, S. A New Light Boson? Phys. Rev. Lett. 1978, 40, 223. [Google Scholar] [CrossRef]
- Wilczek, F. Problem of strong P and T invariance in the presence of instantons. Phys. Rev. Lett. 1978, 40, 279. [Google Scholar] [CrossRef]
- Raffelt, G.G. Axions- motivation, limits and searches. J. Phys. A 2007, 40, 6607. [Google Scholar] [CrossRef]
- Marsch, D.J.E. Axion Cosmology. Phys. Rep. 2016, 643, 1–79. [Google Scholar] [CrossRef]
- Kim, J.E. Weak-Interaction Singlet and Strong CP Invariance. Phys. Rev. Lett. 1979, 43, 103. [Google Scholar] [CrossRef]
- Shifman, M.; Vainshtein, A.; Zakharov, V. Can confinement ensure natural CP invariance of strong interactions? Nucl. Phys. B 1980, 166, 493. [Google Scholar] [CrossRef]
- Zhitnitsky, A.R. On Possible Suppression of the Axion Hadron Interactions. Sov. J. Nucl. Phys. 1980, 31, 260. [Google Scholar]
- Dine, M.; Fischler, W.; Srednicki, M. A Simple Solution to the Strong CP Problem with a Harmless Axion. Phys. Lett. B 1981, 104, 199. [Google Scholar] [CrossRef]
- Capolupo, A.; Giampaolo, S.M.; Lambiase, G.; Quaranta, A. Probing quantum field theory particle mixing and dark-matter-like effects with Rydberg atoms. Eur. Phys. J. C 2020, 80, 423. [Google Scholar] [CrossRef]
- Capolupo, A.; Quaranta, A. Neutrino capture on tritium as a probe of flavor vacuum condensate and dark matter. Phys. Lett. B 2023, 839, 137776. [Google Scholar] [CrossRef]
- Capolupo, A.; Quaranta, A.; Serao, R. Field mixing in curved spacetime and Dark Matter. Symmetry 2023, 15, 807. [Google Scholar] [CrossRef]
- Capolupo, A.; Maria, G.D.; Monda, S.; Quaranta, A.; Serao, R. Quantum field theory of neutrino mixing in spacetime with torsion. Universe 2024, 10, 170. [Google Scholar] [CrossRef]
- Capolupo, A.; Carloni, S.; Quaranta, A. Quantum flavor vacuum in the expanding universe: A possible candidate for cosmological dark matter? Phys. Rev. D 2022, 105, 105013. [Google Scholar] [CrossRef]
- Capolupo, A.; Capozziello, S.; Pisacane, G.; Quaranta, A. Missing matter in galaxies as a neutrino mixing effect. Phys. Dark Universe 2025, 48, 101894. [Google Scholar] [CrossRef]
- Capolupo, A.; Quaranta, A. Boson mixing and flavor vacuum in the expanding universe: A possible candidate for the dark energy. Phys. Lett. B 2023, 840, 137889. [Google Scholar] [CrossRef]
- Capolupo, A.; Quaranta, A. Fermion condensate induced by axial interactions and cosmological implications. J. Phys. G. 2024, 51, 105202. [Google Scholar] [CrossRef]
- Alfinito, E.; Blasone, M.; Iorio, A.; Vitiello, G. Squeezed neutrino oscillations in quantum field theory. Phys. Lett. B 1995, 362, 91–96. [Google Scholar] [CrossRef]
- Blasone, M.; Vitiello, G. Quantum field theory of fermion mixing. Ann. Phys. 1995, 244, 283–311. [Google Scholar] [CrossRef]
- Blasone, M.; Capolupo, A.; Vitiello, G. Quantum field theory of three flavor neutrino mixing and oscillations with CP violation. Phys. Rev. D 2002, 66, 025033. [Google Scholar] [CrossRef]
- Blasone, M.; Capolupo, A.; Capozziello, S.; Carloni, S.; Vitiello, G. Neutrino mixing contribution to the cosmological constant. Phys. Lett. A 2004, 323, 182–189. [Google Scholar] [CrossRef]
- Ji, C.-R.; Mishchenko, Y. The general theory of quantum field mixing. Phys. Rev. D 2002, 65, 096015. [Google Scholar] [CrossRef]
- Capolupo, A.; Ji, C.-R.; Mishchenko, Y.; Vitiello, G. Phenomenology of flavor oscillations with non-perturbative effects from quantum field theory. Phys. Lett. B 2004, 594, 135–140. [Google Scholar] [CrossRef]
- Betti, M.G. et al. [PTOLEMY Collaboration] Neutrino physics with the PTOLEMY project: Active neutrino properties and the light sterile case. arXiv 2019, arXiv:1902.05508. [Google Scholar]
- Long, A.J.; Lunardini, C.; Sabancilar, E. Detecting non-relativistic cosmic neutrinos by capture on tritium: Phenomenology and physics potential. arXiv 2014, arXiv:1405.7654. [Google Scholar] [CrossRef]
- Jusufi, K.; Leon, G.; Millano, A.D. Dark Universe Phenomenology from Yukawa Potential? Phys. Dark Univ. 2023, 42, 101318. [Google Scholar] [CrossRef]
- Cardone, V.F.; Capozziello, S. Systematic biases on galaxy haloes parameters from Yukawa-like gravitational potentials. Mon. Not. Roy. Astron. Soc. 2011, 414, 1301. [Google Scholar] [CrossRef]
- Stabile, A.; Capozziello, S. Galaxy rotation curves in f(R,ϕ) gravity. Phys. Rev. D 2013, 87, 064002. [Google Scholar] [CrossRef]
- Zyla, P.A. et al. [Particle Data Group] Review of particle physics. Prog. Theor. Exp. Phys. 2020, 2022, 083C01. [Google Scholar]
- Gallagher, T.F. Rydberg atoms. Rep. Prog. Phys. 1988, 51, 143. [Google Scholar] [CrossRef]
- Han, J.; Jamil, Y.; Norum, D.V.L.; Tanner, P.J.; Gallagher, T.F. RB nf quantum defects from millimeter-wave spectroscopy of cold 85Rb Rydberg atoms. Phys. Rev. A 2006, 74, 054502. [Google Scholar] [CrossRef]
- Li, W.; Mourachko, I.; Noel, M.W.; Gallagher, T.F. Millimeter-wave spectroscopy of cold Rb Rydberg atoms in a magneto-optical trap: Quantum defects of the ns, np, and nd series. Phys. Rev. A 2003, 67, 052502. [Google Scholar] [CrossRef]
- Weber, K.-H.; Sansonetti, C.J. Accurate energies of nS, nP, nD, nF, and nG levels of neutral cesium. Phys. Rev. A 1987, 35, 4650. [Google Scholar] [CrossRef]
- Cui, J.; van Bijnen, R.; Pohl, T.; Montangero, S.; Calarco, T. Optimal control of Rydberg lattice gases. Quantum Sci. Technol. 2017, 2, 035006. [Google Scholar] [CrossRef]
- Umezawa, H.; Matsumoto, H.; Tachiki, M. Thermo Field Dynamics and Condensed States; North-Holland: New York, NY, USA, 1982. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capolupo, A.; Monda, S.; Pisacane, G.; Quaranta, A.; Serao, R. Dark Universe from QFT Mechanisms and Possible Experimental Probes. Universe 2025, 11, 142. https://doi.org/10.3390/universe11050142
Capolupo A, Monda S, Pisacane G, Quaranta A, Serao R. Dark Universe from QFT Mechanisms and Possible Experimental Probes. Universe. 2025; 11(5):142. https://doi.org/10.3390/universe11050142
Chicago/Turabian StyleCapolupo, A., S. Monda, G. Pisacane, A. Quaranta, and R. Serao. 2025. "Dark Universe from QFT Mechanisms and Possible Experimental Probes" Universe 11, no. 5: 142. https://doi.org/10.3390/universe11050142
APA StyleCapolupo, A., Monda, S., Pisacane, G., Quaranta, A., & Serao, R. (2025). Dark Universe from QFT Mechanisms and Possible Experimental Probes. Universe, 11(5), 142. https://doi.org/10.3390/universe11050142






