Rough Estimates of Solar System Gravitomagnetic Effects in Post-Newtonian Gravity
Abstract
1. Introduction
2. Formalism of Astrophysical Phenomenology
2.1. Gravitomagnetism Originating from MLGR
2.2. Mass Magnetic GR Force
3. Phenomenology of Astrophysical Systems in Gravitomagnetism
3.1. Earth and Moon
3.2. Sun and Solar System Planets
3.3. B Ring of Saturn
4. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
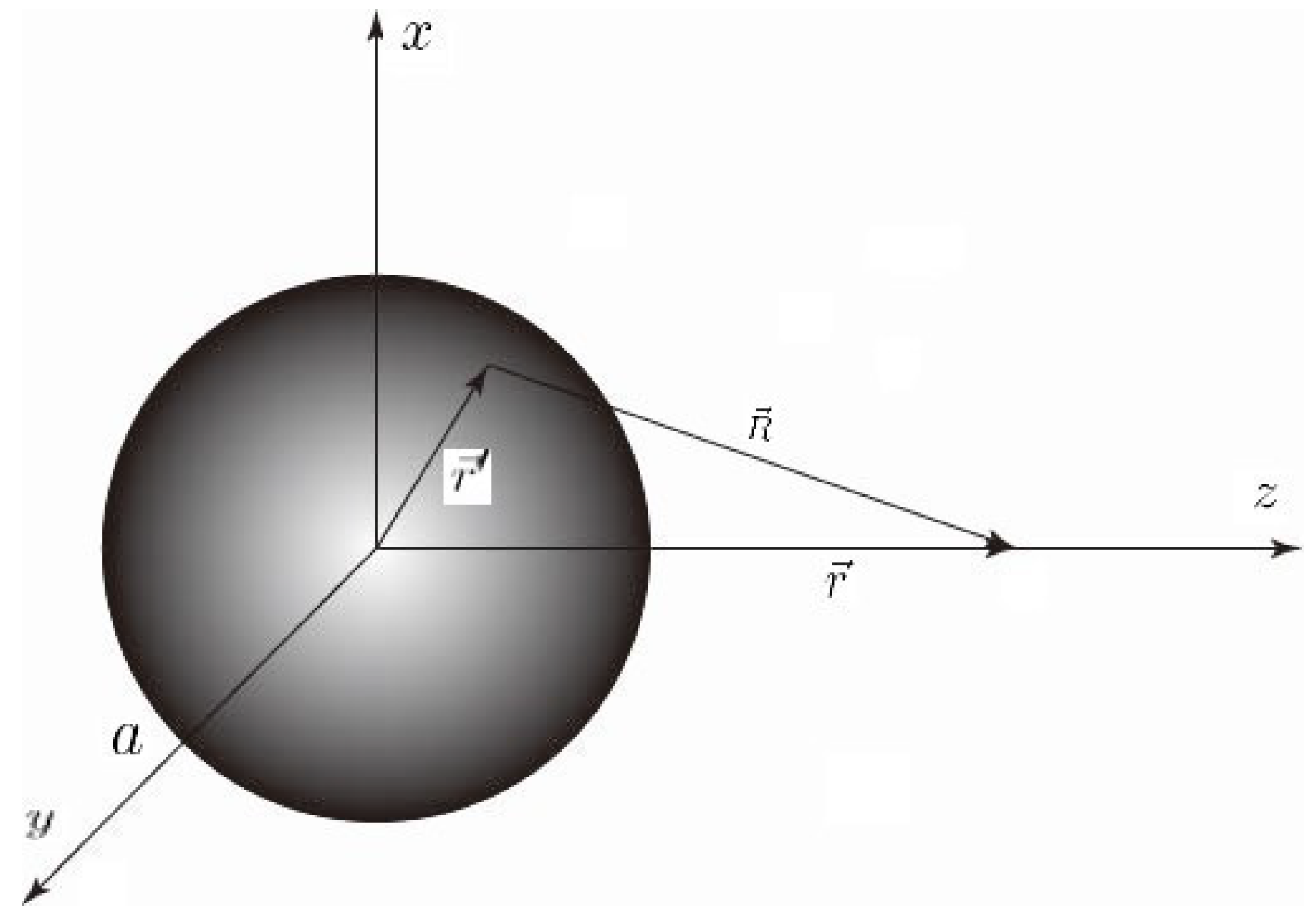
Appendix A. Sketch of EM
| 1 | Superscripts E and B stand for the mass electric Newtonian force and the mass magnetic force, respectively. |
| 2 | Here, we have exploited the identity . |
| 3 | Here, we assume that this observer resides on a space-fixed frame and does not co-rotate together with the Earth so that we can include the spinning effect of the Earth. The same statement is applied to the observers who are located on the surfaces of the Moon, the Sun and the solar system planets. |
| 4 | |
| 5 | From now on, denotes the force () acting on the position at under the field at , for instance. Here, the argument expressed as indicates the vector of the direction from to with a magnitude of . |
| 6 | From now on, the minus sign in indicates the attractive Newtonian force between and , for example. |
| 7 | In Table 1, the magnitudes of and are given in units of , and these values are dimensionless. The minus signs in , again, denote the attractive Newtonian forces between and . |
| 8 | Here, we exploit the approximation at a distant observation point of , where the ellipsis stands for the higher-order terms that can be ignored for the mass-vector potential of a localized mass-current distribution. Note that the first term denotes the mass magnetic monopole term, which vanishes for the closed-loop integral, as expected. Thus, in this paper, we exclude the possibility of a mass magnetic monopole, in addition to that of a charge magnetic monopole. |
| 9 | The recent Cassini data show that the total mass of the rings of Saturn is [16]. In evaluating (48), we exploit this value for the B-ring mass () for simplicity, since the B ring is known to probably be the most massive of Saturn’s rings [24]. Next the orbital radius of the B ring is given by [20]; thus, we use the average value of . Moreover, we ignore the effect of the width of the B ring of Saturn in the evaluation in (48) for simplicity. |
References
- Deriglazov, A.A.; Ramirez, W.G. Frame-dragging effect in the field of non rotating body due to unit gravimagnetic moment. Phys. Lett. B 2018, 779, 210–213. [Google Scholar] [CrossRef]
- Everitt, C.W.F.; Muhlfelder, B.; DeBra, D.B.; Parkinson, B.W.; Turneaure, J.P.; Silbergleit, A.S.; Acworth, E.B.; Adams, M.; Adler, R.; Bencze, W.J.; et al. The Gravity Probe B test of general relativity. Class. Quantum Gravity 2015, 32, 224001. [Google Scholar] [CrossRef]
- Lense, J.; Thirring, H. Ueber den Einfluss der Eigenrotation der Zentralkoerper auf die Bewegung der Planeten und Monde nach der Einsteinschen Gravitationstheorie. Phys. Z. 1918, 19, 156, English translation of this paper appears in Mashhoon, B.; Hehl, F.W.; Theiss, D.S. Gen. Relativ. Gravit. 1984, 16, 711. [Google Scholar]
- Iorio, L. Will the recently approved LARES mission be able to measure the Lense-Thirring effect at 1%? Gen. Relativ. Gravit. 2009, 41, 1717–1724. [Google Scholar] [CrossRef]
- Hobson, M.P.; Efstathiou, G.; Lasenby, A.N. General Relativity: An Introduction for Physicists; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Ludwig, G.O. Galactic rotation curve and dark matter according to gravitomagnetism. Eur. Phys. J. C 2021, 81, 186. [Google Scholar] [CrossRef]
- Ruggiero, M.L.; Ortolan, A.; Speake, C.C. Galactic dynamics in general relativity: The role of gravitomagnetism. Class. Quantum Gravity 2022, 39, 225015. [Google Scholar] [CrossRef]
- Glampedakis, K.; Jones, D.I. Pitfalls in applying gravitomagnetism to galactic rotation curve modelling. Class. Quantum Gravity 2023, 40, 147001. [Google Scholar] [CrossRef]
- Lasenby, A.N.; Hobson, M.P.; Barker, W.E.V. Gravitomagnetism and galaxy rotation curves: A cautionary tale. Class. Quantum Gravity 2023, 40, 215014. [Google Scholar] [CrossRef]
- Hong, S.T. New algorithm of measuring gravitational wave radiation from rotating binary system. Phys. Scripta 2024, 99, 105030. [Google Scholar] [CrossRef]
- Wald, R.M. General Relativity; University of Chicago Press: Chicago, IL, USA, 1984. [Google Scholar]
- Landau, L.D.; Lifschits, E.M. The Classical Theory of Fields; Pergamon Press: Oxford, UK, 1975. [Google Scholar]
- Ward, W.R.; Hamilton, D.P. Tilting Saturn. I. analytic model. Astrophys. J. 2004, 128, 2501. [Google Scholar] [CrossRef]
- Goldreich, P.; Tremaine, S. The dynamics of planetary rings. Ann. Rev. Astron. Astrophys. 1982, 20, 249–283. [Google Scholar] [CrossRef]
- Zhang, Z.; Hayes, A.G.; Janssen, M.A.; Nicholson, P.D.; Cuzzi, J.N.; de Pater, I.; Dunn, D.E. Exposure age of Saturn’s A and B rings, and the Cassini Division as suggested by their non-icy material content. Icarus 2017, 294, 14–42. [Google Scholar] [CrossRef]
- Iess, L.; Militzer, B.; Kaspi, Y.; Nicholson, P.; Durante, D.; Racioppa, P.; Anabtawi, A.; Galanti, E.; Hubbard, W.; Mariani, M.J.; et al. Measurement and implications of Saturn’s gravity field and ring mass. Science 2019, 364, 2965. [Google Scholar] [CrossRef] [PubMed]
- Wisdom, J.; Dbouk, R.; Militzer, B.; Hubbard, W.B.; Nimmo, F.; Downey, B.G.; French, R.G. Loss of a satellite could explain Saturn’s obliquity and young rings. Science 2022, 377, 1285. [Google Scholar] [CrossRef] [PubMed]
- Jackson, J.D. Classical Electrodynamics; John Wiley & Sons: Danvers, MA, USA, 1999. [Google Scholar]
- Griffiths, D. Introduction to Electrodynamics; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Carroll, B.W.; Ostlie, D.A. Modern Astrophysics; Addison-Wesley: New York, NY, USA, 1996. [Google Scholar]
- De Wit, B.; Smith, J. Field Theory in Particle Physics; North-Holland: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Navas, S.; Amsler, C.; Gutsche, T.; Hanhart, C.; Hernández-Rey, J.J.; Lourenço, C.; Masoni, A.; Mikhasenko, M.; Mitchell, R.E.; Patrignani, C.; et al. [Particle Data Group] Review of particle physics. Phys. Rev. D 2024, 110, 030001. [Google Scholar] [CrossRef]
- Padmanabhan, T. Theoretical Astrophysics; Cambridge University Press: Cambridge, UK, 2001; Volume II. [Google Scholar]
- Hedman, M.M.; Nicholson, P.D. The B-rings’s surface mass density from hidden density waves: Less than meets the eye? Icarus 2016, 279, 109. [Google Scholar] [CrossRef]
- Bastin, J.A. Note on the rings of Saturn. Moon Planets 1981, 24, 467. [Google Scholar] [CrossRef]
- Goldstein, H. Classical Mechanics; Addison-Wesley: Boston, MA, USA, 1980. [Google Scholar]
- Dones, L. A recent cometary origin for Saturn’s rings? Icarus 1991, 92, 194–203. [Google Scholar] [CrossRef]
- Iorio, L. Is there still something left that Gravity Probe B can measure? Universe 2020, 6, 85. [Google Scholar] [CrossRef]
| i-th Planet | ||||
|---|---|---|---|---|
| Mercury | ||||
| Venus | * | * | ||
| Earth | ||||
| Mars | ||||
| Jupiter | ||||
| Saturn | ||||
| Uranus | * | * | ||
| Neptune |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, S.-T. Rough Estimates of Solar System Gravitomagnetic Effects in Post-Newtonian Gravity. Universe 2025, 11, 90. https://doi.org/10.3390/universe11030090
Hong S-T. Rough Estimates of Solar System Gravitomagnetic Effects in Post-Newtonian Gravity. Universe. 2025; 11(3):90. https://doi.org/10.3390/universe11030090
Chicago/Turabian StyleHong, Soon-Tae. 2025. "Rough Estimates of Solar System Gravitomagnetic Effects in Post-Newtonian Gravity" Universe 11, no. 3: 90. https://doi.org/10.3390/universe11030090
APA StyleHong, S.-T. (2025). Rough Estimates of Solar System Gravitomagnetic Effects in Post-Newtonian Gravity. Universe, 11(3), 90. https://doi.org/10.3390/universe11030090






