Properties of Heavy Higgs Bosons and Dark Matter Under Current Experimental Limits in the μNMSSM
Abstract
1. Introduction
2. Theoretical Preliminaries
2.1. The Basics of the NMSSM
2.2. The Heavy Higgs Bosons
2.3. The Anomalous Magnetic Moment of the Muon in the NMSSM
2.4. DM-Nucleon Scattering Cross-Section
3. Numerical Results
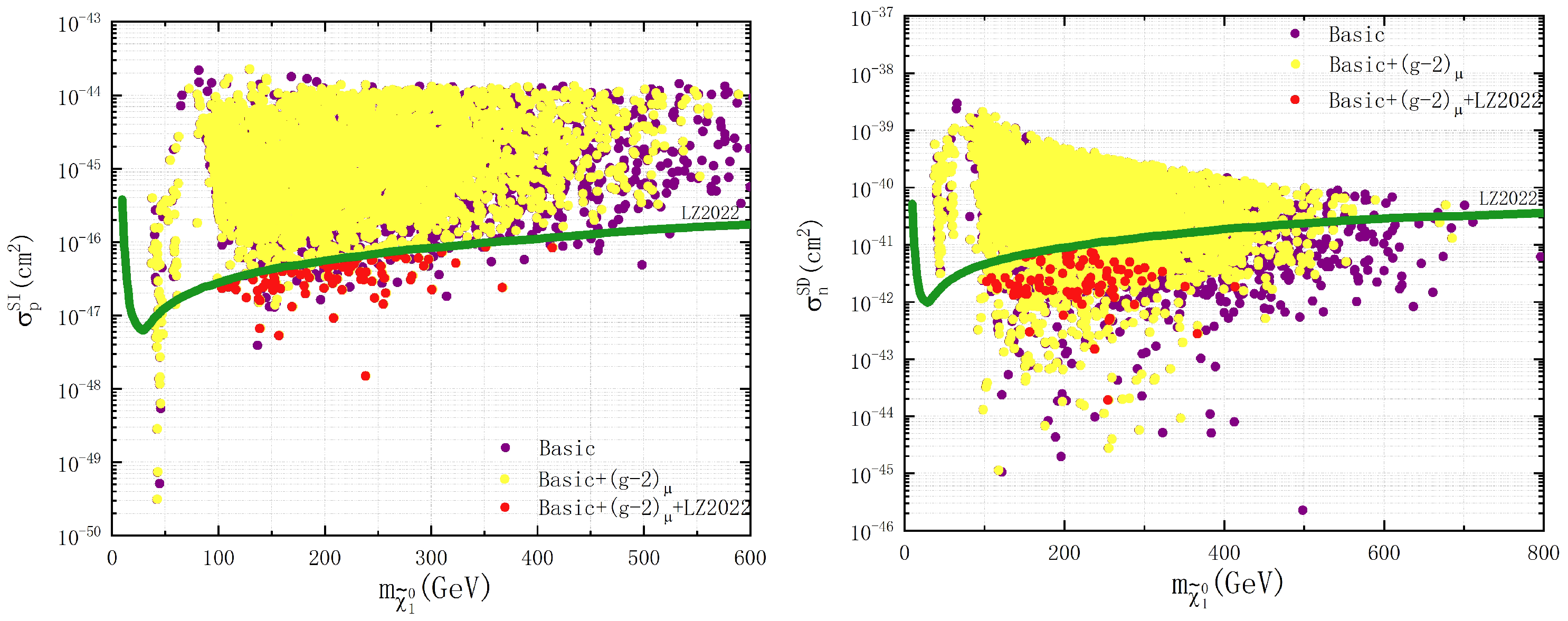
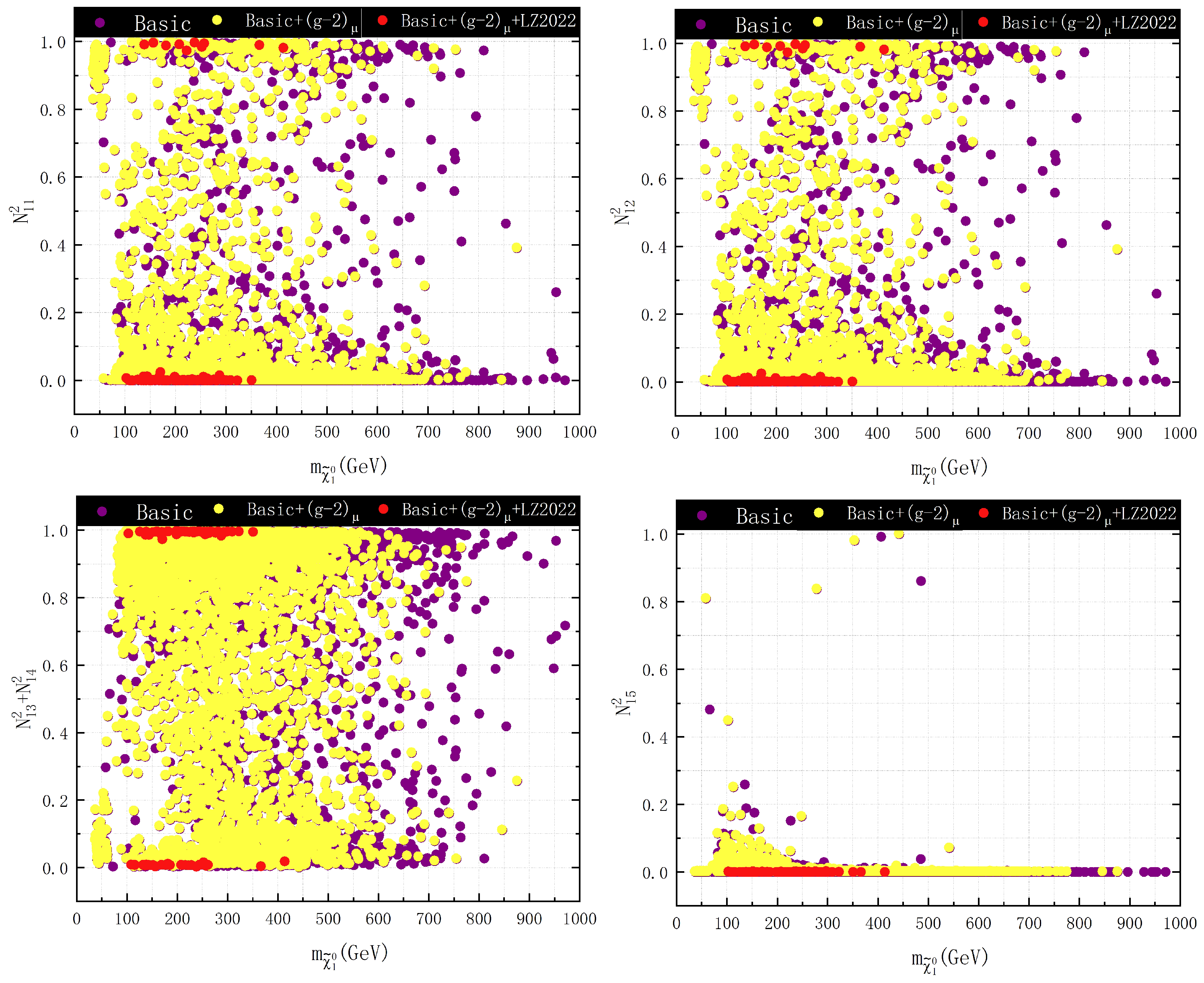
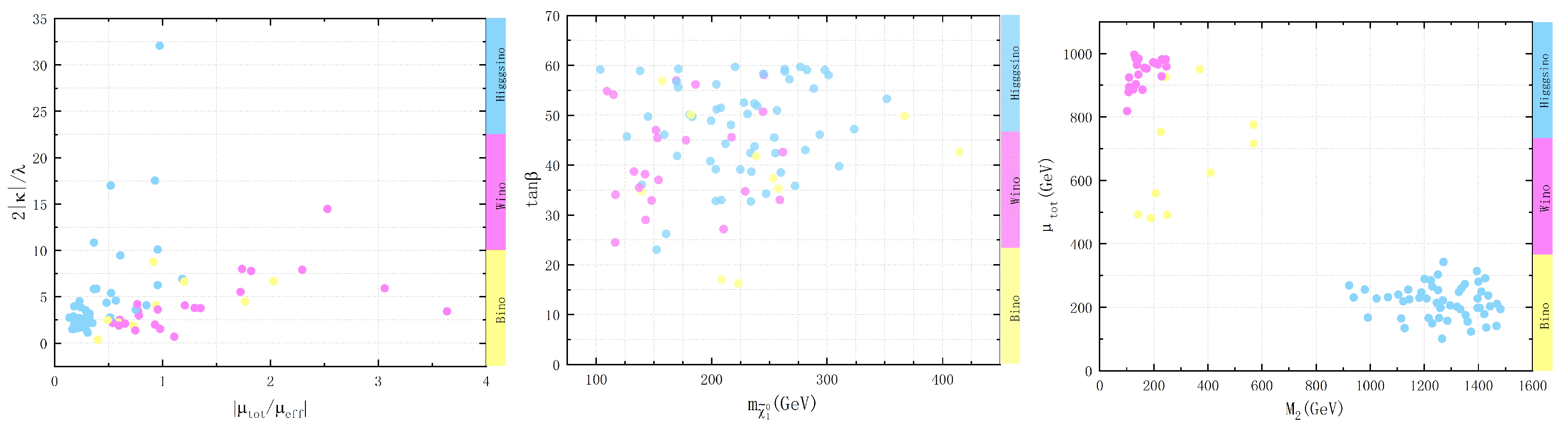
3.1. Properties of Dark Matter
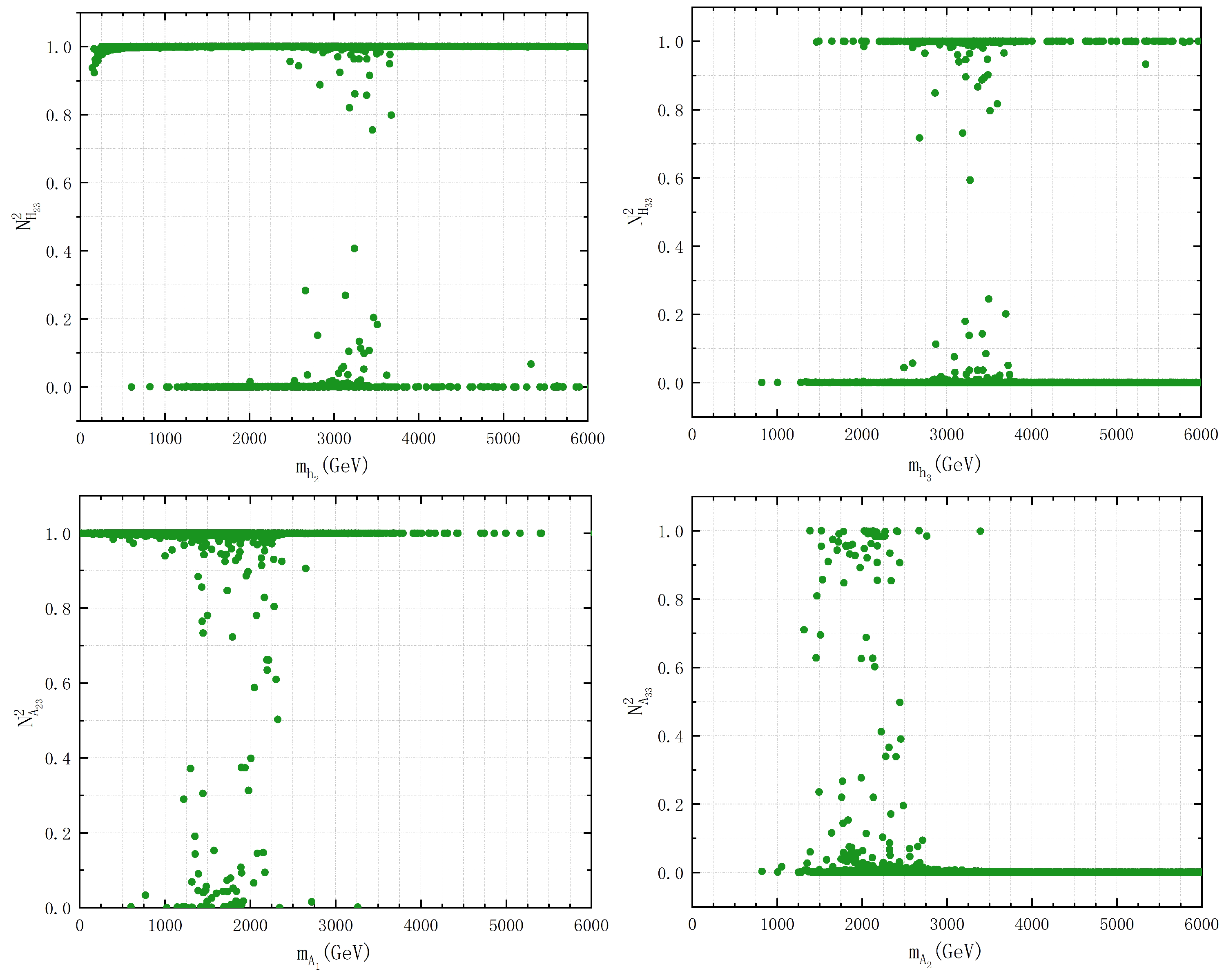
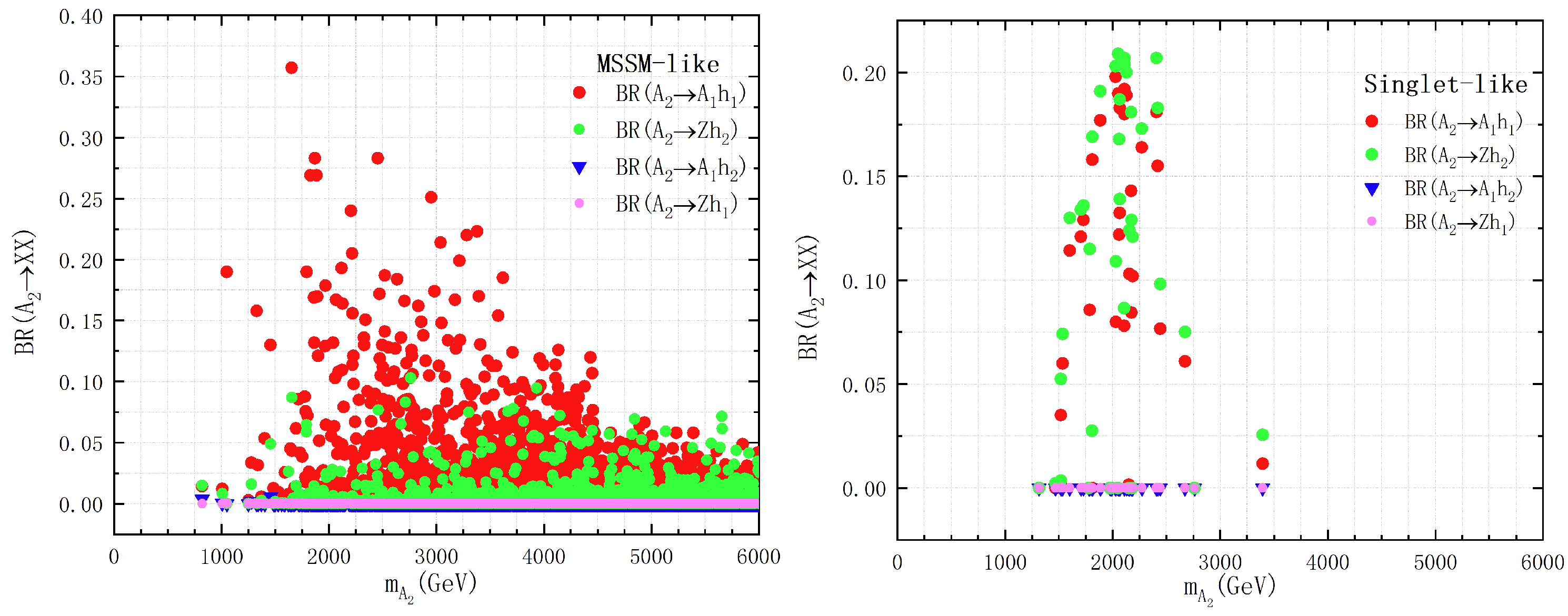
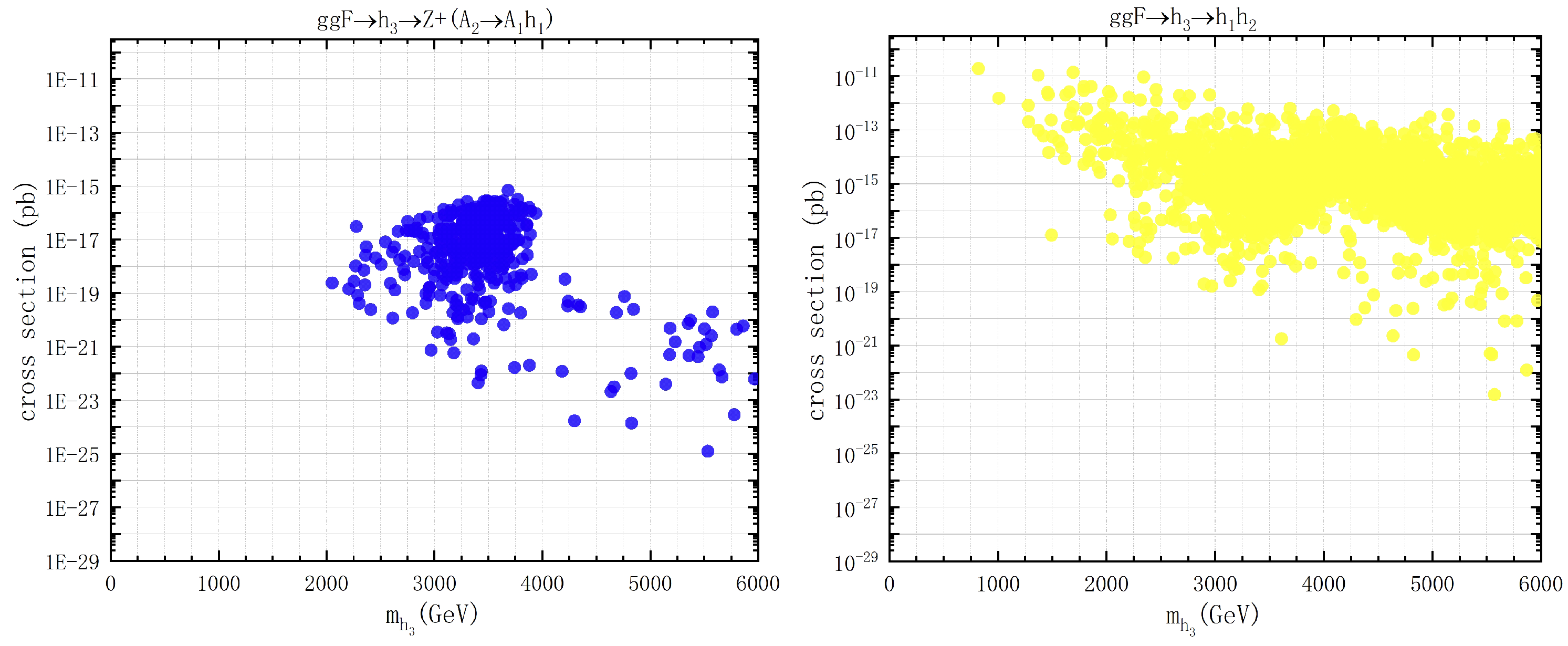
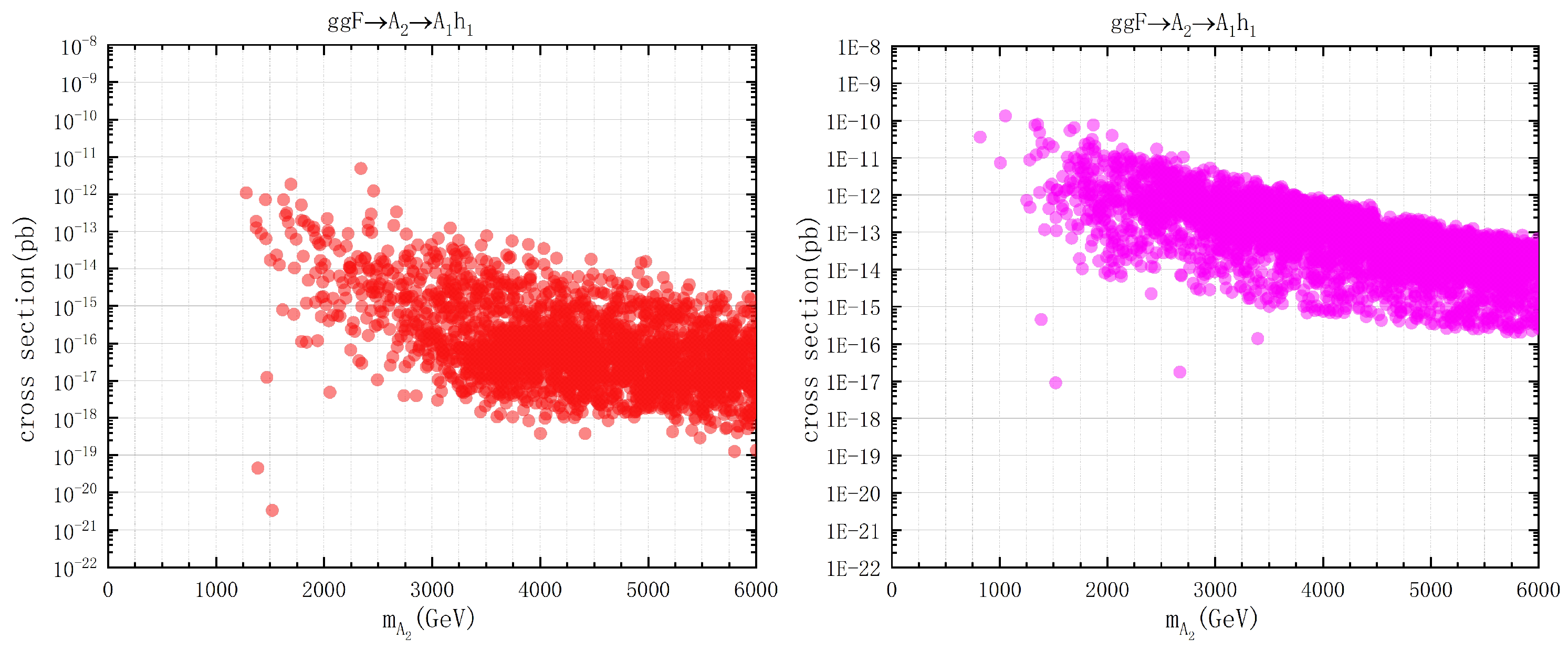
3.2. Properties of Heavy Higgs Bosons
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aad, G. et al. [Atlas Collaboration] Combined search for the Standard Model Higgs boson using up to 4.9 fb−1 of pp collision data at TeV with the ATLAS detector at the LHC. Phys. Lett. B 2012, 710, 49–66. [Google Scholar] [CrossRef]
- Chatrchyan, S. et al. [CMS Collaboration] Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC. Phys. Lett. B 2012, 716, 30–61. [Google Scholar] [CrossRef]
- Chatrchyan, S. et al. [CMS Collaboration] Combined Results of Searches for the Standard Model Higgs Boson in pp Collisions at TeV. Phys. Lett. B 2012, 710, 26–48. [Google Scholar] [CrossRef]
- Abi, B. et al. [(Muon g − 2 Collaboration)] Measurement of the Positive Muon Anomalous Magnetic Moment to 0.46 ppm. Phys. Rev. Lett. 2021, 126, 141801. [Google Scholar] [CrossRef] [PubMed]
- Bennett, G.W. et al. [(Muon g − 2 Collaboration)] Final Report of the Muon E821 Anomalous Magnetic Moment Measurement at BNL. Phys. Rev. D 2006, 73, 072003. [Google Scholar] [CrossRef]
- Franke, F.; Fraas, H. Mass bounds for the neutral Higgs bosons in the next-to-minimal supersymmetric standard model. Phys. Lett. B 1995, 353, 234–242. [Google Scholar] [CrossRef]
- Szleper, M. Search for the NMSSM Higgs bosons at the photon collider. Int. J. Mod. Phys. A 2005, 20, 7404–7411. [Google Scholar] [CrossRef]
- Ellwanger, U. Phenomenological Aspects of the Next-to-Minimal Supersymmetric Standard Model. Nucl. Phys. B Proc. Suppl. 2010, 200–202, 113–119. [Google Scholar] [CrossRef]
- Franke, F.; Fraas, H. Neutralinos and Higgs bosons in the next-to-minimal supersymmetric standard model. Int. J. Mod. Phys. A 1997, 12, 479–534. [Google Scholar] [CrossRef]
- Ellwanger, U.; Hugonie, C.; Teixeira, A.M. The Next-to-Minimal Supersymmetric Standard Model. Phys. Rept. 2010, 496, 1–77. [Google Scholar] [CrossRef]
- Cao, J.; Li, F.; Lian, J.; Pan, Y.; Zhang, D. Impact of LHC probes of SUSY and recent measurement of (g − 2)μ on ℤ3-NMSSM. Sci. China Phys. Mech. Astron. 2022, 65, 291012. [Google Scholar] [CrossRef]
- Cao, J.; Lian, J.; Pan, Y.; Zhang, D.; Zhu, P. Improved (g − 2)μ measurement and singlino dark matter in μ-term extended ℤ3-NMSSM. J. High Energy Phys. 2021, 9, 175. [Google Scholar] [CrossRef]
- Zhou, H.; Cao, J.; Lian, J.; Zhang, D. Singlino-dominated dark matter in Z3-symmetric NMSSM. Phys. Rev. D 2021, 104, 015017. [Google Scholar] [CrossRef]
- Cao, J.; Lian, J.; Pan, Y.; Yue, Y.; Zhang, D. Impact of recent (g − 2)μ measurement on the light CP-even Higgs scenario in general Next-to-Minimal Supersymmetric Standard Model. J. High Energy Phys. 2022, 3, 203. [Google Scholar] [CrossRef]
- Cao, J.; Li, D.; Lian, J.; Yue, Y.; Zhou, H. Singlino-dominated dark matter in general NMSSM. J. High Energy Phys. 2021, 6, 176. [Google Scholar] [CrossRef]
- Cao, J.; Jia, X.; Meng, L.; Yue, Y.; Zhang, D. Status of the singlino-dominated dark matter in general Next-to-Minimal Supersymmetric Standard Model. J. High Energy Phys. 2023, 3, 198. [Google Scholar] [CrossRef]
- Lopez-Fogliani, D.E.; Munoz, C. Proposal for a Supersymmetric Standard Model. Phys. Rev. Lett. 2006, 97, 041801. [Google Scholar] [CrossRef]
- Sirunyan, A.M. et al. [CMS Collaboration] Search for a heavy pseudoscalar boson decaying to a Z and a Higgs boson at TeV. Eur. Phys. J. C 2019, 79, 564. [Google Scholar] [CrossRef]
- Aaboud, M. et al. [The ATLAS Collaboration] Search for heavy resonances decaying into a W or Z boson and a Higgs boson in final states with leptons and b-jets in 36 fb−1 of TeV pp collisions with the ATLAS detector. J. High Energy Phys. 2018, 3, 174, Erratum in J. High Energy Phys. 2018, 11, 51. [Google Scholar] [CrossRef]
- Aad, G. et al. [The ATLAS Collaboration] Search for heavy resonances decaying into a Z or W boson and a Higgs boson in final states with leptons and b-jets in 139 fb−1 of pp collisions at TeV with the ATLAS detector. J. High Energy Phys. 2023, 6, 16. [Google Scholar] [CrossRef]
- Khachatryan, V. et al. [CMS Collaboration] Search for a pseudoscalar boson decaying into a Z boson and the 125 GeV Higgs boson in final states. Phys. Lett. B 2015, 748, 221–243. [Google Scholar] [CrossRef]
- Sirunyan, A.M. et al. [The CMS Collaboration] Search for a heavy pseudoscalar Higgs boson decaying into a 125 GeV Higgs boson and a Z boson in final states with two tau and two light leptons at TeV. J. High Energy Phys. 2020, 3, 65. [Google Scholar] [CrossRef]
- Sirunyan, A.M. et al. [The CMS Collaboration] Search for new neutral Higgs bosons through the H→ ZA process in pp collisions at TeV. J. High Energy Phys. 2020, 3, 55. [Google Scholar] [CrossRef]
- Aad, G. et al. [ATLAS Collaboration] Search for a heavy Higgs boson decaying into a Z boson and another heavy Higgs boson in the and final states in pp collisions at TeV with the ATLAS detector. Eur. Phys. J. C 2021, 81, 396. [Google Scholar] [CrossRef]
- Tumasyan, A. et al. [The CMS Collaboration] Search for a heavy Higgs boson decaying into two lighter Higgs bosons in the bb final state at 13 TeV. J. High Energy Phys. 2021, 11, 57. [Google Scholar] [CrossRef]
- Ellwanger, U.; Hugonie, C. Benchmark planes for Higgs-to-Higgs decays in the NMSSM. Eur. Phys. J. C 2022, 82, 406. [Google Scholar] [CrossRef]
- Kling, F.; Li, H.; Pyarelal, A.; Song, H.; Su, S. Exotic Higgs Decays in Type-II 2HDMs at the LHC and Future 100 TeV Hadron Colliders. J. High Energy Phys. 2019, 6, 31. [Google Scholar] [CrossRef]
- Kling, F.; Li, H.; Li, S.; Pyarelal, A.; Song, H.; Su, S.; Su, W. Exotic Higgs Decays in the Type-II 2HDMs at Current and Future pp Colliders. arXiv 2022, arXiv:2205.12198. [Google Scholar]
- Abel, S.A. Destabilizing divergences in the NMSSM. Nucl. Phys. B 1996, 480, 55–72. [Google Scholar] [CrossRef]
- Maniatis, M. The Next-to-Minimal Supersymmetric extension of the Standard Model reviewed. Int. J. Mod. Phys. A 2010, 25, 3505–3602. [Google Scholar] [CrossRef]
- Panagiotakopoulos, C.; Tamvakis, K. Stabilized NMSSM without domain walls. Phys. Lett. B 1999, 446, 224–227. [Google Scholar] [CrossRef]
- Ferrara, S.; Kallosh, R.; Linde, A.; Marrani, A.; Van Proeyen, A. Superconformal Symmetry, NMSSM, and Inflation. Phys. Rev. D 2011, 83, 025008. [Google Scholar] [CrossRef]
- Hollik, W.G.; Liebler, S.; Moortgat-Pick, G.; Paßehr, S.; Weiglein, G. Phenomenology of the inflation-inspired NMSSM at the electroweak scale. Eur. Phys. J. C 2019, 79, 75. [Google Scholar] [CrossRef]
- Hollik, W.G.; Li, C.; Moortgat-Pick, G.; Paasch, S. Phenomenology of a Supersymmetric Model Inspired by Inflation. Eur. Phys. J. C 2021, 81, 141. [Google Scholar] [CrossRef]
- Kolda, C.F.; Pokorski, S.; Polonsky, N. Stabilized singlets in supergravity as a source of the mu-parameter. Phys. Rev. Lett. 1998, 80, 5263–5266. [Google Scholar] [CrossRef]
- Miller, D.J.; Nevzorov, R.; Zerwas, P.M. The Higgs sector of the next-to-minimal supersymmetric standard model. Nucl. Phys. B 2004, 681, 3–30. [Google Scholar] [CrossRef]
- Cao, J.J.; Heng, Z.X.; Yang, J.M.; Zhang, Y.M.; Zhu, J.Y. A SM-like Higgs near 125 GeV in low energy SUSY: A comparative study for MSSM and NMSSM. J. High Energy Phys. 2012, 3, 86. [Google Scholar] [CrossRef]
- King, S.F.; Mühlleitner, M.; Nevzorov, R.; Walz, K. Natural NMSSM Higgs Bosons. Nucl. Phys. B 2013, 870, 323–352. [Google Scholar] [CrossRef]
- Wang, F.; Wang, W.; Wu, L.; Yang, J.M.; Zhang, M. Probing degenerate heavy Higgs bosons in NMSSM with vector-like particles. Int. J. Mod. Phys. A 2017, 32, 1745005. [Google Scholar] [CrossRef]
- Aoyama, T.; Asmussen, N.; Benayoun, M.; Bijnens, J.; Blum, T.; Bruno, M.; Caprini, I.; Calame, C.C.; Cè, M.; Colangelo, G.; et al. The anomalous magnetic moment of the muon in the Standard Model. Phys. Rep. 2020, 887, 1–166. [Google Scholar] [CrossRef]
- Aoyama, T.; Hayakawa, M.; Kinoshita, T.; Nio, M. Complete Tenth-Order QED Contribution to the Muon g − 2. Phys. Rev. Lett. 2012, 109, 111808. [Google Scholar] [CrossRef] [PubMed]
- Aoyama, T.; Kinoshita, T.; Nio, M. Theory of the Anomalous Magnetic Moment of the Electron. Atoms 2019, 7, 28. [Google Scholar] [CrossRef]
- Czarnecki, A.; Marciano, W.J.; Vainshtein, A. Refinements in electroweak contributions to the muon anomalous magnetic moment. Phys. Rev. D 2003, 67, 073006, Erratum in Phys. Rev. D 2006, 73, 119901. [Google Scholar] [CrossRef]
- Gnendiger, C.; Stöckinger, D.; Stöckinger-Kim, H. The electroweak contributions to (g − 2)μ after the Higgs boson mass measurement. Phys. Rev. D 2013, 88, 053005. [Google Scholar] [CrossRef]
- Keshavarzi, A.; Nomura, D.; Teubner, T. Muon and : A new data-based analysis. Phys. Rev. D 2018, 97, 114025. [Google Scholar] [CrossRef]
- Stoffer, P.; Colangelo, G.; Hoferichter, M. Two-pion contributions to the muon g − 2. PoS 2019, CD2018, 84. [Google Scholar] [CrossRef]
- Colangelo, G.; Hoferichter, M.; Stoffer, P. Two-pion contribution to hadronic vacuum polarization. J. High Energy Phys. 2019, 2, 6. [Google Scholar] [CrossRef]
- Davier, M.; Hoecker, A.; Malaescu, B.; Zhang, Z. Reevaluation of the hadronic vacuum polarisation contributions to the Standard Model predictions of the muon and using newest hadronic cross-section data. Eur. Phys. J. C 2017, 77, 827. [Google Scholar] [CrossRef]
- Keshavarzi, A.; Nomura, D.; Teubner, T. of charged leptons, , and the hyperfine splitting of muonium. Phys. Rev. D 2020, 101, 014029. [Google Scholar] [CrossRef]
- Hoferichter, M.; Hoid, B.L.; Kubis, B. Three-pion contribution to hadronic vacuum polarization. J. High Energy Phys. 2019, 8, 137. [Google Scholar] [CrossRef]
- Kurz, A.; Liu, T.; Marquard, P.; Steinhauser, M. Hadronic contribution to the muon anomalous magnetic moment to next-to-next-to-leading order. Phys. Lett. B 2014, 734, 144–147. [Google Scholar] [CrossRef]
- Melnikov, K.; Vainshtein, A. Hadronic light-by-light scattering contribution to the muon anomalous magnetic moment revisited. Phys. Rev. D 2004, 70, 113006. [Google Scholar] [CrossRef]
- Masjuan, P.; Sanchez-Puertas, P. Pseudoscalar-pole contribution to the (gμ − 2): A rational approach. Phys. Rev. D 2017, 95, 054026. [Google Scholar] [CrossRef]
- Hoferichter, M.; Hoid, B.L.; Kubis, B.; Leupold, S.; Schneider, S.P. Dispersion relation for hadronic light-by-light scattering: Pion pole. J. High Energy Phys. 2018, 10, 141. [Google Scholar] [CrossRef]
- Gérardin, A.; Meyer, H.B.; Nyffeler, A. Lattice calculation of the pion transition form factor with Wilson quarks. Phys. Rev. D 2019, 100, 034520. [Google Scholar] [CrossRef]
- Colangelo, G.; Hagelstein, F.; Hoferichter, M.; Laub, L.; Stoffer, P. Longitudinal short-distance constraints for the hadronic light-by-light contribution to (g − 2)μ with large-Nc Regge models. J. High Energy Phys. 2020, 3, 101. [Google Scholar] [CrossRef]
- Blum, T.; Chowdhury, S.; Hayakawa, M.; Izubuchi, T. Hadronic light-by-light scattering contribution to the muon anomalous magnetic moment from lattice QCD. Phys. Rev. Lett. 2015, 114, 012001. [Google Scholar] [CrossRef]
- Boccaletti, A.; Borsanyi, S.; Davier, M.; Fodor, Z.; Frech, F.; Gerardin, A.; Giusti, D.; Kotov, A.Y.; Lellouch, L.; Lippert, T.; et al. High precision calculation of the hadronic vacuum polarisation contribution to the muon anomaly. arXiv 2024, arXiv:2407.10913. [Google Scholar]
- Aguillard, D.P. et al. [The Muon g - 2 Collaboration] Measurement of the Positive Muon Anomalous Magnetic Moment to 0.20 ppm. Phys. Rev. Lett. 2023, 131, 161802. [Google Scholar] [CrossRef]
- Hunt-Smith, N.T.; Melnitchouk, W.; Sato, N.; Thomas, A.W.; Wang, X.G.; White, M.J. Global QCD analysis and dark photons. J. High Energy Phys. 2023, 9, 96. [Google Scholar] [CrossRef]
- Li, S.; Xiao, Y.; Yang, J.M. Constraining CP-phases in SUSY: An interplay of muon/electron g − 2 and electron EDM. Nucl. Phys. B 2022, 974, 115629. [Google Scholar] [CrossRef]
- Li, Z.; Liu, G.L.; Wang, F.; Yang, J.M.; Zhang, Y. Gluino-SUGRA scenarios in light of FNAL muon g − 2 anomaly. J. High Energy Phys. 2021, 12, 219. [Google Scholar] [CrossRef]
- Du, X.; Wang, F. NMSSM from Alternative Deflection in Generalized Deflected Anomaly Mediated SUSY Breaking. Eur. Phys. J. C 2018, 78, 431. [Google Scholar] [CrossRef]
- Wang, K.; Wang, F.; Zhu, J.; Jie, Q. The semi-constrained NMSSM in light of muon g − 2, LHC, and dark matter constraints. Chin. Phys. C 2018, 42, 103109. [Google Scholar] [CrossRef]
- Cox, P.; Han, C.; Yanagida, T.T. Muon g − 2 and dark matter in the minimal supersymmetric standard model. Phys. Rev. D 2018, 98, 055015. [Google Scholar] [CrossRef]
- Yang, J.L.; Feng, T.F.; Yan, Y.L.; Li, W.; Zhao, S.M.; Zhang, H.B. Lepton-flavor violation and two loop electroweak corrections to (g − 2)μ in the B-L symmetric SSM. Phys. Rev. D 2019, 99, 015002. [Google Scholar] [CrossRef]
- Li, S.; Xiao, Y.; Yang, J.M. Can electron and muon g − 2 anomalies be jointly explained in SUSY? Eur. Phys. J. C 2022, 82, 276. [Google Scholar] [CrossRef]
- Wang, F.; Wu, L.; Xiao, Y.; Yang, J.M.; Zhang, Y. GUT-scale constrained SUSY in light of new muon g − 2 measurement. Nucl. Phys. B 2021, 970, 115486. [Google Scholar] [CrossRef]
- Aboubrahim, A.; Klasen, M.; Nath, P.; Syed, R.M. Tests of gluino-driven radiative breaking of the electroweak symmetry at the LHC. Phys. Scr. 2022, 97, 054002. [Google Scholar] [CrossRef]
- Wang, K.; Zhu, J. Smuon in the NMSSM confronted with the muon g–2 anomaly and SUSY searches. Chin. Phys. C 2023, 47, 013107. [Google Scholar] [CrossRef]
- Zheng, M.D.; Zhang, H.H. Studying the anomalies and in R-parity violating MSSM framework with the inverse seesaw mechanism. Phys. Rev. D 2021, 104, 115023. [Google Scholar] [CrossRef]
- Domingo, F.; Ellwanger, U. Constraints from the Muon g − 2 on the Parameter Space of the NMSSM. J. High Energy Phys. 2008, 7, 79. [Google Scholar] [CrossRef]
- Athron, P.; Bach, M.; Fargnoli, H.G.; Gnendiger, C.; Greifenhagen, R.; Park, J.H.; Paßehr, S.; Stöckinger, D.; Stöckinger-Kim, H.; Voigt, A. GM2Calc: Precise MSSM prediction for (g − 2) of the muon. Eur. Phys. J. C 2016, 76, 62. [Google Scholar] [CrossRef]
- Endo, M.; Hamaguchi, K.; Iwamoto, S.; Kitahara, T. Supersymmetric interpretation of the muon g − 2 anomaly. J. High Energy Phys. 2021, 7, 75. [Google Scholar] [CrossRef]
- Almarashi, M.M.; Alhazmi, F.; Abdulhafidh, R.; Basir, S.A. Dark matter in NMSSM with small and . Results Phys. 2023, 49, 106531. [Google Scholar] [CrossRef]
- Wang, L.; Yang, J.M.; Zhang, Y.; Zhu, P.; Zhu, R. A Concise Review on Some Higgs-Related New Physics Models in Light of Current Experiments. Universe 2023, 9, 178. [Google Scholar] [CrossRef]
- Badziak, M.; Olechowski, M.; Szczerbiak, P. Blind spots for neutralino dark matter in the NMSSM. J. High Energy Phys. 2016, 3, 179. [Google Scholar] [CrossRef]
- Badziak, M.; Olechowski, M.; Szczerbiak, P. Spin-dependent constraints on blind spots for thermal singlino-higgsino dark matter with(out) light singlets. J. High Energy Phys. 2017, 7, 50. [Google Scholar] [CrossRef]
- Badziak, M.; Olechowski, M.; Szczerbiak, P. Blind spots for neutralinos in NMSSM with light singlet scalar. PoS 2015, PLANCK2015, 130. [Google Scholar]
- Pierce, A.; Shah, N.R.; Freese, K. Neutralino Dark Matter with Light Staus. arXiv 2013, arXiv:1309.7351. [Google Scholar]
- Shang, L.; Zhang, Y. EasyScan_HEP: A tool for connecting programs to scan the parameter space of physics models. arXiv 2023, arXiv:2304.03636. [Google Scholar]
- Staub, F. SARAH. arXiv 2008, arXiv:0806.0538. [Google Scholar]
- Staub, F. SARAH 3.2: Dirac Gauginos, UFO output, and more. Comput. Phys. Commun. 2013, 184, 1792–1809. [Google Scholar] [CrossRef]
- Staub, F. SARAH 4: A tool for (not only SUSY) model builders. Comput. Phys. Commun. 2014, 185, 1773–1790. [Google Scholar] [CrossRef]
- Staub, F. Exploring new models in all detail with SARAH. Adv. High Energy Phys. 2015, 2015, 840780. [Google Scholar] [CrossRef]
- Porod, W. SPheno, a program for calculating supersymmetric spectra, SUSY particle decays and SUSY particle production at e+ e- colliders. Comput. Phys. Commun. 2003, 153, 275–315. [Google Scholar] [CrossRef]
- Porod, W.; Staub, F. SPheno 3.1: Extensions including flavour, CP-phases and models beyond the MSSM. Comput. Phys. Commun. 2012, 183, 2458–2469. [Google Scholar] [CrossRef]
- Bélanger, G.; Boudjema, F.; Pukhov, A.; Semenov, A. micrOMEGAs4.1: Two dark matter candidates. Comput. Phys. Commun. 2015, 192, 322–329. [Google Scholar] [CrossRef]
- Belanger, G.; Boudjema, F.; Pukhov, A.; Semenov, A. MicrOMEGAs: A Program for calculating the relic density in the MSSM. Comput. Phys. Commun. 2002, 149, 103–120. [Google Scholar] [CrossRef]
- Belanger, G.; Boudjema, F.; Pukhov, A.; Semenov, A. micrOMEGAs_3: A program for calculating dark matter observables. Comput. Phys. Commun. 2014, 185, 960–985. [Google Scholar] [CrossRef]
- Belanger, G.; Boudjema, F.; Pukhov, A.; Semenov, A. micrOMEGAs: A Tool for dark matter studies. Nuovo Cim. C 2010, 033N2, 111–116. [Google Scholar] [CrossRef]
- Belanger, G.; Boudjema, F.; Brun, P.; Pukhov, A.; Rosier-Lees, S.; Salati, P.; Semenov, A. Indirect search for dark matter with micrOMEGAs2.4. Comput. Phys. Commun. 2011, 182, 842–856. [Google Scholar] [CrossRef]
- Belanger, G.; Boudjema, F.; Pukhov, A.; Semenov, A. Dark matter direct detection rate in a generic model with micrOMEGAs 2.2. Comput. Phys. Commun. 2009, 180, 747–767. [Google Scholar] [CrossRef]
- Belanger, G.; Boudjema, F.; Pukhov, A.; Semenov, A. micrOMEGAs 2.0.7: A program to calculate the relic density of dark matter in a generic model. Comput. Phys. Commun. 2007, 177, 894–895. [Google Scholar] [CrossRef][Green Version]
- Belanger, G.; Boudjema, F.; Pukhov, A.; Semenov, A. MicrOMEGAs 2.0: A Program to calculate the relic density of dark matter in a generic model. Comput. Phys. Commun. 2007, 176, 367–382. [Google Scholar] [CrossRef]
- Belanger, G.; Boudjema, F.; Pukhov, A.; Semenov, A. micrOMEGAs: Version 1.3. Comput. Phys. Commun. 2006, 174, 577–604. [Google Scholar] [CrossRef]
- Belanger, G.; Boudjema, F.; Pukhov, A.; Semenov, A. micrOMEGAs: Recent developments. In Proceedings of the 4th International Workshop on the Identification of Dark Matter, York, UK, 2–6 September 2002; pp. 262–267. [Google Scholar] [CrossRef]
- Bechtle, P.; Heinemeyer, S.; Stål, O.; Stefaniak, T.; Weiglein, G. Probing the Standard Model with Higgs signal rates from the Tevatron, the LHC and a future ILC. J. High Energy Phys. 2014, 11, 39. [Google Scholar] [CrossRef]
- Bechtle, P.; Heinemeyer, S.; Stal, O.; Stefaniak, T.; Weiglein, G. Applying Exclusion Likelihoods from LHC Searches to Extended Higgs Sectors. Eur. Phys. J. C 2015, 75, 421. [Google Scholar] [CrossRef]
- Bagnaschi, E.; Sakurai, K.; Borsato, M.; Buchmueller, O.; Citron, M.; Costa, J.C.; De Roeck, A.; Dolan, M.J.; Ellis, J.R.; Flächer, H.; et al. Likelihood Analysis of the pMSSM11 in Light of LHC 13-TeV Data. Eur. Phys. J. C 2018, 78, 256. [Google Scholar] [CrossRef]
- Khosa, C.K.; Kraml, S.; Lessa, A.; Neuhuber, P.; Waltenberger, W. SModelS Database Update v1.2.3. J. High Energy Phys. 2020, 2020, 158. [Google Scholar] [CrossRef]
- Mahdi Altakach, M.; Kraml, S.; Lessa, A.; Narasimha, S.; Pascal, T.; Waltenberger, W. SModelS v2.3: Enabling global likelihood analyses. arXiv 2023, arXiv:2306.17676. [Google Scholar]
- Dutta, J.; Kraml, S.; Lessa, A.; Waltenberger, W. SModelS extension with the CMS supersymmetry search results from Run 2. J. High Energy Phys. 2018, 1, 5–12. [Google Scholar] [CrossRef]
- Ambrogi, F.; Dutta, J.; Heisig, J.; Kraml, S.; Kulkarni, S.; Laa, U.; Lessa, A.; Neuhuber, P.; Reyes-González, H.; Waltenberger, W.; et al. SModelS v1.2: Long-lived particles, combination of signal regions, and other novelties. Comput. Phys. Commun. 2020, 251, 106848. [Google Scholar] [CrossRef]
- Beenakker, W.; Hopker, R.; Spira, M. PROSPINO: A Program for the production of supersymmetric particles in next-to-leading order QCD. arXiv, 1996; arXiv:hep-ph/9611232. [Google Scholar]
- Aalbers, J. et al. [LUX-ZEPLIN Collaboration] First Dark Matter Search Results from the LUX-ZEPLIN (LZ) Experiment. Phys. Rev. Lett. 2023, 131, 041002. [Google Scholar] [CrossRef] [PubMed]
- Aberle, O.; Adorisio, C.; Adraktas, A.; Ady, M.; Albertone, J.; Alberty, L.; Alcaide Leon, M.; Alekou, A.; Alesini, D.; Almeida Ferreira, B.; et al. High-Luminosity Large Hadron Collider (HL-LHC): Technical Design Report; CERN: Geneva, Switzerland, 2020; Volume 10. [Google Scholar] [CrossRef]
- CEPC Study Group. CEPC Conceptual Design Report: Volume 1—Accelerator. arXiv 2018, arXiv:1809.00285. [Google Scholar]
- Abada, A. et al. [The FCC Collaboration] FCC-hh: The Hadron Collider: Future Circular Collider Conceptual Design Report Volume 3. Eur. Phys. J. Spec. Top. 2019, 228, 755–1107. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heng, Z.; Li, X.; Shang, L. Properties of Heavy Higgs Bosons and Dark Matter Under Current Experimental Limits in the μNMSSM. Universe 2025, 11, 103. https://doi.org/10.3390/universe11030103
Heng Z, Li X, Shang L. Properties of Heavy Higgs Bosons and Dark Matter Under Current Experimental Limits in the μNMSSM. Universe. 2025; 11(3):103. https://doi.org/10.3390/universe11030103
Chicago/Turabian StyleHeng, Zhaoxia, Xingjuan Li, and Liangliang Shang. 2025. "Properties of Heavy Higgs Bosons and Dark Matter Under Current Experimental Limits in the μNMSSM" Universe 11, no. 3: 103. https://doi.org/10.3390/universe11030103
APA StyleHeng, Z., Li, X., & Shang, L. (2025). Properties of Heavy Higgs Bosons and Dark Matter Under Current Experimental Limits in the μNMSSM. Universe, 11(3), 103. https://doi.org/10.3390/universe11030103





