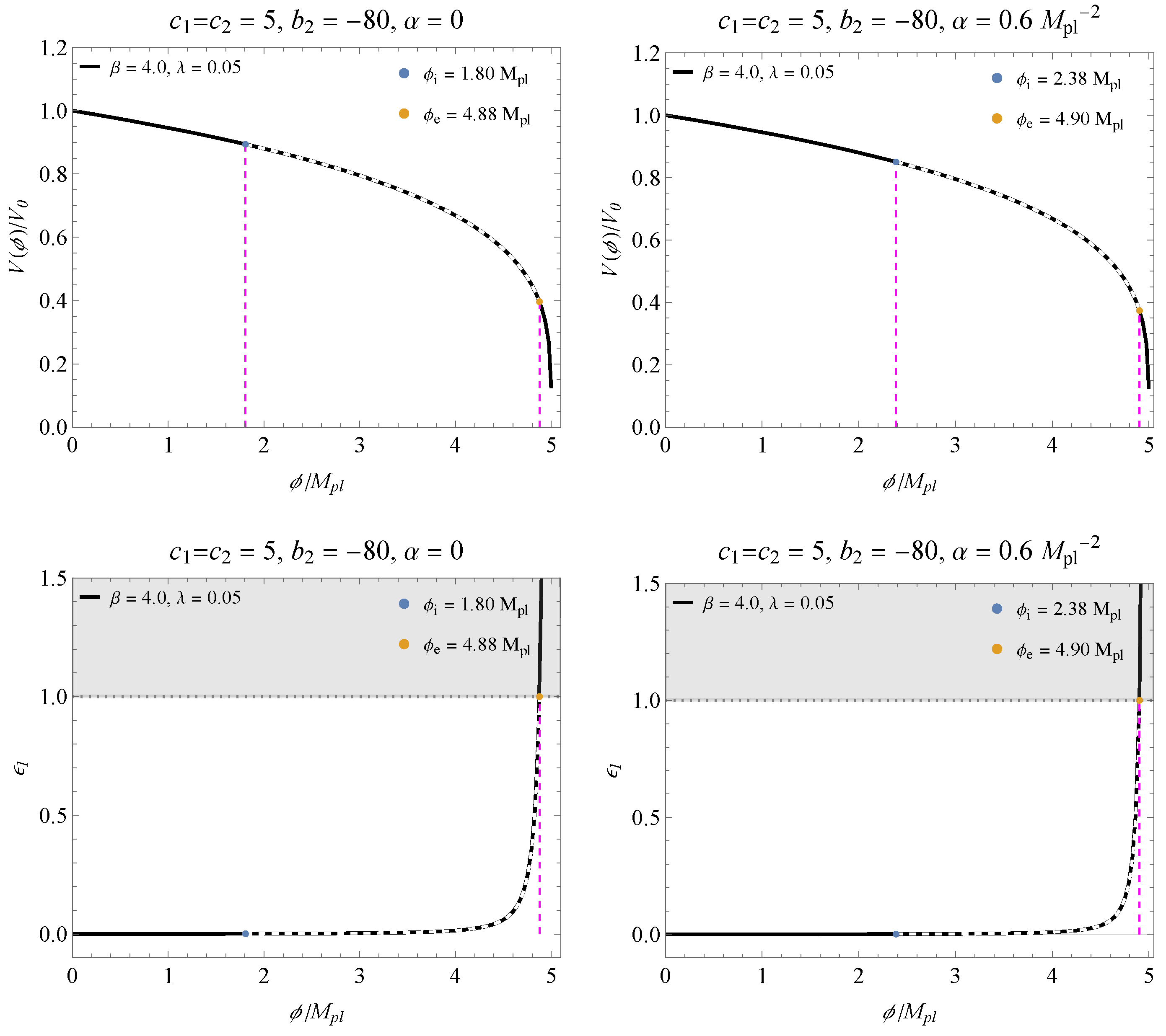Abstract
In the present work, we study cosmology in dilatonic gravity to address the inflationary phase of the early universe. As usual, in dilatonic gravity, the scalar potential assumes the exponential form. However, this potential is not good enough to be in accordance with the Planck 2018 data. More strikingly, the generalized -exponential cannot take this into account either. It is just only presence of the dilatonic sector, in the intermediate coupling regime, that can help the theory to be in full accordance with the observational data.
1. Introduction
Cosmic inflation is a phase undergone by the primordial universe. The cosmic inflation theory, first proposed by Alan Guth, states that in this phase, the universe experienced rapid expansion just after the Big Bang. This rapid expansion occurred on a very tiny scale but had great consequences, explaining many cosmological problems, such as the cosmological horizon and the flatness of the universe [1,2,3]. Currently, the theory of cosmic inflation is widely accepted as a theory which is strongly supported by cosmological observations, such as the detection of temperature fluctuations in cosmic microwave background (CMB) radiation, which are consistent with theoretical predictions of the inflationary scenario. Moreover, investigations of distant galaxies and matter distribution in the universe agree with many aspects of this theory [4,5,6,7].
The inflaton field plays an important role in inflationary cosmology. It concerns a hypothetical scalar field that in some aspects is similar to the Higgs field, accepted to cause the phase of rapid expansion [1]. This field is governed by a scalar potential that, at the limit at which it is predominant, can develop the exponential expansion of spacetime. In particular, the potential of the inflaton field describes the potential energy associated with different configurations of the inflaton. Thus, a specific form of this potential is of great importance in determining the characteristics of inflation, such as for its duration and scale of expansion. Many forms of the inflaton potential have been put forward, from those including quadratic potentials and plateau-like potentials to more complex forms [8,9,10,11,12].
The most common feature of the inflaton potential is that it supports a phase of the rolling inflaton field from high to low potential energy during inflation. Thus, as the field rolls from the top to the bottom of the potential, such that the potential energy is dominant in this phase, it yields an accelerated expansion of the universe. The inflationary phase ends as the inflaton field approaches the minimum of its potential and then starts oscillating. Such oscillations convert the inflaton energy to other particles and fields. This process is called “reheating”, which heats the universe and initiates the radiation phase [13,14,15,16,17,18].
The cosmic inflation theory has been extended to various modified gravity scenarios, which have the , , and theories as good examples. As usual, in gravity, the Ricci scalar R in the Einstein–Hilbert action is formally replaced with a general function . This modification naturally leads to an inflationary phase of the universe, since it introduces additional degrees of freedom via the function , which can lead to an accelerated expansion of the early universe without introducing an inflaton field [19,20,21,22]. Similarly, gravity , that is, the Gauss–Bonnet invariant G, is generalized to a function . As is well known, the Gauss–Bonnet term is a topological term in four-dimensional spacetime, and as a consequence, it does not affect the equations of motion in standard general relativity. However, in extended form, can contribute to the dynamics of the universe, providing a mechanism for inflation. Thus, including terms can naturally produce a richer variety of inflationary solutions, potentially addressing issues such as the so-called graceful exit problem and the generation of primordial perturbations [23]. From the same perspective, gravity makes an interesting modification that leads to teleparallel gravity by replacing the torsion scalar with a function [24]. This theory does not include the curvature of spacetime, but instead uses torsion to describe gravitational interactions. Finally, in a more strict way gravity can lead to an inflationary epoch by appropriately choosing the form of , leading to accelerated expansion. These models have been considered in the recent literature to show that they produce viable inflationary scenarios consistent with observational data, i.e., they survive under constraints from the cosmic microwave background and large-scale structure.
gravity is a modification of general relativity that extends gravity by introducing a dependence on the trace of the energy-momentum tensor T. This addition leads to a theory that accounts for matter and geometry coupling by introducing new dynamical aspects that affect cosmic evolution [25,26,27,28]. The theory has been recently applied to cosmic inflation and has shown promising results, such as the viability of the theory against various cosmological observations. In such a scenario, gravity is coupled to an inflaton field.
A crucial field of superstring models and of cosmological scenarios based on the string effective action is the dilaton field. This field drives the effective strength of all gauge couplings in “grand-unified” models of fundamental interactions [29]. Such coupling strengths can lead the universe towards a strong coupling phase, preceding the phase of standard decelerated evolution. In M-theory, the dilaton is naturally interpreted as the effective “radius” of the eleventh dimension [30]. This field may affect inflationary dynamics and play a fundamental role in generating the primordial spectra of quantum fluctuations, which can be amplified by inflation. As such, the dilaton could naturally provide the coupled quintessence scenario, as long as the cosmological evolution of this field continues after entering the weak coupling regime. Such a regime characterized by a very light (or massless) dilaton is weakly coupled to matter [31]. On the other hand, a massive dilaton is more strongly coupled to macroscopic matter from a gravitational point of view, a sector that was studied in detail in [32].
One should notice that the coupling constant is related to the dilaton field through the expression . Thus, the weak and strong coupling limits are given by and , respectively. Recently, the authors of this study found that -modified theories of gravity in the context of string theory inspired dilaton gravity [33] in the weak coupling limit. It was considered to be a specific model that, under certain conditions, describes the late time universe in accordance with recent observational data. In doing so, we employed numerical methods to obtain several important observable quantities.
On the other hand, the intermediate regime, in which moves between these two extremes, remains little explored. Thus, in the present study, we shall focus on this limit to address inflationary cosmology in dilatonic gravity.
This paper is organized as follows. In Section 2, we review the formalism of pure gravity and introduce dilatonic gravity by explicitly detailing the role of the coupling to be studied in the intermediate regime. In Section 3, we explicitly address the equation of motion for the dilaton playing the role of an inflaton field. In Section 4, we focus on the inflationary parameters and show our main results. Finally, in Section 5, we present our final considerations.
2. Cosmology in Dilatonic Gravity
Let us first take the action given in [34]
where is an arbitrary function of the Ricci scalar curvature , is the trace of the energy–momentum tensor, is the Lagrangian density of matter, and .
Regarding the definition of the energy–momentum tensor, we can express it in such a way that the Lagrangian density of matter depends only on , that is,
By varying the action given in Equation (1) in relation to , we have the field equations given by
so that corresponds to the variation in the trace with respect to the metric tensor, with set in [34]. We will denote and as the derivatives of with respect to the Ricci scalar curvature and the trace of the energy–momentum tensor, respectively.
From the definition of and using Equation (2), we have
In other words, will depend on the Lagrangian of matter, that is, it can refer to the cases of the electromagnetic field, the massless scalar field, and the perfect fluid, among others.
Let us now consider cosmological scenarios related to the effective action that comes from low-energy string theory in which the dilaton field exerts an influence on the dynamics of the universe. We shall focus on the sector of the effective action, coming from a low-energy string theory, given by the tensor field (the metric ) and a scalar field (the dilaton ), where the tilde indicates that we are working on the string frame, and the dilaton couples to the Ricci scalar and dilatonic dynamics in an explicit form—see below. Our starting point is the string-frame, low-energy, gravidilaton effective action, and we advance to the lowest order in the expansion, but including a dilaton-dependent loop and non-perturbative corrections, encoded in a few “form factors”, due to the loop corrections and [35]. is the effective dilaton potential. The model action is [31]
In the cases analyzed in the literature, one can discuss the phenomenology of the relic dilaton background by taking into account two possibilities. First, the massive dilaton is gravitationally more strongly coupled to macroscopic matter. In the strong coupling limit , we assume that is possible to make an asymptotic Taylor expansion in inverse powers of the coupling constant similar to what is done in the context of “induced gravity”. Second, massless dilaton is weakly coupled to matter, that we shall disregard.
We can now characterize the dynamical evolution of the universe with a metric minimally coupled to the dilaton. In this frame, the string effective action is also minimally coupled to perfect fluid sources. Considering the lowest-order , we have [31]. We can use a more convenient coordinate system called the Einstein frame in terms of the metric , which is defined by a conformal transformation . In this frame, if we assume that the action in Equation (5) depends not only on R, but on a function , we can rewrite this gravidilaton action as
In this equation, R is the Ricci scalar curvature, and T is the trace of the energy–momentum tensor of the dilatonic field. In what follows, we will also consider , except where otherwise indicated. We have defined
By varying Equation (6) with respect to , we will obtain
where is the total energy–momentum tensor of the perfect fluid (f) that fills the universe (baryonic matter, radiation and dark matter) plus the dilaton field. Using Equation (4), we can write
with and given by
In general models, the stress–energy tensor of matter is not covariantly conserved. As a consequence, test particles moving in a gravitational field do not follow geodesic lines. There are, however, certain specific forms of the function in which the standard conservation is present. However, we note that such a function must take the particular form . In other words, there is no mixing involving both dependences on R and T [36]. Thus, we can think of the purely T-dependent term as a redefinition of the matter sector in a minimally coupled gravity theory [37], which illustrates the fact that the coupling of matter and energy with gravity interferes with the conservation law to be obeyed by the energy–momentum tensor. Constraints on the function were studied in [38,39]. Recently, some works have explored conservation problems in various contexts of the application of theories [40,41,42,43,44,45,46,47,48,49,50]. In our present study, we shall consider the previously mentioned form which yields to energy–momentum conservation.
We assume that the energy–momentum tensor of the matter and energy is given by , with conditions and , satisfied by the four-velocity . In the following, we will consider a simple example of theories in order to study the inflationary phase of the universe with the presence of a single dilatonic field.
3. Inflation in Dilatonic Gravity
We are interested in studying the dynamics of the inflaton field in the absence of ordinary matter. In other words, we are only interested in the primordial evolution of the universe dominated by the energy contained in a single scalar field represented by the dilaton field minimally coupled to the gravitational field. So, let us introduce a model for an inflationary scenario and obtain the expressions of the inflation observables. Let us now assume a homogeneous and isotropic universe, as described by the Friedmann–Lemaitre–Robertson–Walker (FLRW) metric, whose line element is written as
The specific model is which is the same as that covered in [33] and was first studied by Harko et al. in [34]. For the dilatonic gravity model (6), the field Equation (9), with the Lagrangian (11), can be written as
with
The components of the tensor are given by
Thus, the field equations are
The dilaton equation of motion is given by
where “dot” denotes the derivative with respect to time. From Equations (20) and (21), we have
Let us use the well-known slow-roll approximation, which states a dynamic regime, and . Thus, in this regime, Equations (20) and (22) can be written as
as long as , and consequently, . In this way, the dilatonic field, which plays the role of the inflaton field in this theory, can be written as
This equation can still be written as
Notice that is ensured because it is proportional to the spectral index (see below). And this is in accordance with being very small in the slow-roll regime, where .
In the context of the Gasperini–Veneziano theory, the transition between the pre-Big Bang scenario and the post-Big Bang era is marked by complex dynamics. Before the Big Bang, the universe existed in a state of high density and energy, where the dilaton field plays a crucial role [51,52]. In this regime, the coupling constant is very large, reflecting strong interactions among particles. Thus, we can approximate the form factor to [52]. As the universe expands, an abrupt transition occurs and the inflation field is driven by the dilaton field, which, at the beginning of inflation, takes on very high values [53]. This elevation in the inflaton (dilaton) field, is necessary to provide the potential energy that triggers the rapid expansion of the universe. During this process, decreases significantly as the energy density decreases, allowing the universe to stabilize [52]. After inflation, the value of the inflaton field reduces, resulting in a lower , which facilitates the formation of structures and the dynamics of radiation and matter. This transition is essential for understanding the evolution of the cosmos, connecting the extreme states of the pre-Big Bang to the formation of the observable universe we know today, where the nature of fundamental interactions is profoundly altered. Since we are specifically investigating the impact of a modified theory of gravity on inflationary dynamics and how the dilaton field affects this inflationary scenario, as well as how the inflationary parameters will behave in light of recent experimental data, we will adopt an intermediate form for the term , which preserves the asymptotic values in the weak and strong field limits. Thus, we use the asymptotic form for the general expression of the form factor [52]
The constants and are dimensionless arbitrary constants that come from combinations of original constants from other form factors. The choice of the potential scalar field is very important and characterizes the model we are dealing with. A potential predicted by particle physics is known as a Coleman–Weinberg potential, which arises in the context of grand unified theories [3,54]. Other possibilities are, for example, simpler options such as or . This approach is likely, since we do not know which theory of particle physics describes the early universe. These potentials are considered in detail in reference [55]. Potentials of the type were initially considered in the context of chaotic inflation [53]. Recently, the potential of the type has been used to study inflation in the context of the theories [27]. Another simple and interesting model is based on the usual exponential function given by exp, as originally investigated by Peebles and Ratra [56,57,58,59]. Such exponential potentials arise in four-dimensional effective theories induced by Kaluza–Klein theories [60]. Other examples include supergravity and superstring theories [61] or theories with high derivative terms [62,63]. Although conventional inflation cannot be described by the exponential potential, there is a solution with power-low inflation, and, moreover, this solution is an attractor in the sense of dynamical systems theories [61].
A possible generalization to potential inflation was introduced in [64] and is given by
named -exponential potential.
The -exponential function, , is defined as above for positive values of the term between brackets and zero otherwise, and satisfies the inverse identity , where is the -logarithmic function [65,66]. In the limit , all the above expressions reproduce the usual exponential and logarithm properties. Actually, -exponential potentials present a number of cosmological solutions for a large interval of values of . As we will see in the next section, differently from the conventional result, one can also compute the value of the field at the end of inflation using a slow-roll parameter.
4. Inflationary Parameters
The gravity theories aimed at explaining cosmic inflation seek to provide estimates that are consistent with observations for different parameters related to inflation. These parameters include the scalar spectral index of curvature perturbations , the ratio of tensor to scalar perturbations r and the tensor spectral index [67]. Observational data impose stringent constraints on these quantities. Generally, these observables are analyzed under the slow-roll hypothesis, where all relevant information about any inflationary scenario is encoded in the slow-roll parameters. In the following steps, we will recover the reduced Planck’s mass ; thus, the Equations (24) and (26) can be written, respectively, as
Particularly, one may introduce ln, which leads us to , and [10]. The first two terms of read [68,69], written in terms of the potential (28) and its derivatives as
For the potential adopted in the model, we can express the parameters in terms of as
The end of the inflationary phase is expected to occur at where the condition is satisfied, i.e.,
We can obtain the scalar field at the end of inflation , by numerically solving the above equation. We can also write the equations that describe the model in terms of the number of e-foldings N, defined by ln, where represents the scale factor at the beginning of inflation. Using expansion to , the definition for N and the potential (28), we can write
where is the value of the dilaton that emerges from the end of the pre-Big Bang phase and assumes the initial value of the scalar field in the inflationary period.
We can obtain the amplitude of the potential (28) from the primordial power spectrum of scalar perturbations:
where is the pivot scale, at which the CMB crosses the Hubble horizon during inflation, and its value is fixed at . We also determine that the value of is fixed by Planck Collaboration (2018) , so from (36), we can express the amplitude as follows:
Finally, the spectral scalar index and the tensor-to-scalar ratio can be written in terms of as
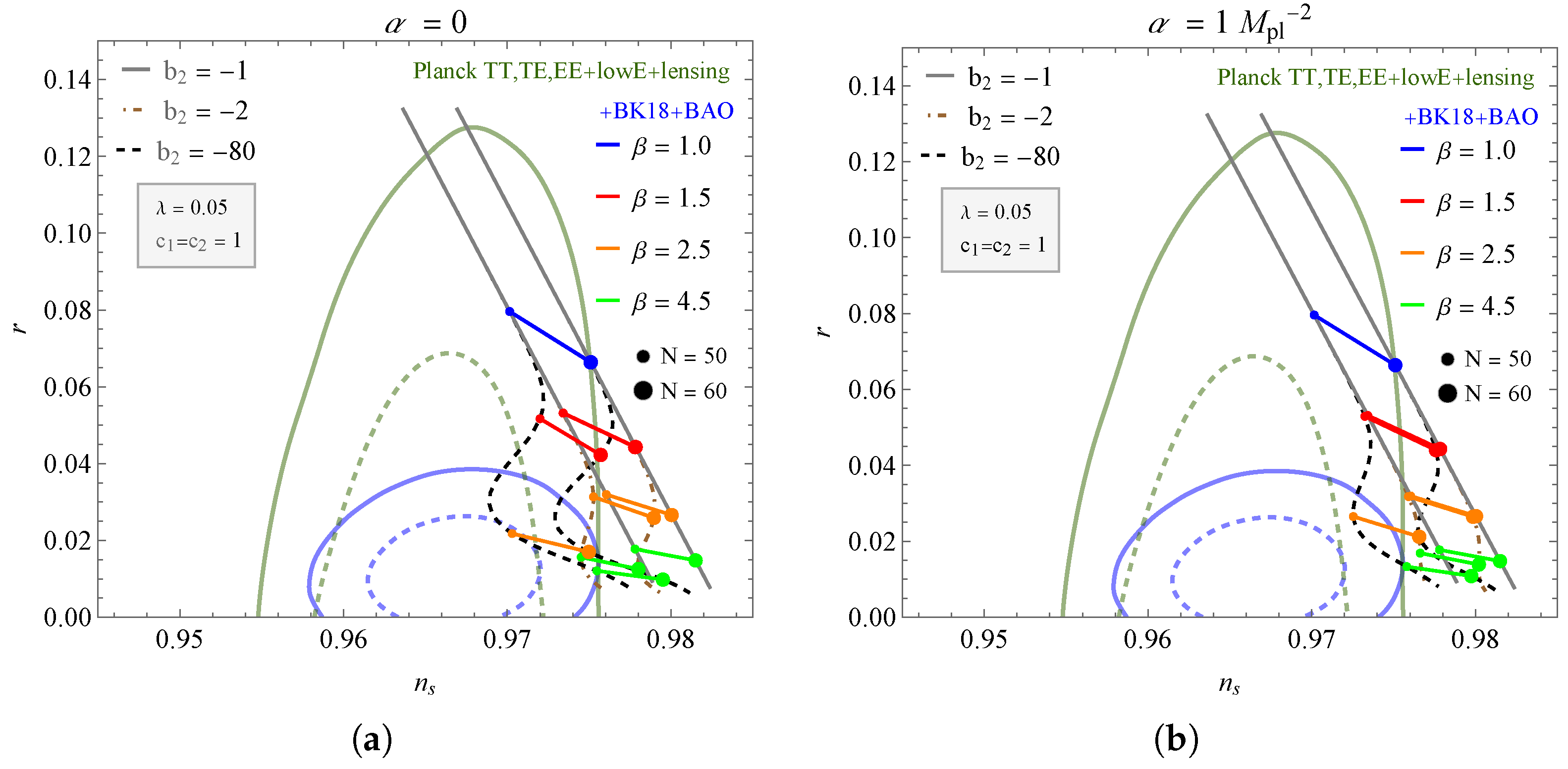
Similarly, as done for , we can obtain the values of by solving (35) numerically. For , and , the expressions and r return to the standard -exponential [70]. In our work, we have while assuming . This way, in Figure 1a, Figure 2 and Figure 3, we check the results for the scalar index and the tensor-to-scalar ratio in a plane , considering two numbers for e-folds and , and compared with the 68% and 95% contours obtained from the Planck(2018)+BAO+BICEP/Keck Array data [71,72]. In Figure 1a, we see the influence of the parameter on the behavior of the curves for . For , we have the result found in [70] outside the regions delimited by the +BK18+BAO data; however, when we vary the parameter , the curves lean towards this region. Comparing Figure 1a,b, we see that contributes to attenuating the effect of . In Table 1 we have the results for the scalar index and the tensor-to-scalar ratio for the values of bounded by the region of the +BK18+BAO data.
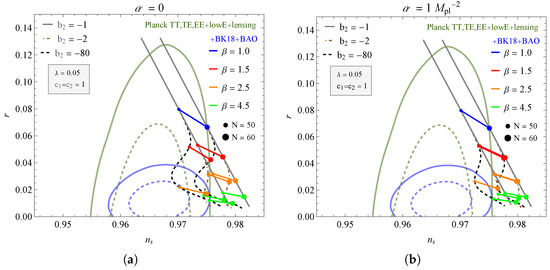
Figure 1.
The plane for different values of and fixed and . The contours correspond to the BK18+BAO data.
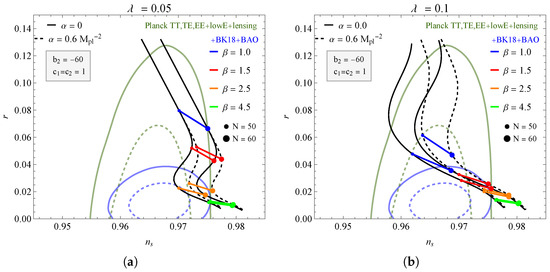
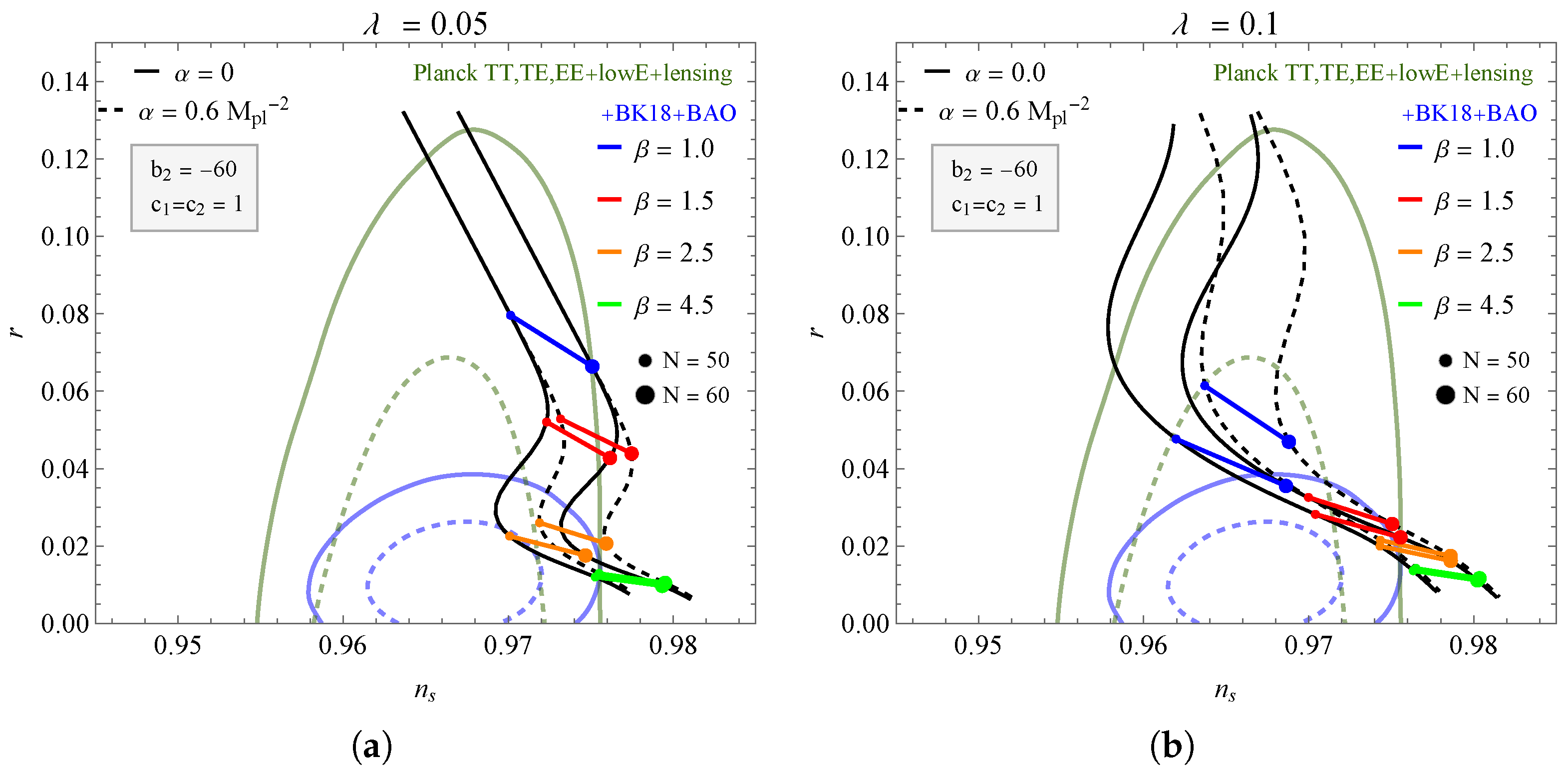
Figure 2.
The plane for different values of and and keeping the values fixed and . The contours correspond to the BK18+BAO data.
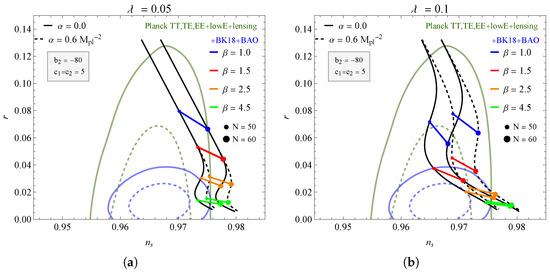
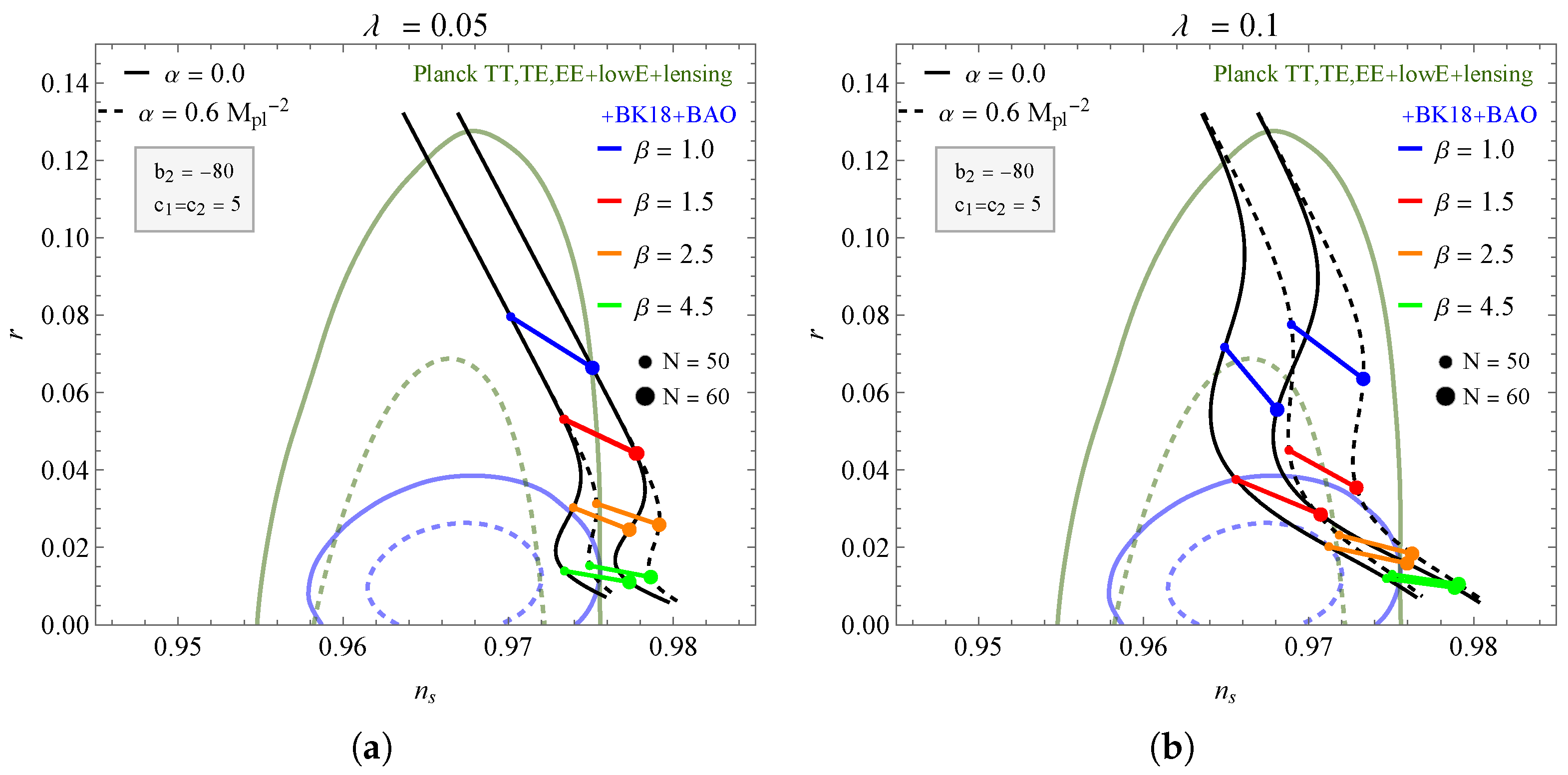
Figure 3.
The plane for different values of and , keeping the values fixed at and . The contours correspond to the BK18+BAO data.

Table 1.
This table summarizes . We fix the e-folding number at , and .
In Figure 2 and Figure 3, we again have the behavior of the curves for two values of e-foldings and . We now test the contribution of the parameters and with the change in in the potential (28). In Figure 2 with , we have a reduction in the possible values of that includes the region delimited by the +BK18 + BAO data in , compared with . Furthermore, reduces the approximation of the curves ( and ) in the regions. We saw in Figure 1 that contributes to the displacement of the curves to the left; however, note that in Figure 3, where we have even for the parameter , the approximation of the curves is reduced, in both cases of , compared to the previous figure, where . In this way, the influence of is similar to the parameter, reducing the approximation of the curves to the delimited region of the data. The results for the scalar index and the tensor-to-scalar ratio corresponding to the two figures mentioned above can be found in Table 2 for values of bounded by the +BK18+BAO data. The fact that BAO tightens r has already been noticed in several scenarios. See, for example, Ref. [73] for a large discussion on this issue.

Table 2.
This table summarizes . We fix the e-folding number at .
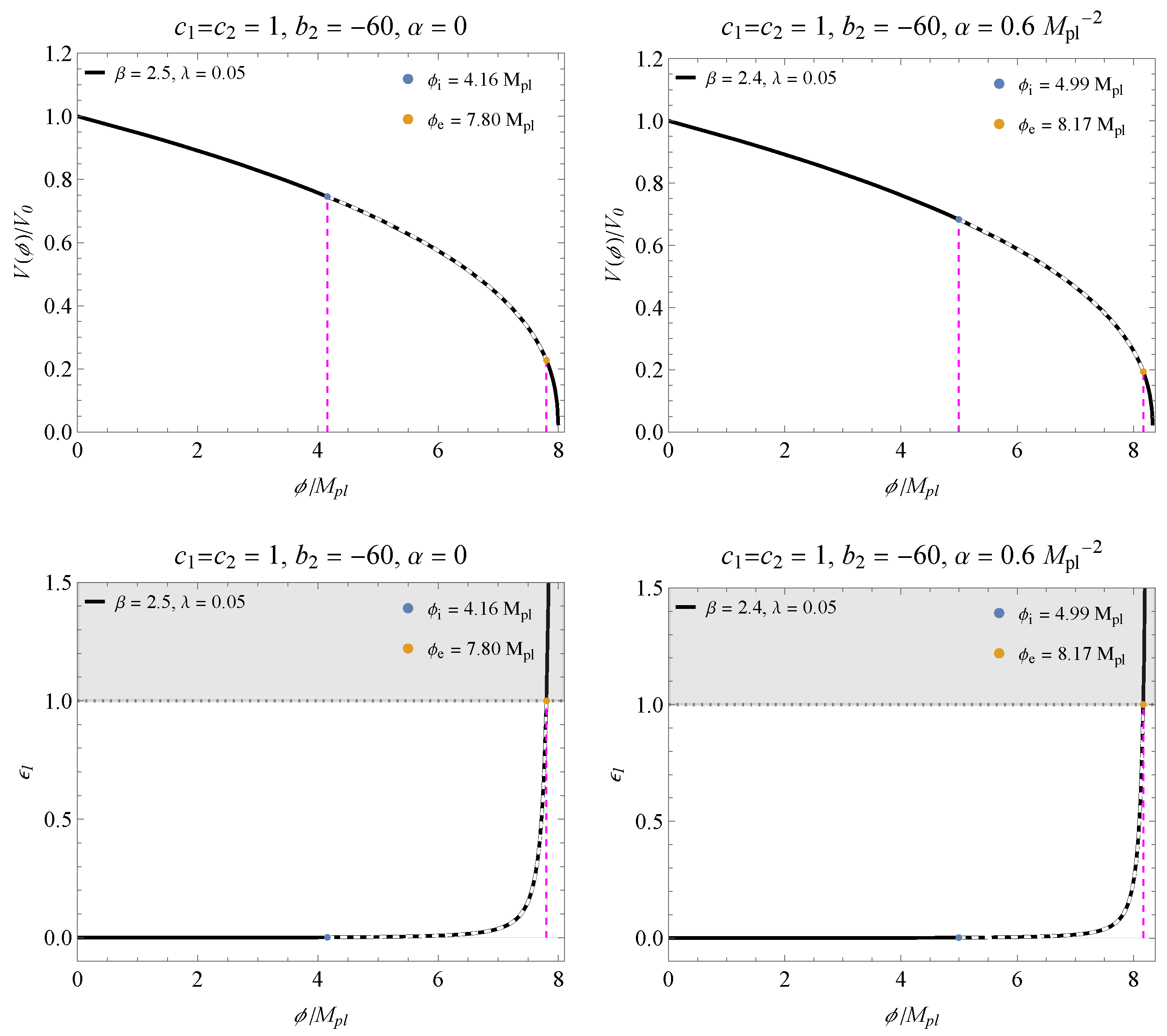
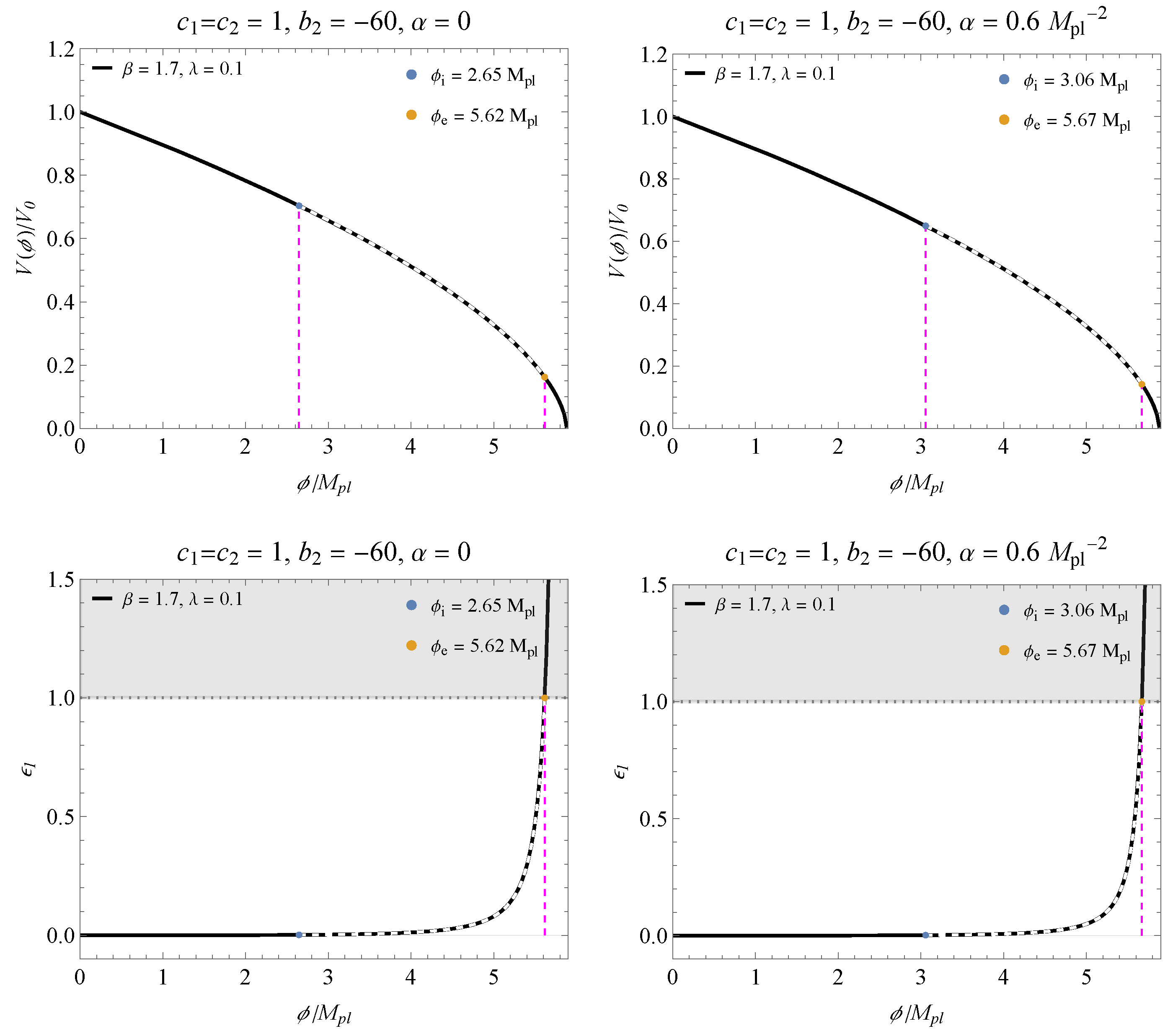
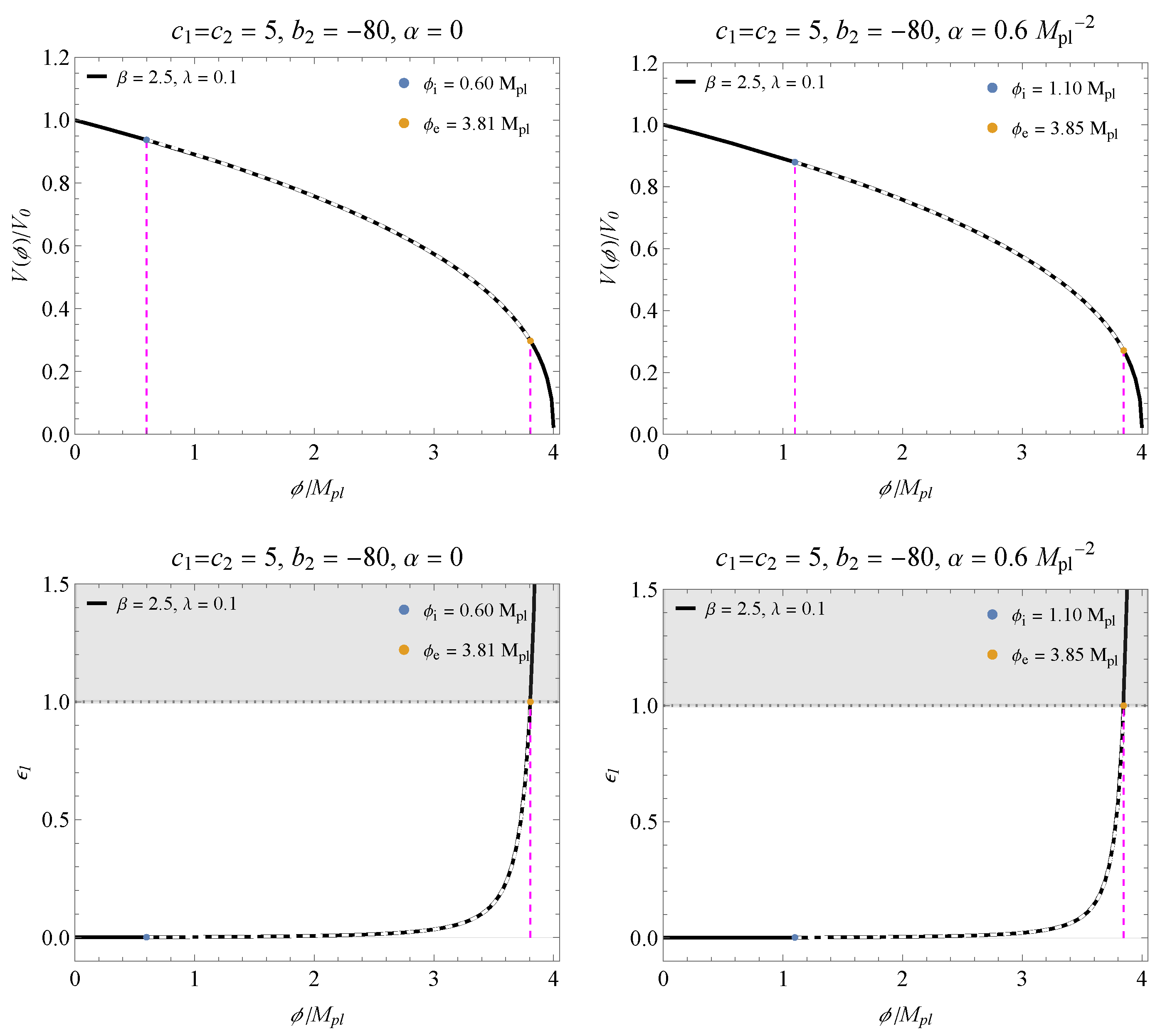
In the following figures, we have the behavior of the potential (28) for the parameters shown in Figure 2 and Figure 3, checking the beginning and end of inflation. We choose an appropriate value for within the region delimited by the BK18+BAO data. In the bottom panels, we have the slow-roll parameter as a function of corresponding to each potential, and the shaded area indicates the breakdown of the slow-roll inflation. Figure 4 and Figure 5 correspond to the cases shown in Figure 2, while Figure 6 and Figure 7 correspond to Figure 3. It is possible to notice that the contribution of reduces the inflation band.
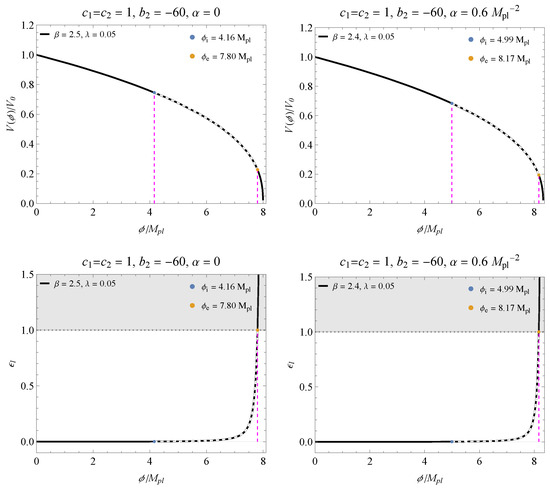
Figure 4.
The (top) graphs present the behavior of the potential for the parameters and within the inflation regime, corresponding to the results presented in Figure 2a. The (bottom) panels are the respective slow-roll parameters as a function of .
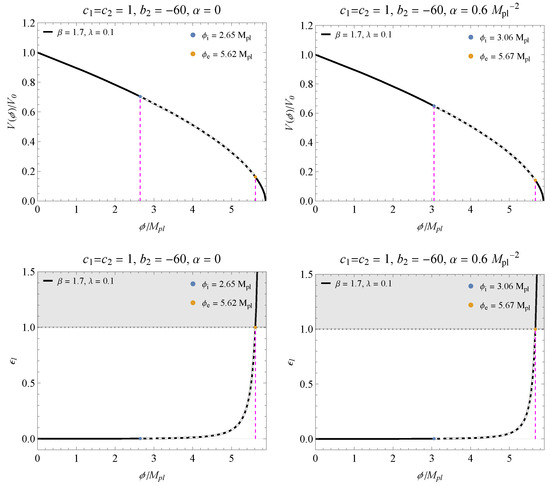
Figure 5.
The (top) graphs present the behavior of the potential for the parameters and within the inflation regime, corresponding to the results presented in Figure 2b. The (bottom) panels are the respective slow-roll parameters as a function of .
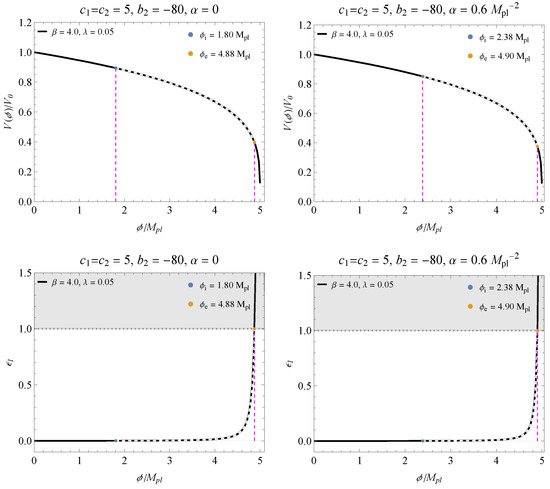
Figure 6.
The (top) graphs present the behavior of the potential for the parameters and within the inflation regime, corresponding to the results presented in Figure 3a. The (bottom) panels are the respective slow-roll parameters as a function of .
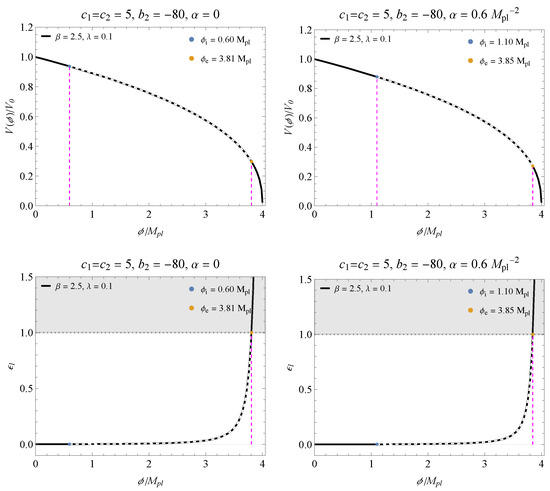
Figure 7.
The (top) graphs present the behavior of the potential for the parameters and within the inflation regime, corresponding to the results presented in Figure 3b. The (bottom) panels are the respective slow-roll parameters as a function of .
For instantaneous reheating in which one finds maximal temperature, we can further estimate the reheating temperature by assuming the energy density , so from the Stefan–Boltzmann law, the reheating temperature is given by
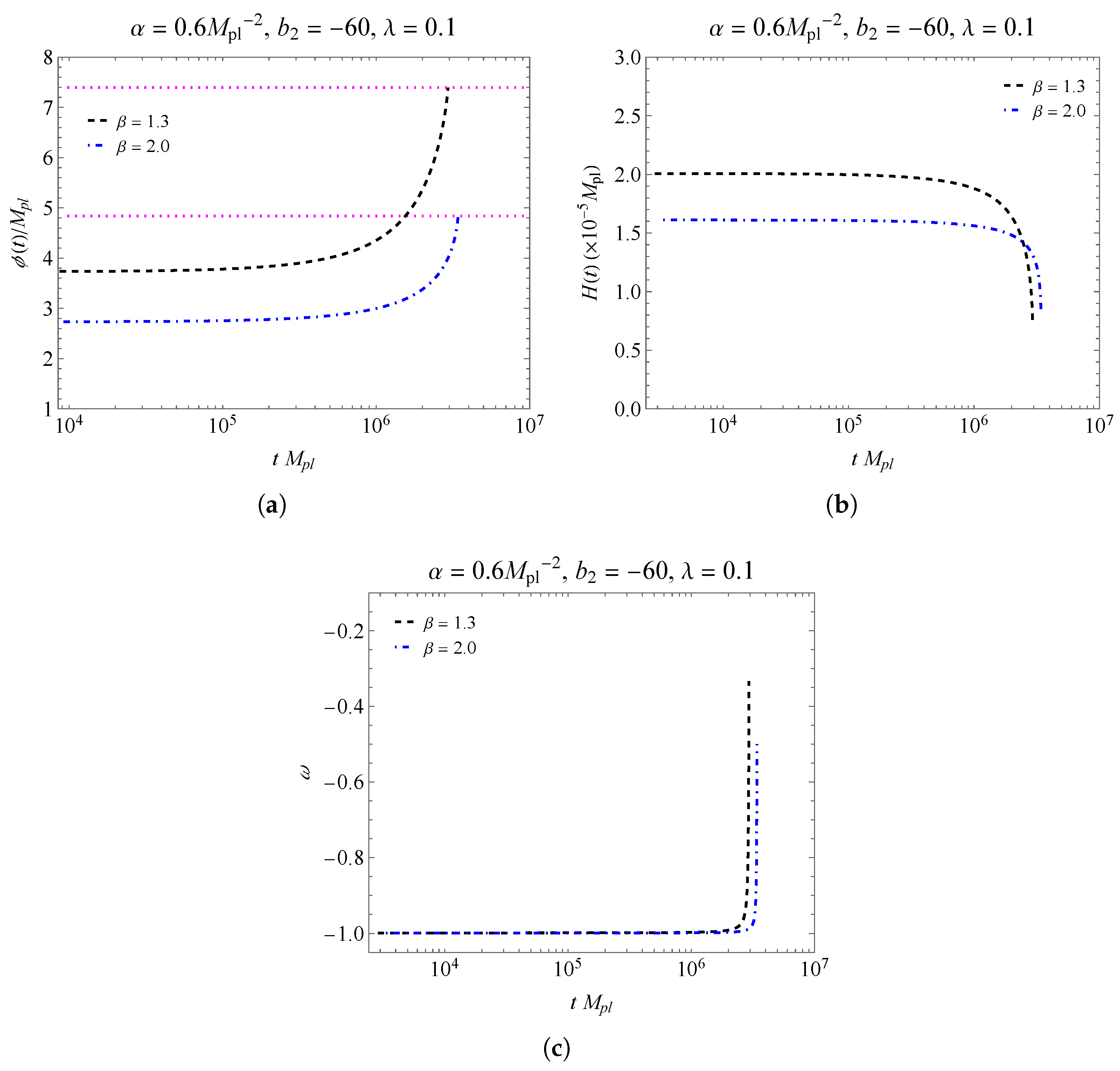
where are the degrees of freedom of the Standard Model. The results for the reheating temperature can be found in Table 3. In Figure 8 and Figure 9, we have the behavior of the parameters , and . Notice the approximately de Sitter regime as before the end of inflation. For the field in Figure 8a and Figure 9a, the behavior of the curves is limited by the horizontal dotted line, which shows the end of inflation in each scenario. In Figure 8b and Figure 9b, we have the behavior of on the scale . We verify that in Figure 8, for the end of inflation with and with using Equation (40), we have the respective values of the reheating temperature and .On the other hand, for Figure 8, we have with and with for the respective temperature values and . Finally, we have, in Figure 8c and Figure 9c, the behavior for the effective equation of state, .

Table 3.
Values for reheating temperature in () for and .
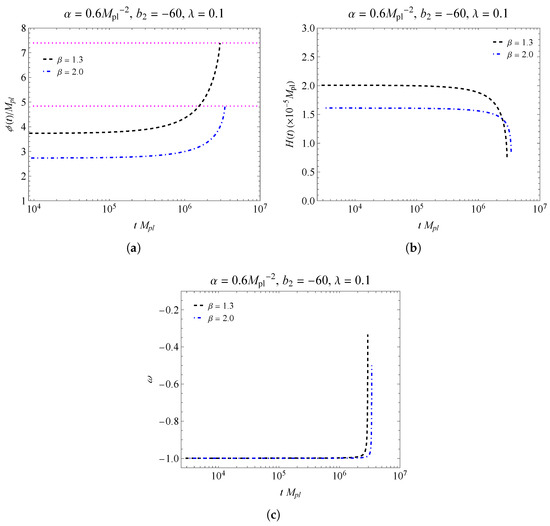
Figure 8.
The figure shows the behavior of , and for the fixed values of , and . In the graph (a), we have the field as a function of time. The horizontal dotted lines delimit the end of inflation. In (b), we have in the order of Planck mass. For the end of inflation, we have for and for . In (c), we have the behavior of the equation of state.
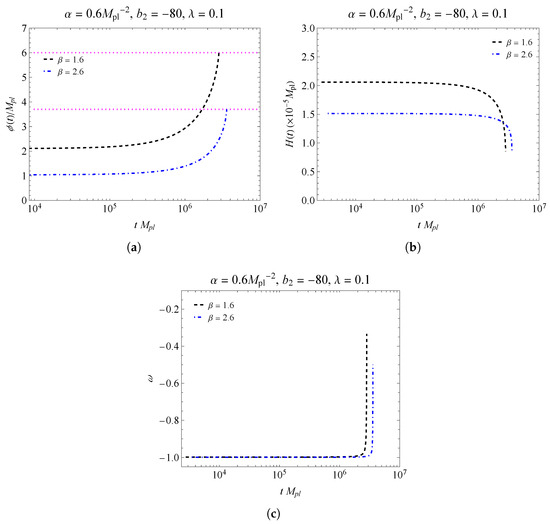
Figure 9.
The figure shows the behavior of , and for the fixed values of , and . In the graph (a), we have the field as a function of time. In (b), we have at the end of inflation, i.e., for and for . In (c), we have the behavior of the equation of state.
5. Conclusions
Our results show how to rescue models in the context of dilatonic gravity in view of the cosmological observations of the Planck 2018 Collaboration. By considering a specific range of parameters adopted in the present analysis, as can be seen in the previous section along with the figures and tables, we check the results for the scalar index and the tensor-to-scalar ratio in a plane by considering two numbers for e-folds and , and compare them with the 68% and 95% contours obtained from the Planck(2018)+BAO+BICEP/Keck Array data [71,72]. The best results, i.e., those that fall inside these contours, are related to , and () or (). For these values of , , this means the universe evolves in the approximately de Sitter regime before the end of inflation. As we know, many interesting models in the past have been ruled out by updated data over time according to revisions of cosmological observational data. In the present study, we turn our attention to the well-explored -exponential. This model, which in our setup corresponds to , is subject to strong restrictions from the Planck 2018 data. However, it was soon rescued in the context of gravity non-minimally coupled to the scalar field [74]. In the present investigation, we reviewed this problem in the context of dilatonic gravity. We show that the presence of dilaton coupling in the intermediate regime plays a fundamental role in rescuing the model. Finally, the model presents a fairly good approximate reheating temperature. In the scope of our present study, we just estimate the instantaneous reheating which leads to the maximal temperature. A study we will conduct in the future will aim to extend the present analysis to consider the decay of the inflaton in several species due to coupling with other fields.
Author Contributions
F.A.B., C.H.A.B.B. and F.G.C. developed the conceptual idea; J.A.V.C. developed the numerics. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by CNPq grant number 309092/2022-1, CNPq/PRONEX/FAPESQ-PB grant number 165/2018 and FAPESQ-PB grant number 77/2022. C.H.A.B. Borges also acknowledges PIQIFPB for financial support, PIQIFPB grant number 23325.003350.2022-84.
Data Availability Statement
The original contributions presented in the study are included in the article. Further inquiries can be directed to the corresponding author/s.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P.J. Cosmology for grand unified theories with radiatively induced symmetry breaking. Phys. Rev. Lett. 1982, 48, 1220. [Google Scholar] [CrossRef]
- Linde, A.D. A new inflationary universe scenario: A possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems. Phys. Lett. B 1982, 108, 389–393. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Chibisov, G. Quantum fluctuations and a nonsingular universe. ZhETF Pisma Redaktsiiu 1981, 33, 549–553. [Google Scholar]
- Guth, A.H.; Pi, S.-Y. Fluctuations in the new inflationary universe. Phys. Rev. Lett. 1982, 49, 1110. [Google Scholar] [CrossRef]
- Hawking, S.W. The development of irregularities in a single bubble inflationary universe. Phys. Lett. B 1982, 115, 295–297. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Dynamics of phase transition in the new inflationary universe scenario and generation of perturbations. Phys. Lett. B 1982, 117, 175–178. [Google Scholar] [CrossRef]
- Hossain, M.W.; Myrzakulov, R.; Sami, M.; Saridakis, E.N. Class of quintessential inflation models with parameter space consistent with bicep2. Phys. Rev. D 2014, 89, 123513. [Google Scholar] [CrossRef]
- Martin, J.; Ringeval, C.; Trotta, R.; Vennin, V. The best inflationary models after planck. J. Cosmol. Astropart. Phys. 2014, 2014, 039. [Google Scholar] [CrossRef]
- Martin, J.; Ringeval, C.; Vennin, V. Encyclopædia inflationaris. Phys. Dark Universe 2014, 5, 75–235. [Google Scholar] [CrossRef]
- Geng, C.-Q.; Hossain, M.W.; Myrzakulov, R.; Sami, M.; Saridakis, E.N. Quintessential inflation with canonical and noncanonical scalar fields and planck 2015 results. Phys. Rev. D 2015, 92, 023522. [Google Scholar] [CrossRef]
- Huang, Q.-G.; Wang, K.; Wang, S. Inflation model constraints from data released in 2015. Phys. Rev. D 2016, 93, 103516. [Google Scholar] [CrossRef]
- Linde, A. Particle physics and inflationary cosmology. arXiv 2005, arXiv:hep-th/0503203. [Google Scholar]
- Dolgov, A.; Linde, A.D. Baryon asymmetry in the inflationary universe. Phys. Lett. B 1982, 116, 329–334. [Google Scholar] [CrossRef]
- Abbott, L.F.; Farhi, E.; Wise, M.B. Particle production in the new inflationary cosmology. Phys. Lett. B 1982, 117, 29–33. [Google Scholar] [CrossRef]
- Starobinsky, A. Nonsingular model of the universe with the quantum-gravitational de sitter stage and its observational consequences. In Quantum Gravity; Springer: Berlin/Heidelberg, Germany, 1984; pp. 103–128. [Google Scholar]
- Dolgov, A.; Hansen, S. Equation of motion of a classical scalar field with back reaction of produced particles. Nucl. Phys. B 1999, 548, 408–426. [Google Scholar] [CrossRef]
- Traschen, J.H.; Brandenberger, R.H. Particle production during out-of-equilibrium phase transitions. Phys. Rev. D 1990, 42, 2491. [Google Scholar] [CrossRef]
- Odintsov, S.; Oikonomou, V. f (r) gravity inflation with string-corrected axion dark matter. Phys. Rev. D 2019, 99, 064049. [Google Scholar] [CrossRef]
- Oikonomou, V. Exponential inflation with f (r) gravity. Phys. Rev. D 2018, 97, 064001. [Google Scholar] [CrossRef]
- Kleidis, K.; Oikonomou, V. Scalar field assisted f (r) gravity inflation. Int. J. Geom. Methods Mod. Phys. 2018, 15, 1850137. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.; Oikonomou, V. Constant-roll inflation in f (r) gravity. Class. Quantum Gravity 2017, 34, 245012. [Google Scholar] [CrossRef]
- Zhong, Y.; Sáez-Chillón Gómez, D. Inflation in mimetic f (g) gravity. Symmetry 2018, 10, 170. [Google Scholar] [CrossRef]
- Rezazadeh, K.; Abdolmaleki, A.; Karami, K. Logamediate inflation in f (t) teleparallel gravity. Astrophys. J. 2017, 836, 228. [Google Scholar] [CrossRef]
- Shabani, H.; Farhoudi, M. Cosmological and solar system consequences of f (r, t) gravity models. Phys. Rev. D 2014, 90, 044031. [Google Scholar] [CrossRef]
- Moraes, P.; Sahoo, P. Modeling wormholes in f (r, t) gravity. Phys. Rev. D 2017, 96, 044038. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Santos, J.; Moraes, P.; Sahoo, P. Inflation in f (r, t) gravity. Eur. Phys. J. Plus 2020, 135, 576. [Google Scholar] [CrossRef]
- Santos, J.R.L.; da Costa, S.S.; Santos, R.S. Cosmological models for f(r,t) − Λ (ϕ) gravity. Phys. Dark Univ. 2023, 42, 101356. [Google Scholar] [CrossRef]
- Witten, E. Some properties of o (32) superstrings. Phys. Lett. B 1984, 149, 351–356. [Google Scholar] [CrossRef]
- Witten, E. String theory dynamics in various dimensions. Nucl. Phys. B 1995, 443, 85–126. [Google Scholar] [CrossRef]
- Gasperini, M. Dilatonic interpretation of quintessence? Phys. Rev. D 2001, 64, 043510. [Google Scholar] [CrossRef]
- Gasperini, M.; Piazza, F.; Veneziano, G. Quintessence as a runaway dilaton. Phys. Rev. D 2001, 65, 023508. [Google Scholar] [CrossRef]
- Brito, F.A.; Borges, C.H.; Campos, J.A.; Costa, F.G. Weak coupling regime in dilatonic f (r, t) cosmology. Universe 2024, 10, 134. [Google Scholar] [CrossRef]
- Harko, T.; Lobo, F.S.; Nojiri, S.; Odintsov, S.D. f (r, t) gravity. Phys. Rev. D-Part. Fields Gravit. Cosmol. 2011, 84, 024020. [Google Scholar] [CrossRef]
- Damour, T.; Polyakov, A.M. The string dilation and a least coupling principle. Nucl. Phys. B 1994, 423, 532–558. [Google Scholar] [CrossRef]
- Alvarenga, F.G.; Cruz-Dombriz, A.d.; Houndjo, M.J.S.; Rodrigues, M.E. Sáez-Gómez Dynamics of scalar perturbations f(R,T) gravity. Phys. Rev. D 2013, 87, 103526, Erratum in Phys. Rev. D 2013, 87, 129905. [Google Scholar] [CrossRef]
- Fisher, S.B.; Carlson, E.D. Reexamining f(R,T) gravity. Phys. Rev. D 2019, 100, 064059. [Google Scholar] [CrossRef]
- Carvalho, G.A.; Lobato, R.V.; Moraes, P.H.R.S.; Arbail, J.D.V.; Marinho, R.M., Jr.; Otoniel, E.; Malheiro, M. Stellar equilibrium configurations of white dwarfs in the f(R, T) gravity. Eur. Phys. J. C 2017, 77, 871. [Google Scholar] [CrossRef]
- Ordines, T.M.; Carlson, E.D. Limits on f(R, T) gravity from Earth’s atmosphere. Phys. Rev. D 2019, 99, 104052. [Google Scholar] [CrossRef]
- Fazlollahi, H.R. Holographic dark energy in non-conserved gravity theory. Commun. Theor. Phys. 2024, 76, 4. [Google Scholar] [CrossRef]
- Fazlollahi, H.R. Non-conserved modified gravity theory. Eur. Phys. J. C 2023, 83, 923. [Google Scholar] [CrossRef]
- Bertini, N.R.; Velten, H. Fully conservative f(R,T) gravity and Solar System constraints. Phys. Rev. D 2023, 107, 124005. [Google Scholar] [CrossRef]
- Pretel, J.M.Z.; Jorás, S.E.; Reis, R.R.R.; Arbañil, J.D.V. Neutron stars in f (R, T) gravity with conserved energy-momentum tensor: Hydrostatic equilibrium and asteroseismology. J. Cosmol. Astropart. Phys. 2021, 8, 055. [Google Scholar] [CrossRef]
- Carvalho, G.A.; Santos, S.I.D.; Moraes, P.H.R.S.; Malheiro, M. Strange stars in energy–momentum-conserved f(R, T) gravity. Int. J. Mod. Phys. D 2020, 29, 2050075. [Google Scholar] [CrossRef]
- Bokhari, A.H.; Kara, A.H.; Gadjagboui, B. On symmetries and conservation laws of some spacetimes in f(R,T) gravity. Mod. Phys. Lett. A 2019, 34, 1975003. [Google Scholar] [CrossRef]
- Singh, V.; Beesham, A. The f(R, Tϕ) gravity models with conservation of energy–momentum tensor. Eur. Phys. J. C 2018, 78, 564. [Google Scholar]
- Lobato, R.V.; Carvalho, G.A.; Martins, A.G.; Moraes, P.H.R.S. Energy nonconservation as a link between f(R, T) gravity and noncommutative quantum theory. Eur. Phys. J. Plus 2019, 134, 132. [Google Scholar] [CrossRef]
- Santos, S.I.D.; Carvalho, G.A.; Moraes, P.H.R.S.; Lenzi, C.H.; Malheiro, M. A conservative energy-momentum tensor in the f(R, T) gravity and its implications for the phenomenology of neutron stars. Eur. Phys. J. Plus. 2019, 134, 398. [Google Scholar] [CrossRef]
- Shabani, H.; Ziaie, A.H. Interpretation of f(R,T) gravity in terms of a conserved effective fluid. Int. J. Mod. Phys. A 2018, 33, 1850050. [Google Scholar] [CrossRef]
- Shabani, H.; Ziaie, A.H. Consequences of energy conservation violation: Late time solutions of Λ(T)CDM subclass of f(R,T) gravity using dynamical system approach. Eur. Phys. J. C 2017, 77, 282. [Google Scholar] [CrossRef]
- Gasperini, M.; Veneziano, G. The pre-big bang scenario in string cosmology. Phys. Rep. 2003, 373, 1–212. [Google Scholar] [CrossRef]
- Gasperini, M. Dilaton cosmology and phenomenology. In String Theory and Fundamental Interactions: Gabriele Veneziano and Theoretical Physics: Historical and Contemporary Perspectives; Springer: Berlin/Heidelberg, Germany, 2008; pp. 787–844. [Google Scholar]
- Linde, A.D. Chaotic inflation. Phys. Lett. B 1983, 129, 177–181. [Google Scholar] [CrossRef]
- Coleman, S.; Weinberg, E. Radiative corrections as the origin of spontaneous symmetry breaking. Phys. Rev. D 1973, 7, 1888. [Google Scholar] [CrossRef]
- Belinsky, V.; Khalatnikov, I.; Grishchuk, L.; Zeldovich, Y.B. Inflationary Stages in Cosmological Models with a Scalar Field. Tech. Rep., International Centre for Theoretical Physics. 1985. Available online: https://inis.iaea.org/records/gxtfj-ses31 (accessed on 4 February 2025).
- Peebles, P.; Ratra, B. Cosmology with a time-variable cosmological’constant’. Astrophys. J. 1988, 325, L17–L20. [Google Scholar] [CrossRef]
- Ratra, B.; Peebles, P.J. Cosmological consequences of a rolling homogeneous scalar field. Phys. Rev. D 1988, 37, 3406. [Google Scholar] [CrossRef] [PubMed]
- Wetterich, C. The cosmon model for an asymptotically vanishing time-dependent cosmological“constant”. arXiv 1994, arXiv:hep-th/9408025. [Google Scholar]
- Ferreira, P.G.; Joyce, M. Cosmology with a primordial scaling field. Phys. Rev. D 1998, 58, 023503. [Google Scholar] [CrossRef]
- Lucchin, F.; Matarrese, S. Power-law inflation. Phys. Rev. D 1985, 32, 1316. [Google Scholar] [CrossRef] [PubMed]
- Halliwell, J.J. Scalar fields in cosmology with an exponential potential. Phys. Lett. B 1987, 185, 341–344. [Google Scholar] [CrossRef]
- Wetterich, C. Kaluza-klein cosmology and the inflationary universe. Nucl. Phys. B 1985, 252, 309–320. [Google Scholar] [CrossRef]
- Shafi, Q.; Wetterich, C. Inflation with higher dimensional gravity. Phys. Lett. B 1985, 152, 51–55. [Google Scholar] [CrossRef]
- Alcaniz, J.S.; Carvalho, F. β-exponential inflation. Europhys. Lett. 2007, 79, 39001. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; US Government Printing Office: Washington, DC, USA, 1968; Volume 55. [Google Scholar]
- Lima, J.; Silva, R.; Plastino, A. Nonextensive thermostatistics and the h theorem. Phys. Rev. Lett. 2001, 86, 2938. [Google Scholar] [CrossRef] [PubMed]
- Benisty, D.; Guendelman, E.I.; Saridakis, E.N. The scale factor potential approach to inflation. Eur. Phys. J. C 2020, 80, 480. [Google Scholar] [CrossRef]
- Liddle, A.R.; Lyth, D.H. Cosmological Inflation and Large-Scale Structure; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Lyth, D.H.; Riotto, A. Particle physics models of inflation and the cosmological density perturbation. Phys. Rep. 1999, 314, 1–146. [Google Scholar] [CrossRef]
- Santos, M.; Benetti, M.; Alcaniz, J.; Brito, F.; Silva, R. Cmb constraints on β-exponential inflationary models. J. Cosmol. Astropart. Phys. 2018, 2018, 023. [Google Scholar] [CrossRef]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.; Bartolo, N.; Basak, S.; et al. Planck 2018 results-x. constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar]
- Ade, P.A.; Ahmed, Z.; Amiri, M.; Barkats, D.; Thakur, R.B.; Bischoff, C.; Beck, D.; Bock, J.; Boenish, H.; Bullock, E.; et al. Improved constraints on primordial gravitational waves using planck, wmap, and bicep/keck observations through the 2018 observing season. Phys. Rev. Lett. 2021, 127, 151301. [Google Scholar] [CrossRef] [PubMed]
- Tristram, M.; Banday, A.J.; Górski, K.M.; Keskitalo, R.; Lawrence, C.R.; Andersen, K.J.; Barreiro, R.B.; Borrill, J.; Colombo, L.P.L.; Eriksen, H.K.; et al. Improved limits on the tensor-to-scalar ratio using BICEP and Planck data. Phys. Rev. D 2022, 105, 083524. [Google Scholar] [CrossRef]
- Santos, F.B.M.D.; da Costa, S.S.; Silva, R.; Benetti, M.; Alcaniz, J. Constraining non-minimally coupled β-exponential inflation with CMB data. J. Cosmol. Astropart. Phys. 2022, 2022, 001. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).