Cosmic Ray Spectra and Anisotropy in an Anisotropic Propagation Model with Spiral Galactic Sources
Abstract
1. Introduction
2. Model Description
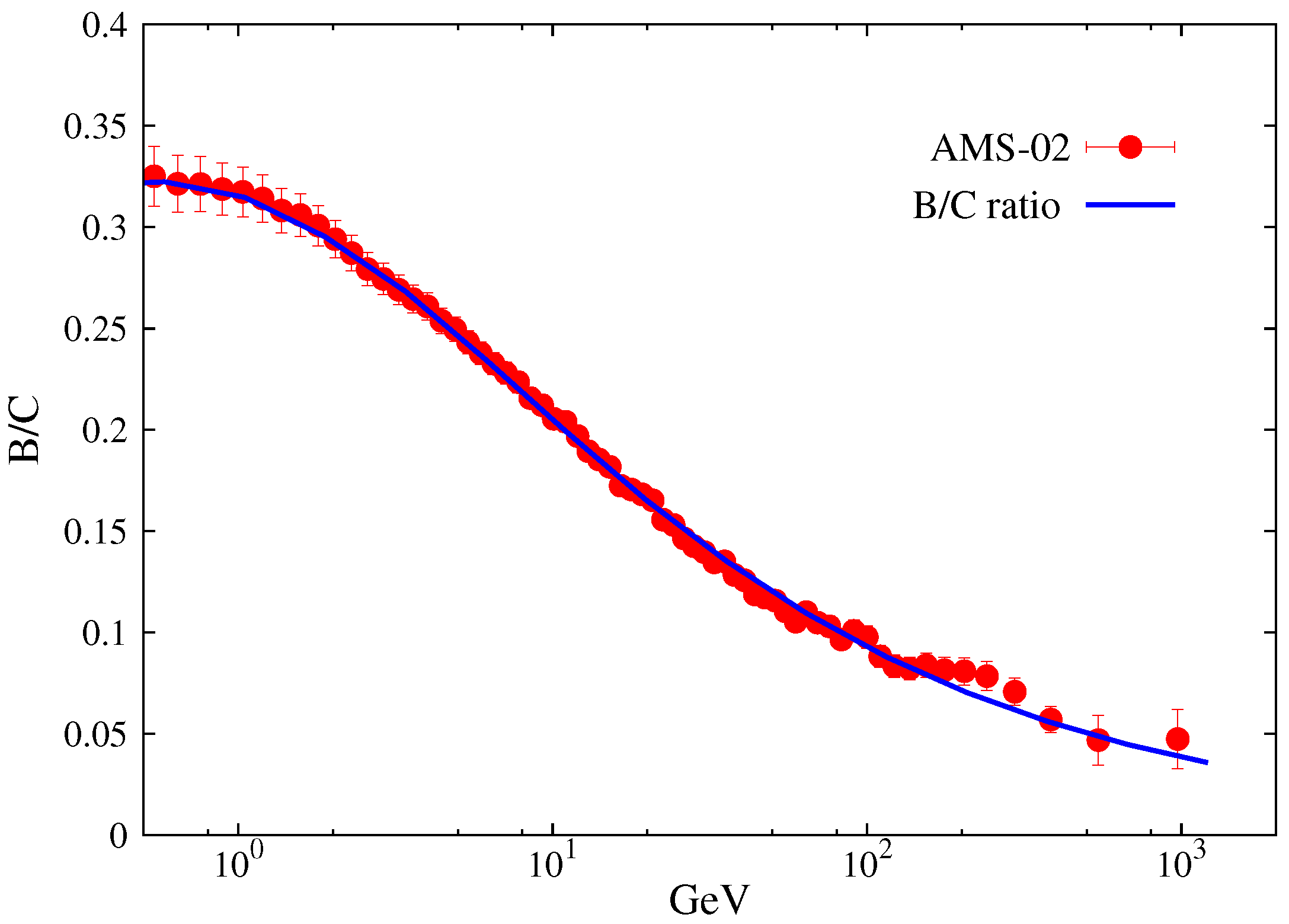
2.1. Spatial-Dependent Propagation Model
2.2. Spiral Distribution of CR Sources
2.3. Nearby Source
2.4. Anisotropic Diffusion and Large-Scale Anisotropy
3. Results and Discussion
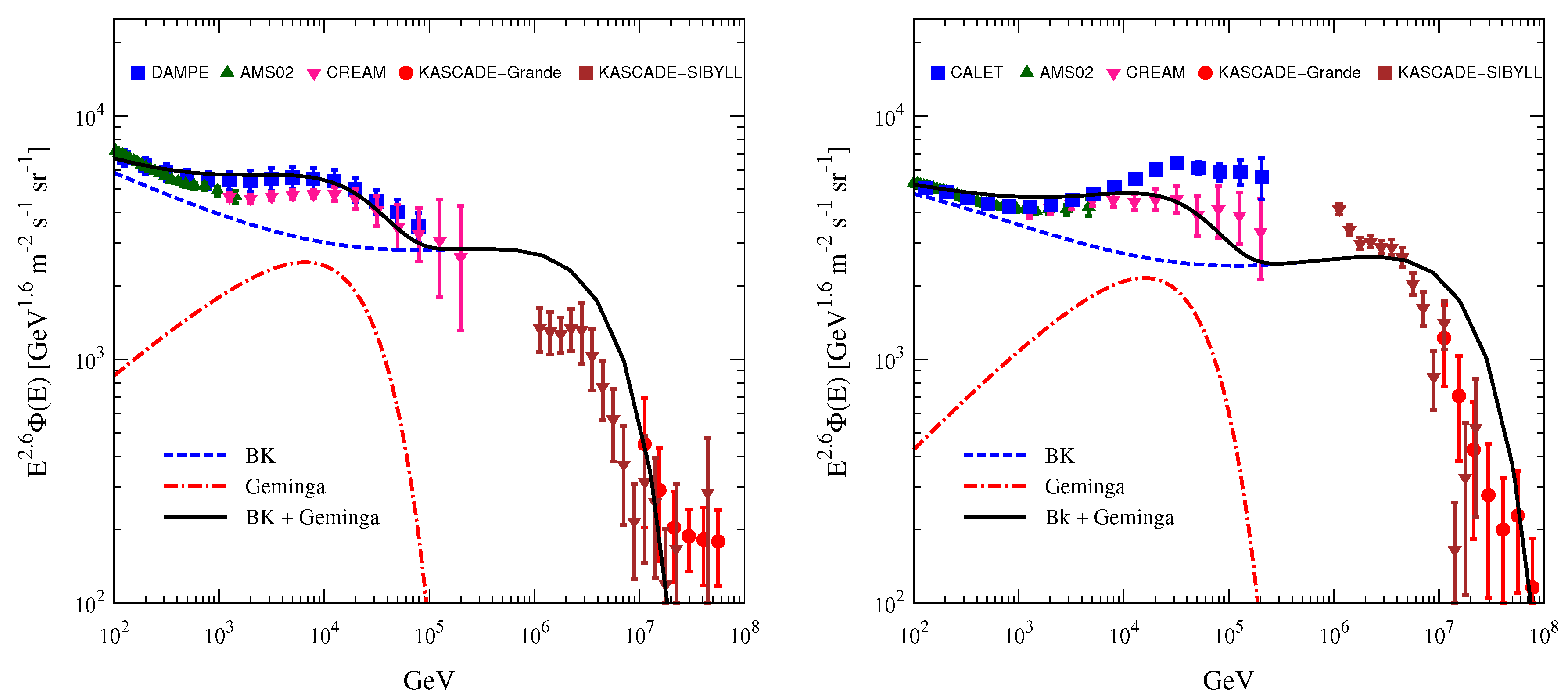
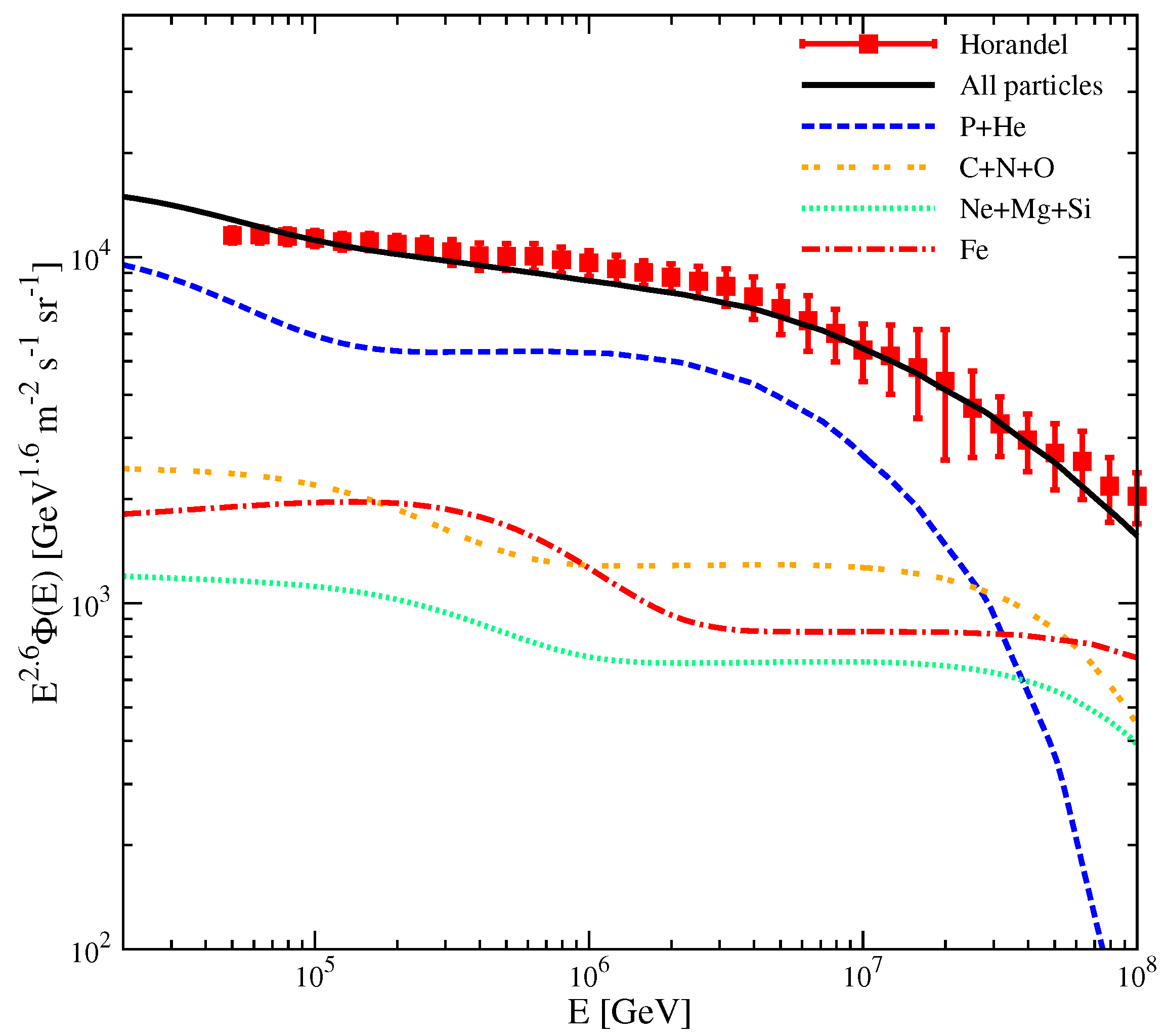
3.1. Proton and Helium Spectra of Nearby Sources
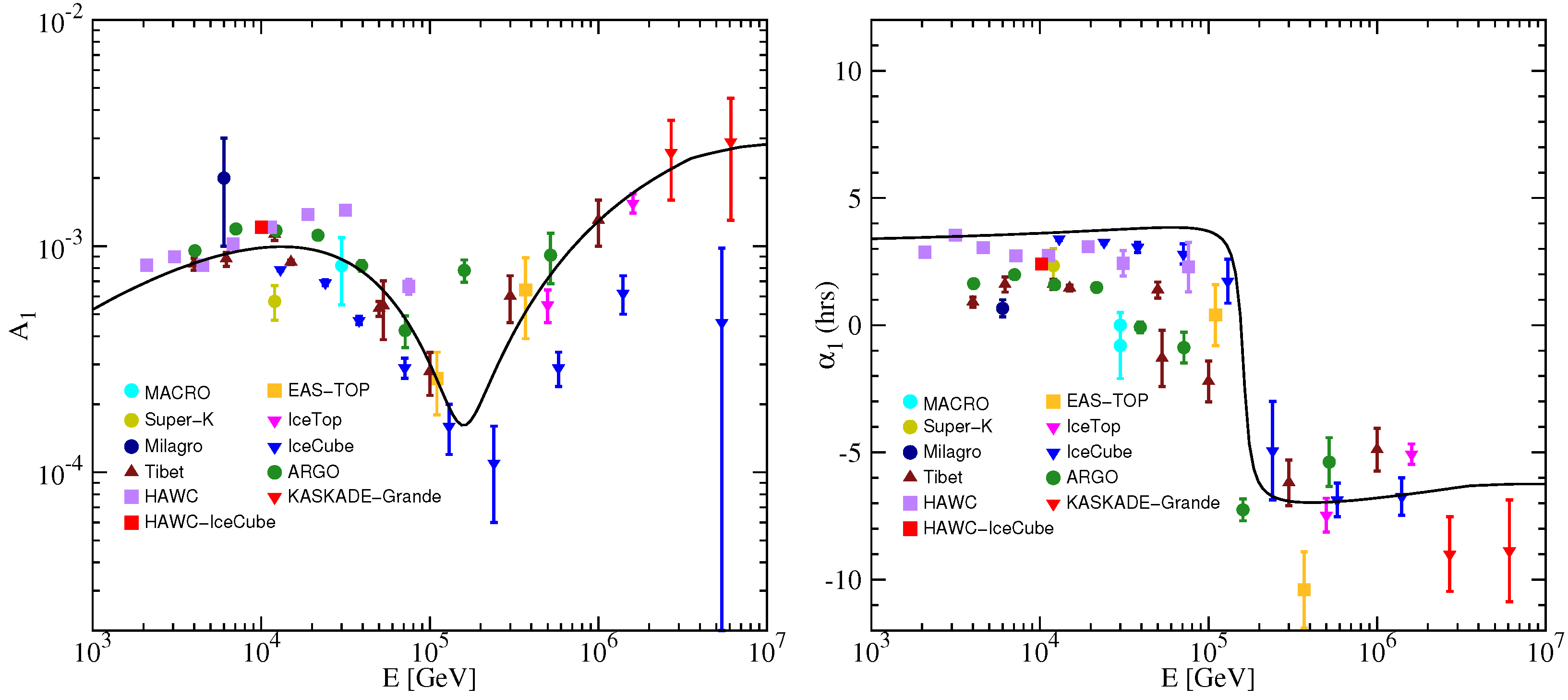
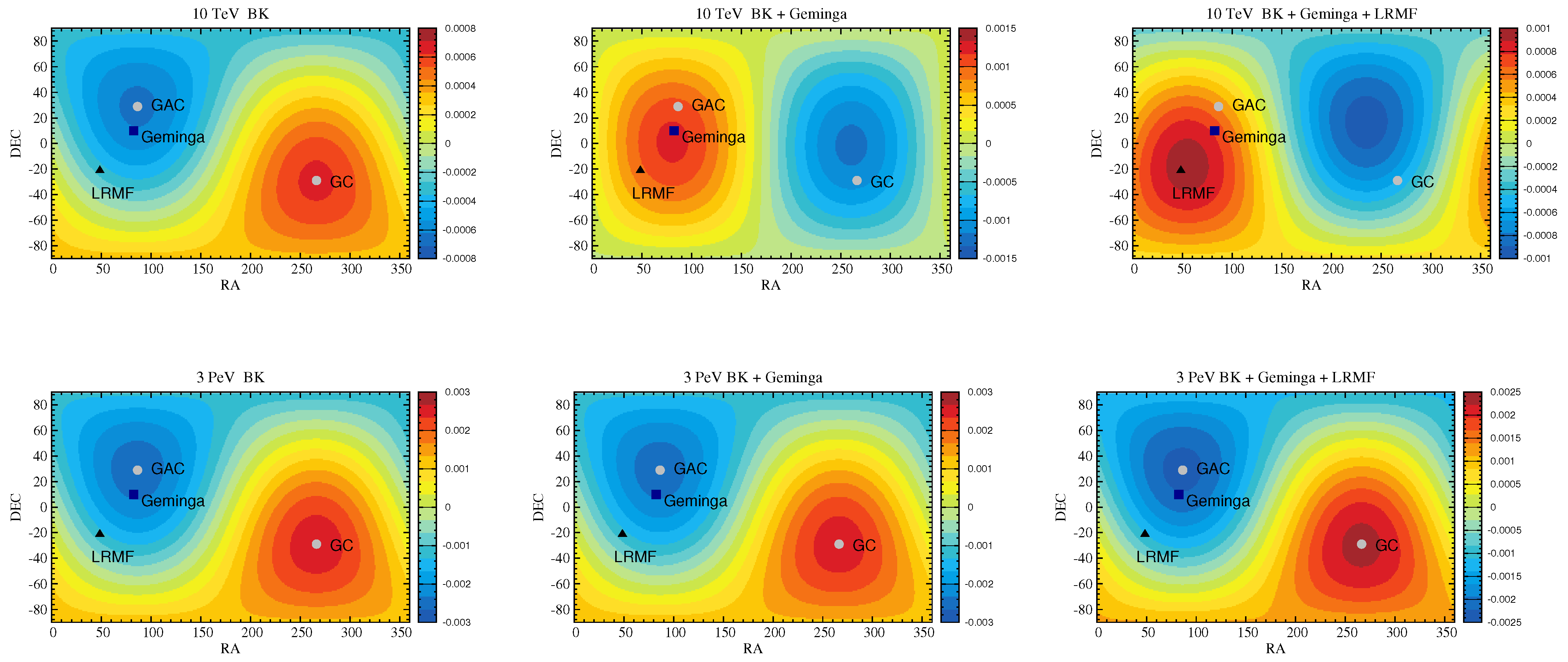
3.2. Anisotropy
4. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Panov, A.D.; Adams, J.H.; Ahn, H.S.; Batkov, K.E.; Bashindzhagyan, G.L.; Watts, J.W.; Wefel, J.P.; Wu, J.; Ganel, O.; Guzik, T.G.; et al. Elemental energy spectra of cosmic rays from the data of the ATIC-2 experiment. Bull. Russ. Acad. Sci. Phys. 2007, 71, 494–497. [Google Scholar] [CrossRef]
- Ahn, H.S.; Allison, P.; Bagliesi, M.G.; Beatty, J.J.; Bigongiari, G.; Childers, J.T.; Conklin, N.B.; Coutu, S.; DuVernois, M.A.; Ganel, O.; et al. Discrepant Hardening Observed in Cosmic-ray Elemental Spectra. Astrophys. J. Lett. 2010, 714, L89–L93. [Google Scholar] [CrossRef]
- Yoon, Y.S.; Ahn, H.S.; Allison, P.S.; Bagliesi, M.G.; Beatty, J.J.; Bigongiari, G.; Boyle, P.J.; Childers, J.T.; Conklin1, N.B.; Coutu, S.; et al. Cosmic-ray Proton and Helium Spectra from the First CREAM Flight. Astrophys. J. 2011, 728, 122. [Google Scholar] [CrossRef]
- Adriani, O.; Barbarino, G.C.; Bazilevskaya, G.A.; Bellotti, R.; Boezio, M.; Bogomolov, E.A.; Bonechi, L.; Bongi, M.; Bonvicini, V.; Borisov, S.; et al. PAMELA Measurements of Cosmic-Ray Proton and Helium Spectra. Science 2011, 332, 69. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, M.; Aisa, D.; Alpat, B.; Alvino, A.; Ambrosi, G.; Andeen, K.; Arruda, L.; Attig, N.; Azzarello, P.; Bachlechner, A.; et al. Precision Measurement of the Proton Flux in Primary Cosmic Rays from Rigidity 1 GV to 1.8 TV with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2015, 114, 171103. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, M.; Aisa, D.; Alpat, B.; Alvino, A.; Ambrosi, G.; Andeen, K.; Arruda, L.; Attig, N.; Azzarello, P.; Bachlechner, A.; et al. Precision Measurement of the Helium Flux in Primary Cosmic Rays of Rigidities 1.9 GV to 3 TV with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2015, 115, 211101. [Google Scholar] [CrossRef] [PubMed]
- DAMPE Collaboration; An, Q.; Asfandiyarov, R.; Azzarello, P.; Bernardini, P.; Bi, X.J.; Cai, M.S.; Chang, J.; Chen, D.Y.; Chen, H.F.; et al. Measurement of the cosmic ray proton spectrum from 40 GeV to 100 TeV with the DAMPE satellite. Sci. Adv. 2019, 5, eaax3793. [Google Scholar]
- Adriani, O.; Akaike, Y.; Asano, K.; Asaoka, Y.; Bagliesi, M.G.; Berti, E.; Bigongiari, G.; Binns, W.R.; Bonechi, S.; Bongi, M.; et al. Direct Measurement of the Cosmic-Ray Proton Spectrum from 50 GeV to 10 TeV with the Calorimetric Electron Telescope on the International Space Station. Phys. Rev. Lett. 2019, 112, 181102. [Google Scholar] [CrossRef]
- Alemanno, F.; An, Q.; Azzarello, P.; Barbato, F.C.T.; Bernardini, P.; Bi, X.J.; Cai, M.S.; Catanzani, E.; Chang, J.; Chen, D.Y.; et al. Measurement of the Cosmic Ray Helium Energy Spectrum from 70 GeV to 80 TeV with the DAMPE Space Mission. Phys. Rev. Lett. 2021, 126, 201102. [Google Scholar] [CrossRef] [PubMed]
- Yoon, Y.S.; Anderson, T.; Barrau, A.; Conklin, N.B.; Coutu, S.; Derome, L.; Han, J.H.; Jeon, J.A.; Kim, K.C.; Kim, M.H.; et al. Proton and Helium Spectra from the CREAM-III Flight. Astrophys. J. 2017, 839, 5. [Google Scholar] [CrossRef]
- Atkin, E.; Bulatov, V.; Dorokhov, V.; Gorbunov, N.; Filippov, S.; Grebenyuk, V.; Karmanov, D.; Kovalev, I.; Kudryashov, I.; Kurganov, A.; et al. New Universal Cosmic-Ray Knee near a Magnetic Rigidity of 10 TV with the NUCLEON Space Observatory. J. Exp. Theor. Phys. Lett. 2018, 108, 5–12. [Google Scholar] [CrossRef]
- Adriani, O.; Akaike, Y.; Asano, K.; Asaoka, Y.; Berti, E.; Bigongiari, G.; Binns, W.R.; Bongi, M.; Brogi, P.; Bruno, A.; et al. Direct Measurement of the Cosmic-Ray Helium Spectrum from 40 GeV to 250 TeV with the Calorimetric Electron Telescope on the International Space Station. J. Exp. Theor. Phys. Lett. 2023, 130, 171002. [Google Scholar] [CrossRef] [PubMed]
- Thoudam, S.; Hörandel, J.R. Nearby supernova remnants and the cosmic ray spectral hardening at high energies. Mon. Not. Roy. Astron. Soc. 2012, 421, 1209–1214. [Google Scholar] [CrossRef][Green Version]
- Liu, W.; Guo, Y.Q.; Yuan, Q. Indication of nearby source signatures of cosmic rays from energy spectra and anisotropies. J. Cosmol. Astropart. Phys. 2019, 10, 010. [Google Scholar] [CrossRef]
- Biermann, P.L.; Becker, J.K.; Dreyer, J.; Meli, A.; Seo, E.S.; Stanev, T. The Origin of Cosmic Rays: Explosions of Massive Stars with Magnetic Winds and Their Supernova Mechanism. Astrophys. J. 2010, 725, 184–187. [Google Scholar] [CrossRef]
- Thoudam, S.; Rachen, J.P.; Van Vliet, A.; Achterberg, A.; Buitink, S.; Falcke, H.; Hörandel, J.R. Cosmic-ray energy spectrum and composition up to the ankle: The case for a second Galactic component. Astron. Astrophys. 2016, 595, A33. [Google Scholar] [CrossRef]
- Tomassetti, N. Origin of the Cosmic-Ray Spectral Hardening. Astrophys. J. Lett. 2012, 752, L13. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, B.; Bi, X.J. Cosmic ray spectral hardening due to dispersion in the source injection spectra. Phys. Rev. D 2011, 84, 043002. [Google Scholar] [CrossRef]
- Zatsepin, V.I.; Sokolskaya, N.V. Three component model of cosmic ray spectra from 10 GeV to 100 PeV. Astron. Astrophys. 2006, 458, 1–5. [Google Scholar] [CrossRef]
- Amenomori, M.; Ayabe, S.; Bi, X.J.; Chen, D.; Cui, S.W.; Danzengluobu; Ding, L.K.; Ding, X.H.; Feng, C.F.; Feng, Z.; et al. Anisotropy and Corotation of Galactic Cosmic Rays. Science 2006, 314, 439–443. [Google Scholar] [CrossRef]
- Amenomori, M.; Bi, X.J.; Chen, D.; Cui, S.W.; Ding, L.K.; Ding, X.H.; Fan, C.; Feng, C.F.; Feng, Z.; Feng, Z.Y.; et al. On Temporal Variations of the Multi-TeV Cosmic Ray Anisotropy using the Tibet III Air Shower Array. Astrophys. J. 2010, 711, 119–124. [Google Scholar]
- Amenomori, M.; Bi, X.J.; Chen, D.; Chen, T.L.; Chen, W.Y.; Cui, S.W.; Danzengluobu; Ding, L.K.; Feng, C.F.; Feng, Z.Y.; et al. Northern Sky Galactic Cosmic Ray Anisotropy between 10 and 1000 TeV with the Tibet Air Shower Array. Astrophys. J. 2017, 836, 153. [Google Scholar] [CrossRef]
- Guillian, G.; Hosaka, J.; Ishihara, K.; Kameda, J.; Koshio, Y.; Minamino, A.; Mitsuda, C.; Miura, M.; Moriyama, S.; Nakahata, M.; et al. Observation of the anisotropy of 10 TeV primary cosmic ray nuclei flux with the Super-Kamiokande-I detector. Phys. Rev. D 2007, 75, 062003. [Google Scholar] [CrossRef]
- Abdo, A.A.; Allen, B.; Aune, T.; Berley, D.; Blaufuss, E.; Casanova, S.; Chen, C.; Dingus, B.L.; Ellsworth, R.W.; Fleysher, L.; et al. Discovery of Localized Regions of Excess 10-TeV Cosmic Rays. Phys. Rev. Lett. 2008, 101, 221101. [Google Scholar] [CrossRef] [PubMed]
- Abdo, A.A.; Allen, B.T.; Aune, T.; Berley, D.; Casanova, S.; Chen, C.; Dingus, L.; Ellsworth, R.W.; Fleysher, L.; Fleysher, R.; et al. The Large-Scale Cosmic-Ray Anisotropy as Observed with Milagro. Astrophys. J. 2009, 698, 2121–2130. [Google Scholar] [CrossRef]
- Abbasi, R.; Abdou, Y.; Abu-Zayyad, T.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Andeen, K.; Auffenberg, J.; Bai, X.; Baker, M.; et al. Measurement of the Anisotropy of Cosmic-ray Arrival Directions with IceCube. Astrophys. J. Lett. 2010, 718, L194–L198. [Google Scholar] [CrossRef]
- Abbasi, R.; Abdou, Y.; Abu-Zayyad, T.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Altmann, D.; Andeen, K.; Auffenberg, J.; Bai, X.; et al. Observation of Anisotropy in the Arrival Directions of Galactic Cosmic Rays at Multiple Angular Scales with IceCube. Astrophys. J. 2011, 740, 16. [Google Scholar] [CrossRef]
- Abbasi, R.; Abdou, Y.; Abu-Zayyad, T.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Allen, M.M.; Altmann, D.; Andeen, K.; et al. Observation of Anisotropy in the Galactic Cosmic-Ray Arrival Directions at 400 TeV with IceCube. Astrophys. J. 2011, 746, 33. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Abbasi, R.; Abdou, Y.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Altmann, D.; Andeen, K.; Auffenberg, J.; et al. Observation of Cosmic-Ray Anisotropy with the IceTop Air Shower Array. Astrophys. J. 2013, 765, 55. [Google Scholar] [CrossRef]
- Aartsen, M.G.; Abraham, K.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Altmann, D.; Anderson, T.; Ansseau, I.; et al. Anisotropy in Cosmic-Ray Arrival Directions in the Southern Hemisphere Based on Six Years of Data from the IceCube Detector. Astrophys. J. 2016, 826, 220. [Google Scholar] [CrossRef]
- Bartoli, B.; Bernardini, P.; Bi, X.J.; Bolognino, I.; Branchini, P.; Budano, A.; Calabrese Melcarne, A.K.; Camarri, P.; Cao, Z.; Cardarelli, R.; et al. Medium scale anisotropy in the TeV cosmic ray flux observed by ARGO-YBJ. Phys. Rev. D 2013, 88, 082001. [Google Scholar] [CrossRef]
- Bartoli, B.; Bernardini, P.; Bi, X.J.; Cao, Z.; Catalanotti, S.; Chen, S.Z.; Chen, T.L.; Cui, S.W.; Dai, B.Z.; D’Amone, A.; et al. ARGO-YBJ Observation of the Large-scale Cosmic Ray Anisotropy During the Solar Minimum between Cycles 23 and 24. Astrophys. J. 2015, 809, 90. [Google Scholar] [CrossRef]
- Aglietta, M.; Alekseenko, V.V.; Alessandro, B.; Antonioli, P.; Arneodo, F.; Bergamasco, L.; Bertaina, M.; Bonino, R.; Castellina, A.; Chiavassa, A.; et al. Evolution of the Cosmic-Ray Anisotropy Above 1014 eV. Astrophys. J. 2009, 692, L130–L133. [Google Scholar] [CrossRef]
- Chiavassa, A.; Apel, W.; Arteaga-Velazquez, J.; Bekk, K.; Bertaina, M.; Blümer, J.; Bozdog, H.; Brancus, I.M.; Cantoni, E.; Cossavella, F.; et al. A study of the first harmonic of the large scale anisotropies with the KASCADE-Grande experiment. In Proceedings of the 34th International Cosmic Ray Conference (ICRC2015), Den Haag, The Netherlands, 30 July–6 August 2015; Volume 236, p. 281. [Google Scholar]
- Apel, W.D.; Arteaga-Velázquez, J.C.; Bekk, K.; Bertaina, M.; Blümer, J.; Bonino, R.; Bozdog, H.; Brancus, I.M.; Cantoni1, E.; Chiavassa, A.; et al. Search for Large-scale Anisotropy in the Arrival Direction of Cosmic Rays with KASCADE-Grande. Astrophys. J. 2019, 870, 91. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Solares, H.A.A.; Barber, A.S.; Baughman, B.M.; Bautista-Elivar, N.; et al. Observation of Small-scale Anisotropy in the Arrival Direction Distribution of TeV Cosmic Rays with HAWC. Astrophys. J. 2014, 796, 108. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Alfaro, R.; Alvarez, C.; Álvarez, J.D.; Arceo, R.; Arteaga-Velázquez, J.C.; Rojas, D.A.; Solares, H.A.A.; Becerril, A.; Belmont-Moreno, E.; et al. Observation of Anisotropy of TeV Cosmic Rays with Two Years of HAWC. Astrophys. J. 2018, 865, 57. [Google Scholar] [CrossRef]
- Li, A.; Yin, S.; Liu, M.; Wang, H.; Li, X.; Li, Y. Interpretation of the Spectra and Anisotropy of Galactic Cosmic Rays. Universe 2022, 8, 307. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Alfaro, R.; Alvarez, C.; Arceo, R.; Arteaga-Velázquez, J.C.; Rojas, D.A.; Belmont-Moreno, E.; BenZvi, S.Y.; Brisbois, C.; Capistrán, T.; et al. All-sky Measurement of the Anisotropy of Cosmic Rays at 10 TeV and Mapping of the Local Interstellar Magnetic Field. Astrophys. J. 2019, 871, 96. [Google Scholar] [CrossRef]
- Ahlers, M. Deciphering the Dipole Anisotropy of Galactic Cosmic Rays. Phys. Rev. Lett. 2016, 117, 151103. [Google Scholar] [CrossRef]
- Compton, A.H.; Getting, I.A. An Apparent Effect of Galactic Rotation on the Intensity of Cosmic Rays. Phys. Rev. 1935, 47, 817–821. [Google Scholar] [CrossRef]
- Li, A.-f.; Yuan, Q.; Liu, W.; Guo, Y.-q. Large-scale Anisotropy of Galactic Cosmic Rays as a Probe of Local Cosmic-Ray Propagation. Astrophys. J. 2024, 962, 43. [Google Scholar] [CrossRef]
- Levine, E.S.; Blitz, L.; Heiles, C. The Spiral Structure of the Outer Milky Way in Hydrogen. Science 2006, 312, 1773–1777. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Hou, L.G.; Bian, S.B.; Hao, C.J.; Liu, D.J.; Li, J.J.; Li, Y.J. Local spiral structure based on the Gaia EDR3 parallaxes. Astron. Astrophys. 2021, 645, L8. [Google Scholar] [CrossRef]
- Tian, Z.; Liu, W.; Yang, B.; Fu, X.-D.; Xu, H.-B.; Yao, Y.-H.; Guo, Y.-Q. Electron and positron spectra in three-dimensional spatial-dependent propagation. model. Chin. Phys. C 2022, 44, 085102. [Google Scholar] [CrossRef]
- Zhang, P.-p.; Qiao, B.-q.; Liu, W.; Cui, S.-w.; Yuan, Q.; Guo, Y.-q. Possible bump structure of cosmic ray electrons unveiled by AMS-02 data and its common origin along with the nuclei and positron. J. Cosmol. Astropart. Phys. 2021, 5, 012. [Google Scholar] [CrossRef]
- Guo, Y.-Q.; Tian, Z.; Jin, C. Spatial-dependent Propagation of Cosmic Rays Results in the Spectrum of Proton, Ratios of p/p, and B/C, and Anisotropy of Nuclei. Astrophys. J. 2016, 819, 54. [Google Scholar] [CrossRef]
- Liu, W.; Yao, Y.-h.; Guo, Y.-Q. Revisiting the Spatially Dependent Propagation Model with the Latest Observations of Cosmic-Ray Nuclei. Astrophys. J. 2016, 869, 176. [Google Scholar] [CrossRef]
- Yuan, Q.; Qiao, B.-Q.; Guo, Y.-Q.; Fan, Y.-Z.; Bi, X.-J. Nearby source interpretation of differences among light and medium composition spectra in cosmic rays. Front. Phys. 2021, 16, 24501. [Google Scholar] [CrossRef]
- Guo, Y.-Q.; Yuan, Q. Understanding the spectral hardenings and radial distribution of Galactic cosmic rays and Fermi diffuse γ rays with spatially-dependent propagation. Phys. Rev. D 2018, 97, 063008. [Google Scholar] [CrossRef]
- Qiao, B.-Q.; Liu, W.; Guo, Y.-Q.; Yuan, Q. Anisotropies of different mass compositions of cosmic rays. J. Cosmol. Astropart. Phys. 2019, 12, 007. [Google Scholar] [CrossRef]
- Zhao, B.; Liu, W.; Yuan, Q.; Hu, H.B.; Bi, X.J.; Wu, H.R.; Zhou, X.-X.; Guo, Y.-Q. Geminga SNR: Possible Candidate of the Local Cosmic-Ray Factory. Astrophys. J. 2022, 926, 41. [Google Scholar] [CrossRef]
- Abeysekara, A.U.; Alfaro, R.; Alvarez, C.; Arceo, R.; Arteaga-Velázquez, J.C.; Avila Rojas, D.; Ayala Solares, H.A.; Barber, A.S.; Bautista-Elivar, N.; Becerril, A.; et al. Extended gamma-ray sources around pulsars constrain the origin of the positron flux at Earth. Science 2017, 358, 911–914. [Google Scholar] [CrossRef] [PubMed]
- Aharonian, F.; An, Q.; Axikegu; Bai, L.X.; Bai, Y.X.; Bao, Y.W.; Bastieri, D.; Bi, X.J.; Cai, H.J.; Cai, T.; et al. Extended Very-High-Energy Gamma-Ray Emission Surrounding PSR J 0622 +3749 Observed by LHAASO-KM2A. Phys. Rev. Lett. 2021, 126, 241103. [Google Scholar] [CrossRef]
- Strong, A.W.; Moskalenko, I.V. Propagation of cosmic-ray nucleons in the galaxy. Astrophys. J. 1998, 509, 212–228. [Google Scholar] [CrossRef]
- Evoli, C.; Gaggero, D.; Vittino, A.; Di Bernardo, G.; Di Mauro, M.; Ligorini, A.; Ullio, P.; Grasso, D. Cosmic-ray propagation with DRAGON2: I. numerical solver and astrophysical ingredients. J. Cosmol. Astropart. Phys. 2017, 2, 015. [Google Scholar] [CrossRef]
- Kissmann, R. PICARD: A novel code for the Galactic Cosmic Ray propagation problem. Astropart. Phys. 2014, 55, 37–50. [Google Scholar] [CrossRef]
- Case, G.; Bhattacharya, D. Revisiting the galactic supernova remnant distribution. Astron. Astrophys. Suppl. 1996, 120, 437–440. [Google Scholar]
- Faucher-Giguère, C.-A.; Kaspi, V.M. Birth and Evolution of Isolated Radio Pulsars. Astrophys. J. 2006, 643, 332–355. [Google Scholar] [CrossRef]
- Blasi, P.; Amato, E. Diffusive propagation of cosmic rays from supernova remnants in the Galaxy. II: Anisotropy. J. Cosmol. Astropart. Phys. 2012, 1, 11. [Google Scholar] [CrossRef][Green Version]
- Sveshnikova, L.G.; Strelnikova, O.N.; Ptuskin, V.S. Spectrum and anisotropy of cosmic rays at TeV-PeV-energies and contribution of nearby sources. Astropart. Phys. 2013, 50–52, 33–46. [Google Scholar] [CrossRef]
- Faherty, J.; Walter, F.M.; Anderson, J. The trigonometric parallax of the neutron star Geminga. Astrophys. Space Sci. 2007, 308, 225–230. [Google Scholar] [CrossRef]
- Manchester, R.N.; Hobbs, G.B.; Teoh, A.; Hobbs, M. The Australia Telescope National Facility Pulsar Catalogue. Astrophys. J. 2005, 129, 1993–2006. [Google Scholar] [CrossRef]
- Funsten, H.O.; DeMajistre, R.; Frisch, P.C.; Heerikhuisen, J.; Higdon, D.M.; Janzen, P.; Larsen, B.A.; Livadiotis, G.; McComas, D.J.; Möbius, E.; et al. Circularity of the Interstellar Boundary Explorer Ribbon of Enhanced Energetic Neutral Atom (ENA) Flux. Astrophys. J. 2013, 776, 30. [Google Scholar] [CrossRef]
- Cerri, S.S.; Gaggero, D.; Vittino, A.; Evoli, C.; Grasso, D. A signature of anisotropic cosmic-ray transport in the gamma-ray sky. J. Cosmol. Astropart. Phys. 2017, 10, 019. [Google Scholar] [CrossRef]
- Aguilar, M.; Cavasonza, L.A.; Ambrosi, G.; Arruda, L.; Attig, N.; Aupetit, S.; Azzarello, P.; Bachlechner, A.; Barao, F.; Barrau, A.; et al. Precision Measurement of the Boron to Carbon Flux Ratio in Cosmic Rays from 1.9 GV to 2.6 TV with the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2016, 117, 231102. [Google Scholar] [CrossRef] [PubMed]
- Aguilar, M.; Cavasonza, L.A.; Ambrosi, G.; Arruda, L.; Attig, N.; Aupetit, S.; Azzarello, P.; Bachlechner, A.; Barao, F.; Barrau, A.; et al. Observation of New Properties of Secondary Cosmic Rays Lithium, Beryllium, and Boron by the Alpha Magnetic Spectrometer on the International Space Station. Phys. Rev. Lett. 2018, 120, 021101. [Google Scholar] [CrossRef]
- Antoni, T.; Apel, W.D.; Badea, A.F.; Bekk, K.; Bercuci, A.; Blümer, J.; Bozdog, H.; Brancus, I.M.; Chilingarian, A.; Daumiller, K.; et al. KASCADE measurements of energy spectra for elemental groups of cosmic rays: Results and open problems. Astropart. Phys. 2005, 24, 1–25. [Google Scholar] [CrossRef]
- Apel, W.D.; Arteaga-Velázquez, J.C.; Bekk, K.; Bertaina, M.; Blümer, J.; Bozdog, H.; Brancus, I.M.; Cantoni, E.; Chiavassa, A.; Cossavella, F.; et al. KASCADE-Grande measurements of energy spectra for elemental groups of cosmic rays. Astropart. Phys. 2013, 47, 54–66. [Google Scholar] [CrossRef]
- Hörandel, J. On the knee in the energy spectrum of cosmic rays. Astropart. Phys. 2003, 19, 193–220. [Google Scholar] [CrossRef]
- Ambrosio, M.; Antolini, R.; Baldini, A.; Barbarino, G.C.; Barish, B.C.; Battistoni, G.; Becherini, Y.; Bellotti, R.; Bemporad, C.; Bernardini, P.; et al. Search for the sidereal and solar diurnal modulations in the total MACRO muon data set. Phys. Rev. D 2003, 67, 042002. [Google Scholar] [CrossRef]
- Aglietta, M.; Alessandro, B.; Antonioli, P.; Arneodo, F.; Bergamasco, L.; Bertaina, M. Study of the Cosmic Ray Anisotropy at Eo ∼100 TeV from EAS-TOP: 1992–1994. In Proceedings of the 24th International Cosmic Ray Conference (ICRC1995), Rome, Italy, 28 August–8 September 1995; Volume 2, p. 800. [Google Scholar]
- Amenomori, M.; Ayabe, S.; Cui, S.W.; Danzengluobu; Ding, L.K.; Ding, X.H.; Feng, C.F.; Feng, Z.Y.; Gao, X.Y.; Geng, Q.X.; et al. Large-Scale Sidereal Anisotropy of Galactic Cosmic-Ray Intensity Observed by the Tibet Air Shower Array. Astrophys. J. 2005, 626, L29–L32. [Google Scholar] [CrossRef]
- Ma, X.-H.; Bi, Y.-J.; Cao, Z.; Chen, M.-J.; Chen, S.-Z. Chapter 1 LHAASO Instruments and Detector technology. Chin. Phys. C 2022, 46, 030001. [Google Scholar] [CrossRef]
| Element | Background | Geminga Source | ||||
|---|---|---|---|---|---|---|
| PV | GeV−1 | TV | ||||
| p | 2.30 | 5 | 2.16 | 22 | ||
| He | 2.21 | 5 | 2.10 | 22 | ||
| C | 2.24 | 5 | 2.13 | 22 | ||
| N | 2.20 | 5 | 2.13 | 22 | ||
| O | 2.25 | 5 | 2.13 | 22 | ||
| Ne | 2.20 | 5 | 2.13 | 22 | ||
| Mg | 2.23 | 5 | 2.13 | 22 | ||
| Si | 2.29 | 5 | 2.13 | 22 | ||
| Fe | 2.26 | 5 | 2.13 | 22 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, A.; Lv, Z.; Liu, W.; Guo, Y.; Zhang, F. Cosmic Ray Spectra and Anisotropy in an Anisotropic Propagation Model with Spiral Galactic Sources. Universe 2025, 11, 53. https://doi.org/10.3390/universe11020053
Li A, Lv Z, Liu W, Guo Y, Zhang F. Cosmic Ray Spectra and Anisotropy in an Anisotropic Propagation Model with Spiral Galactic Sources. Universe. 2025; 11(2):53. https://doi.org/10.3390/universe11020053
Chicago/Turabian StyleLi, Aifeng, Zhaodong Lv, Wei Liu, Yiqing Guo, and Fangheng Zhang. 2025. "Cosmic Ray Spectra and Anisotropy in an Anisotropic Propagation Model with Spiral Galactic Sources" Universe 11, no. 2: 53. https://doi.org/10.3390/universe11020053
APA StyleLi, A., Lv, Z., Liu, W., Guo, Y., & Zhang, F. (2025). Cosmic Ray Spectra and Anisotropy in an Anisotropic Propagation Model with Spiral Galactic Sources. Universe, 11(2), 53. https://doi.org/10.3390/universe11020053






