(Pre)-Inflationary Dynamics with Starobinsky Potential in Noncommutative Effective LQC
Abstract
1. Introduction
2. Brief Review of Noncommutative Effective LQC
2.1. Effective Loop Quantum Cosmology
2.2. Noncommutative Effective LQC
3. Starobinsky Inflation in Noncommutative Effective LQC
3.1. Field Equations and Modified Friedmann Equation
3.2. Energy Stages
3.3. EKE Domination: After the Bounce
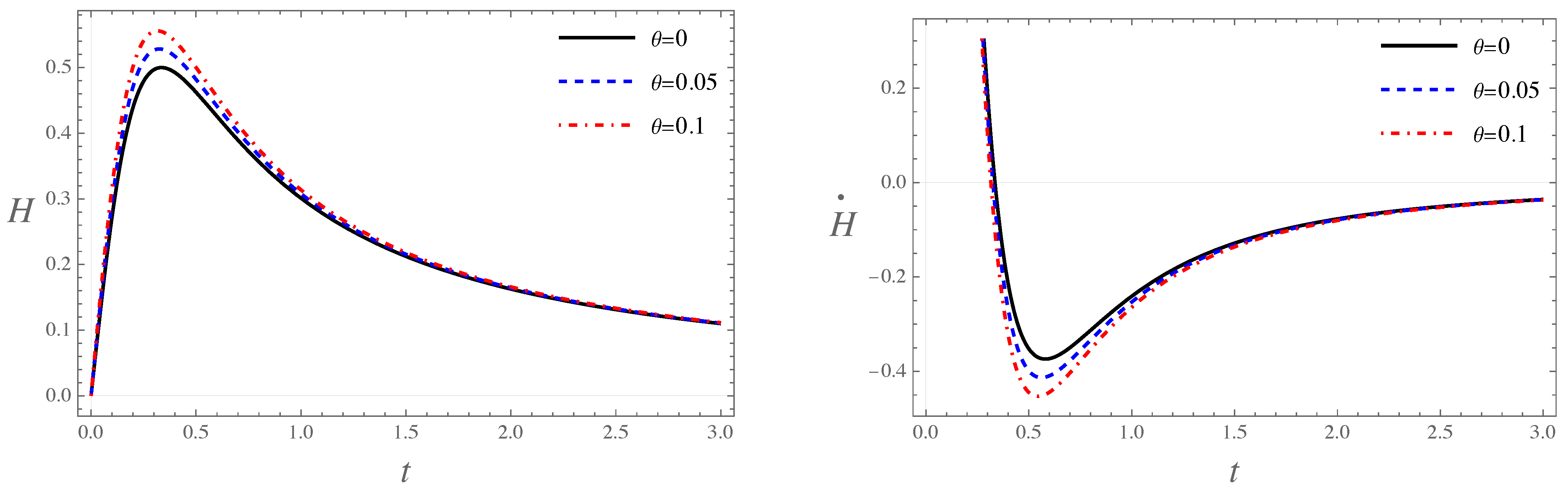
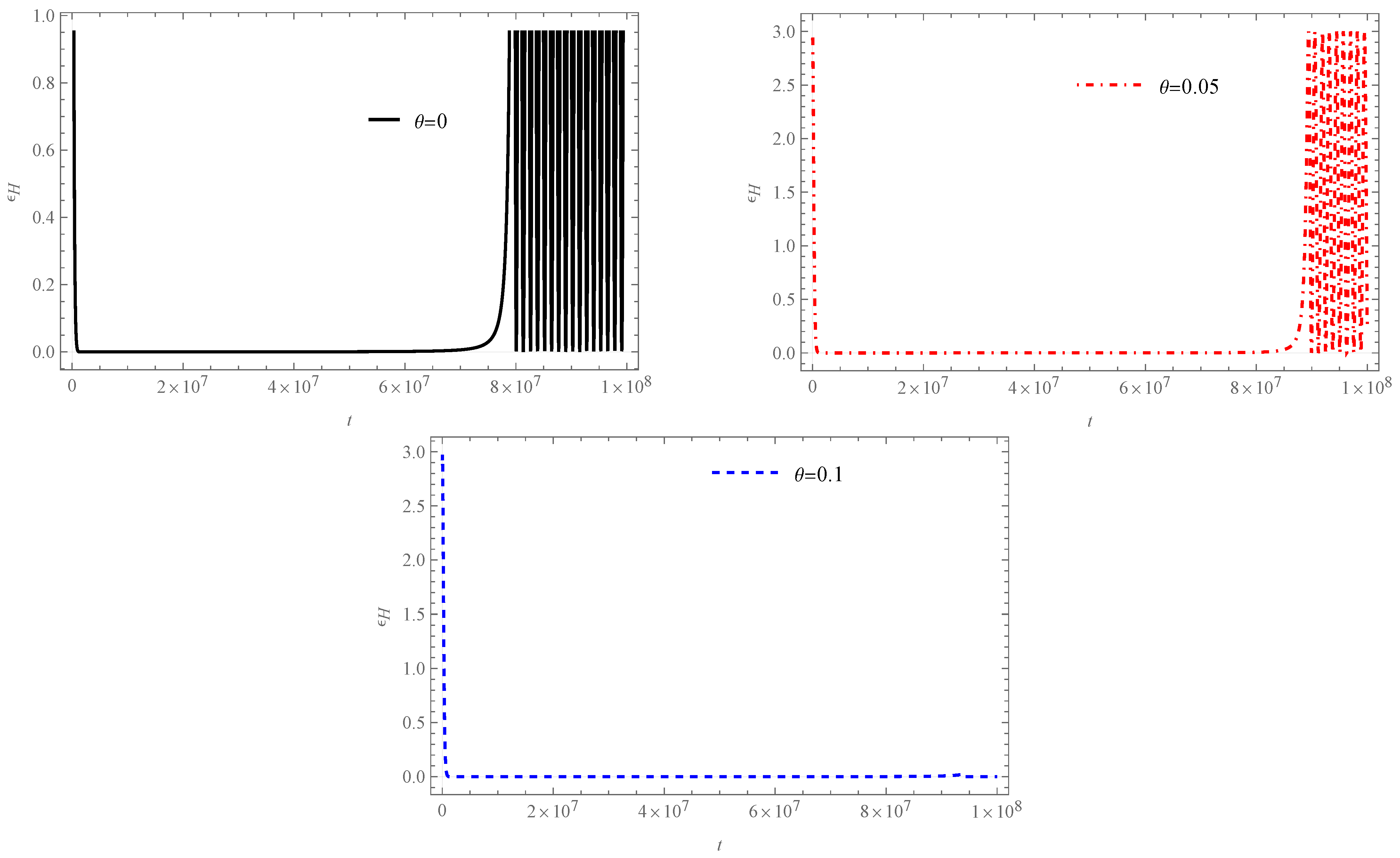
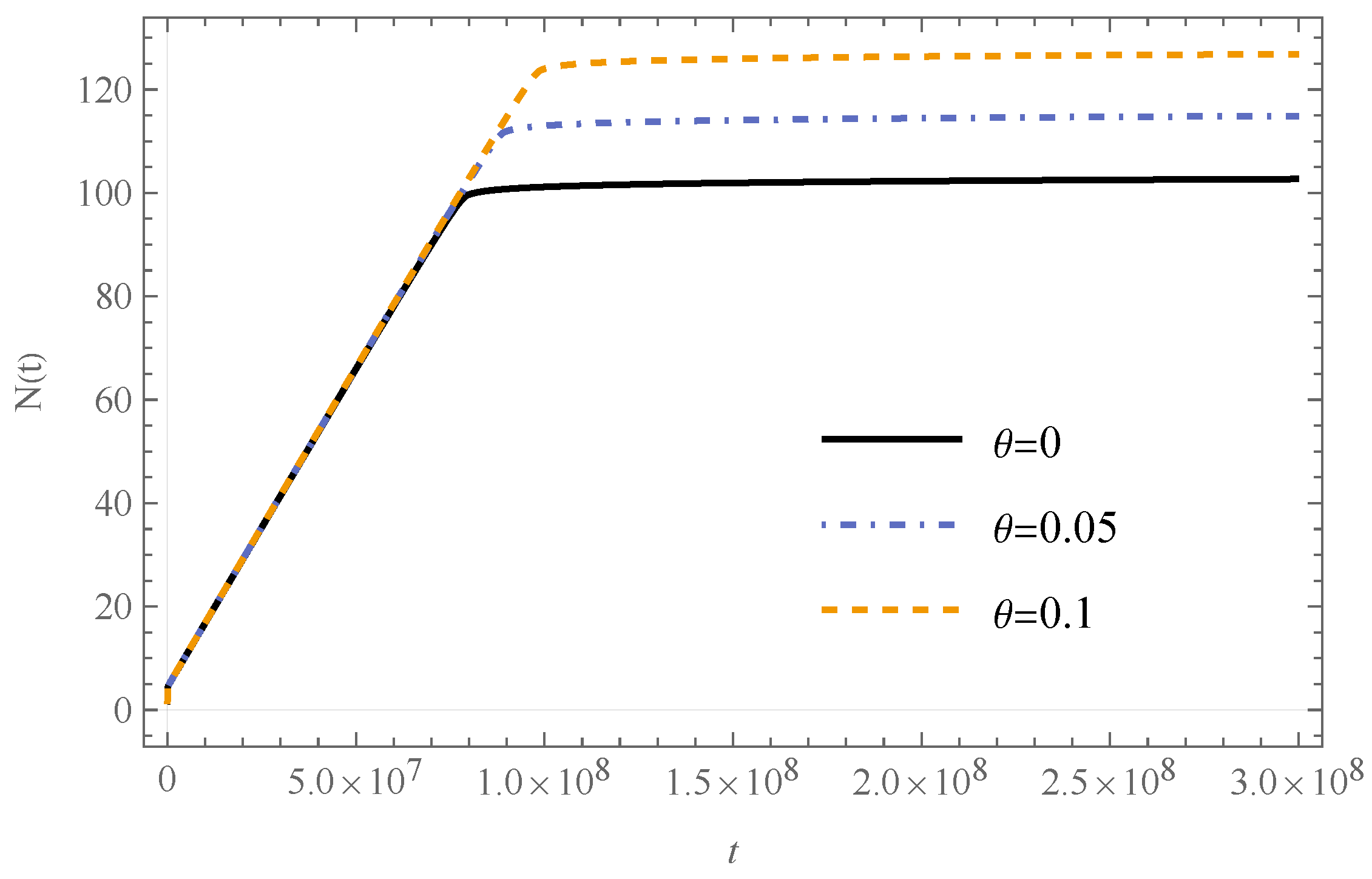
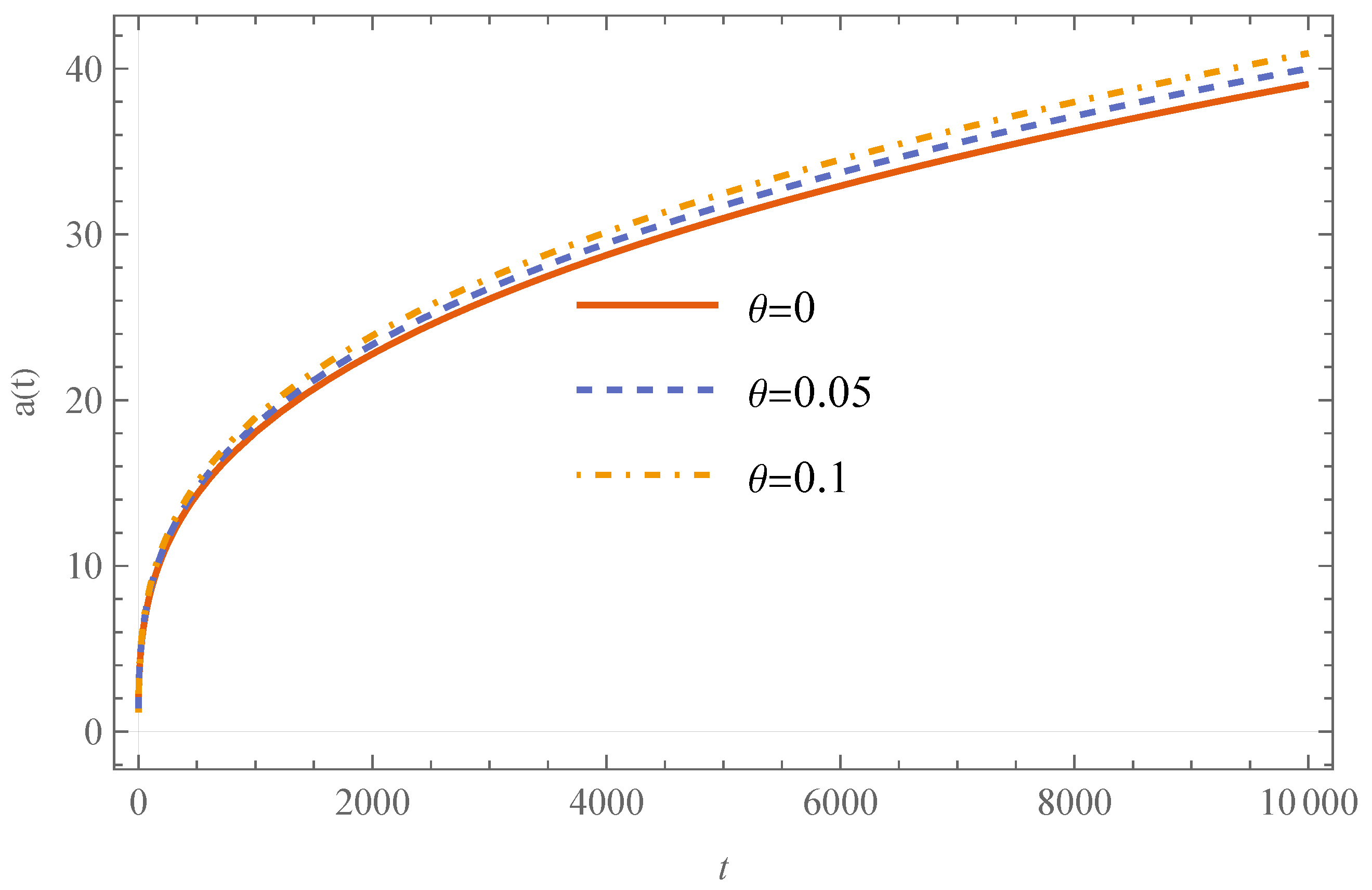
3.3.1. Bouncing Phase
3.3.2. Transition Phase
3.3.3. Slow-Roll Inflation
3.4. KE Domination: After the Bounce
3.4.1. Bouncing Phase
3.4.2. Transition Phase
3.4.3. Slow-Roll Inflation
3.5. PE Domination: After the Bounce
3.5.1. Bouncing Phase
3.5.2. Transition Phase
3.5.3. Slow-Roll Inflation
4. Evolution of the Scalar Field: A Dynamical System Approach
5. Discussion: Starobinsky Potential vs. Quadratic Potential
5.1. Starobinsky Potential vs. Quadratic Potential: EKED Regime
5.2. Starobinsky Potential vs. Quadratic Potential: KED Regime
5.3. Starobinsky Potential vs. Quadratic Potential: PED Regime
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models Without Singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Guth, A.H. The Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Phys. Rev. D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Linde, A.D. A New Inflationary Universe Scenario: A Possible Solution of the Horizon, Flatness, Homogeneity, Isotropy and Primordial Monopole Problems. Phys. Lett. B 1982, 108, 389–393. [Google Scholar] [CrossRef]
- Rovelli, C. Quantum Gravity; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Thiemann, T. Modern Canonical Quantum General Relativity; Cambridge University Press: Cambridge, UK, 2007; ISBN 978-0-511-75568-2/978-0-521-84263-1. [Google Scholar] [CrossRef]
- Ashtekar, A.; Lewandowski, J. Background independent quantum gravity: A Status report. Class. Quant. Grav. 2004, 21, R53. [Google Scholar] [CrossRef]
- Ashtekar, A.; Pawlowski, T.; Singh, P. Quantum nature of the big bang. Phys. Rev. Lett. 2006, 96, 141301. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A.; Pawlowski, T.; Singh, P. Quantum Nature of the Big Bang: Improved dynamics. Phys. Rev. D 2006, 74, 084003. [Google Scholar] [CrossRef]
- Bojowald, M. Loop quantum cosmology. Living Rev. Relativ. 2008, 11, 4. [Google Scholar] [CrossRef]
- Ade, P.A.R. et al. [Planck Collaboration]. Planck 2015 results. XX. Constraints on inflation. Astron. Astrophys. 2016, 594, A20. [Google Scholar] [CrossRef]
- Bonga, B.; Gupt, B. Inflation with the Starobinsky potential in Loop Quantum Cosmology. Gen. Relativ. Gravit. 2016, 48, 71. [Google Scholar] [CrossRef]
- Bhardwaj, A.; Copeland, E.J.; Louko, J. Inflation in Loop Quantum Cosmology. Phys. Rev. D 2019, 99, 063520. [Google Scholar] [CrossRef]
- Bonga, B.; Gupt, B. Phenomenological investigation of a quantum gravity extension of inflation with the Starobinsky potential. Phys. Rev. D 2016, 93, 063513. [Google Scholar] [CrossRef]
- Li, B.F.; Olmedo, J.; Singh, P.; Wang, A. Primordial scalar power spectrum from the hybrid approach in loop cosmologies. Phys. Rev. D 2020, 102, 126025. [Google Scholar] [CrossRef]
- Li, B.F.; Singh, P.; Wang, A. Primordial power spectrum from the dressed metric approach in loop cosmologies. Phys. Rev. D 2020, 101, 086004. [Google Scholar] [CrossRef]
- Saeed, J.; Pan, R.; Brown, C.; Cleaver, G.; Clevear, G.; Wang, A. Universal Properties of the Evolution of the Universe in Modified Loop Quantum Cosmology. Universe 2024, 10, 397. [Google Scholar] [CrossRef]
- Connes, A.; Douglas, M.R.; Schwarz, A.S. Noncommutative geometry and matrix theory: Compactification on tori. J. High Energy Phys. 1998, 02, 003. [Google Scholar] [CrossRef]
- Seiberg, N.; Witten, E. String theory and noncommutative geometry. J. High Energy Phys. 1999, 09, 032. [Google Scholar] [CrossRef]
- Snyder, H.S. Quantized space-time. Phys. Rev. 1947, 71, 38–41. [Google Scholar] [CrossRef]
- Snyder, H.S. The Electromagnetic Field in Quantized Space-Time. Phys. Rev. 1947, 72, 68–71. [Google Scholar] [CrossRef]
- Moffat, J.W. Noncommutative quantum gravity. Phys. Lett. B 2000, 491, 345–352. [Google Scholar] [CrossRef]
- Chamseddine, A.H. Complexified gravity in noncommutative spaces. Commun. Math. Phys. 2001, 218, 283–292. [Google Scholar] [CrossRef]
- Garcia-Compean, H.; Obregon, O.; Ramirez, C.; Sabido, M. Noncommutative selfdual gravity. Phys. Rev. D 2003, 68, 044015. [Google Scholar] [CrossRef]
- Garcia-Compean, H.; Obregon, O.; Ramirez, C.; Sabido, M. Noncommutative topological theories of gravity. Phys. Rev. D 2003, 68, 045010. [Google Scholar] [CrossRef]
- Kober, M. Canonical quantum gravity on noncommutative space–time. Int. J. Mod. Phys. A 2015, 30, 1550085. [Google Scholar] [CrossRef]
- Garcia-Compean, H.; Obregon, O.; Ramirez, C. Noncommutative quantum cosmology. Phys. Rev. Lett. 2002, 88, 161301. [Google Scholar] [CrossRef]
- Barbosa, G.D.; Pinto-Neto, N. Noncommutative geometry and cosmology. Phys. Rev. D 2004, 70, 103512. [Google Scholar] [CrossRef]
- Guzman, W.; Sabido, M.; Socorro, J. Noncommutativity and scalar field cosmology. Phys. Rev. D 2007, 76, 087302. [Google Scholar] [CrossRef]
- Aguero, M.; Ortiz, J.A.A.S.C.; Sabido, M.; Socorro, J. Non commutative Bianchi type II quantum cosmology. Int. J. Theor. Phys. 2007, 46, 2928–2934. [Google Scholar] [CrossRef]
- Guzman, W.; Sabido, M.; Socorro, J. On Noncommutative Minisuperspace and the Friedmann equations. Phys. Lett. B 2011, 697, 271–274. [Google Scholar] [CrossRef]
- Pérez-Payán, S.; Sabido, M.; Yee-Romero, C. Effects of deformed phase space on scalar field cosmology. Phys. Rev. D 2013, 88, 027503. [Google Scholar] [CrossRef]
- Espinoza-García, A.; Torres-Lomas, E.; Pérez-Payán, S.; Díaz-Barrón, L.R. Noncommutativity in Effective Loop Quantum Cosmology. Adv. High Energy Phys. 2019, 2019, 9080218. [Google Scholar] [CrossRef]
- Díaz-Barrón, L.R.; Espinoza-García, A.; Pérez-Payán, S.; Socorro, J. Noncommutative Friedmann Equations in Effective LQC. Int. J. Mod. Phys. D 2020, 29, 2050039. [Google Scholar] [CrossRef]
- Díaz-Barrón, L.R.; Espinoza-García, A.; Pérez-Payán, S.; Socorro, J. Noncommutative effective loop quantum cosmology: Inclusion of a potential term. Phys. Rev. D 2021, 104, 023508. [Google Scholar] [CrossRef]
- Díaz-Barrón, L.R.; Espinoza-García, A.; Pérez-Payán, S.; Socorro, J. Is a loopy and noncommutative early Universe viable? Phys. Lett. B 2023, 847, 138299. [Google Scholar] [CrossRef]
- Mohammadi, A. Non-commutativity in modified loop cosmology. Eur. Phys. J. C 2025, 85, 219. [Google Scholar] [CrossRef]
- Agullo, I.; Ashtkar, A.; Nelson, W. Extension of the quantum theory of cosmological perturbations to the Planck era. Phys. Rev. D 2013, 87, 043507. [Google Scholar] [CrossRef]
- Agullo, I.; Ashtkar, A.; Nelson, W. The pre-inflationary dynamics of loop quantum cosmology: Confronting quantum gravity with observations. Class. Quant. Grav. 2013, 30, 085014. [Google Scholar] [CrossRef]
- Lizzi, F.; Mangano, G.; Miele, G.; Peloso, M. Cosmological perturbations and short distance physics from noncommutative geometry. J. High Energy Phys. 2002, 06, 049. [Google Scholar] [CrossRef]
- Akofor, E.; Balachandran, A.P.; Jo, S.G.; Joseph, A.; Qureshi, B.A. Direction-Dependent CMB Power Spectrum and Statistical Anisotropy from Noncommutative Geometry. J. High Energy Phys. 2008, 2008, 092. [Google Scholar] [CrossRef]
- Guo, R.Y.; Zhang, J.F.; Zhang, X. Can the H0 tension be resolved in extensions to ΛCDM cosmology? J. Cosmol. Astropart. Phys. 2019, 02, 054. [Google Scholar] [CrossRef]
- van Putten, M.H.P.M. Evidence for galaxy dynamics tracing background cosmology below the de Sitter scale of acceleration. Astrophys. J. 2017, 848, 28. [Google Scholar] [CrossRef]
- Colgáin, E.Ó.; van Putten, M.H.P.M.; Yavartanoo, H. de Sitter Swampland, H0 tension & observation. Phys. Lett. B 2019, 793, 126–129. [Google Scholar] [CrossRef]
- van Putten, M.H.P.M. Alleviating tension in CDM and the local distance ladder from first principles with no free parameters. Mon. Not. R. Astron. Soc. 2020, 491, L6–L10. [Google Scholar] [CrossRef]
- Agrawal, P.; Obied, G.; Steinhardt, P.J.; Vafa, C. On the Cosmological Implications of the String Swampland. Phys. Lett. B 2018, 784, 271–276. [Google Scholar] [CrossRef]
- Solà, J.; Gómez-Valent, A.; de Cruz Pérez, J. The H0 tension in light of vacuum dynamics in the Universe. Phys. Lett. B 2017, 774, 317–324. [Google Scholar] [CrossRef]
- Peracaula, J.S.; Gomez-Valent, A.; de Cruz Perez, J.; Moreno-Pulido, C. Running Vacuum in the Universe: Phenomenological Status in Light of the Latest Observations, and Its Impact on the σ8 and H0 Tensions. Universe 2023, 9, 262. [Google Scholar] [CrossRef]
- Peracaula, J.S.; Gómez-Valent, A.; de Cruz Perez, J.; Moreno-Pulido, C. Running vacuum against the H0 and σ8 tensions. Europhys. Lett. 2021, 134, 19001. [Google Scholar] [CrossRef]
- Ashtekar, A.; Singh, P. Loop Quantum Cosmology: A Status Report. Class. Quant. Grav. 2011, 28, 213001. [Google Scholar] [CrossRef]
- Diener, P.; Gupt, B.; Megevand, M.; Singh, P. Numerical evolution of squeezed and non-Gaussian states in loop quantum cosmology. Class. Quant. Grav. 2014, 31, 165006. [Google Scholar] [CrossRef]
- Diener, P.; Joe, A.; Megevand, M.; Singh, P. Numerical simulations of loop quantum Bianchi-I spacetimes. Class. Quant. Grav. 2017, 34, 094004. [Google Scholar] [CrossRef]
- Ashtekar, A.; Corichi, A.; Singh, P. Robustness of key features of loop quantum cosmology. Phys. Rev. D 2008, 77, 024046. [Google Scholar] [CrossRef]
- Corichi, A.; Vukasinac, T. Effective constrained polymeric theories and their continuum limit. Phys. Rev. D 2012, 86, 064019. [Google Scholar] [CrossRef]
- Cordero, R.; Garcia-Compean, H.; Turrubiates, F.J. Deformation quantization of cosmological models. Phys. Rev. D 2011, 83, 125030. [Google Scholar] [CrossRef]
- Vakili, B.; Pedram, P.; Jalalzadeh, S. Late time acceleration in a deformed phase space model of dilaton cosmology. Phys. Lett. B 2010, 687, 119–123. [Google Scholar] [CrossRef]
- Moyal, J.E. Quantum mechanics as a statistical theory. Math. Proc. Camb. Philos. Soc. 1949, 45, 99–124. [Google Scholar] [CrossRef]
- Djemai, A.E.F. On noncommutative classical mechanics. Int. J. Theor. Phys. 2004, 43, 299. [Google Scholar] [CrossRef]
- Perez-Payan, S.; Sabido, M.; Mena, E.; Yee-Romero, C. Analysis of Scalar Field Cosmology with Phase Space Deformations. Adv. High Energy Phys. 2014, 2014, 958137. [Google Scholar] [CrossRef]
- López, J.L.; Sabido, M.; Yee-Romero, C. Phase space deformations in phantom cosmology. Phys. Dark Univ. 2018, 19, 104–108. [Google Scholar] [CrossRef]
- Malekolkalami, B.; Atazadeh, K.; Vakili, B. Late time acceleration in a non-commutative model of modified cosmology. Phys. Lett. B 2014, 739, 400–404. [Google Scholar] [CrossRef]
- Barrow, J.D. The Premature Recollapse Problem in Closed Inflationary Universes. Nucl. Phys. B 1988, 296, 697–709. [Google Scholar] [CrossRef]
- Starobinsky, A.A.; Tsujikawa, S.; Yokoyama, J. Cosmological perturbations from multifield inflation in generalized Einstein theories. Nucl. Phys. B 2001, 610, 383–410. [Google Scholar] [CrossRef]
- De Felice, A.; Tsujikawa, S. f(R) theories. Living Rev. Relativ. 2010, 13, 3. [Google Scholar] [CrossRef] [PubMed]
- Ashtekar, A.; Sloan, D. Loop quantum cosmology and slow roll inflation. Phys. Lett. B 2011, 694, 108–112. [Google Scholar] [CrossRef]
- Ashtekar, A.; Sloan, D. Probability of Inflation in Loop Quantum Cosmology. Gen. Relativ. Gravit. 2011, 43, 3619–3655. [Google Scholar] [CrossRef]
- Li, B.F.; Singh, P.; Wang, A. Genericness of pre-inflationary dynamics and probability of the desired slow-roll inflation in modified loop quantum cosmologies. Phys. Rev. D 2019, 100, 063513. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, A.; Cleaver, G.; Kirsten, K.; Sheng, Q. Pre-inflationary universe in loop quantum cosmology. Phys. Rev. D 2017, 96, 083520. [Google Scholar] [CrossRef]
- Lyth, D.H.; Liddle, A.R. The Primordial Density Perturbation: Cosmology, Inflation and the Origin of Structure; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Akrami, Y. et al. [Planck Collaboration]. Planck 2018 results. X. Constraints on inflation. Astron. Astrophys. 2020, 641, A10. [Google Scholar] [CrossRef]
- Li, B.F.; Singh, P.; Wang, A. Qualitative dynamics and inflationary attractors in loop cosmology. Phys. Rev. D 2018, 98, 066016. [Google Scholar] [CrossRef]
| Event | t | H | N | ||||
|---|---|---|---|---|---|---|---|
| Bounce | 0 | 1 | 0.8 | 3 | 0 | ||
| End SI | 0.3333 | 0.235033 | 0.565686 | 0.5 | 0.115525 | ||
| KE = PE | (a) | 3.76032 | 4.52763 | ||||
| Onset Slow Roll | 3.99535 | 20.1027 | |||||
| End of Inflation | |||||||
| Bounce | 0 | 1 | 0.8 | 3 | 0 | ||
| End SI | 0.332787 | 0.235245 | 0.568538 | 0.497346 | 0.114793 | ||
| KE = PE | (a) | 3.78972 | 4.5230379 | ||||
| Onset Slow Roll | 4.02676 | 9.79795 | |||||
| End of Inflation | |||||||
| Bounce | 0 | 1 | 0.8 | 3 | 0 | ||
| End SI | 0.332211 | 0.235446 | 0.571462 | 0.494674 | 0.114048 | ||
| KE = PE | (a) | 3.82029 | 4.5230377 | ||||
| Onset Slow Roll | 4.05942 | 9.64405 | |||||
| End of Inflation |
| Event | t | H | N | ||||
|---|---|---|---|---|---|---|---|
| Bounce | 0 | −2.8 | 0.8 | 3 | 0 | ||
| End SI | 0.3357 | −2.5631 | 0.5660 | 0.5 | 0.1162 | ||
| KE = PE | 0.9543 | 4.5381 | |||||
| Onset Slow Roll | 1.1816 | 5.9073 | |||||
| End of Inflation | 0.1226 | 93.176 | |||||
| Bounce | 0 | −2.8 | 0.8 | 3 | 0 | ||
| End SI | 0.3252 | −2.5686 | 0.5771 | 0.5283 | 0.1188 | ||
| KE = PE | 0.9814 | 4.5620 | |||||
| Onset Slow Roll | 1.2112 | 5.9696 | |||||
| End of Inflation | 0.1226 | 105.334 | |||||
| Bounce | 0 | −2.8 | 0.8 | 3 | 0 | ||
| End SI | 0.3158 | −2.5737 | 0.5871 | 0.5558 | 0.1213 | ||
| KE = PE | 1.0051 | 4.5843 | |||||
| Onset Slow Roll | 1.2371 | 6.0256 | |||||
| End of Inflation |
| Event | t | H | N | ||||
|---|---|---|---|---|---|---|---|
| Bounce | 0 | −3.3216118 | 0.8 | 0 | |||
| End SI | 0.4850 | −2.9377 | 0.6213 | 0.5 | 0.139605 | ||
| KE = PE | 0.7119 | 4.6159 | |||||
| Onset Slow Roll | 0.9302 | 5.6187 | |||||
| End of Inflation | 0.12263 | 32.9665 | |||||
| Bounce | 0 | −3.3216118 | 0.8 | 0 | |||
| End SI | 0.4715 | −2.9447 | 6378 | 0.530121 | 0.14345 | ||
| KE = PE | 0.7650 | 4.6380 | |||||
| Onset Slow Roll | 0.9918 | 5.7201 | |||||
| End of Inflation | 0.122603 | 42.4349 | |||||
| Bounce | 0 | −3.3216118 | 0.8 | 0 | |||
| End SI | 0.4596 | −2.9511 | 0.6524 | 0.559056 | 0.147063 | ||
| KE = PE | 0.8103 | 4.6596 | |||||
| Onset Slow Roll | 1.0420 | 5.8090 | |||||
| End of Inflation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Díaz-Barrón, L.R.; Espinoza-García, A.; Pérez-Payán, S.; Socorro, J. (Pre)-Inflationary Dynamics with Starobinsky Potential in Noncommutative Effective LQC. Universe 2025, 11, 393. https://doi.org/10.3390/universe11120393
Díaz-Barrón LR, Espinoza-García A, Pérez-Payán S, Socorro J. (Pre)-Inflationary Dynamics with Starobinsky Potential in Noncommutative Effective LQC. Universe. 2025; 11(12):393. https://doi.org/10.3390/universe11120393
Chicago/Turabian StyleDíaz-Barrón, Luis Rey, Abraham Espinoza-García, Sinuhé Pérez-Payán, and José Socorro. 2025. "(Pre)-Inflationary Dynamics with Starobinsky Potential in Noncommutative Effective LQC" Universe 11, no. 12: 393. https://doi.org/10.3390/universe11120393
APA StyleDíaz-Barrón, L. R., Espinoza-García, A., Pérez-Payán, S., & Socorro, J. (2025). (Pre)-Inflationary Dynamics with Starobinsky Potential in Noncommutative Effective LQC. Universe, 11(12), 393. https://doi.org/10.3390/universe11120393






