Thermal Quarks and Polyakov Loops in Two-Color Dense QCD

Abstract

We study confinement and deconfinement in dense two-color QCD by analyzing the dynamics of thermal quarks and gluons. The Polyakov loop is used as a probe of the relevant thermal excitations, distinguishing quark- and hadron-dominated regimes in dense matter. To describe the Polyakov loop, we adopt both lattice-informed phenomenological models and the massive Yang–Mills framework. After calibrating these models at zero density, we investigate in-medium modifications of the Polyakov loops and gluon propagators at finite temperature and density. Diquark gaps control the screening at zero temperature, whereas the screening due to thermal quarks is sensitive to the Polyakov loop. Inclusion of the Polyakov loop helps to reproduce lattice data at low temperature, suggesting that thermal excitations are predominantly hadronic rather than uncorrelated quarks.

1. Introduction

Recently, QCD-like theories such as two-color QCD (QC₂D) and QCD at finite isospin chemical potential (QCD_I) have attracted much attention as laboratories to test methodologies and concepts concerning dense matter in quantum chromodynamics (QCD) [1,2,3,4,5,6,7,8,9,10]. For these theories, lattice Monte Carlo simulations can be carried out without encountering the sign problem [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25], and the results have been used to assess the reliability of effective models as well as weak-coupling approaches, with or without pairing effects [26,27,28]. In recent years, much effort has been devoted to studies of the equation of state (EOS) of dense matter. Notably, several concepts relevant to neutron star EOS—such as the appearance of a sound-speed peak, the stiffening of matter due to pairing effects [29,30,31,32], and the significance of quark effects prior to hadron overlap [33,34,35]—have been confirmed or supported by lattice results in QCD-like theories.

In QC₂D and QCD_I at zero temperature, simple models that incorporate both diquark (meson) and quark degrees of freedom—such as quark–diquark (meson) models [9,36,37]—provide good agreement with lattice results [34,38,39,40,41,42,43]. Although these models do not explicitly realize confinement, they are able to capture the overall features of hadronic matter at low density and quark matter at high density. A notable advantage is that, within a single framework, both causality and thermodynamic stability are automatically satisfied from low to high densities, especially in the domain where hadronic matter transforms into quark matter. By construction, such models implement the essential features of the previous crossover approaches in which hadronic and quark EOS were interpolated phenomenologically [29,30,44,45,46,47,48,49,50,51,52,53]. For more explicit realization of the crossover, see, e.g., recent developments based on the quarkyonic matter picture [35,54,55,56,57,58].

As mentioned, simple quark-hadron models have not directly addressed the nature of confinement–deconfinement transitions; rather this most subtle and intriguing question has been detoured. In this paper, taking dense two-color QCD as our platform, we investigate confinement/deconfinement in dense matter by studying the thermal properties of dense matter. We delineate the lattice data for the Polyakov loop and gluon propagators and compare them with analytic results. Our central question is whether thermal excitations are dominated by quarks or hadrons; answering to this question helps us to understand confinement/deconfinement in dense matter.

In QC₂D, quarks acquire the color-singlet gap and thus generate neither Debye nor Meissner masses [59,60,61,62,63]. As a consequence, infrared gluons are protected from screening and remain confining. With increasing density, the protected phase space gradually shrinks, but it disappears only asymptotically—a scenario known as asymptotic confinement [64,65]. Quark matter with confining gluons provides a concrete realization of the quarkyonic matter proposed by McLerran and Pisarski [66]. Although qualitative arguments for asymptotic confinement are plausible, a detailed characterization remains lacking. Given the significant progress in lattice simulations since the original proposal of asymptotic confinement, it is timely to revisit this concept in a more quantitative manner. In this paper, we pursue this goal through a set of analyses based on effective models.

In thermal models of QCD, the Polyakov loop plays a central role [67]; see Ref. [68] for a review. The expectation value of the Polyakov loop is related to the free energy of an infinitely heavy quark, $\langle L\rangle$∼$e^{-F_Q}$. In pure Yang–Mills (pYM) theory, the flux string from an isolated color charge extends to infinity, implying $F_Q\to \infty$ and hence $\langle L\rangle \to 0$. In contrast, $\langle L\rangle$ becomes finite when the medium is populated with color fields, allowing the flux string of a heavy quark to dissolve. In QCD with light quarks, the string can also be terminated by dynamical quark–antiquark creation, so $\langle L\rangle$ may already be finite even before the medium is saturated with color fields. A key question is how rapidly $\langle L\rangle$ grows with temperature, which directly reflects whether the dominant thermal excitations are hadrons or quarks.

In this paper, we examine two models for the Polyakov loop. The first is the so-called inverse Weiss potential, derived from nonperturbative gluon and ghost propagators [69,70,71,72,73]. In pYM theory, this model successfully reproduces the critical temperature of the confinement–deconfinement transition. Here, we investigate how its predictions are modified once quarks are coupled. The second model is a phenomenological construction calibrated to lattice simulation data, and it has been widely used in Polyakov–Nambu–Jona–Lasinio (PNJL) and Polyakov–Quark–Meson (PQM) frameworks. Although both models describe pYM well, the inclusion of quarks clearly differentiates them: the inverse Weiss potential becomes excessively modified and deviates from lattice results, whereas the phenomenological model continues to reproduce the data. This distinction becomes even more pronounced in the regime of dense quark matter.

We further investigate gluon propagators at various values of ${\mu }_q$ and T, incorporating Polyakov loop effects that suppress thermal quarks. Lattice studies of gluon propagators in two-color dense QCD have been reported in Ref. [74], while model analyses with massive gluon propagators have been carried out both at zero temperature [60] and at finite temperature with quark one-loop corrections [61]. These analytic computations represent finite-${\mu }_q$ applications of the framework successfully developed for pYM [75,76,77,78] and later extended to QCD with dynamical quarks [79,80]; see Ref. [81] for a review. In the present work, we extend these earlier analyses for QC₂D by explicitly including the Polyakov-loop suppression of thermal quarks, and we argue that this effect is helpful to explain the lattice data at low temperature.

The remainder of this paper is organized as follows. In Section 2, we discuss Polyakov loop potentials in pYM theory within both phenomenological and massive-gluon models. In Section 3, we introduce quarks into these Polyakov loop models. In Section 4, the model is calibrated at ${\mu }_q=0$ against lattice results. In Section 5, we analyze the behavior of Polyakov loops at finite density. In Section 6, we compute the in-medium screening of gluon propagators in a Polyakov loop background. In Section 7, we examine the density and temperature dependence of the screening masses. In Section 8, we study gluon propagators at finite momenta. Finally, Section 9 is devoted to discussions and a summary.

2. Polyakov Loop Potential in Pure Yang–Mills

We begin with the gluon sector in the presence of background fields ${\mathcal{A}}_0\equiv {\mathcal{A}}_0^a{\displaystyle \frac{{\lambda }_a}{2}}$, where ${\lambda }_a$ are the Pauli matrices for color. The background field ${\mathcal{A}}_0$ is assumed to be constant in space-time, and we consider amplitudes along the ${\lambda }_3$ direction. The mean-field Polaykov loop is then given as follows:

$$\Phi ={\displaystyle \frac{1}{2}}\mathrm{tr}\left[\mathcal{P}{e}^{\mathrm{i}g\beta {\mathcal{A}}_0^3{\lambda }_3/2}\right]=cos{\displaystyle \frac{\beta \mathcal{R}}{2}},\mathcal{R}\equiv g{\mathcal{A}}_0^3.$$

(1)

In the high temperature limit ($\beta \to 0$), $\Phi$ approaches unity, corresponding to the deconfined phase. At low temperatures, ${\mathcal{A}}_0$ is expected to scale as ∼T. If $\beta \mathcal{R}\to \pi$ is in this limit, the system is in the confined phase ($\Phi =0$). Thus, as the temperature increases, the system undergoes a transition from the confined to the deconfined phase.

Below, we examine two typical models for the Polyakov loop potential: a phenomenological model commonly employed in PNJL and PQM frameworks, and the inverse Weiss potential, which can be computed from nonperturbative gluon and ghost propagators.

2.1. Phenomenological Potential

The phenomenological potentials used in PNJL or PQM models [68] are constructed to reproduce lattice results both with and without quarks. For example, the two-color potential used by Brauner, Fukushima, and Hidaka (BFH) [8] is

$${\Omega }_{\mathrm{BFH}}=-bT\left[24{\Phi }^2{\mathrm{e}}^{-\beta a}+ln(1-{\Phi }^2)\right],$$

(2)

where $b={\left(0.2105\mathrm{GeV}\right)}^3$ and $a=0.8581\mathrm{GeV}$. The potential vanishes for the confined solution $\Phi \to 0$. The first term, proportional to $-T{e}^{-\beta a}$, can be interpreted as an entropic term favoring the deconfined solution. The second term, $ln(1-{\Phi }^2)$, favors the confined solution; it diverges as $\Phi \to 1$, preventing the system from reaching complete deconfinement ($\Phi =1$). The logarithmic form originates from strong-coupling expansions, where the Haar measure yields a logarithmic contribution, and it is related to the presence of ghosts. The three-color version of this model is known to successfully reproduce lattice data at $N_{\mathrm{c}}=3$, and this situation is also true at $N_{\mathrm{c}}=2$, as we see in the following.

2.2. Inverse Weiss Potential

To construct the inverse Weiss potential, we compute the effective potential in the presence of the background field ${\mathcal{A}}_0^3$. For the potential derived from the original perturbative propagators, see Refs. [82,83]. The Lagrangian for the pYM part is

$${\mathcal{L}}_{\mathrm{pYM}}=-{\displaystyle \frac{1}{4}}{G}_{\mu \nu }^A{G}^{A\mu \nu },G_{\mu \nu }^A={\partial }_{\mu }{A}_{\nu }^A-{\partial }_{\nu }{A}_{\mu }^A+g{f}_{ABC}{A}_{\mu }^B{A}_{\nu }^C,$$

(3)

where $f_{ABC}$ is the structure constant and g is the coupling constant. To construct the one-particle-irreducible (1PI) effective potential as a function of ${\mathcal{A}}_0={\mathcal{A}}_0^3{\displaystyle \frac{{\lambda }_3}{2}}$, we first separate the gauge field as $A_{\mu }={\mathcal{A}}_0{\delta }_{\mu 0}+a_{\mu }$, with $a_{\mu }$ being quantum fields. The $G_{\mu \nu }$ can be rewritten as $G_{\mu \nu }^A={\left[{\mathcal{D}}_{\mu }{a}_{\nu }\right]}^A-{\left[{\mathcal{D}}_{\nu }{a}_{\mu }\right]}^A+g{f}_{ABC}{a}_{\mu }^B{a}_{\nu }^C$, with the background covariant derivative defined by ${\mathcal{D}}_{\mu }{a}_{\nu }\equiv {\partial }_{\mu }{a}_{\nu }-\mathrm{i}\mathcal{R}{\delta }_{\mu 0}\left[{\displaystyle \frac{{\lambda }_3}{2}},{\displaystyle \frac{{\lambda }_C}{2}}\right]a_{\nu }^C$. Using the Cartan bases ${\lambda }_3/2$ and ${\lambda }_{\pm }/2=({\lambda }_1\pm \mathrm{i}{\lambda }_2)/2$, one can write

$${\mathcal{D}}_{\mu }{a}_{\nu }={\partial }_{\mu }{a}_{\nu }^3{\displaystyle \frac{{\lambda }_3}{2}}+\left({\partial }_{\mu }-\mathrm{i}\mathcal{R}{\delta }_{\mu 0}\right)a_{\nu }^{-}{\displaystyle \frac{{\lambda }_{+}}{2}}+\left({\partial }_{\mu }+\mathrm{i}\mathcal{R}{\delta }_{\mu 0}\right)a_{\nu }^{+}{\displaystyle \frac{{\lambda }_{-}}{2}}.$$

(4)

We impose the background gauge fixing condition, ${\mathcal{D}}^{\mu }{a}_{\mu }=0$, which breaks the gauge invariance of $a_{\mu }$ but maintains the invariance for ${\mathcal{A}}_{\mu }$.

To model the non-perturbative propagators in the IR, we add a mass term for gluons to capture the qualitative trend of the Landau gauge propagators in a vacuum; see Ref. [81] for a recent review and Refs. [84,85], which give the physical motivation based on the Gribov–Zwanziger framework. We can either add a term $\propto m_g^2{a}_{\mu }^2$, which is local but not gauge invariant, or a term which is non-local but gauge invariant,

$${\mathcal{L}}_{m_g}=-{\displaystyle \frac{m_g^2}{2}}{a}_{\mu }\left(g^{\mu \nu }-{\displaystyle \frac{{\partial }^{\mu }{\partial }^{\nu }}{{\partial }^2}}\right)a_{\nu }.$$

(5)

Including all these elements and using the Faddeev–Popov trick, the massive YM model is

$${\mathcal{L}}_{\mathrm{mYM}}={\mathcal{L}}_{\mathrm{pYM}}+{\displaystyle \frac{{\left({\mathcal{D}}^{\mu }{a}_{\mu }\right)}^2}{2\xi }}+{\mathcal{L}}_{m_g}+\overline{c}{\mathcal{D}}^{\mu }{\mathcal{D}}_{\mu }c+{\mathcal{L}}_{\mathrm{int}},$$

(6)

where c and $\overline{c}$ are ghost and anti-ghost fields. Taking $\xi \to 0$, the gluon and ghost propagators are (the gluon propagator $D_{\mu \nu }^{AB}\propto \langle {\left(a_{\mu }^A\right)}^{*}(-k)a_{\nu }^B\left(k\right)\rangle$)

$${\left[D_{AB}^{\mu \nu }\left(k\right)\right]}_{\mathrm{tree}}=-{\displaystyle \frac{{\delta }_{AB}}{k_A^2-m_g^2}}{P}_{k_A}^{\mu \nu },{\left[D_c^{AB}\left(k\right)\right]}_{\mathrm{tree}}=-{\displaystyle \frac{{\delta }^{AB}}{k_A^2}},$$

(7)

where ${\delta }_{AB}=1$ for $(A,B)=(3,3),(+,+),(-,-)$, with the other components being zero. The projection operator for the transverse component is $P_k^{\mu \nu }=g^{\mu \nu }-k^{\mu }{k}^{\nu }/k^2$. The momentum for $(3,-,+)$-components is given by

$${\left(k_3\right)}_{\mu }=k_{\mu },{\left(k_{\pm }\right)}_{\mu }=k_{\mu }\pm \mathcal{R}{\delta }_{\mu 0}.$$

(8)

With these propagators, one can construct the one-loop effective potential. We define

$$F(r;m)=T\sum _n{\int }_{\overrightarrow{k}}ln\left[{({\omega }_n+r)}^2+{\overrightarrow{k}}^2+m^2\right],$$

(9)

where ${\omega }_n=2n\pi T(n\in \mathbf{Z})$ is the Matsubara frequency for bosons. The free energy densities for gluons and ghosts can be written as

$${\Omega }_g^{\mathrm{mYM}}(T;\mathcal{R})={\displaystyle \frac{1}{2}}\sum _{r=0,\pm \mathcal{R}}\left[3F(r;m_g)+F(r;0)\right],{\Omega }_{gh}^{\mathrm{mYM}}(T;\mathcal{R})=-\sum _{r=0,\pm \mathcal{R}}F(r;0),$$

(10)

where T-independent constants are neglected. The factor 3 in the first term accounts for the trace over the projectors $P^{\mu \nu }$, while the last term arises from the longitudinal component, which decouples from radiative corrections and hence remains massless. Ghosts contribute with the opposite sign to gluons.

Summing the gluon and ghost contributions, the one-loop potential reads

$${\Omega }_{g+gh}^{\mathrm{mYM}}(T;\mathcal{R})={\displaystyle \frac{1}{2}}\sum _{r=0,\pm \mathcal{R}}\left[3F(r;m_g)-F(r;0)\right],$$

(11)

where the sum over r can be explicitly evaluated as

$$\sum _{r=0,\pm \mathcal{R}}F(r;m)=T{\int }_{\overrightarrow{k}}\left(ln\left[1-{\mathrm{e}}^{-\beta E_m}\right]+ln\left[1-2{\mathrm{e}}^{-\beta E_m}(2{\Phi }^2-1)+{\mathrm{e}}^{-2\beta E_m}\right]\right).$$

(12)

In standard perturbation theory, ghosts cancel two gluon modes, leaving only the two transverse modes. In the present massive theory, the massless longitudinal mode is canceled, but the cancellation of one mode is incomplete due to the gluon mass. At low temperatures, massive gluons are suppressed, and the ghost contribution, which favors the confining solution, dominates the potential.

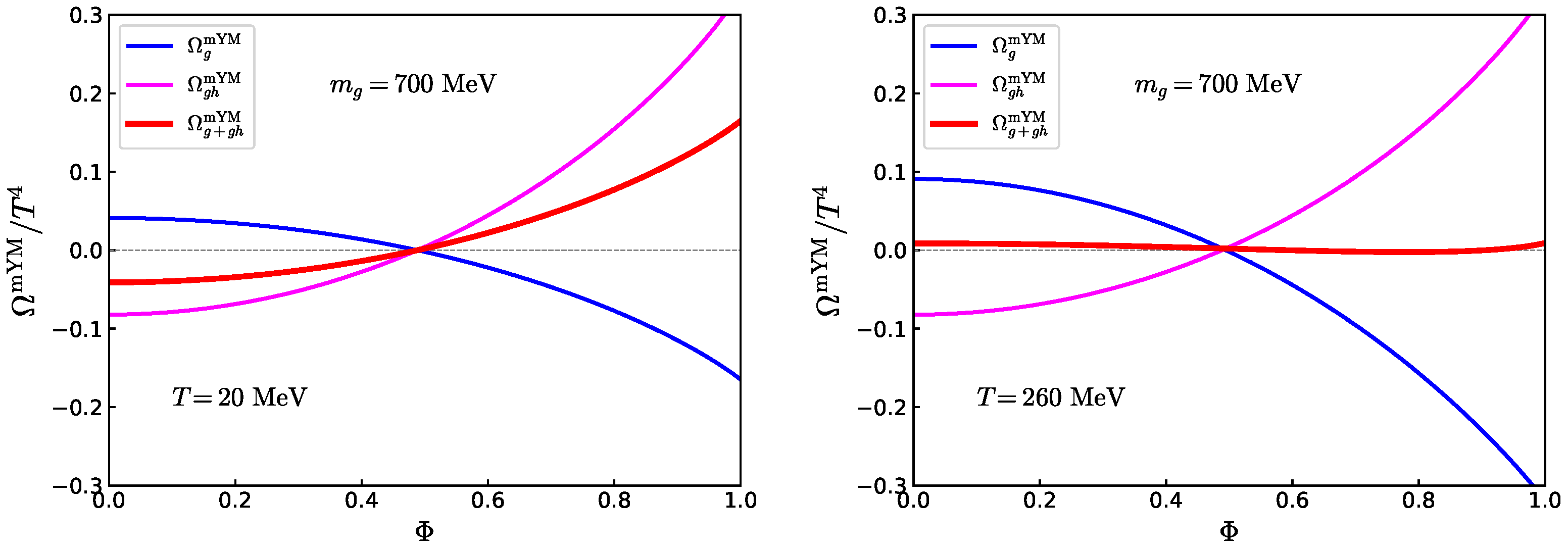
The gluon and ghost potentials are shown in Figure 1 for low temperature ($T=20$ MeV, confined) and high temperature ($T=260$ MeV, deconfined). It should be emphasized that the Polyakov loop in the fundamental representation does not suppress thermal excitations in the adjoint representation. Physically, dynamical gluons screen adjoint charges and form color-singlet states. Indeed, the logarithmic terms with Boltzmann factors can be rewritten as ${\mathrm{Tr}}_{\mathrm{adj}.}\left[1-L_{\mathrm{adj}}{\mathrm{e}}^{-\beta E}\right]$. Here, $L_{\mathrm{adj}}$ denotes the Polyakov loop operator in the adjoint representation, which can be expressed in terms of the fundamental representation $L_{\mathrm{fund}}$ through a group-theoretic relation, $(N_c^2-1)L_{\mathrm{adj}}=N_c^2{L}_{\mathrm{fund}}{\overline{L}}_{\mathrm{fund}}-1$. At the mean-field level, a vanishing Polyakov loop for quarks ($\Phi =0$) necessarily implies a non-vanishing Polyakov loop for gluons and ghosts. As a result, the thermal pressure (=$-{\Omega }^{\mathrm{mYM}}$) is unphysically large at low temperature.

In addition, we examine the temperature and $\Phi$-dependence of the mass $m_g$. Such dependences have been studied in Ref. [86]; see also Ref. [87]. We adopt the following parametrization:

$$m_g^T=\sqrt{{\left(m_g^{\mathrm{vac}}\right)}^2+c_g{\Phi }^{n_g}{T}^2},$$

(13)

which interpolates between the computations at $\Phi =0$ and 1 within the Gribov–Zwanziger framework. We choose $n_g=2$ and $c_g=0$ and 4. At $\Phi =1$, the mass at large T eventually scales as $m_g$∼$g_{s}T$, while for $\Phi =0$, the mass is saturated, $m_g$∼$\mathrm{const}$ for $\Phi =0$. For the vacuum mass, we choose $m_g^{\mathrm{vac}}=800$ MeV, which is consistent with the lattice studies for the Landau gauge propagators in pYM [72,73].

2.3. Comparison of the Polyakov Loop Potential

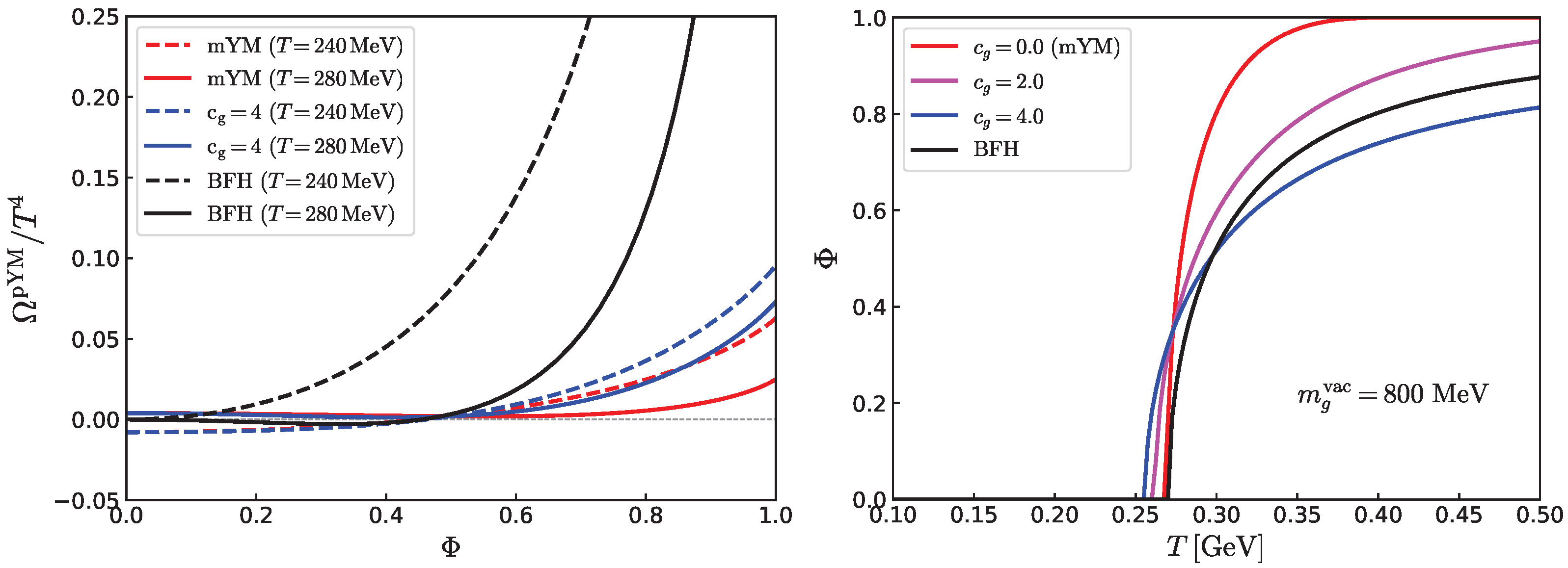
Here, we compare the phenomenological BFH potential with the mYM potential. The left panel of Figure 2 shows both potentials as functions of $\Phi$. In both cases, the critical temperature lies in the range 240–280 MeV. A major difference is that the mYM potential is significantly flatter than the BFH one. Consequently, the Polyakov loop grows much more rapidly with temperature in the mYM case, as illustrated in the right panel of Figure 2. This rapid growth can be moderated by introducing a T- and $\Phi$-dependent gluon mass, which suppresses the gluonic entropic contribution. With $c_g\simeq 2.0$–4.0 and $n_g=2$, the thermal evolution of the Polyakov loop in the mYM model can be brought into qualitative agreement with the BFH result, although the potential structure at $\Phi \gtrsim 0.5$ still shows substantial differences. As we will see in the next section, the behavior of the potential for $\Phi \gtrsim 0.5$ plays a crucial role once quarks are included.

3. Including Quarks: PNJL Model

3.1. Quasi-Quark Excitations

We now include quarks within a quasi-particle description. To be concrete, we use the PNJL model. As a first step, we examine the ${\mu }_q=0$ case to calibrate our models against lattice data. In particular, the lattice data were often obtained for a nonzero diquark source with which quarks form color-singlet diquark condensates and acquire a gap even at ${\mu }_q=0$. Without the diquark source term, the diquark condensate is formed only for ${\mu }_B\ge m_{\pi }$ (equivalently ${\mu }_q\ge m_{\pi }/2$), as predicted by the chiral perturbation theory [88,89].

For later convenience, from the very beginning, we derive the general expression of quark spectra at nonzero ${\mu }_q$ and $\Delta$. In the presence of a temporal background field, the kinetic term reads

$${\mathcal{L}}_{kin,q}=\overline{q}\left[\mathrm{i}\cancel{\partial }+g\cancel{a}+\mathcal{R}{T}_3{\gamma }_0+\mathrm{i}\mu {\gamma }_0-M_q\right]q-q^T\Delta q,$$

(14)

with $T_3={\lambda }_3/2$ and $\Delta ={\gamma }_5{\tau }_2{\lambda }_2\Delta$, where ${\tau }_2$ is the Pauli matrix in flavor space. Employing the Nambu–Gor’kov formalism, we define $\psi =q$ and its charge-conjugated field as ${\psi }_C\left(p\right)={\lambda }_2{\tau }_{2}C{\overline{q}}^T(-p)$. Then,

$$\overline{\psi }\left(p\right)\cancel{p}\psi \left(p\right)={\overline{\psi }}_C\left(p\right)\cancel{p}{\psi }_C\left(p\right),\overline{\psi }\left(p\right){\gamma }_0{\mathcal{A}}^0{T}_3\psi \left(p\right)={\overline{\psi }}_C\left(p\right){\gamma }_0{\mathcal{A}}^0{T}_3{\psi }_C\left(p\right),$$

(15)

where we used ${\lambda }_2(-T_a^T){\lambda }_2=T_a$. The momentum space representation of the Lagrangian now reads

$${\tilde{\mathcal{L}}}_{kin,q}=\overline{\Psi }\left(p\right)\left[\begin{array}{cc}\cancel{p}+\left(\mathcal{R}{T}_3+\mathrm{i}\mu \right){\gamma }_0-M_q& \Delta {\gamma }_5\\ -{\Delta }^{*}{\gamma }_5& \cancel{p}+\left(\mathcal{R}{T}_3-\mathrm{i}\mu \right){\gamma }_0-M_q\end{array}\right]\Psi \left(p\right),$$

(16)

where $\Psi \left(p\right)={(\psi \left(p\right),{\psi }_C\left(p\right))}^T/\sqrt{2}$.

We note that $p_0$ and $\mathcal{R}{T}_3$ always appear in the combination $p_0+\mathcal{R}{T}_3$, while the chemical potential $\mu$ enters the quasiparticle poles as ${\xi }_{\mathrm{p},\mathrm{a}}\left(\overrightarrow{p}\right)=\sqrt{{(E_q\left(\overrightarrow{p}\right)\mp \mu )}^2+{\Delta }^2}$. In the thermodynamic potential, the shift $p_0\to p_0+\mathcal{R}{T}_3$ modifies the standard entropic logarithm according to

$${\mathrm{tr}}_{c}ln\left[1+{\mathrm{e}}^{-\beta ({\xi }_k^i+\mathrm{i}\mathcal{R}{T}_3)}\right]=ln\left[1+{\mathrm{e}}^{-\beta ({\xi }_k^i+\mathrm{i}\mathcal{R}/2)}\right]+ln\left[1+{\mathrm{e}}^{-\beta ({\xi }_k^i-\mathrm{i}\mathcal{R}/2)}\right],$$

(17)

where the trace is taken over color indices. Combining these logarithms, the thermal quark contribution to the free energy (or equivalently, minus the pressure) becomes as follows:

$${\Omega }_{kin,q}^T=-{\mathcal{P}}_{kin,q}^T=-4T\sum _{i=\mathrm{p},\mathrm{a}}{\int }_{\overrightarrow{k}}ln\left(1+2\Phi {\mathrm{e}}^{-\beta {\xi }_k^i}+{\mathrm{e}}^{-2\beta {\xi }_k^i}\right).$$

(18)

The pressure at $\Phi =0$ (confined) or $\Phi =1$ (deconfined) are

$${\mathcal{P}}_{kin,q}^T\to \left\{\begin{array}{ccc}& 4T\sum _{i=\mathrm{p},\mathrm{a}}{\int }_{\overrightarrow{k}}ln\left(1+{\mathrm{e}}^{-\beta N_{\mathrm{c}}{\xi }_k^i}\right)& (\Phi \to 0)\\ & 4N_{\mathrm{c}}T\sum _{i=\mathrm{p},\mathrm{a}}{\int }_{\overrightarrow{k}}ln\left(1+{\mathrm{e}}^{-\beta {\xi }_k^i}\right)& (\Phi \to 1)\end{array}\right.$$

where we write $N_{\mathrm{c}}=2$. The thermal quark pressure is larger at least by a factor $N_{\mathrm{c}}$ in the deconfined phase than in the confined phase. The difference would be even greater in the high temperature limit; for $\Phi =0$ with ${\xi }_k$∼$|\overrightarrow{k}|$, we rescale the variable as $N_{\mathrm{c}}|\overrightarrow{k}|=|{\overrightarrow{k}}^{\prime }|$ to get

$${\mathcal{P}}_{kin,q}^{T\to \infty }(\Phi =0)\sim N_{\mathrm{c}}^{-4}{\mathcal{P}}_{kin,q}^{T\to \infty }(\Phi =1).$$

(19)

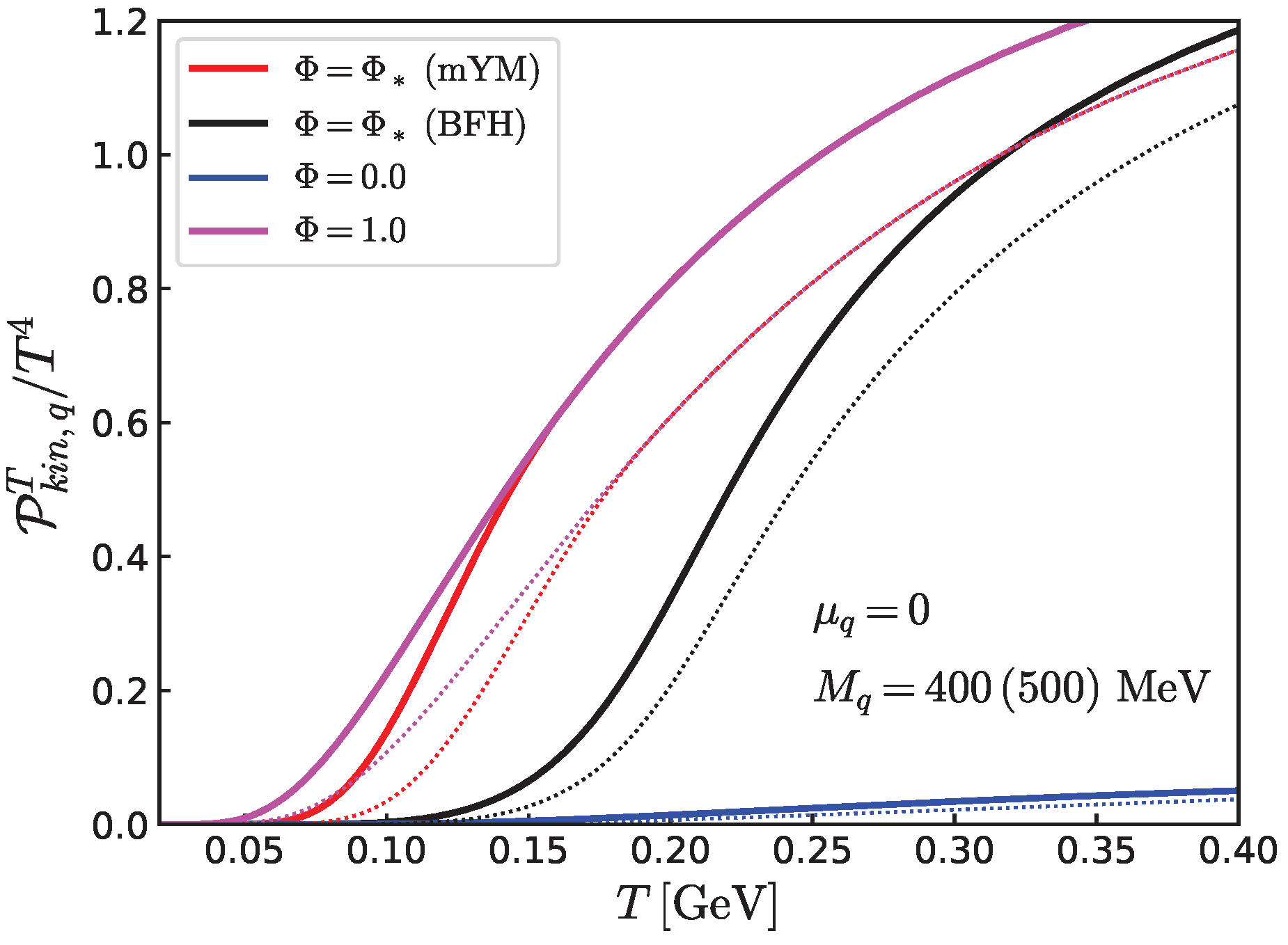
In order to examine the impact of the Polyakov loop, in Figure 3, we fix $M_q=400$ MeV (later, we consider the dynamical evolution of $M_q$) and show the thermal quark pressure at ${\mu }_q=0$ with ${\Phi }_{*}$ minimizing the potentials for mYM + quarks and BFH. We also show the $\Phi =0$ and 1 cases for comparison. It is clear that the suppression effects due to the Polyakov loop are substantial; ${\mathcal{P}}_{kin,q}^T$ at $\Phi =0$ is much smaller than the $\Phi =1$ case, as anticipated from Equation (19) for the quark sector. For dynamical computations allowing the variance of $\Phi$, the growth of $\Phi$ is driven by the thermal quark (hadronic) excitations. Thermal hadronic contributions rise rapidly around T∼150–200 MeV as in the Hagedorn gas, as also does the Polyakov loop. In this regime, hadrons strongly overlap, and there are color fields to which quarks couple become available to form a quark–gluon–plasma; here, hadrons dissociate into a quark–gluon plasma, and quark descriptions should be valid.

3.2. Evolution of Condensates

To determine the evolution of the in-medium gaps, we include both the zero-point energy and the potential terms associated with the gaps and the Polyakov loop. For this purpose, we adopt the pNJL-type thermodynamic potential

$$\begin{array}{c}\hfill {\Omega }_q=-4\sum _{i=\mathrm{p},\mathrm{a}}{\int }_{\overrightarrow{k}}\left[{\xi }_k^i+Tln\left(1+2\Phi {\mathrm{e}}^{-\beta {\xi }_k^i}+{\mathrm{e}}^{-2\beta {\xi }_k^i}\right)\right]+{\displaystyle \frac{{(M_q-m_q)}^2+{(\Delta -{\Delta }_{\mathrm{ext}})}^2}{2G}},\end{array}$$

(20)

where G denotes the NJL coupling constant, $m_q$ the current quark mass, and ${\Delta }_{\mathrm{ext}}$ an external diquark source term. The current quark mass $m_q$ is adjusted to reproduce the pion mass employed in the lattice simulations. In the lattice setup, the diquark source term ${\Delta }_{\mathrm{ext}}$ is introduced to stabilize the numerical calculations; we take its value accordingly to ensure consistency with the lattice data.

Including the pYM term, the gap equations for $\Phi$, $M_q$, and $\Delta$ are (${\Omega }_{{\mathrm{QC}}_2\mathrm{D}}={\Omega }_{\mathrm{pYM}}+{\Omega }_q$)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial {\Omega }_{{\mathrm{QC}}_2\mathrm{D}}}{\partial \Phi }}& ={\displaystyle \frac{\partial {\Omega }_{\mathrm{pYM}}}{\partial \Phi }}-4T\sum _{i=\mathrm{p},\mathrm{a}}{\int }_{\overrightarrow{k}}\left[{\displaystyle \frac{\Theta ({\Lambda }_{\mathrm{NJL}}-|\overrightarrow{k}|)}{cosh\left(\beta {\xi }_k^i\right)+\Phi }}+{\displaystyle \frac{\Theta (|\overrightarrow{k}|-{\Lambda }_{\mathrm{NJL}})}{cosh\left(\beta {\xi }_k^i{|}_{\eta ={\eta }_{\mathrm{ext}}}\right)+\Phi }}\right],\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial {\Omega }_{{\mathrm{QC}}_2\mathrm{D}}}{\partial \eta }}& =-4\sum _{i=\mathrm{p},\mathrm{a}}{\int }_{\overrightarrow{k}}\Theta ({\Lambda }_{\mathrm{NJL}}-|\overrightarrow{k}\left|\right){\displaystyle \frac{\partial {\xi }_k^i}{\partial \eta }}{\displaystyle \frac{sinh\left(\beta {\xi }_k^i\right)}{cosh\left(\beta {\xi }_k^i\right)+\Phi }}+{\displaystyle \frac{\eta -{\eta }_{\mathrm{ext}}}{2G}},\hfill \end{array}$$

(21)

where $\eta =M_q$ or $\Delta$. In the low temperature limit ($\beta \to +\infty$), the thermal factors in the integrand depend on $\Phi$ very weakly; the thermal factor behaves as $1/(cosh\left(\beta {\xi }_k^i\right)+\Phi )\simeq {\mathrm{e}}^{-\beta {\xi }_k^i}$ for the $\Phi$ part and $sinh\left(\beta {\xi }_k^i\right)/(cosh\left(\beta {\xi }_k^i\right)+\Phi )\simeq 1$ for the $M_q$ and $\Delta$ parts.

Here, we have assumed that the gaps damp at high energy and parametrize such damping scale as ${\Lambda }_{\mathrm{NJL}}$. This scale appears automatically if we use momentum-dependent interactions, e.g., the ∼$1/p^2$ type. In the NJL model, the contact interactions yield only momentum-independent gaps. Thus, we have to impose such a scale ${\Lambda }_{\mathrm{NJL}}$ by hand so that $\partial {\xi }_k^i/\partial \eta$ is nonzero only for $|\overrightarrow{k}|\le {\Lambda }_{\mathrm{NJL}}$. This results in the standard NJL gap equations. Meanwhile, the integral in the equation for $\Phi$ should include both thermal quarks with and without the effective masses, so we should keep the integral for $|\overrightarrow{k}|\ge {\Lambda }_{\mathrm{NJL}}$.

3.3. The Pion Mass

To calibrate our model parameters to the lattice setup, we first compute the pion mass within the model. In the framework of the RPA, the pion mass at ${\mu }_q=T=0$ is determined by

$$1-4G{N}_{\mathrm{c}}{\delta }_{ab}{\int }_{\overrightarrow{p}}{\displaystyle \frac{\Theta ({\Lambda }_{\mathrm{NJL}}-|\overrightarrow{k}\left|\right)}{E_p-m_{\pi }^2/4E_p}}=0.$$

(22)

In the chiral limit, this equation reduces to the gap equation for $M_q$ at $m_{\pi }=0$, in accordance with the Nambu–Goldstone theorem.

4. The Polyakov Loop in QC₂D: Calibration at ${\mathbf{\mu }}_{\mathbf{q}}=\mathbf{0}$

We first briefly summarize the qualitative differences between the mYM and phenomenological BFH potentials after including quarks, then we proceed to quantitative comparisons with lattice results.

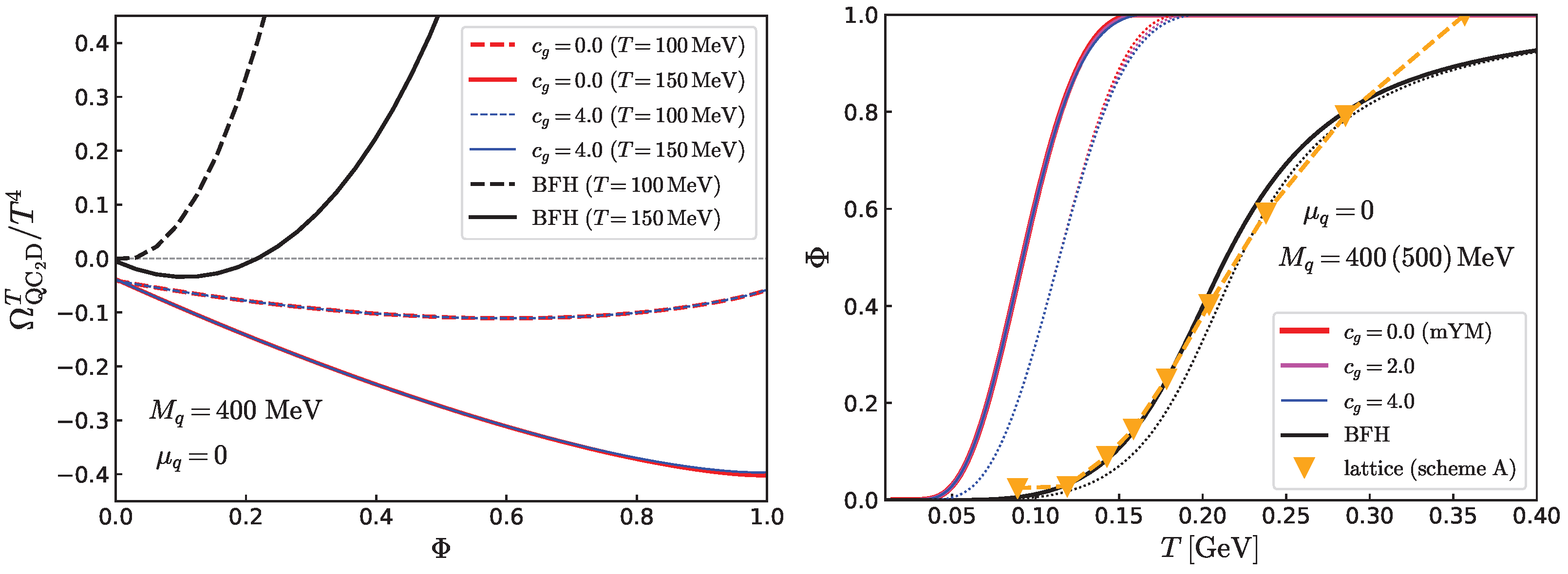
We begin by examining the structure of the Polyakov loop potentials at ${\mu }_q=0$. Figure 4 shows the Polyakov loop potential, ${\Omega }_{{\mathrm{QC}}_2\mathrm{D}}^T\equiv {\Omega }_{\mathrm{pYM}}+{\Omega }_q^T$, with quarks included (left), and the corresponding temperature dependence of the Polyakov loop (right). Here, ${\Omega }_{\mathrm{pYM}}$ is replaced by either ${\Omega }_{gl+gh}$ for the mYM or ${\Omega }_{\mathrm{BFH}}$ for the phenomenological model. For the mYM potential, we consider $c_g=0.0$ and $4.0$ with $n_g=2$ and $m_g^{\mathrm{vac}}=800$ MeV.

Adding quarks to the pYM potential significantly alters its qualitative structure, leading to distinct behaviors between the mYM and BFH models. While both models exhibit similar transition temperatures in the pYM case, the mYM potential is much flatter with respect to $\Phi$, so the deconfined solution is strongly favored once quarks are included. In contrast, the BFH potential incurs a large energy cost near $\Phi \simeq 1$ (diverging as $\Phi \to 1$) due to the Haar measure term ∼$ln(1-{\Phi }^2)$, which delays the growth of $\Phi$. These differences are directly reflected in the temperature dependence of the Polyakov loop.

We now turn to more quantitative discussions. To compare our model calculations with lattice simulation results, we must use model parameters adjusted to the setup used in lattice computations. First, we note that there is no unique way to set the scale in QC₂D [14] since there are no real-world counterparts. In this work, we consider the lattice results in which the string tension is fixed as $\sqrt{{\sigma }_s}\simeq 440$ MeV. For the current quark masses, the “fine ensemble” lattice simulations [15] use a relatively heavy quark mass that yields a pion-to-rho mass ratio of $m_{\pi }/m_{\rho }$∼$0.8$, which is substantially larger than the corresponding ratio in the real world, $m_{\pi }/m_{\rho }\simeq 0.18$. The heavy pion mass of $m_{\pi }\simeq 637$ MeV was used to reduce the computational cost for extensions to finite ${\mu }_q$. We take into account this heavy current quark mass in our model predictions. We test two parameter sets, set I and set II, in

Table 1. Two parameter sets are used for the quark model. We tune the current quark mass $m_q$ for a given coupling G so that the RPA yields a pion pole at $m_{\pi }=637$ MeV. The cutoff ${\Lambda }_{\mathrm{NJL}}$ is chosen to be the same for both parameter sets.

Name	${\mathit{m}}_{\mathit{\pi }}\left[\mathbf{MeV}\right]$	${\mathbf{\Lambda }}_{\mathbf{NJL}}\left[\mathbf{MeV}\right]$	$\mathit{G}\left[{\mathbf{GeV}}^{-2}\right]$	${\mathit{m}}_{\mathit{q}}\left[\mathbf{MeV}\right]$	${\mathit{M}}_{\mathit{q}}\left[\mathbf{MeV}\right]$
set I	637	657	5.42	121	378
set II			7.23	110	512

.

Another important step is to set the renormalization factor of the Polyakov loop. We are not aware of how to rigorously match the Polyakov loop in our model and lattice data. For this reason, we simply choose the renormalization factor for the lattice results to make model results and lattice data consistent at ${\mu }_q=0$ (Figure 5), then we make model predictions for the Polyakov loop at ${\mu }_q\ne 0$. Later, these model predictions are compared with the lattice results.

The renormalized and bare Polyakov loops are related by (in Ref. [15], the notation “L” is used in place of $\Phi$)

$${\Phi }_R\left(T\right)=Z_{\Phi }^{N_{\tau }}{\Phi }_0\left({\left(N_{\tau }a\right)}^{-1}\right)$$

(23)

where $T={\left(N_{\tau }a\right)}^{-1}$ and $Z_{\Phi }$ is the renormalization factor. Ref. [15] discussed two renormalization schemes,

$${\Phi }_R^{\mathrm{scheme}\mathrm{A}}(T=1/4a)=1.0,{\Phi }_R^{\mathrm{scheme}\mathrm{B}}(T=1/4a)=0.5,$$

(24)

where $1/4a\simeq 356.875$ MeV. In Ref. [15], most results are presented in scheme B. In the continuum expression, the renormalization factors correspond to the choice of the zero-point energy,

$$Z_{\Phi }^{N_{\tau }}=exp\left[\beta {\displaystyle \frac{ln{Z}_{\Phi }}{a}}\right]\equiv {\mathrm{e}}^{\beta (E_R-E_0)}.$$

(25)

The Polyakov loops in schemes A and B can be written as follows:

$${\Phi }_R^{\mathrm{scheme}\mathrm{A}/\mathrm{B}}(T;E_R)={\mathrm{e}}^{\beta (E_R^{A/B}-E_0)}{\Phi }_0\left(T\right).$$

(26)

In Ref. [15], most of the data are given in scheme B. Hence, it is convenient to write the Polyakov loops at the energy scale $E_R$ as follows:

$${\Phi }_R(T;E_R)={\mathrm{e}}^{\beta (E_R-E_B)}{\Phi }_R^{\mathrm{scheme}\mathrm{B}}\left(T\right).$$

(27)

For instance, to convert the data from scheme B to A, we substitute $E_R^A$ such that $E_R^A-E_R^B\simeq 247$ MeV. For fitting to our model at ${\mu }_q=0$, we use $E_R\simeq 270$ MeV unless otherwise stated.

It is important to note that these renormalization factors affect not only the magnitude of the Polyakov loop but also its temperature derivatives. For instance, the location of the susceptibility peak depends on the renormalization scheme. This scheme dependence can be eliminated by considering the ratio ${\Phi }_R(T;{\mu }_q)/{\Phi }_R(T;{\mu }_q=0)$, allowing a physically meaningful discussion of ${\mu }_q$ effects. At low temperatures, this ratio is inconvenient since both numerators and denominators become vanishing. For this reason, we do not show the ratio but plot $\Phi$ itself after calibrating $E_R-E_B$ so that our $\Phi$ at ${\mu }_q=0$ matches the lattice results. We then examine the ${\mu }_q$-dependence of the Polyakov loop.

5. The Polyakov Loop in Baryonic and Quark Matter

Outline

We now explore the finite ${\mu }_q$ domain, beginning with the overall behavior of various condensates. It is well established that for ${\Delta }_{\mathrm{ext}}=0$, a diquark condensate forms when ${\mu }_q\ge m_{\pi }/2$. Initially, the diquarks are of the Bose–Einstein condensation (BEC) type, forming molecule-like pairs, but with increasing density, they evolve into Bardeen–Cooper–Schrieffer (BCS)-type pairs near the quark Fermi surface. For finite ${\Delta }_{\mathrm{ext}}\ne 0$, diquark condensates can form even before ${\mu }_q=m_{\pi }/2$. 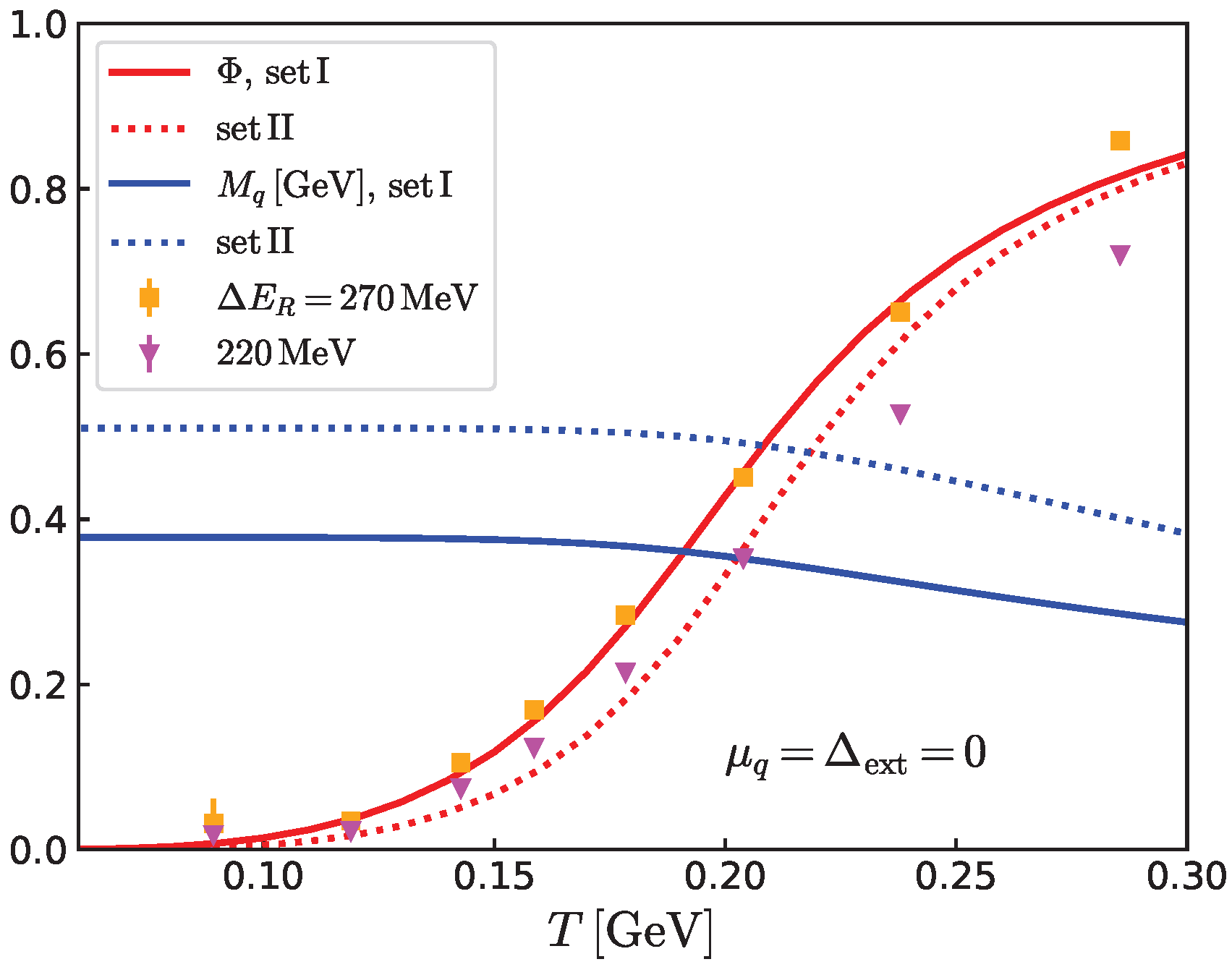Figure 6 shows $M_q$, $\Delta$, and $\Phi$ at a fixed temperature $T=10$ MeV for various ${\mu }_q$ using parameter set I. The solid (dotted) lines correspond to ${\Delta }_{\mathrm{ext}}=45$ MeV, which matches $ja=0.03$ in the lattice results of Ref. [15]. As mentioned, nonzero ${\Delta }_{\mathrm{ext}}$ allows the diquark condensate to form even for ${\mu }_q<m_{\pi }/2$. Meanwhile, the reduction of $\Delta$ at very large ${\mu }_q$ is simply an artifact of the UV cutoff; beyond the Fermi surface, with increasing ${\mu }_q$, the available phase space for pairing diminishes because of the UV cutoff; hence, diquarks cannot form at very large densities. The gap $\Delta$ vanishes around ${\mu }_q\simeq 800$ MeV, leaving quarks gapless on the Fermi surface. In this regime, even a small temperature of T∼10 MeV is sufficient to induce substantial Polyakov loop expectation values.

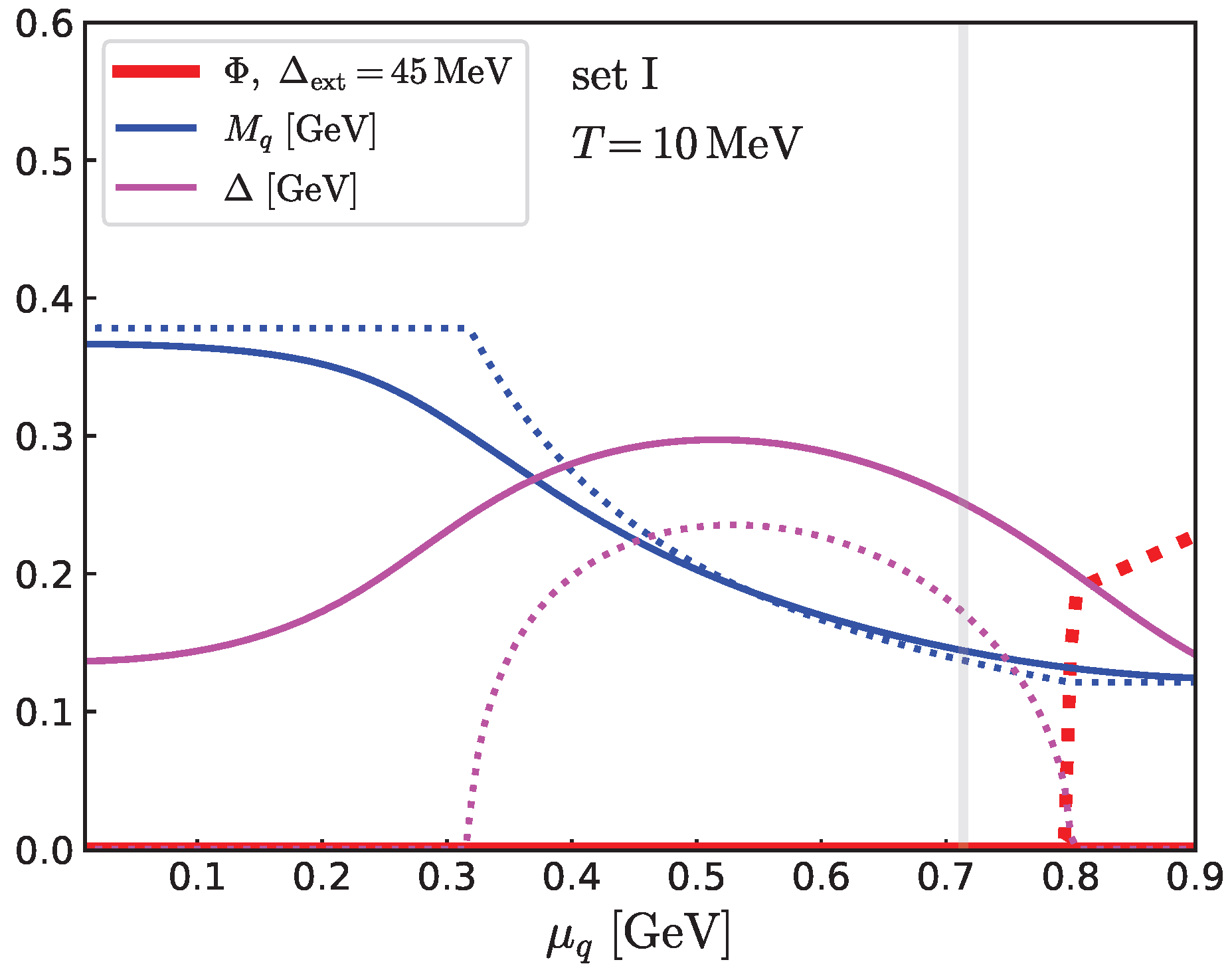
Figure 7 shows the diquark gaps $\Delta$ for ${\mu }_q=286,428,571,$ and 714 MeV as a function of temperature. For ${\Delta }_{\mathrm{ext}}=0$ MeV, parameter set I predicts a second-order transition at $T_s$∼110–140 MeV. In Ref. [15], the results at finite j are extrapolated to $j\to 0$, giving an estimate $T_s\simeq 100$–120 MeV, which is roughly consistent with set I. In contrast, set II, used with the BFH potential, predicts $T_s\simeq 170$–200 MeV, indicating a different definition of the theory from that in Ref. [15]. This explains why the NJL coupling G in set I is approximately 0.75 times smaller than in the BFH setup. For comparisons, in Figure 8 we also show the results for fixed values of Polyakov loop at $\Phi =0$ and 1.

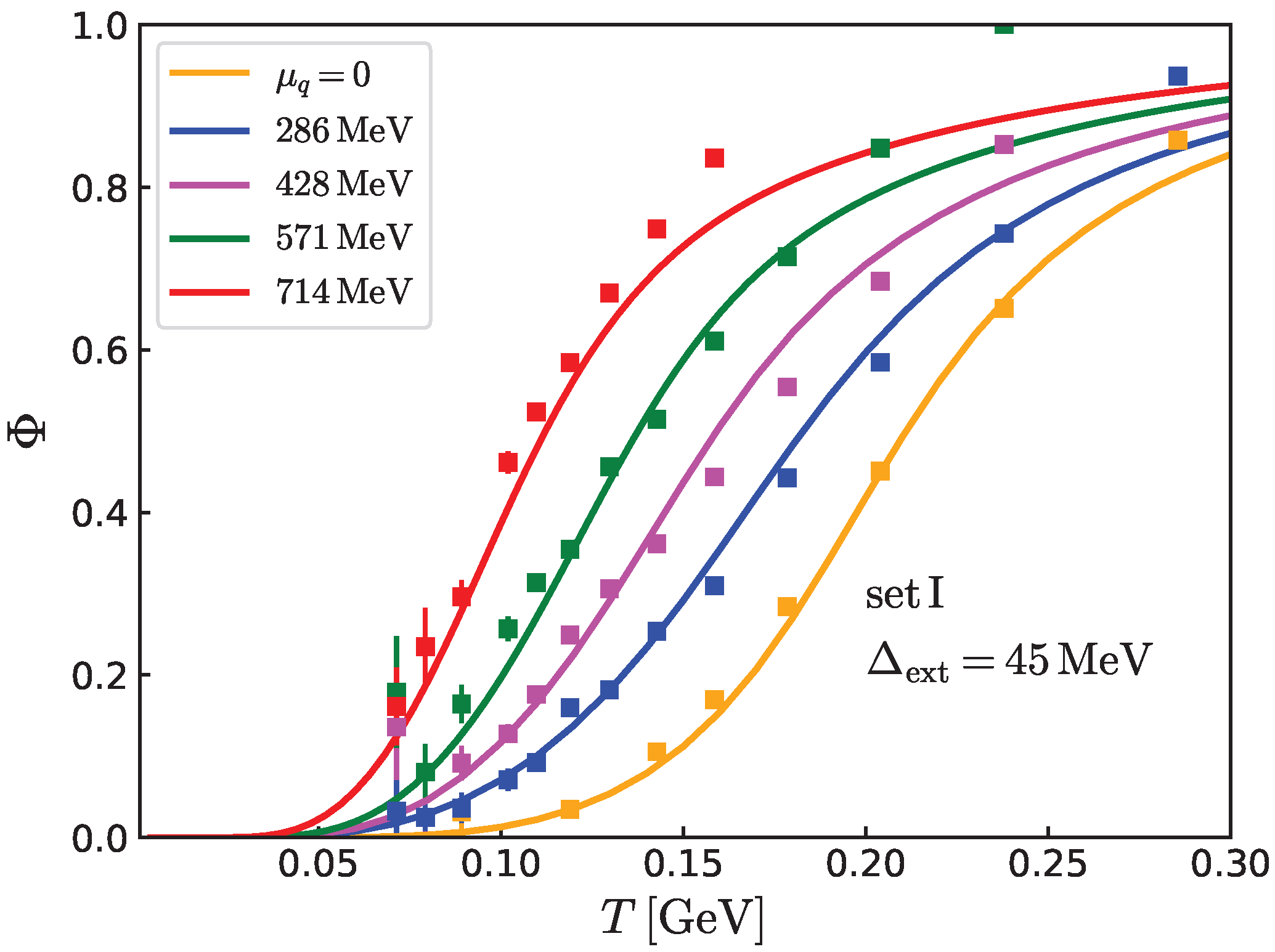
Having established reasonable consistency in $T_s$ and $\Delta$ between model set I and the lattice results of Ref. [15], we now extend the comparison to finite ${\mu }_q$. Figure 9 shows the Polyakov loop $\Phi$ for set I with ${\Delta }_{\mathrm{ext}}=45$ MeV, together with the lattice data at $ja=0.03$. At low temperatures, corresponding to $\Phi \lesssim 0.8$, the model reproduces the lattice results well. At higher temperatures ($\Phi \gtrsim 0.8$), the model $\Phi$ begins to saturate, while the lattice $\Phi$ continues to grow, as the renormalization factor allows $\Phi$ to exceed unity. This high-temperature deviation occurs for all ${\mu }_q$ studied, and its origin remains unclear. Nevertheless, our model is expected to be more reliable at low energies, and the agreement in this regime is noteworthy.

At low temperatures, it is crucial to maintain a sizable $\Delta$. Figure 10 illustrates that if $\Delta$ is artificially set to zero, quarks become gapless. These gapless excitations induce a rapid rise of the Polyakov loop, resulting in substantial disagreement between our model and the lattice data.

We emphasize that, in all these analyses, the parameters for the gluonic part of the Polyakov loop potential, ${\Omega }_{\mathrm{pYM}}$, are kept unchanged. In principle, in-medium gluon screening could modify the gluon propagator and weaken confinement. Nevertheless, our minimal setup—without major modifications to ${\Omega }_{\mathrm{pYM}}$—yields reasonable agreement with lattice results, suggesting that drastic changes in ${\Omega }_{\mathrm{pYM}}$ are disfavored for the density range considered here. In the next section, we reinforce this conclusion by examining the effect of the diquark gap on the gluon propagators.

6. Gluon Propagators at One-Loop with Polyakov Loops

We focus on medium corrections to the static gluon propagators, $D\left(k\right)$, at zero frequency ($k_0=0$). Processes with $k_0\ll {\mu }_q$ keep quarks near the Fermi surface and hence are most relevant for non-perturbative effects. At the same time, the momentum transfer $|\overrightarrow{k}|$ can be large if quarks remain close to the Fermi surface before and after scattering. Therefore, we concentrate on small $k_0$ while considering a wide range of $|\overrightarrow{k}|$ to ∼$2{\mu }_q$.

To reproduce the lattice results of Ref. [74], it is crucial to suppress quark excitations in the infrared region. Gapless quarks would otherwise over-screen the electric gluons [62]. Including a diquark gap of $\Delta$∼200 MeV reduces the electric screening, improving agreement with lattice data [60,61]. In contrast, in the magnetic sector, static screening remains absent for any value of $\Delta$, as in the normal phase. The magnetic screening is usually regarded as non-perturbative effects.

At finite temperatures, thermally excited particles—either quarks or hadrons—respond to external momenta as gapless modes [61,90]. If the thermal excitations are quark-dominated, they induce static electric screening as in the normal phase, while the static magnetic modes remain unscreened. In contrast, if the thermal excitations are confined, the electric screening is expected to be weaker, since color-singlet objects of typical size $R_{\mathrm{size}}$ cannot respond effectively to external fields at wavelengths much longer than their size ($k\ll R_{\mathrm{size}}^{-1}$).

We account for the suppression of thermal quarks by including Polyakov loops. The gluon self-energy is described by the polarization function

$$-\mathrm{i}{\Pi }_{\mu \nu }^{AB}\left(k_A\right)\equiv {\left(\mathrm{i}{g}_s\right)}^2{\int }_{x,y}{\mathrm{e}}^{-\mathrm{i}k(x-y)}〈\left(\overline{q}{\gamma }_{\mu }{\displaystyle \frac{{\lambda }_A}{2}}q\right)\left(x\right)\left(\overline{q}{\gamma }_{\nu }{\displaystyle \frac{{\lambda }_B}{2}}q\right)\left(y\right)〉.$$

(28)

where $k_A$ was defined in Equation (8). Explicit evaluation shows that ${\Pi }^{AB}$ depends on $k_A$ and is diagonal in color space, with nonzero components only for $(A,B)=(3,3),(+,+),(-,-)$. All other combinations vanish.

As usual, we decompose the gluon self-energy into electric and magnetic components. In the presence of the background field, the momenta entering the projection tensors are $k_A$, which ensures the Ward–Takahashi identity, $k_A^{\mu }{\Pi }_{\mu \nu }^{AB}=0$, is satisfied. The decomposition then reads

$${\Pi }_{\mu \nu }^{AB}\left(k_A\right)={\delta }^{AB}{P}_{\mu \nu }^E\left(k_A\right){\Pi }_E\left(k_A\right)+{\delta }^{AB}{P}_{\mu \nu }^M\left(k_A\right){\Pi }_M\left(k_A\right)$$

(29)

where $k_A$ was defined in Equation (8).

6.1. The Vacuum Subtraction

The polarization function is formally UV divergent. We extract the UV divergent vacuum contribution and combine it with the counter terms for the renormalization,

$$\begin{array}{}& {\left[{\Pi }_{\mu \nu }^{AB}\left(k_A\right)\right]}^R\equiv \left[{\Pi }_{\mu \nu }^{AB}\left(k_A\right)\right]+\delta Z_g{k}_A^2{P}_{\mu \nu }^{k_A}\hfill \mathrm{(30)}& ={\delta }^{AB}{P}_{\mu \nu }^{k_A}\left[{\Pi }_{\mathrm{vac}}\left(k_A\right)+\delta Z_g{k}_A^2\right]+P_{\mu \nu }^E\left(k_A\right)\delta {\Pi }_E^{AB}\left(k_A\right)+P_{\mu \nu }^M\left(k_A\right)\delta {\Pi }_M^{AB}\left(k_A\right),\hfill \end{array}$$

where the renormalized vacuum part is ($K^2\equiv -{\left(k_A\right)}^2$, ${\alpha }_s=g_s^2/4\pi$)

$${\Pi }_{\mathrm{vac}}^R\left(k_A\right)={\Pi }_{\mathrm{vac}}\left(k_A\right)+\delta Z_g{k}_A^2=-K^2{\displaystyle \frac{2{\alpha }_s^q}{\pi }}{\int }_0^1\mathrm{d}xx(1-x)ln{\displaystyle \frac{{\left(M_q^{\mathrm{vac}}\right)}^2+x(1-x)K^2}{{\left(M_q^{\mathrm{vac}}\right)}^2+x(1-x){\mu }_R^2}},$$

(31)

with ${\mu }_R$ being the renormalization scale. The medium part is defined by subtracting the vacuum part,

$$\delta {\Pi }_{E,M}\equiv {\Pi }_{E,M}-{\Pi }_{\mathrm{vac}},$$

(32)

where the subscript $AB$ is omitted for the moment.

This subtracted function is UV convergent, but its finite part depends on regularization methods. In particular, if we integrate $q_0$ first to pick up poles and then integrate $\overrightarrow{q}$, there emerge UV finite terms which violate the conservation law $k_A^{\mu }{\Pi }_{\mu \nu }^{AB}\left(k_A\right)=0$ when the quark propagators in ${\Pi }_{E,M}$ and ${\Pi }_{\mathrm{vac}}$ contain, e.g., different $M_q$ or $\Delta$ [59].

One way to restore the conservation law is to introduce counterterms that cancel regularization artifacts [59]. Another approach is to split the vacuum subtraction into two steps [61]:

$$\delta {\Pi }_{E,M}={\delta }_S{\Pi }_{E,M}+{\delta }_{{\mu }_q}{\Pi }_{E,M}={\left[{\Pi }_{\mathrm{vac}}^{M_q\to {\tilde{M}}_q}-{\Pi }_{\mathrm{vac}}\right]}_{\dim \mathrm{reg}}+{\left[{\Pi }_{E,M}-{\Pi }_{\mathrm{vac}}^{M_q\to {\tilde{M}}_q}\right]}_{3\mathrm{d}\mathrm{reg}}.$$

(33)

Here, ${\delta }_{{\mu }_q}{\Pi }_{E,M}$—which is the difference between ${\Pi }_{E,M}$ and ${\Pi }_{\mathrm{vac}}$ evaluated with the same gap parameters but different ${\mu }_q$—has no regularization artifacts; hence, one can evaluate it using the standard residue method with a three-dimensional cutoff. Meanwhile, each term in ${\delta }_S{\Pi }_{E,M}$ can be evaluated via dimensional regularization; hence, ${\delta }_S{\Pi }_{E,M}$ can be made artifact-free. The parameter ${\tilde{M}}_q({\mu }_q,T)\equiv \sqrt{M_q^2+{\Delta }^2}$, determined at a given ${\mu }_q$, is uniquely fixed to ensure that the conservation law is maintained. Explicitly, ${\delta }_S{\Pi }_{E,M}$ reads as follows:

$${\delta }_S{\Pi }_{E,M}=-K^2{\displaystyle \frac{2{\alpha }_s^q}{\pi }}{\int }_0^1\mathrm{d}xx(1-x)ln{\displaystyle \frac{{\tilde{M}}_q^2+x(1-x)K^2}{{\left(M_q^{\mathrm{vac}}\right)}^2+x(1-x)K^2}}.$$

(34)

If the gap parameters in vacuum and medium remain the same, i.e., ${\tilde{M}}_q=M_q^{\mathrm{vac}}$, then ${\delta }_S{\Pi }_{E,M}$ vanishes by construction.

6.2. The Medium Corrections

Physical medium effects are largely reflected by ${\delta }_{{\mu }_q}{\Pi }_{E,M}$. Decomposing the normal and anomalous quark propagators into the particle and antiparticle components, then calculating the residue integral for $q_0$, we find (before the vacuum subtraction)

$$-\mathrm{i}{\Pi }_{E,M}^{AB}\left(k_A\right)={\displaystyle \frac{g_s^2}{2}}\sum _{s,s^{\prime }=p,a}{\int }_{\overrightarrow{q}}{K}_{E,M}^{s{s}^{\prime }}\left[C_{E,M}^{s{s}^{\prime }}{\mathcal{G}}_{AB}^{s{s}^{\prime }}+{\tilde{C}}_{E,M}^{s{s}^{\prime }}{\tilde{\mathcal{G}}}_{AB}^{s{s}^{\prime }}\right]({\overrightarrow{q}}_{+},{\overrightarrow{q}}_{-};k_0),$$

(35)

where ${\overrightarrow{q}}_{\pm }=\overrightarrow{q}\pm \overrightarrow{k}/2$. We call $K_{E,M}^{s{s}^{\prime }}$, $C_{E,M}^{s{s}^{\prime }}$, and ${\mathcal{G}}_{AB}^{s{s}^{\prime }},{\tilde{\mathcal{G}}}_{AB}^{s{s}^{\prime }}$ the kinematic, coherence, and propagator factors. The propagator $\tilde{\mathcal{G}}$ is non-vanishing only at nonzero temperatures.

6.2.1. Kinematic Factors

The explicit forms of the kinematic factors are

$$\begin{array}{}& {\mathcal{K}}_E^{\mathrm{p}\mathrm{p}}={\mathcal{K}}_E^{\mathrm{a}\mathrm{a}}=-{\displaystyle \frac{k^2}{{\overrightarrow{k}}^2}}\left(1+{\displaystyle \frac{{\overrightarrow{q}}^2-{\overrightarrow{k}}^2/4+M_q^2}{E_{q_{+}}{E}_{q_{-}}}}\right),\hfill & {\mathcal{K}}_E^{\mathrm{p}\mathrm{a}}={\mathcal{K}}_E^{\mathrm{a}\mathrm{p}}=-{\displaystyle \frac{k^2}{{\overrightarrow{k}}^2}}\left(1-{\displaystyle \frac{{\overrightarrow{q}}^2-{\overrightarrow{k}}^2/4+M_q^2}{E_{q_{+}}{E}_{q_{-}}}}\right),\hfill & {\mathcal{K}}_M^{\mathrm{p}\mathrm{p}}={\mathcal{K}}_M^{\mathrm{a}\mathrm{a}}=-1+{\displaystyle \frac{\left(\right|\overrightarrow{q}{|cos\theta )}^2-{\overrightarrow{k}}^2/4+M_q^2}{E_{q_{+}}{E}_{q_{-}}}},\hfill \mathrm{(36)}& {\mathcal{K}}_M^{\mathrm{p}\mathrm{a}}={\mathcal{K}}_M^{\mathrm{a}\mathrm{p}}=-1-{\displaystyle \frac{\left(\right|\overrightarrow{q}{|cos\theta )}^2-{\overrightarrow{k}}^2/4+M_q^2}{E_{q_{+}}{E}_{q_{-}}}},\hfill \end{array}$$

where $\theta$ in $cos\theta$ is the angle between $\overrightarrow{q}$ and $\overrightarrow{k}$. These kinematic factors depend on $M_q$ and the spatial momenta, and they are common across different states of matter. It is useful to note that, at low momenta, the electric components behave as ${\mathcal{K}}_E^{\mathrm{p}\mathrm{p}}\to 2+O({\overrightarrow{k}}^2)$ and ${\mathcal{K}}_E^{\mathrm{p}\mathrm{a}}\to O({\overrightarrow{k}}^2)$. This indicates that in-medium corrections to the electric part are dominated by particle–hole excitations.

6.2.2. Coherence Factors

The coherence factors, which characterize the diquark condensed phase, are

$$\begin{array}{}& {\mathcal{C}}_{E,M}^{\mathrm{p}\mathrm{p}}\hfill & ={\displaystyle \frac{1}{2}}\left(1-{\displaystyle \frac{(E_{q_{+}}-{\mu }_q)(E_{q_{-}}-{\mu }_q)\pm {|\Delta |}^2}{{\xi }_{\mathrm{p}}^{+}{\xi }_{\mathrm{p}}^{-}}}\right),\hfill & {\mathcal{C}}_{E,M}^{\mathrm{a}\mathrm{a}}\hfill & ={\displaystyle \frac{1}{2}}\left(1-{\displaystyle \frac{(E_{q_{+}}+{\mu }_q)(E_{q_{-}}+{\mu }_q)\pm {|\Delta |}^2}{{\xi }_{\mathrm{a}}^{+}{\xi }_{\mathrm{a}}^{-}}}\right),\hfill \mathrm{(37)}& {\mathcal{C}}_{E,M}^{\mathrm{p}\mathrm{a}}\hfill & ={\displaystyle \frac{1}{2}}\left(1+{\displaystyle \frac{(E_{q_{+}}-{\mu }_q)(E_{q_{-}}+{\mu }_q)\mp {|\Delta |}^2}{{\xi }_{\mathrm{p}}^{+}{\xi }_{\mathrm{a}}^{-}}}\right),\hfill \end{array}$$

and the factor relevant only at finite temperature (since $\tilde{\mathcal{G}}$ is nonzero only at finite temperature, see below),

$$\begin{array}{}& \hfill {\tilde{\mathcal{C}}}_{E,M}^{\mathrm{p}\mathrm{p}}& ={\displaystyle \frac{1}{2}}\left(1+{\displaystyle \frac{(E_{q_{+}}-{\mu }_q)(E_{q_{-}}-{\mu }_q)\pm {|\Delta |}^2}{{\xi }_{\mathrm{p}}^{+}{\xi }_{\mathrm{p}}^{-}}}\right),\hfill & \hfill {\tilde{\mathcal{C}}}_{E,M}^{\mathrm{a}\mathrm{a}}& ={\displaystyle \frac{1}{2}}\left(1+{\displaystyle \frac{(E_{q_{+}}+{\mu }_q)(E_{q_{-}}+{\mu }_q)\pm {|\Delta |}^2}{{\xi }_{\mathrm{a}}^{+}{\xi }_{\mathrm{a}}^{-}}}\right),\hfill \mathrm{(38)}& \hfill {\tilde{\mathcal{C}}}_{E,M}^{\mathrm{p}\mathrm{a}}& ={\displaystyle \frac{1}{2}}\left(1-{\displaystyle \frac{(E_{q_{+}}-{\mu }_q)(E_{q_{-}}+{\mu }_q)\mp {|\Delta |}^2}{{\xi }_{\mathrm{p}}^{+}{\xi }_{\mathrm{a}}^{-}}}\right),\hfill \end{array}$$

where ${\mathcal{C}}_{E,M}^{\mathrm{p}\mathrm{a}}(q_{+},q_{-})={\mathcal{C}}_{E,M}^{\mathrm{a}\mathrm{p}}(q_{-},q_{+})$ and ${\tilde{\mathcal{C}}}_{E,M}^{\mathrm{p}\mathrm{a}}(q_{+},q_{-})={\tilde{\mathcal{C}}}_{E,M}^{\mathrm{a}\mathrm{p}}(q_{-},q_{+})$. It is important to note that, at zero temperature, the electric component is vanishing in the small momentum limit, ${\mathcal{C}}_E^{\mathrm{p}\mathrm{p}}$∼$O(\overrightarrow{q}·\overrightarrow{k})$. Later, we see that the propagator factor ${\mathcal{G}}_E^{\mathrm{p}\mathrm{p}}$ remains finite for $\overrightarrow{k}\to 0$ so that the product ${\mathcal{C}}_E^{\mathrm{p}\mathrm{p}}{\mathcal{G}}_E^{\mathrm{p}\mathrm{p}}$ vanishes, meaning that the electric screening is absent in the diquark condensed phase. This situation differs from the normal phase where the propagator exhibits a singularity $\overrightarrow{k}$ as ∼$1/\overrightarrow{q}·\overrightarrow{k}$ for small $|\overrightarrow{k}|$ and hence makes the product ${\mathcal{C}}_E^{\mathrm{p}\mathrm{p}}{\mathcal{G}}_E^{\mathrm{p}\mathrm{p}}$ finite. In this case, the Debye mass emerges, cutting off gluons in the IR. In contrast, the particle–hole contribution to the magnetic component is finite, ${\mathcal{C}}_M^{\mathrm{p}\mathrm{p}}$∼${\Delta }^2/{\xi }_p^2$.

6.2.3. Propagator Factors

Finally, we examine the propagator factors where the effects of the Polyakov loop enter. First, we generalize the Fermi–Dirac distribution for quarks as

$$n_F(x\pm \mathrm{i}Q/2)={\displaystyle \frac{1+\Phi {\mathrm{e}}^{\beta x}}{{\mathrm{e}}^{2\beta x}+2\Phi {\mathrm{e}}^{\beta x}+1}}\pm \mathrm{i}{\displaystyle \frac{\tilde{\Phi }{\mathrm{e}}^{\beta x}}{{\mathrm{e}}^{2\beta x}+2\Phi {\mathrm{e}}^{\beta x}+1}}\equiv L_F^{\Phi }\left(x\right)\pm \mathrm{i}{\tilde{L}}_F^{\Phi }\left(x\right),$$

(39)

where $\Phi =\Phi +\mathrm{i}\tilde{\Phi }=cos(\beta \mathcal{R}/2)+\mathrm{i}sin(\beta \mathcal{R}/2)$.

For deconfined quarks at $(\Phi ,\tilde{\Phi })=(1,0)$, this function is reduced to the usual Fermi–Dirac distribution, $L_F^{\Phi =1}\left(x\right)\to n_F\left(x\right)$ and ${\tilde{L}}_F^{\Phi =1}\left(x\right)\to 0$. The low temperature behavior of the real part is $L_F^{\Phi =1}\left({\xi }_s\right)$∼${\mathrm{e}}^{-\beta {\xi }_s}$.

For confined quarks at $(\Phi ,\tilde{\Phi })=(0,1)$, we find $L_F^{\Phi =\mathrm{i}}\left(x\right)\to n_F\left(2x\right)$ and ${\tilde{L}}_F^{\Phi =\mathrm{i}}\left(x\right)\to {\mathrm{e}}^{\beta x}{n}_F\left(2x\right)$. At low temperatures, their behaviors are $L_F^{\Phi =\mathrm{i}}\left({\xi }_s\right)$∼${\mathrm{e}}^{-2\beta {\xi }_s}$ and ${\tilde{L}}_F^{\Phi =\mathrm{i}}\left({\xi }_s\right)$∼${\mathrm{e}}^{-\beta {\xi }_s}$, respectively. For low energy excitations, the real part exhibits a stronger suppression, ∼${\mathrm{e}}^{-2\beta \Delta }$, which can be interpreted as the Boltzmann factor for hadronic excitations. Meanwhile, the imaginary part is suppressed as ∼$e^{-\beta \Delta }$, reflecting quark excitations decaying into the colored background.

Using these generalized distribution functions, the $A=B=3$ components of the propagator factors are

$$\begin{array}{}& \hfill {\mathcal{G}}_{s{s}^{\prime }}^{A=B=3}(q_{+},q_{-};\Phi )& =\left[1-L_F^{\Phi }\left({\xi }_s^{-}\right)-L_F^{\Phi }\left({\xi }_{s^{\prime }}^{+}\right)\right]\left({\displaystyle \frac{1}{k_0+{\xi }_s^{-}+{\xi }_{s^{\prime }}^{+}}}+{\displaystyle \frac{1}{-k_0+{\xi }_s^{-}+{\xi }_{s^{\prime }}^{+}}}\right),\hfill \mathrm{(40)}& \hfill {\tilde{\mathcal{G}}}_{s{s}^{\prime }}^{A=B=3}(q_{+},q_{-};\Phi )& =\left[L_F^{\Phi }\left({\xi }_s^{-}\right)-L_F^{\Phi }\left({\xi }_{s^{\prime }}^{+}\right)\right]\left({\displaystyle \frac{1}{k_0-{\xi }_s^{-}+{\xi }_{s^{\prime }}^{+}}}+{\displaystyle \frac{1}{-k_0-{\xi }_s^{-}+{\xi }_{s^{\prime }}^{+}}}\right),\hfill \end{array}$$

which contain only the real part of the thermal distribution functions. On the other hand, the $(A,B)=(\mp ,\mp )$ components are

$$\begin{array}{}& \hfill {\mathcal{G}}_{s{s}^{\prime }}^{\mp \mp }& =\left[1-L_F^{\Phi }\left({\xi }_s^{-}\right)-L_F^{\Phi }\left({\xi }_{s^{\prime }}^{+}\right)\right]\left({\displaystyle \frac{1}{k_0\mp \mathrm{i}\mathcal{R}+{\xi }_s^{-}+{\xi }_{s^{\prime }}^{+}}}+{\displaystyle \frac{1}{-(k_0\mp \mathrm{i}\mathcal{R})+{\xi }_s^{-}+{\xi }_{s^{\prime }}^{+}}}\right)\hfill & & \pm \mathrm{i}\left[{\tilde{L}}_F^{\Phi }\left({\xi }_s^{-}\right)+{\tilde{L}}_F^{\Phi }\left({\xi }_{s^{\prime }}^{+}\right)\right]\left({\displaystyle \frac{1}{k_0\mp \mathrm{i}\mathcal{R}-{\xi }_s^{-}+{\xi }_{s^{\prime }}^{+}}}-{\displaystyle \frac{1}{-(k_0\mp \mathrm{i}\mathcal{R})-{\xi }_s^{-}+{\xi }_{s^{\prime }}^{+}}}\right),\hfill & \hfill {\tilde{\mathcal{G}}}_{s{s}^{\prime }}^{\mp \mp }& =\left[L_F^{\Phi }\left({\xi }_s^{-}\right)-L_F^{\Phi }\left({\xi }_{s^{\prime }}^{+}\right)\right]\left({\displaystyle \frac{1}{k_0\mp \mathrm{i}\mathcal{R}-{\xi }_s^{-}+{\xi }_{s^{\prime }}^{+}}}+{\displaystyle \frac{1}{-(k_0\mp \mathrm{i}\mathcal{R})-{\xi }_s^{-}+{\xi }_{s^{\prime }}^{+}}}\right)\hfill \mathrm{(41)}& & \pm \mathrm{i}\left[{\tilde{L}}_F^{\Phi }\left({\xi }_s^{-}\right)+{\tilde{L}}_F^{\Phi }\left({\xi }_{s^{\prime }}^{+}\right)\right]\left({\displaystyle \frac{1}{k_0\mp \mathrm{i}\mathcal{R}-{\xi }_s^{-}+{\xi }_{s^{\prime }}^{+}}}-{\displaystyle \frac{1}{-(k_0\mp \mathrm{i}\mathcal{R})-{\xi }_s^{-}+{\xi }_{s^{\prime }}^{+}}}\right),\hfill \end{array}$$

which contain the real and imaginary parts of the thermal distribution functions. It is important to note that ${\mathcal{G}}^{AB}$ and ${\tilde{\mathcal{G}}}^{AB}$ are functions of $k_A$; this verifies Equation (28), where we wrote ${\Pi }^{AB}$ as functions of $k_A$. We also note that the imaginary parts of $\mathcal{G}$ and $\tilde{\mathcal{G}}$ are common, $\mathrm{Im}{\mathcal{G}}_{s{s}^{\prime }}^{\mp \mp }=\mathrm{Im}{\tilde{\mathcal{G}}}_{s{s}^{\prime }}^{\mp \mp }$. These functions vanish at ${\left(k_A\right)}_0=0$, and we will therefore not discuss them further.

6.2.4. The Full Expression After Adding the pYM Type Self-Energy

Below, we examine the electric and magnetic propagators at $K^2=-k_A^2$. It is known that the vacuum propagators in the pYM theories are well described by the massive gluon propagator, including the gluon one-loop polarization function, ${\Pi }_{\mathrm{vac}}^G(k;m_g,{\alpha }_s^G,{\mu }_R)$, whose explicit expression is given by Equation (17) in Ref. [75]. Here, ${\mu }_R$ is the renormalization scale for which we take ${\mu }_R=1$ GeV, and ${\alpha }_s^G$ is the coupling in the gluon sector, which generally differs from the quark–gluon coupling ${\alpha }_s^q$. In the following, we begin with the vacuum propagators fitted to lattice data and then examine the impact of in-medium quark contributions. The propagators are expressed as

$$D_{\mu \nu }^{AB}\left(k_A\right)=D_E^{AB}{P}_{\mu \nu }^E+D_M^{AB}{P}_{\mu \nu }^M,D_{E,M}^{AB}\left(k_A\right)={\displaystyle \frac{{\delta }^{AB}}{K^2+m_g^2+{\Pi }_{\mathrm{vac}}^G+{\Pi }_{\mathrm{vac}}^R+\delta {\Pi }_{E,M}}},$$

(42)

where ${\Pi }_{\mathrm{vac}}^R$ and $\delta {\Pi }_{E,M}$ are defined in Equations (31) and (33).

7. One Loop vs. Lattice Results: Screening Masses

From now on, we compare our computations with the lattice results of Ref. [74]. For concreteness, we focus on the data at $\beta =2.1$, with the inverse lattice spacing $a^{-1}=1.41$ GeV, the pion mass $m_{\pi }\simeq 637$ MeV, spatial size $L_s\simeq 2.21$ fm, and temporal size $L_t$ corresponding to temperatures ranging from $T\simeq 44$ MeV to 353 MeV. This setup is very similar to the “fine ensemble” lattice data in Ref. [15] for the Polyakov loop in the previous section, where $\beta \simeq 2.1$, $a^{-1}=1.43$ GeV, and $m_{\pi }\simeq 637$ MeV. In Ref. [74], the results at $T\simeq 44$ MeV are regarded as effectively zero temperature data. Here, however, we explicitly treat them as $T=44$ MeV results, since analytic calculations at $T=0$ and $T=44$ MeV show considerable deviations at high densities.

Unfortunately, the lattice data at small momenta are sensitive to system size, and the statistical errors are non-negligible. Moreover, the lattice propagators were not renormalized, so the overall normalization of the field amplitude is arbitrary. To minimize both statistical and systematic uncertainties, we normalize each propagator by its value at $K^2=0$ at a chosen reference point of $({\mu }_q,T)$.

For the analytic results, we generally use $(\Phi ,M_q,\Delta )$ obtained from our gap Equation (21) with ${\Delta }_{\mathrm{ext}}=45$ MeV, except for the ${\mu }_q=0$ case, where the lattice computations set the external field to ${\Delta }_{\mathrm{ext}}=0$. Unless otherwise stated, we take ${\alpha }_s^G=1.0$; variations in ${\alpha }_s^G$ can largely be compensated by adjusting $m_g$, for which we test several values.

7.1. Density Evolution of the Screening Masses: Qualitative Guides from Fixed $\Phi$ and $\Delta$

To establish theoretical baselines, we first examine the screening masses with Polyakov loops set to $\Phi =0$ (confined) and $\Phi =1$ (deconfined) for various diquark gaps, $\Delta =1,100,$ and 200 MeV. The quark mass $M_q$ is determined by solving the gap equations for each $(\Phi ,\Delta )$ configuration. These results serve as guidelines for comparison with the lattice data.

We define the screening masses as follows:

$$m_{E/M}^2({\mu }_q,T)\equiv 1/D_{E/M}(k=0;{\mu }_q,T).$$

(43)

However, these expressions are not directly usable until a normalization is specified. To remove this arbitrariness and reduce statistical fluctuations in the lattice data, we normalize the screening masses by their values at zero density and "zero temperature" for each ${\mu }_q$:

$${\overline{m}}_{E/M}({\mu }_q,T)\equiv {\displaystyle \frac{m_{E/M}({\mu }_q,T)}{m_{E/M}({\mu }_q^{*},T^{*})}},({\mu }_q^{*},T^{*})=(0,44)\mathrm{MeV}.$$

(44)

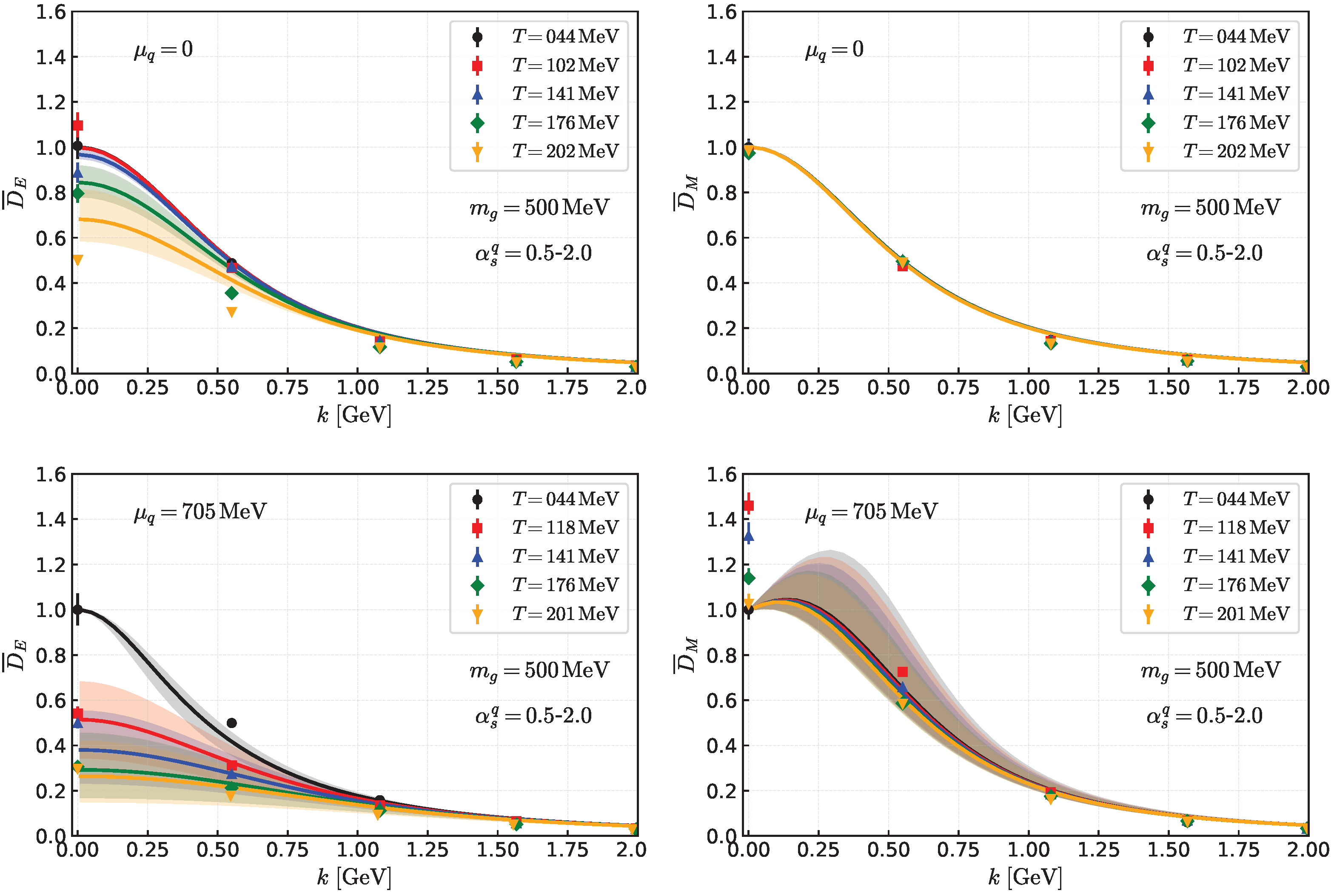
Shown in Figure 11 are the normalized electric (left panels) and magnetic (right panels) screening masses at low temperature, $T\simeq 44$ MeV. For the analytic results, we display two cases: $\Phi =1$ (upper panels, deconfined) and $\Phi =0$ (lower panels, confined). The error bands on the theoretical curves correspond to variations of ${\alpha }_s^q$ from 0.5 to 2, with the central solid curve representing ${\alpha }_s^q=1$.

For the electric sector, it is essential to consider a relatively large gap, $\Delta$∼200 MeV, and/or to include the Polyakov loop suppression of thermal quarks. The theoretical curves for the electric screening mass suggest that, for $\Delta \lesssim 100$ MeV, the screening masses increase too rapidly once the BCS regime sets in. This estimate of $\Delta$∼200 MeV is consistent with the lattice results for the superfluid critical temperature, $T_s\simeq 100$ MeV, in the BCS region; applying the BCS estimate, ${\Delta }^{\mathrm{BCS}}\simeq T_s/0.57$∼180 MeV [91], supports this observation.

Including the Polyakov loop suppresses thermal quark contributions, tempering the evolution of the electric screening toward high densities. Near the Fermi surface, the abundance of thermal quarks and baryons (diquarks) scales as ∼$\Phi e^{-\beta {\xi }_p}$∼$\Phi e^{-\beta \Delta }$ and ∼$e^{-2\beta \Delta }$, respectively, controlling the strength of quark screening effects. The impact of the Polyakov loop is small for $\Delta \simeq 0$ as ${\mathrm{e}}^{-\beta \Delta }\simeq {\mathrm{e}}^{-2\beta \Delta }\simeq 1$, while for a substantial $\Delta$, roughly twice the temperature is required for the confined case ($\Phi =0$) to develop a screening mass as large as in the deconfined case ($\Phi =1$). Equivalently, for a fixed T, the results for $\Delta$ with $\Phi =0$ resemble those for $2\Delta$ with $\Phi =1$. This correspondence can be verified by comparing the curve for $\Delta =100$ MeV with $\Phi =0$ to that for $\Delta =200$ MeV with $\Phi =1$, i.e., ${\mathrm{e}}^{-2\beta \times 100\mathrm{MeV}}={\mathrm{e}}^{-\beta \times 200\mathrm{MeV}}$, as shown in Figure 11.

The situation is very different in the magnetic sector. The theoretical curves show essentially no in-medium modifications of the magnetic screening mass with increasing ${\mu }_q$ (and also with increasing T, see Figure 12). The lattice results, however, suggest that the magnetic mass starts to increase from ${\mu }_q$∼700 MeV, a trend that cannot be captured by the present one-loop calculations.

The values of $(\Phi ,\Delta )$ dynamically determined from the gap equations remain within the range $\Phi$∼0 and $\Delta$∼200–300 MeV. Consequently, the screening masses closely follow the curves for $\Delta =200$ MeV and $\Phi =0$, where both the electric and magnetic masses remain nearly constant over the range of ${\mu }_q$ explored in this work. For this reason, we do not separately display the results of dynamically determined gaps here.

7.2. Thermal Evolution of the Screening Masses

Next, we examine the temperature evolution of the static screening masses for ${\mu }_q=$ 0, 282, 423, 564, and 705 MeV. Shown in Figure 12 are the normalized electric and magnetic screening masses. For the analytic results, we present two cases with $m_g=$ 400 MeV (upper panels) and 500 MeV (lower panels). The error bands for the theoretical curves reflect the variation in ${\alpha }_s^q$ from 0.5 to 2, with the central solid curve corresponding to ${\alpha }_s^q=1$.

For the electric sector, the screening mass increases with T, as expected from the conventional picture of the thermal Debye mass. The electric screening is primarily governed by the gap $\Delta$; in the absence of $\Delta$, the electric mass of order ∼$g_s{\mu }_q$ already emerges at $T=0$. The Polyakov loop suppresses thermal quark fluctuations and thereby moderates the growth of thermal contributions to the screening. The results with $m_g=400$ MeV appear to reproduce the lattice data well, whereas those with $m_g=500$ MeV tend to slightly underestimate them. At present, however, it is difficult to pin down the optimal value of $m_g$ from these computations, since its effect can be compensated by the behavior of $\Delta$, which is not yet conclusively determined. In fact, our determination of $\Delta$ is not entirely free from cutoff artifacts, as already mentioned. We suspect that the value of $\Delta$ in our PNJL model—estimated as ≃220–300 MeV for ${\Delta }_{\mathrm{ex}}=45$ MeV—and the resulting superfluid critical temperature $T_c$∼150 MeV may be somewhat too large. If this expectation is correct, the quark contributions to $m_g$ should be more pronounced than in the present computations, in which case a larger $m_g$ or ${\alpha }_s^q$ value may be acceptable.

For the magnetic sector, the quark contributions to the screening mass vanish for all ${\mu }_q$ and T. Consequently, the magnetic screening mass remains insensitive to variations in ${\mu }_q$ and T. This trend is consistent with the lattice data up to $T\simeq 250$ MeV. At zero momentum ($|\overrightarrow{k}|=0$), we find no in-medium modifications for the analytically computed magnetic propagators, whereas at finite spatial momenta such modifications do appear, as will be discussed in the next subsection.

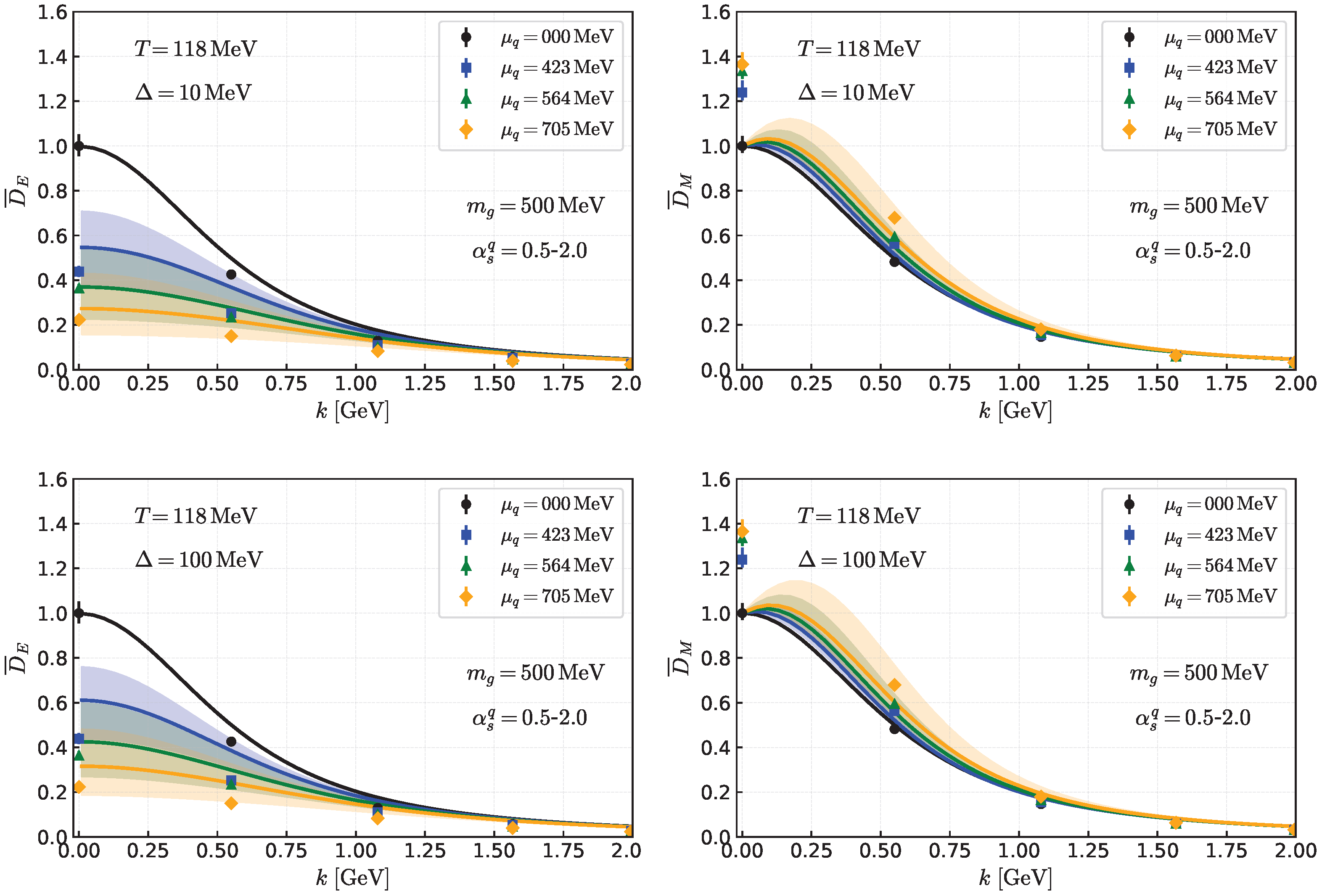
8. One Loop vs. Lattice Results: Gluon Propagators at Finite Momenta

Next, we examine the momentum dependence of the gluon propagators. We focus on the static case with $k_0=0$ but cover a wide range of spatial momenta, since such modes play the dominant role in low-energy processes. We select specific $({\mu }_q,T)$ points where lattice data are available [74]. Our analysis begins with the thermal evolution at ${\mu }_q=0$ and ${\mu }_q=705$ MeV, followed by the density evolution at $T=44$ MeV and $T=118$ MeV. The results at $T=118$ MeV, however, turn out to be very sensitive to the location of the diquark critical temperature and therefore require some additional analysis.

8.1. Thermal Evolution at ${\mu }_q=0$ and ${\mu }_q=705$ MeV

First, we examine the thermal evolution of the propagators at ${\mu }_q=0$ and ${\mu }_q=705$ MeV. Figure 13 compares our analytic results with the lattice data. The propagators are normalized as follows:

$${\overline{D}}_{E/M}({\mu }_q,T)\equiv {\displaystyle \frac{D_{E/M}({\mu }_q,T)}{D_{E/M}({\mu }_q,T^{*})}},T^{*}=44\mathrm{MeV}.$$

(45)

Here, we show the results for $m_g=500$ MeV, with the range of ${\alpha }_s^q$ varied between 0.5 and 2.0, as in the previous analyses.

For ${\mu }_q=0$, the electric propagators in the lattice data show a slightly stronger suppression than in our analytic results. This discrepancy becomes less pronounced if we reduce the value of $m_g$, so we consider it to lie within the range of theoretical uncertainties. The magnetic propagators, on the other hand, are well reproduced across the entire temperature range studied.

Next, we turn to the ${\mu }_q=705$ MeV case. The electric propagators show good consistency between the analytic and lattice results. In contrast, the magnetic propagators exhibit a sizable discrepancy at $|\overrightarrow{k}|=0$, for which we currently have no clear explanation. This suggests that computations beyond one-loop order or genuinely non-perturbative effects may be required. Meanwhile, the analytic and lattice results are in good agreement for $|\overrightarrow{k}|\gtrsim 500$ MeV.

8.2. Density Evolution at $T=44$ MeV and $T=118$ MeV

Here, we examine the density evolution of the propagators at fixed temperatures, $T=44$ MeV and $T=118$ MeV. Shown in Figure 14 are comparisons between the analytic results and lattice data. Here, the propagators are normalized as follows:

$${\overline{D}}_{E/M}({\mu }_q,T)\equiv {\displaystyle \frac{D_{E/M}({\mu }_q,T)}{D_{E/M}({\mu }_q^{*},T)}},{\mu }_q^{*}=0.$$

(46)

First, we consider the $T=44$ MeV results. In the lattice data, the electric propagators at ${\mu }_q=423$ and 564 MeV show an enhancement at low momenta, but we suspect that this feature is simply due to statistical fluctuations (see also Figure 11). For ${\mu }_q=282$ and 705 MeV, the analytic results are consistent with the lattice data at $|\overrightarrow{k}|$∼0 but remain slightly smaller than the lattice values for $|\overrightarrow{k}|\gtrsim$ MeV. This tension can be alleviated by increasing $m_g$. Taking these observations together, we conclude that the agreement between the analytic and lattice results at $T=44$ MeV is acceptable.

As for the magnetic propagators at finite momenta, we observe a significant quark contribution through paramagnetic enhancement, which grows with increasing ${\mu }_q$. It is important to note that choosing too large a value of ${\alpha }_s^q$ leads to a serious disagreement between the analytic and lattice results. Furthermore, extrapolating the one-loop results with fixed ${\alpha }_s^q$ to very high density eventually causes chromo-magnetic instability [92,93], which has been extensively discussed in the context of gapless color superconductivity [94,95]. A possible way to avoid such an instability is to invoke a “gluon saturation” mechanism, as in the Gribov–Zwanziger model [84,85], which would drive $m_g$ to increase with ${\mu }_q$ before the paramagnetic enhancement causes the instability. This conceptual issue, however, lies beyond the scope of the present paper.

Now, we turn to the case of $T=118$ MeV. Our analytic results show substantially weaker electric screening compared to the lattice results. This discrepancy may be understood as follows. As mentioned earlier, the $\Delta$ and the superfluid critical temperature $T_s$ in our PNJL model are about 1.2–1.5 times larger than those inferred from the lattice. Consequently, while $T=118$ MeV lies slightly above the lattice $T_s$, it is still smaller than our model’s $T_s$ by about 20–50 MeV. To examine how this discrepancy affects the results, we compute the analytic propagators with fixed values of $\Delta$ of $\Delta =10$ and 100 MeV while determining $(\Phi ,M_q)$ self-consistently from the gap equation. The corresponding results are shown in Figure 15. Using smaller $\Delta$ than predicted in our PNJL model enhances electric screening and hence suppresses the propagators, thereby improving agreement with the lattice data.

For the magnetic propagators at $T=118$ MeV, the agreement with the lattice results is generally good, as shown in Figure 14 and Figure 15. We also notice that reducing $\Delta$ slightly weakens the paramagnetic enhancement at finite $|\overrightarrow{k}|$.

9. Discussion and Summary

In this paper, we delineate the role of thermal quarks in dense QC₂D and their impact on gluon dynamics, focusing specifically on the Polyakov loop and gluon propagators.

Our initial approach was to start from the massive gluon propagators constrained by lattice data and then use them to compute the Polyakov loop potential. However, the resulting potential for the pYM turns out to be too flat; the inclusion of quark contributions drastically deforms the structure of the Polyakov loop potential, leading to an overly rapid deconfinement that disagrees with lattice QCD results. We therefore speculate that the massive gluons appearing in the propagators and those responsible for confinement (the Polyakov loop potential) are somewhat distinct: the former corresponds to excitations above the confining vacuum, while the gluons forming the Polyakov loop potential are not like quasi-particles and appear to be more robust against quark-induced perturbations.

To investigate the nature of thermal excitations in dense matter, we employ phenomenological Polyakov loop potentials used in the literature and examine their correlation with thermal quarks in a manner similar to the PNJL and PQM models. We tune our setup to be consistent with lattice results; in particular, we adjust our model parameters to reproduce a pion mass of $m_{\pi }$∼640 MeV and introduce a finite diquark source term, ${\Delta }_{\mathrm{ex}}=45$ MeV, which is commonly used to stabilize lattice simulations. The renormalization of the Polyakov loop is also taken into account.

After calibrating our model to reproduce lattice results at ${\mu }_q=0$, we study the Polyakov loop at finite ${\mu }_q$ and find reasonable agreement with the lattice data. Achieving this agreement requires a diquark gap of $\Delta$∼200–300 MeV and a finite ${\Delta }_{\mathrm{ex}}$. If $\Delta$ is artificially set to zero, the Polyakov loop reaches the deconfined solution too rapidly due to the large abundance of gapless quarks.

We next delineate in-medium gluon propagators in the Landau–DeWitt gauge. At the one-loop level, it is known that at zero temperature, the color-singlet diquark gap protects gluons from screening by quarks. Thermal quarks overcoming the gap energy contribute to the screening as in the normal phase; hence, the thermal modifications of the gluon mass can be used to study the nature of thermal excitations and how confinement affects them.

The Polyakov loop effects quenches the colored quarks and suppresses their contributions to the screening. These confining effects are important at the lowest temperature measured on the lattice, T∼44 MeV, and should be taken into account when confronting theoretical computations with the lattice data. The thermal evolution of the screening masses at various ${\mu }_q$ appears reasonably consistent with the lattice results for the range of our parameters, ${\alpha }_s^q=0.5$–2.0 and $m_g=400$–500 MeV.

Overall, our analyses with the current lattice data suggest that thermal colored excitations in dense two-color QCD matter are strongly suppressed. In the $\Phi =1$ case, the electric screening grows too rapidly compared to lattice results, unless $\Delta$ is considerably larger than ∼200 MeV (this is unlikely however), allowing thermal quarks to be effectively neglected even without Polyakov loop suppression. Including the Polyakov loop increases the minimum excitation from ∼$\Delta$ to ∼$2\Delta$, corresponding to the energy scale of baryonic (diquark) excitations.

To draw more definitive conclusions about confinement and deconfinement in dense QC₂D matter, however, lattice data with smaller statistical fluctuations and better-controlled finite-volume and lattice-spacing effects are called for. On the theoretical side, the analytic computations should be improved by including higher-order loop corrections and genuinely non-perturbative effects.

While this work focuses on the proof of principle about confinement/deconfinement in dense quark matter, ultimately, the framework should be applied to three-color QCD. The quark back reaction to the gluon sector highly depends on the phase structure. For instance, in the case of the color-flavor-locked phase, there are both Debye and Meissner masses with which both electric and magnetic gluons are screened. Another probability, as suggested in the quarkyonic mater scenario, is that the Fermi surface is dominated by color-singlet composites which do not strongly screen gluons, as in the color-singlet diquarks in QC₂D. These physics, dependent on the phase structure, are left for future studies.