Evaluating Gaia Astrometric Quality and Distances for Galactic Hot Supergiants
Abstract
1. Introduction
2. Materials and Methods
2.1. Distance Determination Pipeline
2.1.1. Object Identification and Data Retrieval
Cone Searches and Source Association
2.1.2. Parallax Processing and Error Recalibration
Zero-Point Correction
RUWE-Based Uncertainty Inflation
Catalogue Choice (DR3 vs. EDR3)
Implementation Notes
2.1.3. Bayesian Distance Inference
2.1.4. Quality Control and Final Distance Adoption
- The new Bayesian distance is preferred if it meets strict quality standards:
- The parallax signal-to-noise ratio () is .
- The relative distance error is .
- Key Gaia quality metrics are nominal (e.g., and the source is not flagged as duplicated).
- Otherwise, the old Bailer-Jones et al. [29] distance is used as a fallback, provided its relative error does not exceed 60%.
- If neither estimate is reliable, the value with the smaller relative error is adopted, but it is flagged as having low quality.
Code Availability
3. Results
3.1. Overview of the Sample
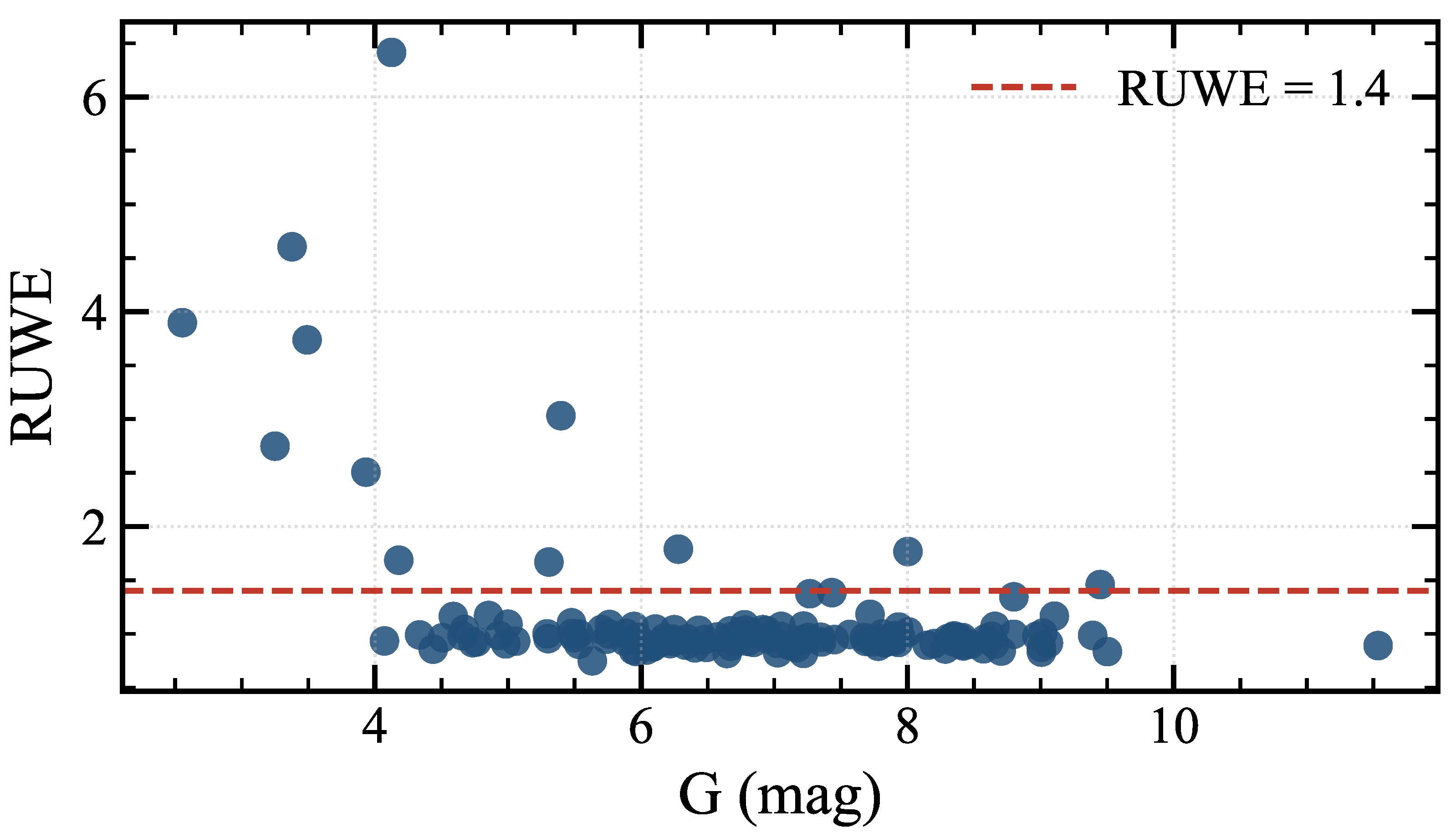
3.2. Astrometric Quality of the Sample
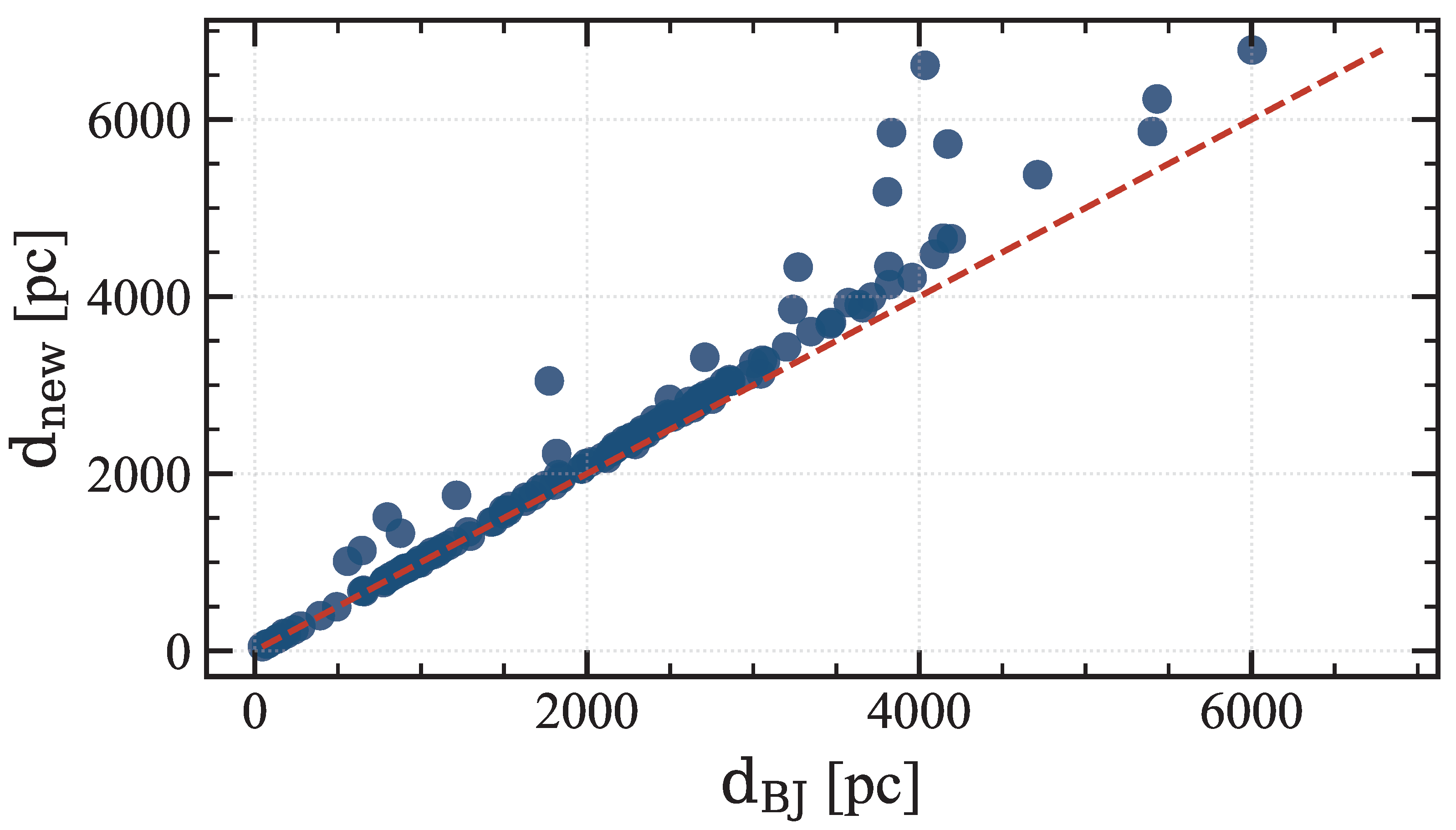
3.3. Recomputed Distances Versus Bailer-Jones
3.4. Comparison with Previous Works
3.5. Adoption Outcomes
3.6. Outliers and Informative Counterexamples
3.7. Tables and Recommended Usage
4. Conclusions
- Operational quantity. RUWE is a diagnostic, but adoption is governed by the effective information content computed after all corrections.
- Agreement at high S/N. For informative parallaxes (large ), the recalculated distances closely match Bailer-Jones values ; differences are dominated by ZP shifts and slightly broader posteriors.
- Intermediate regime. At , we find modest, interpretable offsets (typically ∼10–30% at large distances) arising from the combination of ZP, catalogue choice, and the EDSD prior.
- Low-information cases. For or problematic Gaia QC, the posterior becomes prior-dominated and we do not adopt , reverting to .
- Adoption logic. We adopt only when (i) , (ii) , and (iii) Gaia QC is satisfactory; otherwise, we label the entry BJ_old and record the cause in quality_note.
- Practical outcome. The catalogue provides one adopted distance per star with transparent flags and uncertainties, enabling safe propagation to absolute magnitudes, luminosities, and radii while avoiding overconfident inferences for high-RUWE/low-S/N objects.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HRD | Hertzsprung–Russell diagram |
| RUWE | Renormalised Unit Weight Error |
| MCMC | Markov-Chain Monte-Carlo |
| EDSD | Exponentially decreasing space density |
| SNR | Signal to noise ratio |
| ZP | Zero-point |
Appendix A
| N | Name | [pc] [29] | [pc] | RUWE | G [mag] | [pc] | [pc] | L [pc] | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | HD 1070 | 2516.03 | 97.81 | 0.92 | 7.83 | 2641.01 | 174.85 | 15.32 | 2012.80 |
| 2 | BD+60 51 | 3638.11 | 126.18 | 0.83 | 9.01 | 3909.82 | 385.57 | 10.46 | 2500.00 |
| 3 | HD 2928 | 3470.70 | 203.04 | 0.90 | 8.42 | 3707.81 | 346.55 | 11.02 | 2500.00 |
| 4 | HD 3283 | 905.65 | 23.96 | 1.04 | 5.70 | 924.96 | 34.35 | 26.96 | 724.52 |
| 5 | V755 Cas | 3003.46 | 119.14 | 0.82 | 7.03 | 3246.23 | 265.09 | 12.53 | 2402.77 |
| 6 | BD+61 153 | 2678.26 | 91.62 | 0.98 | 8.97 | 2836.91 | 201.97 | 14.28 | 2142.61 |
| 7 | HD 4717 | 2649.40 | 115.80 | 0.94 | 7.87 | 2790.89 | 195.42 | 14.51 | 2119.52 |
| 8 | HD 4841 | 2865.90 | 126.44 | 0.98 | 6.69 | 3044.85 | 232.95 | 13.33 | 2292.72 |
| 9 | HD 5776 | 2762.44 | 144.38 | 0.97 | 7.89 | 2928.01 | 215.26 | 13.85 | 2209.95 |
| 10 | HD 7902 | 2486.87 | 93.87 | 0.92 | 6.84 | 2671.20 | 178.88 | 15.15 | 1989.50 |
| 11 | HD 7720 | 2689.60 | 102.29 | 0.92 | 8.65 | 2848.03 | 203.57 | 14.23 | 2151.68 |
| 12 | HD 8065 | 1422.80 | 77.63 | 0.85 | 5.94 | 1454.44 | 96.62 | 15.27 | 1138.24 |
| 13 | BD+62 246 | 2755.14 | 117.73 | 0.93 | 8.40 | 2902.38 | 211.49 | 13.97 | 2204.11 |
| 14 | HD 9233 | 3055.95 | 175.56 | 0.88 | 7.78 | 3281.61 | 270.98 | 12.40 | 2444.76 |
| 15 | HD 9311 | 2682.46 | 126.20 | 0.93 | 7.17 | 2853.45 | 204.34 | 14.20 | 2145.97 |
| 16 | HD 9811 | 2489.39 | 101.69 | 0.93 | 6.16 | 2630.70 | 173.47 | 15.37 | 1991.51 |
| 17 | HD 15316 | 2392.85 | 118.71 | 1.03 | 6.94 | 2533.83 | 179.86 | 14.32 | 1914.28 |
| 18 | HD 62888 | 3573.01 | 268.11 | 1.18 | 7.72 | 3931.83 | 737.39 | 5.97 | 2500.00 |
| 19 | BD+60 331 | 2672.52 | 97.41 | 0.98 | 8.63 | 2800.26 | 196.76 | 14.47 | 2138.02 |
| 20 | BD+60 333 | 2764.91 | 134.23 | 1.07 | 8.66 | 2898.32 | 232.99 | 12.73 | 2211.93 |
| 21 | BD+60 339 | 2636.87 | 103.49 | 0.86 | 8.29 | 2744.04 | 188.88 | 14.76 | 2109.49 |
| 22 | V819 Cas | 2712.90 | 129.14 | 0.82 | 6.65 | 2886.33 | 209.12 | 14.05 | 2170.32 |
| 23 | BD+56 386 | 658.79 | 11.91 | 0.96 | 7.68 | 668.68 | 15.06 | 44.27 | 527.03 |
| 24 | HD 11831 | 2857.63 | 132.35 | 0.92 | 7.74 | 3061.94 | 235.58 | 13.26 | 2286.11 |
| 25 | 53 Cas | 904.55 | 36.27 | 1.00 | 5.48 | 923.89 | 41.38 | 22.42 | 723.64 |
| 26 | V472 Per | 2495.27 | 331.56 | 1.10 | 5.48 | 2838.95 | 655.00 | 5.17 | 1996.22 |
| 27 | HD 13476 | 2333.18 | 109.95 | 1.04 | 6.25 | 2493.47 | 187.99 | 13.52 | 1866.55 |
| 28 | HD 13744 | 2309.02 | 99.28 | 0.93 | 7.35 | 2436.47 | 148.65 | 16.57 | 1847.22 |
| 29 | HD 14010 | 2358.87 | 86.65 | 0.96 | 6.94 | 2457.91 | 151.30 | 16.43 | 1887.09 |
| 30 | HD 14322 | 2316.43 | 93.66 | 0.93 | 6.69 | 2443.34 | 149.50 | 16.53 | 1853.14 |
| 31 | HD 14433 | 2094.68 | 82.48 | 0.95 | 6.23 | 2184.89 | 119.40 | 18.45 | 1675.74 |
| 32 | V474 Per | 1297.55 | 144.55 | 0.93 | 5.06 | 1294.72 | 139.53 | 9.709 | 1038.04 |
| 33 | V553 Per | 2439.60 | 106.20 | 1.07 | 7.22 | 2586.58 | 211.78 | 12.504 | 1951.68 |
| 34 | HD 14542 | 2143.04 | 99.86 | 0.93 | 6.80 | 2244.92 | 126.08 | 17.961 | 1714.43 |
| 35 | HD 14899 | 2166.67 | 86.64 | 0.97 | 7.26 | 2278.07 | 132.39 | 17.374 | 1733.33 |
| 36 | V425 Per | 2502.90 | 131.77 | 0.99 | 6.78 | 2659.64 | 177.33 | 15.210 | 2002.32 |
| 37 | HD 15620 | 2256.84 | 107.41 | 1.02 | 8.01 | 2344.08 | 153.33 | 15.496 | 1805.47 |
| 38 | HD 16778 | 2416.62 | 117.91 | 0.97 | 7.35 | 2540.80 | 161.74 | 15.906 | 1933.30 |
| 39 | HD 236995 | 2248.83 | 94.23 | 0.97 | 8.34 | 2390.97 | 143.11 | 16.881 | 1799.06 |
| 40 | HD 17088 | 2708.47 | 248.03 | 1.37 | 7.27 | 3315.13 | 879.98 | 4.636 | 2166.78 |
| 41 | HD 17145 | 2224.57 | 91.21 | 0.95 | 7.81 | 2376.82 | 146.03 | 16.46 | 1779.66 |
| 42 | V480 Per | 2173.80 | 136.90 | 1.01 | 5.89 | 2292.00 | 168.91 | 13.82 | 1739.04 |
| 43 | HD 20041 | 924.89 | 45.72 | 1.00 | 5.53 | 939.27 | 53.42 | 17.75 | 739.91 |
| 44 | CS Cam | 972.28 | 113.12 | 0.93 | 4.07 | 983.37 | 130.80 | 8.06 | 777.83 |
| 45 | CE Cam | 1067.36 | 125.38 | 0.99 | 4.34 | 1113.95 | 152.70 | 7.84 | 853.89 |
| 46 | HD 237153 | 2269.98 | 57.80 | 1.00 | 8.80 | 2414.17 | 145.92 | 16.72 | 1815.98 |
| 47 | BD+55 838 | 4143.10 | 183.91 | 0.87 | 9.01 | 4659.88 | 548.23 | 8.83 | 2500.00 |
| 48 | AZ CMi | 148.30 | 1.09 | 1.03 | 6.43 | 148.66 | 1.58 | 93.47 | 300.00 |
| 49 | HD 19978 | 78.93 | 0.98 | 3.03 | 5.40 | 79.65 | 3.76 | 21.37 | 300.00 |
| 50 | BD+43 1168 | 3816.67 | 183.15 | 1.01 | 9.02 | 4340.53 | 475.59 | 9.46 | 2500.00 |
| 51 | 19 Aur | 1164.20 | 144.37 | 0.98 | 4.93 | 1189.11 | 138.46 | 9.05 | 931.36 |
| 52 | HD 35600 | 880.38 | 29.83 | 0.75 | 5.63 | 901.34 | 36.32 | 24.87 | 704.31 |
| 53 | HD 248587 | 2405.98 | 131.82 | 0.93 | 7.69 | 2608.82 | 193.46 | 13.73 | 1924.78 |
| 54 | HD 39970 | 1748.44 | 89.53 | 0.93 | 5.88 | 1866.62 | 124.42 | 15.21 | 1398.76 |
| 55 | HD 40297 | 1845.22 | 79.19 | 0.87 | 7.17 | 1945.99 | 100.82 | 19.43 | 1476.18 |
| 56 | HD 40589 | 1632.58 | 92.97 | 1.07 | 5.95 | 1734.28 | 148.78 | 11.97 | 1306.06 |
| 57 | HD 42400 | 1513.45 | 62.08 | 1.09 | 6.78 | 1589.54 | 114.39 | 14.14 | 1210.76 |
| 58 | HD 253250 | 2613.94 | 143.99 | 1.17 | 9.10 | 2815.77 | 314.09 | 9.39 | 2091.15 |
| 59 | 9 Gem | 1713.19 | 98.60 | 1.05 | 6.11 | 1823.50 | 144.99 | 12.86 | 1370.55 |
| 60 | HD 43910 | 2023.94 | 102.62 | 0.95 | 7.21 | 2133.92 | 126.73 | 17.01 | 1619.15 |
| 61 | 13 Mon | 816.45 | 82.32 | 0.86 | 4.44 | 833.54 | 78.71 | 10.95 | 653.16 |
| 62 | HR 2409 | 773.37 | 51.53 | 1.00 | 5.76 | 770.03 | 51.40 | 15.20 | 618.70 |
| 63 | HD 46783 | 1842.53 | 69.05 | 0.98 | 7.95 | 1963.23 | 102.94 | 19.20 | 1474.03 |
| 64 | HD 48452 | 4192.87 | 360.64 | 0.97 | 8.41 | 4652.44 | 613.30 | 7.96 | 2500.00 |
| 65 | MWC 536 | 4711.58 | 538.24 | 0.93 | 7.90 | 5375.84 | 852.42 | 6.66 | 2500.00 |
| 66 | HD 55036 | 3346.96 | 250.72 | 1.04 | 6.91 | 3604.67 | 383.99 | 9.77 | 2500.00 |
| 67 | HD 58439 | 3045.25 | 296.61 | 0.96 | 6.17 | 3127.35 | 304.66 | 10.64 | 2436.20 |
| 68 | HD 59612 | 1283.74 | 117.67 | 0.93 | 4.77 | 1343.25 | 137.62 | 10.15 | 1026.99 |
| 69 | HR 3183 | 493.17 | 14.64 | 0.96 | 5.30 | 496.66 | 16.58 | 29.95 | 394.54 |
| 70 | HR 3345 | 393.84 | 5.62 | 1.03 | 6.67 | 397.42 | 7.05 | 56.19 | 315.07 |
| 71 | HD 164865 | 1498.81 | 47.44 | 0.82 | 7.22 | 1546.98 | 60.48 | 25.62 | 1199.05 |
| 72 | HD 165784 | 1496.85 | 94.48 | 0.89 | 6.10 | 1586.69 | 101.20 | 15.88 | 1197.48 |
| 73 | V4387 Sgr | 1967.68 | 165.63 | 0.84 | 5.96 | 2052.42 | 188.85 | 11.22 | 1574.14 |
| 74 | HD 167838 | 1675.29 | 66.41 | 0.97 | 6.57 | 1751.84 | 100.29 | 17.63 | 1340.23 |
| 75 | BD-12 4970 | 1994.59 | 90.17 | 0.96 | 8.30 | 2114.58 | 112.15 | 18.99 | 1595.67 |
| 76 | AS 314 | 1620.24 | 30.77 | 0.84 | 9.50 | 1688.66 | 71.18 | 23.79 | 1296.19 |
| 77 | HD 175687 | 655.83 | 62.98 | 0.91 | 4.98 | 682.96 | 44.14 | 15.68 | 524.67 |
| 78 | HD 332757 | 5402.02 | 523.13 | 0.91 | 8.20 | 5863.48 | 864.09 | 7.05 | 2500.00 |
| 79 | HT Sge | 2168.42 | 120.57 | 0.93 | 6.25 | 2307.81 | 152.49 | 15.34 | 1734.74 |
| 80 | HR 7699 | 1204.73 | 32.14 | 0.88 | 6.09 | 1233.24 | 43.72 | 28.23 | 963.78 |
| 81 | 42 Cyg | 1128.54 | 24.61 | 0.95 | 5.74 | 1155.33 | 37.00 | 31.21 | 902.83 |
| 82 | 55 Cyg | 1827.14 | 265.45 | 1.04 | 4.67 | 1988.52 | 416.10 | 5.58 | 1461.72 |
| 83 | HD 199478 | 2423.10 | 222.36 | 0.90 | 5.53 | 2566.64 | 286.47 | 9.39 | 1938.48 |
| 84 | 9 Cep | 996.03 | 84.07 | 0.98 | 4.65 | 993.88 | 105.73 | 9.82 | 796.82 |
| 85 | Nu Cep | 994.02 | 14.86 | 0.89 | 11.54 | 1022.91 | 26.07 | 39.15 | 795.22 |
| 86 | HD 207673 | 1524.55 | 35.04 | 0.95 | 6.34 | 1579.30 | 62.23 | 25.42 | 1219.64 |
| 87 | 13 Cep | 1076.95 | 43.92 | 0.96 | 5.50 | 1088.93 | 46.18 | 23.65 | 861.56 |
| 88 | HD 209900 | 3659.71 | 176.50 | 0.86 | 8.57 | 3873.49 | 378.40 | 10.56 | 2500.00 |
| 89 | V399 Lac | 2289.32 | 173.34 | 0.85 | 6.04 | 2330.67 | 199.96 | 11.97 | 1831.46 |
| 90 | HD 239886 | 3463.39 | 178.85 | 0.90 | 8.48 | 3688.59 | 342.95 | 11.07 | 2500.00 |
| 91 | HD 239895 | 3712.42 | 302.20 | 0.89 | 8.15 | 3993.59 | 402.36 | 10.25 | 2500.00 |
| 92 | HD 211971 | 1104.51 | 17.89 | 0.95 | 6.48 | 1117.52 | 31.12 | 35.85 | 883.61 |
| 93 | 4 Lac | 785.87 | 50.84 | 0.96 | 4.51 | 793.63 | 57.16 | 14.14 | 628.70 |
| 94 | HD 239950 | 3956.84 | 187.56 | 0.99 | 9.39 | 4214.75 | 448.35 | 9.73 | 2500.00 |
| 95 | HD 213470 | 3819.55 | 215.93 | 0.87 | 6.49 | 4135.61 | 431.61 | 9.91 | 2500.00 |
| 96 | BD+62 2210 | 2643.54 | 99.68 | 0.98 | 7.91 | 2774.32 | 193.10 | 14.60 | 2114.83 |
| 97 | BD+60 2542 | 3073.78 | 141.42 | 0.95 | 8.59 | 3268.04 | 268.75 | 12.45 | 2459.02 |
| 98 | BD+61 2472 | 2574.31 | 72.51 | 0.92 | 9.06 | 2694.84 | 182.11 | 15.02 | 2059.45 |
| 99 | HD 22227 | 979.64 | 19.75 | 0.87 | 6.40 | 991.69 | 24.50 | 40.38 | 783.71 |
| 100 | 6 Cas | 2319.84 | 330.23 | 1.00 | 5.29 | 2460.86 | 427.28 | 6.45 | 1855.87 |
| 101 | BD+62 2313 | 2750.29 | 83.12 | 0.84 | 8.70 | 2841.36 | 202.64 | 14.26 | 2200.24 |
| 102 | HD 223767 | 2858.64 | 126.34 | 0.91 | 7.02 | 3042.45 | 232.58 | 13.34 | 2286.91 |
| 103 | HD 186745 | 1968.87 | 64.68 | 0.89 | 6.67 | 2057.47 | 105.81 | 19.57 | 1575.10 |
| 104 | HD 184943 | 4090.44 | 235.91 | 0.92 | 7.93 | 4478.59 | 506.39 | 9.17 | 2500.00 |
| 105 | HD 161695 | 1800.44 | 82.27 | 0.91 | 6.22 | 1872.66 | 103.81 | 18.19 | 1440.35 |
| 106 | HD 43820 | 190.69 | 0.95 | 0.98 | 8.35 | 191.53 | 1.13 | 168.50 | 300.00 |
| 107 | HD 17086 | 780.54 | 10.08 | 0.90 | 6.33 | 792.66 | 15.65 | 50.49 | 624.43 |
| 108 | HD 17857 | 2331.07 | 81.29 | 0.95 | 7.45 | 2435.92 | 148.59 | 16.58 | 1864.86 |
| 109 | HD 216912 | 235.09 | 1.67 | 0.98 | 7.05 | 235.59 | 2.06 | 113.64 | 300.00 |
| 110 | HD 13717 | 1044.92 | 27.13 | 1.00 | 7.81 | 1070.89 | 34.73 | 30.83 | 835.93 |
| 111 | HD 28747 | 843.69 | 19.28 | 1.00 | 7.57 | 861.97 | 20.64 | 41.66 | 674.95 |
| 112 | BD+60 2582 | 2972.21 | 124.72 | 0.92 | 8.35 | 3115.06 | 243.96 | 13.04 | 2377.77 |
| 113 | HD 58131 | 3200.86 | 241.41 | 0.94 | 7.23 | 3431.40 | 381.71 | 9.41 | 2500.00 |
| 114 | HD 47314 | 902.82 | 26.91 | 0.89 | 8.42 | 931.36 | 34.07 | 27.36 | 722.25 |
| 115 | HD 58585 | 1437.45 | 40.42 | 0.97 | 5.97 | 1460.79 | 56.71 | 25.80 | 1149.96 |
| 116 | HD 58764 | 2119.39 | 88.52 | 0.89 | 7.12 | 2173.08 | 119.64 | 18.31 | 1695.52 |
| 117 | 44 Cas | 277.18 | 2.87 | 1.09 | 5.76 | 279.25 | 6.02 | 46.27 | 300.00 |
| 118 | GQ Cam | 5431.24 | 614.88 | 0.93 | 7.84 | 6232.23 | 972.80 | 6.64 | 2500.00 |
| 119 | CMa | 131.01 | 0.35 | 0.96 | 8.38 | 131.05 | 0.46 | 283.79 | 300.00 |
| N | Name | [pc] [29] | [pc] | RUWE | G [mag] | [pc] | [pc] | L [pc] | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Cas | 4171.53 | 1012.79 | 0.92 | 4.74 | 5723.41 | 2433.01 | 2.63 | 2500.00 |
| 2 | Cyg | 876.46 | 111.66 | 1.69 | 4.18 | 1328.49 | 697.28 | 2.49 | 701.17 |
| 3 | HD 10756 | 3238.28 | 247.73 | 1.38 | 7.43 | 3855.04 | 1062.31 | 4.51 | 2500.00 |
| 4 | Aql | 70.39 | 2.69 | 2.75 | 3.25 | 75.60 | 11.64 | 7.44 | 300.00 |
| 5 | 5 Per | 1816.45 | 108.88 | 1.79 | 6.28 | 2227.79 | 690.05 | 4.18 | 1453.16 |
| 6 | HD 55493 | 6002.90 | 692.51 | 1.06 | 7.93 | 6784.44 | 1463.86 | 4.81 | 2500.00 |
| 7 | V455 Cep | 3270.64 | 325.32 | 1.77 | 8.00 | 4332.08 | 1694.60 | 3.42 | 2500.00 |
| 8 | 67 Oph | 797.18 | 162.31 | 2.51 | 3.93 | 1510.49 | 879.10 | 1.33 | 637.74 |
| 9 | Leo | 558.27 | 86.20 | 3.74 | 3.49 | 1011.80 | 562.32 | 1.62 | 446.61 |
| 10 | HD 187982 | 1772.63 | 365.72 | 1.67 | 5.31 | 3047.79 | 1693.48 | 1.63 | 1418.10 |
| 11 | Tau | 45.84 | 0.89 | 4.61 | 3.38 | 46.80 | 3.55 | 13.61 | 300.00 |
| 12 | o Sco | 175.54 | 7.11 | 6.42 | 4.12 | 195.87 | 39.63 | 6.02 | 300.00 |
| 13 | Aur | 1213.98 | 299.79 | 1.16 | 4.59 | 1755.71 | 940.05 | 2.53 | 971.18 |
References
- Vink, J.S.; Brott, I.; Gräfener, G.; Langer, N.; de Koter, A.; Lennon, D.J. The nature of B supergiants: Clues from a steep drop in rotation rates at 22 000 K. The possibility of bi-stability braking. Astron. Astrophys. 2010, 512, L7. [Google Scholar] [CrossRef]
- Kudritzki, R.-P.; Puls, J. Winds from Hot Stars. Annu. Rev. Astron. Astrophys. 2000, 38, 613–666. [Google Scholar] [CrossRef]
- Meynet, G.; Kudritzki, R.-P.; Georgy, C. The flux-weighted gravity–luminosity relationship of blue supergiant stars as a constraint for stellar evolution. Astron. Astrophys. 2015, 581, A36. [Google Scholar] [CrossRef]
- Vaidman, N.L.; Khokhlov, S.A.; Agishev, A.T. Unveiling the Evolution of MWC 728: Non-Conservative Mass Transfer in an FS CMa Binary. Galaxies 2025, 13, 78. [Google Scholar] [CrossRef]
- Nurmakhametova, S.T.; Vaidman, N.L.; Miroshnichenko, A.S.; Khokhlov, A.A.; Agishev, A.T.; Yermekbayev, B.S.; Danford, S.; Aarnio, A.N. HR 4049: A Spectroscopic Analysis of a Post-AGB Object. Galaxies 2025, 13, 26. [Google Scholar] [CrossRef]
- Walborn, N.R.; Nichols-Bohlin, J. Ultraviolet spectral morphology of the O stars. IV. The OB supergiant sequence. Publ. Astron. Soc. Pac. 1987, 99, 40–53. [Google Scholar] [CrossRef]
- Kudritzki, R.P.; Bresolin, F.; Przybilla, N. A New Extragalactic Distance Determination Method Using the Flux-weighted Gravity of Late B and Early A Supergiants. Astrophys. J. 2003, 582, L83. [Google Scholar] [CrossRef]
- Verdugo, E.; Talavera, A.; Gómez de Castro, A.I. Spectroscopic properties of early-type supergiants. I. Astron. Astrophys. Suppl. Ser. 1999, 137, 351–364. [Google Scholar] [CrossRef]
- Verdugo, E.; Talavera, A.; Gómez de Castro, A.I. Spectroscopic properties of early-type supergiants. II. Astron. Astrophys. 1999, 346, 819–834. [Google Scholar]
- Firnstein, M.; Przybilla, N. Quantitative spectroscopy of Galactic BA-type supergiants. I. Atmospheric parameters. Astron. Astrophys. 2012, 543, A80. [Google Scholar] [CrossRef]
- Weßmayer, D.; Przybilla, N.; Butler, K. Quantitative spectroscopy of A-type supergiants. Astron. Astrophys. 2022, 688, A92. [Google Scholar] [CrossRef]
- de Burgos, A.; Simón-Díaz, S.; Urbaneja, M.A.; Negueruela, I. Building a Modern Empirical Database of Galactic O9–B9 Supergiants: Sample Selection, Description, and Completeness. Astron. Astrophys. 2023, 674, A212. [Google Scholar] [CrossRef]
- Miroshnichenko, A.S.; Chari, R.; Danford, S.; Prendergast, P.; Aarnio, A.N.; Andronov, I.L.; Chinarova, L.L.; Lytle, A.; Amantayeva, A.; Gabitova, I.A.; et al. Searching for Phase-Locked Variations of the Emission-Line Profiles in Binary Be Stars. Galaxies 2023, 11, 83. [Google Scholar] [CrossRef]
- Miroshnichenko, A.; Danford, S.; Verdugo, E.; Klochkova, V.G.; Chentsov, E.L.; Zharikov, S.V. Spectroscopic Criteria for Luminosity Calibration of Massive B5–A5 Stars. In Proceedings of the Conference “Massive Stars: From Alpha to Omega”, Rhodes, Greece, 10–14 June 2013; p. 169. Available online: https://ui.adsabs.harvard.edu/abs/2013msao.confE.169M (accessed on 25 October 2025).
- Kovtyukh, V.V. High-Precision Effective Temperatures of 161 FGK Supergiants from Line-Depth Ratios. Mon. Not. R. Astron. Soc. 2007, 378, 617–624. [Google Scholar] [CrossRef]
- Arellano Ferro, A.; Giridhar, S.; Rojo Arellano, E. Spectroscopy of Galactic supergiants. Rev. Mex. Astron. Astrofis. 2003, 39, 3–15. [Google Scholar]
- Humphreys, R.M.; Davidson, K. Studies of luminous stars in nearby galaxies. III. Comments on the evolution of the most massive stars in the Milky Way and the Large Magellanic Cloud. Astrophys. J. 1979, 232, 409–420. [Google Scholar] [CrossRef]
- Vaidman, N.L.; Miroshnichenko, A.S.; Zharikov, S.V.; Khokhlov, S.A.; Agishev, A.T.; Yermekbayev, B.S. Fundamental Parameters and Evolutionary Scenario of HD 327083. Galaxies 2025, 13, 47. [Google Scholar] [CrossRef]
- Vaidman, N.L.; Nurmakhametova, S.T.; Miroshnichenko, A.S.; Khokhlov, S.A.; Agishev, A.T.; Khokhlov, A.A.; Ashimov, Y.K.; Yermekbayev, B.S. Determination of Orbital Parameters of Binary Star Systems Using the MCMC Method. Galaxies 2025, 13, 101. [Google Scholar] [CrossRef]
- Kochanek, C.S. A non-detection of red supergiant convection in Gaia. Mon. Not. R. Astron. Soc. 2023, 520, 3510–3513. [Google Scholar] [CrossRef]
- Beitia-Antero, L.; Gómez de Castro, A.I.; de la Fuente Marcos, R. High reddening patches in Gaia DR2. Possible artifacts or indication of star formation at the edge of the Galactic disk. Astron. Astrophys. 2020, 634, A33. [Google Scholar] [CrossRef]
- Castro-Ginard, A.; Penoyre, Z.; Casey, A.R.; Brown, A.G.A.; Belokurov, V.; Cantat-Gaudin, T.; Drimmel, R.; Fouesneau, M.; Khanna, S.; Kurbatov, E.P.; et al. Gaia DR3 detectability of unresolved binary systems. Astron. Astrophys. 2024, 688, A1. [Google Scholar] [CrossRef]
- Weßmayer, D.; Przybilla, N.; Ebenbichler, A.; Aschenbrenner, P.; Butler, K. The blue supergiant Sher 25 revisited in the Gaia era. Astron. Astrophys. 2023, 677, A175. [Google Scholar] [CrossRef]
- Smith, N.; Aghakhanloo, M.; Murphy, J.W.; Drout, M.R.; Stassun, K.G.; Groh, J.H. On the Gaia DR2 distances for Galactic luminous blue variables. Mon. Not. R. Astron. Soc. 2019, 488, 1760–1778. [Google Scholar] [CrossRef]
- Vink, J.S.; Oudmaijer, R.D. The Blue Supergiant Problem and the Main-Sequence Width. Galaxies 2025, 13, 19. [Google Scholar] [CrossRef]
- Crowther, P.A.; Lennon, D.J.; Walborn, N.R. Physical parameters and wind properties of Galactic early B supergiants. Astron. Astrophys. 2006, 446, 279–293. [Google Scholar] [CrossRef]
- Wenger, M.; Ochsenbein, F.; Egret, D.; Dubois, P.; Bonnarel, F.; Borde, S.; Genova, F.; Jasniewicz, G.; Laloë, S.; Lesteven, S.; et al. The SIMBAD astronomical database. The CDS reference database for astronomical objects. Astron. Astrophys. Suppl. Ser. 2000, 143, 9–22. [Google Scholar] [CrossRef]
- Ochsenbein, F.; Bauer, P.; Marcout, J. The VizieR database of astronomical catalogues. Astron. Astrophys. Suppl. Ser. 2000, 143, 23–32. [Google Scholar] [CrossRef]
- Bailer-Jones, C.A.L.; Rybizki, J.; Fouesneau, M.; Demleitner, M.; Andrae, R. VizieR Online Data Catalog: Distances to 1.47 Billion Stars in Gaia EDR3 (Bailer-Jones+, 2021). 2021. Available online: https://ui.adsabs.harvard.edu/abs/2021yCat.1352....0B (accessed on 20 October 2025).
- Vallenari, A. et al. [Gaia Collaboration] Gaia Data Release 3. Summary of the content and survey properties. Astron. Astrophys. 2023, 674, A1. [Google Scholar] [CrossRef]
- Brown, A.G.A. et al. [Gaia Collaboration] Gaia Early Data Release 3. Summary of the contents and survey properties. Astron. Astrophys. 2021, 649, A1. [Google Scholar] [CrossRef]
- Brown, A.G.A. et al. [Gaia Collaboration] VizieR Online Data Catalog: Gaia EDR3 (Gaia Collaboration, 2020). Astron. Astrophys. 2021, 649, A1, Erratum in Astron. Astrophys. 2021, 650, C3. [Google Scholar] [CrossRef]
- Ginsburg, A. et al. [Astroquery Collaboration]. astroquery: An Astronomical Web-querying Package in Python. Astron. J. 2019, 157, 98. [CrossRef]
- Price-Whelan, A.M. et al. [Astropy Collaboration]. The Astropy Project: Sustaining and Growing a Community-oriented Open-source Project and the Latest Major Release (v5.0) of the Core Package. Astrophys. J. 2022, 935, 167. [CrossRef]
- Lindegren, L.; Bastian, U.; Biermann, M.; Bombrun, A.; de Torres, A.; Gerlach, E.; Geyer, R.; Hernández, J.; Hilger, T.; Hobbs, D.; et al. Gaia Early Data Release 3. Parallax bias versus magnitude, colour, and position. Astron. Astrophys. 2021, 649, A4. [Google Scholar] [CrossRef]
- Groenewegen, M.A.T. The parallax zero-point offset from Gaia EDR3 data. Astron. Astrophys. 2021, 654, A20. [Google Scholar] [CrossRef]
- Fabricius, C.; Luri, X.; Arenou, F.; Babusiaux, C.; Helmi, A.; Muraveva, T.; Reyl’e, C.; Spoto, F.; Vallenari, A.; Antoja, T.; et al. Gaia Early Data Release 3. Catalogue validation. Astron. Astrophys. 2021, 649, A5. [Google Scholar] [CrossRef]
- El-Badry, K. How to use Gaia parallaxes for stars with poor astrometric fits. Open J. Astrophys. 2025, 8, 62. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vaidman, N.L.; Nurmakhametova, S.T.; Umirova, A.B.; Khokhlov, S.A.; Agishev, A.T.; Yermekbayev, B.S. Evaluating Gaia Astrometric Quality and Distances for Galactic Hot Supergiants. Universe 2025, 11, 359. https://doi.org/10.3390/universe11110359
Vaidman NL, Nurmakhametova ST, Umirova AB, Khokhlov SA, Agishev AT, Yermekbayev BS. Evaluating Gaia Astrometric Quality and Distances for Galactic Hot Supergiants. Universe. 2025; 11(11):359. https://doi.org/10.3390/universe11110359
Chicago/Turabian StyleVaidman, Nadezhda L., Shakhida T. Nurmakhametova, Aziza B. Umirova, Serik A. Khokhlov, Aldiyar T. Agishev, and Berik S. Yermekbayev. 2025. "Evaluating Gaia Astrometric Quality and Distances for Galactic Hot Supergiants" Universe 11, no. 11: 359. https://doi.org/10.3390/universe11110359
APA StyleVaidman, N. L., Nurmakhametova, S. T., Umirova, A. B., Khokhlov, S. A., Agishev, A. T., & Yermekbayev, B. S. (2025). Evaluating Gaia Astrometric Quality and Distances for Galactic Hot Supergiants. Universe, 11(11), 359. https://doi.org/10.3390/universe11110359






