Abstract
Recently, a link between gravitational tension (GT) and energy density via the Kretschmann scalar (KS) was proposed to construct regular black holes (RBHs) in pure Lovelock (PL) gravity. However, including a negative cosmological constant in PL gravity leads to a curvature singularity. Here, we choose the coupling constants such that the Lovelock equations admit an n-fold degenerate AdS vacuum (LnFDGS), allowing us to construct an RBH with , where the energy density is analogous to the previously mentioned model. To achieve this, we propose alternative definitions for both the KS and GT. We find that, for mass parameter values greater than the extremal value , our RBH solution becomes indistinguishable from the AdS vacuum black hole from inside the event horizon out to infinity. At small scales, quantum effects modify the geometry and thermodynamics, removing the singularity. Furthermore, due to the lack of analytical relationships between the event horizon, photon sphere, and shadow in LnFDGS, we propose a numerical method to represent these quantities.
1. Introduction
The detection of gravitational waves [1,2] has significantly strengthened the position of general relativity (GR), even surpassing its already well-established success at the Solar System scale [3]. Nevertheless, some inconsistencies in GR at quantum scales, along with the still unknown nature of dark energy and dark matter, have driven the scientific community to investigate modified theories of gravity. As a first example of these alternative frameworks, the Horndeski scalar–tensor theory [4] generalizes GR by introducing one or more scalar degrees of freedom. This theory is carefully constructed so that its equations of motion prevent the emergence of an unwanted extra degree of freedom, commonly referred to as a ‘ghost’, which would carry negative energy. As a second example, we consider the theories of gravity [5]. As noted in reference [6], this framework offers a gravitational alternative for a unified description of inflation, dark energy, and dark matter, without the need to manually introduce an inflaton field or additional dark components. It is also worth mentioning that black hole solutions have been studied within this theory [7].
In line with the previous paragraph, in recent decades, modified gravity theories predicting the existence of extra dimensions have also attracted significant attention. Although several experiments have attempted to test this hypothesis, extra dimensions have not yet been observed. As a result, any theory that incorporates extra dimensions must be consistent with general relativity in four dimensions. One such theory is Lovelock gravity. The Lagrangian of Lovelock gravity incorporates higher curvature terms as corrections to the Einstein–Hilbert action [8]. Additionally, Lovelock’s theories respect the core principles of general relativity; for instance, their equations of motion are of second order. It is worth noting that one particular case of Lovelock theories, namely, Einstein–Gauss–Bonnet gravity, has gained attention in recent years in the context of inflationary models and has been confronted with the GW170817 observational results [9,10].
On the other hand, it is well known that vacuum solutions describing black holes possess a physical singularity, referring to a location where curvature invariants diverge and the tidal forces near a black hole’s singularity become infinite, which can lead to the unbounded stretching of an object, a phenomenon known as spaghettification. One way to address the existence of physical singularities is to define appropriate forms for the matter sources in the energy–momentum tensor such that the central singularity is suppressed. Black holes that are free of a physical singularity are usually referred to as regular black holes (RBHs).
In recent years, the relationship between the gravitational tension associated with the Kretschmann scalar in the vacuum case and the energy density has been investigated to eliminate the existence of singularities. The Kretschmann scalar is an invariant associated with the measurement of tidal forces [11]. In a four-dimensional, vacuum, spherically symmetric space, this scalar is proportional to , leading to infinite tidal forces at the origin. Gravitational field tension in the spherically symmetric case is characterized by the curvature term given by the square root of the Kretschmann scalar of the vacuum solution: in . This correlation is logical, as the spacetime tension should increase with the mass of the vacuum source [12]. In this connection, as a way to address the problem of singularities while including an appropriate structure for the energy–momentum tensor, a higher-dimensional model was recently constructed in reference [13] for pure Lovelock (PL) gravity, where the energy density encodes the gravitational information of the vacuum solution through the Kretschmann scalar. Near the radial origin, where tidal forces and the gravitational tension in the vacuum solution diverge, the tidal forces in the model become finite. Specifically, the energy density is written as
with and a being constants. In summary, the model proposed in [13] is such that its energy density encodes the gravitational information of the vacuum solution. Thus, near the central singularity, where the gravitational tension and tidal forces of the vacuum black hole become infinite, the energy density of the model remains finite, suppressing the singularity and giving rise to a regular black hole (RBH). This model coincides with the RBH of Dymnikova [14] in the four-dimensional case. On the other hand, in a speculative sense, in four dimensions, this way of relating gravitational tension to energy density is analogous to the particle production ratio in the quantum Schwinger effect [15]. We can find studies related to this latter topic in references [12,16,17]. However, this is a topic that requires deeper investigation.
Since the origin of general relativity, there has been an interest in understanding the role of the cosmological constant. The observed accelerated expansion of the universe can be attributed to a small, yet strictly positive, four-dimensional cosmological constant of approximately [18]. Unfortunately, a positive cosmological constant introduces several technical complications. First, the presence of a positive cosmological constant leads to the existence of a cosmological horizon; thus, it prevents the definition of a proper asymptotic regime and complicates an unambiguous identification of a black hole’s ADM mass. Second, a positive cosmological constant is commonly linked to negative pressure, which implies thermodynamic instability.
During the last three decades, primarily due to the AdS/CFT conjecture, considering a negative cosmological constant has been of paramount interest in theoretical physics. From a theoretical point of view, considering asymptotically AdS spaces has advantages, such as the construction of a proper action principle—one that admits the definition of an asymptotic boundary where well-defined boundary conditions can be imposed and where unambiguous conserved charges can be computed.
Despite the above-mentioned issues regarding physical problems being addressed by including a negative cosmological constant, there has been little speculation in the literature about a possible negative numerical value for this constant. For example, references [19,20], using observations of stars near the Galactic Center, estimate a negative value for the cosmological constant, in [19], for anti-de Sitter spacetimes, corresponding to a negative term of approximately . The authors claim that this value is consistent with some ideas within the framework of a certain class of multidimensional string models. In [20], also using observations of stars near the Galactic Center, the orbital precession in the Reissner–Nordström–AdS solution is studied, obtaining values of . The authors state that their constraints on the cosmological constant are much weaker not only than their cosmological estimates but also than the constraints obtained from Solar System data.
In the context of this work, that is, within Lovelock theories, some authors assume that the coupling constants of the theory could be of the order of Planck scale quantities [21]. This makes sense if one considers that the theory might only be testable at high energies. As we will see in detail below, the zeroth-order coupling constant is proportional to the cosmological constant. Under this idea, a negative cosmological constant would be of the order of powers of the Planck length, . That is, an AdS radius on the order of the Planck length. However, there are also works that define intermediate energies as those which are weak enough to be testable at energy scales below the Planck scale, but still high enough to feel the effects of the higher-curvature terms in Lovelock theory [22]. Under this latter assumption, , with . That is, an AdS radius sufficiently larger than the Planck length, in order to satisfy what has been mentioned above.
When higher dimensions () are considered, several families of gravitational theories emerge that satisfy the same conditions of general relativity, such as second-order differential equations. Arguably, the simplest of these families is the d-dimensional Lovelock gravity, which corresponds to the addition of all of the lower-dimensional topological densities. General relativity corresponds to the simplest case.
A special case of Lovelock theories is pure Lovelock theory (PL) [23,24]. This theory considers only a single term in the Lagrangian. Related to those theories discussed above, a disadvantage of PL theory is that considering the presence of a negative cosmological constant in a spherically symmetric spacetime leads to the appearance of a curvature singularity [23]. This singularity is such that, although the metric tensor is regular for a radius greater than the event horizon, the Ricci and Kretschmann invariants diverge at a point within this location. This issue has not been extensively investigated; therefore, it may be related to a potential breakdown of spacetime. Thus, studying the recent analogy between gravitational tension and energy density, as carried out in [13], appears to be unfeasible within the framework of PL theory in the presence of a negative cosmological constant for the construction of RBH solutions.
To address the issue above—namely, the apparent impossibility of studying the recent analogy between gravitational tension and energy density in pure Lovelock theory under the influence of a negative cosmological constant—this work will take the following into account: One potential drawback of generic Lovelock gravity is the existence of multiple ground states, meaning more than one solution with constant curvature spaces, or equivalently, more than one potential effective cosmological constant [25]. These effective cosmological constants can be complex numbers, which can lead to instability of the ground states under dynamical evolution. To address this issue, one can choose the coupling constant in such a way that the equations of motion roughly take the form [26]. In this case, there is a single ground state, but it is n-fold degenerate with constant curvature. This scenario is referred to as Lovelock with an n-fold degenerate ground state (LnFDGS). This is also known as the degenerate vacuum. In the context of this work, this coupling constant structure allows for the observation of a single negative effective cosmological constant, which, among other things, has facilitated the development of techniques for determining conserved charges [27]. This also seems to make sense in the framework of the AdS/CFT correspondence, as two or more negative cosmological constants would lead to different asymptotic boundary structures for the same background; see some recent applications of LnFDGS theory in references [27,28,29,30,31,32].
PL has significant differences compared to the LnFDGS theory [26,27]. While PL considers only a single term from the Lovelock series, LnFDGS includes all the terms from this series up to , where the square brackets represent the floor function. Moreover, PL cannot be factored into several equivalent negative effective cosmological constants, unlike LnFDGS. Remarkably, LnFDGS does not exhibit a curvature singularity of the type mentioned earlier. This offers the advantage of displaying a well-defined asymptotically AdS structure. In the context of this work, the absence of the aforementioned pathology in LnFDGS enables the construction of RBH solutions with a negative cosmological constant, allowing for the testing of the physical consequences of its presence from both geometric and thermodynamic perspectives.
On the other hand, it is well known that light is not directly observable at the event horizon of a black hole. Instead, what can be detected is the so-called shadow of a black hole, a dark region surrounded by light, resulting from gravitational lensing around the event horizon. One of the major achievements of the Event Horizon Telescope (EHT) collaboration has been the imaging of the shadows of the supermassive black holes M87 [33] and Sgr A [34]. It is worth mentioning that, given the theoretical interest driven by the presence of a negative cosmological constant, the study of shadows in an asymptotically AdS regime has also been explored in some references (see, for example, [35,36]). In this context, there has also been strong motivation, from a theoretical perspective, to study shadows in extra-dimensional scenarios; see, for example, reference [37] for scalar–tensor–vector theories, and reference [38] (and references therein) for rotating black hole shadows; see also [39]. As previously mentioned, the study of the physical properties of black holes in Lovelock gravity has attracted considerable attention in recent years [27,28,29,30,31,40,41]. Along this line, it is natural to investigate the physical properties of their shadows. It is worth noting that in reference [42], analytical relations were established for the photon sphere radius and the shadow radius of singular vacuum black holes in pure Lovelock (PL) gravity. However, for most specific cases within Lovelock theory, such analytical results are not attainable. Therefore, it is of physical interest to develop a numerical methodology for representing black hole shadows.
Regarding the points above, in this work, we provide a methodology to study the analogy between gravitational tension and energy density, aiming to construct regular black hole solutions in LnFDGS gravity in the presence of a negative cosmological constant. It is worth mentioning that directly relating the gravitational tension to the Kretschmann scalar of the vacuum LnFDGS solution, in the same way as for PL theory, is complicated because several additional terms would appear in the gravitational tension. Due to this, unlike [13], we define an alternative version of the Kretschmann scalar suitable for the LnFDGS AdS theory, and consequently, a redefinition of the gravitational tension. We test how the presence of the negative cosmological constant influences the obtained RBH solution, both in terms of its geometric and thermodynamic properties. Additionally, since it is not possible to find analytical relationships between the event horizon, the photon sphere radius, and the shadow size in LnFDGS, we propose a method to numerically and graphically obtain these relationships and analyze their physical behavior.
2. A Brief Revision of Lovelock Gravity with n-Fold Degenerate Ground State
Given that this family of theories is well known, it is only worthwhile recalling the features relevant for the discussion. First, the d-dimensional Lovelock (LL) Lagrangian is given by
where is the Riemann tensor, stands for the integer part of X, and is a set of dimensionful constants. As mentioned in the introduction, since they are dimensionful coupling constants, they can be defined such that they have units of [43]. Thus, it is possible to define , with having units of . Therefore, for , corresponding to the Einstein–Hilbert case, we have . The LL equations of motion can be written as
Here, denotes an n-th order generalization of the Einstein tensor, which is influenced by the order of the Riemann tensor of the Lagrangian L. For instance, represents the Einstein tensor associated with the Ricci scalar (with the Einstein–Hilbert theory being a specific case of Lovelock theory), corresponds to the Lanczos tensor related to the Gauss–Bonnet Lagrangian, and corresponds to the cubic tensor.
It is straightforward to notice that not even in a vacuum can these equations of motion be solved for an arbitrary set of ’s. Not even the ground-states, i.e., the locally constant curvature solutions, can be obtained in for a general set of ’s. The problem of obtaining these constant curvature solutions reduces to obtaining the roots of a polynomial of order , which, as it is well known, is not unattainable for . Moreover, these roots can be complex numbers with nonvanishing imaginary parts. A way to avoid this discussion is to fix the asymptotic behavior to a single asymptotically locally flat or AdS behavior.
As mentioned in the Introduction, Lovelock theory can be factorized into several effective cosmological constants [25]. In this connection, for and from , the vacuum equations of motion can be written as [27]
This shows, as expected, that the Lovelock gravity can be factorized into several ground states of constant curvature. In this work, we aim to complete the analysis considering asymptotically locally AdS spaces, i.e., spaces satisfying
In the simplest cases where Equation (5) is satisfied, the vacuum is n-fold degenerate, and the EOMs in Equations (3) and (4), after an appropriate choice of the coupling constants [26,40], take the simple form
with .
The static vacuum solution of (6) was obtained in [26,40]. In Schwarzschild coordinates, this is given by
where corresponds to the transversal section of a -sphere. The vacuum solution is
It must be stressed that stands for any of the n different roots of (X). It is straightforward to check the presence of a singularity at . Nonetheless, this is not enough, and in general, what characterizes the interesting physical solutions is that they satisfy , for . If such that , this defines a Killing horizon and thus the line element above Equations (7) and (8) describe a black hole geometry. One can notice how similar this solution is to the corresponding Schwarzschild solution. (Nonetheless, there is at least one significant difference. For an n even integer, since there are always two ± real roots in the expression, can be considered allowed).
It is worth stressing that, as mentioned in the Introduction, the structure of the equations of motion leading to the last solution is quite different from that of PL, as PL considers only a single term in the Lovelock series. At the same time, LnFDGS includes all the terms of the mentioned series up to under the particular choice of coupling constants previously mentioned. This choice allows the equations of motion to be factorized into AdS vacua, as described above (which is not possible for PL).
3. About the Nature of the Matter Source Proposed for Lovelock with n-Fold Degenerate Ground State AdS
Given the aforementioned differences between PL and LnFDGS theories, providing a form for the energy density analogous to the one described earlier is not straightforward. This is because several additional terms would appear when directly substituting the Kretschmann scalar of the vacuum LnFDGS solution. To address this, we will provide some of the necessary ingredients. First, we will define gravitational tension through the gauge curvature tensor , which is the Poincaré (group) curvature. Second, we will define an appropriate tensor for LnFDGS, which we will refer to as the Poincaré AdS-like curvature. From this, we will provide an alternative version of the Kretschmann scalar associated with gravitational tension. Finally, we will describe, from a physical perspective, the resulting structure of the energy density.
3.1. Defining Gravitational Tension Through the Gauge Curvature and a Glimpse of the Analogy with the Schwinger Effect
Although the analogy between gravitational tension and the production ratio in the Schwinger effect requires further study, this work provides some insights into the subject, allowing us to speculate. As discussed in [14,16], one could argue that the Schwinger effect should play a role in one of two ways. Firstly, it would give rise to corrections to the vacuum expectation value of the fields. These corrections can be expressed in terms of powers of the Riemann tensor [44]. Furthermore, gravitation itself should self-correct due to the presence of singularities. It is expected that these effects cannot be separated for large curvature. To address any of these approximations, after considering Equation (1), one can recall that in asymptotically (Riemannian) flat spaces (i.e., with a vanishing cosmological constant), one analogy to the gauge curvature is the Poincaré (group) curvature. In this way, we can also interpret the gravitational tension as , where
where span the Poincare algebra. Here, is the curvature tensor and the torsion tensor. However, since on a Riemannian manifold the torsion tensor vanishes and the curvature tensor is the Riemann tensor, the Schwinger effect could be characterized by the Kretschmann scalar [11,15,16]:
Now, as mentioned earlier, in order to propose an energy density, one can observe that for the four-dimensional Schwarzschild solution, the Kretschmann scalar is proportional to , and thus, by substituting it into Equation (1), the energy density proposed by Dymnikova is reproduced.
Before proceeding, it is worth mentioning that the prescription above has been further explored in many works; see [12,15,16,17]. Essentially, the results are regular black hole and wormhole solutions. In [45,46], the mentioned relationship between the Kretschmann scalar and the Schwinger effect was explored in a different (gravitational) context.
3.2. An Alternative Definition of the Kretschmann Scalar for Our Anti-De Sitter Space
To extend the framework to asymptotically (locally) anti-de Sitter spaces, it is enough to consider an ) curvature [47] instead of the Poincare one. One option is [48]
In this work, for simplicity, we will refer to the tensor as Poincaré AdS-like curvature, where l is called the AdS radius and are a set of generators of . Since the discussion is for a Riemannian manifold, where , in order to simplify the calculations, one can define an adequate Kretschmann scalar :
As above, one can evaluate on the four-dimensional Schwarzschild-AdS solution, which yields
This leads to the same energy density, see Equation (1), as in the case. This must be expected as for the effects of the different asymptotical structure should be irrelevant.
3.3. The Proposed Model
As mentioned earlier, to define the energy density in (1), we associate the gravitational tension with the value of our definition provided above for the Kretschmann scalar for the vacuum AdS LnFDGS solution. From Equations (6) and (12),
where
Now, evaluating, using (8), yields
Building on the idea previously described, where gravitational tension is proportional to the square root of the Kretschmann scalar of the vacuum solution,
In this way, the steps previously taken, namely, defining a tensor analogous to the gauge curvature, which we call the Poincaré AdS-like curvature, and providing an alternative definition for the Kretschmann scalar, now allow us to model an energy density. Thus, in analogy with (1), the energy density can be defined as
where, for simplicity, the constant A has been adjusted to
where a is an arbitrary constant. It is worth mentioning that this density model satisfies what was described earlier. While the gravitational tension associated with the tidal forces of the vacuum LnFDGS AdS solution diverges near the origin, the energy density encodes the information of the aforementioned case in such a way that, at the origin, the density takes a finite value, which, as we will see below, is associated with the suppression of the singularity usually present at the radial origin.
4. A New Static Regular Solution in Lovelock with n-Fold Degenerate Ground State AdS
The energy–momentum tensor corresponds to a neutral perfect fluid:
On the one hand, it is well known that this form of the metric imposes the condition . To obtain the regular solution it is enough to solve (6)
The components and of the equations of motion take the form
where l corresponds to the AdS radius, which is related to the cosmological constant such that and where
On the other hand, due to the transverse symmetry, we have for all the angular coordinates. Thus, using the aforementioned condition , the conservation law gives
Using the static ansatz (7) with
the direct integration yields
We replace the energy density in the last equation using Equations (18) and (19), obtaining the mass function.
By choosing as the integration constant, the mass function is given by
In the expression above, we have chosen as the integration constant. As we will see below, this choice allows the function to behave as a de Sitter core close to the origin, and thus, the solution is regular.
It is worth noting that the coordinate r defines the regions of interest. While corresponds to the asymptotic region, must define the center of the solution. Below, we analyze the regions associated with the event horizons present in the solution.
4.1. Structure of Horizons
We begin by mentioning that the mass parameter at which our solution, Equations (25) and (26), vanishes is given by the following expression:
where is such that .
In Figure 1, we can observe the generic behavior of the mass parameter as a function of the radial values where the function vanishes. The behavior in the vacuum LnFDGS AdS case [26,40] is shown in dashed red, while the behavior of our RBH LUV AdS solution with our matter sources is shown in blue. Thus, the regions where M decreases correspond to the values of the inner horizon , and the regions where M increases correspond to the values of the black hole horizon in our solution. Therefore, for , there exist an inner horizon and a black hole horizon for the same value of the parameter M. The value corresponds to the point where the inner and black hole horizons coincide, i.e., an extremal black hole.
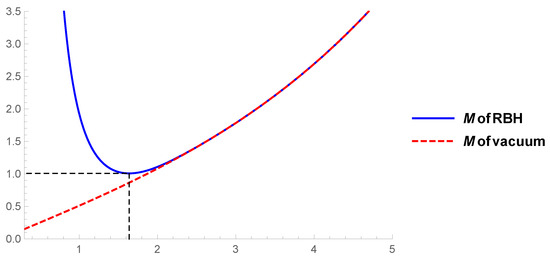
Figure 1.
On horizontal axis: . On vertical axis: M of our RBH is shown in blue and M in the vacuum case [40] in dashed red. We have used . We can check that this behavior is generic by using other parameter values. The decreasing part of the blue curve corresponds to the inner horizon of the RBH solution, while the increasing part represents the event horizon. The minimum point marks the extremal radius. The red curve represents the vacuum AdS solution. For a value slightly greater than the extremal radius, both solutions become indistinguishable for radial values equal to or greater than the event horizon.
A remarkable feature is that, under a small rightward deviation in the value of the extremal radius , that is, (which corresponds to a small upper-right deviation in the value of M with respect to ), our regular AdS solution and its vacuum AdS counterpart become indistinguishable, as the dashed red and blue curves also become indistinguishable. More specifically, for a value slightly above , both the vacuum solution and the regular solution share the same event horizon radius. In this case, the two solutions can only be distinguished inside the event horizon.
For values on the vertical axis smaller than , our solution exhibits a regular geometry without horizons. It is worthwhile to stress that, unlike the vacuum LnFDGS AdS solutions in [26,40], due to the absence of singularities, regular solutions do not need to be black holes; i.e., they do not require the presence of a horizon to be well defined. In other words, regular solutions are not constrained by the cosmic censorship hypothesis.
If we take the Planck length as a reference on the horizontal axis of the figure, such that the extremal radius is and , then for values slightly greater than these, , both solutions become indistinguishable. In this scenario, physics at Planck scales becomes particularly interesting, as the nature of the matter sources contributes to the suppression of the singularity.
As a consequence of the above, we also note that for values considerably larger than the Planck scales, such as the observed values of mass and radius of rotating black holes observed in LIGO GW150914, about 35 solar masses [49], both the vacuum and regular solutions are also indistinguishable. Thus, it becomes intriguing to observe the properties of black holes at scales much smaller than those that have been observed to date.
It is worth discussing the potential case where , in which, as a consequence of the previous discussion, the Schwarzschild LnFDGS AdS solution [26,40] becomes indistinguishable from our regular black hole (RBH) solution with LnFDGS AdS. This scenario makes sense if one considers the case in which the parameter a is of the order of the Planck length, , and the radius is of the order of the rotating black hole observed in LIGO GW150914 [49], km. In this way, the parameter a can be interpreted essentially as the length scale at which quantum corrections become not only non-negligible but also relevant. Depending on the model considered, this length scale can be as small as the Planck length.
4.2. Merging Zone
A remarkable feature of our regular solution is the existence, in general, of a radial coordinate value at which the regular solution converges toward the vacuum LnFDGS AdS solution found in Refs. [26,40], which corresponds to Equation (8). However, analytically estimating the precise radial value beyond which our regular AdS solution and its vacuum AdS counterpart become indistinguishable is difficult. Numerically, we observe in the first panel of Figure 2 that, for a value of the mass parameter , associated with the existence of an extremal horizon , both solutions become indistinguishable for a radial value greater than the extremal horizon. In the second panel, we observe that for mass values greater than , corresponding to an event horizon , both solutions become indistinguishable before reaching the mentioned event horizon. It is straightforward to verify that the behavior shown in this figure is generic for other parameter choices. In this way, the obtained solution is such that, for a mass parameter value slightly greater than (associated with an extremal radius), our RBH solution LnFDGS becomes indistinguishable from its vacuum counterpart LnFDGS [26,40] inside the event horizon, from a radial value up to infinity. If is on the order of the Planck scale, the geometric differences between both solutions, particularly the suppression of the singularity, would occur at quantum scales.
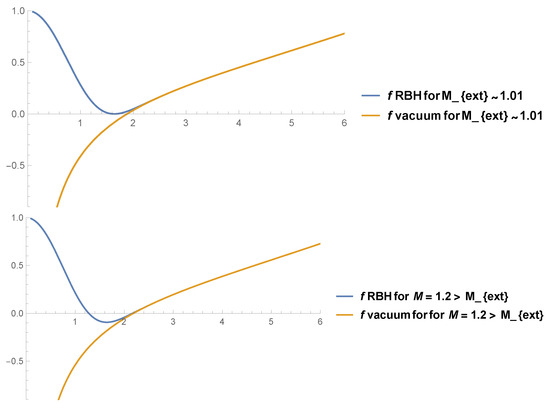
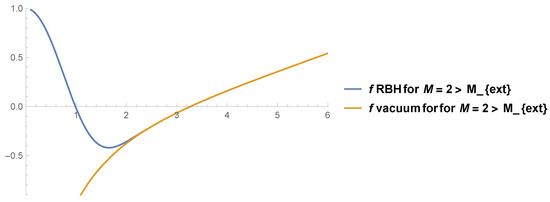
Figure 2.
On the horizontal axis: r. On the vertical axis: the function for , , and in the first, second, and third panels, respectively. We have used , , , . We can check that this behavior is generic for other parameter values. We observe that for mass parameter values greater than the extremal mass, , both solutions become indistinguishable from within the event horizon.
4.3. Behavior near Region
One must analyze the region near , which essentially separates the regular solution from its black hole counterpart. At , the absence of any singularity can be demonstrated. This becomes evident simply by taking the limit:
In principle, this defines a (nearly) (anti-) de Sitter or flat region near . However, the presence of the term can be observed, and therefore, given that in a realistic physical setup , where l represents the AdS radius, even for small masses M, a de Sitter-like region is expected near .
From the last equation, it is straightforward to check that the Kretschmann invariant takes a finite value near the origin:
4.4. AdS Asymptotic Region
Firstly, one needs to address how our regular solution, Equations (25) and (26), evolves as the asymptotic region is approached, roughly as . As expected, the regular solution, as ,
defining an asymptotically locally AdS space as r grows but also a merging into the vacuum solution counterpart [26,40]. As is well known, an asymptotically AdS behavior allows for a proper definition of conserved quantities at the boundary [50]. Along these lines, shadows have also been studied in spacetimes with this type of asymptotics [35,36].
5. Shadows
We study the spherically symmetric line element given by (7). Thus, the transversal section can be written as
We can notice that the metric tensor is independent of the angular coordinate and the temporal coordinate. In this way, we can identify the following Killing vectors:
These Killing vectors lead to conserved quantities such that
where the dot indicates the derivative with respect to the affine parameter. We consider a movement of a photon in an equatorial plane described by , with being constant. Thus,
where, in our case, E and L represent the energy and angular momentum of the photon as measured by an observer at infinity.
It is straightforward to check that the norm of the tangent vector to the geodesic is also conserved. In this line, we have
We use for null geodesics; for time-like geodesics (massive particles), , and for space-like geodesics, . As indicated in [42], due to the spherical symmetry, it is sufficient to consider the motion of null geodesics in an equatorial plane. From the previous equations, we obtain
where the effective potential is
and where the impact parameter b is the perpendicular distance between the position of a photon moving towards the black hole and its center.
We say that the radius of each circular orbit is the distance between the center of the black hole and a point in spacetime where photons follow a circular motion. The geodesic for these distances is a closed circle. This forms the so-called photon sphere, whose radius we denote as .
Minima in the effective potential function correspond to stable circular orbits. Maxima, on the other hand, correspond to unstable circular orbits. It is important to mention that in several solutions, such as the Schwarzschild solution or the vacuum black hole solution of pure Lovelock, the photon sphere is unstable because it corresponds to a maximum of the effective potential [42]. However, it plays an important physical role. The photon sphere is the union of all closed null geodesics. Thus, there are no other types of closed null geodesics in the spacetime. Photons tangential to the photon sphere will remain on the photon sphere. However, since the photon sphere is unstable, small perturbations will cause the photon to either fall into the black hole or escape from it. In this way, the radius of the photon sphere is determined by the following equation:
where the prime indicates differentiation with respect to the radial coordinate. Following reference [42], for simplicity, we assume that all light sources are placed uniformly at infinity. The critical impact parameter of the system is the impact parameter for which the photon will precisely fall into the circular orbit around the black hole. For an impact parameter smaller than the critical impact parameter, the photon will always end up inside the black hole. For an impact parameter larger than the critical impact parameter, the photon will end up at an infinite distance from the black hole. Following [42], an observer located at infinity leads to the critical impact parameter being equal to the shadow radius, ; see the scheme in Figure 3. This can be computed by setting in Equation (41):
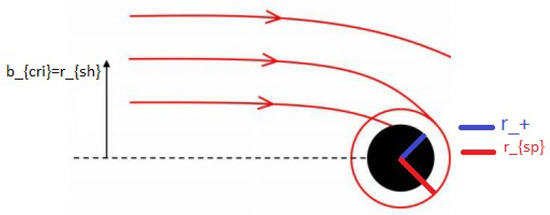
Figure 3.
Scheme: We observe that photons launched with an impact parameter smaller than the shadow radius fall into the black hole. Photons with an impact parameter equal to the shadow radius fall into an unstable circular orbit. Photons launched with an impact parameter greater than the shadow radius escape toward the boundary of spacetime.
As previously mentioned, the study of black holes in Lovelock gravity has attracted significant attention in recent years from a theoretical perspective. This naturally motivates the investigation of their shadow properties. In this regard, given the lack of analytical expressions for the event horizon, the photon sphere radius, and the shadow size in our case study, it is particularly interesting to establish numerical relationships between these shadow-related features within the context of Lovelock theories. In what follows, we propose a numerical methodology to achieve this. In the subsection below, we propose a method to achieve this. We use the case as an example, but it is straightforward to check that our proposal is applicable to other values of n and d.
A Recipe for Determining the Size of the Photon Sphere and the Shadow
- 1.
- First, since it is not possible to obtain an analytical value for the photon sphere radius from Equation (41), we obtain the mass parameter from this equation for our RBH solution, Equations (25) and (27).As an example, we study the case in Figure 4. The values of the ascending curve (in the example, as shown by the orange dashed vertical line; values greater than ∼6.5 on the horizontal axis) represent the candidate values of the photon sphere radius. We use the word “candidate” because later we need to ensure that the condition is satisfied. The vertical axis shows the values of the mass parameter. Thus, each ordered pair represents values of the candidate photon sphere and the mass parameter in the parameter space such that Equation (41) is satisfied, i.e., where the potential reaches an unstable maximum. On the other hand, the orange dashed horizontal line in Figure 4 represents the maximum value of the mass parameter for the parameters used. Below, we detail what the black horizontal line in the figure represents.
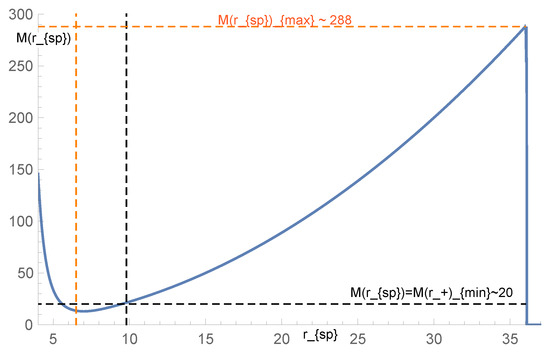 Figure 4. This figure displays the range of possible values for the photon sphere. On the horizontal axis: the candidate values of the photon sphere radius . On the vertical axis: the mass parameter . Using .
Figure 4. This figure displays the range of possible values for the photon sphere. On the horizontal axis: the candidate values of the photon sphere radius . On the vertical axis: the mass parameter . Using . - 2.
- From Equation (42) we can obtain the following relation between the photon sphere radius and the shadow’s radius:We are interested in testing the parameter values that satisfy the condition that the shadow radius is greater than the photon sphere radius, . Due to the highly nonlinear nature of our equations, obtaining analytical relations for this condition becomes extremely difficult.From Equation (43) and Figure 4, we extract the ordered pairs , which allow us to identify the possible values of the photon sphere radius. On the other hand, from Equation (44), we obtain the corresponding shadow radius values. Using this information, we determine the potential values of both the photon sphere radius and the shadow radius as given by Equation (44).However, as previously mentioned, we are interested in identifying the values of the parameter l that satisfy the condition that the shadow radius is greater than the photon sphere radius. To this end, using Equations (43) and (44), we employ the RegionPlot command in Mathematica. This is facilitated by the fact that Equation (43) is independent of the parameter l.As shown in Figure 5, for the parameters considered, the condition is fulfilled for approximately across all values of . Therefore, in the following step, we must use a value of l that satisfies this condition.
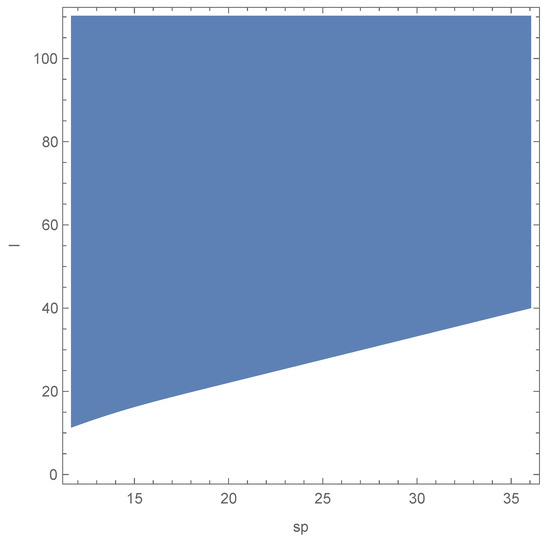 Figure 5. In blue, we observe the values of the photon sphere radius and the AdS radius l that satisfy the condition , using .
Figure 5. In blue, we observe the values of the photon sphere radius and the AdS radius l that satisfy the condition , using . - 3.
- To display the numerical behavior of the mass parameter, we use Equation (28), where, as previously mentioned, the values on the horizontal axis in the ascending curve correspond to the values taken by the event horizon, .In Figure 6, we display the behavior of the mass parameter. We must be consistent with the previous point and choose a value of l that satisfies the description provided there. In this way, on the ascending curve, we have an ordered pair of the form . The black dashed horizontal line represents the extremal minimum value of the mass for the chosen parameters, emphasizing that l is not arbitrary.
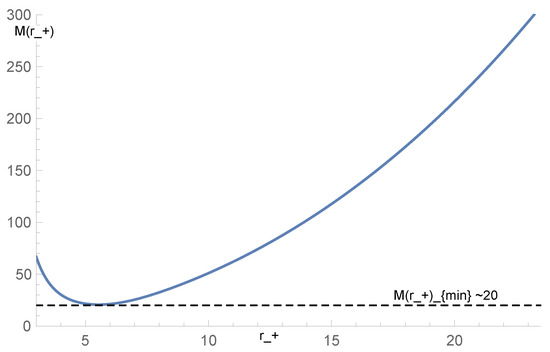 Figure 6. This figure displays the values of the event horizon corresponding to different values of the mass parameter. The values on the horizontal axis of the ascending curve represent the event horizon radius . On the vertical axis, we have the mass parameter . Using .
Figure 6. This figure displays the values of the event horizon corresponding to different values of the mass parameter. The values on the horizontal axis of the ascending curve represent the event horizon radius . On the vertical axis, we have the mass parameter . Using . - 4.
- In Figure 4, we have the ordered pairs , while in Figure 6, we have the ordered pairs . In this regard, we note the following:
- The mass parameter must be the same in both cases when the remaining parameters are fixed. This is because M represents the mass parameter of the solution and must have the same value for both and . Thus, to numerically test the relationship between and , we must consider that
- Once the appropriate ranges for and have been determined in the previous steps, we can numerically plot the relationship between and in Figure 7, using condition (45) on the ordered pairs and from Figure 4 and Figure 6, respectively. As expected, we observe that the value of the photon sphere is greater than that of the event horizon. That is, photons follow a circular motion due to the geometric distortion of spacetime caused by the presence of the black hole. We also note that as increases, the value of also increases in the parameter space.
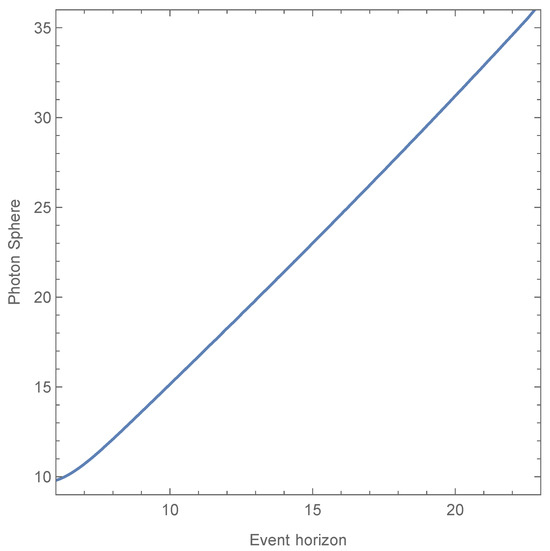
Figure 7.
This figure displays the values of the photon sphere radius versus the values of the event horizon radius. The values on the horizontal axis represent the event horizon radius . The values on the vertical axis represent the sphere photon radius . Using .
- 5.
- Once the appropriate ranges for and l have been determined in the previous steps, using Equation (44), we plot the relationship between the photon sphere radius and the shadow radius in Figure 8. As expected, we observe that the value of the photon sphere radius is smaller than that of the shadow radius. That is, photons that are directed with an impact parameter equal to towards the black hole curve their trajectory towards the unstable photon sphere.
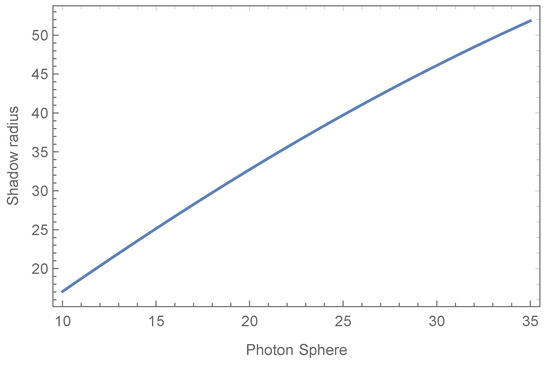 Figure 8. This figure displays the values of the shadow radius corresponding to different values of the photon sphere radius. Using .
Figure 8. This figure displays the values of the shadow radius corresponding to different values of the photon sphere radius. Using .
Following the methodology described earlier, in Figure 9 we display the behavior of the event horizon versus the photon sphere radius for (left panel) and (right panel). It is important to note that, in agreement with the analysis carried out above, for each case, depending on the values of in the parameter space, there are different ranges for the values of the event horizon and the photon sphere radius. We can note that if we use a common event horizon value as a reference for the same value of n, the photon sphere radius decreases as the number of dimensions increases.
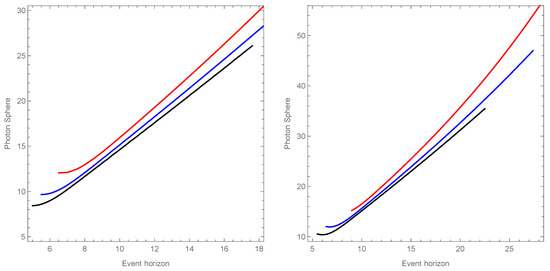
Figure 9.
This figure displays the values of the photon sphere radius corresponding to different values of the event horizon radius. The values on the horizontal axis represent the event horizon radius . The values on the vertical axis represent the sphere photon radius . In the left panel we have used , (red), (blue), and (black). In the right panel we have used , (red), (blue), and (black).
In Figure 10, we display the behavior of the photon sphere radius versus the black hole shadow radius for (left panel) and (right panel). In the same way as in the previous figure, and in agreement with the analysis carried out above, for each case, depending on the values of in the parameter space, there are different ranges for the values of the photon sphere radius and the shadow radius. We can note that if we use a common photon sphere radius value as a reference for the same value of n, the size of the black hole shadow radius tends to decrease as the number of dimensions increases.
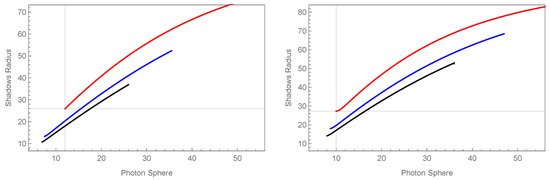
Figure 10.
This figure displays the values of the shadow radius corresponding to different values of the photon sphere radius. The values on the horizontal axis represent the sphere photon radius . The values on the vertical axis represent the shadow radius . In the left panel we have used , (red), (blue), and (black). In the right panel we have used , (red), (blue), and (black).
From a physical point of view, our methodology allows us to estimate the parameter ranges for which the condition that the shadow radius fully encloses the photon sphere radius, and the latter, in turn, fully encloses the event horizon, is satisfied, that is, the condition holds. This is consistent with the analytical treatment of the vacuum pure Lovelock case presented in Reference [42], which appears to be the only analytically solvable case currently known for Lovelock gravity.
In this way, our numerical approach could eventually be used for a deeper investigation in a future work, enabling, for example, the estimation of the deflection angle or the characterization of a linearly uniformly accelerated trajectory. In addition to the above, we would like to point out that establishing a direct comparison between the AdS radius values used in our figures and those estimated by other authors in the context of Lovelock theories would require, at the very least, theoretical justification regarding the behavior of the full set of black hole parameters within the AdS–Lovelock framework. This latter aspect goes beyond the scope of the present work. As mentioned, the values of the AdS radius currently available in the literature for Lovelock gravity remain speculative [21,22].
6. Thermodynamics
First of all, it is worth noting that the energy can be computed as a conserved charge by following the methodology in Reference [40], which involves a regularization process. In this case, the conserved charge associated with the energy, computed using a time-like Killing vector, is obtained in an analogous way to Reference [27]:
In this way, the black hole energy is directly related to the parameter M.
On the other hand, in Reference [31] it was shown, using the conditions and , which can be viewed as constraints on the evolution along the space of parameters, that the first law of thermodynamics takes the form
The above equation can be rewritten as
where we can identify the temperature and entropy terms as
where corresponds to a local definition of the variation of the energy at the horizon. On the other hand, the definitions of entropy and temperature coincide with those of the vacuum case. That is, our matter sources influence the behavior of the aforementioned definition .
In this section, we study the thermodynamics at the event horizon, that is, where the mass parameter satisfies , where , as previously mentioned, is associated with the extremal radius, where the inner and event horizons coincide, . It is worth emphasizing, as mentioned earlier, that an interesting feature of our solution is that, for a value of M slightly greater than , the behavior of the mass parameter in our solution becomes indistinguishable from the vacuum case. Therefore, under this condition, the event horizons of both solutions coincide. As also discussed, this implies that the geometry of both cases becomes indistinguishable beyond the event horizon.
6.1. Temperature
The temperature is defined by
In Equation (51), we can notice that the first two terms are independent of a, and furthermore, they match the expression for the temperature found in [26,40] for the vacuum LnFDGS AdS solution. Regarding the third term in Equation (51), we can analytically observe that for a scenario where , the condition
holds. Thus, we find analytically that in a regime where the temperature of the vacuum LnFDGS AdS solution becomes indistinguishable from that of our RBH LnFDGS AdS solution. This regime could be of physical interest in the case where a is on the order of the Planck scale, while corresponds to a realistic radius—on the order of the radius of the rotating black hole observed in LIGO GW150914, —which is much larger than the Planck scale.
Numerically, we can note that for the value of where , the temperature vanishes. In this sense, it is well known that the zero temperature point is associated with a black remnant, known as what remains once evaporation stops. In this context, in Figure 11 below we observe that a remnant indeed forms in this extremal case.
In Figure 11, the generic numerical behavior of the temperature as a function of the event horizon is displayed. We can observe that this behavior is generic for other values of the parameters involved. In this figure, the horizontal axis can be considered to be on the order of Planck units, . Two curves are shown. The blue curve represents the temperature of the vacuum LnFDGS AdS solution [26,40] as a function of the event horizon. The orange curve corresponds to the temperature of our RBH LnFDGS AdS solution. It can be observed that there exists a finite value slightly greater than the extremal radius, , where the temperatures of both cases become indistinguishable.
It is of interest to discuss what happens for values smaller than , that is, radial values prior (from left to right) to the point where both temperatures become indistinguishable:
- The temperature of the vacuum solution increases and hypothetically diverges in the limit .
- On the other hand, in the case of the regular solution, we can note that the temperature decreases until it vanishes for the value , where .
In this sense, it is well known that the point of zero temperature is associated with a black hole remnant, what remains once evaporation ceases. In this context, in Figure 11 below we observe that a remnant indeed forms in this extremal case.
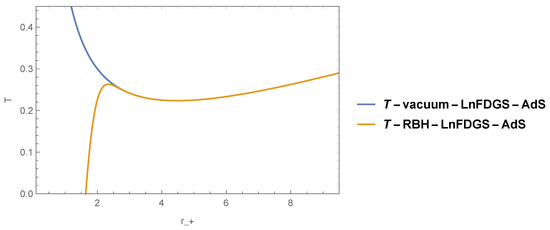
Figure 11.
This figure displays the values of the temperature corresponding to different values of the event horizon radius for , , , and .
Thus, at the small Planck scale, quantum effects would emerge. This implies that, instead of the temperature diverging as in the vacuum case, the matter sources proposed in this work lead the temperature to decrease until a black hole remnant is reached at and .
In other words, the behavior of temperature suggests that our forms of matter in the energy–momentum tensor play a role in eliminating divergences in LnFDGS AdS theories. This is analogous to the role of non-commutative matter sources in general relativity (GR), which in turn play the same role in quantum field theory and string theory [51,52]. Therefore, it would be of interest to study the role of our LnFDGS AdS energy sources in quantum field theory in a future work. As shown, the role of our matter sources is to cool the black hole in the final stage. Consequently, analogous to the non-commutative case studied in GR [51], this could be interpreted as a suppression of the quantum back-reaction of Hawking radiation once the temperature has already reached its maximum, as the black hole emits progressively less energy. As mentioned, these effects could be tested at Planck scales.
6.2. Heat Capacity and Radial Evolution
We use the standard definition of heat capacity:
In this section, we are interested in identifying the regions where the heat capacity is positive (stable), negative (unstable), and where it diverges, indicating the presence of phase transitions. In this connection, from Figure 1 the derivative is always positive, i.e., .
Since the sign of the derivative depends only on the sign of the derivative , it follows that the sign of the heat capacity also depends solely on this latter derivative. In connection with the previous paragraph, from Figure 11, we can observe that, for our solution, the temperature exhibits three regions from left to right: (i) due to the influence of matter sources at small scales; (ii) and (iii), which coincide with the vacuum LnFDGS AdS case where and , respectively. Thus, in our solution there would be two phase transitions (analyzed from right to left): (i) where ; (ii) where (these two coincide with the vacuum LnFDGS AdS case, where both solutions become indistinguishable); (iii) where .
Once both the vacuum solution and our regular black hole (RBH) become distinguishable, the heat capacities of the two solutions also differ at small scales. In this way, we can observe the following: Moving from right to left, while the heat capacity of the vacuum AdS solution remains negative, implying complete evaporation, as the parameter M decreases toward , would cause the temperature to diverge to infinity; in our regular AdS solution, the matter sources induce a new phase transition such that the heat capacity changes from negative to positive. This implies that, as the mass decreases to reach the extremal value , the temperature decreases until a black hole remnant is reached at , at which point the evaporation process halts. As mentioned earlier, this could occur at scales close to the Planck scale. That is, the nature of our matter sources, along with the avoidance of singularity formation, would lead to the existence of a remnant.
7. Discussion and Summary
As mentioned in the Introduction, a model was recently proposed in Ref. [13] to suppress physical singularities in pure Lovelock (PL) gravity, where the energy density encodes the gravitational information of the vacuum solution through the Kretschmann scalar. However, in the PL framework, the inclusion of a negative cosmological constant is unfeasible, as its presence leads to the appearance of a curvature singularity in the spherically symmetric case.
To address the aforementioned issue, namely, the introduction of an energy density analogous to that in Ref. [13] within Lovelock theories under the presence of a negative cosmological constant, in this work, instead of considering the PL action, which includes only a single term in the Lovelock series, we adopt the definition of the coupling constants given in Refs. [26,40]. By including all terms in the Lovelock series up to order , the resulting equations of motion possess an n-fold degenerate AdS ground state. In this way, the inclusion of a negative cosmological constant does not lead to the emergence of curvature singularities.
Given the structure of the equations of motion in LnFDGS theories, providing a form for the energy density analogous to the one described earlier is not straightforward. This is because several additional terms would appear when directly substituting the Kretschmann scalar of the vacuum LnFDGS solution. To address this, we have defined an appropriate gauge curvature tensor for LnFDGS, , which we have called the Poincaré AdS-like curvature. From this, we provide an alternative version of the Kretschmann scalar associated with gravitational tension. In this way, using the structure provided for gravitational tension, we have defined the energy density, which maintains the physical arguments provided in reference [17] for PL.
The obtained solution is such that, for a mass parameter value slightly greater than (associated with an extremal radius), our RBH solution LnFDGS becomes indistinguishable from its vacuum counterpart LnFDGS [26,40] inside the event horizon, from a radial value up to infinity. If is on the order of the Planck scale, the geometric differences between both solutions, particularly the suppression of the singularity, would occur at quantum scales.
On the other hand, due to the high theoretical interest that the study of black holes in Lovelock gravity has garnered, it is natural to explore the properties of their shadows. However, in most solutions within this theory—such as our case of interest, the LnFDGS AdS solution—the analytical study of these shadows becomes challenging. In this regard, related to the study of shadows, a method has been proposed to obtain numerical graphical relationships between the event horizon, the photon sphere radius, and the shadow size in our case study. The case , has been used as an example to explain our procedure. However, it is straightforward to verify that our proposal is applicable to other values of n and d. We have also presented the graphical behavior for the cases , and , . We note that, when using a common event horizon value as a reference for the same value of n, the photon sphere radius decreases as the number of dimensions increases. Additionally, when using a common photon sphere radius value as a reference for the same value of n, the size of the black hole shadow radius tends to decrease as the number of dimensions increases. It is also important to mention that, in all the cases studied numerically, the condition is satisfied.
From the analysis of the temperature, it can be observed that there exists a finite value slightly greater than the extremal radius, , where the temperatures of both cases also become indistinguishable. Thus, at the Planck scales, quantum effects would arise, meaning that instead of the temperature evolving to infinity, as in the vacuum LnFDGS case, the matter sources proposed in this work cause the temperature to decrease until a black hole remnant is reached at and .
Regarding radial evolution and heat capacity, once the heat capacities of both the vacuum solution and our regular solution are distinguishable at short scales, we observe a key difference: while the heat capacity of the vacuum AdS solution remains negative, implying complete evaporation, the parameter M decreasing toward would cause the temperature to diverge to infinity. In our regular AdS solution, the matter sources induce a new phase transition such that the heat capacity changes from negative to positive. This implies that as the mass decreases and approaches the extremal value , the temperature also decreases until a black hole remnant is reached at , at which point the evaporation process halts. As mentioned earlier, this could occur at scales close to the Planck scale. That is, the nature of our matter sources, along with the avoidance of singularity formation, would lead to the existence of a remnant.
Author Contributions
Conceptualization, R.A., M.E. and B.A.; Methodology, R.A., M.E. and B.A.; Software, M.E.; Validation, R.P.-F., R.A., M.E. and B.A.; Formal analysis, R.A., M.E. and B.A.; Investigation, R.A., M.E. and B.A.; Data curation, R.P.-F. and M.E.; Writing—original draft, R.A. and M.E.; Writing—review and editing, R.A. and M.E.; Visualization, R.P.-F., R.A., M.E. and B.A.; Supervision, R.A. and M.E.; Project administration, R.A. and M.E. All authors have read and agreed to the published version of the manuscript.
Funding
The work of RA was partially funded through FONDECYT-Chile 1220335. Milko Estrada is funded by the FONDECYT Iniciación Grant 11230247.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170814: A Three-Detector Observation of Gravitational Waves from a Binary Black Hole Coalescence. Phys. Rev. Lett. 2017, 119, 141101. [Google Scholar] [CrossRef]
- Damour, T. General Relativity today. In Gravitation and Experiment: Poincaré Seminar 2006; Alimi, J.M., Füzfa, A., Eds.; Birkhäuser Basel: Basel, Switzerland, 2007; pp. 1–49. [Google Scholar] [CrossRef]
- Horndeski, G.W. Second-order scalar-tensor field equations in a four-dimensional space. Int. J. Theor. Phys. 1974, 10, 363–384. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Introduction to modified gravity and gravitational alternative for dark energy. Int. J. Geom. Methods Mod. Phys. 2007, 4, 115–145. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Saez-Gomez, D. Cosmological reconstruction of realistic modified F(R) gravities. Phys. Lett. B 2009, 681, 74–80. [Google Scholar] [CrossRef]
- de la Cruz-Dombriz, A.; Dobado, A.; Maroto, A.L. Black Holes in f(R) theories. Phys. Rev. D 2009, 80, 124011, Erratum in Phys. Rev. D 2011, 83, 029903. [Google Scholar] [CrossRef]
- Lovelock, D. The Einstein tensor and its generalizations. J. Math. Phys. 1971, 12, 498–501. [Google Scholar] [CrossRef]
- Oikonomou, V.K. A refined Einstein–Gauss–Bonnet inflationary theoretical framework. Class. Quant. Grav. 2021, 38, 195025. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Swampland implications of GW170817-compatible Einstein-Gauss-Bonnet gravity. Phys. Lett. B 2020, 805, 135437. [Google Scholar] [CrossRef]
- Bena, I.; Houppe, A.; Warner, N.P. Delaying the Inevitable: Tidal Disruption in Microstate Geometries. J. High Energy Phys. 2021, 2, 103. [Google Scholar] [CrossRef]
- Alencar, G.; Estrada, M.; Muniz, C.R.; Olmo, G.J. Dymnikova GUP-corrected black holes. J. Cosmol. Astropart. Phys. 2023, 11, 100. [Google Scholar] [CrossRef]
- Estrada, M.; Aros, R. Pure Lovelock gravity regular black holes. J. Cosmol. Astropart. Phys. 2025, 01, 032. [Google Scholar] [CrossRef]
- Dymnikova, I. Vacuum nonsingular black hole. Gen. Rel. Grav. 1992, 24, 235–242. [Google Scholar] [CrossRef]
- Dymnikova, I. De sitter-schwarzschild black hole: Its particlelike core and thermodynamical properties. Int. J. Mod. Phys. D 1996, 5, 529–540. [Google Scholar] [CrossRef]
- Ansoldi, S. Spherical black holes with regular center: A Review of existing models including a recent realization with Gaussian sources. arXiv 2008, arXiv:0802.0330. [Google Scholar] [CrossRef]
- Estrada, M.; Muniz, C.R. Dymnikova-Schwinger traversable wormholes. J. Cosmol. Astropart. Phys. 2023, 03, 055. [Google Scholar] [CrossRef]
- Barrow, J.D.; Shaw, D.J. The Value of the Cosmological Constant. Gen. Rel. Grav. 2011, 43, 2555–2560. [Google Scholar] [CrossRef]
- Zakharov, A.F. Are signatures of anti-de-Sitter black hole at the Galactic Center? arXiv 2014, arXiv:1407.2591. [Google Scholar] [CrossRef]
- Zakharov, A.F. Constraints on tidal charge of the supermassive black hole at the Galactic Center with trajectories of bright stars. Eur. Phys. J. C 2018, 78, 689. [Google Scholar] [CrossRef]
- Chernicoff, M.; Giribet, G.; Oliva, J. Hairy Lovelock black holes and Stueckelberg mechanism for Weyl symmetry. J. Phys. Conf. Ser. 2016, 761, 012074. [Google Scholar] [CrossRef]
- Camanho, X.O.; Edelstein, J.D.; Maldacena, J.; Zhiboedov, A. Causality Constraints on Corrections to the Graviton Three-Point Coupling. J. High Energy Phys. 2016, 2016, 20. [Google Scholar] [CrossRef]
- Cai, R.G.; Ohta, N. Black Holes in Pure Lovelock Gravities. Phys. Rev. D 2006, 74, 064001. [Google Scholar] [CrossRef]
- Dadhich, N.; Ghosh, S.G.; Jhingan, S. The Lovelock gravity in the critical spacetime dimension. Phys. Lett. B 2012, 711, 196–198. [Google Scholar] [CrossRef]
- Camanho, X.O.; Edelstein, J.D. A Lovelock black hole bestiary. Class. Quant. Grav. 2013, 30, 035009. [Google Scholar] [CrossRef]
- Crisostomo, J.; Troncoso, R.; Zanelli, J. Black hole scan. Phys. Rev. D 2000, 62, 084013. [Google Scholar] [CrossRef]
- Aros, R.; Estrada, M. Regular black holes and its thermodynamics in Lovelock gravity. Eur. Phys. J. C 2019, 79, 259. [Google Scholar] [CrossRef]
- Xu, H.; Yung, M.H. Black hole evaporation in Lovelock gravity with diverse dimensions. Phys. Lett. B 2019, 794, 77–82. [Google Scholar] [CrossRef]
- Estrada, M.; Aros, R. Regular black holes with Λ > 0 and its evolution in Lovelock gravity. Eur. Phys. J. C 2019, 79, 810. [Google Scholar] [CrossRef]
- Aros, R.; Estrada, M.; Pereira, P. An Alternative Study about the Geometry and the First Law of Thermodynamics for AdS Lovelock Gravity, Using the Definition of Conserved Charges. Entropy 2022, 24, 1197. [Google Scholar] [CrossRef] [PubMed]
- Estrada, M. Gravitational Decoupling algorithm modifies the value of the conserved charges and thermodynamics properties in Lovelock Unique Vacuum theory. Annals Phys. 2022, 439, 168792. [Google Scholar] [CrossRef]
- Aros, R.; Estrada, M. Study about black hole solutions with nonconstant transversal curvature and its conserved charges in Lovelock gravity. Phys. Rev. D 2024, 109, 104044. [Google Scholar] [CrossRef]
- Akiyama, K.; Algaba, J.C.; Alberdi, A.; Alef, W.; Anantua, R.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; et al. First M87 Event Horizon Telescope Results. VIII. Magnetic Field Structure near The Event Horizon. Astrophys. J. Lett. 2021, 910, L13. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Algaba, J.C.; Anantua, R.; Asada, K.; Azulay, R.; Bach, U.; Baczko, A.K.; Ball, D.; et al. First Sagittarius A* Event Horizon Telescope Results. VI. Testing the Black Hole Metric. Astrophys. J. Lett. 2022, 930, L17. [Google Scholar] [CrossRef]
- Belhaj, A.; Belmahi, H.; Benali, M. Superentropic AdS black hole shadows. Phys. Lett. B 2021, 821, 136619. [Google Scholar] [CrossRef]
- Hamil, B.; Lütfüoğlu, B.C.; Dahbi, L. Quantum-corrected Schwarzschild AdS black hole surrounded by quintessence: Thermodynamics and shadows. Mod. Phys. Lett. A 2024, 39, 2450161. [Google Scholar] [CrossRef]
- Nozari, K.; Saghafi, S.; Mohammadpour, A. Higher-dimensional MOG dark compact object: Shadow behaviour in the light of EHT observations. Eur. Phys. J. C 2024, 84, 778. [Google Scholar] [CrossRef]
- Singh, B.P.; Kumar, R.; Ghosh, S.G. Effect of higher dimensions on rotating black holes shadow. New Astron. 2023, 99, 101945. [Google Scholar] [CrossRef]
- Vagnozzi, S.; Visinelli, L. Hunting for extra dimensions in the shadow of M87*. Phys. Rev. D 2019, 100, 024020. [Google Scholar] [CrossRef]
- Aros, R.; Troncoso, R.; Zanelli, J. Black holes with topologically nontrivial AdS asymptotics. Phys. Rev. D 2001, 63, 084015. [Google Scholar] [CrossRef]
- Bueno, P.; Cano, P.A.; Hennigar, R.A. Regular black holes from pure gravity. Phys. Lett. B 2025, 861, 139260. [Google Scholar] [CrossRef]
- Paithankar, K.; Kolekar, S. Black hole shadow and acceleration bounds for spherically symmetric spacetimes. Phys. Rev. D 2023, 108, 104042. [Google Scholar] [CrossRef]
- Garraffo, C.; Giribet, G. The Lovelock Black Holes. Mod. Phys. Lett. A 2008, 23, 1801–1818. [Google Scholar] [CrossRef]
- Birrell, N.D.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar] [CrossRef]
- Wondrak, M.F.; van Suijlekom, W.D.; Falcke, H. Gravitational Pair Production and Black Hole Evaporation. Phys. Rev. Lett. 2023, 130, 221502. [Google Scholar] [CrossRef]
- Chernodub, M.N. Conformal anomaly and gravitational pair production. arXiv 2023, arXiv:2306.03892. [Google Scholar] [CrossRef]
- Hassaine, M.; Zanelli, J. Chern-Simons (Super)Gravity, 2016 ed.; 100 years of general relativity; World Scientific: Hackensack, NJ, USA, 2016; Volume 2. [Google Scholar] [CrossRef]
- Hassaine, M.; Troncoso, R.; Zanelli, J. 11D supergravity as a gauge theory for the M-algebra. Proc. Sci. 2005, WC2004, 006. [Google Scholar] [CrossRef]
- LIGO Scientific and Virgo Collaborations; Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; et al. The basic physics of the binary black hole merger GW150914. Annalen Phys. 2017, 529, 1600209. [Google Scholar] [CrossRef]
- Aros, R.; Contreras, M.; Olea, R.; Troncoso, R.; Zanelli, J. Conserved charges for even dimensional asymptotically AdS gravity theories. Phys. Rev. D 2000, 62, 044002. [Google Scholar] [CrossRef]
- Nicolini, P.; Smailagic, A.; Spallucci, E. Noncommutative geometry inspired Schwarzschild black hole. Phys. Lett. B 2006, 632, 547–551. [Google Scholar] [CrossRef]
- Smailagic, A.; Spallucci, E. Thermodynamical phases of a regular SAdS black hole. Int. J. Mod. Phys. D 2013, 22, 1350010. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).