Abstract
It has long been debated whether gamma-ray bursts (GRBs) could serve as potential sources of ultra-high-energy cosmic rays (UHECRs). In this study, we consider GRBs as sources of UHECR injection with an injection index of and propagate them through the extragalactic magnetic field within the framework of CRPropa 3. The baryon loading factor is taken into account to quantify the rate of UHECR energy injection. In the benchmark case with a jet opening angle of and , we find that both high- and low-luminosity populations contribute to less than 10% of the UHECR spectrum. The most constrained scenario suggests , indicating that GRBs are less efficient in producing the all-sky UHECR intensity. The high-energy diffuse neutrinos and gamma rays resulting from interactions between UHECRs from GRBs and extragalactic background photons do not dominate the observations of Fermi-LAT or IceCube.
1. Introduction
As the most violent and energetic phenomena in gamma-ray bands, gamma-ray bursts (GRBs) have long been considered as one of the potential accelerators of ultra-high-energy cosmic rays (UHECRs) [1,2,3]. Those with a long duration can be classified into high-luminosity (HL) and low-luminosity (LL) categories based on whether the isotropic peak luminosity exceeds erg/s. Recent data sets from the Auger Observatory suggest a light-to-heavy composition for the primary mass of UHECRs in the energy range of eV, with a possible proton component fraction of 10% above eV [4]. For LL GRBs, heavy compositions can survive more easily and account for the spectrum of UHECRs with an energy injection rate erg [5,6]. For HL GRBs, they have a lower local rate and a higher energy budget with a potential proton-dominated outflow, as photodisintegration near the acceleration site occurs due to a high effective optical depth .
The diffuse neutrinos can be produced when UHECRs are launched or ejected in regions with dense photons or protons (e.g., jet base or the accretion disk). Neutrinos and gamma rays can also be produced by hadronuclear (pp) or photohadronic (p) interactions when UHECRs propagate in the photon fields of the extragalactic background light (EBL) and cosmic microwave background (CMB).
The energy scale of the isotropic diffuse gamma-ray background (IGRB), diffuse neutrinos, and UHECRs are comparable, at erg [7]. Although a common origin for these cosmic radiations is possible, the intensity of IGRB appears to be lower than the neutrino-associated hadronic flux, suggesting the presence of a population of UHECR accelerators that are opaque to gamma rays [8] (e.g., choked jets in GRBs or AGN). Cross-correlations between high-energy gamma rays from GRBs detected by the Fermi Large Area Telescope (LAT) and UHECRs detected by the Telescope Array and Auger have shown no significant correlation [9]. The stack analysis of the correlation between gamma rays from GRBs and IceCube TeV-PeV neutrinos also found no significance [10]. Additionally, for the brightest GRB of all time, GRB 221009A, no evidence of neutrino emission was found [11]. However, we cannot yet exclude the possibility that GRBs UHECRs could dominate the all-sky intensity of diffuse gamma rays, neutrinos, and cosmic rays. In this work, we use Monte Carlo simulations within the framework of CRPropa 3 to estimate the potential multi-messenger contribution of the propagation process of GRBs UHECRs.
This paper is organised as follows: Section 2 introduces the UHECR propagating configuration. Section 3 depicts our synthetic GRB samples and energy scale. The calculations, robustness analysis, and conclusions are described in Section 4. The cold dark universe is adopted in this work assuming cosmological parameters with and 71 .
2. Propagation with CRPROPA 3
To understand how UHECRs obtain nonthermal energy from GRBs, two leading scenarios are magnetic reconnection [12] and shock acceleration [13], both of which predict that UHECRs can be accelerated to energies up to eV. Diffuse neutrinos and gamma rays can be produced when these extremely energetic nuclei propagate through the cosmological photon field. For a nuclei with primary mass A and charge Z, the dominate photohadronic processes are photopion production (e.g., ), Bethe–Heitler pair production ) and photodisintegration ). The induced charged pion will decay into a muon and a neutrino, while gamma rays result from neutral pion decay. UHECRs are deflected by the extragalactic magnetic field (EMGF) before reaching Earth. The average deflection angle is given by [14]
for first order highly magnetized voids (), where is the rigidity of UHECR that travel a distance of D, (equals 1 Mpc is accepted in this work) is the coherence length, and B is the RMS magnetic field strength.
To simulate the interaction and deflection of UHECRs, we utilize the framework of CRPropa 3.2 to randomly propagate UHECRs [15]. The photohadronic interactions mentioned earlier are all included. For the secondary electromagnetic (EM) particles, an EM cascade can be induced with energy loss processes such as pair production, including double and triple pair production, and inverse-Compton scattering. We use the EBL model of Gilmore et al. [16], and the universal radio background model of Protheroe and Biermann [17] in this work. Similar to Das et al. [18], the EM cascade is managed by a numerical method named DINT in CRPropa 3 to reduce the calculation time. We select an observed sphere around the Earth with a radius of 1 Mpc to avoid the apparent deflection in the inner space. All UHECRs and secondary particles that reach the observed sphere are recorded. For GRB 221009A, protons with an energy spectrum between 0.1 EeV–100 EeV are injected at the location (on the X axis) with an initial direction (−1,0,0), and the arrival location on the observed sphere is plotted in Figure 1. After deflection by the extragalactic magnetic field and interactions, only one-tenth of the protons reach the observed sphere for a simulated minimal energy of 0.1 EeV.
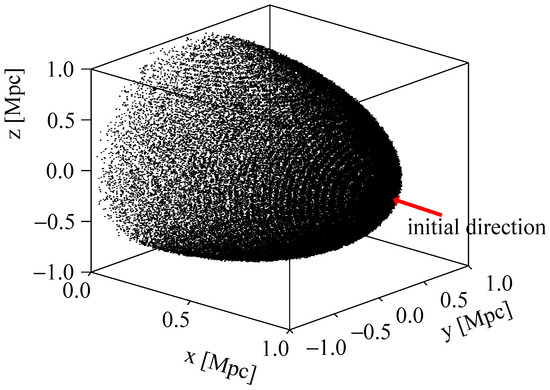
Figure 1.
The spatial distribution of arriving UHECRs on the observed sphere. The initial direction of UHECR injection is opposite to the x axis.
After presuming the magnetic field configuration with nG [19] and 1 Mpc for a random turbulent EGMF with Kolmogorov power spectrum, we need the redshift and baryon energy information to simulate all GRBs hadronic samples with an injection spectrum between 0.1 EeV and 100 EeV.
The redshift interval (0,5] is divided into 50 bins with a bin width of 0.1, and the total observed spectrum is processed by weighting the redshift distribution.
3. Simulation Data Set
The distribution of the isotropic peak luminosity L of GRBs is generally described by the luminosity function . The local burst rate is observationally related to the parameters of after considering the threshold and exposure of the correspond detector. The number of GRBs per unit time in the interval and is given by
where is the event rate in units of at redshift z, is the comoving volume element, while is the Hubble parameter. The luminosity function is normalized to 1 and is widely adopted as a broken power law
where a and b are the lower and upper index, respectively, and is the break luminosity. In this work, we adopt the luminosity function of HL GRB populations, with the best value of fit, , , , , . The burst rate following the empirical broken power law (EBPL) form is
where the local event rate is fixed by Fermi-LAT observation and the empirical parameters , , [20]. The validity of all parameter values has been tested by Yao et al. [21], who concluded that the star formation rate is not favoured. The redshift distribution of our model samples is shown in Figure 2.
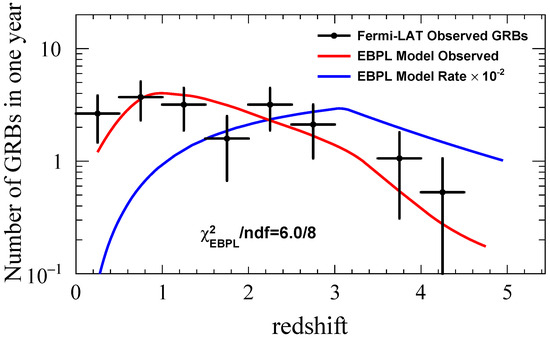
Figure 2.
The redshift distribution of our GRB samples for one year of detection. The blue line indicates the EBPL model rate multiplied by a factor of for clarity. The red line represents the predicted annual detection of GRBs, accounting for detection effects.
If we consider LL GRBs as a distinct subgroup compared with HL GRBs, they exhibit a wider jet opening angle and a significantly higher local burst rate than the latter. Referring to Liang et al. [22], LL GRBs have a local burst rate of with the star formation rate model [23]
The Fermi-GBM Gamma-Ray Burst Spectral Catalog [24] analyzed the gamma-ray energy emission on the extend band of 1 keV–10 MeV for 135 GRBs, and the long GRBs were picked and fitted using a Gaussian . Assuming as a representation of the total leptonic emission for GRBs, the total baryon energy of HL GRBs is estimated as . The factor denotes the baryon loading factor as the traditional definition, which describes the ratio of leptonic and baryonic acceleration energy. The baryon loading factor is model-dependent (for different acceleration sites) and observation-constrained. For instance, the neutrino observation implies for GRB 221009A [10]. A high-energy cut is implemented to prevent overestimation resulting from the high-energy portion of the Gaussian distribution, which exceeds the observation of the most energetic GRB 160625B with erg. In the calculation of the total hadronic emission energy scale, the assumption that is set in the following analysis.
All of the simulated GRBs are considered EeV proton sources, with an injection spectrum of in the energy band of 0.1–100 EeV. All the EeV protons are launched in the jet cone, interacted by background photons, and deflected by the extragalactic magnetic field. In Section 4, we calculate the diffuse cosmic ray flux on the observed sphere to determine the contribution to UHECRs. The secondary neutrinos are propagated in 1D with solid angle correction, while the DINT algorithm is involved for secondary gamma rays from the hadronic interaction as a potential contributor of IGRB.
4. Result
4.1. Calculation of All-Sky Isotropic Emission
UHECRs are propagated by Monte Carlo simulation within the framework of CRPropa 3.2 and are captured by the observed sphere. Over a time duration equivalent to one year and an observed area of ( Mpc), we calculate the observed UHECRs spectrum. Denoting the burst rate in one year as a dimensionless function of redshift z as , the spectrum of UHECRs can be obtained by
where is the differential number of particles with energy in the interval (E, E+dE) from a burst with hadronic energy at redshift z, and is the normalized Gaussian (to burst rate ) introduced in Section 3. For the same UHECR injection spectrum, the intensity of the observed spectral energy distribution is proportional to the total injection energy, which means
To simplify the problem, a top-hat jet is considered with a benchmark jet opening angle . The distribution weighted UHECR injection energy is erg and . The value of can be increased by a factor of 2 if the high energy cut on is removed. Then, the observed flux is
The distribution of the UHECR energy injection rate on a certain redshift in Equation (7) is simplified by the average injection energy described by Equation (6). Given that the UHECR energy injection rate is outlined by the right-hand term of Equation (6), the energy scales of PeV neutrinos and cascade-induced gamma rays are also validated. The electromagnetic (EM) cascade and neutrino production are simulated in one dimension, with nearly all the total energy of the EM cascade being transformed into gamma-ray energy. The conversion of gamma-rays and neutrinos involves multiplying by the effective geometry factor that describes the ratio of the solid angle of the observed sphere occupied by the GRB jet. The diffuse gamma ray and neutrinos spectrum takes the expression of
for a cone isotropic emission, where is the half opening angle of the observed sphere corresponding to the injection site sin Mpc/, is the luminosity distance on redshift z, and is the gamma ray or neutrinos energy injection rate normalized to the UHECR energy injection rate.
4.2. Hadronic Mutimessenger Contribution from HL GRBs
The baryon loading factor is connected to the acceleration mechanism and the launch site. For the internal shock model, the lepton and proton are simultaneously accelerated at the internal shock radius. The can be as large as the part of internal energy converted into electrons . Meanwhile, for dissipative photosphere models and magnetic dissipation models, a lower is expected [25]. The best constraint from the highest neutrino signal expectation GRB 221009A is as the function of Lorentz factor for the neutron–proton collision scenario [10]. The solid colorful line shows the isotropic gamma rays, neutrinos, and UHECRs spectrum from the propagation of simulated GRB EeV protons in Figure 3 for the case. The dash and dotted line represent a higher value of of 10 for certain models’ prediction and 26 for the purpose to fit the UHECRs spectrum, respectively.
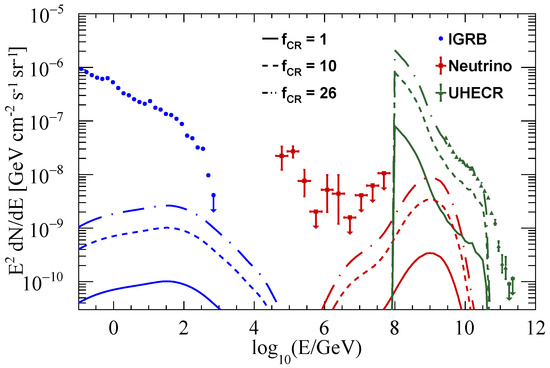
Figure 3.
Multimessenger contribution from HL GRB populations. Solid lines denote the diffuse gamma rays, neutrinos, and cosmic ray protons from the propagation of GRB UHECRs with a baryon loading factor . The dash line and dotted line are from the UHECR propagation with and . The spectrum of isotropic diffuse gamma ray background deducted by the foreground model A from Fermi−LAT is taken from Ackermann et al. [26], the diffuse neutrinos and UHECRs are taken from The IceCube Collaboration [27] and Halim et al. [4], respectively.
Generally speaking, the extragalactic gamma-ray background including point sources are supposed to be dominated by blazars [28]. Star-forming galaxies account for the majority of IGRB [29]. The secondary gamma rays from the EM cascade induced by proton propagation contribute two orders of magnitude less than the intensity of the IGRB, even if the energy injection rate satisfies the requirement for the all-sky UHECR spectrum, implying a leptonic origin for astrophysical sources. To dominate the intensity of UHECR, the escaped protons from HL GRBs should satisfy a maximal energy injection of erg corresponding to at redshift . The defection of the simulated 100 EeV protons is due to the minimal burst radius that exceeds the GZK radius, which is about 100 Mpc for 100 EeV protons. Beyond the end of the energy band in the simulation, the Auger composition analysis showed a mixed-heavy composition was dominant [4]. The proton composition of HL GRBs could hardly explain the UHECR spectrum. The all-flavor neutrinos spectrum is also plotted in Figure 3. The detection of EeV neutrinos from the propagation of UHECRs is consistent with observations from IceCube. If we consider EeV neutrinos as an extension of PeV neutrinos, the overall diffuse neutrino flux seems to surpass the index of observed for PeV neutrinos [30], which argues against a baryon loading factor greater than 1.8. Our findings suggest that the assumption that IGRB originates from the propagation of UHECRs that have escaped from GRBs or sources with GRB-like evolution should be disregarded.
4.3. Hadronic Mutimessenger for the LL GRB Case
The nature of LL GRBs is still unclear. Their lower gamma-ray luminosity, perhaps caused by the lower bulk Lorentz factors of the outflow [31], or a wider even quasi-spherical jet. The off-beam LL GRBs seems to be associated with 10% of Type Ic supernovae (e.g., GRB 980425 and GRB130427A [32,33,34]). Up to date, the most complete LL GRB burst energy samples suggest the emission energy erg [35]. The lower gamma-ray luminosity makes the photon environment more transparent for ultra-high energy nuclei, with an effective optical depth of at a loading site cm [6]. We take the total cosmic ray nuclei energy , erg temporarily for the Si-F 1 presupernova model composition of Zhang et al. [6] and calculate the nuclei propagation spectrum, which is shown in Figure 4.
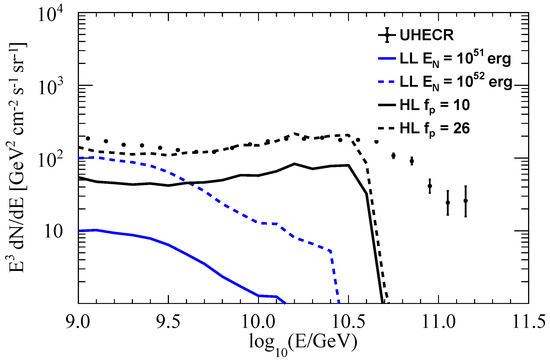
Figure 4.
UHECRs after propagation from LL (blue line) and HL GRBs (black line). For LL GRBs hadronic emission, the Si−R 1 composition of Zhang et al. [6] is applied with a rigidity-dependent injection spectrum , and the results of total cosmic ray nuclei energy of erg and erg are marked in solid and dash lines. The observed UHECRs spectrum of HL GRBs with and marked by black solid and dash lines.
The nuclei seem to fit badly with the UHECR all-particle spectrum. The main difference bewteen this work and the Si-R 1 model of Zhang et al. [6] is the injection spectrum of the escaped nuclei from GRBs. The latter used a delta-like function to estimate the escaped nuclei energy spectrum. If we assume a power law proton production rate with an index of s and exponential cut at as a function of dynamical evolution of the accelerator, the time-integrated spectrum in momentum space can be given by [36]:
where is the local emission rate of the proton production at . If both and follow the power law forms with index and , then the time-integrated spectrum also follows the power law form, , and the index of the escaping particles is . Here, we suppose the index of in the analysis. The UHECR spectrum might be fitted well using a harder power law index of 1.5, as suggested by Zhang et al. [6]. For a nuclei energy injection rate of erg corresponding to erg, the contributions of the diffuse gamma ray and neutrinos towards the background intensity are an more order of magnitude lower, similar to the HL scenario. Our results imply a comparable nuclei energy injection rate to that of Zhang et al. [6], which demands a injection rate of erg . However, the role of LL GRBs is still not determined by direct evidence due to the limit observation and unclear physical mechanism.
4.4. The Tightest Constraint from GeV Photons
For the potential GeV photon emission, the LAT observation consists of hadronic emission and leptonic emission: . The biggest constraint is , which provides the upper limit of UHECR energy, presuming that the total gamma-ray energy is from the EM cascade of hadronic emission. So, the hadronic emission energy on the tLAT band (0.1–10 GeV) is
where 10 is the empirical relationship of fluence, and 10 is the GBM fluence on the 10 keV–1MeV band [37], and the second term on the right hand is 1/2 for a photon spectrum . So, we can obtain the upper limit of the multimessenger contribution for the condition in Figure 5.
Figure 5.
The same as Figure 2, but the gamma-ray energy scales is measured using . See more details in the text.
It is observed that, under the most stringent constraint, protons originating from gamma-ray bursts appear to play a subdominant role in contributing to Ultra-High Energy Cosmic Rays (UHECRs) with a baryon loading factor of . This constraint should be interpreted cautiously, as the value of is notably higher than the predictions of various GRB models. Additionally, the burst energy is somewhat overestimated, given that only bursts with measured redshifts are statistically included in the analysis.
4.5. The Robustness of the Analysis
It is important to note that the calculations discussed in the preceding sections assume a narrow jet opening angle of . It is crucial to highlight that our results are not dependent on the jet opening angle due to the geometric relationship elucidated in Section 4.1. The total energy flux of the secondary particles and UHECRs that we observe is associated with the solid angle occupied by the observed sphere. Recently, a delay of 400 GeV photon observed by Fermi-LAT has been reported, which is believed to be a secondary EM cascade photon resulting from the propagation of UHECRs [38]. The delay time corresponding to the strength of the intergalactic magnetic field is approximately nG. We also conducted the simulation with an RMS magnetic field strength of nG and discovered that the outcomes were consistent with previous analyses. This consistency reinforces the robustness of our findings and supports the conclusions drawn from the simulations.
To estimate the influence brought by nearby GRBs with a redshift of , we compared the value of cos on redshift Mpc and . The former value of cos is about an order of magnitude lower than the latter value, demonstrating that the nearby GRBs are negligible compared with the whole samples.
5. Conclusions
The dominant sources of UHECRs are still uncertain. In this study, we conduct an analysis to assess the potential role of GRB as an UHECRs injection source using CRPropa 3.2. Regardless of the specifics regarding the jet opening angle and EMGF, our findings suggest that the Auger UHECR spectrum can be well-fitted by a composition consisting purely of protons originating from HL GRBs with a baryon loading of . This implies an escape radius with approximately the size of the internal shock region. Our analysis indicates that, even when assuming hadronic emission dominates the gamma-ray emission in the LAT band, GRBs are not likely to be the main contributor to the all-sky UHECRs intensity, even when overestimating the actual gamma-ray energy emission. If we consider a power-law extension for EeV neutrinos, the baryon loading should be lower than 1.8. We anticipate that observations and spectral measurements of EeV neutrinos and UHECRs from GRBs in the future could validate or further constrain our analysis.
Author Contributions
Conceptualization, F.M.; Methodology, Y.J.; Writing—original draft, Z.L.; Supervision, Y.G. All of the authors have contributed to writing. All authors have read and agreed to the published version of the manuscript.
Funding
Thank for the support from the Key Research and Development Program of the National Science and Technology Platform Project (2022YFC3700801), and the National Natural Science Foundation of China (No. 12275279, No. 12373105), and the Open Project of Guangxi Key Laboratory of Nuclear Physics and Nuclear Technology under Grant No. NLK2021-07.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Milgrom, M.; Usov, V. Possible Association of Ultra-High-Energy Cosmic-Ray Events with Strong Gamma-Ray Bursts. Astrophys. J. 1995, 449, L37. [Google Scholar] [CrossRef]
- Vietri, M. The Acceleration of Ultra–High-Energy Cosmic Rays in Gamma-Ray Bursts. arXiv, 1995; arXiv:astro-ph/9506081. [Google Scholar]
- Waxman, E.; Bahcall, J. High Energy Neutrinos from Cosmological Gamma-Ray Burst Fireballs. Phys. Rev. Lett. 1997, 78, 2292–2295. [Google Scholar] [CrossRef]
- Halim, A.A.; Abreu, P.; Aglietta, M.; Allekotte, I.; Cheminant, K.A.; Almela, A.; Alvarez-Muñiz, J.; Yebra, J.A.; Anastasi, G.; Anchordoqui, L.; et al. Constraining the Sources of Ultra-High-Energy Cosmic Rays across and above the Ankle with the Spectrum and Composition Data Measured at the Pierre Auger Observatory. J. Cosmol. Astropart. Phys. 2023, 2023, 24. [Google Scholar] [CrossRef]
- Murase, K.; Ioka, K.; Nagataki, S.; Nakamura, T. High-Energy Cosmic-Ray Nuclei from High- and Low-Luminosity Gamma-Ray Bursts and Implications for Multimessenger Astronomy. Phys. Rev. D 2008, 78, 023005. [Google Scholar] [CrossRef]
- Zhang, B.T.; Murase, K.; Kimura, S.S.; Horiuchi, S.; Mészáros, P. Low-Luminosity Gamma-Ray Bursts as the Sources of Ultrahigh-Energy Cosmic Ray Nuclei. Phys. Rev. D 2018, 97, 083010. [Google Scholar] [CrossRef]
- Murase, K.; Fukugita, M. Energetics of High-Energy Cosmic Radiations. Phys. Rev. D 2019, 99, 063012. [Google Scholar] [CrossRef]
- Murase, K.; Guetta, D.; Ahlers, M. Hidden Cosmic-Ray Accelerators as an Origin of TeV-PeV Cosmic Neutrinos. Phys. Rev. Lett. 2016, 116, 071101. [Google Scholar] [CrossRef]
- Álvarez, E.; Cuoco, A.; Mirabal, N.; Zaharijas, G. Searches for Correlation between UHECR Events and High-Energy Gamma-Ray Fermi-LAT Data. J. Cosmol. Astropart. Phys. 2016, 2016, 023. [Google Scholar] [CrossRef]
- Abbasi, R.; Ackermann, M.; Adams, J.; Agarwalla, S.K.; Aguilar, J.A.; Ahlers, M.; Alameddine, J.M.; Amin, N.M.; Andeen, K.; Anton, G.; et al. Search for 10–1000 GeV Neutrinos from Gamma-Ray Bursts with IceCube. Astrophys. J. 2024, 964, 126. [Google Scholar] [CrossRef]
- Abbasi, R.; Ackermann, M.; Adams, J.; Agarwalla, S.K.; Aggarwal, N.; Aguilar, J.A.; Ahlers, M.; Alameddine, J.M.; Amin, N.M.; Andeen, K.; et al. Limits on Neutrino Emission from GRB 221009A from MeV to PeV Using the IceCube Neutrino Observatory. Astrophys. J. Lett. 2023, 946, L26. [Google Scholar] [CrossRef]
- Giannios, D. UHECRs from Magnetic Reconnection in Relativistic Jets. Mon. Not. R. Astron. Soc. Lett. 2010, 408, L46–L50. [Google Scholar] [CrossRef]
- Dermer, C.D.; Razzaque, S. Acceleration of Ultra-high-energy Cosmic Rays in the Colliding Shells of Blazars and Gamma-ray Bursts: Constraints from the Fermi Gamma-ray Space Telescope. Astrophys. J. 2010, 724, 1366. [Google Scholar] [CrossRef]
- Alves Batista, R.; Shin, M.S.; Devriendt, J.; Semikoz, D.; Sigl, G. Implications of Strong Intergalactic Magnetic Fields for Ultrahigh-Energy Cosmic-Ray Astronomy. Phys. Rev. D 2017, 96, 023010. [Google Scholar] [CrossRef]
- Batista, R.A.; Dundovic, A.; Erdmann, M.; Kampert, K.H.; Kuempel, D.; Müller, G.; Sigl, G.; van Vliet, A.; Walz, D.; Winchen, T. CRPropa 3—A Public Astrophysical Simulation Framework for Propagating Extraterrestrial Ultra-High Energy Particles. J. Cosmol. Astropart. Phys. 2016, 2016, 38. [Google Scholar] [CrossRef]
- Gilmore, R.C.; Somerville, R.S.; Primack, J.R.; Domínguez, A. Semi-Analytic Modelling of the Extragalactic Background Light and Consequences for Extragalactic Gamma-Ray Spectra. Mon. Not. R. Astron. Soc. 2012, 422, 3189–3207. [Google Scholar] [CrossRef]
- Protheroe, R.; Biermann, P. A New Estimate of the Extragalactic Radio Background and Implications for Ultra-High-Energy γ-ray Propagation. Astropart. Phys. 1996, 6, 45–54. [Google Scholar] [CrossRef]
- Das, S.; Gupta, N.; Razzaque, S. Ultrahigh-energy Cosmic-Ray Interactions as the Origin of Very High-energy γ-Rays from BL Lacertae Objects. Astrophys. J. 2020, 889, 149. [Google Scholar] [CrossRef]
- Das, S.; Razzaque, S. Ultrahigh-Energy Cosmic-Ray Signature in GRB 221009A. Astron. Astrophys. 2023, 670, L12. [Google Scholar] [CrossRef]
- Wanderman, D.; Piran, T. The Luminosity Function and the Rate of Swift’s Gamma-Ray Bursts. Mon. Not. R. Astron. Soc. 2010, 406, 1944–1958. [Google Scholar] [CrossRef]
- Yao, Y.H.; Chang, X.C.; Hu, H.B.; Pan, Y.B.; Zhang, H.M.; Li, H.Y.; Qiao, B.Q.; Kang, M.M.; Yang, C.W.; Liu, W.; et al. Contribution of High-energy GRB Emissions to the Spectrum of the Isotropic Diffuse γ-Ray Background. Astrophys. J. 2020, 901, 106. [Google Scholar] [CrossRef]
- Liang, E.; Zhang, B.; Virgili, F.; Dai, Z.G. Low-Luminosity Gamma-Ray Bursts as a Unique Population: Luminosity Function, Local Rate, and Beaming Factor. Astrophys. J. 2007, 662, 1111. [Google Scholar] [CrossRef]
- Porciani, C.; Madau, P. On the Association of Gamma-Ray Bursts with Massive Stars: Implications for Number Counts and Lensing Statistics. Astrophys. J. 2001, 548, 522. [Google Scholar] [CrossRef]
- Poolakkil, S.; Preece, R.; Fletcher, C.; Goldstein, A.; Bhat, P.N.; Bissaldi, E.; Briggs, M.S.; Burns, E.; Cleveland, W.H.; Giles, M.M.; et al. The Fermi-GBM Gamma-Ray Burst Spectral Catalog: 10 yr of Data. Astrophys. J. 2021, 913, 60. [Google Scholar] [CrossRef]
- Zhang, B.; Kumar, P. Model-Dependent High-Energy Neutrino Flux from Gamma-Ray Bursts. Phys. Rev. Lett. 2013, 110, 121101. [Google Scholar] [CrossRef] [PubMed]
- Ackermann, M.; Ajello, M.; Albert, A.; Atwood, W.B.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; et al. The Spectrum of Isotropic Diffuse Gamma-Ray Emission Between 100 MeV and 820 GeV. Astrophys. J. 2015, 799, 86. [Google Scholar] [CrossRef]
- Aguilar, J.A.; Allison, P.; Beatty, J.J.; Bernhoff, H.; Besson, D.; Bingefors, N.; Botner, O.; Buitink, S.; Carter, K.; Clark, B.A.; et al. The IceCube Neutrino Observatory–Contributions to ICRC 2017 Part II: Properties of the Atmospheric and Astrophysical Neutrino Flux. arXiv 2017, arXiv:1710.01191. [Google Scholar]
- Qu, Y.; Zeng, H.; Yan, D. Gamma-ray Luminosity Function of BL Lac Objects and Contribution to the Extragalactic Gamma-Ray Background. Mon. Not. R. Astron. Soc. 2019, 490, 758–765. [Google Scholar] [CrossRef]
- Roth, M.A.; Krumholz, M.R.; Crocker, R.M.; Celli, S. The Diffuse γ-ray Background is Dominated by Star-Forming Galaxies. Nature 2021, 597, 341–344. [Google Scholar] [CrossRef] [PubMed]
- Aartsen, M.G.; Abraham, K.; Ackermann, M.; Adams, J.; Aguilar, J.A.; Ahlers, M.; Ahrens, M.; Altmann, D.; Anderson, T.; Archinger, M.; et al. A Combined Maximum-Likelihood Analysis of the High-Energy Astrophysical Neutrino Flux Measured with IceCube. Astrophys. J. 2015, 809, 98. [Google Scholar] [CrossRef]
- Liang, E.W.; Yi, S.X.; Zhang, J.; Lü, H.J.; Zhang, B.B.; Zhang, B. Constraining Gamma-ray Burst Initial Lorentz Factor with the Afterglow Onset Feature and Discovery of a Tight Γ0-E γ,iso Correlation. Astrophys. J. 2010, 725, 2209. [Google Scholar] [CrossRef]
- Galama, T.J.; Vreeswijk, P.M.; van Paradijs, J.; Kouveliotou, C.; Augusteijn, T.; Böhnhardt, H.; Brewer, J.P.; Doublier, V.; Gonzalez, J.F.; Leibundgut, B.; et al. An Unusual Supernova in the Error Box of the γ-ray Burst of 25 April 1998. Nature 1998, 395, 670–672. [Google Scholar] [CrossRef]
- Soderberg, A.M.; Nakar, E.; Berger, E.; Kulkarni, S.R. Late-Time Radio Observations of 68 Type Ibc Supernovae: Strong Constraints on Off-Axis Gamma-Ray Bursts. Astrophys. J. 2006, 638, 930. [Google Scholar] [CrossRef]
- Xu, D.; de Ugarte Postigo, A.; Leloudas, G.; Krühler, T.; Cano, Z.; Hjorth, J.; Malesani, D.; Fynbo, J.P.U.; Thöne, C.C.; Sánchez-Ramírez, R.; et al. Discovery of the Broad-Lined Type Ic SN 2013cq Associated with the very Energetic GRB 130427A. Astrophys. J. 2013, 776, 98. [Google Scholar] [CrossRef]
- Dereli, H.; Boër, M.; Gendre, B.; Amati, L.; Dichiara, S.; Orange, N.B. A Study of GRBs with Low-luminosity Afterglows. Astrophys. J. 2017, 850, 117. [Google Scholar] [CrossRef]
- Ohira, Y.; Murase, K.; Yamazaki, R. Escape-Limited Model of Cosmic-ray Acceleration Revisited. Astron. Astrophys. 2010, 513, A17. [Google Scholar] [CrossRef]
- Ackermann, M.; Ajello, M.; Asano, K.; Axelsson, M.; Baldini, L.; Ballet, J.; Barbiellini, G.; Bastieri, D.; Bechtol, K.; Bellazzini, R.; et al. The First Fermi-LAT Gamma-Ray Burst Catalog. Astrophys. J. Suppl. Ser. 2013, 209, 11. [Google Scholar] [CrossRef]
- Xia, Z.Q.; Wang, Y.; Yuan, Q.; Fan, Y.Z. A Delayed 400 GeV Photon from GRB 221009A and Implication on the Intergalactic Magnetic Field. Nat. Commun. 2024, 15, 4280. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).