Weak Deflection Angle by the Einstein–Cartan Traversable Wormhole Using Gauss–Bonnet Theorem with Time Delay

Abstract

In this article, we estimate the gravitational deflection angles of light in the spacetime of Einstein–Cartan wormholes supported by normal matter or phantom energy utilizing the Gauss–Bonnet theorem. The obtained deflection angles are examined in relation to the wormhole throat radius $r_0$ and the equation of state parameter $\omega$ across four scenarios, and it has been seen that the larger throat radii $r_0$ result in higher deflection angles. Moreover, the wormholes filled with phantom energy exhibit greater deflection angles compared to those filled with normal matter. The reported deflection angles are influenced by dark matter and Maxwell’s fish eye matter: Dark matter, as well as Maxwell’s fish eye matter, increases the deflection angles. The deflection angle is also estimated using the Keeton and Petters method, which is proportional to wormhole throat $r_0$ and inversely proportional to the impact parameter b. Additionally, a comparative study is performed on the deflection angles obtained from four different scenarios. Finally, analytical results for time delay due to Einstein–Cartan wormholes are estimated for the four $\omega$ cases which are decreasing for increasing values of $r_c$.

1. Introduction

Wormholes are tunnels in spacetime that can link either two parallel universes or two locations within the same universe. This intriguing nature continuously motivates physicists to find precise solutions describing the wormhole structures within both the framework of general relativity and modified theories of gravity. The concept of a wormhole was first proposed by Weyl [1], and later, Einstein and Rosen [2] formulated an interesting model that presents a bridge connecting two identical regions, termed the Einstein–Rosen bridge. It has been seen that the Einstein–Rosen bridge is non-traversable and collapses shortly after formation [3]. In 1988, Morris and Thorne [4] first formulated the traversable wormhole in the context of general relativity, in which the traversability depends on the presence of the exotic matter within the wormhole [5]. Indeed, the traversable wormhole in general relativity demands the violation of the null energy condition at least within the vicinity of the wormhole’s throat [6]. After the seminal work of Morris–Thorne, several theoretical researchers explored the different facets of wormhole structures [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]. In the recent past, Konoplya et al. [23] studied the traversable asymmetry wormholes endowed by the smooth gravitational and charged Dirac fields in the context of general relativity. Their study claimed that a stationary observer at the wormhole throat does not feel the gravitational force for the physically relevant condition on the wormhole throat; however, this condition is unnecessary [24]. Kain [25] investigated the relationship between entangled particles and wormholes within the framework of general relativity. Additionally, the wormhole solutions are also investigated in the context of the modified theories of gravity, such as $f\left(R\right)$ gravity [26,27,28], Horava gravity [29], $f(R,T)$ gravity [30], $\kappa (R,T)$ gravity [31], semiclassical gravity [32,33], Einstein–Gauss–Bonnet gravity [34,35], bumblebee gravity [36], exponential $f(R,T)$ gravity [37], teleparallel gravity [38], Brans–Dicke gravity [39,40,41,42], born-infield gravity [43,44], Kaluza–Klein gravity [45,46], etc. Moreover, Luis Blázquez-Salced et al. [47] introduced a detailed calculation of an Ansatz that can demonstrate the spherically symmetric Einstein–Dirac configurations in d-dimensional space. They also explored a regular wormhole solution supported by the Dirac fields by applying the Ansatz. It has been found that traversable wormholes can exist in four-dimensional Einstein–Dirac–Maxwell gravity without requiring the exotic matter [48], and this study has been thoroughly discussed in Ref. [49]. In the scenario of wormhole study, Moraes [50] introduced the general solutions for static wormholes in $f(R,T)$ gravity; Chew et al. [51] studied the spinning wormhole solutions in the context of scalar–tensor theory; Brihaye et al. [52] studied the scalarized–charged wormholes in the framework of Einstein–Gauss–Bonnet gravity; Barros et al. [53] studied the wormhole solutions with matter haunted by conformally coupled ghosts; Rosa et al. [54] analyzed the traversable wormholes in the energy–momentum squared gravity.

The Einstein–Cartan theory of gravity represents a groundbreaking approach that incorporates the effects of mass with spin, expanding upon the theory of relativity and offering a new perspective on the cosmos [55,56]. Indeed, the Einstein-Cartan theory suggests that spacetime is not merely characterized by matter and energy but also encompasses an additional dimension known as spinors, often conceptualized as the fifth dimension. The Einstein-Cartan theory also predicted the expansion of the universe; especially, the cosmological settings in this theory suggest the elimination of the Big Bang singularity by a non-singular state of finite minimum radius [57,58,59,60,61,62,63,64,65]. Recently, Falco and Battista [66] studied the binary dynamics at the first post-Newtonian order within the framework of the Einstein-Cartan theory; Ranjbar et al. [67] studied the gravitational slip parameter and gravitational waves in the Einstein–Cartan theory. Furthermore, in the background of the Einstein–Cartan theory, Akhshabi and Zamani [68] investigated the measurement of cosmological distances in the presence of torsion; Luz [69] found the cosmological solutions where matter is represented by a perfect fluid with inherent spin; Elizalde et al. [70] studied the impact of the spin tensor of dark matter on the transmission of gravitational waves; He et al. [71] studied the different scalaron-induced inflation along with the Starobinsky inflation. Apart from that, the Einstein–Cartan theory also received much attention in studying several traversable wormhole structures. Bronnikov and Galiakhmetov [72] introduced the possibility of the existence of static traversable wormholes without any requirement for exotic matter in the context of Einstein–Cartan gravity, and Mehdizadeh et al. [73] investigated the wormhole structures filled with Weyssenhoff fluid and anisotropic matter in the Einstein–Cartan theory. Additionally, several researchers introduced different wormhole structures in the context of the Einstein–Cartan theory [74,75,76,77].

Einstein’s general theory of relativity has been confirmed by several experiments over the years. In this regard, gravitational lensing is one of the famous tools for the confirmation of general relativity that was carried out by studying solar eclipses in modern observational cosmology [78,79]. Gravitational lensing can also be employed to determine the mass of galaxies and clusters, as well as to detect dark matter [80]. For the first time, Soldner suggested gravitational lensing in the background of Newtonian theory. Later, Liebes [81] and Refsdal [82] developed the basic theories of gravitational lensing. In the literature, there are three types of gravitational lensing, namely, strong gravitational lensing, weak gravitational lensing, and micro gravitational lensing. These three types of gravitational lensing can be analyzed using various types of methods available in the literature. Gibbons and Werner [83] introduced a very renowned method to calculate the deflection angle of light by using the Gauss–Bonnet theorem, and this method evaluated the exact deflection angle in the weak limit approximation for the Schwarzschild black hole [83]. Moreover, this method was used to estimate the deflection angle in the gravitational field of the Kerr black hole [84], rotating the global monopole and cosmic string [85,86,87], under the Lorentz symmetry breaking and quantum effects [88,89], Rindler-modified Schwarzschild black hole [90], etc. Furthermore, adopting Gibbons and Werner’s method, Crisnejo et al., [91] estimated the deflection angles of light and massive particles in a plasma medium in the spacetime of the Schwarzschild black hole. Jusufi estimated the deflection angles of massive particles in the gravitational field of the Kerr black hole [92], and he extended the study for charged particles in Kerr–Newman spacetime [93].

On the other hand, there is no experimental evidence for the existence of wormhole geometry up to the present. In this respect, the scientific community has been studying gravitational lensing in wormhole spacetimes using various renowned methods. Taking Gibbons and Werner’s method into account, Jusifi et al. [94] calculated the weak deflection angles of light by wormholes supported by electric charge, magnetic charge, and scalar fields. The deflection angle of light by charged wormholes in the content of Einstein–Maxwell-dilation theory was estimated in Ref. [95]. Jusufi and Ovgun [96] explored the gravitational lensing for rotation wormholes. Kuhfittig [97] calculated the deflection angle of light by the wormholes that existed in the galactic halo region. Shaikh et al. [98] studied the gravitational lensing and the energy conditions in the spacetime of the scalar–tensor wormholes. In addition, the deflection angles of light are estimated in the background of various types of wormholes that are studied in the literature [99,100,101,102,103,104,105,106,107,108,109,110,111,112,113]. Additionally, the deflection angle of spherically symmetric lenses can be computed up to the post-post-Newtonian (PPN), introduced by Keeton and Petters [114,115], and Sereno and de Luca [116] expanded the PPN approximation for Kerr black holes.

Dark matter consists of particles that do not interact with or emit light, making them undetectable through electromagnetic radiation observation. The Standard Model of Cosmology has established that the dark sector of the universe comprises 27% dark matter (DM). In 1933, Zwicky [117,118] discovered the existence of DM in the galaxy cluster. The Milky Way Galaxy also contains dark matter content that has been shown with the help of sound observational grounds [119,120,121]. The presence of dark matter is inferred primarily through its gravitational effects, although it also exhibits a minimal non-gravitational interaction and is of a non-relativistic nature [122]. The dark matter candidate affects the deflection angle of light in wormhole spacetimes [123]. In this article, we have estimated the deflection angles of light in the spacetime of the Einstein–Cartan wormhole using Gibbons and Werner’s method and Keeton–Petters’ method, and we also analyzed the dark matter and Maxwell’s fish eye matter influences on the deflection angles. The present article has been designed as follows: We have formulated the Einstein–Cartan traversable wormhole solutions in Section 2. The Gauss–Bonnet method is described in Section 3. The Gaussian optical curvature is formulated in Section 3.1, and the Gauss–Bonnet theorem is described in Section 3.2. We have analyzed the dark matter influences on the deflection angle in Section 4. Section 5 deals with the influences of Maxwell’s fish eye matter on the deflection angle. We have estimated the deflection angle using the Keeton and Petters method in Section 6. The time delay is estimated in Section 7. Finally, the results and conclusion have been derived in Section 8.

2. Einstein–Cartan Traversable Wormhole Solutions

The Einstein–Cartan theory (ECT) is developed to describe the spin effects on the gravitational theory by considering a four-dimensional differential manifold endowed with a metric tensor and a linear connection [55,56]. Indeed, the mass and spin of the matter configuration simultaneously affect the structure of spacetime in the framework of the ECT. The action integral in this formulation can be expressed as [55,56]

$$\begin{array}{ccc}\hfill S& =& \int d^{4}x\sqrt{g}\left[{\displaystyle \frac{-1}{2k}}(R+2\mathsf{\Lambda })+{\mathcal{L}}_m\right]\hfill \\ & =& \int d^{4}x\sqrt{g}\left[{\displaystyle \frac{-1}{2k}}\left\{R\left(\left\{\right\}\right)+C_{\beta \lambda }^{\alpha }{C}_{\alpha }^{\beta \lambda }-C_{\beta \alpha }^{\alpha }{C}_{\lambda }^{\beta \lambda }+2\mathsf{\Lambda }\right\}+{\mathcal{L}}_m\right].\hfill \end{array}$$

(1)

where $k=8\pi G/c^4$, R, ${\mathcal{L}}_m$, and $\mathsf{\Lambda }$ are the gravitational coupling constant, Ricci scalar, Lagrangian of the matter fields, and the cosmological constant, respectively. Furthermore, the contortion tensor $C_{\alpha \beta }^{\mu }$ can be defined in the following form:

$$C_{\alpha \beta }^{\mu }=T_{\alpha \beta }^{\mu }+T_{\alpha \beta }^{\mu }+T_{\beta \alpha }^{\mu }.$$

(2)

Here, $T_{\mu \nu }^{\alpha }$ denotes the spacetime torsion tensor, defined as

$$T_{\alpha \beta }^{\mu }={\displaystyle \frac{1}{2}}\left[{\mathsf{\Gamma }}_{\alpha \beta }^{\mu }-{\mathsf{\Gamma }}_{\beta \alpha }^{\mu }\right].$$

(3)

The Cartan field equations can be derived from the variation of the action (1) with respect to the contortion tensor, as follows:

$$T_{\mu \beta }^{\alpha }-{\delta }_{\beta }^{\alpha }{T}_{\mu \gamma }^{\gamma }+{\delta }_{\mu }^{\alpha }{T}_{\beta \gamma }^{\gamma }=-{\displaystyle \frac{1}{2}}k{\tau }_{\mu \beta }^{\alpha },$$

(4)

where ${\tau }^{\mu \alpha \beta }=2(\delta {\mathcal{L}}_m/\delta C_{\mu \alpha \beta })/\sqrt{-g}$ represents the spin tensor of matter [55]. The governing equation of the torsion tensor is algebraic and does not permit the generation of torsion waves outside the matter distribution [55]. As a result, spacetime torsion exists solely within the matter configuration. Therefore, the variation of the action (1) formed the EC field equation as [55,124,125,126]

$$G_{\mu \nu }\left(\left\{\right\}\right)-\mathsf{\Lambda }{g}_{\mu \nu }=\kappa (T_{\mu \beta }+{\theta }_{\mu \beta }),$$

(5)

where $\left(\right)$ represents the symmetrization, and ${\theta }_{\mu \beta }$ is defined as

$$\begin{array}{ccc}\hfill {\theta }_{\mu \beta }& =& {\displaystyle \frac{1}{\kappa }}[4T_{\mu \eta }^{\eta }{T}_{\mu \beta }^{\beta }-2g_{\mu \nu }{T}_{\rho }^{\rho \sigma }{T}_{ϵ\sigma }^{\sigma }-\left(T_{\mu ϵ}^{\rho }+2T_{\left(\mu ϵ\right)}^{\rho }\right)\left(T_{\nu \rho }^{ϵ}+2T_{\left(\nu \rho \right)}^{ϵ}\right)\hfill \\ & & +{\displaystyle \frac{g_{\mu \nu }}{2}}\left(T^{\rho \sigma ϵ}+2T^{\left(\sigma ϵ\right)\rho }\right)\left(T_{ϵ\sigma \rho }+2T_{\left(\sigma \rho \right)ϵ}\right)],\hfill \end{array}$$

(6)

where the tensor ${\theta }_{\mu \nu }$ is a correction in the dynamical energy–momentum tensor $T_{\mu \beta }=2(\delta {\mathcal{L}}_m/\delta g^{\mu \beta })/\sqrt{-g}$. It is noted that field Equation (5) reduces to the standard Einstein field equation with a cosmological constant for ${\theta }_{\mu \nu }$ = 0. However, field Equation (5) can also be expressed as

$$\begin{array}{c}\hfill R_{\mu \nu }-{\displaystyle \frac{1}{2}}R{g}_{\mu \nu }-\mathsf{\Lambda }{g}_{\mu \nu }=\kappa {\mathsf{\Delta }}_{\mu \nu },\end{array}$$

(7)

where $R_{\mu \nu }$, and ${\mathsf{\Delta }}_{\mu \nu }$ are the Ricci tensor and canonical energy–momentum tensor, respectively. Moreover, ${\mathsf{\Delta }}_{\mu \nu }$ is related to $T_{\mu \beta }$ through the Belinfante–Rosenfeld relation, defined as

$$\begin{array}{c}\hfill {\mathsf{\Delta }}_{\alpha \beta }=T_{\alpha \beta }+{\displaystyle \frac{1}{2}}\left({\nabla }_{\mu }-2T_{\mu \gamma }^{\gamma }\right)\left({\tau }_{\alpha \beta }^{\mu }-{\tau }_{\beta \alpha }^{\mu }+{\tau }_{\alpha \beta }^{\mu }\right),\end{array}$$

(8)

where ${\nabla }_{\mu }$ represents the covariant derivative with respect to the asymmetric connection [127]. It is observed that the Bianchi identities (4) and EC field Equation (7) together yield the conservation laws for both the canonical energy–momentum tensor and the spin tensor [55,56,128,129,130,131,132,133,134,135,136,137]. Now, we take into account a classical representation of spin, defined as [137,138,139,140]

$$\begin{array}{c}\hfill {\tau }_{\mu \nu }^{\alpha }=S_{\mu \nu }{u}^{\alpha },S_{\mu \nu }{u}^{\mu }=0,\end{array}$$

(9)

where $u^{\alpha }$ and $S_{\mu \nu }$ are the four-velocity and spin density tensor, respectively.

Therefore, the total energy–momentum tensor can be expressed as comprising the usual fluid component and an intrinsic spin component, given by [141]

$$\begin{array}{ccc}\hfill T_{\alpha \beta }^{total}& =& T_{\alpha \beta }+{\theta }_{\alpha \beta }\hfill \\ & =& \left[(\rho \left(r\right)+P_t\left(r\right))u_{\alpha }{u}_{\beta }+P_t\left(r\right)g_{\alpha \beta }+(P_r\left(r\right)-P_t\left(r\right))v_{\alpha }{v}_{\beta }\right]+u_{(\alpha }{S}_{\beta )}^{\mu }{u}^{\nu }{C}_{\mu \nu }^{\rho }{u}_{\rho }\hfill \\ & & +u^{\rho }{C}_{\rho \sigma }^{\mu }{u}^{\sigma }{u}_{(\alpha }{S}_{\beta )\mu }-{\displaystyle \frac{1}{2}}{u}_{(\alpha }{T}_{\beta )\mu \nu }{S}^{\mu \nu }+{\displaystyle \frac{1}{2}}{T}_{\mu \nu (\alpha }{S}_{\beta )}^{\mu }{u}^{\nu },\hfill \end{array}$$

(10)

where $v_{\mu }$ is the radial unit spacelike vector field, and $\rho \left(r\right)$, $P_r\left(r\right)$, and $P_t\left(r\right)$ are the energy density, radial pressure, and tangential pressure of the fluid, respectively. Therefore, Einstein’s field equation for anisotropic matter distribution with spin correction terms can be written from Equations (5) and (6) together with Equations (9) and (10) in the following form

$$\begin{array}{ccc}\hfill G_{\mu \nu }-\mathsf{\Lambda }{g}_{\mu \nu }& =& \kappa \left(\rho +P_t-{\displaystyle \frac{\kappa }{2}}{S}^2\right)u_{\mu }{u}_{\nu }+\kappa \left(P_t-{\displaystyle \frac{\kappa }{4}}{S}^2\right)g_{\mu \nu }+\left(P_r-P_t\right)v_{\mu }{v}_{\nu }.\hfill \end{array}$$

(11)

With $S^2={\displaystyle \frac{1}{2}}⟨S_{\mu \nu }{S}^{\mu \nu }⟩$.

Now, the Morris–Thorne traversable wormhole spacetime metric is defined as [4]

$$d{s}^2=-e^{2\mathsf{\Phi }\left(r\right)}d{t}^2+{\left(1-{\displaystyle \frac{\mathsf{\Omega }\left(r\right)\left(r\right)}{r}}\right)}^{-1}d{r}^2+r^2(d{\theta }^2+si{n}^2\theta d{\varphi }^2)$$

(12)

where $\mathsf{\Phi }\left(r\right)$ and $\mathsf{\Omega }\left(r\right)\left(r\right)$ are the redshift function and shape function, respectively.

Therefore, for metric (12), EC field Equation (11) reads as (considering the units $\kappa$ = c = 1)

$$\begin{array}{ccc}\hfill \rho \left(r\right)& =& {\displaystyle \frac{1}{4r^2}}\left[4{\mathsf{\Omega }}^{\prime }\left(r\right)\left(r\right)+r^2{S}^2\left(r\right)-4\mathsf{\Lambda }{r}^2\right],\hfill \end{array}$$

(13)

$$\begin{array}{ccc}\hfill P_r\left(r\right)& =& {\displaystyle \frac{1}{4r^3}}\left[8r{\mathsf{\Phi }}^{\prime }\left(r\right)\left(r-\mathsf{\Omega }\left(r\right)\left(r\right)\right)-4\mathsf{\Omega }\left(r\right)\left(r\right)+r^3{S}^2\left(r\right)+4\mathsf{\Lambda }{r}^3\right],\hfill \end{array}$$

(14)

$$\begin{array}{ccc}\hfill P_t\left(r\right)& =& {\displaystyle \frac{1}{4r^3}}[4r^2\left({\mathsf{\Phi }}^{″}\left(r\right)+{\mathsf{\Phi }}^{\prime 2}\left(r\right)\right)\left(r-\mathsf{\Omega }\left(r\right)\left(r\right)\right)-2r{\mathsf{\Phi }}^{\prime }\left(r\right)\left(r{\mathsf{\Omega }}^{\prime }\left(r\right)\left(r\right)-2r+\mathsf{\Omega }\left(r\right)\left(r\right)\right)\hfill \\ & & +r^3{S}^2\left(r\right)-2r{\mathsf{\Omega }}^{\prime }\left(r\right)\left(r\right)+2\mathsf{\Omega }\left(r\right)\left(r\right)].\hfill \end{array}$$

(15)

where ′ stands for ${\displaystyle \frac{d}{dr}}$. The conservation equation of the total energy–momentum tensor can be expressed as

$$\begin{array}{c}\hfill {\mathsf{\Phi }}^{\prime }(\rho \left(r\right)+P_r\left(r\right))+P_r^{\prime }\left(r\right)+{\displaystyle \frac{2}{r}}(P_r\left(r\right)-P_t\left(r\right))-{\displaystyle \frac{1}{2}}\left[{\mathsf{\Phi }}^{\prime }{S}^2+{\displaystyle \frac{1}{2}}{\left(S^2\right)}^{\prime }\right]=0.\end{array}$$

(16)

Furthermore, we can assume that the spin component of the conservation equation is satisfied independently, leading to

$$\begin{array}{c}\hfill {\mathsf{\Phi }}^{\prime }{S}^2+{\displaystyle \frac{1}{2}}{\left(S^2\right)}^{\prime }=0\end{array}$$

(17)

Thus, we acquire

$$\begin{array}{c}\hfill S^2=S_0^{2}exp(-2{\varphi }^{\prime }\left(r\right))\end{array}$$

(18)

where $S_0$ is a constant of integration.

Recently, Mehdizadeh et al. [73] introduced the traversable wormhole solutions in the context of the Einstein–Cartan gravity by adopting a linear equation of state (EoS), $P_r\left(r\right)=\omega \rho \left(r\right)$; $\omega$ is a constant termed as an EoS parameter and a constant redshift function, defined as ${\mathsf{\Phi }}^{\prime }\left(r\right)$ = 0. Substituting $P_r\left(r\right)$ and $\rho \left(r\right)$ into the EoS $P_r\left(r\right)=\omega \rho \left(r\right)$, one obtains the following expression:

$$\begin{array}{c}\hfill {\mathsf{\Omega }}^{\prime }\left(r\right)={\displaystyle \frac{8r(r-\mathsf{\Omega }\left(r\right)){\mathsf{\Phi }}^{\prime }\left(r\right)-4\mathsf{\Omega }\left(r\right)+(1-\omega )r^3{S}^2\left(r\right)+4\mathsf{\Lambda }{r}^3(1+\omega )}{4\omega r}}.\end{array}$$

(19)

Now, for the constant redshift function, ${\mathsf{\Phi }}^{\prime }\left(r\right)$ = 0, the share function $\mathsf{\Omega }\left(r\right)$ is obtained from Equation (19) in the following form

$$\begin{array}{c}\hfill \mathsf{\Omega }\left(r\right)={\displaystyle \frac{\xi r^3}{4(1+3\omega )}}+{\displaystyle \frac{C}{r^{\frac{1}{\omega }}}},\end{array}$$

(20)

where C is the integration constant, and $\xi =4\mathsf{\Lambda }(1+\omega )-S_0^2(\omega -1)$. Now, the condition $\mathsf{\Omega }\left(r_0\right)=r_0$ yields the following result:

$$\begin{array}{c}\hfill C={\displaystyle \frac{4r_0(3w+1)-\xi r_0^3}{4(3w+1)r_0^{-\frac{1}{w}}}}\end{array}$$

(21)

Mehdizadeh et al. [73] set the values of $\mathsf{\Lambda }$ and $S_0$ to ensure that $\xi$ = 0. Therefore, the value of C reads as

$$\begin{array}{c}\hfill C=r_0^{1+{\displaystyle \frac{1}{w}}}\end{array}$$

(22)

Thus, the shape function reads as

$$\begin{array}{c}\hfill \mathsf{\Omega }\left(r\right)=r_0{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{1}{\omega }}}.\end{array}$$

(23)

Now, we can obtain the following result:

$$\begin{array}{c}\hfill {\mathsf{\Omega }}^{\prime }\left(r_0\right)=-{\displaystyle \frac{1}{\omega }}.\end{array}$$

(24)

The above result ensures that the shape function satisfies the flare-out condition ${\mathsf{\Omega }}^{\prime }\left(r_0\right)<1$ for $\omega >0$ or $\omega <-1$. Moreover, Mehdizadeh et al. [73] described that their presented wormholes are supported by normal matter or matter made of phantom energy corresponding to $\omega >0$ or $\omega <-1$. In this scenario, therefore, the Einstein–Cartan traversable wormhole solutions can be expressed as

$$d{s}^2=-d{t}^2+{\left[1-{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{\omega +1}{\omega }}}\right]}^{-1}d{r}^2+r^2(d{\theta }^2+sin\theta d{\varphi }^2),$$

(25)

The above Einstein–Cartan traversable wormholes are asymptotically flat, which permits the estimation of the deflection angle in the spacetime of these wormholes by using the Gauss–Bonnet (GB) method in the weak field limit. Indeed, the asymptotically flat nature of the present wormholes motivates us to consider them in this study.

3. Gauss–Bonnet (GB) Method

In this section, we are going to estimate the deflection angles in the spacetimes of both kinds of Einstein–Cartan traversable wormholes: filled with normal matter and matter made of phantom energy by the use of the GB method.

3.1. Gaussian Optical Curvature

To obtain the Gaussian optical curvature, we take into account the null geodesics deflected by Einstein–Cartan wormholes. At the equatorial plane $\theta =\pi /2$, the null geodesic equations $d{s}^2$ = 0 for the wormhole spacetime metric (2) read as

$$d{t}^2={\left[1-{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{\omega +1}{\omega }}}\right]}^{-1}d{r}^2+r^{2}d{\varphi }^2.$$

(26)

Now, we consider the static radial Regge–Wheeler tortoise coordinate $r^{★}$ that helps to express the optical metric with a new function $f\left(r^{★}\right)$ in the following form:

$$d{t}^2\equiv g_{ab}^{op}d{x}^{a}d{x}^b={d{r}^{★}}^2+{f\left(r^{★}\right)}^{2}d{\phi }^2.$$

(27)

It is important to note that the static radial Regge–Wheeler tortoise coordinate $r^{★}$ ensures that the equatorial plane in the optical metric can be described as a surface of revolution whenever it is embedded in ${\mathbb{R}}^3$. Now, comparing Equations (26) and (27), we obtain the following results:

$$\begin{array}{ccc}\hfill d{r}^{★}& =& {\left[1-{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{\omega +1}{\omega }}}\right]}^{-1/2}dr,\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill f\left(r^{★}\right)& =& r.\hfill \end{array}$$

(29)

The mathematical formula to calculate the Gaussian curvature $\mathbf{G}$ of the optical surface is defined as [83]

$$\begin{array}{ccc}\hfill \mathcal{G}& =& -{\displaystyle \frac{1}{f\left(r^{★}\right)}}{\displaystyle \frac{d^{2}f\left(r^{★}\right)}{d{r^{★}}^2}}=-{\displaystyle \frac{1}{f\left(r^{★}\right)}}\left[{\displaystyle \frac{dr}{d{r}^{★}}}{\displaystyle \frac{d}{dr}}\left({\displaystyle \frac{dr}{d{r}^{★}}}\right){\displaystyle \frac{df}{dr}}+{\left({\displaystyle \frac{dr}{d{r}^{★}}}\right)}^2{\displaystyle \frac{d^{2}f}{d{r}^2}}\right].\hfill \end{array}$$

Using the above formula (30), we obtain the optical Gaussian curvature for the Einstein–Cartan wormholes (2) as

$$\begin{array}{ccc}\hfill \mathcal{G}& =& -{\displaystyle \frac{(\omega +1)r_0^{\frac{\omega +1}{\omega }}}{2\omega r^{\frac{3\omega +1}{\omega }}}}.\hfill \end{array}$$

(30)

The above optical Gaussian curvature can be used to calculate the deflection angle of light by the Einstein–Cartan wormholes.

3.2. Deflection Angle

In the realm of the weak gravitational field, the bending angle of light observed from a distant source can be calculated using the Gauss–Bonnet theorem. For a non-singular region ${\mathcal{S}}_R$ surrounded by the beam of light with boundary $\partial {\mathcal{S}}_R={\gamma }_{g^{op}}\cup {\gamma }_R$, having the Euler characteristic element $\chi$ and metric g in the focal region where the light rays meet with both the source and the viewer, the GB theorem reads as [83]

$$\underset{{\mathcal{S}}_R}{\int \int }\mathcal{G}\mathrm{d}\mathcal{A}+\underset{\partial {\mathcal{S}}_R}{\oint }\kappa \mathrm{d}t+\sum _i{\theta }_i=2\pi \chi \left({\mathcal{S}}_R\right),$$

(31)

where ${\theta }_i$ stands for the exterior angle at the $i^{th}$ vertex, $\mathrm{d}\mathcal{A}$ is the the surface element, and $\kappa$ represents the geodesic curvature. It is noted that $\chi \left({\mathcal{S}}_R\right)=1$ for a non-singular domain outside of the light ray and $\chi \left({\mathcal{S}}_R\right)=0$ for a singular domain outside of the light ray. We go further for the non-singular domain outside of the light ray.

Now, the geodesic curvature can be computed using the following formula:

$$\kappa =g^{\mathrm{op}}\left({\nabla }_{\dot{\gamma }}\dot{\gamma },\ddot{\gamma }\right)\mathrm{with}{g}^{op}(\dot{\gamma },\dot{\gamma })=1,$$

(32)

where $\ddot{\gamma }$ represents the unit acceleration vector. It is noted that the jump angles of the viewer ${\theta }_v$ and source ${\theta }_s$ satisfy the condition ${\theta }_v$ + ${\theta }_s\to \pi$ for $R\to \infty$ [83]. Furthermore, for a geodesic ${\gamma }_{g^{op}}$, $\kappa \left({\gamma }_{g^{op}}\right)=0$. Therefore, geodesic curvature $\kappa$ becomes

$$\kappa \left({\gamma }_R\right)=\left|{\nabla }_{{\dot{\gamma }}_R}{\dot{\gamma }}_R\right|,$$

(33)

Now, the radial part of the geodesic curvature $\kappa$ with the condition ${\gamma }_R:=r\left(\phi \right)=R=\mathrm{constant}$ can be expressed as

$${\left({\nabla }_{{\dot{\gamma }}_R}{\dot{\gamma }}_R\right)}^r={\dot{\gamma }}_R^{\phi }\left({\partial }_{\phi }{\dot{\gamma }}_R^r\right)+{\tilde{\mathsf{\Gamma }}}_{\phi \phi }^r{\left({\dot{\gamma }}_R^{\phi }\right)}^2,$$

(34)

where ${\tilde{\mathsf{\Gamma }}}_{\phi \phi }^r$ stands for the Christoffel symbol of the optical metric. The first term in the expression above nullifies and the subsequent term can be derived using the unit speed condition ${\tilde{g}}_{\phi \phi }{\dot{\gamma }}_R^{\phi }{\dot{\gamma }}_R^{\phi }=1$, this results in

$$\begin{array}{ccc}\hfill \underset{R\to \infty }{lim}\kappa \left({\gamma }_R\right)& =& \underset{R\to \infty }{lim}\left|{\nabla }_{{\dot{\gamma }}_R}{\dot{\gamma }}_R\right|,\to {\displaystyle \frac{1}{R}}.\hfill \end{array}$$

For the optical metric (26), ${lim}_{R\to \infty }dt\to Rd\phi$ at the significantly vast radial distances. Therefore, the GB theorem (31) can be expressed as

$$\underset{{\mathcal{S}}_R}{\int \int }\mathcal{G}d\mathcal{A}+\underset{{\gamma }_R}{\oint }\kappa dt\stackrel{R\to \infty }{=}\underset{{\mathcal{S}}_{\infty }}{\int \int }\mathcal{G}d\mathcal{A}+\underset{0}{\overset{\pi +\widehat{\alpha }}{\int }}d\phi =\pi ,$$

(35)

where $d\mathcal{A}=\sqrt{det{g}^{op}}d{r}^{★}d\phi .$ Finally, the mathematical formula for the deflection angle can be expressed as

$$\begin{array}{ccc}\hfill \widehat{\alpha }& =& -\underset{0}{\overset{\pi }{\int }}\underset{r_{\gamma }}{\overset{\infty }{\int }}\mathcal{G}\sqrt{det{g}^{op}}d{r}^{★}d\phi .\hfill \end{array}$$

(36)

We can estimate the deflection angle from the above formula (36) by choosing the light ray as $r\left(\phi \right)=b/sin\phi$, where b is the impact parameter. Next, we compute the deflection angle of light in the spacetime of the Einstein–Cartan wormholes associated with the normal matter, $\omega =1/3,1/6$, and the matter with phantom energy, $\omega =-6/5,-3/2$.

3.2.1. Case-I: $\omega ={\displaystyle \frac{1}{3}}$

First, we compute the Gaussian optical curvature using formula (30) for the case $\omega =1/3$ as

$${\mathcal{G}}_{\omega ={\displaystyle \frac{1}{3}}}=-{\displaystyle \frac{2r_0^4}{r^6}}.$$

(37)

Then, the deflection angle with the above Gaussian optical curvature can be expressed in terms of the following integral:

$$\begin{array}{ccc}\hfill {\widehat{\alpha }}_{\omega ={\displaystyle \frac{1}{3}}}& =& \underset{0}{\overset{\pi }{\int }}\underset{r_{\gamma }}{\overset{\infty }{\int }}{\displaystyle \frac{2r_0^4}{r^6}}\sqrt{det{g}^{op}}d{r}^{★}d\phi .\hfill \end{array}$$

(38)

To evaluate the integral above, it is important to recognize that

$$\sqrt{det{g}^{op}}d{r}^{★}=r{\left[1-{\left({\displaystyle \frac{r_0}{r}}\right)}^4\right]}^{-1/2}dr$$

(39)

Expanding the last equation in the Taylor series we obtain

$$\sqrt{det{g}^{op}}d{r}^{★}=rdr\left[1+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{r_0}{r}}\right)}^4+{\displaystyle \frac{3}{8}}{\left({\displaystyle \frac{r_0}{r}}\right)}^8+{\displaystyle \frac{5}{16}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{12}+{\displaystyle \frac{35}{128}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{16}+.....+O\left({\left({\displaystyle \frac{r_0}{r}}\right)}^{4n}\right)\right].$$

(40)

After imposing the above result in Equation (36), we obtain the deflection angle as

$${\widehat{\alpha }}_{\omega ={\displaystyle \frac{1}{3}}}\simeq {\displaystyle \frac{3\pi }{16}}{\left({\displaystyle \frac{r_0}{b}}\right)}^4+{\displaystyle \frac{35\pi }{1024}}{\left({\displaystyle \frac{r_0}{b}}\right)}^8+{\displaystyle \frac{231\pi }{16384}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{12}+{\displaystyle \frac{32175\pi }{4194304}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{16}+{\displaystyle \frac{323323\pi }{67108864}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{20}.$$

(41)

This deflection angle is graphically depicted in Figure 1 (Left), which ensures that it decreases in increasing values of impact parameter b and increases for increasing values of wormhole throat radius $r_0$. Furthermore, one can see that the deflection angle becomes zero for $r_0=0$, the absence of Einstein–Cartan wormholes.

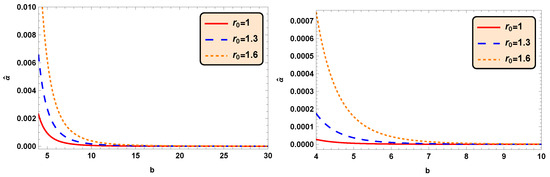
Figure 1. Deflection angle $\widehat{\alpha }$ against the impact parameter b corresponding to $\omega ={\displaystyle \frac{1}{3}}$ (Left) and $\omega ={\displaystyle \frac{1}{6}}$ (Right).

3.2.2. Case-II: $\omega ={\displaystyle \frac{1}{6}}$

The Gaussian optical curvature for $\omega =1/6$ is obtained from Equation (30) as

$${\mathcal{G}}_{\omega ={\displaystyle \frac{1}{6}}}=-{\displaystyle \frac{7r_0^7}{2r^9}}$$

(42)

With the above Gaussian curvature (42), the deflection angle reads as

$$\begin{array}{ccc}\hfill {\widehat{\alpha }}_{\omega ={\displaystyle \frac{1}{6}}}& =& \underset{0}{\overset{\pi }{\int }}\underset{r_{\gamma }}{\overset{\infty }{\int }}{\displaystyle \frac{7r_0^7}{2r^9}}\sqrt{det{g}^{op}}\mathrm{d}{r}^{★}\mathrm{d}\phi .\hfill \end{array}$$

(43)

To find the result of the above integral, let us note that

$$\sqrt{det{g}^{op}}d{r}^{★}=r{\left[1-{\left({\displaystyle \frac{r_0}{r}}\right)}^7\right]}^{-1/2}dr=rdr\left[1+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{r_0}{r}}\right)}^7+{\displaystyle \frac{3}{8}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{14}+{\displaystyle \frac{5}{16}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{21}+{\displaystyle \frac{35}{128}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{28}+.....+O\left({\left({\displaystyle \frac{r_0}{r}}\right)}^{7n}\right)\right].$$

(44)

Therefore, in this case, the deflection angle is obtained as

$${\widehat{\alpha }}_{\omega ={\displaystyle \frac{1}{6}}}\simeq {\displaystyle \frac{16}{35}}{\left({\displaystyle \frac{r_0}{b}}\right)}^7+{\displaystyle \frac{429\pi }{16384}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{14}+{\displaystyle \frac{32768}{969969}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{21}+{\displaystyle \frac{25072875\pi }{4294967296}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{28}+{\displaystyle \frac{33554432}{2917007775}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{35}.$$

(45)

We graphically demonstrate the deflection angle ${\widehat{\alpha }}_{\omega ={\displaystyle \frac{1}{6}}}$ in Figure 1 (Right). One can see that this deflection angle has the same behaviors as the deflection angle ${\widehat{\alpha }}_{\omega ={\displaystyle \frac{1}{6}}}$, but it is smaller in amount compared to ${\widehat{\alpha }}_{\omega ={\displaystyle \frac{1}{3}}}$. In week limit filed approximation, the deflection angle (SC) of the Schwarzschild black hole = 4M/b, M is the mass of the black hole [142]. From Figure 2, it is clear that the rate of decreasing of our reported deflection angles ${\widehat{\alpha }}_{\omega ={\displaystyle \frac{1}{3}}}$ and ${\widehat{\alpha }}_{\omega ={\displaystyle \frac{1}{6}}}$ is higher than the rate of decreasing of the deflection angle SC against the impact parameter b. Therefore, these deflection angles cannot mimic the deflection angle (SC) of the Schwarzschild black hole.

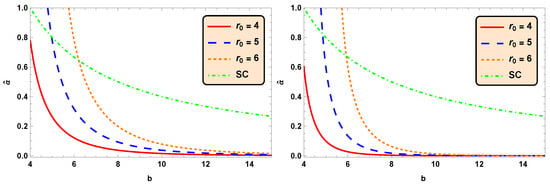
Figure 2. Deflection angle $\widehat{\alpha }$ against the impact parameter b corresponding to $\omega ={\displaystyle \frac{1}{3}}$ (Left) and $\omega ={\displaystyle \frac{1}{6}}$ (Right) with the deflection angle (SC) of the Schwarzschild black hole for mass $M=1$.

3.2.3. Case-III: $\omega =-{\displaystyle \frac{6}{5}}$

In this case, the Gaussian optical curvature is found as

$${\mathcal{G}}_{\omega =-{\displaystyle \frac{6}{5}}}=-{\displaystyle \frac{r_0^{1/6}}{12r^{13/6}}}$$

(46)

Then, we find that the deflection angle in terms of the following integral is

$$\begin{array}{ccc}\hfill {\widehat{\alpha }}_{\omega =-{\displaystyle \frac{6}{5}}}& =& \underset{0}{\overset{\pi }{\int }}\underset{r_{\gamma }}{\overset{\infty }{\int }}{\displaystyle \frac{r_0^{1/6}}{12r^{13/6}}}\sqrt{det{g}^{op}}\mathrm{d}{r}^{★}\mathrm{d}\phi ,\hfill \end{array}$$

(47)

With the surface element

$$\sqrt{det{g}^{op}}d{r}^{★}=r{\left[1-{\left({\displaystyle \frac{r_0}{r}}\right)}^{1/6}\right]}^{-1/2}dr=rdr\left[1+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{1/6}+{\displaystyle \frac{3}{8}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{1/3}+{\displaystyle \frac{5}{16}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{1/2}+{\displaystyle \frac{35}{128}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{2/3}+..+O\left({\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{n}{6}}}\right)\right].$$

(48)

Therefore, on using the above result, we find the deflection angle as

$${\widehat{\alpha }}_{\omega =-{\displaystyle \frac{6}{5}}}\simeq {\displaystyle \frac{6\sqrt{\pi }\mathsf{\Gamma }\left(\frac{19}{12}\right)}{7\mathsf{\Gamma }\left(\frac{13}{12}\right)}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{{\displaystyle \frac{1}{6}}}+{\displaystyle \frac{3\sqrt{\pi }\mathsf{\Gamma }\left(\frac{5}{3}\right)}{16\mathsf{\Gamma }\left(\frac{7}{6}\right)}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{{\displaystyle \frac{1}{3}}}+{\displaystyle \frac{\mathsf{\Gamma }{\left(\frac{3}{4}\right)}^2}{4\sqrt{2\pi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{{\displaystyle \frac{1}{2}}}+{\displaystyle \frac{3\sqrt{\pi }\mathsf{\Gamma }\left(\frac{11}{6}\right)}{64\mathsf{\Gamma }\left(\frac{4}{3}\right)}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{{\displaystyle \frac{2}{3}}}+{\displaystyle \frac{21\sqrt{\pi }\mathsf{\Gamma }\left(\frac{23}{12}\right)}{704\mathsf{\Gamma }\left(\frac{17}{12}\right)}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{{\displaystyle \frac{5}{6}}}.$$

(49)

This deflection angle also decreases in increasing values of impact parameter b and increases for increasing values of wormhole throat radius $r_0$ (See Figure 3). Interestingly, from the above expression, we can conclude that there is no deflection angle for $r_0=0$, the absence of Einstein–Cartan wormholes.

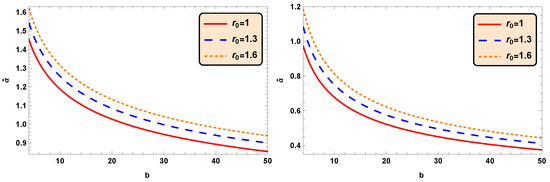
Figure 3. Deflection angle $\widehat{\alpha }$ against the impact parameter b corresponding to $\omega =-{\displaystyle \frac{6}{5}}$ (Left) and $\omega =-{\displaystyle \frac{3}{2}}$ (Right).

3.2.4. Case-IV: $\omega =-{\displaystyle \frac{3}{2}}$

The Gaussian optical curvature in this case is found as

$${\mathcal{G}}_{\omega =-{\displaystyle \frac{3}{2}}}=-{\displaystyle \frac{r_0^{1/3}}{6r^{7/3}}}.$$

(50)

Similarly, we find the deflection angle as

$$\begin{array}{ccc}\hfill {\widehat{\alpha }}_{\omega =-{\displaystyle \frac{3}{2}}}& =& \underset{0}{\overset{\pi }{\int }}\underset{r_{\gamma }}{\overset{\infty }{\int }}{\displaystyle \frac{r_0^{1/3}}{6r^{7/3}}}\sqrt{det{g}^{op}}\mathrm{d}{r}^{★}\mathrm{d}\phi ,\hfill \end{array}$$

(51)

with

$$\sqrt{det{g}^{op}}d{r}^{★}=r{\left[1-{\left({\displaystyle \frac{r_0}{r}}\right)}^{1/3}\right]}^{-1/2}dr=rdr\left[1+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{1/3}+{\displaystyle \frac{3}{8}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{2/3}+{\displaystyle \frac{5}{16}}\left({\displaystyle \frac{r_0}{r}}\right)+{\displaystyle \frac{35}{128}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{4/3}+...+O\left({\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{n}{3}}}\right)\right].$$

(52)

Therefore, the above result yields the deflection angle as

$${\widehat{\alpha }}_{\omega =-{\displaystyle \frac{3}{2}}}\simeq {\displaystyle \frac{{\pi }^{3/2}}{\sqrt{3}\mathsf{\Gamma }\left(\frac{1}{3}\right)\mathsf{\Gamma }\left(\frac{7}{6}\right)}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{{\displaystyle \frac{1}{3}}}+{\displaystyle \frac{{\pi }^{\frac{2}{3}}}{4\mathsf{\Gamma }\left(\frac{1}{6}\right)\mathsf{\Gamma }\left(\frac{4}{3}\right)}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{2/3}+{\displaystyle \frac{r_0}{8b}}+{\displaystyle \frac{5{\pi }^{3/2}}{256\mathsf{\Gamma }\left(\frac{2}{3}\right)\mathsf{\Gamma }\left(\frac{5}{6}\right)}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{{\displaystyle \frac{4}{3}}}+{\displaystyle \frac{7{\pi }^{3/2}}{320\sqrt{3}\mathsf{\Gamma }\left(\frac{2}{3}\right)\mathsf{\Gamma }\left(\frac{5}{6}\right)}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{{\displaystyle \frac{5}{3}}}.$$

(53)

The deflection angle ${\widehat{\alpha }}_{\omega =-{\displaystyle \frac{3}{2}}}$ behaves similarly to the deflection angle ${\widehat{\alpha }}_{\omega =-{\displaystyle \frac{6}{5}}}$ with respect to the impact parameter b and wormhole throat $r_0$; moreover, the deflection angle ${\widehat{\alpha }}_{\omega =-{\displaystyle \frac{3}{2}}}$ is lesser than the deflection angle ${\widehat{\alpha }}_{\omega =-{\displaystyle \frac{6}{5}}}$ (See Figure 3 (Right)).

We now compare the approximated deflection angles with their exact numerical values using graphical representation. In order to carry this out, we have solved Equation (36) using a numerical technique corresponding to $r_0=1$ and $\omega =\{1/3,1/6,-6/5,-3/2\}$ with step length = 1. The approximated deflection angles for all the cases $\omega =\{1/3,1/6,-6/5,-3/2\}$ associated with $r_0=1$ are slightly lower than their respective exact numerical values, as is clear from Figure 4.

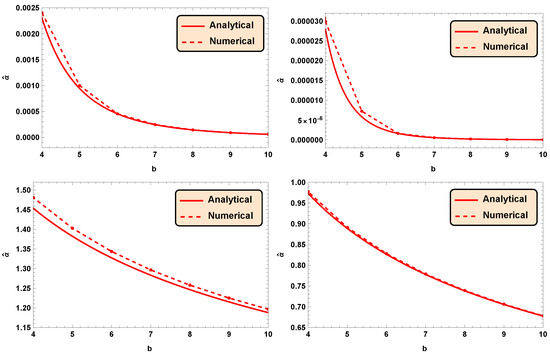
Figure 4. Analytical and numerical deflection angles $\widehat{\alpha }$ against the impact parameter b corresponding to the above panel: $\omega ={\displaystyle \frac{1}{3}}$, $r_0$ = 1 (Left) and $\omega ={\displaystyle \frac{1}{6}}$, $r_0$ = 1 (Right); below panel: $\omega =-{\displaystyle \frac{6}{5}}$, $r_0$ = 1 (Left) and $\omega =-{\displaystyle \frac{3}{2}}$, $r_0$ = 1 (Right).

4. Dark Matter’s Influence on Deflection Angle

Here, we are willing to study the influences of dark matter on the weak deflection angle of light in the spacetime of Einstein–Cartan wormholes. In this regard, we consider the refractive index for the dark matter medium, defined as [143]

$$\begin{array}{c}\hfill n\left(\xi \right)=1+\beta A_0+A_2{\xi }^2\end{array}$$

(54)

where $\xi$ is the frequency of light, $\beta ={\rho }_0/4m^2{\xi }^2$ and ${\rho }_0$ are the mass density of the scattered dark-matter particles, $A_0=-2{ϵ}^2{e}^2$, and $A_2\ge 0$.

The optical geometry of the Einstein–Cartan wormholes with the effect of the dark matter can be given as

$$\begin{array}{c}\hfill d{t}^2=n^2\left(\xi \right){\left[1-{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{\omega +1}{\omega }}}\right]}^{-1}d{r}^2+n^2\left(\xi \right)r^{2}d{\varphi }^2\end{array}$$

(55)

For the above optical geometry, we obtain the Gaussian optical curvature ${\mathcal{G}}_{DM}$ with the dark matter influence as follows:

$$\begin{array}{c}\hfill {\mathcal{G}}^{DM}=-{\displaystyle \frac{(\omega +1)r_0^{\frac{\omega +1}{\omega }}}{2\omega {\left(1+\beta A_0+A_2{\xi }^2\right)}^2{r}^{\frac{3\omega +1}{\omega }}}}.\end{array}$$

(56)

Imposing the above result in the formula of the deflection angle (36), we obtain the deflection angles in the following forms:

$$\begin{array}{ccc}\hfill {\widehat{\alpha }}_{\omega ={\displaystyle \frac{1}{3}}}^{DM}& \simeq & {\displaystyle \frac{3\pi }{16\mathsf{\Psi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^4+{\displaystyle \frac{35\pi }{1024\mathsf{\Psi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^8+{\displaystyle \frac{231\pi }{16384\mathsf{\Psi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{12}+{\displaystyle \frac{32175\pi }{4194304\mathsf{\Psi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{16}+{\displaystyle \frac{323323\pi }{67108864\mathsf{\Psi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{20},\hfill \end{array}$$

(57)

$$\begin{array}{ccc}\hfill {\widehat{\alpha }}_{\omega ={\displaystyle \frac{1}{6}}}^{DM}& \simeq & {\displaystyle \frac{16}{35\mathsf{\Psi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^7+{\displaystyle \frac{429\pi }{16384\mathsf{\Psi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{14}+{\displaystyle \frac{32768}{969969\mathsf{\Psi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{21}+{\displaystyle \frac{25072875\pi }{4294967296\mathsf{\Psi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{28}+{\displaystyle \frac{33554432}{2917007775\mathsf{\Psi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{35},\hfill \end{array}$$

(58)

$$\begin{array}{ccc}\hfill {\widehat{\alpha }}_{\omega =-{\displaystyle \frac{6}{5}}}^{DM}& \simeq & {\displaystyle \frac{6\sqrt{\pi }\mathsf{\Gamma }\left(\frac{19}{12}\right)}{7\mathsf{\Gamma }\left(\frac{13}{12}\right)\mathsf{\Psi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{{\displaystyle \frac{1}{6}}}+{\displaystyle \frac{3\sqrt{\pi }\mathsf{\Gamma }\left(\frac{5}{3}\right)}{16\mathsf{\Gamma }\left(\frac{7}{6}\right)\mathsf{\Psi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{{\displaystyle \frac{1}{3}}}+{\displaystyle \frac{\mathsf{\Gamma }{\left(\frac{3}{4}\right)}^2}{4\sqrt{2\pi }\mathsf{\Psi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{{\displaystyle \frac{1}{2}}}+{\displaystyle \frac{3\sqrt{\pi }\mathsf{\Gamma }\left(\frac{11}{6}\right)}{64\mathsf{\Gamma }\left(\frac{4}{3}\right)\mathsf{\Psi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{{\displaystyle \frac{2}{3}}}+{\displaystyle \frac{21\sqrt{\pi }\mathsf{\Gamma }\left(\frac{23}{12}\right)}{704\mathsf{\Gamma }\left(\frac{17}{12}\right)\mathsf{\Psi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{{\displaystyle \frac{5}{6}}},\hfill \end{array}$$

(59)

$$\begin{array}{ccc}\hfill {\widehat{\alpha }}_{\omega =-{\displaystyle \frac{3}{2}}}^{DM}& \simeq & {\displaystyle \frac{{\pi }^{3/2}}{\sqrt{3}\mathsf{\Gamma }\left(\frac{1}{3}\right)\mathsf{\Gamma }\left(\frac{7}{6}\right)\mathsf{\Psi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{{\displaystyle \frac{1}{3}}}+{\displaystyle \frac{{\pi }^{\frac{2}{3}}}{4\mathsf{\Gamma }\left(\frac{1}{6}\right)\mathsf{\Gamma }\left(\frac{4}{3}\right)\mathsf{\Psi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{{\displaystyle \frac{2}{2}}}+{\displaystyle \frac{r_0}{8\mathsf{\Psi }b}}+{\displaystyle \frac{5{\pi }^{3/2}}{256\mathsf{\Gamma }\left(\frac{2}{3}\right)\mathsf{\Gamma }\left(\frac{5}{6}\right)\mathsf{\Psi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{{\displaystyle \frac{4}{3}}}\hfill \\ & & +{\displaystyle \frac{7{\pi }^{3/2}}{320\sqrt{3}\mathsf{\Gamma }\left(\frac{2}{3}\right)\mathsf{\Gamma }\left(\frac{5}{6}\right)\mathsf{\Psi }}}{\left({\displaystyle \frac{r_0}{b}}\right)}^{{\displaystyle \frac{5}{3}}},\hfill \end{array}$$

(60)

where $\mathsf{\Psi }=A_0^2{\beta }^2+2A_0{A}_2\beta {\xi }^2+2A_0\beta +A_2^2{\xi }^4+2A_2{\xi }^2+1$. Here, we can find that the deflection angles through the dark matter around the Einstein–Cartan traversable wormholes have been increased compared to the deflection angles by Einstein–Cartan traversable wormholes in general cases.

5. Maxwell’s Fish Eye Matter Influences on Deflection Angle

In this section, we discuss the effect of Maxwell’s fish eye (MFE) matter influences on the obtained deflection angles in the Einstein–Cartan wormhole spacetime. For that, we consider the refractive-index profile of the MFE-like medium, defined as [144]

$$\begin{array}{c}\hfill n={\displaystyle \frac{z_0}{1+z^2}}\end{array}$$

(61)

where $z_0$ is a constant and z is the complex coordinate of the wave propagation in a two-dimensional Cartesian $(x,y)$ plane. Now, we find the Gaussian optical curvature for optical metric with the refractive-index profile of the MFE-like medium as follows:

$$\begin{array}{c}\hfill {\mathcal{G}}^{MFE}=-{\displaystyle \frac{d(\omega +1){\left(z^2+1\right)}^2{\left(\frac{r_0}{r}\right)}^{1/\omega }}{2\omega z_0^2{r}^3}}.\end{array}$$

(62)

The deflection angles corresponding to the above Gaussian optical curvature are obtained as

$$\begin{array}{ccc}\hfill {\widehat{\alpha }}_{\omega ={\displaystyle \frac{1}{3}}}^{MFE}& \simeq & {\displaystyle \frac{1}{z_0}}{\widehat{\alpha }}_{\omega ={\displaystyle \frac{1}{3}}}+{\displaystyle \frac{2z^2}{z_0}}{\widehat{\alpha }}_{\omega ={\displaystyle \frac{1}{3}}},\hfill \end{array}$$

(63)

$$\begin{array}{ccc}\hfill {\widehat{\alpha }}_{\omega ={\displaystyle \frac{1}{6}}}^{MFE}& \simeq & {\displaystyle \frac{1}{z_0}}{\widehat{\alpha }}_{\omega ={\displaystyle \frac{1}{6}}}+{\displaystyle \frac{2z^2}{z_0}}{\widehat{\alpha }}_{\omega ={\displaystyle \frac{1}{6}}},\hfill \end{array}$$

(64)

$$\begin{array}{ccc}\hfill {\widehat{\alpha }}_{\omega =-{\displaystyle \frac{6}{5}}}^{MFE}& \simeq & {\displaystyle \frac{1}{z_0}}{\widehat{\alpha }}_{\omega =-{\displaystyle \frac{6}{5}}}+{\displaystyle \frac{2z^2}{z_0}}{\widehat{\alpha }}_{\omega =-{\displaystyle \frac{6}{5}}},\hfill \end{array}$$

(65)

$$\begin{array}{ccc}\hfill {\widehat{\alpha }}_{\omega =-{\displaystyle \frac{3}{2}}}^{MFE}& \simeq & {\displaystyle \frac{1}{z_0}}{\widehat{\alpha }}_{\omega =-{\displaystyle \frac{3}{2}}}+{\displaystyle \frac{2z^2}{z_0}}{\widehat{\alpha }}_{\omega =-{\displaystyle \frac{3}{2}}},\hfill \end{array}$$

(66)

From the above results, we can see that the deflection angles of the photon through the MFE matter around the Einstein–Cartan traversable wormholes are higher than the general cases. It is noted that the above deflection angles reduce to the deflection angles of general cases for $z_0=1$ and $z=0$, in the absence of MFE matter.

6. Deflection Angle Using the Keeton and Petters Method

In the year 2006, Keeton and Petters [114,115] introduced a completely new method to compute the deflection angle in the asymptotically flat spacetime of static spherically symmetric astrophysical objects. The Keeton and Petters (KP) method determines the deflection angle of light using the post-post-Newtonian (PPN) coefficients corrected up to the third order.

Let us consider that the light is propagating in a static spherically symmetric spacetime, defined by

$$d{s}^2=-A\left(r\right)d{t}^2+B\left(r\right)d{r}^2+C\left(r\right)(d{\theta }^2+{sin}^2\theta d{\varphi }^2).$$

(67)

Now, at the equatorial plane $\theta =\pi /2$, the above metric reads as

$$d{s}^2=-A\left(r\right)d{t}^2+B\left(r\right)d{r}^2+C\left(r\right)d{\varphi }^2.$$

(68)

It is noted that whenever $A\left(r\right)\to 1$, $B\left(r\right)\to 1$ and $C\left(r\right)\to r^2$ i.e., in the absence of the lens, the spacetime metric becomes flat. Furthermore, at the equatorial plane $\theta =\pi /2$, the Einstein–Cartan traversable wormhole metric becomes

$$d{s}^2=-d{t}^2+{\left[1-{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{\omega +1}{\omega }}}\right]}^{-1}d{r}^2+r^{2}d{\varphi }^2,$$

(69)

Comparing the last two Equations (68) and (69), we obtain the metric coefficient as

$$\begin{array}{ccc}\hfill A\left(r\right)& =& 1,\mathrm{and}B\left(r\right)={\left[1-{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{\omega +1}{\omega }}}\right]}^{-1}.\hfill \end{array}$$

(70)

Furthermore, the general form of the PPN series for the coefficient metric can be expressed as [115]

$$\begin{array}{ccc}\hfill A\left(r\right)& =& 1+2a_1\left({\displaystyle \frac{\varphi }{c}}\right)+2a_2{\left({\displaystyle \frac{\varphi }{c}}\right)}^2+2a_3{\left({\displaystyle \frac{\varphi }{c}}\right)}^3+...+O\left({\left({\displaystyle \frac{\varphi }{c}}\right)}^n\right),\hfill \end{array}$$

(71)

$$\begin{array}{ccc}\hfill B\left(r\right)& =& 1-2b_1\left({\displaystyle \frac{\varphi }{c}}\right)+4b_2{\left({\displaystyle \frac{\varphi }{c}}\right)}^2-8b_2{\left({\displaystyle \frac{\varphi }{c}}\right)}^3+......+O\left({\left({\displaystyle \frac{\varphi }{c}}\right)}^n\right),\hfill \end{array}$$

(72)

where $\varphi$ represents the three-dimensional Newtonian perspective, and $a_i$ and $b_i$ are called the PPN coefficients. To determine the PPN coefficients, we compare the PPN series with the Taylor series form of the metric functions. In this order, we take

$$\begin{array}{c}\hfill {\displaystyle \frac{\varphi }{c}}=-{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{\omega +1}{\omega }}}.\end{array}$$

(73)

Therefore, we find the values of PPN coefficients as

$$\begin{array}{c}\hfill a_1=a_2=a_3=0\mathrm{and}{b}_1=-{\displaystyle \frac{1}{2}},b_2={\displaystyle \frac{1}{4}},b_3=-{\displaystyle \frac{1}{8}}.\end{array}$$

(74)

Now, the Keeton and Petters method yields the deflection angle of light in the following form:

$$\begin{array}{c}\hfill {\widehat{\alpha }}^{KP}={\mathcal{F}}_1\left({\displaystyle \frac{m}{b}}\right)+{\mathcal{F}}_2{\left({\displaystyle \frac{m}{b}}\right)}^2+{\mathcal{F}}_3{\left({\displaystyle \frac{m}{b}}\right)}^3+O{\left({\displaystyle \frac{m}{b}}\right)}^4.\end{array}$$

(75)

where

$$\begin{array}{ccc}\hfill {\mathcal{F}}_1& =& 2(a_1+b_1),\hfill \end{array}$$

(76)

$$\begin{array}{ccc}\hfill {\mathcal{F}}_2& =& \left(2a_1^2-a_2+a_1{b}_1+b_2-{\displaystyle \frac{b_1^2}{4}}\right)\pi ,\hfill \end{array}$$

(77)

$$\begin{array}{ccc}\hfill {\mathcal{F}}_3& =& {\displaystyle \frac{2}{3}}\left(35a_1^3+15a_1^2{b}_1-3a_1\left(10a_2+b_1^2-4b_2\right)+6a_3+b_1^3-6a_2{b}_1-4b_1{b}_2+8b_3\right).\hfill \end{array}$$

(78)

To compute the desired deflection angle, we consider $m=r_0$ and calculate the values of the coefficients of bending angle using the above equations, obtained as

$$\begin{array}{c}\hfill A_1=1,A_2={\displaystyle \frac{3\pi }{16}},\mathrm{and}{A}_3={\displaystyle \frac{1}{16}}.\end{array}$$

(79)

Finally, the Keeton and Petters method provides the deflection angle of light in the gravitational field of the Einstein–Cartan traversable wormhole as

$$\begin{array}{c}\hfill {\widehat{\alpha }}^{KP}=\left({\displaystyle \frac{r_0}{b}}\right)+{\displaystyle \frac{3\pi }{16}}{\left({\displaystyle \frac{r_0}{b}}\right)}^2+{\displaystyle \frac{1}{16}}{\left({\displaystyle \frac{r_0}{b}}\right)}^3+O{\left({\displaystyle \frac{r_0}{b}}\right)}^4.\end{array}$$

(80)

From the above expression, we can conclude that the deflection angle is directly proportional to wormhole throat radius $r_0$ and inversely proportional to the impact parameter b.

To enhance the qualitative aspect of our study, we compare the present deflection angles obtained in the general case (GC) with dark matter’s influence (DM), with Maxwell’s fish eye matter influences (MFE), and in Keeton and Petters method (KPM) graphically in Figure 5 for $r_0=1$. It is noted that the DM is depicted for $\mathsf{\Psi }=1/2$, and MFE is depicted for $z_0=1$ and $z=0.5$. For all the values of $\omega =\{1/3,1/6,-6/5,-3/2\}$, one can see that $MEF>DM>GC$, and hence, the influences of dark matter, as well as Maxwell’s fish eye matter, increased the deflection angle in spacetime of the Einstein–Cartan wormhole. The deflection angle obtained in the Keeton and Petters method is also decreasing in nature for increasing values of impact parameter b, as is clear from Figure 5 (Below Panel (Right)). From Figure 5, we can also conclude that the deflection angles associated with the matter made of phantom energy $\omega =\{-6/5,-3/2\}$> the deflection angle obtained in Keeton and Petters method > the deflection angles associated with the normal matter $\omega =\{1/6,1/3\}$.

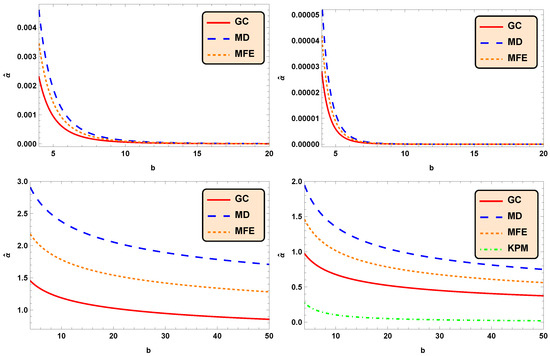
Figure 5. Deflection angle $\widehat{\alpha }$ against the impact parameter b corresponding to the above panel: $\omega ={\displaystyle \frac{1}{3}}$, $r_0$ = 1 (Left) and $\omega ={\displaystyle \frac{1}{6}}$, $r_0$ = 1; below panel: $\omega =-{\displaystyle \frac{6}{5}}$, $r_0$ = 1 (Left) and $\omega =-{\displaystyle \frac{3}{2}}$, $r_0$ = 1 (Right). The panel below (right) also displays the deflection angle (KPM) obtained using the Keeton and Petters method for $r_0=1$.

7. Time Delay

Here, we focus on discussing the time delay due to the gravitational field of Einstein–Cartan wormholes. The time delay is the difference in time of the situation where two photons are released simultaneously from the source but traversing distinct paths toward the viewer. Let us suppose that the light is propagating in a static spherically symmetric spacetime (67), then the time delay of the light passing through its gravitational field can be defined as [145]

$$\begin{array}{c}\hfill \mathsf{\Delta }T=2{\int }_{r_0}^{r_e}\left[{\displaystyle \frac{1}{\sqrt{\left[\frac{A\left(r\right)}{B\left(r\right)}-\frac{A^2\left(r\right)}{B\left(r\right)C\left(r\right)}\frac{C\left(r_c\right)}{A\left(r_c\right)}\right]}}}-{\displaystyle \frac{1}{\sqrt{\left[1-\frac{r_c^2}{r^2}\right]}}}\right]dr+2{\int }_{r_0}^{r_s}\left[{\displaystyle \frac{1}{\sqrt{\left[\frac{A\left(r\right)}{B\left(r\right)}-\frac{A^2\left(r\right)}{B\left(r\right)C\left(r\right)}\frac{C\left(r_c\right)}{A\left(r_c\right)}\right]}}}-{\displaystyle \frac{1}{\sqrt{\left[1-\frac{r_c^2}{r^2}\right]}}}\right]dr,\end{array}$$

(81)

where $r_v$ and $r_s$ represent the distances of the viewer and the source from the considered astrophysical object, and $r_c$ represents the closest approach to that object. We estimate the time delay in the gravitational field of Einstein–Cartan wormholes filled with normal matter and matter with phantom energy using the above algorithm.

Now, the total duration for a light signal to travel through the gravitational field of the Einstein–Cartan wormholes (2), journeying from the viewer (Earth) to the source, and returning after reflecting from the source, is given as [145]

$$T_{total}=2\left[T(r_v,r_c)+T(r_s,r_c)\right]$$

(82)

where

$$T(r_v,r_c)={\int }_{r_c}^{r_v}{\left[{\displaystyle \frac{A\left(r\right)}{B\left(r\right)}}-{\displaystyle \frac{A^2\left(r\right)}{B\left(r\right)C\left(r\right)}}{\displaystyle \frac{C\left(r_c\right)}{A\left(r_c\right)}}\right]}^{-{\displaystyle \frac{1}{2}}}dr={\int }_{r_c}^{r_v}{\left(1-{\displaystyle \frac{r_c^2}{r^2}}\right)}^{-{\displaystyle \frac{1}{2}}}{\left[1-{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{\omega +1}{\omega }}}\right]}^{-{\displaystyle \frac{1}{2}}}dr,$$

(83)

and

$$T(r_s,r_c)={\int }_{r_c}^{r_s}{\left[{\displaystyle \frac{A\left(r\right)}{B\left(r\right)}}-{\displaystyle \frac{A^2\left(r\right)}{B\left(r\right)C\left(r\right)}}{\displaystyle \frac{C\left(r_c\right)}{A\left(r_c\right)}}\right]}^{-{\displaystyle \frac{1}{2}}}dr={\int }_{r_c}^{r_s}{\left(1-{\displaystyle \frac{r_c^2}{r^2}}\right)}^{-{\displaystyle \frac{1}{2}}}{\left[1-{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{\omega +1}{\omega }}}\right]}^{-{\displaystyle \frac{1}{2}}}dr.$$

(84)

The integrand of the above integration can be written as

$$\begin{array}{ccc}\hfill \mathcal{I}& =& {\left(1-{\displaystyle \frac{r_c^2}{r^2}}\right)}^{-{\displaystyle \frac{1}{2}}}{\left[1-{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{\omega +1}{\omega }}}\right]}^{-{\displaystyle \frac{1}{2}}}\hfill \end{array}$$

(85)

$$\begin{array}{ccc}& =& {\left(1-{\displaystyle \frac{r_c^2}{r^2}}\right)}^{-{\displaystyle \frac{1}{2}}}\left[1+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{\omega +1}{\omega }}}+{\displaystyle \frac{3}{8}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{2(\omega +1)}{\omega }}}+{\displaystyle \frac{5}{16}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{3(\omega +1)}{\omega }}}+{\displaystyle \frac{35}{128}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{4(\omega +1)}{\omega }}}+...+O\left({\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{n(\omega +1)}{\omega }}}\right)\right],\hfill \end{array}$$

(86)

$$\begin{array}{ccc}& \simeq & {\left(1-{\displaystyle \frac{r_c^2}{r^2}}\right)}^{-{\displaystyle \frac{1}{2}}}\left[1+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{\omega +1}{\omega }}}+{\displaystyle \frac{3}{8}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{2(\omega +1)}{\omega }}}+{\displaystyle \frac{5}{16}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{3(\omega +1)}{\omega }}}+{\displaystyle \frac{35}{128}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{4(\omega +1)}{\omega }}}\right].\hfill \end{array}$$

(87)

Considering the above approximate values of the integrand $\mathcal{I}$, we find

$$T_{total}=2{\int }_{r_c}^{r_e}{\left(1-{\displaystyle \frac{r_c^2}{r^2}}\right)}^{-{\displaystyle \frac{1}{2}}}\left[1+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{\omega +1}{\omega }}}+{\displaystyle \frac{3}{8}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{2(\omega +1)}{\omega }}}+{\displaystyle \frac{5}{16}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{3(\omega +1)}{\omega }}}+{\displaystyle \frac{35}{128}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{4(\omega +1)}{\omega }}}\right]dr$$

$$+2{\int }_{r_c}^{r_s}{\left(1-{\displaystyle \frac{r_c^2}{r^2}}\right)}^{-{\displaystyle \frac{1}{2}}}\left[1+{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{\omega +1}{\omega }}}+{\displaystyle \frac{3}{8}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{2(\omega +1)}{\omega }}}+{\displaystyle \frac{5}{16}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{3(\omega +1)}{\omega }}}+{\displaystyle \frac{35}{128}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{4(\omega +1)}{\omega }}}\right]dr.$$

(88)

Therefore, from Equation (81) we can estimate the time delay in the gravitational field of Einstein–Cartan wormholes as

$$\mathsf{\Delta }T=2{\int }_{r_c}^{r_v}{\left(1-{\displaystyle \frac{r_c^2}{r^2}}\right)}^{-{\displaystyle \frac{1}{2}}}\left[{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{\omega +1}{\omega }}}+{\displaystyle \frac{3}{8}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{2(\omega +1)}{\omega }}}+{\displaystyle \frac{5}{16}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{3(\omega +1)}{\omega }}}+{\displaystyle \frac{35}{128}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{4(\omega +1)}{\omega }}}\right]dr$$

$$+2{\int }_{r_c}^{r_s}{\left(1-{\displaystyle \frac{r_c^2}{r^2}}\right)}^{-{\displaystyle \frac{1}{2}}}\left[{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{\omega +1}{\omega }}}+{\displaystyle \frac{3}{8}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{2(\omega +1)}{\omega }}}+{\displaystyle \frac{5}{16}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{3(\omega +1)}{\omega }}}+{\displaystyle \frac{35}{128}}{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{4(\omega +1)}{\omega }}}\right]dr.$$

(89)

Now, we estimate the delay in time for the cases corresponding to the values of $\omega =1/3,1/6$ (normal matter), and $\omega =-6/5,3/2$ (matter with phantom energy), respectively. On using the above result (89), we obtain the following delays in time due to the gravitational field of Einstein–Cartan wormholes:

$$\begin{array}{ccc}\hfill \mathsf{\Delta }T{\mid }_{\lambda ={\displaystyle \frac{1}{3}}}& =& {\displaystyle \frac{r_0^4/r_c^{11}}{2048}}\left[{\displaystyle \frac{r_c\sqrt{r_v^2-r_c^2}}{r_v^{10}}}{T}_1\left(r_v\right)+{\displaystyle \frac{r_c\sqrt{r_s^2-r_c^2}}{s^{10}}}{T}_1\left(r_s\right)+(1024r_c^8+480r_c^4{r}_0^4+315r_0^8)\left\{T_2\left(r_v\right)+T_2\left(r_s\right)\right\}\right],\hfill \end{array}$$

(90)

$$\begin{array}{ccc}\hfill \mathsf{\Delta }T{\mid }_{\lambda ={\displaystyle \frac{1}{6}}}& =& {\displaystyle \frac{r_0^7/r_c^{20}}{2837852160}}\left[{\displaystyle \frac{\sqrt{r_v^2-r_c^2}}{r_v^{19}}}{T}_3\left(r_v\right)+{\displaystyle \frac{\sqrt{r_s^2-r_c^2}}{r_s^{19}}}{T}_3\left(r_s\right)+960269310r_c^7{r}_0^7\left\{T_4\left(r_v\right)+T_4\left(r_s\right)\right\}\right],\hfill \end{array}$$

(91)

$$\begin{array}{ccc}\hfill \mathsf{\Delta }{T}_{\omega =-{\displaystyle \frac{6}{5}}}& =& {\displaystyle \frac{1}{660}}[9\left\{{\left({\displaystyle \frac{r_0}{r_v}}\right)}^{{\displaystyle \frac{1}{6}}}{T}_5\left(r_v\right)+{\left({\displaystyle \frac{r_0}{r_s}}\right)}^{{\displaystyle \frac{1}{6}}}{T}_5\left(r_s\right)\right\}+275\sqrt{r_0{r}_v}F\left[{\displaystyle \frac{1}{2}},{\displaystyle \frac{3}{4}};{\displaystyle \frac{7}{4}};{\displaystyle \frac{r_v^2}{r_c^2}}\right]+275\sqrt{r_0{r}_s}F\left[{\displaystyle \frac{1}{2}},{\displaystyle \frac{3}{4}};{\displaystyle \frac{7}{4}};{\displaystyle \frac{r_s^2}{r_c^2}}\right]\hfill \\ & & -22\sqrt{\pi }c{\left({\displaystyle \frac{r_0}{r_c}}\right)}^{{\displaystyle \frac{1}{6}}}\left\{{\displaystyle \frac{25{\left(\frac{r_0}{r_c}\right)}^{\frac{1}{3}}\mathsf{\Gamma }\left(\frac{7}{4}\right)}{\mathsf{\Gamma }\left(\frac{5}{4}\right)}}+{\displaystyle \frac{27{\left(\frac{r_0}{r_c}\right)}^{\frac{1}{6}}\mathsf{\Gamma }\left(\frac{11}{6}\right)}{\mathsf{\Gamma }\left(\frac{4}{3}\right)}}+{\displaystyle \frac{30\mathsf{\Gamma }\left(\frac{11}{12}\right)}{\mathsf{\Gamma }\left(\frac{17}{12}\right)}}\right\}],\hfill \end{array}$$

(92)

$$\begin{array}{ccc}\hfill \mathsf{\Delta }{T}_{\omega =-{\displaystyle \frac{3}{2}}}& =& {\displaystyle \frac{1}{80}}[50\left\{(T_6\left(r_v\right)+T_6\left(r_s\right)\right\}+45T_7\left(r_v\right){\left({\displaystyle \frac{r_0}{r_v}}\right)}^{{\displaystyle \frac{2}{3}}}+45T_7\left(r_s\right){\left({\displaystyle \frac{r_0}{r_s}}\right)}^{{\displaystyle \frac{2}{3}}}+48T_8\left(r_v\right){\left({\displaystyle \frac{r_0}{r_v}}\right)}^{{\displaystyle \frac{1}{3}}}+48T_8{\left({\displaystyle \frac{r_0}{r_s}}\right)}^{{\displaystyle \frac{1}{3}}}\hfill \\ \hfill -& & {\displaystyle \frac{96\sqrt{\pi }{r}_c^2{\left(\frac{r_0}{r_c}\right)}^{\frac{2}{3}}\mathsf{\Gamma }\left(\frac{11}{6}\right)}{\mathsf{\Gamma }\left(\frac{4}{3}\right)}}-{\displaystyle \frac{90\sqrt{\pi }{r}_c^2{\left(\frac{r_0}{r_c}\right)}^{\frac{2}{3}}\mathsf{\Gamma }\left(\frac{5}{3}\right)}{\mathsf{\Gamma }\left(\frac{7}{6}\right)}}],\hfill \end{array}$$

(93)

where

$$\begin{array}{ccc}\hfill T_1\left(r\right)& =& 128c^8\left(r_0^8+2r_0^4{r}^4+8r^8\right)+16r_c^6\left(9r_0^8{r}^2+20r_0^4{r}^6\right)+210r_c^2{r}_0^8{r}^6+315r_0^8{r}^8+24r_c^4\left(7r_0^8{r}^4+20r_0^4{r}^8\right),\hfill \end{array}$$

$$\begin{array}{ccc}\hfill T_2\left(r\right)& =& {cot}^{-1}\left[{\displaystyle \frac{r_c}{\sqrt{r^2-r_c^2}}}\right],\hfill \\ \hfill T_3\left(r\right)& =& 1,867,008r_c^{18}\left(50r_0^{14}+95r_0^7{r}^7+304r^{14}\right)+18,304r_c^{16}\left(5400r_0^{14}{r}^2+10,659r_0^7{r}^9+41,344r^{16}\right)+2288r_c^{14}{r}^4\hfill \\ & & \times \left(46,080r_0^{14}+95,931r_0^7{r}^7+661,504r^{14}\right)+5544r_c^{12}{r}_0^7{r}^6\left(20,480r_0^7+46,189r^7\right)+630r_c^{10}{r}_0^7{r}^8(196,608r_0^7\hfill \\ & & +508,079r^7)+105r_c^8{r}_0^7{r}^{10}\left(1,310,720r_0^7+4,572,711r^7\right)+157,286,400r_c^6{r}_0^{14}{r}^{12}+188,743,680r_c^4{r}_0^{14}{r}^{14}\hfill \\ & & +251,658,240r_c^2{r}_0^{14}{r}^{16}+503,316,480r_0^{14}{r}^{18},\hfill \\ \hfill T_4\left(r\right)& =& \sqrt{r^2-r_c^2}{tan}^{-1}\left[{\displaystyle \frac{\sqrt{r^2-r_c^2}-r}{r_c}}\right],T_5\left(r\right)=r\left[33{\left({\displaystyle \frac{r_0}{r}}\right)}^{{\displaystyle \frac{1}{6}}}F\left[{\displaystyle \frac{1}{2}},{\displaystyle \frac{5}{6}};{\displaystyle \frac{11}{6}};{\displaystyle \frac{r^2}{r_c^2}}\right]+40F\left[{\displaystyle \frac{1}{2}},{\displaystyle \frac{11}{12}};{\displaystyle \frac{23}{12}};{\displaystyle \frac{r^2}{r_c^2}}\right]\right],\hfill \end{array}$$

$$\begin{array}{ccc}\hfill T_6\left(r\right)& =& r_0{tanh}^{-1}\left[r\sqrt{r^2-r_c^2}\right],T_7\left(r\right)=r^{2}F\left[{\displaystyle \frac{1}{2}},{\displaystyle \frac{2}{3}};{\displaystyle \frac{5}{3}};{\displaystyle \frac{r^2}{r_c^2}}\right],T_8\left(r\right)=r^{2}F\left[{\displaystyle \frac{1}{2}},{\displaystyle \frac{5}{6}};{\displaystyle \frac{11}{6}};{\displaystyle \frac{r^2}{r_c^2}}\right].\hfill \end{array}$$

(94)

With $F[a,b;c;r]$ as the hypergeometric function. It is noted that the obtained delays in time become zero for $r_0=0$, the absence of wormholes, as desired. The time delay decreases with the increasing values of the closest approach to the lens $r_c$ for $\omega =\{1/3,1/6,-6/5,-3/2\}$, as is clear from Figure 6. It is important to note that the time delay in gravitational lensing is closely connected to the deflection angle, as both are determined by the light’s path and the gravitational field it traverses. A larger deflection angle results in a longer, more delayed journey for the light, and the gravitational time dilation is increased. Interestingly, our results have followed the same relationship, clear from Figure 5 and Figure 6.

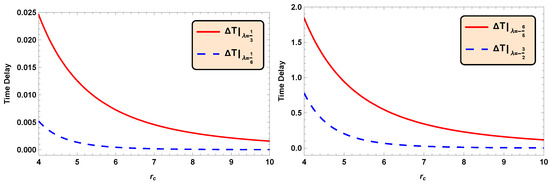
Figure 6. Time delay against the closest approach $r_c$ corresponding to $\omega ={\displaystyle \frac{1}{3}}$, $\omega ={\displaystyle \frac{1}{6}}$ (Left) and $\omega =-{\displaystyle \frac{6}{5}}$$\omega =-{\displaystyle \frac{3}{2}}$ (Right) with $r_0=1$, $r_v=3\times {10}^6$ and $r_s=2\times {10}^6$.

8. Results and Conclusions

The study of gravitational lensing is one of the most significant tools for observing the wormhole geometries in the universe. In this article, we have studied gravitational lensing in the spacetime of the Einstein–Cartan wormholes supported by the normal matter ($\omega >0$) or matter with phantom energy ($\omega <-1$) using the Gauss–Bonnet method. Adopting the weak deflection limit, we have estimated the deflection angle of light by the Einstein–Cartan wormholes corresponding to $\omega =1/3,1/6$ (normal matter) and $\omega =-6/5,-3/2$ (matter with phantom energy). The obtained deflection angles for $\omega =1/3,1/6$ are decreasing in nature against the impact parameter, as expected; moreover, the deflection angle for $\omega =1/3$ is higher than the deflection angle for $\omega =1/6$, i.e., the deflection angle decreases for decreasing values of $\omega$ (see Figure 1). In the case of wormholes filled by the matter with phantom energy, the deflection angles are also decreasing for the increasing impact parameter; here, it is also found that the deflection angles have decreasing behavior with the decreasing values of $\omega$ (see Figure 3). On the other hand, the deflection angles by the Einstein–Cartan wormholes supported by the matter with phantom energy are higher than the deflection angles by the Einstein–Cartan wormholes supported by normal matter; therefore, matter with phantom energy creates a higher deflection angle than the normal matter in the spacetime of Einstein–Cartan wormholes. Interestingly, one can see that all the obtained deflection angles vanish for $r_0$ = 0, the absence of Einstein–Cartan wormholes. It has been seen that the reported approximated deflection angles for all the cases $\omega =\{1/3,1/6,-6/5,-3/2\}$ associated with $r_0=1$ are slightly lower than their respective exact numerical values (see Figure 4). We have also studied the influences of the dark matter content and Maxwell’s fish eye matter on the obtained deflection angles. The deflection angles increase with the effect of the dark matter content, as well as the effect of Maxwell’s fish eye matter. We have also estimated the deflection angle using the Keeton and Petters method and found that the deflection angle is directly proportional to the wormhole throat radius and inversely proportional to the impact parameter. Moreover, we compare the present deflection angles obtained in the general case (GC), with dark matter’s influence (DM), with Maxwell’s fish eye matter influences (MFE), and in Keeton and Petters method (KPM) graphically in Figure 5 for $r_0=1$. For all the values of $\omega =\{1/3,1/6,-6/5,-3/2\}$, we have found that $MEF>DM>GC$. Therefore, the influences of dark matter, as well as Maxwell’s fish eye matter, increased the deflection angle. Additionally, it has been seen that the deflection angles associated with the matter made of phantom energy $\omega =\{-6/5,-3/2\}$> the deflection angle obtained in Keeton and Petters method > the deflection angles associated with the normal matter $\omega =\{1/6,1/3\}$, as is clear from Figure 5. The expressions for time delays by the considered wormholes are also calculated corresponding to $\omega =\{1/3,1/6,-6/5,-3/2\}$, which helps to measure the delays in time in the spacetime of the Einstein–Cartan wormholes filled by normal matter or matter with phantom energy. It is also noted that the time delays become zero for $r_0=0$, i.e., for the absence of Einstein–Cartan wormholes. The time delay decreases with the increasing values of the closest approach to the lens $r_c$ for all the values of $\omega =\{1/3,1/6,-6/5,-3/2\}$, as is clear from Figure 6. Moreover, the matter made of phantom energy creates a higher time delay than the normal matter case. Especially, one can see from Figure 6 that $\mathsf{\Delta }{T}_{{\displaystyle \frac{1}{6}}}<\mathsf{\Delta }{T}_{{\displaystyle \frac{1}{3}}}<\mathsf{\Delta }{T}_{-{\displaystyle \frac{3}{2}}}<\mathsf{\Delta }{T}_{-{\displaystyle \frac{6}{5}}}$.

Finally, the significance of gravitational lensing in astrophysics has piqued our curiosity in investigating the deflection angle by the Einstein–Cartan wormholes. The present study may inspire the scientific community to search the Einstein–Cartan wormholes observationally and to do fruitful research work on the gravitational lensing by other astrophysical objects.