The Algorithm of the Two Neutron Monitors for the Analysis of the Rigidity Spectrum Variations of Galactic Cosmic Ray Intensity Flux in Solar Cycle 24
Abstract
1. Introduction
2. Two-Station Method for Determining Rigidity Spectrum Exponent γ of the GCR Intensity Variation
3. Experimental Results and Discussion
4. Conclusions
- (i)
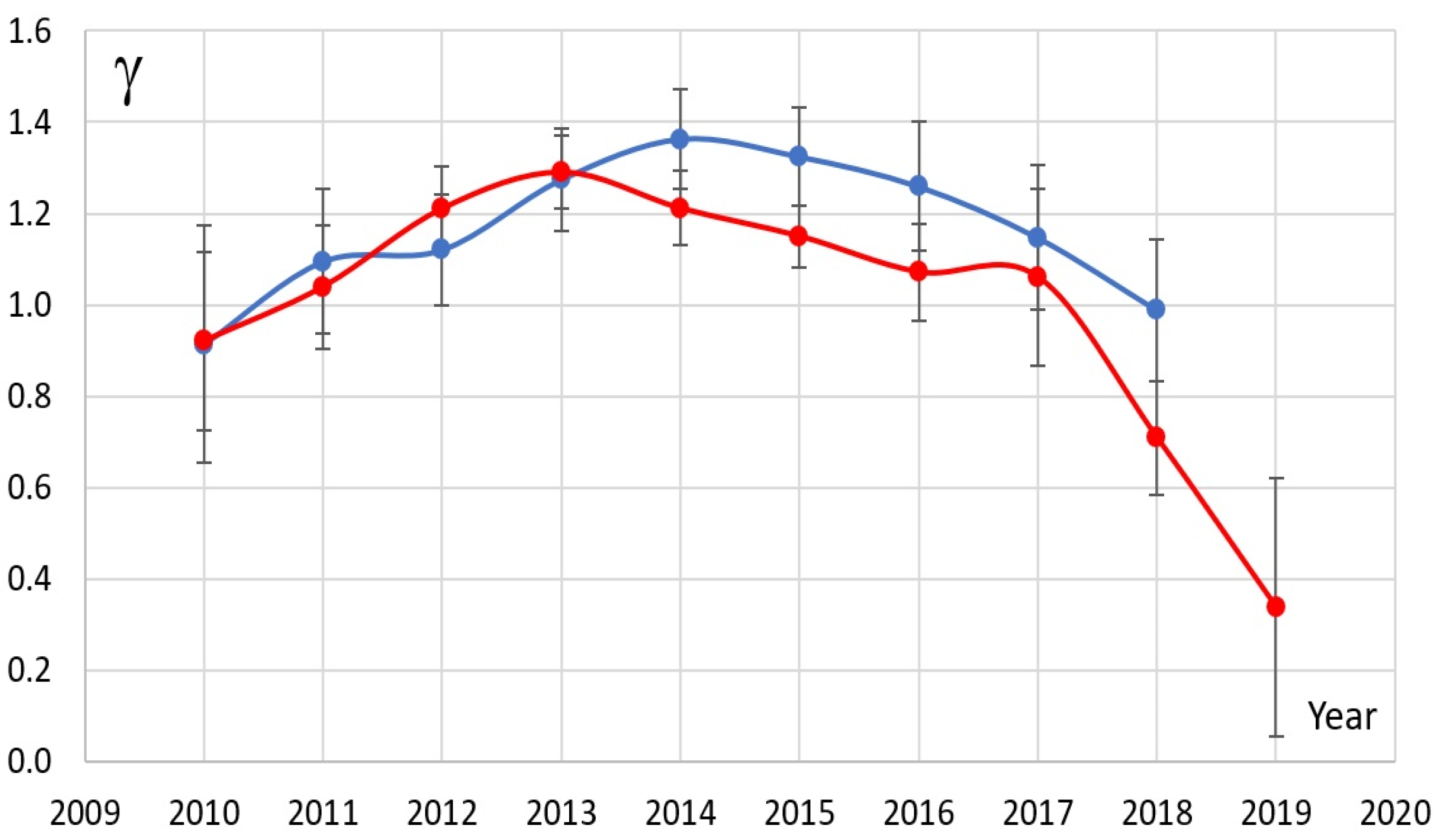
- Based on the method of two stations for two pair monitors (Oulu–Potchefstroom and Mexico–Apatity), the changes in the RSV exponent γ of the GCR flux in the 24th cycle of solar activity were obtained. In solar activity minima and around the minima, the γ exponent varies in a range γ = 0.6–0.9, while in the SA maxima and in the vicinity, the gamma exponent changes in the range γ = 1.2–1.3;
- (ii)
- The RSV of GCR isotropic flux is soft in the SA maxima and in the vicinity of the SA, while in the SA minima and in the vicinity of the SA, it is hard in the considered period from 2009 to 2019. Thus, the universality of the temporal changes in the RSV of GCR isotropic flux for all 11 cycles of SA from 1965 to 2019 has been confirmed;
- (iii)
- The results obtained indicate the change in the character of the diffusion of GCR during the decreasing and increasing epochs of SA caused by the changes in the structure of HMF turbulences. In the period of increasing SA, the RSV of the GCR flux quickly becomes soft (i.e., the exponent γ quickly reaches its maximum value: γ = 1.3, while in the period of decreasing SA, the rigidity spectrum gradually becomes hard (i.e., the γ gradually changes from 1.29 to 0.64);
- (iv)
- The structural changes in HMF turbulence play a decisive role in the formation of long-term GCR variations in the heliosphere;
- (v)
- The presented two-monitor method is an alternative to the least squares method when there are only a few monitors working stably in a given period. Because of the lack of data, we cannot use the least squares method;
- (vi)
- The two-monitor method and the least squares method give similar results and confirm universal RSV changes in different periods of solar activity.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Calculation of Exponent γ by the Least Squares Method
References
- Stozhkov, Y.; Makhmutov, V.; Svirzhevsky, N. About Cosmic Ray Modulation in the Heliosphere. Universe 2022, 8, 558. [Google Scholar] [CrossRef]
- Alania, M.V.; Modzelewska, R.; Wawrzynczak, A. Peculiarities of cosmic ray modulation in the solar minimum 23/24. J. Geophys. Res. Space Phys. 2014, 119, 4164. [Google Scholar] [CrossRef]
- Bieber, J.W.; Matthaeus, W.H.; Smith, C.W.; Wanner, W.; Kallenrode, M.-B.; Wibberenz, G. Proton and electron mean free paths: The Palmer consensus revisited. Astrophys. J. 1994, 420, 294. [Google Scholar] [CrossRef]
- Jokipii, J.R. Propagation of cosmic rays in the solar wind. Rev. Geophys. Space Phys. 1971, 9, 27–87. [Google Scholar] [CrossRef]
- Melnikov, Y.P. General correlation scales of random component of IMF. Geomagn. Aeoronomia 2005, 45, 445. [Google Scholar]
- Siluszyk, M.; Iskra, K.; Alania, M.V.; Miernicki, S. Interplanetary magnetic field turbulence and rigidity spectrum of the galactic cosmic rays intensity variation (1968–2012). J. Geophys. Res. 2018, 123, 30–38. [Google Scholar] [CrossRef]
- Siluszyk, M.; Iskra, K. Modeling the Time Delay Problem of Galactic Cosmic Ray Flux in Solar Cycles 21 and 23. Sol. Phys. 2020, 295, 68. [Google Scholar] [CrossRef]
- Toptygin, I.N. Cosmic Rays in Interplanetary Magnetic Fields; Dordrecht, D. Reidel Publishing Co.: Dordrecht, The Netherlands, 1985; Available online: https://link.springer.com/book/10.1007/978-94-009-5257-7 (accessed on 1 May 2024).
- Alania, M.V.; Iskra, K. Features of the Solar Wind Large-Scale Structure in the Different Periods of Solar Activity Based on the Variations of Cosmic Rays. Adv. Space Res. 1995, 16, 241. [Google Scholar] [CrossRef]
- Dorman, L.I. Cosmic ray variations, Moscow: State Publishing House for Technical and Theoretical Literature. J. Phys. Soc. Jpn. 1957, 13, 8. [Google Scholar] [CrossRef]
- Dorman, L.I. Cosmic Rays Variations and Space Explorations; North-Holland: Amsterdam, The Netherlands, 1974. [Google Scholar]
- Dorman, L.I. Variations of Galactic Cosmic Rays; Izdatel’stvo Moskovskogo Universiteta: Moscow, Russia, 1975; p. 214. Available online: https://ui.adsabs.harvard.edu/abs/1975MIzMU.........D/abstract (accessed on 1 May 2024). (In Russian)
- Dorman, L.I. Cosmic ray long-term variation: Even-odd cycle effect, role of drifts, and the onset of cycle 23. Adv. Space Res. 2001, 27, 601–606. [Google Scholar] [CrossRef]
- Yasue, S.; Mori, S.; Sakakibara, S.; Nagashima, K. Coupling Coefficients of Cosmic Ray Daily Variations for Neutron Monitor Stations; Report of Cosmic-Ray Research Laboratory: Nagoya, Japan, 1982. [Google Scholar]
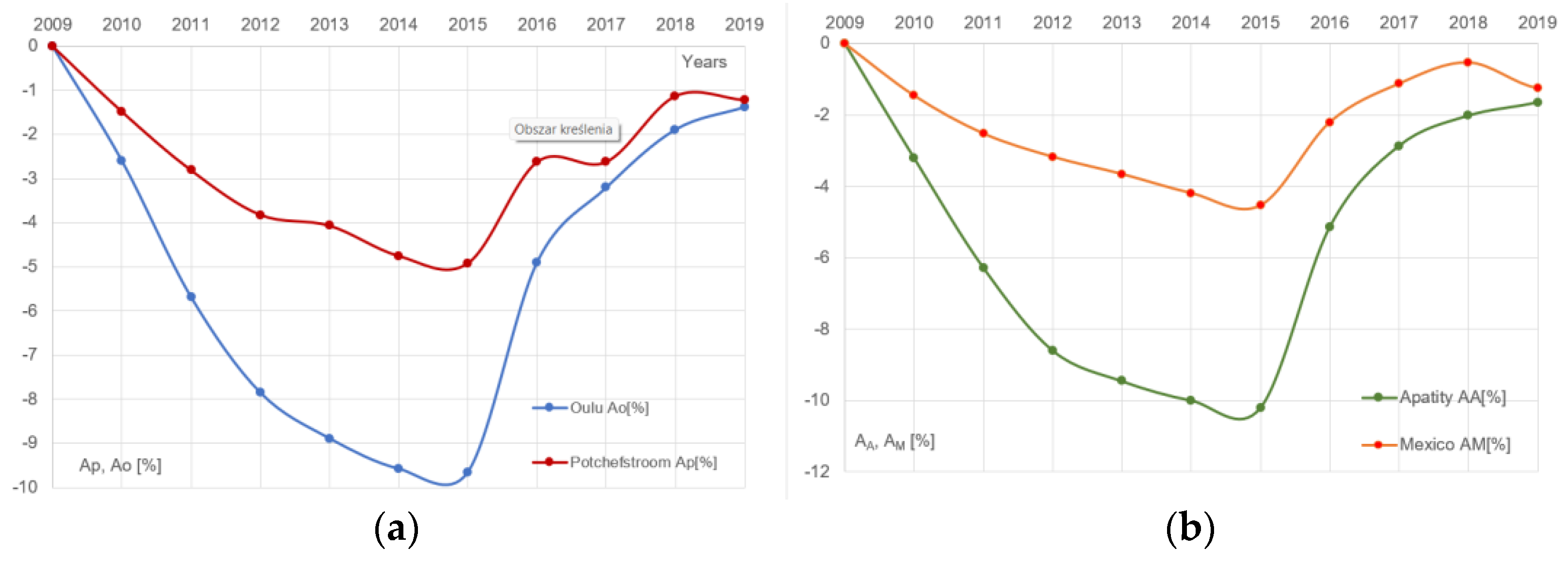
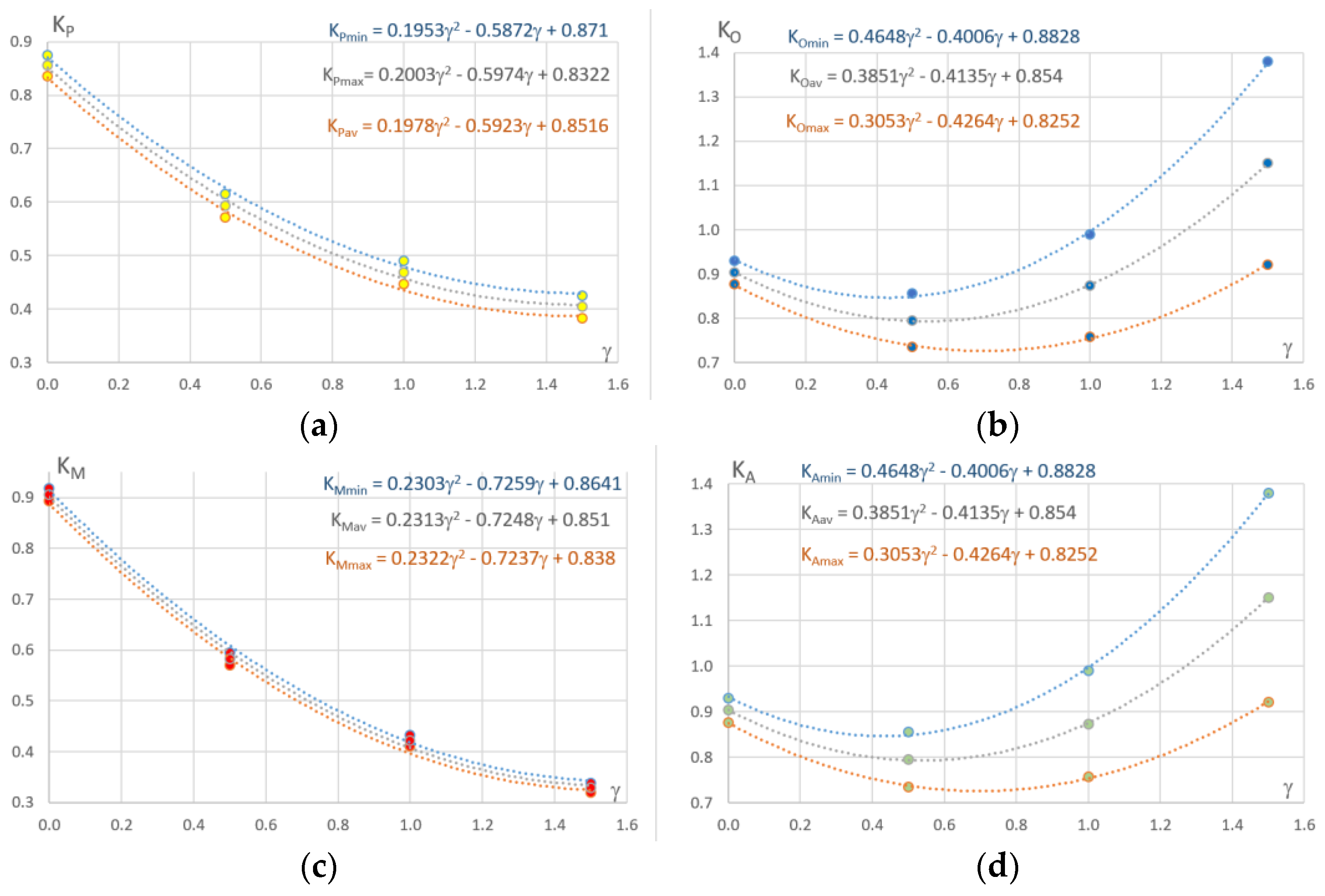
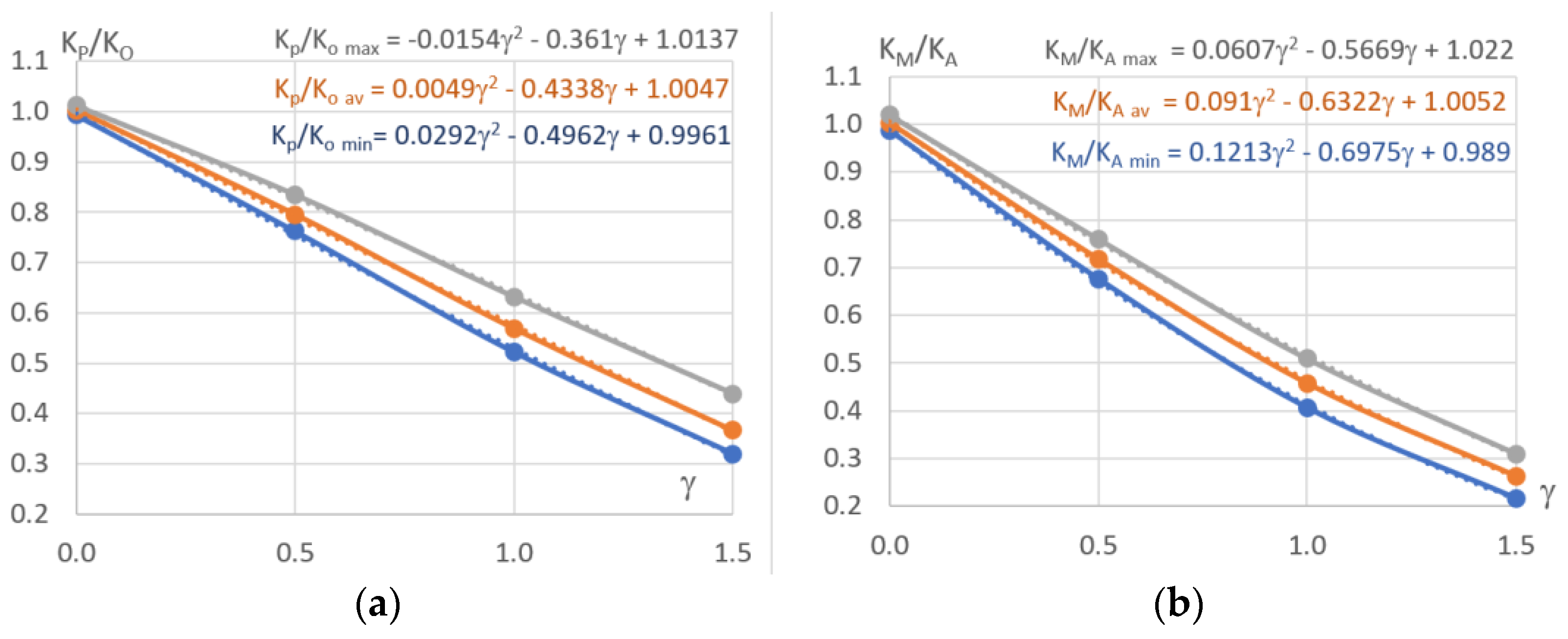
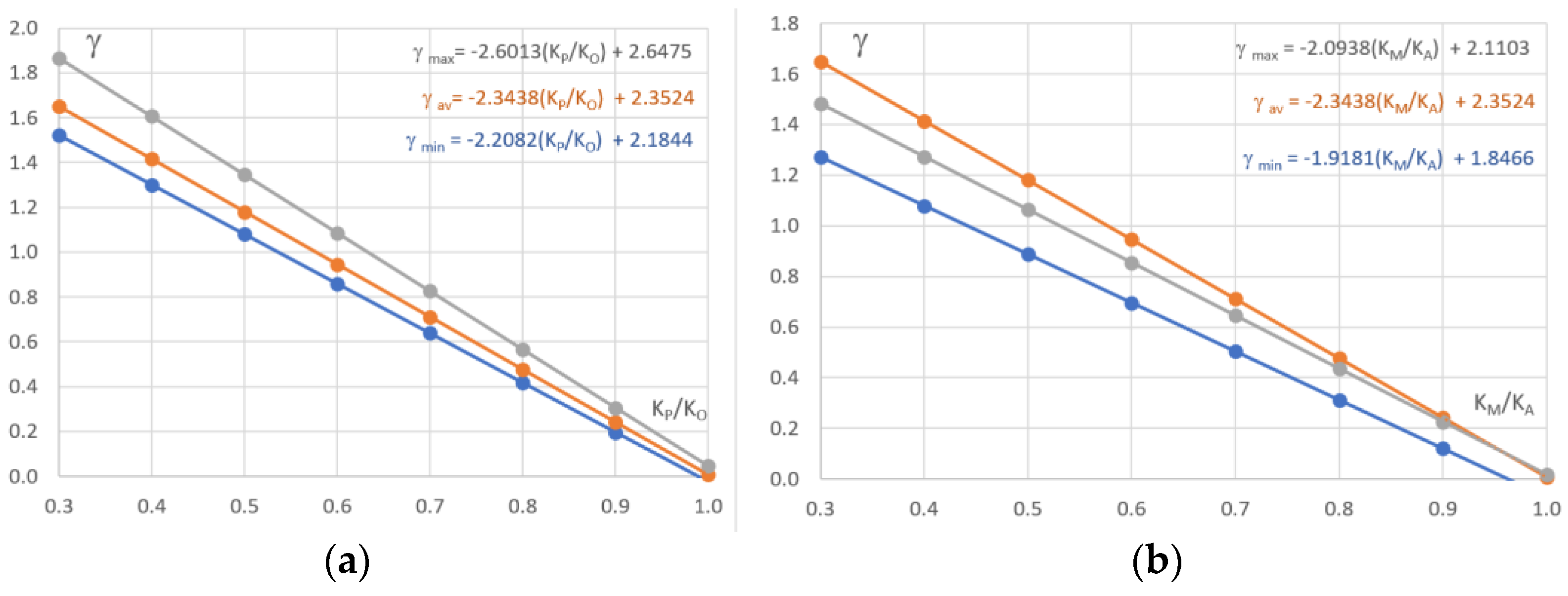
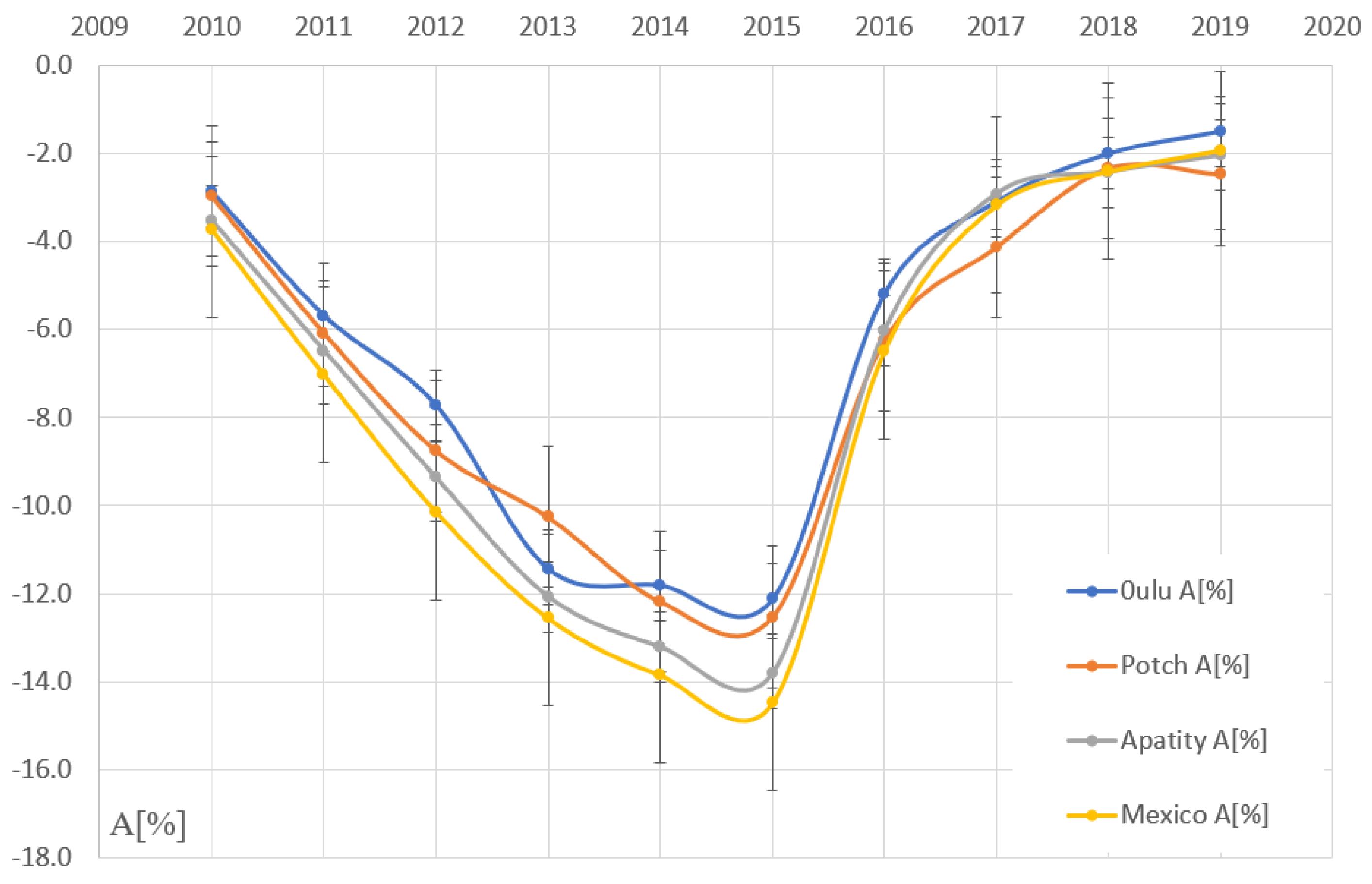
| Year | AP | AO | AP/AO | AM | AA | AM/AA |
|---|---|---|---|---|---|---|
| 2009 | 0 | 0 | --- | 0 | 0 | --- |
| 2010 | −1.48 ± 0.50 | −2.59 ± 0.11 | 0.57 ± 0.12 | −1.46 ± 0.08 | −3.20 ± 0.06 | 0.45 ± 0.10 |
| 2011 | −2.81 ± 0.20 | −5.69 ± 0.03 | 0.49 ± 0.07 | −2.52 ± 0.04 | −6.28 ± 0.02 | 0.40 ± 0.07 |
| 2012 | −3.82 ± 0.10 | −7.85 ± 0.01 | 0.49 ± 0.05 | −3.17 ± 0.02 | −8.59 ± 0.01 | 0.37 ± 0.05 |
| 2013 | −4.07 ± 0.09 | −8.89 ± 0.01 | 0.46 ± 0.04 | −3.65 ± 0.02 | −9.45 ± 0.01 | 0.39 ± 0.04 |
| 2014 | −4.75 ± 0.08 | −9.58 ± 0.01 | 0.50 ± 0.04 | −4.19 ± 0.01 | −9.99 ± 0.01 | 0.42 ± 0.04 |
| 2015 | −4.92 ± 0.06 | −9.65 ± 0.01 | 0.51 ± 0.04 | −4.53 ± 0.01 | −10.2 ± 0.01 | 0.44 ± 0.03 |
| 2016 | −2.62 ± 0.18 | −4.89 ± 0.03 | 0.54 ± 0.06 | −2.20 ± 0.03 | −5.14 ± 0.02 | 0.43 ± 0.05 |
| 2017 | −2.62 ± 0.26 | −3.20 ± 0.06 | 0.82 ± 0.07 | −1.12 ± 0.14 | −2.86 ± 0.06 | 0.39 ± 0.10 |
| 2018 | −1.13 ± 0.62 | −1.89 ± 0.12 | 0.60 ± 0.07 | −0.53 ± 0.36 | −2.02 ± 0.11 | 0.26 ± 0.06 |
| 2019 | −1.22 ± 2.17 | −1.38 ± 0.22 | 0.89 ± 0.49 | −1.24 ± 0.07 | −1.64 ± 0.16 | 0.76 ± 0.15 |
| R = 200 GV | KP | KO | KM | KA | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| γ | min | av | max | min | av | max | min | av | max | min | av | max |
| 0.0 | 0.8748 | 0.8555 | 0.8362 | 0.8803 | 0.8534 | 0.8264 | 0.8686 | 0.8556 | 0.8426 | 0.8803 | 0.8534 | 0.8264 |
| 0.5 | 0.6148 | 0.5932 | 0.5716 | 0.8063 | 0.7455 | 0.6846 | 0.5452 | 0.5328 | 0.5203 | 0.8063 | 0.7455 | 0.6846 |
| 1.0 | 0.4905 | 0.4688 | 0.4471 | 0.9395 | 0.8237 | 0.7078 | 0.3820 | 0.3712 | 0.3603 | 0.9395 | 0.8237 | 0.7078 |
| 1.5 | 0.4258 | 0.4043 | 0.3828 | 1.3303 | 1.1008 | 0.8713 | 0.2889 | 0.2796 | 0.2702 | 1.3303 | 1.1008 | 0.8713 |
| Rmax = 200 GV | KP/KO | KM/KA | ||||
|---|---|---|---|---|---|---|
| γ | min | av | max | min | av | max |
| 0.0 | 0.994 | 1.003 | 1.012 | 0.987 | 1.003 | 1.020 |
| 0.5 | 0.762 | 0.796 | 0.835 | 0.676 | 0.718 | 0.760 |
| 1.0 | 0.522 | 0.569 | 0.632 | 0.407 | 0.458 | 0.509 |
| 1.5 | 0.320 | 0.367 | 0.439 | 0.217 | 0.264 | 0.310 |
| YEAR | γ(P-O) | γ(M-A) | KO | KP | KA | KM |
|---|---|---|---|---|---|---|
| 2010 | 0.91 ± 0.26 | 0.92 ± 0.20 | 0.90 | 0.50 | 0.91 | 0.39 |
| 2011 | 1.09 ± 0.16 | 1.04 ± 0.14 | 1.00 | 0.46 | 0.97 | 0.36 |
| 2012 | 1.12 ± 0.12 | 1.21 ± 0.09 | 1.02 | 0.44 | 0.92 | 0.31 |
| 2013 | 1.27 ± 0.11 | 1.29 ± 0.08 | 0.78 | 0.40 | 0.78 | 0.29 |
| 2014 | 1.36 ± 0.11 | 1.21 ± 0.08 | 0.81 | 0.39 | 0.76 | 0.30 |
| 2015 | 1.32 ± 0.11 | 1.15 ± 0.07 | 0.80 | 0.39 | 0.74 | 0.31 |
| 2016 | 1.26 ± 0.14 | 1.07 ± 0.11 | 0.94 | 0.42 | 0.85 | 0.34 |
| 2017 | 1.15 ± 0.16 | 1.06 ± 0.19 | 1.03 | 0.45 | 0.98 | 0.35 |
| 2018 | 0.99 ± 0.16 | 0.71 ± 0.12 | 0.94 | 0.48 | 0.83 | 0.47 |
| 2019 | 0.94 ± 1.09 | 0.34 ± 0.28 | 0.92 | 0.49 | 0.80 | 0.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iskra, K.; Siluszyk, M.; Wozniak, W. The Algorithm of the Two Neutron Monitors for the Analysis of the Rigidity Spectrum Variations of Galactic Cosmic Ray Intensity Flux in Solar Cycle 24. Universe 2024, 10, 311. https://doi.org/10.3390/universe10080311
Iskra K, Siluszyk M, Wozniak W. The Algorithm of the Two Neutron Monitors for the Analysis of the Rigidity Spectrum Variations of Galactic Cosmic Ray Intensity Flux in Solar Cycle 24. Universe. 2024; 10(8):311. https://doi.org/10.3390/universe10080311
Chicago/Turabian StyleIskra, Krzysztof, Marek Siluszyk, and Witold Wozniak. 2024. "The Algorithm of the Two Neutron Monitors for the Analysis of the Rigidity Spectrum Variations of Galactic Cosmic Ray Intensity Flux in Solar Cycle 24" Universe 10, no. 8: 311. https://doi.org/10.3390/universe10080311
APA StyleIskra, K., Siluszyk, M., & Wozniak, W. (2024). The Algorithm of the Two Neutron Monitors for the Analysis of the Rigidity Spectrum Variations of Galactic Cosmic Ray Intensity Flux in Solar Cycle 24. Universe, 10(8), 311. https://doi.org/10.3390/universe10080311





