Mono-Higgs and Mono-Z Production in the Minimal Vector Dark Matter Model

Abstract

The minimal vector dark matter is a viable realization of the minimal dark matter paradigm. It extends the standard model by the inclusion of a vector matter field in the adjoint representation of $\mathrm{SU}{\left(2\right)}_L$. The dark matter candidate corresponds to the neutral component of the new vector field ($V^0$). Previous studies have shown that the model can explain the observed dark matter abundance while evading direct and indirect searches. At colliders, the attention has been put on the production of the charged companions of the dark matter candidate. In this work, we focus on the mono-Higgs and mono-Z signals at Hadron colliders. The new charged vectors ($V^{\pm }$) are invisible unless a dedicated search is performed. Consequently, we assume that the mono-Higgs and mono-Z processes correspond to the $pp\to h{V}^{+,0}{V}^{-,0}$ and $pp\to Z{V}^{+,0}{V}^{-,0}$ reactions, respectively. We show that, while the $pp\to h{V}^{+,0}{V}^{-,0}$ is more important, both channels may produce significant signals at the HL-LHC and colliders running at $\sqrt{s}=27$ TeV and 100 TeV, probing almost the complete parameter space.

1. Introduction

The quest for an explanation of dark matter’s nature is one of the main drivers in the current high-energy physics research program. Although more exotic alternatives exist, the general lore assumes that dark matter (DM) is, in fact, a new kind of particle. We already know that such a particle should be massive, electrically neutral (or with a very small electric charge), and stable (or with a lifetime of the order of the age of the universe). However, current data do not significantly constrain its mass nor its spin. Still, an intriguing coincidence can be noticed: if the DM’s mass is of the order of the GeV’s, and it interacts with the standard particles with a strength comparable to weak interaction, then the observed abundance of DM is naturally reproduced. This is called “WIMP Miracle” because it characterizes a “Weakly Interacting Massive Particle” as a well-motivated candidate for DM. This observation makes natural the assumption that the DM feels the weak interaction or, in more technical words, it should be a neutral component of a $\mathrm{SU}{\left(2\right)}_L$ multiplet. This idea has been developed in the so-called “Minimal Dark Matter” program [1]. Originally, this theoretical setup was studied only for the cases of particles with spin-0 and spin-$\frac{1}{2}$ in several $\mathrm{SU}{\left(2\right)}_L$ representations. However, there are no fundamental reasons for excluding spin-1 particles from this program. Indeed, the cases of vector particles in the fundamental [2] and adjoint [3] representations have already been proposed as viable sources for DM candidates. Typically, these models must be treated as effective theories, since the presence of massive vector particles induces perturbative unitarity violations. Nevertheless, this is not an insurmountable difficulty, especially in the case of the adjoint representation. In this case, it has been shown that the scale of unitarity violation is rather high (around 100 TeV) [3]. Although an ultraviolet completion of the model has been constructed [4], the effective low-energy model is completely adequate for phenomenological purposes. For this reason, in this paper, we focus on the effective theory which extends the standard model by the inclusion of a massive vector field in the adjoint representation (the so-called “Minimal Vector Dark Matter” or MVDM model) [3]. The neutral component of the new massive vector triplet ($V^0$) becomes the dark matter candidate and is stabilized by a $Z_2$ symmetry, which is imposed by reasons related to unitarity preservation [3,5]. Previous studies [3] have shown that the model can explain the observed dark matter abundance while evading direct and indirect searches, in fact, the expected sensitivity of future experiments such as XENONnT at 20 ton-years [6] could strongly constrain the parameter space of the studied model. At colliders, the attention has been put on the production of the charged companions of the dark matter and the mono-jet signal (both processes were studied in [3]). Additionally, in reference [7], the possibility of the charged companions of the dark matter as long-lived particles, producing displaced vertices in ATLAS and CMS was studied. In this work, we focus on the mono-Higgs and mono-Z signals at Hadron colliders. The study of these two processes is motivated by the fact that the MVDM has only two free parameters and, as will be shown below, mono-Higgs and mono-Z production can provide complementary information on these parameters. We show that, while the $pp\to h{V}^{+,0}{V}^{-,0}$ is more important, both channels may produce significant signals at the HL-LHC and colliders running at $\sqrt{s}=27$ TeV and 100 TeV.

The rest of the paper is organized in the following way. In Section 2, we briefly describe the main aspects of the MVDM model. Then, in Section 3, we explain our methodology. In Section 4, we discuss our results, while in Section 5, we state our conclusions.

2. The Model

For the reader’s convenience, we briefly recall the main characteristics of the model, which was fully developed in Ref. [3]. The standard model (SM) is extended by the introduction of a new triplet vector field ($V_{\mu }={(V_{\mu }^{+},V_{\mu }^0,V_{\mu }^{-})}^T$) transforming homogeneously in the adjoint representations of $\mathrm{SU}{\left(2\right)}_L$ with no hypercharge, that is,

$$V_{\mu }\to U_L^{†}{V}_{\mu }{U}_L$$

(1)

with $U_L\in \mathrm{SU}{\left(2\right)}_L$. Additionally, a $Z_2$ symmetry is imposed, under which all the standard fields are even and $V_{\mu }$ is odd. The model is, then, defined by the following Lagrangian:

$$\begin{array}{ccc}\hfill \mathcal{L}& =& {\mathcal{L}}_{SM}-\mathrm{Tr}\left\{D_{\mu }{V}_{\nu }{D}^{\mu }{V}^{\nu }\right\}+\mathrm{Tr}\left\{D_{\mu }{V}_{\nu }{D}^{\nu }{V}^{\mu }\right\}\hfill \\ & & -\frac{g^2}{2}\mathrm{Tr}\left\{[V_{\mu },V_{\nu }][V^{\mu },V^{\nu }]\right\}\hfill \\ & & -ig\mathrm{Tr}\left\{W_{\mu \nu }[V^{\mu },V^{\nu }]\right\}+{\tilde{M}}^2\mathrm{Tr}\left\{V_{\nu }{V}^{\nu }\right\}\hfill \\ & & +a\left({\mathsf{\Phi }}^{†}\mathsf{\Phi }\right)\mathrm{Tr}\left\{V_{\nu }{V}^{\nu }\right\}\hfill \end{array}$$

(2)

where the covariant derivative $D_{\mu }={\partial }_{\mu }-ig[W_{\mu },·]$ is the usual one for the adjoint representation of $\mathrm{SU}{\left(2\right)}_L$. After the electroweak symmetry breaking, the physical mass of the new vector triplet is:

$$M_V^2={\tilde{M}}^2+\frac{1}{2}a{v}^2$$

(3)

where v is the vacuum expectation value of the Higgs field $⟨\mathsf{\Phi }⟩=v$.

We want to emphasize that this construction is rather minimal, in the sense that only two new free parameters are added: the mass of the vector triplet $M_V$ and the Higgs–vector coupling constant a.

At this point, it is worth recalling that radiative electroweak corrections at the loop level induce a mass splitting between the charged components of $V_{\mu }$ and the neutral component. Concretely speaking, the charged components of $V_{\mu }$ receive an additional electromagnetic correction to their propagator, which is absent for the case of $V^0$. For large values of $M_V$, the mass splitting is given by:

$$\Delta M\equiv M_{V^{\pm }}-M_{V^0}\approx 200\mathrm{MeV},$$

(4)

making $V^0$ the lightest particle, which is odd under the $Z_2$ symmetry. Consequently, $V^0$ happens to be stable and a good DM candidate. Indeed, the model reproduces the observed relic density [8] while remaining consistent with all the experimental constraints if $M_V$ is in the range from 3 to 4 TeV. In Figure 1, we show the region of the parameter space which is allowed by current experimental constraints.

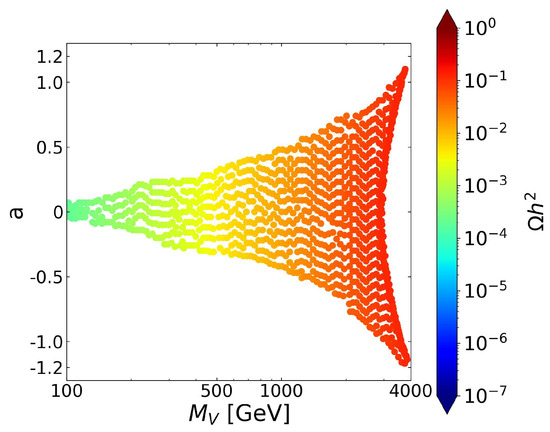
Figure 1. Parameter space allowed by experimental and observational constraints. This includes direct and indirect dark matter searches, dark matter abundance, and consistency with perturbative unitarity. The color scale indicates the value of the relic density. Notice that we have included the case of subabundance.

As a consequence of the tiny mass splitting, the only decay channel available to the charged components of the vector triplet is $V^{\pm }\to V^0{\pi }^{\pm }$, where the pion happens to be very soft. Consequently, it is very difficult to detect any $V^{\pm }$ except by dedicated searches for long living particles [7,9,10,11]. As a result, we assume that $V^0$ and $V^{\pm }$ contribute to the missing energy when they are present in the final state.

3. Methodology

We start by considering the mono-Higgs signal associated with the $V^{\pm ,0}$ production. Our main and irreducible background is the Higgs–Strahlung with a Z-boson decaying into neutrinos [7]. Although there are other sources of background, such as $t\overline{t}$ and $Zb\overline{b}$ processes, they can be filtered out by applying appropriate kinematic cuts, implementing a lepton veto, and enhancing the trigger in future experiments [12,13,14,15,16], consequently they will not be taken into account in this analysis.

We used the CalcHEP [17] package to perform our simulations. The signal was computed using the CalcHEP implementation of the model [18] available at the High Energy Physics Model Database [19].

The main process contributing to the signal of $V^0$ production is $gg\to h{V}^0{V}^0$. Since the $V^0$ does not couple to fermions and a $Z{V}^0{V}^0$ vertex does not exist, the only way to have a $q\overline{q}\to h{V}^0{V}^0$ process is through the direct coupling of the Higgs boson to quarks, making it highly suppressed.

Additionally, we took into account the Higgs boson decay into two b-quarks. The reconstruction efficiency for this channel is estimated to be ${ϵ}_{eff-b}\approx 0.80$ [20,21,22,23] and the $h\to b\overline{b}$ decay probability [24], $Br(h\to b\overline{b})\approx 0.58$. Using the standard definition of statistical significance as a function of the integrated luminosity on the collider:

$$S=\sqrt{{ϵ}_{eff-b}·Br(h\to b\overline{b})·L}·{\displaystyle \frac{{\sigma }_s}{\sqrt{{\sigma }_s+{\sigma }_b}}}$$

(5)

where ${\sigma }_s=\sigma (pp\to h{V}^{+,0}{V}^{-,0})$ and ${\sigma }_b=\sigma (pp\to Zh\to \nu \overline{\nu }h)$ are the cross-section for the signal and the background respectively, extracted from the simulations made on CalcHEP and L is the integrated luminosity.

On the other hand, the main contribution to the background for Mono-Z production comes from the $pp\to ZZ$ channel. In this case, we have to impose that one of the Z-bosons decays into visible particles while the other one, into neutrinos. Consequently, for the mono-Z process, our significance formula can be written as:

$$S=\sqrt{Br(Z\to visible)·L}·{\displaystyle \frac{{\sigma }_s}{\sqrt{{\sigma }_s+{\sigma }_b}}}$$

(6)

where this time ${\sigma }_s=\sigma (pp\to Z{V}^{+,0}{V}^{-,0})$ and ${\sigma }_b=\sigma (pp\to ZZ\to \nu \overline{\nu }Z)$. In our discussion, we will pay attention to the regions of the parameter space where we get $S>2$. Of course, a low significance like $S=2$ indicates only a weak hint of the possible existence of New Physics, and only regions with $S>5$ provide the conditions needed for discovery.

At this point, it is valuable to remark that the cross-section for the process $pp\to X{V}^{+}{V}^{-}$ ($X=h,Z$) is, in general, much bigger than $\sigma (pp\to X{V}^0{V}^0)$ due to the fact the first one contains electroweak contributions that the last one lacks (see the production diagrams in Figure 2).

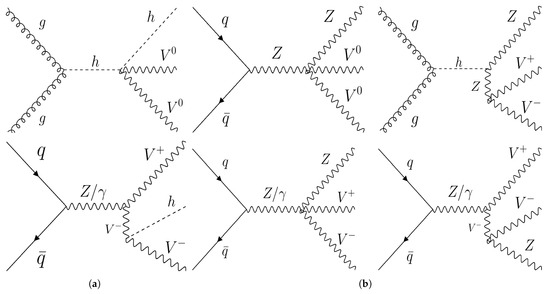
Figure 2. Representative diagrams of the signal process used in the analysis. The diagrams include the effective $hgg$ vertex generated by a loop of top quarks. (a) $pp\to hVV$; (b) $pp\to ZVV$.

We performed simulations for three future facilities: the HL-LHC, the HE-LHC, and the FCC-hh. Their projected energies and expected maximum integrated luminosities are shown in Table 1.

Table 1. Integrated luminosities and energies used in our simulations. The values were taken from [25,26].

Collider	HL-LHC	HE-LHC	FCC-hh
$\sqrt{s}$ [TeV]	13.6	27	100
$L\left[a{b}^{-1}\right]$	3	10	30

An important aspect of our simulations was to set up kinematic cuts in order to optimize the statistical significance of the signal. We focused on the missing transverse momentum ($p_T^{\mathrm{miss}}$, which corresponds to the apparently unbalanced transverse momentum of the h or Z bosons) as our relevant kinematic variable. We explored the parameter space using different cuts in $p_T^{\mathrm{miss}}$ until we obtained an optimal cut. An example of this process is shown in Figure 3.

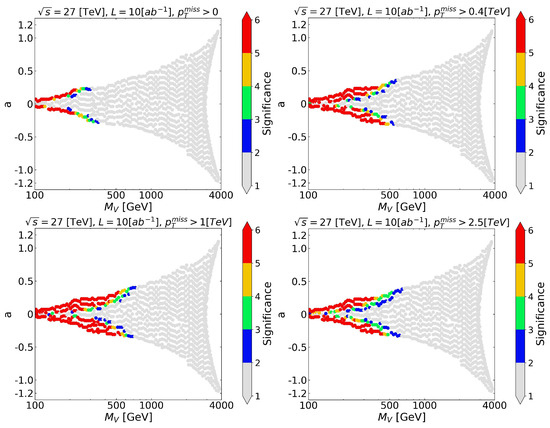
Figure 3. Parameter space displaying the statistical significance and satisfying the condition $S>2$, for the HE-LHC with an integrated luminosity $L=10a{b}^{-1}$ under various kinematic cuts in the mono-Higgs event.

The optimal kinematic cut results for mono-Higgs and mono-Z events across the three accelerators are shown in Table 2.

Table 2. Optimal kinematic cuts for the missing momentum transverse of the Higgs and Z-boson, according to the collider.

Collider	HL-LHC	HE-LHC	FCC-hh
$p_T^{\mathrm{miss}}$ [TeV]	0.4	1	3.5

In all our simulations, we employed the cteq6l(proton) parton distribution function  [27]. Finally, we will base our work on the final parameter space found in reference [3] and represented in Figure 1.

4. Results

4.1. Mono-Higgs Production

We start by considering the mono-Higgs production. As explained above, this process receives contributions not only from the associated production of a Higgs boson and two $V^0$’s, but also from the production of a Higgs with a pair of charged massive vectors. In order to visualize the relative importance of each subprocess, we will discuss first the $h{V}^0{V}^0$ channel, and later, we will consider the mono-Higgs production, taking into account all the contributions.

4.1.1. $V^0$ Production

To estimate the observability potential of our model in the $h{V}^0{V}^0$ channel, we computed the signal-to-background ratio and the statistical significance of the signal as functions of the DM mass ($M_V$) and the Higgs-DM coupling constant (a). In Figure 4, we show the signal-to-background ratio as a function of $M_V$ under the condition that the statistical significance is larger than 2. Meanwhile, in Figure 5, we show which region of the parameter space is tested with the same criterion.

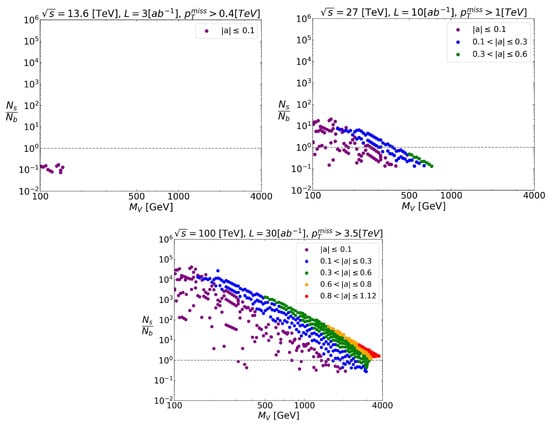
Figure 4. Ratio between signal and background events for each accelerator for the process $pp\to h{V}^0{V}^0$. The dashed gray lines indicate when the ratio is 1. All the points satisfy the constrain $S>2$.

Figure 5. Parameter space displaying the value of the ratio between signal and background events in the color scale, for each accelerator for the process $pp\to h{V}^0{V}^0$.

Figure 6 and Figure 7 are similar to the previous ones, but this time, the statistical significance is the relevant quantity. We see that the HL-LHC cannot prove the model (reaching S ≃ 4), and the FCC has the potential to test almost the whole parameter space except for a small region of high DM mass and small Higgs–DM coupling. In fact, if the $V^0$ were the only source of missing energy, the mono-Higgs production could provide a relevant signal of the model for $M_V\lesssim$ 550 GeV at the HE-LHC and $M_V\lesssim 4$ TeV for the FCC.

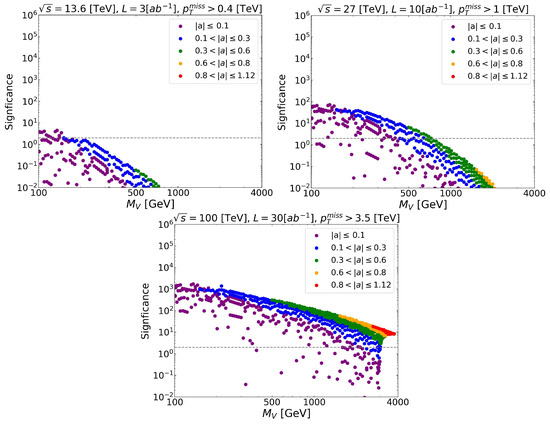
Figure 6. Statistical significance as a function of the vector mass for the process $pp\to h{V}^0{V}^0$. The dashed gray lines indicates when the significance reaches the 68% confidence level ($S=2$).

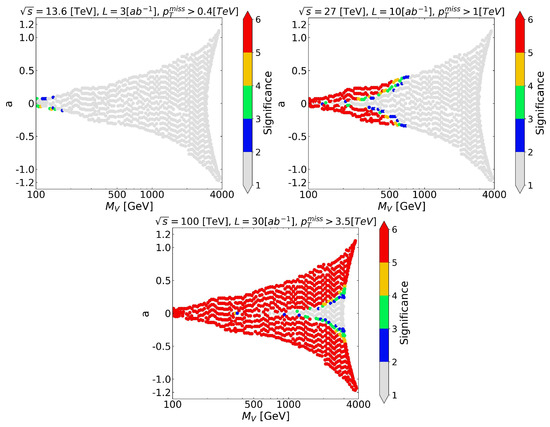
Figure 7. Parameter space showing the significance in the color bar for the process $pp\to h{V}^0{V}^0$ @ 13.6; 27 and 100 TeV of energy center of mass with its respective optimal kinematic cut and maximum integrated luminosity.

4.1.2. $V^{\pm ,0}$ Production

However, as explained above, the charged companions for our DM candidate may also contribute to missing energy. In this case, the mono-Higgs production originated from both the $pp\to h{V}^0{V}^0$ and $pp\to h{V}^{+}{V}^{-}$ channels. The $pp\to h{V}^{+}{V}^{-}$ is favored by electroweak contributions that are absent $pp\to h{V}^0{V}^0$, making the mono-Higgs production much stronger when the two sub-processes are taken into account. The difference is evident when we compare Figure 4 and Figure 8. The signal-to-background ratio increases as much as four orders of magnitude at the low mass region and one order of magnitude at the highest masses. Of course, the statistical significance is also improved (see Figure 9 and Figure 10).

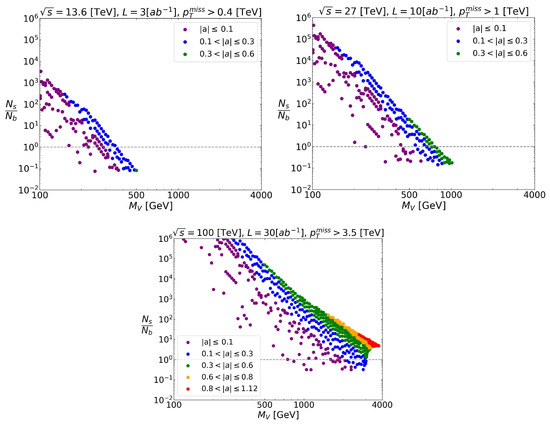
Figure 8. Ratio between signal and background events for each accelerator for the process $pp\to h{V}^{+,0}{V}^{-,0}$. The dashed gray lines indicate when the ratio is 1. All the points satisfy the constraint $S>2$.

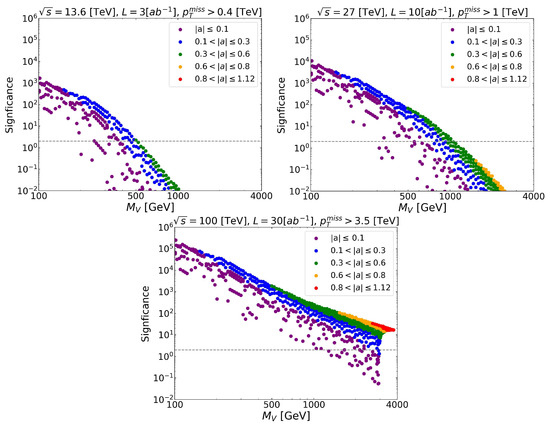
Figure 9. Statistical significance as a function of the vector mass for the process $pp\to h{V}^{+,0}{V}^{-,0}$. The dashed gray lines indicates when the significance reaches the 68% confidence level ($S=2$).

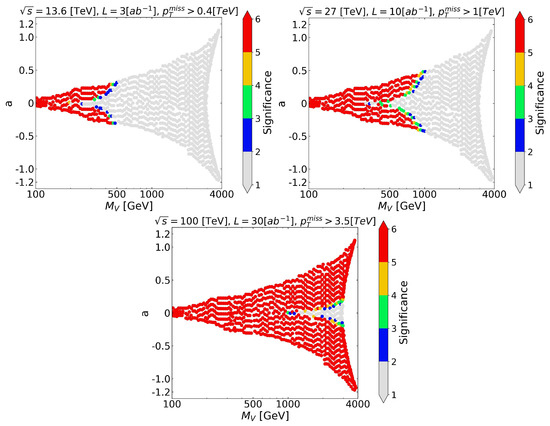
Figure 10. Parameter space showing the Significance in the color bar for the process $pp\to h{V}^{+,0}{V}^{-,0}$ @ 13.6; 27 and 100 TeV of energy center of mass with its respective optimal kinematic cut and maximum integrated luminosity.

Following the same conditions of Figure 4 and Figure 5, in Figure 8 and Figure 11, the excess of events in each collider is presented, assuming in each case the maximum projected luminosity. As the result of a greater signal-to-background ratio, the HL-LHC can prove the model for $M_V\lesssim 500$ GeV and $\left|a\right|\lesssim$$0.3$ (blue and purple dots in Figure 8). In the case of the HE-LHC, the model can be tested for masses as large as 1 TeV.

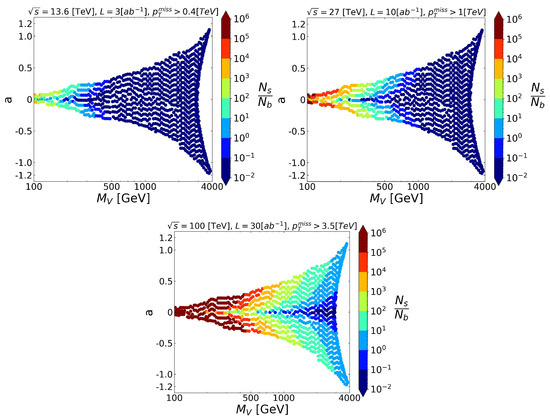
Figure 11. Parameter space displaying the value of the ratio between signal and background events in the color scale, for each accelerator for the process $pp\to h{V}^{+,0}{V}^{-,0}$.

The FCC-hh, on the other hand, can prove most of the parameter space, even part of the region for which there is saturation of the relic density.

4.2. Mono-Z Production

Now, we turn our attention to the mono-Z production process. Again, this process receives two contributions in our model: $pp\to V^0{V}^{0}Z$ and $pp\to V^{+,0}{V}^{-,0}Z$. Similarly to the analysis made for the mono-Higgs production, we study these two sub-processes separately.

4.2.1. $V^0$ Production

In Figure 12, we show the behavior of statistical significance for the $pp\to Z{V}^0{V}^0$ at the FCC-hh with $L=30a{b}^{-1}$, which represents the highest expected luminosity for this collider. As we can see, the signals produced by this particular sub-process are not statistically significant, even for the largest luminosity. Consequently, we will turn our attention toward the production of a Z boson in association with the charged companions of the DM candidate.

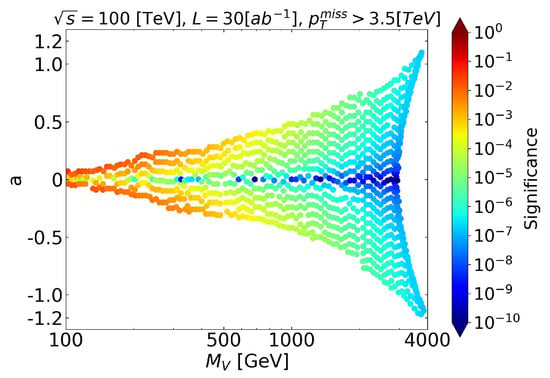
Figure 12. Statistical significance in the parameter space for $pp\to Z{V}^0{V}^0$.

4.2.2. $V^{\pm ,0}$ Production

Although we are faced with the same large background as before, here, the signal is much more powerful due to the electroweak channels. As we did in the mono-Higgs production case, we study the signal-to-background ratio (Figure 13) and its statistical significance (Figure 14) at different colliders. This time, significant excesses of events are produced in most parts of the allowed parameter space, making the model testable through this channel for masses up to a few TeV.

Figure 13. Parameter space displaying the value of the ratio between signal and background events in the color scale, for each accelerator in the process $pp\to Z{V}^{+,0}{V}^{-,0}$.

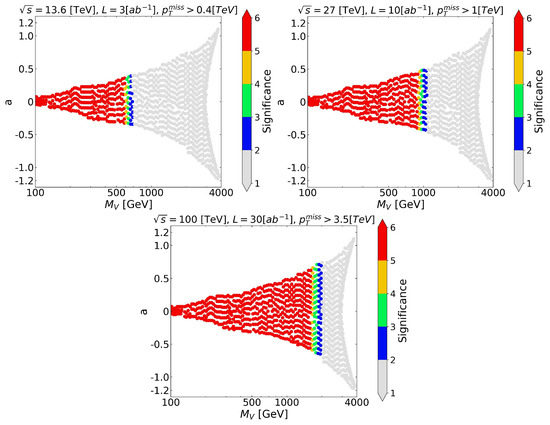
Figure 14. Parameter space showing the significance in the color bar for the process $pp\to Z{V}^{+,0}{V}^{-,0}$ @ 13.6; 27 and 100 TeV of energy center of mass with its respective optimal kinematic cut and maximum integrated luminosity.

The main feature of the Mono-Z event is its independence of the Higgs–DM coupling parameter $\left(a\right)$, thus the mass of the vector $\left(M_V\right)$ is the only important parameter to consider. In this sense, the mono-Z production is complementary to the mono-Higgs channel.

5. Conclusions

In this work, we have studied the mono-Higgs and the mono-Z production channels in the minimal vector dark matter model. We argue that the production of the Higgs and the Z boson in association with the charged companions of the DM candidate must be taken into account and contribute significantly to the studied channels. The study of the mono-Higgs production at the FCC may, in principle, test the whole parameter space with the exception of a small region at high DM masses and very low Higgs–DM coupling. For this reason, the mono-Higgs channel may represent the best opportunity to discover or rule out this model at future colliders. Although the mono-Higgs is always the most important channel, the mono-Z is complementary and, in the case of discovery in the mono-Higgs, it may help in determining the values of the parameters of the model.