Further Study of the Relationship between Transient Effects in Energetic Proton and Cosmic Ray Fluxes Induced by Coronal Mass Ejections

Abstract

The study and better understanding of energetic transient phenomena caused by disturbances occurring on our Sun are of great importance, primarily due to the potential negative effects those events can have on Earth’s environment. Here, we present the continuation of our previous work on understanding the connection between disturbances in the flux of energetic particles induced in the near-Earth environment by the passage of interplanetary coronal mass ejections and related Forbush decrease events. The relationship between the shape of fluence spectra of energetic protons measured by the instruments on the SOHO/ERNE probe at Lagrange point L1, Forbush decrease parameters measured by the worldwide network of neutron monitors, and coronal mass ejection parameters measured in situ is investigated. Various parameters used to characterize transient phenomena and their impact on the heliosphere, provided by the WIND spacecraft, were utilized to improve the accuracy of the calculation of the associated energetic proton fluence. The single and double power laws with exponential rollover were used to model the fluence spectra, and their effectiveness was compared. Correlation analysis between exponents used to characterize the shape of fluence spectra and Forbush decrease parameters is presented, and the results obtained by the two models are discussed.

1. Introduction

The study of eruptive events on the sun and associated disturbances in the heliosphere is of great importance, largely due to the potential hazards they can pose to many areas of modern life. This is especially true at the present time, given the increased likelihood of their occurrence in the rising phase of solar cycle 25.

Magnetic reconnection on the sun involves violent processes through which magnetic energy is transformed into other forms of energy, often resulting in solar flares (SFs) or coronal mass ejections (CMEs). SFs are sudden eruptive phenomena in the solar atmosphere’s active regions, observed as a flash of electromagnetic radiation, and are frequently associated with CMEs [1,2]. CMEs are large-scale eruptions of magnetized plasma from the sun’s corona into the interplanetary medium, where they can be referred to as interplanetary coronal mass ejections (ICMEs).

Solar flares and coronal mass ejections may induce complex disturbances in the heliosphere and Earth’s magnetosphere. One such phenomenon includes particle acceleration that results in a flux enhancement of protons, electrons, and ions. These enhancements, typically referred to as solar energetic particle (SEP) events, can be measured in interplanetary space by detectors onboard space probes, and in extreme cases, by Earth-based detectors. High-energy particles can be ejected and accelerated from the sun during SF events [3,4], or they can be accelerated by CME- and ICME-induced shock waves. These phenomena can accelerate SEPs to $\mathrm{MeV}$ or even $\mathrm{GeV}$ energies, reaching Earth usually within a day after their occurrence or even faster [5]. It is important to study not just the strong SEP events, which have the potential to affect our civilization [6], but also the weaker and more frequent ones. It is crucial to understand the circumstances under which they occur but also the parameters that describe the propagation and strength of these events [7].

Another way eruptive events on the sun can affect the near-Earth environment is through their impact on cosmic rays (CRs). Cosmic rays are high-energy charged particles that predominantly originate from outside our solar system, although some of these particles can originate from the sun. In the heliosphere, CRs interact with the interplanetary magnetic field (IMF), which is carried by the stream of supersonic plasma blowing outward from the sun known as the solar wind. Transients such as CMEs and ICMEs with accompanied bow shocks, created due to the interaction of faster ICME with slower solar wind, can modulate CRs [8,9]. This modulation of CRs can be detected on Earth as a sudden offset in the CR flux, followed by a gradual recovery phase that can last several days [10,11], an effect commonly known as a nonrecurrent Forbush decrease (FD). Thus, the observed change in CR flux can be used as a proxy for solar activity.

These are just some of the numerous phenomena that can occur in the heliosphere and are associated with the sun’s activity. To maximize our understanding of such complex events, we must investigate all the interconnections among the various induced processes. In this work, we expand on our previous study of one such relationship [12], specifically the connection between the enhanced flux of solar energetic particles and the properties of concurrent Forbush decreases, which have also been observed and studied by other authors [13,14]. The main idea behind the study is that, on one hand, the passage of a CME/ICME can lead to particle acceleration and an increase in the detected flux of energetic particles, while on the other hand, it may cause a decrease in the observed flux of CRs or the aforementioned Forbush decrease. To investigate the connection between these two phenomena, we examined the correlation between the shape of the event-integrated differential SEP flux, or differential fluence, measured at Lagrange point 1 (L1), and the magnitudes of associated FDs. To extend and potentially refine our previous study, we implemented several improvements. These features include the utilization of high-resolution data for the IMF, solar wind, and CME speeds in order to increase the precision in determining the onset and duration of events. Furthermore, we introduced an additional model for the description of the fluence spectra to be used alongside and compared with the previously used one. Finally, we applied a new fitting procedure based on the Monte Carlo approach. We believe these improvements lead to noticeably more precise and reliable results that further support the proposed relationship between the shape of the differential fluence spectra and the magnitudes of FDs.

In the article, we first discuss various data sources used in the analysis and justify the selection of events from solar cycles 23 and 24. We then describe in detail the procedure used to determine the differential SEP fluence spectra. In the next section, we introduce two models that were used to parameterize the fluence spectra and compare how well they were able to fit the data. Finally, we perform the correlation analysis to study the dependence between FD parameters and the spectral indices of SEP fluence spectra, as well as the selected CME parameters. We discuss the results in terms of the models applied and evaluate the usefulness of obtained indices as predictors of FD properties.

2. Data and Event Selection

2.1. Data Sources

Various types of data were necessary for the presented study, including energetic proton data measured near Earth, selected IMF, CME, solar wind, and geomagnetic field parameters, as well as CR measurements by Earth-based detectors. The data are available either in the form of time series or as extreme and averaged values over the duration of the event. Two main repositories were used to acquire these data: the OMNIWeb Plus repository provided by the NASA/Goddard Space Flight Center [15] (for energetic proton data and time series of IMF and solar wind speeds) and the IZMIRAN Forbush decrease database provided by the Pushkov Institute of Terrestrial Magnetism, Ionosphere, and Radio Wave Propagation, Russian Academy of Sciences [16] (for Forbush decrease and averaged space weather parameters).

Energetic proton data in the OMNIWeb Plus repository are provided by the Energetic and Relativistic Nuclei and Electron (ERNE) sensor unit onboard the Solar and Heliospheric Observatory (SOHO) [17]. SOHO is situated in a halo orbit around L1. SOHO/ERNE has two energetic particle sensors: the Low-Energy Detector (LED) and the High-Energy Detector (HED), each with ten energy channels measuring ion fluxes and count rates in the ranges of 1.3–13 MeV/nucleon and 13–130 MeV/nucleon, respectively. This setup has been actively monitoring differential proton flux over the course of the last three solar cycles [18,19]. For this study, hourly data of energetic protons were used.

IMF and solar wind speed data in the OMNIWeb Plus repository were provided by the Global Geospace Science (GGS) WIND spacecraft. The spacecraft was positioned upstream of Earth at L1, initially in a Lissajous orbit and then, more recently, inserted into a halo orbit around L1. The primary goal of the mission has been to monitor the properties of the solar wind, a task that its onboard instruments have successfully performed over the last three decades [20].

Various space weather parameters associated with a specific FD event were taken from the database of Forbush decreases compiled by researchers from IZMIRAN. FD magnitudes in the database are obtained using measurements from the worldwide network of neutron monitors (the most widely used type of ground-level CR detectors). Neutron monitor data were corrected for efficiency and atmospheric effects. Other space weather data in the IZMIRAN database were assembled from various sources to produce a comprehensive repository containing various associated parameters of FDs, the heliosphere, and the geomagnetic field. In this study, we used parameters related to CMEs and solar wind, such as average CME speed and maximum solar wind speed, as well as the minimal Disturbance Storm-Time index (Dst) over the duration of the FD event. We also used FD magnitudes calculated by the IZMIRAN researchers using the global survey method (GSM) technique [21]. GSM integrates measurements from a worldwide network of neutron monitors, accounting for all effects caused by various anisotropies and disturbances of atmospheric and geomagnetic origin, to derive the hourly variation of primary cosmic ray flux outside Earth’s atmosphere. In addition to FD magnitudes measured at Earth, they also provide the values of FD magnitudes corrected for the magnetospheric effect, which should remove the contribution of the disturbances introduced by variations in the geomagnetic field.

2.2. Event Selection

In this study, we focused on the events that occurred during most of the solar cycle 23 and 24. To establish the connection between the shape of energetic proton fluence spectra and the properties of concurrent Forbush decrease (FD) events, we decided to focus on events with larger magnitudes, expecting the correlation to be more pronounced in such cases due to less noise from noncontributing processes. The lower boundary for FD magnitude for event selection was somewhat arbitrarily set to $4\%$. Further lowering this bound would certainly increase the statistics in the analysis, but we do not believe it would add much support to the proposed relationship, due to the non-negligible likelihood that events of lower magnitude may exhibit different behavior from events of larger magnitudes (which is further discussed in Section 5). However, there are plans to investigate this in more detail in the future and possibly extend the analysis to include events of lower magnitudes.

The term SEP event can be somewhat misleading due to two possible processes leading to particle acceleration, so we feel we should clarify the nature of the events used in this work. Evidence of two distinctive physical mechanisms of SEP acceleration has been accumulating for the last half-century [4]. The first of the two mechanisms is associated with type II radio bursts from coronal and interplanetary shock waves, while the second is associated with type III radio bursts produced by streaming electrons. The former is driven by fast CMEs, is proton-dominated, and produces “gradual” SEP events (sometimes also referred to as Energetic Storm Particle, or ESP events) that have high SEP flux intensity near Earth. The latter mechanism is predominantly connected to magnetic reconnection with open magnetic field lines and resonant wave–particle interactions in impulsive SFs and jets. It produces “impulsive” SEP events that last for hours, in contrast to gradual events, which can last for days partly due to the continuing acceleration of the shock. Even though all of the CMEs used in the analysis can be associated with SFs, we believe all of them belong to the gradual SEP event class.

Determining event-integrated SEP fluence was not always simple, especially in the case of complex events where structures that appear to have different sources are superimposed. That is why we have decided to eliminate all events for which we did not find a clear association with the passage of a specific CME, leaving us with 20 events to be used in the analysis. Selected FD events and their respective parameters from the IZMIRAN database are shown in

Table 1. Selected parameters from the IZMIRAN database associated with FD events: FD magnitude for particles with $10\mathrm{GV}$ rigidity (M), FD magnitude for particles with $10\mathrm{GV}$ rigidity corrected for magnetospheric effect ($M_M$), average CME speed between the Sun and the Earth calculated from the beginning of the associated CME ($V_{meanC}$), maximal hourly solar wind speed during the event ($V_{max}$), and minimal Dst index during the event ($Ds{t}_{min}$).

Date/Time of FD Onset	M $[\%]$	${\mathit{M}}_{\mathit{M}}$ $[\%]$	${\mathit{V}}_{\mathit{meanC}}$ $\left[{\mathbf{kms}}^{-1}\right]$	${\mathit{V}}_{\mathit{max}}$ $\left[{\mathbf{kms}}^{-1}\right]$	${\mathit{Dst}}_{\mathit{min}}$ $\left[\mathbf{nT}\right]$
29−Sep−2001 09:40:00	4.3	4.4	831	694.0	−56.0
11−Oct−2001 17:01:00	7.0	6.9	769	572.0	−71.0
21−Oct−2001 16:48:00	5.4	7.3	858	677.0	−187.0
24−Nov−2001 05:56:00	9.2	9.8	1366	1024.0	−221.0
17−Apr−2002 11:07:00	6.2	7.0	745	611.0	−127.0
07−Sep−2002 16:36:00	4.6	5.1	863	550.0	181.0
30−Oct−2003 16:19:00	14.3	9.4	2140	1876.0	383.0
20−Nov−2003 08:03:00	4.7	6.8	872	703.0	422.0
26−Jul−2004 22:49:00	13.5	14.4	1290	1053.0	197.0
13−Sep−2004 20:03:00	5.0	5.3	948	613.0	50.0
15−May−2005 02:38:00	9.5	12.2	1231	987.0	263.0
14−Dec−2006 14:14:00	8.6	9.6	1165	955.0	146.0
05−Aug−2011 17:51:00	4.3	4.8	1104	611.0	−115.0
24−Oct−2011 18:31:00	4.9	6.5	633	516.0	−147.0
08−Mar−2012 11:03:00	11.7	11.2	1188	737.0	143.0
14−Jul−2012 18:09:00	6.4	7.6	834	667.0	−127.0
23−Jun−2013 04:26:00	5.9	5.3	844	697.0	−49.0
12−Sep−2014 15:53:00	8.5	5.9	897	730.0	−75.0
22−Jun−2015 18:33:00	8.4	9.1	1040	742.0	−204.0
07−Sep−2017 23:00:00	6.9	7.7	1190	817.0	−124.0

.

3. Determination of Energetic Proton Fluence Spectra

Establishing a clear connection between a CME originating on the sun and a consequent FD is often not straightforward [22]. Due to the many potential interactions that can occur in the heliosphere, the same can be true when one tries to establish the effect of an ICME passage on the observed flux of energetic protons in interplanetary space.

Complex events on the sun and related disturbances in the heliosphere include various processes that can lead to particle acceleration and contribute to an increased flux of energetic protons [23]. Hence, the direct link between the structures observed in the energetic proton flux time series and the passage of an ICME is not always obvious. To establish this link as reliably as possible, we utilized data provided by various instruments onboard the WIND spacecraft. As our primary interest was the determination of the precise timing of the onset and duration of the interaction, we found the time series of the IMF and CME velocity to be the most useful parameters for this purpose available in the WIND data.

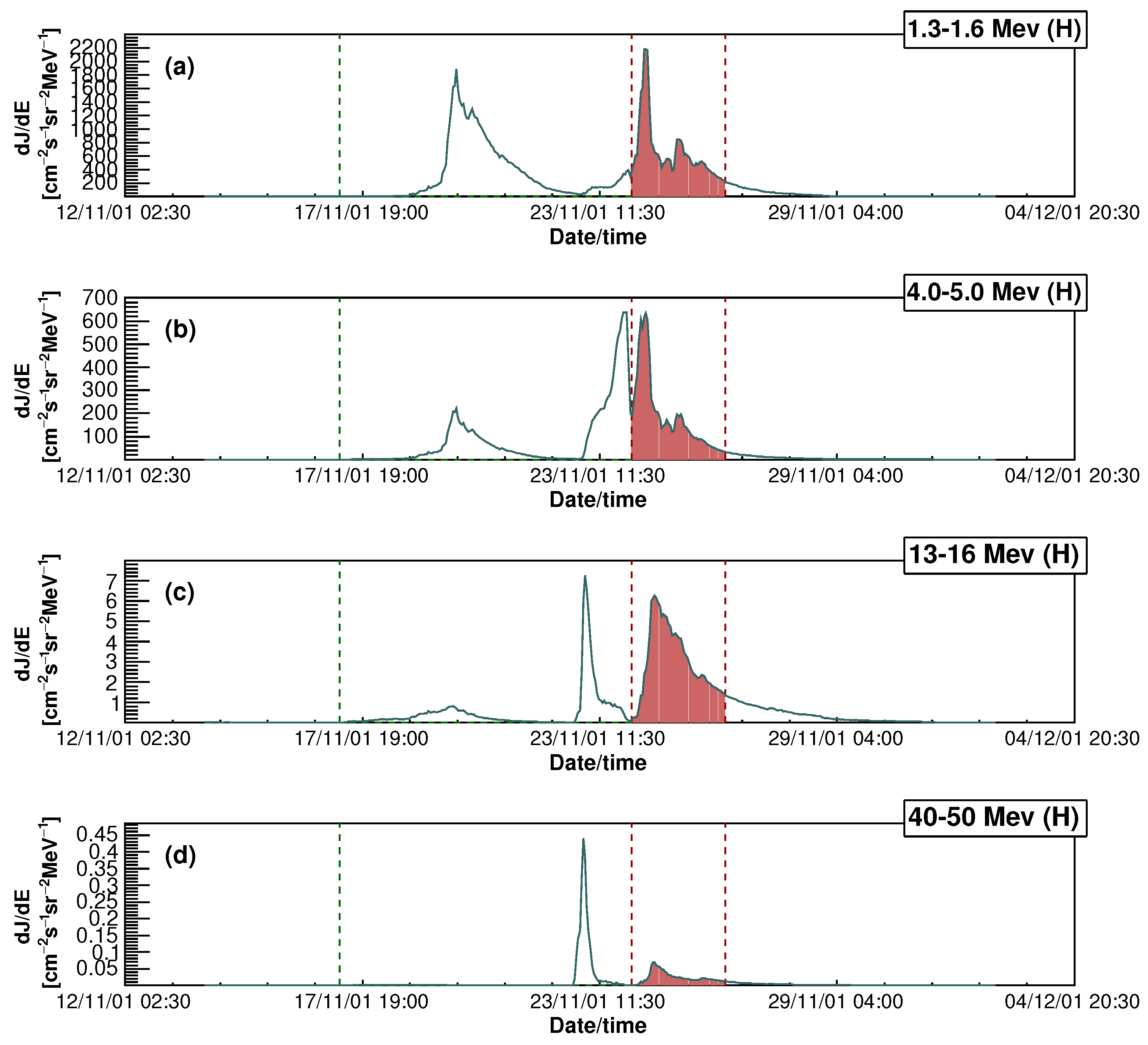
To illustrate the usefulness of WIND data for this purpose, Figure 1 shows the time series for the IMF (both the total magnitude and its components), solar wind velocity, and the flux of energetic protons for one selected channel (1.3–1.6 MeV/nucleon) measured by the SOHO/ERNE instrument for the November 2001 event. Vertical dashed lines indicate the time intervals associated with the shock-sheath region and the ICME itself (from left to right, respectively). Some of the analyzed events are forming complex magneto-plasma structures, which can be explained by interactions with high-speed solar wind streams or other ICMEs.

Considering the different time resolutions of WIND ($92\mathrm{s}$) and SOHO/ERNE data ($1\mathrm{h}$), which can result in slight hour-round-off time shifts of the time series for the latter, we observe a clear impact of the arrival of the ICME shock on the flux of energetic protons. In addition to the increase in proton flux attributed to the passage of the ICME, there is a noticeable structure that seemingly precedes the ICME shock. This structure does not appear to be directly related to the variations in the IMF or solar wind velocity. Due to the general complexity of events on the sun, which typically lead to the formation of CMEs, and the different mechanisms of particle acceleration and interaction with the solar wind, it is possible that the detected increase in proton flux preceding the shock is induced by some other aspect of such phenomena or could be some kind of event precursor. We discuss the possible nature of this structure below; however, we believe that the absence of a detailed explanation of the mechanism behind its origin will not critically affect the procedure of determining differential proton fluence and the presented results. Nonetheless, it is definitely a feature that we will try to investigate in our future work, as we believe it will lead to a better overall understanding of complex space weather phenomena.

The times marking the shock and the end of ICME interaction, determined as explained in the previous paragraphs, are now used as integration bounds to calculate event-integrated flux (or differential fluence) for each of the SOHO/ERNE energy channels. An illustration of this procedure is shown in Figure 2 for four selected SOHO/ERNE channels.

Among the three vertical dashed lines, the second and the third ones mark the integration bounds, while the first one indicates the end of the time interval used to calculate the baseline value (the beginning of the baseline interval being the same as the beginning of the interval shown on the graph). In several cases where energetic proton flux preceding the event was disturbed for a longer period of time, a time interval after the event, when the flux has recovered and was stable, was used. The duration of time intervals used for baseline determination ranged from a day and a half to several days. The filled area under the graph represents the differential fluence value for a given channel calculated relative to the baseline.

One can observe that part of the proton flux time series associated with the structure preceding the arrival of the shock exhibits a different energy dependence to the part we assume is induced by the passage of the ICME and its interaction with the local particles [24], as the relative ratio of the areas under respective profiles increases with increasing energy. This could indicate that the observed structure is not related to the CME but is a consequence of some other interaction.

In our previous work [12], due to the lack of high-resolution WIND data, integration intervals were more loosely defined. We were unable to precisely separate only the CME-induced part of the energetic proton flux, often including the precursor structure. We believe the new approach is a significant improvement and should lead to more reliable results.

4. Parametrization of Fluence Spectra

Using the values for differential energetic proton flux in different energy channels integrated over the duration of the event (as detailed in Section 3), we form the differential fluence spectra for selected events. The average energy in $\mathrm{MeV}$ was used for particle energy bin values [25].

Several models have been proposed over the years to describe the observed spectra [26]. One feature that has proven somewhat challenging to accurately describe is the characteristic brake or “knee”, which can be prominent in extreme events [27,28], possibly occurring due to the effect of interplanetary transport [29]. Previously [12], we relied on the model proposed by Band et al. [29,30] to fit the event-integrated fluence spectra. The model, originally developed to describe gamma-ray burst spectra but also successfully used to model fluence spectra [31], is based on the double power law in the following form:

$$\frac{dJ}{dE}=\left\{\begin{array}{cc}A{E}^{\alpha }exp\left(-\frac{E}{E_B}\right)\hfill & E\le (\alpha -\beta )E_B,\hfill \\ A{E}^{\beta }{\left[\left(\alpha -\beta \right)E_B\right]}^{\alpha -\beta }exp\left(\beta -\alpha \right)\hfill & E>(\alpha -\beta )E_B,\hfill \end{array}\right.$$

(1)

where E is the particle energy, $E_B$ is the “knee” energy, $\alpha$ is the power law index that characterizes the low-energy part of the spectrum, $\beta$ is the power law index that characterizes the high-energy part of the fluence spectrum, and A is the spectral coefficient.

While this model reasonably described the observed spectra for a number of events, in some cases, it seemed that the agreement could be better. Attempting to use the “knee” energy as a free parameter in the fitting procedure resulted in either fit instability or divergent fits. We believed this to be a consequence of the limitations of standard minimizers in handling a relatively large number of free parameters. To overcome this issue, in our previous analysis, we decided to treat the “knee” energy as a fixed parameter, determining $E_B$ by relying on the dependence of this parameter on the integral fluence reported by some authors [28,32]. Additionally, the range conditions in Equation (1) were approximated using the expected values for indices $\alpha$ and $\beta$ of $-1$ and $-2$, respectively, as suggested in [30], effectively reducing the conditions for the low-energy and high-energy ranges to $E\le E_B$ and $E>E_B$. However, the number of approximations needed to stabilize the fitting procedure seemed excessive, so considering an alternative approach seemed advisable.

To reduce potentially significant uncertainties and to increase the reliability of the fitting, in this study, we resorted to employing the procedure based on the Monte Carlo approach, specifically utilizing the emcee Python package. emcee is a robust, well-tested, and user-friendly MIT-licensed tool for Bayesian inference, which uses Markov Chain Monte Carlo (MCMC) sampling. It is based on the affine-invariant ensemble sampler and is widely and successfully applied in various research disciplines and data science domains, including astrophysics, biostatistics, and machine learning. We performed the fitting procedure using Equation (1) and setting all four parameters as free variables. The fitting algorithm performed exceptionally well, rapidly and reliably converging to optimal parameter values with very high precision and minimal deviation between independent walkers. The approach led to a significantly improved and more stable fitting procedure, ultimately resulting in noticeably more reliable outcomes compared with our previous method.

Although fitting the energetic proton fluence spectra with the Band function using the MCMC method eventually performed remarkably well, the function was not so straightforward to implement when the fitting procedure was based on standard minimizer algorithms. Hence, we were interested in investigating whether a simpler and more robust model could be comparably effective in describing energetic proton spectra while also being easier to implement. One such model, proposed by Ellison and Ramaty, was developed based on observations of particle acceleration at interplanetary shocks [33], and was successfully used to model spectra of several particle species during large SEP events [34]. In these studies, it was concluded that for strong events it mainly fits the lower energy range satisfactorily. However, we felt it performed well enough to test it on the set of events we selected for the presented analysis. The model assumes the form of a power law with an exponential rollover to describe the energetic particle fluence spectra:

$$\frac{dJ}{dE}=A{E}^{\gamma }exp\left(-\frac{E}{E_0}\right),$$

(2)

where E is the particle energy, $E_0$ is the cutoff exponent parameter, $\gamma$ is the spectral index, and A is the spectral coefficient.

Even though it is one of the older proposed models, and some authors had objections to the somewhat arbitrary introduction of the rollover correction [32], we found the Ellison–Ramaty model to be mostly in good agreement with the observed data. Additionally, it proved to be robust in terms of the convergence of the fit. Hence, we felt it is a good candidate to compare against the model proposed by Band et al. to possibly determine if one is more suited than the other for the purpose of our analysis.

We fitted the fluence data with both Band and Ellison–Ramaty models and compared how accurately they described the observed spectra. The Ellison–Ramaty model mostly converged stably and performed reasonably well when used with standard minimizers. However, for a more accurate comparison of both models, we utilized the aforementioned implementation using the emcee package for the Ellison–Ramaty function as well. This indeed led to further improvements, greater accuracy, and increased precision of the fit results.

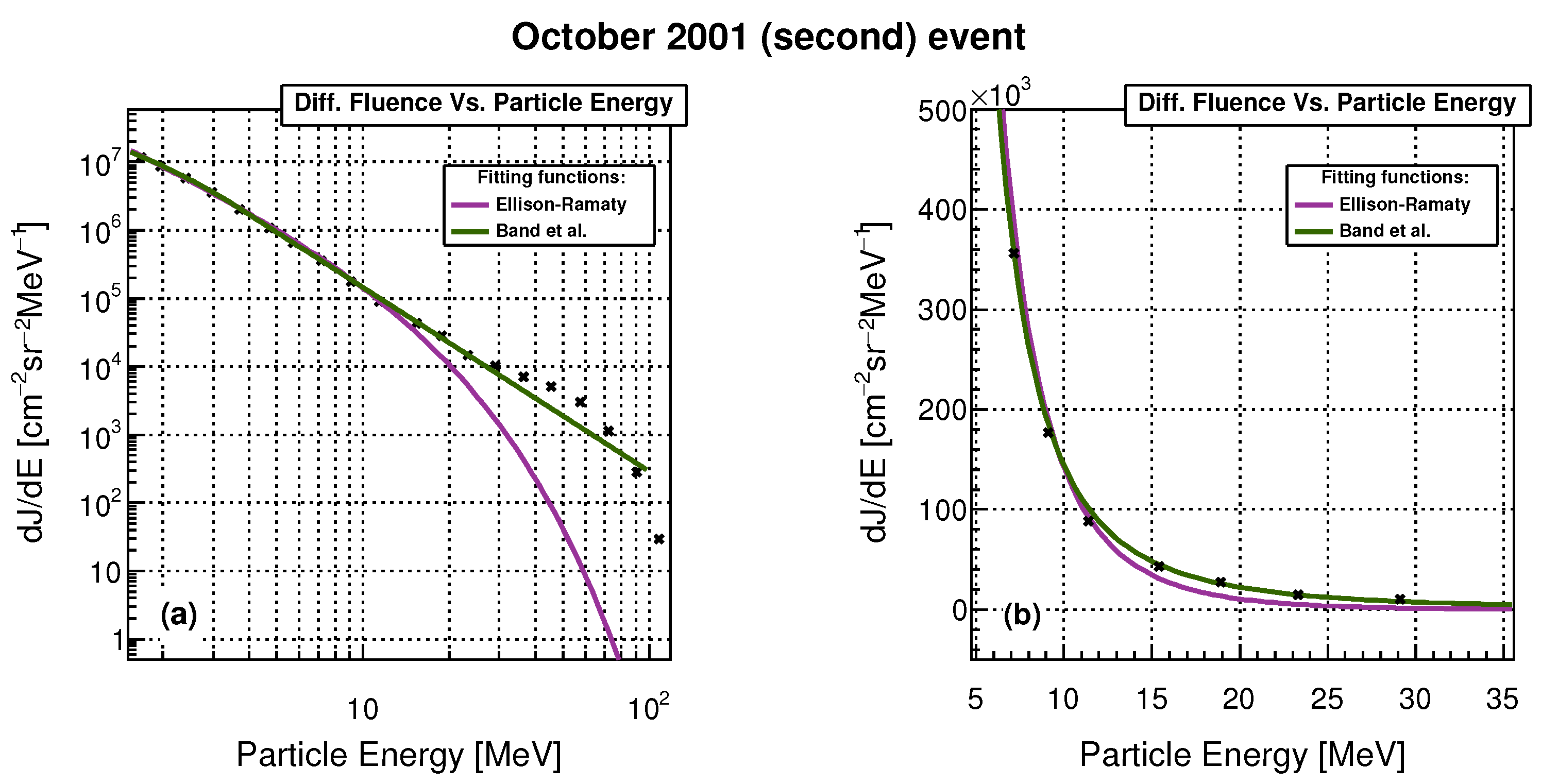
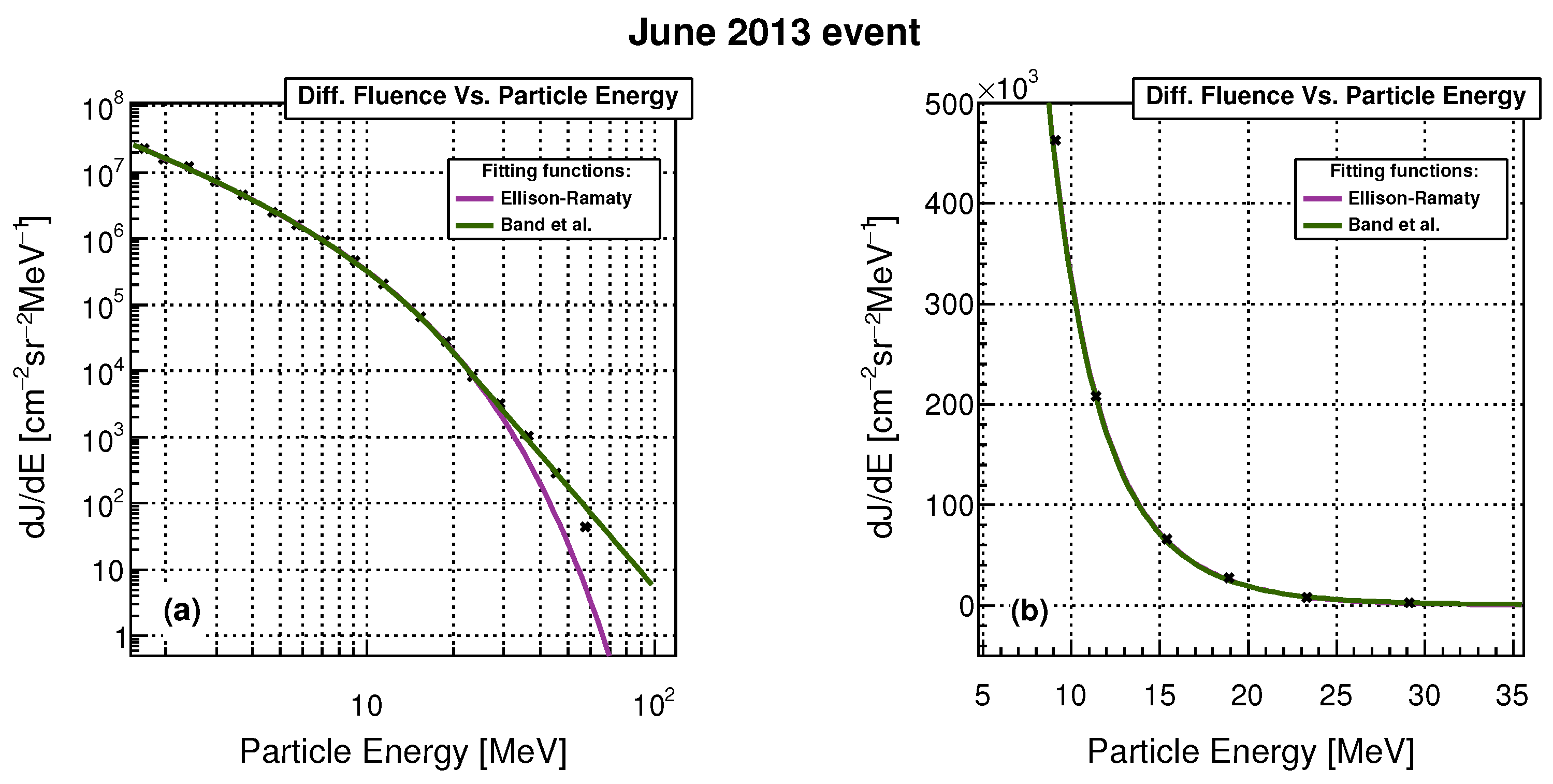
In direct comparison, the Band function proved to be an overall more flexible model, describing the spectra more accurately, particularly apparent in its ability to effectively model the “knee” feature. While in some cases this difference in performance was more evident, for the majority of events, the Ellison–Ramaty model seemed to describe the spectra sufficiently well, offering only a moderately poorer fit. In Figure 3 and Figure 4, we show two events that best illustrate the different cases of the level of agreement between the two models.

The green line in Figure 3 and Figure 4 represents the fit function given by Equation (1) (Band et al.), and the magenta line represents the fit function given by Equation (2) (Ellison–Ramaty). The left panels on both figures show the fluence spectrum in log–log scale, while the right panels zoom in on the region around the “knee” energy in linear scale, which proved to be the most demanding to fit adequately.

An example where the difference in performance between the two models is most apparent is the second event in October 2001 (occurring around October 21), shown in Figure 3. Here, the observed spectrum is clearly better described by Equation (1). The Ellison–Ramaty fit starts to diverge just after the “knee”, and although the divergence is not dramatic, it is still noticeable. However, in the case of the June 2013 event (Figure 4), the difference between the two models is much smaller, with Ellison–Ramaty providing only a marginally less accurate fit. We believe that the fact that the second situation is encountered more often provides sufficient justification for continuing to use both models in the remainder of the analysis.

The obtained spectral indices $\alpha$, $\beta$, and $\gamma$, as well as the values for the ‘knee’ and roll-over energies, are shown in

Table 2. Parameters for the two models used to fit the fluence spectra for all events: spectral indices ($\alpha$, $\beta$) and “knee” energy ($E_B$) for the Band et al. model, and spectral index ($\gamma$) and roll-over energy ($E_0$) for the Ellison–Ramaty model.

Date/Time of FD Onset	$\mathit{\alpha }$	$\mathit{\beta }$	${\mathit{E}}_{\mathit{B}}$ $\left[\mathbf{MeV}\right]$	$\mathit{\gamma }$	${\mathit{E}}_0$ $\left[\mathbf{MeV}\right]$
29−Sep−2001 09:40:00	−1.859(1)	−3.60(2)	11.71(5)	−1.806(1)	10.000(1)
11−Oct−2001 17:01:00	−1.229(8)	−4.130(4)	1.354(6)	−1.798(4)	1.999(6)
21−Oct−2001 16:48:00	−1.169(6)	−2.695(1)	2.44(2)	−1.918(2)	7.93(4)
24−Nov−2001 05:56:00	−0.375(1)	−5.537(5)	3.535(1)	−0.378(1)	3.548(1)
17−Apr−2002 11:07:00	−1.422(2)	−3.783(2)	2.529(4)	−1.667(1)	3.271(4)
07−Sep−2002 16:36:00	−1.866(1)	−4.73(2)	4.991(8)	−1.882(1)	5.122(7)
30−Oct−2003 16:19:00	−0.100(1)	−5.876(4)	3.271(1)	0.000(1)	3.071(1)
20−Nov−2003 08:03:00	−1.599(4)	−3.419(5)	3.45(2)	−1.801(2)	4.58(2)
26−Jul−2004 22:49:00	−1.234(1)	−4.910(7)	3.328(2)	−1.255(1)	3.404(2)
13−Sep−2004 20:03:00	−0.949(1)	−6.54(2)	3.467(1)	−0.951(1)	3.474(1)
15−May−2005 02:38:00	−0.431(1)	−7.37(4)	2.811(1)	−0.432(1)	2.813(1)
14−Dec−2006 14:14:00	−0.721(1)	−4.038(2)	2.200(1)	−0.841(1)	2.427(1)
05−Aug−2011 17:51:00	−1.532(1)	−4.70(1)	4.742(5)	−1.545(1)	4.837(5)
24−Oct−2011 18:31:00	−1.112(2)	−7.57(5)	1.641(1)	−1.119(1)	1.648(1)
08−Mar−2012 11:03:00	−0.677(1)	−3.642(1)	5.129(1)	−0.698(1)	5.286(1)
14−Jul−2012 18:09:00	−1.246(1)	−9.999(1)	2.496(1)	−1.245(1)	2.494(1)
23−Jun−2013 04:26:00	−1.560(1)	−5.08(3)	5.71(1)	−1.564(1)	5.752(9)
12−Sep−2014 15:53:00	−0.551(3)	−3.350(1)	1.287(2)	−1.699(1)	3.232(4)
22−Jun−2015 18:33:00	−1.382(1)	−6.21(2)	3.424(1)	−1.386(1)	3.437(1)
07−Sep−2017 23:00:00	−1.210(1)	−5.11(1)	4.553(3)	−1.216(1)	4.590(2)

. Fit errors for all parameters are given in parentheses.

To further study and compare the usefulness of the models in describing the measured spectra, we performed a correlative analysis, presenting the results of both models in parallel.

5. Correlation between Spectral Indices and Forbush Decrease Parameters

To study the relationship between the enhanced flux of energetic protons accelerated by a CME/ICME-related interplanetary shock and the effect of the passage of these disturbances on cosmic rays, we investigate the correlation between spectral indices used to parameterize the shape of the energetic proton fluence spectra and the magnitudes of coincident Forbush decreases. FD magnitudes for $10\mathrm{GV}$ rigidity particles, calculated using GSM applied to neutron monitor data provided by the global neutron monitor network [35], are available in the IZMIRAN database. In addition to FD magnitudes measured at Earth, the database offers calculated values of FD magnitudes for $10\mathrm{GV}$ rigidity particles corrected for magnetospheric effects using the Dst index.

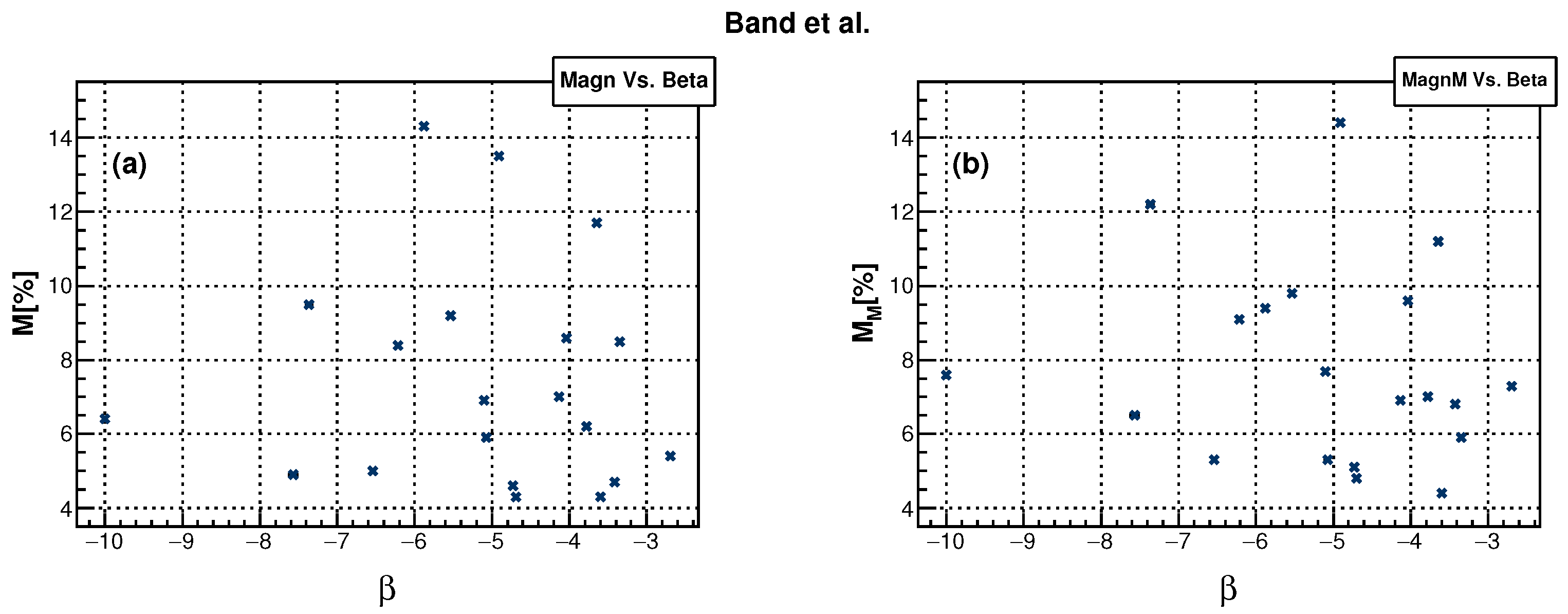
Figure 5 shows the dependence between the spectral index $\alpha$, obtained by fitting the fluence spectra with the function proposed by Band et al., and FD magnitudes. The dependence for the measured FD magnitude (M) is shown in the left panel, while the dependence for FD magnitude corrected for magnetospheric effects ($M_M$) is shown in the right panel.

Equivalent plots for spectral index $\beta$ are shown in Figure 6.

Figure 7 shows the relationship between FD magnitude and the spectral index $\gamma$, obtained by fitting the fluence spectra with the Ellison–Ramaty function. As in the previous figure, the dependence for the measured FD magnitude is shown on the left panel, while one for the FD magnitude corrected for magnetospheric effects is shown on the right panel.

The new fitting procedure has undoubtedly improved the reliability with which spectral index $\alpha$ is determined, and for some events, the newly obtained values have changed non-negligibly. However, the effect of the new results on the dependence shown in Figure 5 was not dramatic. A much larger change was observed in new values for the parameter $\beta$ (Figure 6). Where before it exhibited similar dependence as spectral index $\alpha$ in relation to FD magnitudes, now it is clear there is little correlation between these quantities. A few reasons come to mind to explain this observation, which could be related to the origin, acceleration mechanisms, and potential transport effects of the higher energy protons. However, we feel such a discussion is probably beyond the scope of this study, so for now this feature should be noted and further investigation left for future analysis. When it comes to the spectral index obtained from the Ellison–Ramaty fit, we observe a very similar relationship between $\gamma$ and FD magnitudes as we do for $\alpha$. This could indicate that the poorer fit of the Ellison–Ramaty function does not have a significant impact on this relationship. The observation seems consistent with our assumption, based on the negligible correlation between the spectral index $\beta$ and FD magnitudes, that the importance of the shape of the high-energy part of the spectrum appears to be less significant for the relationship we are investigating.

It is worth noting that in the distributions shown in Figure 5 and Figure 7, we observe what could be an outlier event (the July 2004 event with the value for M slightly below and the value for $M_M$ slightly above $14\%$) A potential reason for the deviation could be the overestimation of the FD magnitude for this event. The July 2004 event occurred on 26 July at 22:49:00 (according to the IZMIRAN database). It was preceded by two other events: one on 22 July at 10:36:00 (with a magnitude of $5.2\%$) and the second one on 24 July at 06:13:00 (with a magnitude of $4.6\%$). Cosmic ray flux had not yet recovered from these two events before the occurrence of the 26 July FD. We believe that if that was not the case, the magnitude for this event would be several percent smaller, hence it would deviate less in distributions presented in Figure 5 and Figure 7.

Previously [12], we noticed the possibility of the existence of two classes of events, where a different trend was observed for the events of smaller and events of larger FD magnitude, the boundary between them somewhat arbitrarily set to a magnitude of $6\%$. After refining the analysis in this work, the possibility of such classification is not eliminated but is somewhat less evident, and it appears to require a more careful analysis, which could be considered in a possible future extension of this study.

To quantify the proposed correlations between the spectral indices and FD magnitudes, we have performed a standard correlation analysis. Pearson correlation coefficients between FD magnitudes and spectral indices $\alpha$, $\beta$, and $\gamma$, as well as several selected space weather parameters, are shown in

Table 3. Correlation coefficients between FD magnitudes and spectral indices, as well as selected space weather parameters.

	$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\gamma }$	${\mathit{V}}_{\mathit{meanC}}$ $\left[{\mathbf{kms}}^{-1}\right]$	${\mathit{V}}_{\mathit{max}}$ $\left[{\mathbf{kms}}^{-1}\right]$	${\mathit{Dst}}_{\mathit{min}}$ $\left[\mathbf{nT}\right]$
$\mathit{M}[\%]$	0.70	−0.05	0.68	0.78	0.79	−0.38
${\mathit{M}}_{\mathit{M}}[\%]$	0.54	−0.15	0.59	0.54	0.53	−0.42

. We omitted to include the results for the parameters $E_B$ and $E_0$, as they exhibited an insignificant correlation with other parameters of interest. Additionally, aside from a relatively modest correlation between $\gamma$ and $E_0$ of $-41\%$, they also showed negligible correlations with the spectral indices themselves.

The correlation between spectral index $\alpha$ and FD magnitude M is roughly the same as previously reported ($70\%$ instead of $67\%$), while the correlation with FD magnitude corrected for the magnetospheric effect $M_M$ is somewhat smaller ($54\%$ instead of $64\%$). There is barely any correlation between spectral index $\beta$ with any of the FD magnitudes, as was indicated by the plots in Figure 6. Correlation coefficients for the spectral index $\gamma$ have values comparable to those obtained for $\alpha$–$68\%$ and $59\%$ for M and $M_M$, respectively. We believe that these results are non-negligibly affected by the observed deviation of the July 2004 event and that the actual correlations are stronger. Indeed, if the July 2004 event is removed, the correlations increase for both spectral indices $\alpha$ and $\gamma$, as shown in

Table 4. Correlation coefficients between FD magnitudes, spectral indices, as well as selected space weather parameters, with the July 2004 event excluded.

	$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\gamma }$	${\mathit{V}}_{\mathit{meanC}}$ $\left[{\mathbf{kms}}^{-1}\right]$	${\mathit{V}}_{\mathit{max}}$ $\left[{\mathbf{kms}}^{-1}\right]$	${\mathit{Dst}}_{\mathit{min}}$ $\left[\mathbf{nT}\right]$
$\mathit{M}[\%]$	0.83	−0.07	0.77	0.81	0.80	−0.39
${\mathit{M}}_{\mathit{M}}[\%]$	0.71	−0.20	0.73	0.54	0.52	−0.47

.

Based on the results in Table 3, we see that the correlation between FD magnitude M and spectral indices $\alpha$ and $\gamma$ are only slightly smaller than the correlations between M and the maximum hourly solar wind speed ($V_{\max }$) and average CME velocity ($V_{\mathrm{meanC}}$), which are quantities that typically show the largest correlation with FD magnitudes [36], and could be considered as the best predictors for FD magnitudes among space weather parameters. On the other hand, the correlations between the corrected FD magnitude $M_M$ and spectral indices are comparable to the correlations between $M_M$ and $V_{\max }$ and $V_{\mathrm{meanC}}$. If the July 2004 event is not taken into account (results presented in Table 4), the correlations with M for both spectral indices become comparable to those for $V_{\max }$ and $V_{\mathrm{meanC}}$. More importantly, for $M_M$, the correlations are significantly larger for both indices, indicating the extent to which the results in Table 3 were negatively influenced by the deviation of the July 2004 event.

Presented results, particularly the ones in Table 4, indicate even more strongly than in our previous work the significant correlation between spectral indices used to parameterize the shape of fluence spectra of energetic protons and FD magnitudes. The level of correlation for magnitude M suggests that spectral indices $\alpha$ and $\gamma$ serve as equally effective predictors of FD magnitude for particles with $10\mathrm{GV}$ rigidity obtained by the GSM model (M) as other space weather parameters, while for the FD magnitude for particles with $10\mathrm{GV}$ rigidity corrected for magnetospheric effects ($M_M$), they appear to be better predictors than other parameters. The results for both $\alpha$ and $\gamma$ are largely comparable, and they seem to be almost equally useful for our study. However, if we had to choose the recommended model for use in this type of analysis, it would be the model proposed by Band et al. This model proved to be more flexible, especially in modeling the “knee” and the higher energy part of the energetic proton fluence spectra. The potential downside of this model is that it requires some effort in implementation. In that sense, we believe the Ellison–Ramaty model remains a useful tool due to its robustness and ‘out-of-the-box’ applicability.

It was shown [1] that even during complex heliospheric events, involving multiple CMEs in succession, it was possible to calculate with sufficient accuracy the magnitude of the FD outside the geomagnetic field (corrected for the magnetospheric effect) using the established correlation. The obtained value for the FD magnitude corrected for magnetospheric effects was $-8.3\%$, which was in good agreement with the value of $-7.7\%$ obtained from the GSM (the relative difference between the two methods being $7\%$). In the case of the FD magnitude measured at Earth relative difference was somewhat larger ($15\%$), where we obtained the value of $-8.1\%$, while the value calculated based on the GSM was $-6.9\%$. These results indicate that the established correlations, even without additional refinement, can reliably predict FD amplitudes.

6. Conclusions

We presented an extension of our work, focusing on studying the connection between disturbances in the flux of energetic particles in the heliosphere and concurrent variations in the cosmic ray flux induced by the passage of a CME/ICME. Energetic proton flux, measured by the SOHO/ERNE instrument at L1 in twenty energy channels, was integrated over the duration of the event to obtain differential fluence spectra. To enhance the accuracy of this procedure, IMF and CME speed data provided by the WIND satellite were utilized. Fluence spectra were fitted with both the Ellison–Ramaty model and the model proposed by Band et al., and their effectiveness was compared. Cross-correlation between the spectral power indices obtained from the models and FD magnitudes, calculated by the GSM model for $10\mathrm{GV}$ particles from the IZMIRAN database, was performed. The correlation between spectral indices and FD magnitude for events of moderate-to-high magnitude proved to be significant and, with the exception of the July 2004 event, comparable to the correlation with other space weather parameters that could be considered good predictors of FD magnitude. In the case of FD magnitude corrected for magnetospheric effects, the correlation with spectral indices is greater than for any other space weather parameter. Even though the Ellison–Ramaty model was able to model the energetic proton fluence spectra well in many cases, the model proposed by Band et al. performed better overall. Therefore, in our opinion, it should be the recommended model for similar studies.