Jets Studies in Central and Forward Regions at Current and Expected Large Hadron Collider Future Energies
Abstract
1. Introduction
2. Monte Carlo Event Generators
2.1. PYTHIA Event Generator
Brief Description of the Lund String Model
2.2. HERWIG Event Generator
Brief Description of the Cluster Hadronization Model of HERWIG
2.3. EPOS-LHC Event Generator
Brief Description of Hadronization Model of EPOS-LHC
3. Event Selections
4. Results and Discussion
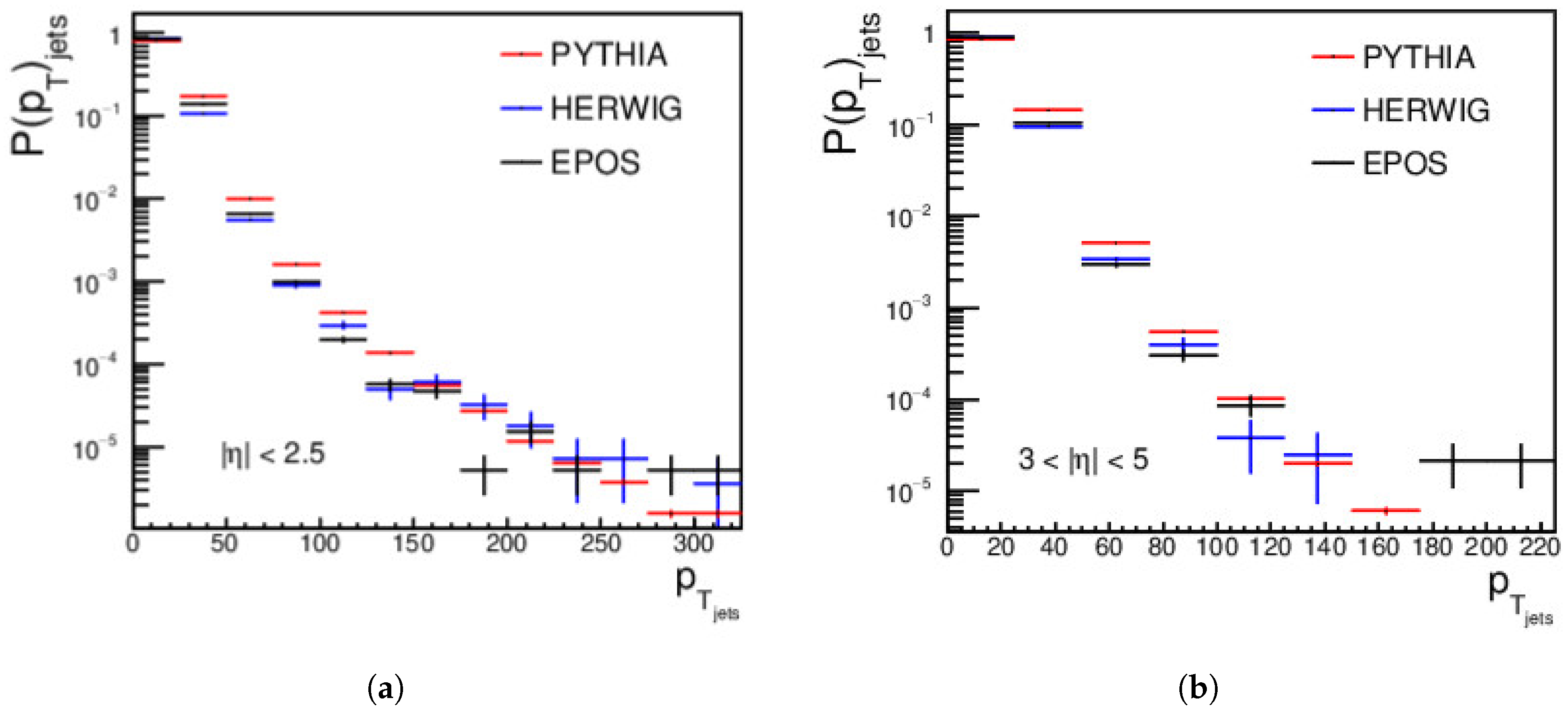
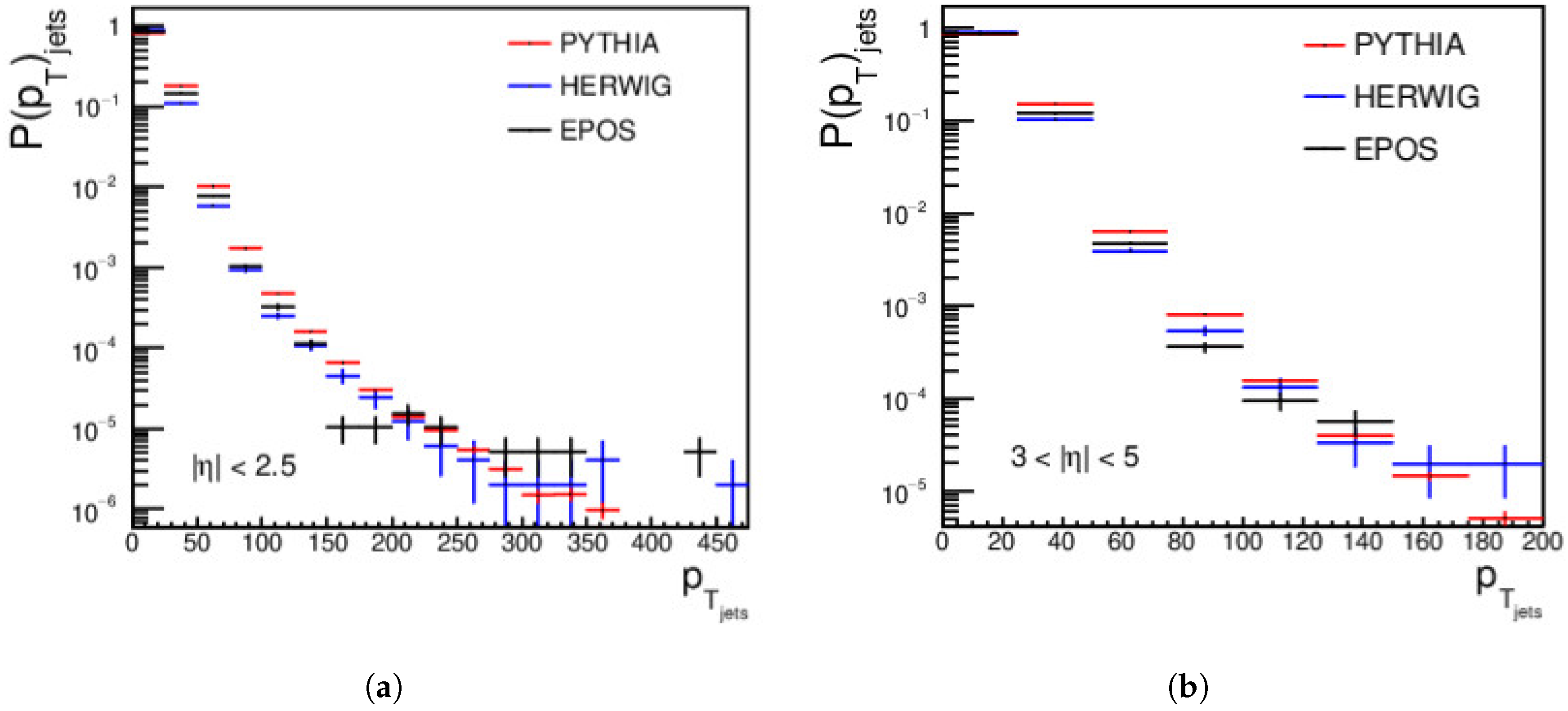
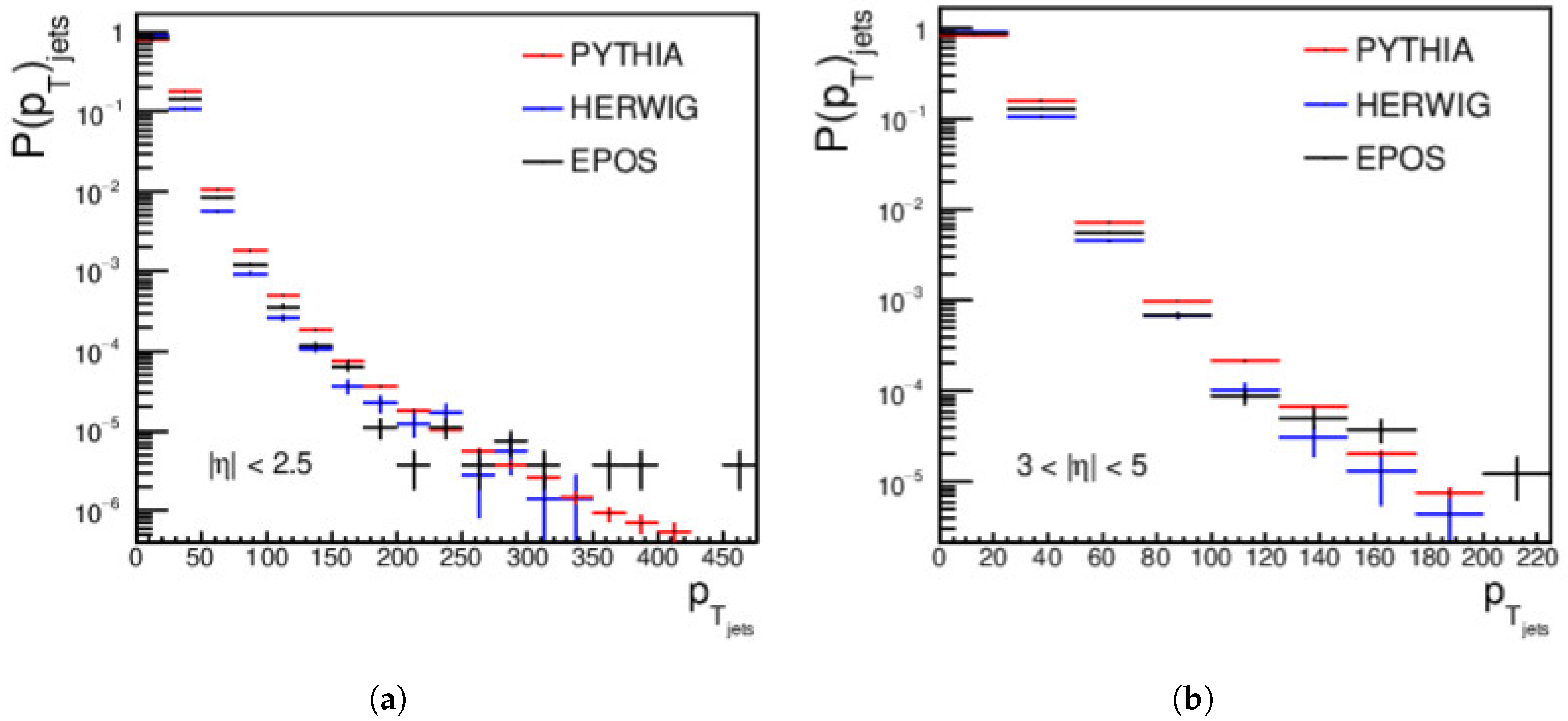
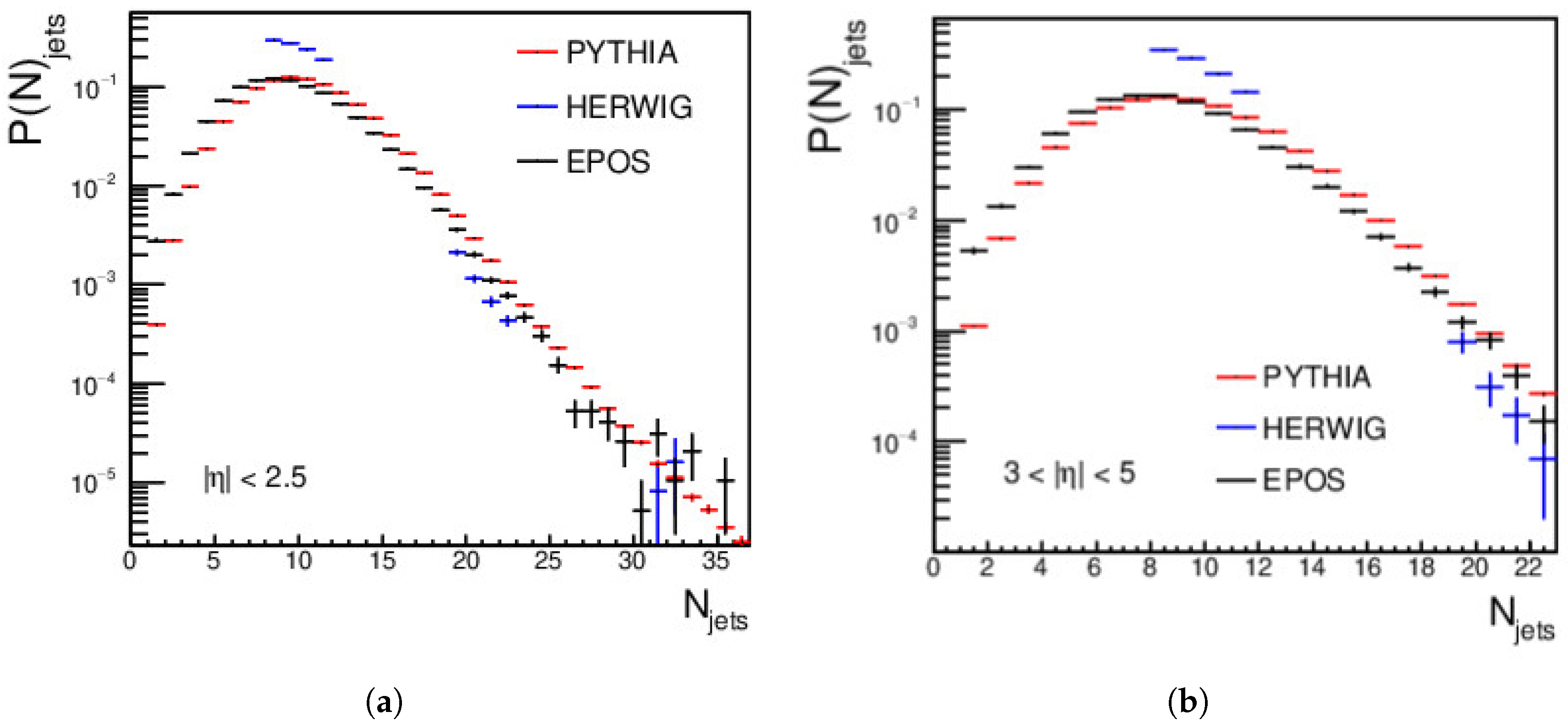
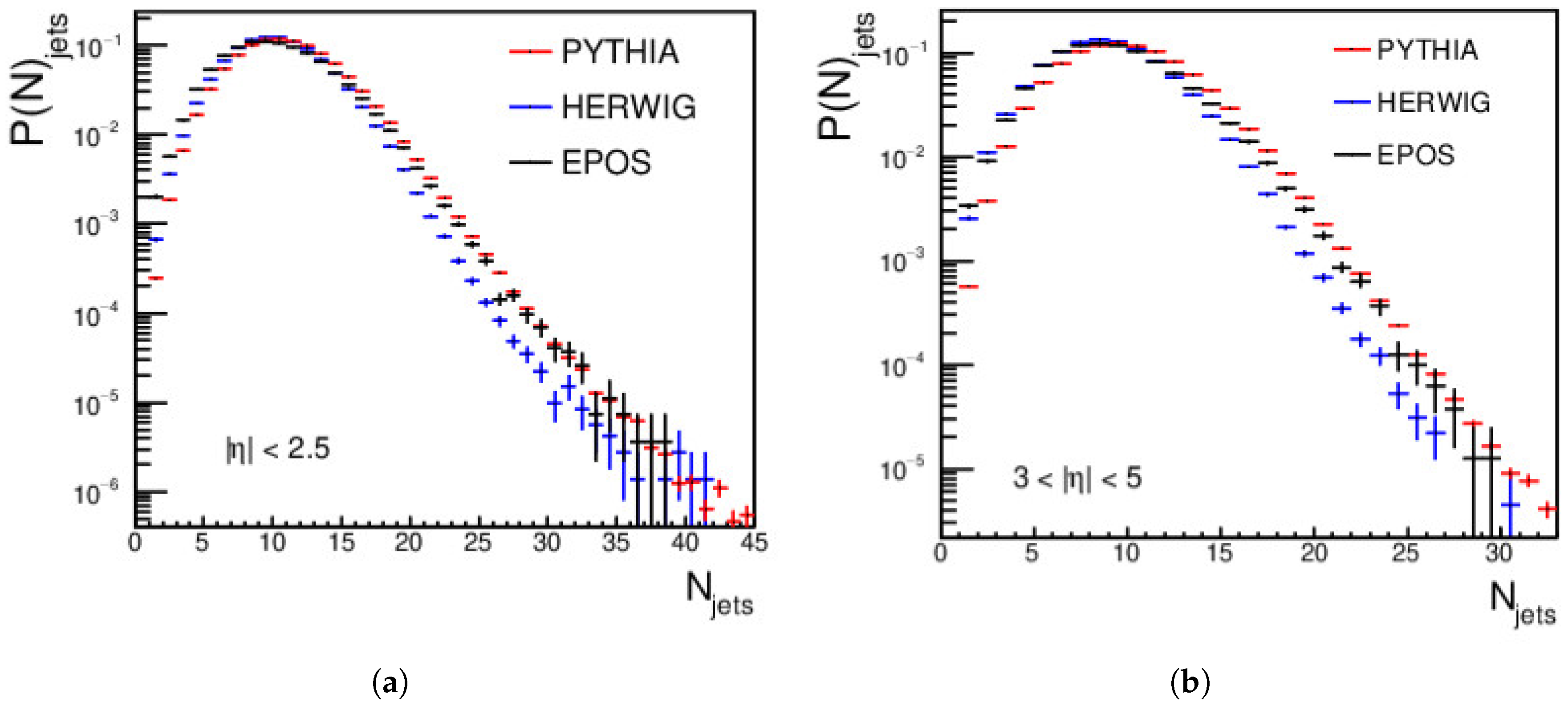
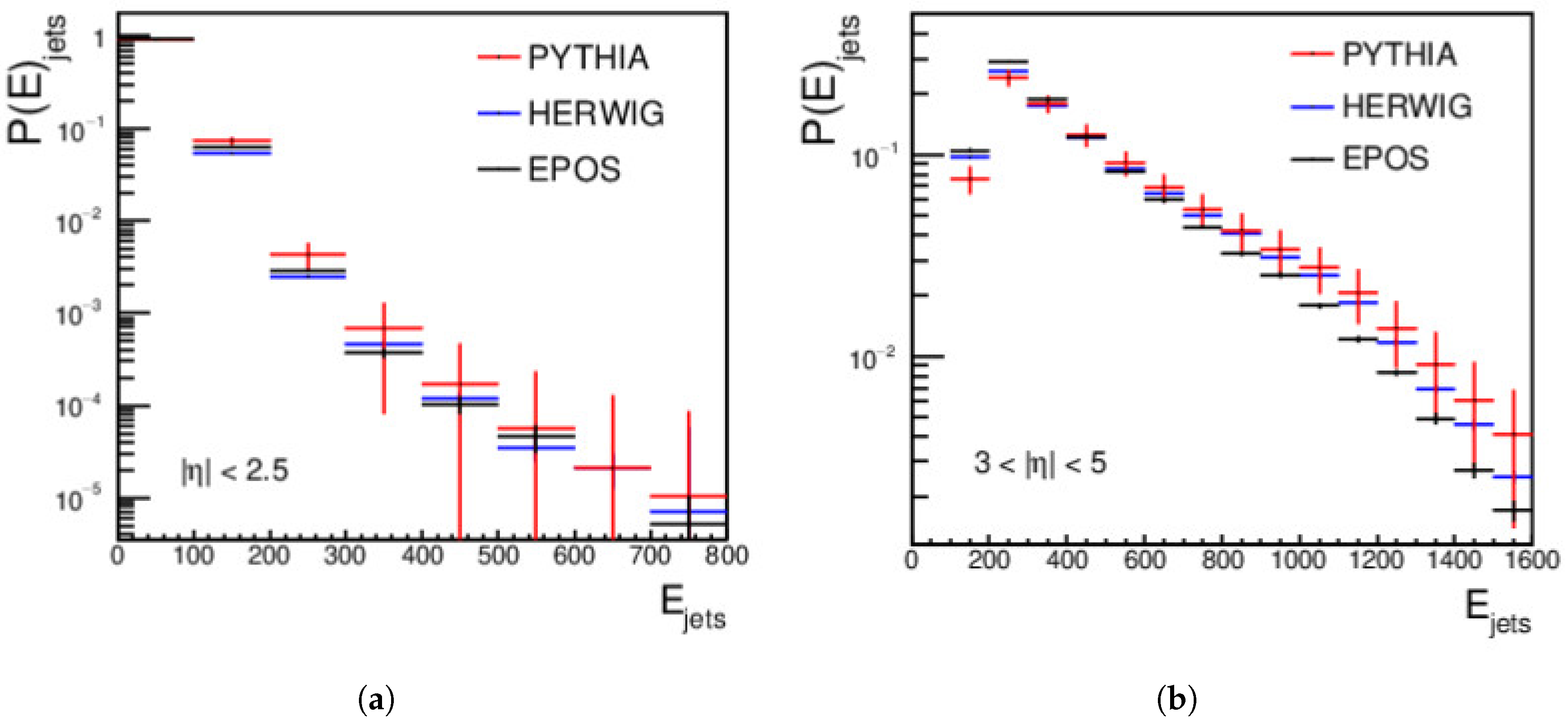
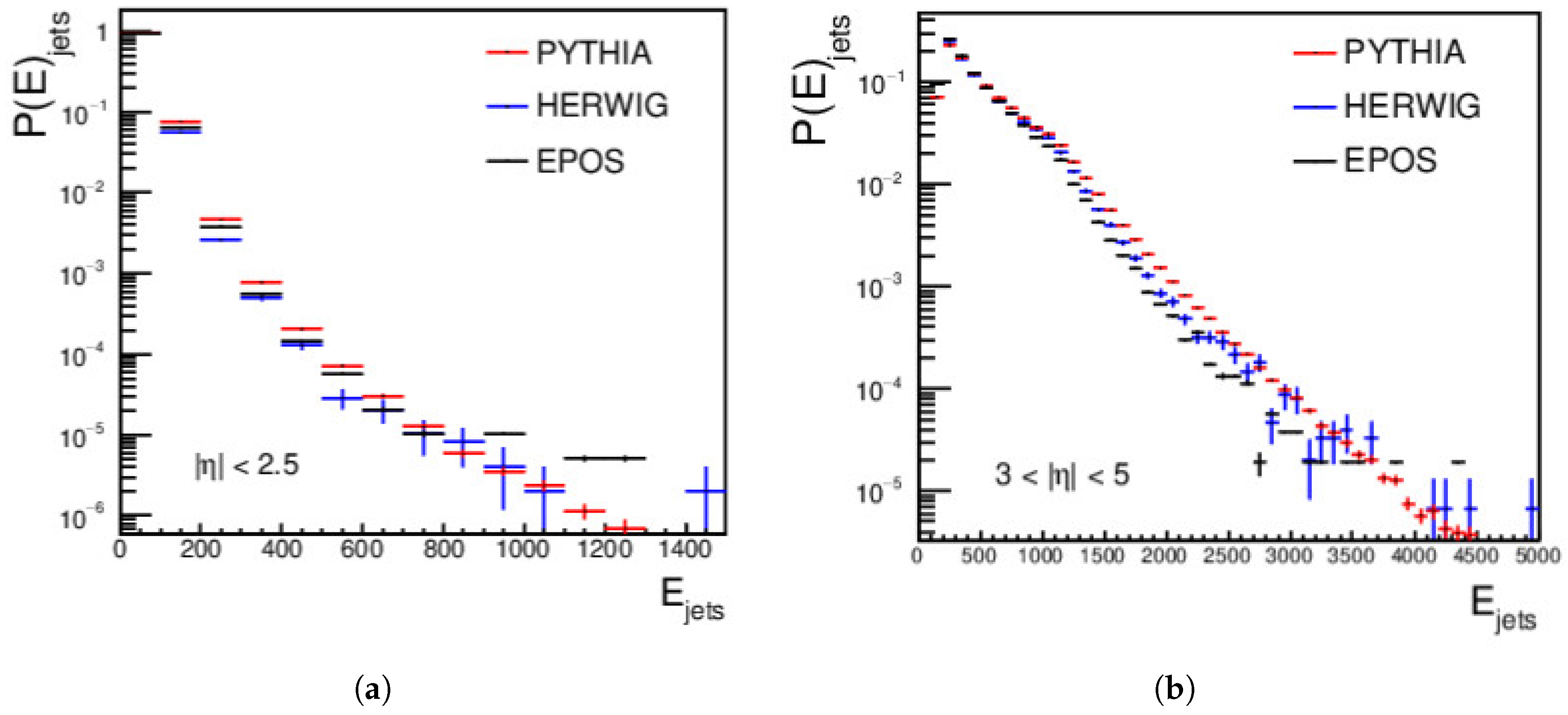
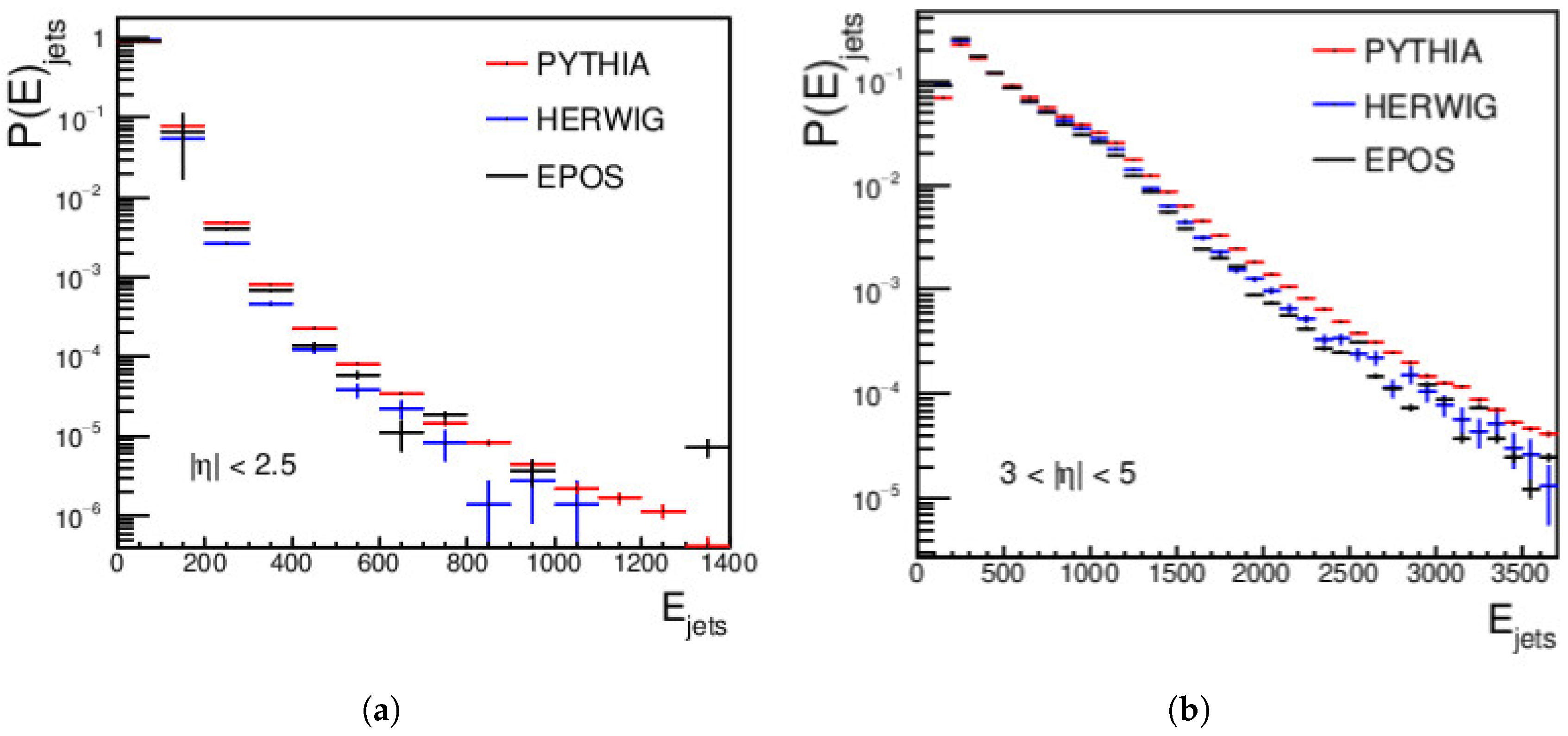
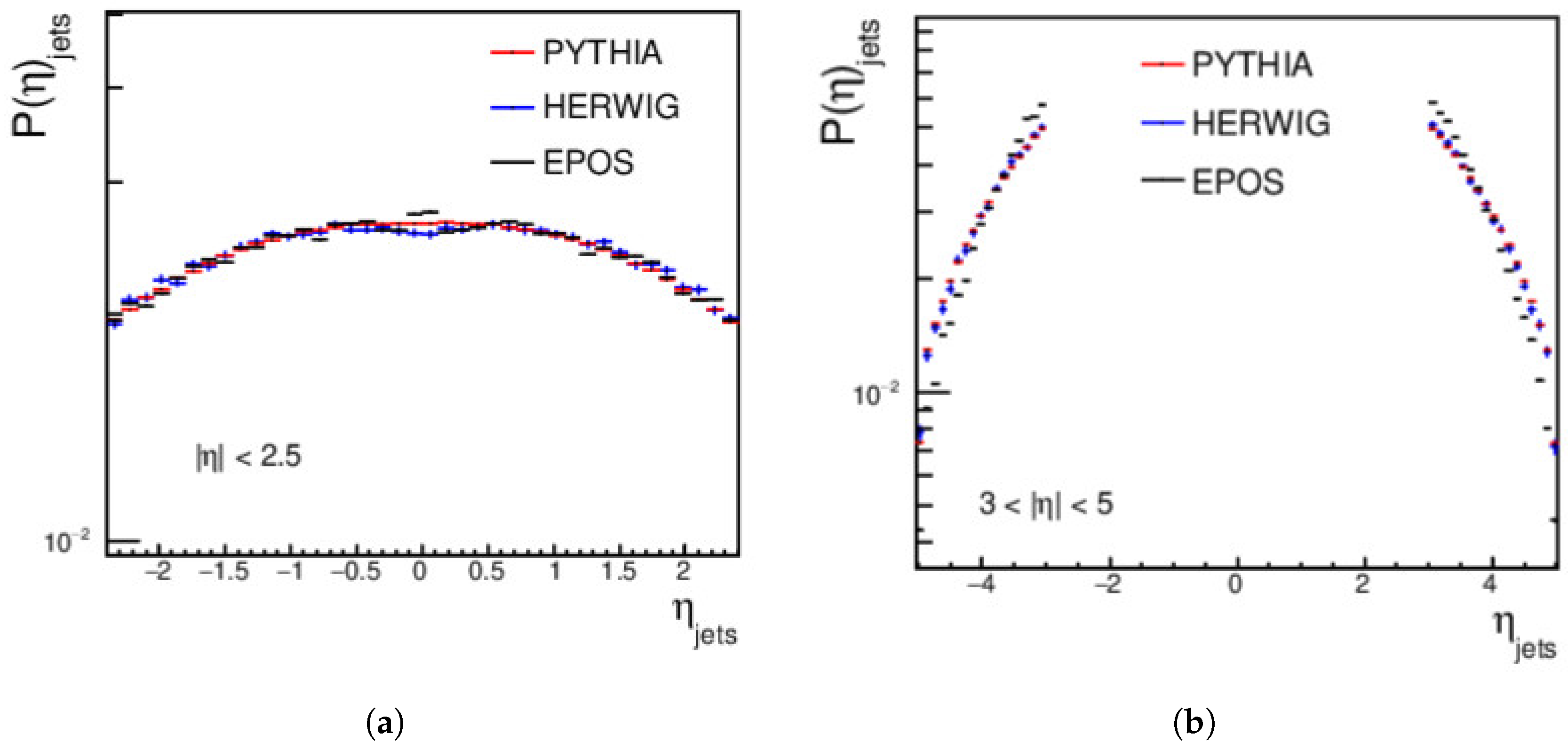
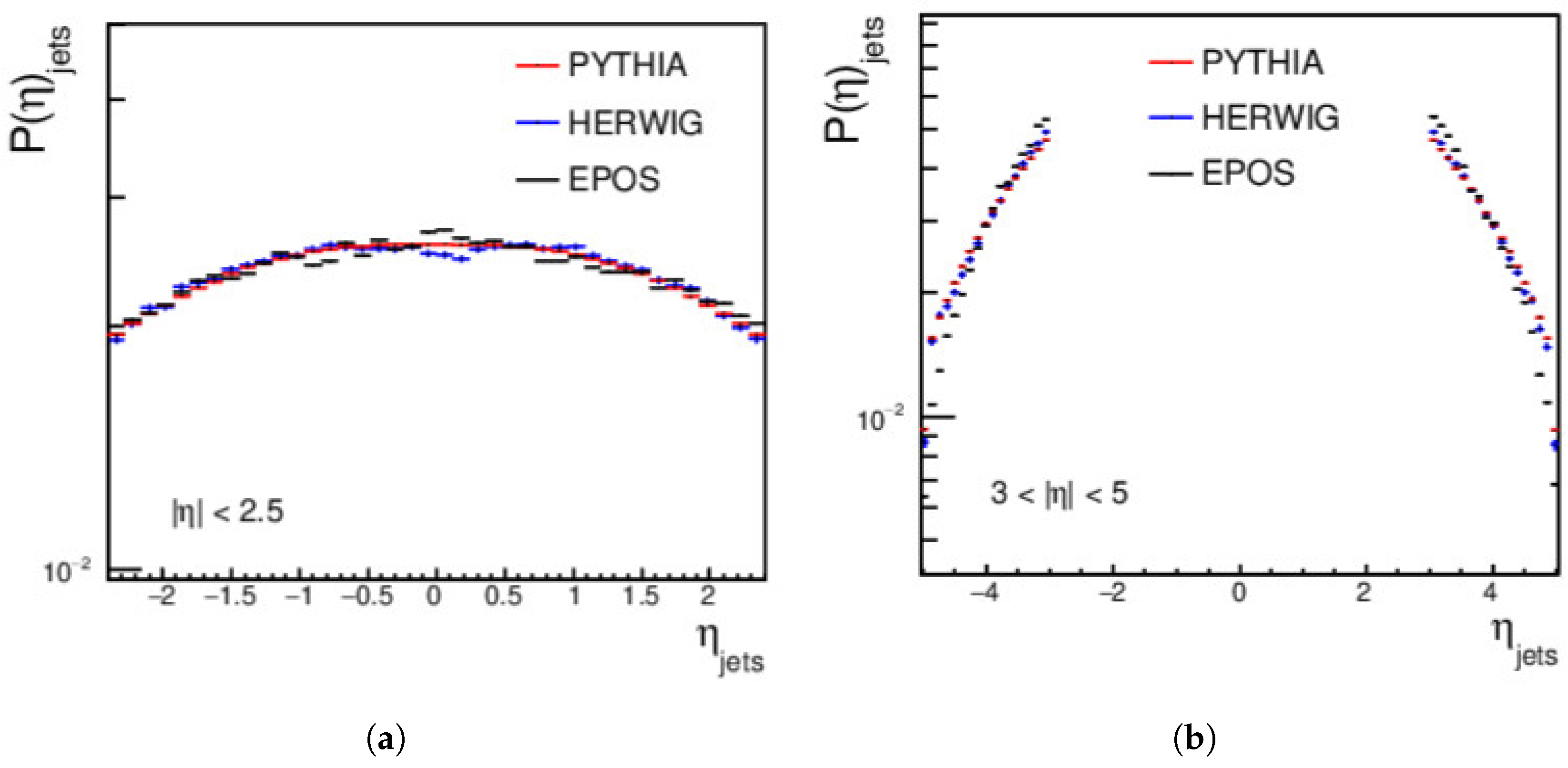
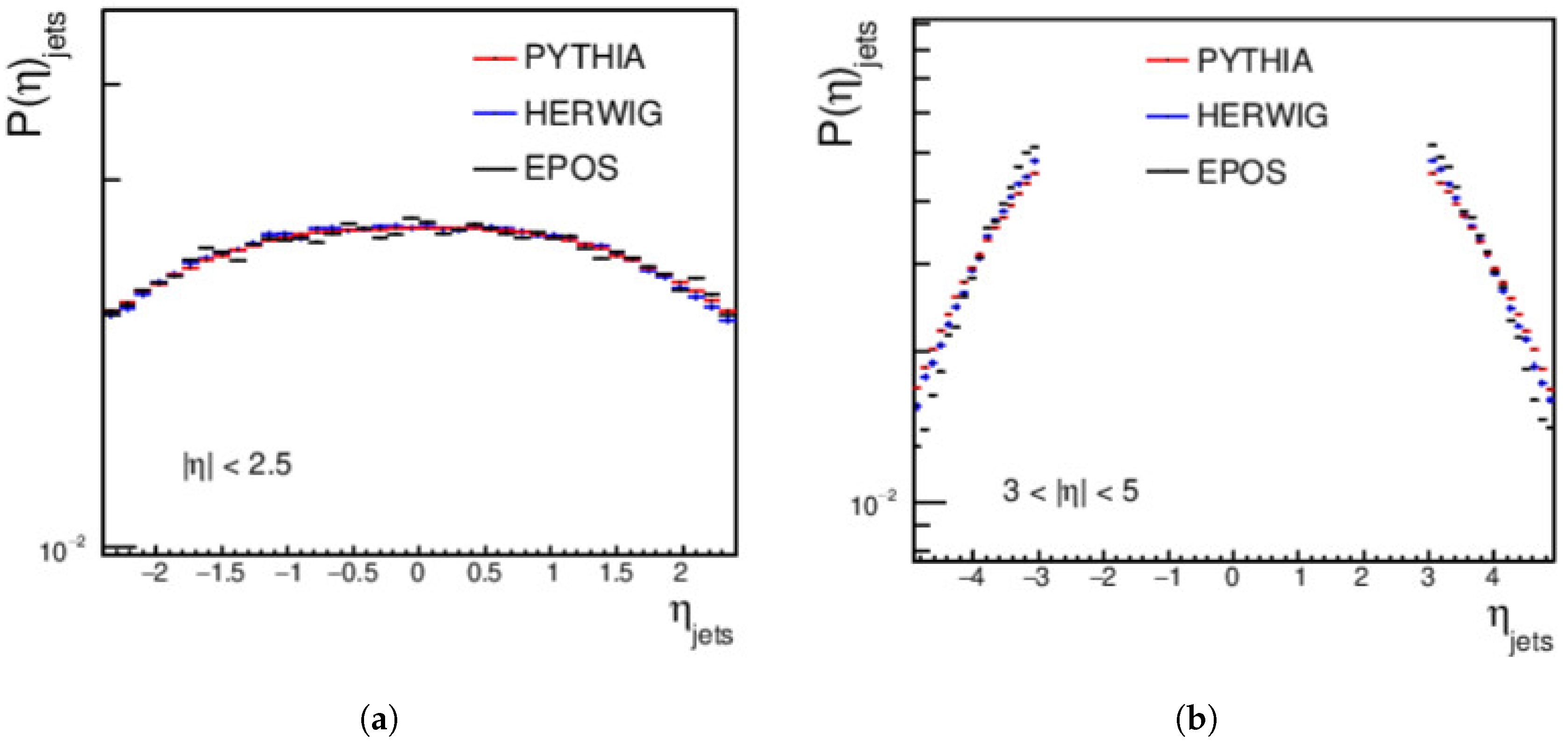
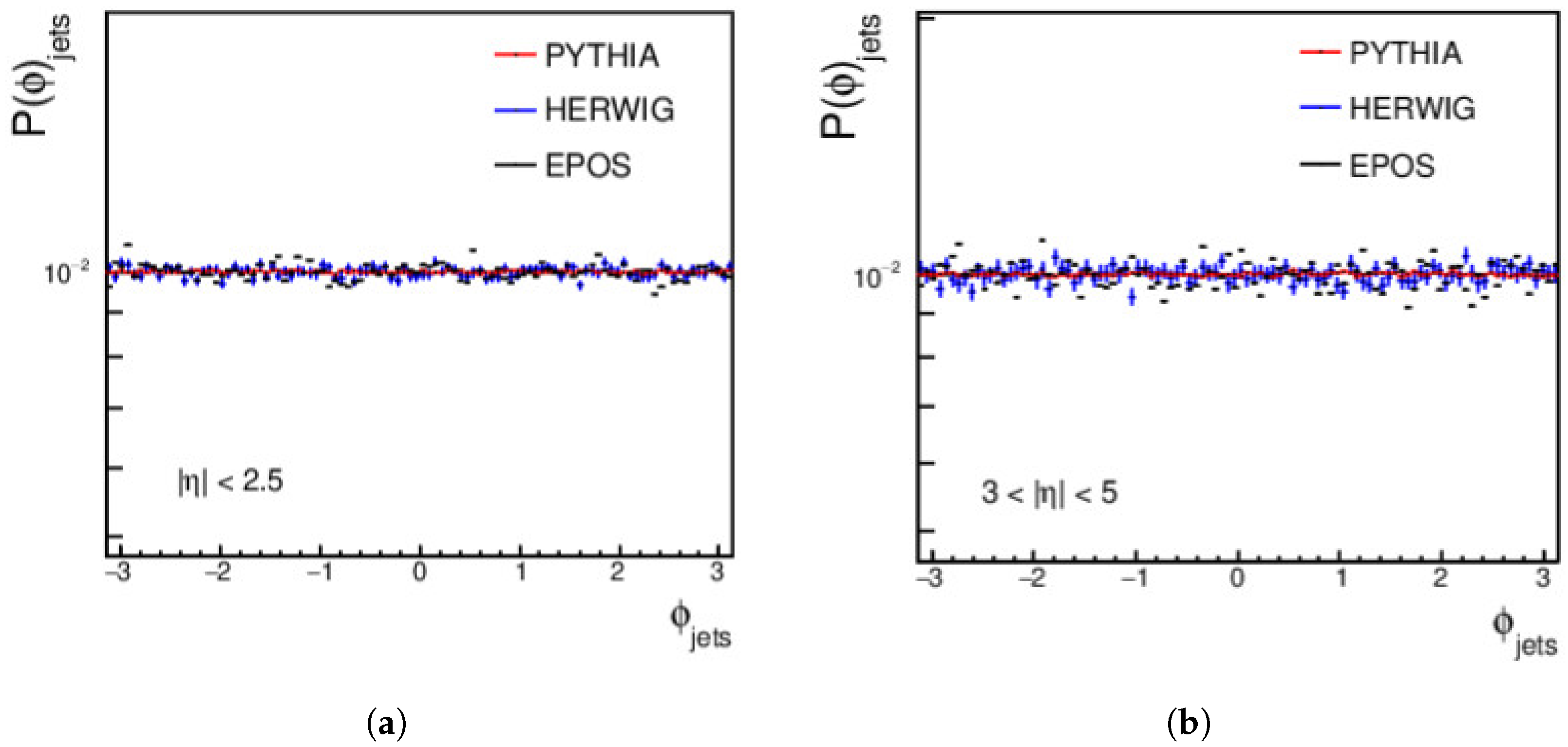
4.1. Jets Measurements
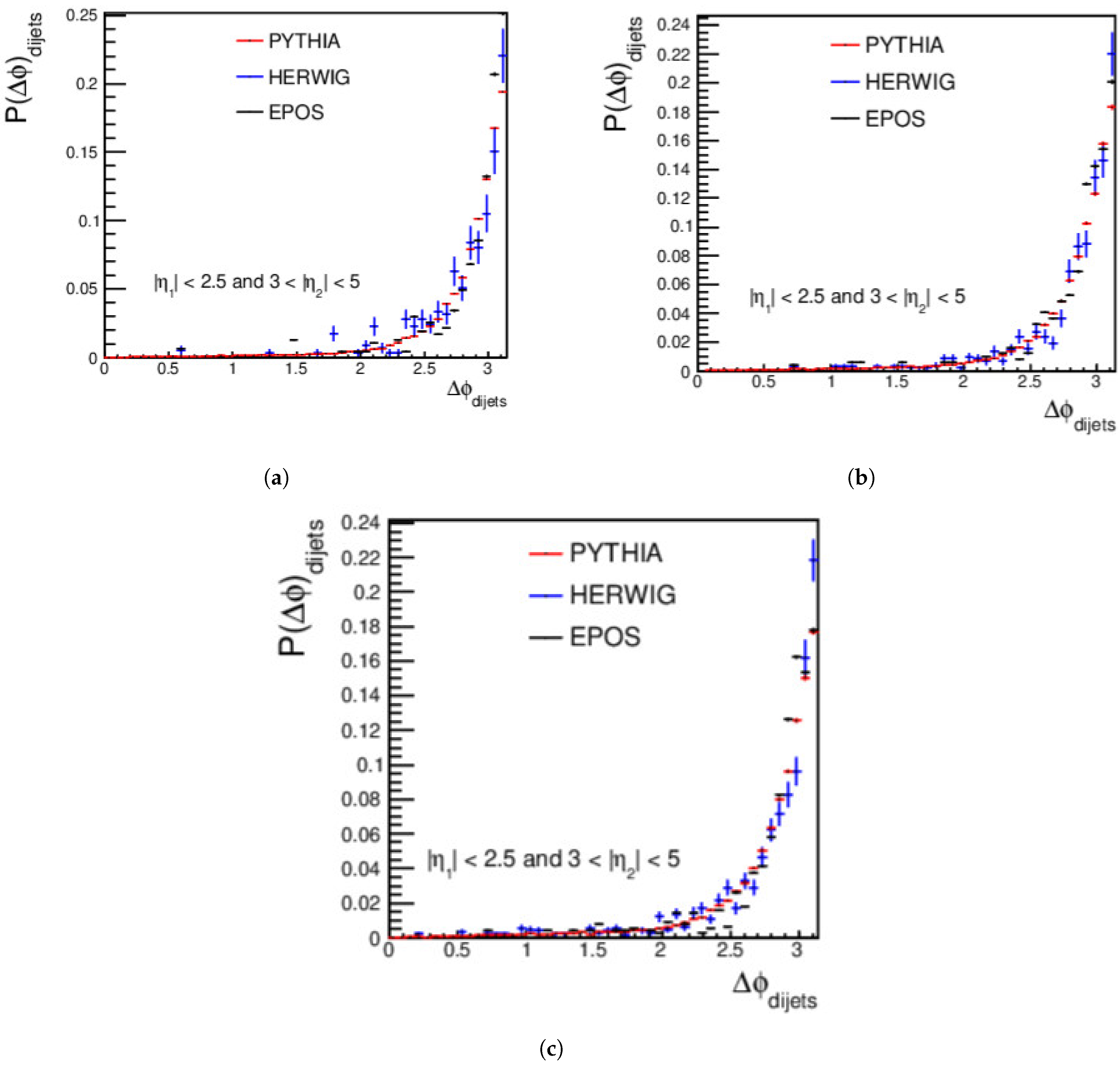
4.2. Dijets Measurements
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| QCD | quantum chromodynamics |
| MC | Monte Carlo |
| LHC | Large Hadron Collider |
| SM | standard model |
| BSM | beyond standard model |
| MPI | multiple parton interaction |
| ISR | initial-state radiation |
| FSR | final-state radiation |
| DM | dark matter |
| LO | leading order |
| HI | heavy ions |
| HEP | high-energy physics |
| PS | parton scattering |
References
- Frye, C.; Larkoski, A.J.; Thaler, J.; Zhou, K. Casimir meets Poisson: Improved quark/gluon discrimination with counting observables. J. High Energy Phys. 2017, 2017, 83. [Google Scholar] [CrossRef]
- Gras, P.; Höche, S.; Kar, D.; Larkoski, A.; Lönnblad, L.; Plätzer, S.; Siódmok, A.; Skands, P.; Soyez, G.; Thaler, J. Systematics of quark/gluon tagging. J. High Energy Phys. 2017, 2017, 91. [Google Scholar] [CrossRef]
- Gromov, N. Elementary particles in the early Universe. J. Cosmol. Astropart. Phys. 2016, 2016, 053. [Google Scholar] [CrossRef][Green Version]
- Choudhury, S. Performance of the High-Level Trigger System at CMS in LHC Run-2. IEEE Trans. Nucl. Sci. 2021, 68, 2035–2042. [Google Scholar] [CrossRef]
- He, M.; Rapp, R. Hadronization and Charm-Hadron Ratios in Heavy-Ion Collisions. Phys. Rev. Lett. 2020, 124, 042301. [Google Scholar] [CrossRef]
- Qu, H.; Gouskos, L. Jet tagging via particle clouds. Phys. Rev. D 2020, 101, 056019. [Google Scholar] [CrossRef]
- Kasieczka, G.; Plehn, T.; Schell, T.; Strebler, T.; Salam, G.P. Resonance searches with an updated top tagger. J. High Energy Phys. 2015, 2015, 203. [Google Scholar] [CrossRef]
- Kim, C. Exclusive Heavy Quark Dijet cross-section. J. Korean Phys. Soc. 2020, 77, 469–476. [Google Scholar] [CrossRef]
- Khosa, C.K.; Marzani, S. Higgs boson tagging with the Lund jet plane. Phys. Rev. D 2021, 104, 055043. [Google Scholar] [CrossRef]
- Sipio, R.D.; Giannelli, M.F.; Haghighat, S.K.; Palazzo, S. DijetGAN: A Generative-Adversarial Network approach for the simulation of QCD dijet events at the LHC. J. High Energy Phys. 2019, 2019, 110. [Google Scholar] [CrossRef]
- Freytsis, M.; Volansky, T.; Walsh, J.R. Tagging partially reconstructed objects with jet substructure. Phys. Lett. B 2017, 769. [Google Scholar] [CrossRef]
- Mukhopadhyaya, B.; Samui, T.; Singh, R.K. Dynamic radius jet clustering algorithm. J. High Energy Phys. 2023, 2023, 19. [Google Scholar] [CrossRef]
- de Lejarza, J.J.M.; Cieri, L.; Rodrigo, G. Quantum clustering and jet reconstruction at the LHC. Phys. Rev. D 2022, 106, 036021. [Google Scholar] [CrossRef]
- Stewart, I.W.; Tackmann, F.J.; Thaler, J.; Vermilion, C.K.; Wilkason, T.F. XCone: N-jettiness as an exclusive cone jet algorithm. J. High Energy Phys. 2015, 2015, 72. [Google Scholar] [CrossRef]
- Marzani, S.; Soyez, G.; Spannowsky, M. Looking Inside Jets: An Introduction to Jet Substructure and Boosted-Object Phenomenology; Springer International Publishing: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Boronat, M.; Fuster, J.; Garcia, I.; Roloff, P.; Simoniello, R.; Vos, M. Jet reconstruction at high-energy electron–positron colliders. Eur. Phys. J. C 2018, 78, 144. [Google Scholar] [CrossRef]
- Moreno, E.A.; Cerri, O.; Duarte, J.M.; Newman, H.B.; Nguyen, T.Q.; Periwal, A.; Pierini, M.; Serikova, A.; Spiropulu, M.; Vlimant, J.R. JEDI-net: A jet identification algorithm based on interaction networks. Eur. Phys. J. C 2020, 80, 58. [Google Scholar] [CrossRef]
- Tseng, J.; Evans, H. Sequential recombination algorithm for jet clustering and background subtraction. Phys. Rev. D 2013, 88, 014044. [Google Scholar] [CrossRef]
- Sirunyan, A.; Tumasyan, A.; Adam, W.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Erö, J.; Flechl, M.; et al. Particle-flow reconstruction and global event description with the CMS detector. J. Instrum. 2017, 12, P10003. [Google Scholar] [CrossRef]
- Cerro, G.; Dasmahapatra, S.; Day-Hall, H.A.; Ford, B.; Moretti, S.; Shepherd-Themistocleous, C.H. Spectral clustering for jet physics. J. High Energy Phys. 2022, 2022, 165. [Google Scholar] [CrossRef]
- Gauld, R.; Huss, A.; Stagnitto, G. Flavor Identification of Reconstructed Hadronic Jets. Address of flavour to suit any jet. Phys. Rev. Lett. 2023, 130, 161901. [Google Scholar] [CrossRef]
- Cukierman, A.R. Searches for New Physics Using Jets with the ATLAS Detector; Stanford University: Stanford, CA, USA, 2020; Volume 2020. [Google Scholar]
- Haisch, U.; Polesello, G. Searching for dark matter in final states with two jets and missing transverse energy. J. High Energy Phys. 2019, 2019, 128. [Google Scholar] [CrossRef]
- Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Asilar, E.; Bergauer, T.; Brandstetter, J.; Brondolin, E.; Dragicevic, M.; Erö, J.; et al. Combined search for electroweak production of charginos and neutralinos in proton–proton collisions at = 13 TeV. J. High Energy Phys. 2018, 2018, 160. [Google Scholar] [CrossRef]
- Klein, S.R.; Nystrand, J.; Seger, J.; Gorbunov, Y.; Butterworth, J. STARlight: A Monte Carlo simulation program for ultra-peripheral collisions of relativistic ions. Comput. Phys. Commun. 2017, 212, 258–268. [Google Scholar] [CrossRef]
- Czyż, H.; Kisza, P. EKHARA 3.0: An update of the EKHARA Monte Carlo event generator. Comput. Phys. Commun. 2019, 234, 245–255. [Google Scholar] [CrossRef]
- Baranov, S.; Martinez, A.B.; Banos, L.I.E.; Guzman, F.; Hautmann, F.; Jung, H.; Lelek, A.; Lidrych, J.; Lipatov, A.; Malyshev, M.; et al. CASCADE3 A Monte Carlo event generator based on TMDs. Eur. Phys. J. C 2021, 81, 5. [Google Scholar] [CrossRef]
- Naseebullah; Olimov, K.K.; Khan, I.; Ali, Y.; Ajaz, M.; Ahmad, A. Analysis of production of ∑(1385)±, (1530)0 and their anti-particles in inelastic pp collisions at = 7 TeV. Eur. Phys. J. Plus 2023, 138, 556. [Google Scholar] [CrossRef]
- Sjöstrand, T. The Pythia event generator: Past, present and future. Comput. Phys. Commun. 2020, 246, 106910. [Google Scholar] [CrossRef]
- Bellm, J.; Bewick, G.; Ravasio, S.F.; Gieseke, S.; Grellscheid, D.; Kirchgaeßer, P.; Loshaj, F.; Masouminia, M.R.; Nail, G.; Papaefstathiou, A.; et al. Herwig 7.2 release note. Eur. Phys. J. C 2020, 80, 452. [Google Scholar] [CrossRef]
- Frixione, S.; Fuks, B.; Hirschi, V.; Mawatari, K.; Shao, H.S.; Sunder, M.P.A.; Zaro, M. Automated simulations beyond the Standard Model: Supersymmetry. J. High Energy Phys. 2019, 2019, 8. [Google Scholar] [CrossRef]
- Bothmann, E.; Chahal, G.S.; Höche, S.; Krause, J.; Krauss, F.; Kuttimalai, S.; Liebschner, S.; Napoletano, D.; Schönherr, M.; Schulz, H.; et al. Event generation with Sherpa 2.2. SciPost Phys. 2019, 7, 3. [Google Scholar] [CrossRef]
- Ajaz, M.; Haj Ismail, A.A.K.; Muhammad, M.; Suleymanov, M.; Abdelkader, A.; Suleymanov, R. Pseudorapidity dependence of the bulk properties of hadronic medium in pp collisions at 7 TeV. Sci. Rep. 2022, 12, 8142. [Google Scholar] [CrossRef] [PubMed]
- Tumasyan, A.; Adam, W.; Andrejkovic, J.W.; Bergauer, T.; Chatterjee, S.; Damanakis, K.; Dragicevic, M.; Escalante Del Valle, A.; Fruehwirth, R.; Jeitler, M.; et al. CMS pythia 8 colour reconnection tunes based on underlying-event data. Eur. Phys. J. C 2023, 83, 587. [Google Scholar] [CrossRef] [PubMed]
- Brass, S.; Kilian, W.; Reuter, J. Parallel adaptive Monte Carlo integration with the event generator WHIZARD. Eur. Phys. J. C 2019, 79, 344. [Google Scholar] [CrossRef]
- Ajaz, M.; Waqas, M.; Khan, R.; Adil Khan, M.; Li, L.L.; Alrebdi, H.I.; Abdel-Aty, A.H. Inclusive Charged-Particle Kinematic Distributions at LHC Energies: Data versus Theory. Symmetry 2022, 14, 2401. [Google Scholar] [CrossRef]
- Bierlich, C.; Gustafson, G.; Lönnblad, L.; Tarasov, A. Effects of Overlapping Strings in pp Collisions. J. High Energy Phys. 2015, 2015, 148. [Google Scholar] [CrossRef]
- Bellm, J.; Gieseke, S.; Grellscheid, D.; Plätzer, S.; Rauch, M.; Reuschle, C.; Richardson, P.; Schichtel, P.; Seymour, M.H.; Siódmok, A.; et al. Herwig 7.0/Herwig++ 3.0 release note. Eur. Phys. J. C 2016, 76, 196. [Google Scholar] [CrossRef]
- Webber, B. A QCD model for jet fragmentation including soft gluon interference. Nucl. Phys. B 1984, 238, 492–528. [Google Scholar] [CrossRef]
- Bähr, M.; Gieseke, S.; Gigg, M.A.; Grellscheid, D.; Hamilton, K.; Latunde-Dada, O.; Plätzer, S.; Richardson, P.; Seymour, M.H.; Sherstnev, A.; et al. Herwig++ physics and manual. Eur. Phys. J. C 2008, 58, 639–707. [Google Scholar] [CrossRef]
- Ene, A.C.; Jipa, A.; Giubega, L.E. Study of Monte Carlo event generators for proton–proton collisions at LHC energies in the forward region. Chin. Phys. C 2019, 43, 083001. [Google Scholar] [CrossRef]
- Pierog, T.; Guiot, B.; Karpenko, I.; Sophys, G.; Stefaniak, M.; Werner, K. EPOS 3 and Air Showers. EPJ Web Conf. 2019, 210, 02008. [Google Scholar] [CrossRef]
- Drescher, H.J.; Hladik, M.; Ostapchenko, S.; Pierog, T.; Werner, K. Parton-based Gribov—Regge theory. Phys. Rep. 2001, 350, 93–289. [Google Scholar] [CrossRef]
- Pierog, T.; Werner, K. EPOS Model and Ultra High Energy Cosmic Rays. Nucl. Phys. B—Proc. Suppl. 2009, 196, 102–105. [Google Scholar] [CrossRef]
- Werner, K. Revealing a deep connection between factorization and saturation: New insight into modeling high-energy proton–proton and nucleus-nucleus scattering in the EPOS4 framework. Phys. Rev. C 2023, 108, 064903. [Google Scholar] [CrossRef]
- Werner, K.; Karpenko, I.; Pierog, T.; Bleicher, M.; Mikhailov, K. Evidence for hydrodynamic evolution in proton–proton scattering at 900 GeV. Phys. Rev. C 2011, 83, 044915. [Google Scholar] [CrossRef]
- Pierog, T.; Karpenko, I.; Katzy, J.M.; Yatsenko, E.; Werner, K. EPOS LHC: Test of collective hadronization with data measured at the CERN Large Hadron Collider. Phys. Rev. C 2015, 92, 034906. [Google Scholar] [CrossRef]
- Bierlich, C.; Buckley, A.; Butterworth, J.; Christensen, C.H.; Corpe, L.; Grellscheid, D.; Grosse-Oetringhaus, J.F.; Gutschow, C.; Karczmarczyk, P.; Klein, J.; et al. Robust independent validation of experiment and theory: Rivet version 3. SciPost Phys. 2020, 8, 26. [Google Scholar] [CrossRef]
- The CMS Collaboration; Sirunyan, A.M.; Tumasyan, A.; Adam, W.; Ambrogi, F.; Bergauer, T.; Dragicevic, M.; Erö, J.; Valle, A.E.D.; Flechl, M.; et al. Search for high mass dijet resonances with a new background prediction method in proton–proton collisions at = 13 TeV. J. High Energy Phys. 2020, 2020, 33. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmoud, M.A.; Hamdi, S.; Radi, A.; El-Borie, M.A.; Tayel, E.A. Jets Studies in Central and Forward Regions at Current and Expected Large Hadron Collider Future Energies. Universe 2024, 10, 154. https://doi.org/10.3390/universe10040154
Mahmoud MA, Hamdi S, Radi A, El-Borie MA, Tayel EA. Jets Studies in Central and Forward Regions at Current and Expected Large Hadron Collider Future Energies. Universe. 2024; 10(4):154. https://doi.org/10.3390/universe10040154
Chicago/Turabian StyleMahmoud, M. A., Somaia Hamdi, A. Radi, M. A. El-Borie, and E. A. Tayel. 2024. "Jets Studies in Central and Forward Regions at Current and Expected Large Hadron Collider Future Energies" Universe 10, no. 4: 154. https://doi.org/10.3390/universe10040154
APA StyleMahmoud, M. A., Hamdi, S., Radi, A., El-Borie, M. A., & Tayel, E. A. (2024). Jets Studies in Central and Forward Regions at Current and Expected Large Hadron Collider Future Energies. Universe, 10(4), 154. https://doi.org/10.3390/universe10040154






