A Simple Direct Empirical Observation of Systematic Bias of the Redshift as a Distance Indicator
Abstract
1. Introduction
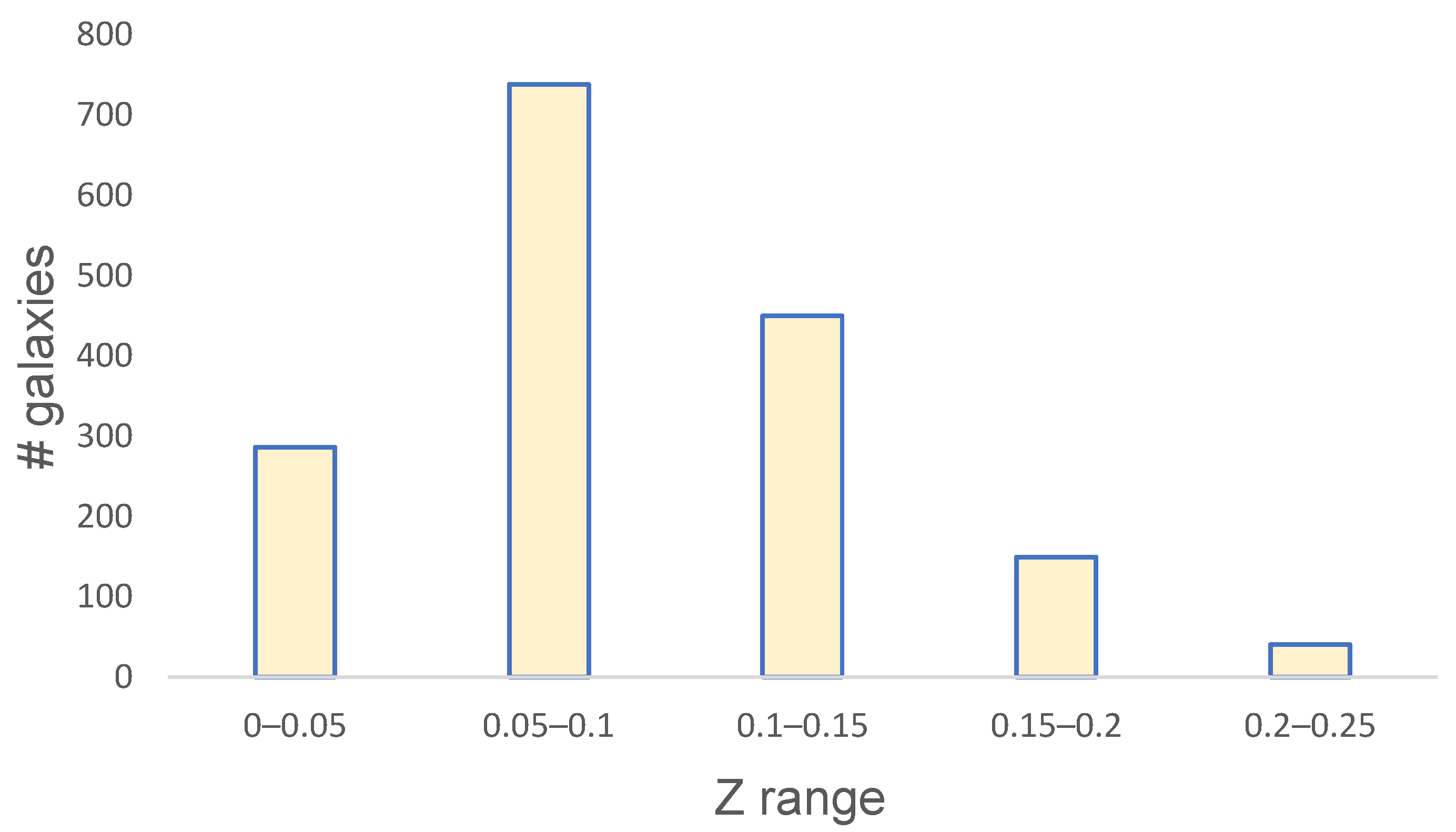
2. Data
3. Results
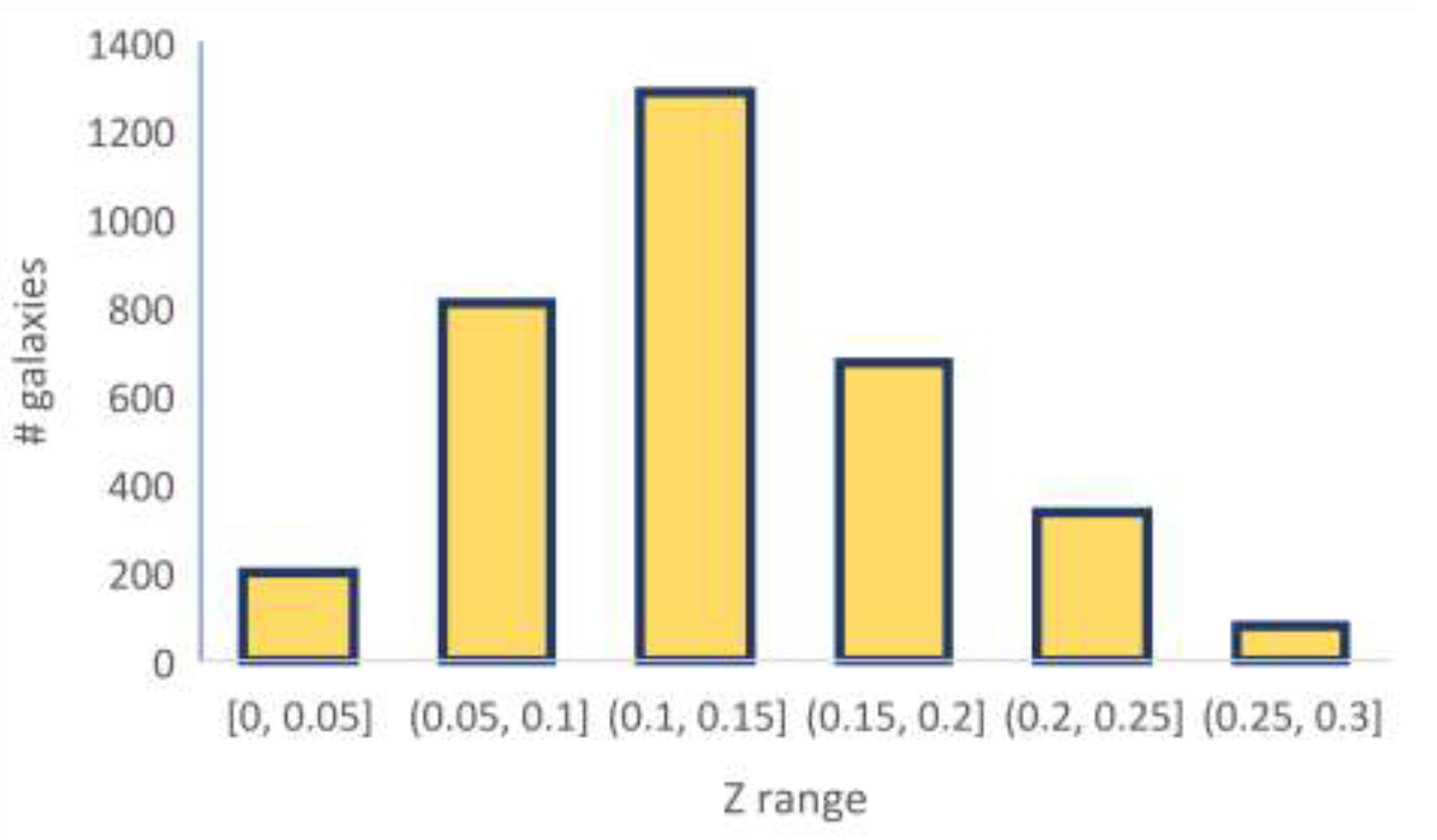
4. Comparison with Other Datasets
4.1. Comparison with Annotations by Galaxy Zoo
4.2. Comparison with Annotations by SpArcFiRe
4.3. Comparison with Galaxies from the Southern Galactic Pole
5. Possible Explanations and Future Experiments
6. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, H.Y.; Huterer, D. Sample variance in the local measurements of the Hubble constant. Mon. Not. R. Astron. Soc. 2017, 471, 4946–4955. [Google Scholar] [CrossRef]
- Mörtsell, E.; Dhawan, S. Does the Hubble constant tension call for new physics? J. Cosmol. Astropart. Phys. 2018, 2018, 025. [Google Scholar] [CrossRef]
- Bolejko, K. Emerging spatial curvature can resolve the tension between high-redshift CMB and low-redshift distance ladder measurements of the Hubble constant. Phys. Rev. D 2018, 97, 103529. [Google Scholar] [CrossRef]
- Davis, T.M.; Hinton, S.R.; Howlett, C.; Calcino, J. Can redshift errors bias measurements of the Hubble Constant? Mon. Not. R. Astron. Soc. 2019, 490, 2948–2957. [Google Scholar] [CrossRef]
- Pandey, S.; Raveri, M.; Jain, B. Model independent comparison of supernova and strong lensing cosmography: Implications for the Hubble constant tension. Phys. Rev. D 2020, 102, 023505. [Google Scholar] [CrossRef]
- Camarena, D.; Marra, V. Local determination of the Hubble constant and the deceleration parameter. Phys. Rev. Res. 2020, 2, 013028. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—A review of solutions. Class. Quantum Gravity 2021, 38, 153001. [Google Scholar] [CrossRef]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Anand, G.S.; Breuval, L.; et al. A comprehensive measurement of the local value of the Hubble constant with 1 km s−1 Mpc−1 uncertainty from the Hubble Space Telescope and the SH0ES team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Whitler, L.; Endsley, R.; Stark, D.P.; Topping, M.; Chen, Z.; Charlot, S. On the ages of bright galaxies 500 Myr after the big bang: Insights into star formation activity at z > 15 with JWST. Mon. Not. R. Astron. Soc. 2023, 519, 157–171. [Google Scholar] [CrossRef]
- Neeleman, M.; Prochaska, J.X.; Kanekar, N.; Rafelski, M. A cold, massive, rotating disk galaxy 1.5 billion years after the Big Bang. Nature 2020, 581, 269–272. [Google Scholar] [CrossRef] [PubMed]
- Cowley, W.I.; Baugh, C.M.; Cole, S.; Frenk, C.S.; Lacey, C.G. Predictions for deep galaxy surveys with JWST from ΛCDM. Mon. Not. R. Astron. Soc. 2018, 474, 2352–2372. [Google Scholar] [CrossRef]
- Crawford, D.F. Curvature pressure in a cosmology with a tired-light redshift. Aust. J. Phys. 1999, 52, 753–777. [Google Scholar] [CrossRef]
- Pletcher, A.E. Why Mature Galaxies Seem to have Filled the Universe shortly after the Big Bang. Qeios 2023. [Google Scholar] [CrossRef]
- Gupta, R. JWST early Universe observations and ΛCDM cosmology. Mon. Not. R. Astron. Soc. 2023, 524, 3385. [Google Scholar] [CrossRef]
- Lee, S. The cosmological evolution condition of the Planck constant in the varying speed of light models through adiabatic expansion. Phys. Dark Universe 2023, 42, 101286. [Google Scholar] [CrossRef]
- Seshavatharam, U.S.; Lakshminarayana, S. A Rotating Model of a Light Speed Expanding Hubble-Hawking Universe. Phys. Sci. Forum 2023, 7, 43. [Google Scholar]
- Seshavatharam, U.; Lakshminarayana, S. Understanding nearby Cosmic Halt with 4G Model of Final Unification—Is Universe Really Accelerating? Am. J. Planet. Space Sci. 2023, 2, 118. [Google Scholar]
- Lovyagin, N.; Raikov, A.; Yershov, V.; Lovyagin, Y. Cosmological model tests with JWST. Galaxies 2022, 10, 108. [Google Scholar] [CrossRef]
- Marrucci, L. Spinning the Doppler effect. Science 2013, 341, 464–465. [Google Scholar] [CrossRef] [PubMed]
- Lavery, M.P.; Barnett, S.M.; Speirits, F.C.; Padgett, M.J. Observation of the rotational Doppler shift of a white-light, orbital-angular-momentum-carrying beam backscattered from a rotating body. Optica 2014, 1, 1–4. [Google Scholar] [CrossRef]
- Liu, B.; Chu, H.; Giddens, H.; Li, R.; Hao, Y. Experimental observation of linear and rotational Doppler shifts from several designer surfaces. Sci. Rep. 2019, 9, 8971. [Google Scholar] [CrossRef]
- Zwicky, F. On the Masses of Nebulae and of Clusters of Nebulae. Astrophys. J. 1937, 86, 217. [Google Scholar] [CrossRef]
- Oort, J.H. Some Problems Concerning the Structure and Dynamics of the Galactic System and the Elliptical Nebulae NGC 3115 and 4494. Astrophys. J. 1940, 91, 273. [Google Scholar] [CrossRef]
- Rubin, V.C. The rotation of spiral galaxies. Science 1983, 220, 1339–1344. [Google Scholar] [CrossRef] [PubMed]
- El-Neaj, Y.A.; Alpigiani, C.; Amairi-Pyka, S.; Araújo, H.; Balaž, A.; Bassi, A.; Bathe-Peters, L.; Battelier, B.; Belić, A.; Bentine, E.; et al. AEDGE: Atomic experiment for dark matter and gravity exploration in space. EPJ Quantum Technol. 2020, 7, 6. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Milgrom, M. MOND and the mass discrepancies in tidal dwarf galaxies. Astrophys. J. Lett. 2007, 667, L45. [Google Scholar] [CrossRef][Green Version]
- De Blok, W.; McGaugh, S. Testing modified newtonian dynamics with low surface brightness galaxies: Rotation curve fits. Astrophys. J. 1998, 508, 132. [Google Scholar] [CrossRef]
- Sanders, R. The virial discrepancy in clusters of galaxies in the context of modified Newtonian dynamics. Astrophys. J. Lett. 1998, 512, L23. [Google Scholar] [CrossRef]
- Sanders, R.H.; McGaugh, S.S. Modified Newtonian dynamics as an alternative to dark matter. Annu. Rev. Astron. Astrophys. 2002, 40, 263–317. [Google Scholar] [CrossRef]
- Swaters, R.; Sanders, R.; McGaugh, S. Testing modified Newtonian dynamics with rotation curves of dwarf and low surface brightness galaxies. Astrophys. J. 2010, 718, 380. [Google Scholar] [CrossRef]
- Sanders, R. NGC 2419 does not challenge modified Newtonian dynamics. Mon. Not. R. Astron. Soc. 2012, 419, L6–L8. [Google Scholar] [CrossRef]
- Iocco, F.; Pato, M.; Bertone, G. Testing modified Newtonian dynamics in the Milky Way. Phys. Rev. D 2015, 92, 084046. [Google Scholar] [CrossRef]
- Díaz-Saldaña, I.; López-Domínguez, J.; Sabido, M. On emergent gravity, black hole entropy and galactic rotation curves. Phys. Dark Universe 2018, 22, 147–151. [Google Scholar] [CrossRef]
- Falcon, N. A large-scale heuristic modification of Newtonian gravity as an alternative approach to dark energy and dark matter. J. Astrophys. Astron. 2021, 42, 102. [Google Scholar] [CrossRef]
- Sanders, R. Mass discrepancies in galaxies: Dark matter and alternatives. Astron. Astrophys. Rev. 1990, 2, 1–28. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M. The dark matter problem from f (R) gravity viewpoint. Ann. Phys. 2012, 524, 545–578. [Google Scholar] [CrossRef]
- Chadwick, E.A.; Hodgkinson, T.F.; McDonald, G.S. Gravitational theoretical development supporting MOND. Phys. Rev. D 2013, 88, 024036. [Google Scholar] [CrossRef]
- Farnes, J.S. A unifying theory of dark energy and dark matter: Negative masses and matter creation within a modified ΛCDM framework. Astron. Astrophys. 2018, 620, A92. [Google Scholar] [CrossRef]
- Rivera, P.C. An Alternative Model of Rotation Curve that Explains Anomalous Orbital Velocity, Mass Discrepancy and Structure of Some Galaxies. Am. J. Astron. Astrophys. 2020, 7, 73–79. [Google Scholar] [CrossRef]
- Nagao, S. Galactic Evolution Showing a Constant Circulating Speed of Stars in a Galactic Disc without Requiring Dark Matter. Rep. Adv. Phys. Sci. 2020, 4, 2050004. [Google Scholar] [CrossRef]
- Blake, B.C. Relativistic Beaming of Gravity and the Missing Mass Problem. Bull. Am. Phys. Soc. 2021, 2021, B17.00002. [Google Scholar]
- Gomel, R.; Zimmerman, T. The Effects of Inertial Forces on the Dynamics of Disk Galaxies. Galaxies 2021, 9, 34. [Google Scholar] [CrossRef]
- Skordis, C.; Złośnik, T. New relativistic theory for modified Newtonian dynamics. Pattern Recognit. Lett. 2021, 127, 161302. [Google Scholar] [CrossRef]
- Larin, S.A. Towards the Explanation of Flatness of Galaxies Rotation Curves. Universe 2022, 8, 632. [Google Scholar] [CrossRef]
- Mannheim, P.D. Alternatives to dark matter and dark energy. Prog. Part. Nucl. Phys. 2006, 56, 340–445. [Google Scholar] [CrossRef]
- Kroupa, P. The dark matter crisis: Falsification of the current standard model of cosmology. Publ. Astron. Soc. Aust. 2012, 29, 395–433. [Google Scholar] [CrossRef]
- Kroupa, P.; Pawlowski, M.; Milgrom, M. The failures of the standard model of cosmology require a new paradigm. Int. J. Mod. Phys. D 2012, 21, 1230003. [Google Scholar] [CrossRef]
- Kroupa, P. Galaxies as simple dynamical systems: Observational data disfavor dark matter and stochastic star formation. Can. J. Phys. 2015, 93, 169–202. [Google Scholar] [CrossRef]
- Arun, K.; Gudennavar, S.; Sivaram, C. Dark matter, dark energy, and alternate models: A review. Adv. Space Res. 2017, 60, 166–186. [Google Scholar] [CrossRef]
- Akerib, D.S.; Alsum, S.; Araújo, H.M.; Bai, X.; Bailey, A.J.; Balajthy, J.; Beltrame, P.; Bernard, E.P.; Bernstein, A.; Biesiadzinski, T.P.; et al. Results from a Search for Dark Matter in the Complete LUX Exposure. Phys. Rev. Lett. 2017, 118, 021303. [Google Scholar] [CrossRef]
- Bertone, G.; Tait, T.M. A new era in the search for dark matter. Nature 2018, 562, 51–56. [Google Scholar] [CrossRef] [PubMed]
- Aprile, E.; Aalbers, J.; Agostini, F.; Alfonsi, M.; Althueser, L.; Amaro, F.D.; Anthony, M.; Arneodo, F.; Baudis, L.; Bauermeister, B.; et al. Dark Matter Search Results from a One Ton-Year Exposure of XENON1T. Phys. Rev. Lett. 2018, 121, 111302. [Google Scholar] [CrossRef] [PubMed]
- Skordis, C.; Złośnik, T. Gravitational alternatives to dark matter with tensor mode speed equaling the speed of light. Phys. Rev. D 2019, 100, 104013. [Google Scholar] [CrossRef]
- Sivaram, C.; Arun, K.; Rebecca, L. MOND, MONG, MORG as alternatives to dark matter and dark energy, and consequences for cosmic structures. J. Astrophys. Astron. 2020, 41, 4. [Google Scholar] [CrossRef]
- Hofmeister, A.M.; Criss, R.E. Debate on the Physics of Galactic Rotation and the Existence of Dark Matter. Galaxies 2020, 8, 54. [Google Scholar] [CrossRef]
- Byrd, G.; Howard, S. Spiral galaxies when disks dominate their halos (using arm pitches and rotation curves). J. Wash. Acad. Sci. 2021, 107, 1–10. [Google Scholar]
- Haslbauer, M.; Banik, I.; Kroupa, P.; Wittenburg, N.; Javanmardi, B. The high fraction of thin disk galaxies continues to challenge ΛCDM cosmology. Astrophys. J. 2022, 925, 183. [Google Scholar] [CrossRef]
- Haslbauer, M.; Kroupa, P.; Zonoozi, A.H.; Haghi, H. Has JWST already falsified dark-matter-driven galaxy formation? Astrophys. J. Lett. 2022, 939, L31. [Google Scholar] [CrossRef]
- Shamir, L. Patterns of galaxy spin directions in SDSS and Pan-STARRS show parity violation and multipoles. Astrophys. Space Sci. 2020, 365, 136. [Google Scholar] [CrossRef]
- Shamir, L. Asymmetry between galaxies with clockwise handedness and counterclockwise handedness. Astrophys. J. 2016, 823, 32. [Google Scholar] [CrossRef]
- Shamir, L. Asymmetry between galaxies with different spin patterns: A comparison between COSMOS, SDSS, and Pan-STARRS. Open Astron. 2020, 29, 15–27. [Google Scholar] [CrossRef]
- Shamir, L. Analysis of spin directions of galaxies in the DESI Legacy Survey. Mon. Not. R. Astron. Soc. 2022, 516, 2281–2291. [Google Scholar] [CrossRef]
- Shamir, L. Using 3D and 2D analysis for analyzing large-scale asymmetry in galaxy spin directions. PASJ 2022, 74, 1114–1130. [Google Scholar] [CrossRef]
- Shamir, L. Asymmetry in galaxy spin directions - analysis of data from DES and comparison to four other sky surveys. Universe 2022, 8, 8. [Google Scholar] [CrossRef]
- Mcadam, D.; Shamir, L.; others. Reanalysis of the spin direction distribution of Galaxy Zoo SDSS spiral galaxies. Adv. Astron. 2023, 2023, 4114004. [Google Scholar] [CrossRef]
- Shamir, L.; McAdam, D. A possible tension between galaxy rotational velocity and observed physical properties. arXiv 2022, arXiv:2212.04044. [Google Scholar]
- Shamir, L. Ganalyzer: A tool for automatic galaxy image analysis. Astrophys. J. 2011, 736, 141. [Google Scholar] [CrossRef]
- Shamir, L. Large-scale asymmetry in galaxy spin directions: Evidence from the Southern hemisphere. Publ. Astron. Soc. Aust. 2021, 38, e037. [Google Scholar] [CrossRef]
- Lintott, C.J.; Schawinski, K.; Slosar, A.; Land, K.; Bamford, S.; Thomas, D.; Raddick, M.J.; Nichol, R.C.; Szalay, A.; Andreescu, D.; et al. Galaxy Zoo: Morphologies derived from visual inspection of galaxies from the Sloan Digital Sky Survey. Mon. Not. R. Astron. Soc. 2008, 389, 1179–1189. [Google Scholar] [CrossRef]
- Davis, D.R.; Hayes, W.B. SpArcFiRe: Scalable Automated Detection of Spiral Galaxy Arm Segments. Astrophys. J. 2014, 790, 87. [Google Scholar] [CrossRef]
- Hayes, W.B.; Davis, D.; Silva, P. On the nature and correction of the spurious S-wise spiral galaxy winding bias in Galaxy Zoo 1. Mon. Not. R. Astron. Soc. 2017, 466, 3928–3936. [Google Scholar] [CrossRef]
- Dhar, S.; Shamir, L. Systematic biases when using deep neural networks for annotating large catalogs of astronomical images. Astron. Comput. 2022, 38, 100545. [Google Scholar] [CrossRef]
- McAdam, D.; Shamir, L. Asymmetry between galaxy apparent magnitudes shows a possible tension between physical properties of galaxies and their rotational velocity. Symmetry 2023, 15, 1190. [Google Scholar] [CrossRef]
- Wenger, M.; Ochsenbein, F.; Egret, D.; Dubois, P.; Bonnarel, F.; Borde, S.; Genova, F.; Jasniewicz, G.; Laloë, S.; Lesteven, S.; et al. The SIMBAD astronomical database-The CDS reference database for astronomical objects. Astron. Astrophys. Suppl. Ser. 2000, 143, 9–22. [Google Scholar] [CrossRef]
- d’Assignies D, W.; Chisari, N.E.; Hamaus, N.; Singh, S. Intrinsic alignments of galaxies around cosmic voids. Mon. Not. R. Astron. Soc. 2022, 509, 1985–1994. [Google Scholar] [CrossRef]
- Kraljic, K.; Davé, R.; Pichon, C. And yet it flips: Connecting galactic spin and the cosmic web. Mon. Not. R. Astron. Soc. 2020, 493, 362–381. [Google Scholar] [CrossRef]
- Aluri, P.K.; Cea, P.; Chingangbam, P.; Chu, M.C.; Clowes, R.G.; Hutsemékers, D.; Kochappan, J.P.; Krasiński, A.; Lopez, A.M.; Liu, L.; et al. Is the observable Universe consistent with the cosmological principle? Class. Quantum Gravity 2023, 40, 094001. [Google Scholar] [CrossRef]
- Shamir, L. Analysis of ∼106 spiral galaxies from four telescopes shows large-scale patterns of asymmetry in galaxy spin directions. Adv. Astron. 2022, 2022, 8462363. [Google Scholar] [CrossRef]
- Shamir, L. Large-scale asymmetry in galaxy spin directions: Analysis of galaxies with spectra in DES, SDSS, and DESI Legacy Survey. Astron. Notes 2022, 343, e20220010. [Google Scholar] [CrossRef]
- Shamir, L. A possible large-scale alignment of galaxy spin directions—Analysis of 10 datasets from SDSS, Pan-STARRS, and HST. New Astron. 2022, 95, 101819. [Google Scholar] [CrossRef]
- Shamir, L. Large-scale asymmetry in the distribution of galaxy spin directions—Analysis and reproduction. Symmetry 2023, 15, 1704. [Google Scholar] [CrossRef]
- Ebrahimian, E.; Krishnan, C.; Mondol, R.; Sheikh-Jabbari, M. Towards a realistic dipole cosmology: The dipole Λ CDM model. arXiv 2023, arXiv:2305.16177. [Google Scholar]
- Krishnan, C.; Mondol, R.; Sheikh-Jabbari, M. A Tilt Instability in the Cosmological Principle. arXiv 2022, arXiv:2211.08093. [Google Scholar] [CrossRef]
- Allahyari, A.; Ebrahimian, E.; Mondol, R.; Sheikh-Jabbari, M. Big Bang in Dipole Cosmology. arXiv 2023, arXiv:2307.15791. [Google Scholar]
- Krishnan, C.; Mondol, R.; Sheikh-Jabbari, M. Dipole cosmology: The Copernican paradigm beyond FLRW. J. Cosmol. Astropart. Phys. 2023, 2023, 020. [Google Scholar] [CrossRef]
- Krishnan, C.; Mondol, R.; Jabbari, M.S. Copernican paradigm beyond FLRW. Symmetry 2023, 15, 428. [Google Scholar] [CrossRef]
- Gödel, K. An example of a new type of cosmological solutions of Einstein’s field equations of gravitation. Rev. Mod. Phys. 1949, 21, 447. [Google Scholar] [CrossRef]
- Ozsváth, I.; Schücking, E. Finite rotating universe. Nature 1962, 193, 1168–1169. [Google Scholar] [CrossRef]
- Gödel, K. Rotating universes in general relativity theory. Gen. Relativ. Gravit. 2000, 32, 1419–1427. [Google Scholar] [CrossRef]
- Chechin, L. Rotation of the Universe at different cosmological epochs. Astron. Rep. 2016, 60, 535–541. [Google Scholar] [CrossRef]
- Campanelli, L. A conjecture on the neutrality of matter. Found. Phys. 2021, 51, 56. [Google Scholar] [CrossRef]
- Pathria, R. The universe as a black hole. Nature 1972, 240, 298–299. [Google Scholar] [CrossRef]
- Stuckey, W. The observable universe inside a black hole. Am. J. Phys. 1994, 62, 788–795. [Google Scholar] [CrossRef]
- Easson, D.A.; Brandenberger, R.H. Universe generation from black hole interiors. J. High Energy Phys. 2001, 2001, 024. [Google Scholar] [CrossRef]
- Seshavatharam, U. Physics of rotating and expanding black hole universe. Prog. Phys. 2010, 2, 7–14. [Google Scholar]
- Popławski, N.J. Radial motion into an Einstein–Rosen bridge. Phys. Lett. B 2010, 687, 110–113. [Google Scholar] [CrossRef]
- Christillin, P. The Machian origin of linear inertial forces from our gravitationally radiating black hole Universe. Eur. Phys. J. Plus 2014, 129, 175. [Google Scholar] [CrossRef]
- Dymnikova, I. Universes Inside a Black Hole with the de Sitter Interior. Universe 2019, 5, 111. [Google Scholar] [CrossRef]
- Chakrabarty, H.; Abdujabbarov, A.; Malafarina, D.; Bambi, C. A toy model for a baby universe inside a black hole. Eur. Phys. J. C 2020, 80, 373. [Google Scholar] [CrossRef]
- Popławski, N.J. A nonsingular, anisotropic universe in a black hole with torsion and particle production. Gen. Relativ. Gravit. 2021, 53, 18. [Google Scholar] [CrossRef]
- Seshavatharam, U.V.S.; Lakshminarayana, S. Concepts and results of a Practical Model of Quantum Cosmology: Light Speed Expanding Black Hole Cosmology. Mapana J. Sci. 2022, 21, 13. [Google Scholar]
- Gaztanaga, E. The Black Hole Universe, part I. Symmetry 2022, 14, 1849. [Google Scholar] [CrossRef]
- Gaztanaga, E. The Black Hole Universe, Part II. Symmetry 2022, 14, 1984. [Google Scholar] [CrossRef]
- Susskind, L. The world as a hologram. J. Math. Phys. 1995, 36, 6377–6396. [Google Scholar] [CrossRef]
- Bak, D.; Rey, S.J. Holographic principle and string cosmology. Class. Quantum Gravity 2000, 17, L1. [Google Scholar] [CrossRef]
- Bousso, R. The holographic principle. Rev. Mod. Phys. 2002, 74, 825. [Google Scholar] [CrossRef]
- Myung, Y.S. Holographic principle and dark energy. Phys. Lett. B 2005, 610, 18–22. [Google Scholar] [CrossRef]
- Hu, B.; Ling, Y. Interacting dark energy, holographic principle, and coincidence problem. Phys. Rev. D 2006, 73, 123510. [Google Scholar] [CrossRef]
- Rinaldi, E.; Han, X.; Hassan, M.; Feng, Y.; Nori, F.; McGuigan, M.; Hanada, M. Matrix-Model Simulations Using Quantum Computing, Deep Learning, and Lattice Monte Carlo. PRX Quantum 2022, 3, 010324. [Google Scholar] [CrossRef]
- Campanelli, L.; Cea, P.; Tedesco, L. Ellipsoidal universe can solve the cosmic microwave background quadrupole problem. PRL 2006, 97, 131302. [Google Scholar] [CrossRef] [PubMed]
- Campanelli, L.; Cea, P.; Tedesco, L. Cosmic microwave background quadrupole and ellipsoidal universe. Phys. Rev. D 2007, 76, 063007. [Google Scholar] [CrossRef]
- Gruppuso, A. Complete statistical analysis for the quadrupole amplitude in an ellipsoidal universe. Phys. Rev. D 2007, 76, 083010. [Google Scholar] [CrossRef]
- Campanelli, L.; Cea, P.; Fogli, G.; Tedesco, L. Cosmic parallax in ellipsoidal universe. Mod. Phys. Lett. A 2011, 26, 1169–1181. [Google Scholar] [CrossRef]
- Cea, P. The ellipsoidal universe in the Planck satellite era. Mon. Not. R. Astron. Soc. 2014, 441, 1646–1661. [Google Scholar] [CrossRef]
- Sanejouand, Y.H. A framework for the next generation of stationary cosmological models. Int. J. Mod. Phys. D 2022, 31, 2250084. [Google Scholar] [CrossRef]
- Javanmardi, B.; Porciani, C.; Kroupa, P.; Pflam-Altenburg, J. Probing the isotropy of cosmic acceleration traced by type Ia supernovae. Astrophys. J. 2015, 810, 47. [Google Scholar] [CrossRef]
- Krishnan, C.; Mohayaee, R.; Colgáin, E.Ó.; Sheikh-Jabbari, M.; Yin, L. Hints of FLRW breakdown from supernovae. Phys. Rev. D 2022, 105, 063514. [Google Scholar] [CrossRef]
- Cowell, J.A.; Dhawan, S.; Macpherson, H.J. Potential signature of a quadrupolar Hubble expansion in Pantheon+ supernovae. arXiv 2022, arXiv:2212.13569. [Google Scholar] [CrossRef]
- McConville, R.; Colgain, E. Anisotropic distance ladder in Pantheon+ supernovae. arXiv 2023, arXiv:2304.02718. [Google Scholar]
- Perivolaropoulos, L. Isotropy properties of the absolute luminosity magnitudes of SnIa in the Pantheon+ and SH0ES samples. Phys. Rev. D 2023, 108, 063509. [Google Scholar] [CrossRef]
- Khetan, N.; Izzo, L.; Branchesi, M.; Wojtak, R.; Cantiello, M.; Murugeshan, C.; Agnello, A.; Cappellaro, E.; Della Valle, M.; Gall, C.; et al. A new measurement of the Hubble constant using Type Ia supernovae calibrated with surface brightness fluctuations. Astron. Astrophys. 2021, 647, A72. [Google Scholar] [CrossRef]
- Vagnozzi, S. Seven hints that early-time new physics alone is not sufficient to solve the Hubble tension. Universe 2023, 9, 393. [Google Scholar] [CrossRef]
- Loeb, A.; Gaudi, B.S. Periodic flux variability of stars due to the reflex Doppler effect induced by planetary companions. Astrophys. J. Lett. 2003, 588, L117. [Google Scholar] [CrossRef]
- Opik, E. An estimate of the distance of the Andromeda Nebula. Astrophys. J. 1922, 55, 406–410. [Google Scholar] [CrossRef]
- Babcock, H.W. The rotation of the Andromeda Nebula. Lick Obs. Bull. 1939, 19, 41–51. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, W.K., Jr. Rotation of the Andromeda nebula from a spectroscopic survey of emission regions. Astrophys. J. 1970, 159, 379. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, W.K., Jr.; Thonnard, N. Extended rotation curves of high-luminosity spiral galaxies. IV-Systematic dynamical properties, SA through SC. Astrophys. J. 1978, 225, L107–L111. [Google Scholar] [CrossRef]
- Rubin, V.C.; Ford, W.K., Jr.; Thonnard, N. Rotational properties of 21 SC galaxies with a large range of luminosities and radii, from NGC 4605/R = 4kpc/to UGC 2885/R = 122 kpc. Astrophys. J. 1980, 238, 471–487. [Google Scholar] [CrossRef]
- Rubin, V.C.; Burstein, D.; Ford Jr, W.K.; Thonnard, N. Rotation velocities of 16 Sa galaxies and a comparison of Sa, Sb, and Sc rotation properties. Astrophys. J. 1985, 289, 81–98. [Google Scholar] [CrossRef]
- Sofue, Y.; Rubin, V. Rotation curves of spiral galaxies. Annu. Rev. Astron. Astrophys. 2001, 39, 137–174. [Google Scholar] [CrossRef]

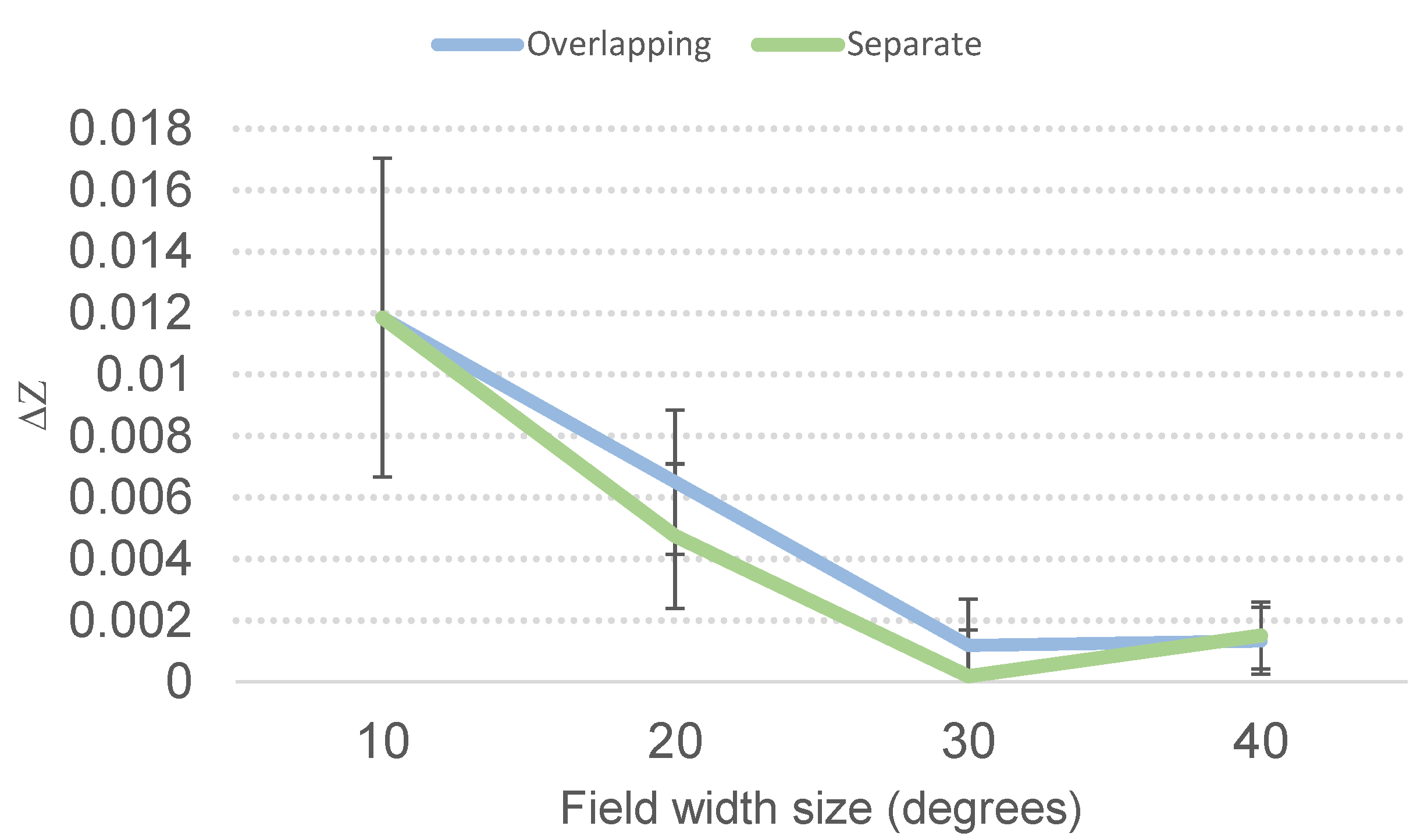
| Field (∘) | # MW | # OMW | z | t-Test p | ||
|---|---|---|---|---|---|---|
| 10 × 10 | 204 | 202 | 0.0996 ± 0.0036 | 0.08774 ± 0.0036 | 0.01185 ± 0.005 | 0.02 |
| 20 × 20 | 817 | 825 | 0.09545 ± 0.0017 | 0.08895 ± 0.0016 | 0.0065 ± 0.0023 | 0.0058 |
| z Range | # MW | # OMW | z | ||
|---|---|---|---|---|---|
| z < 0.1 | 491 | 521 | 0.0629 ± 0.001 | 0.0601 ± 0.001 | 0.0028 ± 0.0013 |
| z > 0.1 | 326 | 304 | 0.1441 ± 0.002 | 0.1388 ± 0.002 | 0.0053 ± 0.0028 |
| Band | MW | OMW | t-Test p | |
|---|---|---|---|---|
| spectroFlux_g | 25.969 ± 0.8669 | 28.554 ± 1.0918 | −2.585 | 0.063 |
| spectroFlux_r | 53.2433 ± 1.765 | 58.6214 ± 2.3422 | −5.378 | 0.066 |
| spectroFlux_i | 77.4189 ± 2.513 | 85.0868 ± 3.407 | −7.667 | 0.067 |
| Field (∘) | # MW | # OMW | z | t-Test p | ||
|---|---|---|---|---|---|---|
| Original 10 × 10 | 710 | 732 | 0.07197 ± 0.0015 | 0.06234 ± 0.0014 | 0.00963 ± 0.002 | <0.0001 |
| Mirrored 10 × 10 | 728 | 709 | 0.06375 ± 0.0014 | 0.07191 ± 0.0014 | −0.00816 ± 0.002 | <0.0001 |
| Original 20 × 20 | 2903 | 2976 | 0.07285 ± 0.0007 | 0.071164 ± 0.0007 | 0.001686 ± 0.0009 | 0.04 |
| Mirrored 20 × 20 | 3003 | 2914 | 0.07113 ± 0.0007 | 0.07271 ± 0.0007 | −0.00158 ± 0.0009 | 0.05 |
| Field (∘) | # OMW | # MW | z | t-Test p | ||
|---|---|---|---|---|---|---|
| 10 × 10 | 414 | 376 | 0.1270 ± 0.0025 | 0.1352 ± 0.0027 | −0.0082 ± 0.0036 | 0.018 |
| 20 × 20 | 1702 | 1681 | 0.1273 ± 0.0014 | 0.1317 ±0.0013 | −0.0044 ± 0.0018 | 0.008 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shamir, L. A Simple Direct Empirical Observation of Systematic Bias of the Redshift as a Distance Indicator. Universe 2024, 10, 129. https://doi.org/10.3390/universe10030129
Shamir L. A Simple Direct Empirical Observation of Systematic Bias of the Redshift as a Distance Indicator. Universe. 2024; 10(3):129. https://doi.org/10.3390/universe10030129
Chicago/Turabian StyleShamir, Lior. 2024. "A Simple Direct Empirical Observation of Systematic Bias of the Redshift as a Distance Indicator" Universe 10, no. 3: 129. https://doi.org/10.3390/universe10030129
APA StyleShamir, L. (2024). A Simple Direct Empirical Observation of Systematic Bias of the Redshift as a Distance Indicator. Universe, 10(3), 129. https://doi.org/10.3390/universe10030129






