The QCD Vacuum as a Disordered Chromomagnetic Condensate

Abstract

An attempt is made to describe from first principles the large-scale structure of the confining vacuum in quantum chromodynamics. Starting from our previous variational studies of the SU(2) pure gauge theory in an external Abelian chromomagnetic field and extending Feynman’s qualitative analysis in (2+1)-dimensional SU(2) gauge theory, we show that the SU(3) vacuum in three-space and one-time dimensions behaves like a disordered chromomagnetic condensate. Color confinement is assured by the presence of a mass gap together with the absence of color long-range correlations. We offer a clear physical picture for the formation of the flux tube between static quark charges that allows us to determine the color structure and the transverse profile of the flux-tube chromoelectric field. The transverse profile of the flux-tube chromoelectric field turns out to be in reasonable agreement with lattice data. We, also, show that our quantum vacuum allows for both the color and ordinary Meissner effect. We find that for massless quarks, the quantum vacuum can accommodate a finite non-zero density of fermion zero modes leading to the dynamical breaking of the chiral symmetry.

1. Introduction

The most challenging aspect of high-energy physics is understanding color and quark confinement (for an overview see Refs. [1,2,3,4,5,6,7,8,9,10]). Despite the fact that the theory of the strong interactions, Quantum Chromodynamics (QCD), has been known for decades, and not withstanding large efforts with numerical simulations aimed at unravelling the nature of the QCD vacuum, we still lack a fundamental understanding of the corresponding physics. As a matter of fact, the mechanism that leads to color confinement remains an open question in spite of intense non-perturbative lattice studies for more than three decades.

According to a model conjectured a long time ago by G. ’t Hooft [11,12,13] and S. Mandelstam [14] the confining vacuum behaves as a coherent state of color magnetic monopoles, or, equivalently, the vacuum resembles a magnetic (dual) superconductor (for a more complete discussion, see Refs. [5,8,10,15,16] and references therein). Up to now, there have been extensive numerical studies of monopole condensation. However, even if magnetic monopoles do condense in the confinement mode, the actual mechanism of confinement could depend on additional dynamical forces.

An alternative model for color confinement is based on the special role of center vortices. By means of lattice simulations, evidence has been accumulated that center vortices are responsible for confinement (for instance, see Refs. [6,10] and references therein). A different confinement picture was advanced by V. N. Gribov [17,18] and further elaborated by D. Zwanzinger [19] where it is argued that the gauge field configurations that are relevant for confinement are concentrated on the so-called Gribov horizon (for a pedagogic overview, see Ref. [20] and references therein). As a matter of fact, it has been suggested [21,22,23] that both Gribov–Zwanzinger and the center vortex picture of confinement are compatible. On the other hand, interestingly enough, in Refs. [24,25,26], pure Yang–Mills theories have been investigated within the Schrödinger representation in the Coulomb gauge. These authors, by using vacuum functionals that are strongly peaked at the Gribov horizon, showed that the vacuum functional becomes field independent in the infrared consistent with a stochastic vacuum at large distances.

One could conclude that there is no totally convincing explanation of the confinement phenomenon and that a full understanding of the QCD vacuum dynamics is still lacking. However, previous different pictures of confinement can be reconciled if the confining vacuum behaves like a disordered chromomagnetic condensate. In this case, the condensation of vortices and chromomagnetic monopoles are only a symptom rather than the origin of confinement.

In a seminal paper, R. P. Feynman [27] argued that in (2+1)-dimensions the SU(2) confining vacuum at large distances is a chromomagnetic condensate disordered by the gauge symmetry. The confinement of colors comes from the existence of a mass gap and the absence of color long-range order. In this paper, we will show that, indeed, the Yang–Mills vacuum in (3+1)-dimensions does display at a large distance a mass gap and no color long-range order. On the other hand, we will argue that the color dynamics at very short distances is governed by the perturbative regime.

In Refs. [28,29,30], by means of the lattice Schrödinger functional, a gauge invariant effective action was introduced for external static background fields that allowed the dynamics of gauge theories to be probed non-perturbatively. In particular [31,32,33,34], the Yang–Mills vacuum was probed by means of an external constant Abelian chromomagnetic field on the lattice. Actually, up to now, the lattice studies have been limited to the SU(3) pure gauge theory or to QCD with two degenerate massive quarks. It turned out that, by increasing the strength of the applied external field, the deconfinement temperature decreases towards zero. In other words, there is a critical field $g{H}_c$ such that, for $gH>g{H}_c$, the gauge system is in the deconfined phase. More precisely, it resulted that:

$$\frac{T_c\left(gH\right)}{T_c\left(0\right)}=1-\frac{\sqrt{gH}}{\sqrt{g{H}_c}}.$$

(1)

As a consequence, one is led to suspect that there must be an intimate connection between Abelian chromomagnetic fields and color confinement. The existence of a critical chromomagnetic field is not easily understandable within the coherent magnetic monopole or vortex condensate picture of the confining vacuum, but it could be compatible with the disordered chromomagnetic condensate picture, for strong-enough chromomagnetic field strengths to enforce long-range color order, thereby destroying confinement. On the other hand, the peculiar color Meissner effect, Equation (1), could be easily explained if the vacuum behaves as an ordinary relativistic color superconductor. Thus, we have to reconcile two apparently different aspects. On one hand, the confining vacuum does display condensation of both Abelian magnetic monopoles and vortices; on the other hand, the relation between the deconfinement temperature and the applied Abelian chromomagnetic field, Equation (1), would imply that the magnetic length $a_H\sim 1/\sqrt{gH}$ is the only relevant scale of the problem. Indeed, Equation (1) suggests that the vacuum behaves as a condensate of a color charged scalar field whose mass is proportional to the inverse of the magnetic length. Interestingly enough, a long time ago it was pointed out that in the Yang–Mills theory, a ferro-chromomagnetic state could have a lower energy with respect to the perturbative vacuum [35,36,37,38]. However, it was soon shown by N. K. Nielsen and P. Olesen [39,40] (also, see Ref. [41]) that such a state is affected by unstable modes. Thus, we see that a natural candidate for the tachyonic color charged scalar fields are the Nielsen–Olesen unstable modes, for the eventual condensation of these modes should make the vacuum a dynamical color superconductor. This kind of argument led a long time ago to the proposal of the so-called Copenhagen vacuum [42,43,44,45,46,47,48], where vacuum field configurations that differ from the classical external field only in the unstable mode sector would result in the formation of a quantum liquid. However, in Refs. [49,50], we showed that, by using variational techniques on a class of gauge-invariant Gaussian wave functionals, the stabilization of the Nielsen–Olesen modes contributes to the energy density with a negative classical term, which cancels the classical magnetic energy. Moreover, the stabilization of the Nielsen–Olesen modes induces a further background field that behaves non-analytically in the coupling constant and screens almost completely the external chromomagnetic field. As a consequence, even in the strong-field regime, the naive perturbative regime, one deals with the non-perturbative regime. This means that the calculation of the energy density, even in the one-loop approximation, is non-perturbative. Nevertheless, we believe that the gauge-invariant variational perturbative approach presented in Refs. [49,50] convincingly showed that the Nielsen–Olesen instability is an artifact of the one-loop approximation and that the correct treatment of this one-loop instability leads to a drastic reduction in the energy density of the trial vacuum functional. Indeed, this kind of effect has already been checked by means of non-perturbative numerical simulations in lattice gauge theories [51,52,53,54,55]. On the other hand, the inevitable presence of the induced background field needed to overcome the one-loop instability was not appreciated until the remarkable evidence from the lattice of the color Meissner effect that leads us to reconsider the dynamics of the stabilizing chromomagnetic background field and, finally, to unravelling the nature of the confining vacuum.

The main aims of the present paper are twofold. Firstly, we shall extend the variational perturbative calculations following our previous papers in SU(2) [49,50] to the SU(3) gauge theory in the presence of an external constant Abelian chromomagnetic field directed along the third direction in color space. In Section 2, following Ref. [50] (henceforth referred to as I), we consider the SU(3) pure gauge theory in the Schrödinger representation, and we show explicitly that in the one-loop approximation, there are three different kinds of unstable modes. Section 3 is devoted to the variational minimization of the ground-state energy density. We find that the tachyonic condensation of the unstable modes leads to stabilizing chromomagnetic background fields with peculiar kink structures. We, also, show that the resulting ground-state wavefunctional is not energetically favored with respect to a perturbative vacuum. In Section 4, we present a careful analysis of the induced background fields and we show that they allow the presence of vacuum chromomagnetic charges.

In the second part of the present paper, we set up the QCD vacuum wavefunctional and try a punctual comparison with hadron phenomenology and lattice data. In Section 5, we present our picture on the structure of the vacuum as a disordered chromomagnetic condensate. This is achieved after taking into account the kink structure of the background fields dynamically generated by the unstable mode condensation together with Feynman’s analysis adapted to the SU(3) gauge theory in three spatial dimensions. In Section 6, we show that our QCD vacuum is characterized by non-zero gluon condensate, mass gap and the absence of color long-range correlations. We reach a clear physical picture for the generation of a squeezed flux tube between a static quark pair that allows us to determine both the color structure and the transverse profile of the flux-tube chromoelectric fields. In addition, we show that our proposal for the confining QCD vacuum allows for the color Meissner effect as well as the Meissner effect recently suggested by numerical simulations of full QCD on the lattice in the presence of extreme magnetic fields. In Section 7, we evaluate the contributions of dynamical quarks to the vacuum energy in the one-loop approximation. Moreover, we suggest that for massless quarks, the dynamically generated background fields could account for a finite non-zero density of fermion zero modes, fulfilling, thereby, the breaking of the chiral symmetry. Finally, the summary of the main results and some concluding remarks are given in Section 8.

It is worthwhile stressing that we are not claiming that we have solved completely the confinement problem in QCD. However, we feel that the results of the present paper could offer a promising path towards the complete understanding of confinement in quantum chromodynamics.

2. Constant Chromomagnetic Background Field in SU(3)

In this section, we consider the (3+1) dimensional pure SU(3) gauge theory. We shall work in the temporal gauge and follow closely the approach developed in I. In the temporal gauge $A_0^a=0$, the Hamiltonian reads:

$$\mathcal{H}=\frac{1}{2}\int d\overrightarrow{x}\left\{{\left(E_i^a\left(\overrightarrow{x}\right)\right)}^2+{\left(B_i^a\left(\overrightarrow{x}\right)\right)}^2\right\},$$

(2)

where

$$B_i^a\left(\overrightarrow{x}\right)=\frac{1}{2}{ϵ}_{ijk}{F}_{ij}^a\left(\overrightarrow{x}\right),$$

(3)

and

$$F_{ij}^a\left(\overrightarrow{x}\right)={\partial }_i{A}_j^a\left(\overrightarrow{x}\right)-{\partial }_j{A}_i^a\left(\overrightarrow{x}\right)+g{f}^{abc}{A}_i^b\left(\overrightarrow{x}\right)A_j^c\left(\overrightarrow{x}\right).$$

(4)

We shall use the fixed-time Schrödinger representation for quantized fields. In fact, the Schrödinger approach to quantum field theories permits a direct study of the vacuum structure through the analysis of the vacuum wavefunctional of the theory. The structure of the vacuum wavefunctional should reflect the nature of color confinement and other non-perturbative features of QCD, more notably, the quark confinement and the chiral symmetry breaking. Actually, the Schrödinger approach may allow the study of the vacuum structure through variational methods implemented by means of trial wavefunctionals.

In the fixed-time Schrödinger representation, the chromoelectric field $E_i^a\left(\overrightarrow{x}\right)$ acts as functional derivative:

$$E_i^a\left(\overrightarrow{x}\right)=+i\frac{\delta }{\delta A_i^a\left(\overrightarrow{x}\right)}$$

(5)

on the physical states that are functionals obeying the Gauss law (see, e.g., Ref. [56]):

$$\left[{\partial }_i{\delta }^{ab}+g{f}^{acb}{A}_i^c\left(\overrightarrow{x}\right)\right]\frac{\delta }{\delta A_i^b\left(\overrightarrow{x}\right)}\mathcal{G}\left[A\right]=0.$$

(6)

The effects of an external background field are incorporated by writing

$$A_i^a\left(\overrightarrow{x}\right)={\overline{A}}_i^a\left(\overrightarrow{x}\right)+{\eta }_i^a\left(\overrightarrow{x}\right)$$

(7)

where ${\overline{A}}_i^a\left(\overrightarrow{x}\right)$ is the background field, and ${\eta }_i^a\left(\overrightarrow{x}\right)$ the fluctuating field. We are interested in a constant Abelian chromomagnetic field:

$${\overline{A}}_k^a\left(\overrightarrow{x}\right)={\overline{A}}_k\left(\overrightarrow{x}\right){\delta }^{a,3},{\overline{A}}_k\left(\overrightarrow{x}\right)={\delta }_{k,2}{x}_{1}H,\overrightarrow{x}=(x_1,x_2,x_3).$$

(8)

It is straightforward to rewrite the Hamiltonian in terms of the fluctuating fields. We obtain:

$$\mathcal{H}=V\frac{H^2}{2}+{\mathcal{H}}^{\left(2\right)}+{\mathcal{H}}^{\left(3\right)}+{\mathcal{H}}^{\left(4\right)},$$

(9)

where

$${\mathcal{H}}^{\left(2\right)}=\frac{1}{2}\int d\overrightarrow{x}\left\{-\frac{{\delta }^2}{\delta {\eta }_i^a\left(\overrightarrow{x}\right)\delta {\eta }_i^a\left(\overrightarrow{x}\right)}+{\eta }_i^a\left(\overrightarrow{x}\right){\mathcal{O}}_{ij}^{ab}\left(\overrightarrow{x}\right){\eta }_j^b\left(\overrightarrow{x}\right)-{\left[D_i^{ab}\left(\overrightarrow{x}\right){\eta }_i^b\left(\overrightarrow{x}\right)\right]}^2\right\},$$

(10)

$${\mathcal{H}}^{\left(3\right)}=\frac{g}{2}{ϵ}_{ijk}{ϵ}_{i{j}^{\prime }{k}^{\prime }}{f}^{abc}\int d\overrightarrow{x}{\eta }_j^b\left(\overrightarrow{x}\right){\eta }_k^c\left(\overrightarrow{x}\right)D_{j^{\prime }}^{ad}\left(\overrightarrow{x}\right){\eta }_{k^{\prime }}^d\left(\overrightarrow{x}\right),$$

(11)

$${\mathcal{H}}^{\left(4\right)}=\frac{g^2}{8}{ϵ}_{ijk}{ϵ}_{i{j}^{\prime }{k}^{\prime }}{f}^{abc}{f}^{a{b}^{\prime }{c}^{\prime }}\int d\overrightarrow{x}{\eta }_j^b\left(\overrightarrow{x}\right){\eta }_k^c\left(\overrightarrow{x}\right){\eta }_{j^{\prime }}^{b^{\prime }}\left(\overrightarrow{x}\right){\eta }_{k^{\prime }}^{c^{\prime }}\left(\overrightarrow{x}\right).$$

(12)

In Equations (10) and (11), $D_i^{ab}\left(\overrightarrow{x}\right)$ is the covariant derivative with respect to the background field:

$$D_i^{ab}\left(\overrightarrow{x}\right)={\partial }_i{\delta }^{ab}+g{f}^{acb}{\overline{A}}_i^c\left(\overrightarrow{x}\right),$$

(13)

while ${\mathcal{O}}_{ij}^{ab}(\overline{A},\overrightarrow{x})$ is the operator

$${\mathcal{O}}_{ij}^{ab}\left(\overrightarrow{x}\right)=-{\delta }_{ij}{D}_k^{ac}\left(\overrightarrow{x}\right)D_k^{cb}\left(\overrightarrow{x}\right)+2gH{ϵ}_{3ij}{f}^{3ab}.$$

(14)

The Gauss constraints, Equation (6), can be rewritten as:

$$\left[D_i^{ab}\left(\overrightarrow{x}\right)+g{f}^{acb}{\eta }_i^c\left(\overrightarrow{x}\right)\right]\frac{\delta }{\delta {\eta }_i^b\left(\overrightarrow{x}\right)}\mathcal{G}\left[\eta \right]=0.$$

(15)

As is well known (see, for instance, Ref. [56]), the Gauss constraints ensure that the physical states are invariant against time-independent gauge transformations. It follows, then, that the physical states are not normalizable. To overcome this problem, one must fix the residual gauge invariance. Following I, we impose the covariant Coulomb constraints:

$$D_i^{ab}\left(\overrightarrow{x}\right){\eta }_i^b\left(\overrightarrow{x}\right)=0.$$

(16)

Accordingly, the functional measure in the scalar product between two physical states gets modified by the Faddeev–Popov determinant associated to the gauge-fixing Equation (16) so that we are left with the following scalar product between physical states:

$$<{\mathcal{G}}_1|{\mathcal{G}}_2>=\int \mathcal{D}\eta {\mathcal{G}}_1^{*}\left[\eta \right]{\mathcal{G}}_2\left[\eta \right]{\Delta }_{F-P}\left[\eta \right]\delta \left[D_i^{ab}\left(\overrightarrow{x}\right){\eta }_i^b\left(\overrightarrow{x}\right)\right].$$

(17)

A long time ago, it was suggested [35,36,37] that states with a constant chromomagnetic field could lie below the perturbative ground state. This was the main motivation that led us to investigate non-perturbatively the structure of the vacuum functional in the presence of Abelian chromomagnetic background field, Equation (8). To this end, we need to set up trial vacuum wavefunctionals and, then, to evaluate the expectation value of the Hamiltonian on these states. This strategy, however, is not easily implementable due to the Gauss constraints on physical states. Nevertheless, if one assumes that the quantum fluctuations over the background field can be dealt with perturbatively, then there is a natural strategy to follow. In fact, the lowest-order approximation (the one-loop approximation) leads us to consider the quadratic piece of the Hamiltonian, Equation (9):

$${\mathcal{H}}_0=V\frac{H^2}{2}+{\mathcal{H}}^{\left(2\right)}.$$

(18)

In the same approximation, the Gauss constraint reduces to:

$$D_i^{ab}\left(\overrightarrow{x}\right)\frac{\delta \mathcal{G}\left[\eta \right]}{\delta {\eta }_i^b\left(\overrightarrow{x}\right)}=0.$$

(19)

It is quite easy to show that Equation (19) is satisfied by wavefunctionals that depend only on transverse fields, i.e., satisfying Equation (16). To diagonalize ${\mathcal{H}}_0$, it suffices to solve the eigenvalue equations:

$${\mathcal{O}}_{ij}^{ab}\left(\overrightarrow{x}\right){\varphi }_j^b\left(\overrightarrow{x}\right)=\lambda {\varphi }_i^a\left(\overrightarrow{x}\right)$$

(20)

with the conditions

$$D_i^{ab}\left(\overrightarrow{x}\right){\varphi }_i^b\left(\overrightarrow{x}\right)=0.$$

(21)

Fortunately, the solutions of Equations (20) and (21) have been discussed in detail in I. This will greatly simplify the analyses in the present case. To see this, let us consider Equation (20) assuming that $a,b=1,2$. From Equation (14), we obtain:

$${\mathcal{O}}_{ij}^{ab}\left(\overrightarrow{x}\right)=\left[-{\partial }^2{\delta }^{ab}+2gH{f}^{3ab}{x}_1{\partial }_2+g^2{H}^2{x}_1^2{f}^{3ca}{f}^{3cb}\right]{\delta }_{ij}+2gH{ϵ}_{3ij}{f}^{3ab}.$$

(22)

Since for $a,b=1,2$ we have $f^{3ab}={ϵ}^{3ab}$, Equation (22) reduces to the SU(2) operator discussed in I, Appendix B. As a consequence, we obtain the following spectrum:

$$\begin{array}{c}\hfill \lambda (n,p_2,p_3,\alpha =1)=p_3^2+gH(2n+1),n\ge 0\\ \hfill \lambda (n,p_2,p_3,\alpha =2)=p_3^2+gH(2n+1),n\ge 1\end{array}$$

(23)

with transverse eigenvector ${\varphi }_j^a(N_1;\overrightarrow{x})$, $N_1=(n,p_2,p_3,\alpha )$. We have, also, the tachyonic modes (u-modes):

$$\lambda \left(N_u\right)=p_3^2-gH,N_u=(p_2,p_3)$$

(24)

with transverse eigenvectors ${\varphi }_j^a(N_u;\overrightarrow{x})$. The explicit construction of the transverse eigenfunctions is discussed in detail in I, Appendix B.

For $a,b=3$ we obtain:

$${\mathcal{O}}_{ij}^{ab}\left(\overrightarrow{x}\right)=-{\partial }^2{\delta }^{a3}{\delta }^{b3}{\delta }_{ij}$$

(25)

with eigenvalues:

$$\lambda \left(N_2\right)={\overrightarrow{p}}^2,N_2=(p_1,p_2,p_3,\alpha ),\alpha =\pm 1$$

(26)

and the eigenstates ${\varphi }_j^a(N_2;\overrightarrow{x})$ are transverse plane waves.

For $a,b=4,5$ we have that $f^{3ab}=\frac{1}{2}{ϵ}^{3ab}$, so that:

$${\mathcal{O}}_{ij}^{ab}\left(\overrightarrow{x}\right)=\left[-{\partial }^2{\delta }^{ab}+2gH\frac{{ϵ}^{3ab}}{2}{x}_1{\partial }_2+\frac{g^2{H}^2}{4}{x}_1^2{\delta }^{ab}\right]{\delta }_{ij}+2gH{ϵ}_{3ij}\frac{{ϵ}^{3ab}}{2}$$

(27)

that coincides with the operator ${\mathcal{O}}_{ij}^{ab}\left(\overrightarrow{x}\right)$ in Equation (22) with $gH$ replaced by $\frac{gH}{2}$. As a consequence, we easily find the spectrum:

$$\begin{array}{c}\hfill \lambda (n,p_2,p_3,\alpha =1)=\sqrt{p_3^2+\frac{gH}{2}(2n+1)},n\ge 0\\ \hfill \lambda (n,p_2,p_3,\alpha =2)=\sqrt{p_3^2+\frac{gH}{2}(2n+1)},n\ge 1\end{array}$$

(28)

with transverse eigenvector ${\varphi }_j^a(N_3;\overrightarrow{x})$, $N_3=(n,p_2,p_3,\alpha )$. Obviously, we have, also, the tachyonic v-modes:

$$\lambda \left(N_v\right)=p_3^2-\frac{gH}{2},N_v=(p_2,p_3)$$

(29)

with transverse eigenvectors ${\varphi }_j^a(N_v;\overrightarrow{x})$.

For $a,b=6,7$, using $f^{3ab}=-\frac{1}{2}{ϵ}^{3ab}$, we obtain:

$${\mathcal{O}}_{ij}^{ab}\left(\overrightarrow{x}\right)=\left[-{\partial }^2{\delta }^{ab}-2gH\frac{{ϵ}^{3ab}}{2}{x}_1{\partial }_2+\frac{g^2{H}^2}{4}{x}_1^2{\delta }^{ab}\right]{\delta }_{ij}-2gH{ϵ}_{3ij}\frac{{ϵ}^{3ab}}{2},$$

(30)

with spectrum:

$$\begin{array}{c}\hfill \lambda (n,p_2,p_3,\alpha =1)=\sqrt{p_3^2+\frac{gH}{2}(2n+1)},n\ge 0\\ \hfill \lambda (n,p_2,p_3,\alpha =2)=\sqrt{p_3^2+\frac{gH}{2}(2n+1)},n\ge 1\end{array}$$

(31)

with transverse eigenvector ${\varphi }_j^a(N_4;\overrightarrow{x})$, $N_4=(n,p_2,p_3,\alpha )$. We have, also, the tachyonic w-modes:

$$\lambda \left(N_w\right)=p_3^2-\frac{gH}{2},N_w=(p_2,p_3)$$

(32)

with transverse eigenvectors ${\varphi }_j^a(N_w;\overrightarrow{x})$.

Finally, for $a,b=8$, we have:

$${\mathcal{O}}_{ij}^{ab}\left(\overrightarrow{x}\right)=-{\partial }^2{\delta }^{a8}{\delta }^{b8}{\delta }_{ij}$$

(33)

with eigenvalues:

$$\lambda \left(N_5\right)={\overrightarrow{p}}^2,N_5=(p_1,p_2,p_3,\alpha ),\alpha =\pm 1$$

(34)

and the transverse eigenvectors ${\varphi }_j^a(N_5;\overrightarrow{x})$ correspond to the familiar plane waves.

The eigenvectors ${\varphi }_j^a(N_3;\overrightarrow{x})$, ${\varphi }_j^a(N_4;\overrightarrow{x})$ as well as the unstable mode eigenvectors ${\varphi }_j^a(N_v;\overrightarrow{x})$, ${\varphi }_j^a(N_w;\overrightarrow{x})$ can be inferred from the results in I, Appendix B after replacing $gH$ with $\pm \frac{gH}{2}$.

It is, now, straightforward to find the ground-state wavefunctional and energy of the quadratic Hamiltonian, Equation (18). Evidently, we can write:

$${\mathcal{W}}_0\left[\eta \right]={\mathcal{V}}_0\left[{\eta }_s\right]{\mathcal{Z}}_0\left[{\eta }_u\right],$$

(35)

where the quantum fluctuations have been separated into stable and unstable modes according to:

$${\eta }_i^a\left(\overrightarrow{x}\right)={\eta }_{si}^a\left(\overrightarrow{x}\right)+{\eta }_{ui}^a\left(\overrightarrow{x}\right)$$

(36)

and

$${\eta }_{si}^a\left(\overrightarrow{x}\right)=\sum _{k=1}^5\sum _{N_k}c\left(N_k\right){\varphi }_i^a(N_k;\overrightarrow{x}),$$

(37)

$${\eta }_{ui}^a\left(\overrightarrow{x}\right)=\sum _{\beta =u,v,w}\sum _{N_{\beta }}c\left(N_{\beta }\right){\varphi }_i^a(N_{\beta };\overrightarrow{x}).$$

(38)

Evidently, we have:

$${\mathcal{V}}_0\left[{\eta }_s\right]=exp\left\{-\frac{1}{4}\int d\overrightarrow{x}d\overrightarrow{y}{\eta }_{si}^a\left(\overrightarrow{x}\right){\left(G_s\right)}_{ij}^{ab}(\overrightarrow{x},\overrightarrow{y}){\eta }_{sj}^b\left(\overrightarrow{y}\right)\right\},$$

(39)

with

$${\left(G_s\right)}_{ij}^{ab}(\overrightarrow{x},\overrightarrow{y})=\sum _{k=1}^5\sum _{N_k}2{\lambda }^{\frac{1}{2}}\left(N_k\right){\varphi }_i^{a*}(N_k;\overrightarrow{x}){\varphi }_j^b(N_k;\overrightarrow{y}).$$

(40)

The ground-state energy of the stable modes is:

$$\begin{array}{c}\hfill E_S\left(gH\right)=\frac{1}{2}\sum _{k=1}^5\sum _{N_k}{\lambda }^{\frac{1}{2}}\left(N_k\right)=V\left\{2\int \frac{d\overrightarrow{p}}{{\left(2\pi \right)}^3}\sqrt{{\overrightarrow{p}}^2}\right.\\ \hfill +\frac{gH}{4{\pi }^2}{\int }_{-\infty }^{+\infty }d{p}_3\left[\sum _{n=0}^{\infty }\sqrt{p_3^2+gH(2n+1)}+\sum _{n=1}^{\infty }\sqrt{p_3^2+gH(2n+1)}\right]\\ \hfill \left.+2\times \frac{gH}{8{\pi }^2}{\int }_{-\infty }^{+\infty }d{p}_3\left[\sum _{n=0}^{\infty }\sqrt{p_3^2+\frac{gH}{2}(2n+1)}+\sum _{n=1}^{\infty }\sqrt{p_3^2+\frac{gH}{2}(2n+1)}\right]\right\}.\end{array}$$

(41)

As concerns the unstable mode sector, since the eigenvalues $\lambda \left(N_u\right)$, $\lambda \left(N_v\right)$ and $\lambda \left(N_w\right)$ are not positive definite, the analogous expressions of Equations (39) and (40) for the wavefunctional ${\mathcal{Z}}_0\left({\eta }_u\right)$ would lead to an non-physical ground-state wavefunctional. At this point, it is necessary to mention that, at variance with the SU(2) gauge theory where one deals with only the Nielsen–Olesen unstable modes, in the SU(3) gauge theory, we exposed for the first time the presence of three different kinds of instabilities. Curiously enough, such a circumstance was never mentioned in the literature. On the contrary, it is widely believed that the unique instabilities in both the SU(2) and SU(3) gauge theories are due to the Nielsen–Olesen unstable modes. In any case, the origin of the instability is due to the fact that our u-, v- and w-modes behave like charged scalar fields with negative squared masses. In I, this led us to assume that the unstable modes were naturally driven to a dynamical Bose–Einstein condensation very similar to the Higgs mechanism where the condensation is stabilized by the short-range repulsive interaction due to the positive quartic self-coupling. However, as discussed at length in I, one must take care of the gauge invariance assured by the Gauss constraints to obtain physically meaningful results. For completeness, we briefly recap the strategy we followed in I. Firstly, one must set up a physical basis and, after that, define a perturbative strategy. To overcome the instabilities, we must modify the wavefunctional ${\mathcal{Z}}_0\left({\eta }_u\right)$ in Equation (35) by assuming that:

$${\mathcal{Z}}_0\left[{\eta }_u\right]=exp\left\{-\frac{1}{4}\int d\overrightarrow{x}d\overrightarrow{y}{\eta }_{ui}^a\left(\overrightarrow{x}\right){\left(G_u\right)}_{ij}^{ab}(\overrightarrow{x},\overrightarrow{y}){\eta }_{uj}^b\left(\overrightarrow{y}\right)\right\},$$

(42)

with

$${\left(G_u\right)}_{ij}^{ab}(\overrightarrow{x},\overrightarrow{y})=\sum _{\beta =u,v,w}\sum _{N_{\beta }}2\rho \left(N_{\beta }\right){\varphi }_i^{a*}(N_{\beta };\overrightarrow{x}){\varphi }_j^b(N_{\beta };\overrightarrow{y}),$$

(43)

where $\rho \left(N_{\beta }\right)$ are variational parameters. Note that the resulting wavefunctional ${\mathcal{W}}_0\left[\eta \right]$ satisfies:

$$D_i^{ab}\left(\overrightarrow{x}\right)\frac{\delta {\mathcal{W}}_0\left[\eta \right]}{\delta {\eta }_i^b\left(\overrightarrow{x}\right)}=0.$$

(44)

Starting from ${\mathcal{W}}_0\left[\eta \right]$, one can obtain a basis $\left\{{\mathcal{W}}_n\left[\eta \right]\right\}$ of the wavefunctional satisfying the Gauss constraints, Equation (44), by acting on ${\mathcal{W}}_0\left[\eta \right]$ with a suitable creation operator as defined in I, Appendix B. Starting from the orthogonal basis $\left\{{\mathcal{W}}_n\left[\eta \right]\right\}$, we can set up a physical basis 1:

$${\mathcal{G}}_n\left[\eta \right]={\mathcal{W}}_n\left[\eta \right]exp\left\{{\Gamma }_n\left[\eta \right]\right\}$$

(45)

satisfying the Gauss law:

$$\left[D_i^{ab}\left(\overrightarrow{x}\right)+g{f}^{acb}{\eta }_i^c\left(\overrightarrow{x}\right)\right]\frac{\delta }{\delta {\eta }_i^b\left(\overrightarrow{x}\right)}{\mathcal{G}}_n\left[\eta \right]=0.$$

(46)

In the spirit of considering perturbatively the quantum fluctuations over the background field, one can solve Equation (46) by writing:

$${\Gamma }_n\left[\eta \right]=g{\Gamma }_n^{\left(1\right)}\left[\eta \right]+g^2{\Gamma }_n^{\left(2\right)}\left[\eta \right]+...$$

(47)

Indeed, as shown in I, after inserting Equations (45) and (47) into Equation (46), one can iteratively determine the functional ${\Gamma }_n^{\left(1\right)}\left[\eta \right],{\Gamma }_n^{\left(2\right)}\left[\eta \right],...$. Subsequently, we can implement a perturbative expansion for the ground-state energy by means of the well-known Brueckner–Goldstone formula (see, e.g., Ref. [57]):

$$E=<{\mathcal{G}}_0\left|\mathcal{H}\right|{\mathcal{G}}_0>+<{\mathcal{G}}_0\left|{\mathcal{H}}_I\sum _{k\ge 0}{\left[\frac{{\mathcal{H}}_I}{<{\mathcal{G}}_0\left|\mathcal{H}\right|{\mathcal{G}}_0>-{\mathcal{H}}_0}\right]}^k\right|{\mathcal{G}}_0{>}_{connected}$$

(48)

where:

$${\left({\mathcal{H}}_0\right)}_{nm}=<{\mathcal{G}}_n\left|\mathcal{H}\right|{\mathcal{G}}_n>{\delta }_{nm},$$

(49)

$${\left({\mathcal{H}}_I\right)}_{nm}=<{\mathcal{G}}_n\left|\mathcal{H}\right|{\mathcal{G}}_m>(1-{\delta }_{nm}).$$

(50)

In other words, the unperturbed Hamiltonian is given by the diagonal expectation values of the full Hamiltonian $\mathcal{H}$, while the perturbations are the off-diagonal elements of $\mathcal{H}$. If the ground-state wavefunctional ${\mathcal{G}}_0\left[\eta \right]$ turns out to be close to the true ground-state wavefunctional, then we have that ${\mathcal{H}}_I$ is a genuine small perturbation.

Since we shall work up to the second perturbative order, Equation (48) reduces to:

$$E=<{\mathcal{G}}_0\left|\mathcal{H}\right|{\mathcal{G}}_0>+\sum _{n>0}\frac{1}{{\left(\mathcal{H}\right)}_{00}-{\left(\mathcal{H}\right)}_{nn}}{\left|<{\mathcal{G}}_n\left|\mathcal{H}\right|{\mathcal{G}}_0>\right|}^2.$$

(51)

One further problem arises from the circumstance that the physical basis $\left\{{\mathcal{G}}_n\left[\eta \right]\right\}$ is not orthogonal. Actually, one can transform the basis $\left\{{\mathcal{G}}_n\left[\eta \right]\right\}$ into an orthogonal basis through the Löwdin’s transformation [58] (see I for further details). Our aim is to evaluate the ground-state energy in the lowest order, i.e., in the one-loop approximation. However, we already remarked that the dynamical condensation of the tachyonic modes forced us to consider the quartic self-coupling Hamiltonian ${\mathcal{H}}^{\left(4\right)}$ that is of order $g^2$ corresponding to a two-loop contribution to the ground-state energy. As a consequence, to respect the gauge symmetry, we must extend the calculation of the ground-state energy up to the second order in our perturbative scheme with a variational physical basis so that our strategy is to evaluate the ground-state energy by means of Equation (51) and, after the stabilization of the tachyonic modes, we will retain only the lowest-order terms.

3. The Variational Minimization of the Vacuum Energy

The central issue of this section is the calculation of the ground-state energy after the stabilization of the tachyonic modes. In I, we showed that the Nielsen–Olesen modes were stabilized by the dynamical Bose–Einstein condensation leading to a peculiar non-perturbative background field ${\overrightarrow{u}}^a\left(\overrightarrow{x}\right)$. In the present case, we expect that the condensation of three different kinds of tachyonic modes will induce three non-perturbative background fields ${\overrightarrow{u}}^a\left(\overrightarrow{x}\right),a=1,2$, ${\overrightarrow{v}}^a\left(\overrightarrow{x}\right),a=4,5$ and ${\overrightarrow{w}}^a\left(\overrightarrow{x}\right),a=6,7$. It is convenient to introduce the SU(3) non-perturbative background field vector:

$$\overrightarrow{U}\left(\overrightarrow{x}\right)=\left\{\begin{array}{cc}{\overrightarrow{u}}^a\left(\overrightarrow{x}\right)\hfill & a=1,2\hfill \\ {\overrightarrow{v}}^a\left(\overrightarrow{x}\right)\hfill & a=4,5\hfill \\ {\overrightarrow{w}}^a\left(\overrightarrow{x}\right)\hfill & a=6,7\hfill \\ 0\hfill & a=3,8\hfill \end{array}\right..$$

(52)

We may also introduce the $8\times 8$ block-diagonal SU(3) matrix:

$$G_{Uij}(\overrightarrow{x},\overrightarrow{y})=\left(\begin{array}{ccccc}{G}_{u,ij}^{ab}(\overrightarrow{x},\overrightarrow{y})& & & & \\ & 0& & & \\ & & G_{v,ij}^{cd}(\overrightarrow{x},\overrightarrow{y})& & \\ & & & G_{w,ij}^{ef}(\overrightarrow{x},\overrightarrow{y})& \\ & & & & 0\end{array}\right)$$

(53)

with

$$G_{u,ij}^{ab}(\overrightarrow{x},\overrightarrow{y})=\sum _{p_2,p_3}2{\rho }_u(p_2,p_3){\varphi }_{ui}^{a*}\left(\overrightarrow{x}\right){\varphi }_{uj}^b\left(\overrightarrow{y}\right),a,b=1,2$$

(54)

$$G_{v,ij}^{cd}(\overrightarrow{x},\overrightarrow{y})=\sum _{p_2,p_3}2{\rho }_v(p_2,p_3){\varphi }_{vi}^{c*}\left(\overrightarrow{x}\right){\varphi }_{vj}^d\left(\overrightarrow{y}\right),c,d=4,5$$

(55)

$$G_{w,ij}^{ef}(\overrightarrow{x},\overrightarrow{y})=\sum _{p_2,p_3}2{\rho }_w(p_2,p_3){\varphi }_{wi}^{e*}\left(\overrightarrow{x}\right){\varphi }_{wj}^f\left(\overrightarrow{y}\right),e,f=6,7$$

(56)

where we have explicated the indices $N_u,N_v$ and $N_w$ and the unstable-mode eigenvectors. We may also introduce the fluctuating SU(3) vector:

$${\overrightarrow{\eta }}_U\left(\overrightarrow{x}\right)=\left\{\begin{array}{cc}{\overrightarrow{\eta }}_u^a\left(\overrightarrow{x}\right)\hfill & a=1,2\hfill \\ {\overrightarrow{\eta }}_v^a\left(\overrightarrow{x}\right)\hfill & a=4,5\hfill \\ {\overrightarrow{\eta }}_w^a\left(\overrightarrow{x}\right)\hfill & a=6,7\hfill \\ 0\hfill & a=3,8\hfill \end{array}\right.$$

(57)

where

$$\begin{array}{c}\hfill {\overrightarrow{\eta }}_u^a\left(\overrightarrow{x}\right)=\sum _{p_2,p_3}{c}_u(p_2,p_3){\overrightarrow{\varphi }}_u^a\left(\overrightarrow{x}\right).\\ \hfill {\overrightarrow{\eta }}_v^a\left(\overrightarrow{x}\right)=\sum _{p_2,p_3}{c}_v(p_2,p_3){\overrightarrow{\varphi }}_v^a\left(\overrightarrow{x}\right).\\ \hfill {\overrightarrow{\eta }}_w^a\left(\overrightarrow{x}\right)=\sum _{p_2,p_3}{c}_w(p_2,p_3){\overrightarrow{\varphi }}_w^a\left(\overrightarrow{x}\right).\end{array}$$

(58)

Now, following I, we replace the wavefunctional ${\mathcal{Z}}_0$, Equation (42), with:

$${\mathcal{Z}}_0\left[{\eta }_U\right]=exp\left\{-\frac{1}{4}\int d\overrightarrow{x}d\overrightarrow{y}\left[{\eta }_{Ui}^a\left(\overrightarrow{x}\right)-U_i^a\left(\overrightarrow{x}\right)\right]G_{Uij}^{ab}(\overrightarrow{x},\overrightarrow{y})\left[{\eta }_{Uj}^b\left(\overrightarrow{y}\right)-U_j^b\left(\overrightarrow{y}\right)\right]\right\}.$$

(59)

The main advantage of using this compact notation is that we can follow step by step the calculations presented in I for the SU(2) gauge theory. The resulting calculations are rather involved and quite difficult to follow in detail; nevertheless, they can be borrowed quite easily from I after replacing the SU(2) structure constants ${ϵ}^{abc}$ with the SU(3) structure constants $f^{abc}$. As a consequence, one finds that, in order to determine configurations that are able to stabilize the tachyonic modes, it is enough to evaluate only the energy of the unstable sector so that we have for the ground-state energy:

$$E=V\frac{H^2}{2}+E_S+E_U,$$

(60)

where the first term in the right hand site is the classical energy, the second the one-loop contributions due to the stable modes given by Equation (41), and finally:

$$E_U=\frac{1}{8}\int d\overrightarrow{x}{G}_{Uii}^{aa}(\overrightarrow{x},\overrightarrow{x})+\frac{1}{2}\int d\overrightarrow{x}{\mathcal{O}}_{ij}^{ab}\left(\overrightarrow{x}\right)\left[G_{Uij}^{-1ab}(\overrightarrow{x},\overrightarrow{x})+U_i^a\left(\overrightarrow{x}\right)U_j^b\left(\overrightarrow{x}\right)\right]+E_U^{\left(4\right)}$$

(61)

with

$$\begin{array}{l}{E}_U^{\left(4\right)}=\frac{g^2}{8}{ϵ}_{ijk}{ϵ}_{i{j}^{\prime }{k}^{\prime }}{f}^{abc}{f}^{a{b}^{\prime }{c}^{\prime }}\int d\overrightarrow{x}\{U_j^b\left(\overrightarrow{x}\right)U_k^c\left(\overrightarrow{x}\right)U_{j^{\prime }}^{b^{\prime }}\left(\overrightarrow{x}\right)U_{k^{\prime }}^{c^{\prime }}\left(\overrightarrow{x}\right)+\hfill \\ [G_{Uj{j}^{\prime }}^{-1b{b}^{\prime }}(\overrightarrow{x},\overrightarrow{x})U_k^c\left(\overrightarrow{x}\right)U_{k^{\prime }}^{c^{\prime }}\left(\overrightarrow{x}\right)+G_{Uj{k}^{\prime }}^{-1b{c}^{\prime }}(\overrightarrow{x},\overrightarrow{x})U_k^c\left(\overrightarrow{x}\right)U_{j^{\prime }}^{b^{\prime }}\left(\overrightarrow{x}\right)+G_{Uk{j}^{\prime }}^{-1c{b}^{\prime }}(\overrightarrow{x},\overrightarrow{x})U_j^b\left(\overrightarrow{x}\right)U_{k^{\prime }}^{c^{\prime }}\left(\overrightarrow{x}\right)\hfill \\ +permutations\left]\right\}.\hfill \end{array}$$

(62)

From these equations, we see that the ground-state energy is a functional of ${\rho }_u(p_2,p_3)$, ${\rho }_v(p_2,p_3)$, ${\rho }_u(p_2,p_3)$ and ${\overrightarrow{u}}^a\left(\overrightarrow{x}\right)$, ${\overrightarrow{v}}^a\left(\overrightarrow{x}\right)$, ${\overrightarrow{w}}^a\left(\overrightarrow{x}\right)$. Our variational procedure leads us to minimize the vacuum energy with respect to the variational parameters. To this end, we note that:

$${\overrightarrow{u}}^a\left(\overrightarrow{x}\right)=\sum _{p_2,p_3}{b}_u(p_2,p_3){\overrightarrow{\varphi }}_u^a\left(\overrightarrow{x}\right).$$

(63)

As in I, we may assume that in Equation (63), $b_u(p_2,p_3)$ factorizes. As a consequence, we obtain:

$$\begin{array}{c}\hfill u_k^{\pm }\left(\overrightarrow{x}\right)=\frac{1}{\sqrt{2}}\left(u_k^1\left(\overrightarrow{x}\right)\pm i{u}_k^2\left(\overrightarrow{x}\right)\right)\\ \hfill u_k^{\pm }\left(\overrightarrow{x}\right)=\frac{f_u\left(x_3\right)}{\sqrt{2}}\left(\begin{array}{c}1\\ \mp i\\ 0\end{array}\right)g_{\pm }^u(x_1,x_2)\end{array}$$

(64)

where $f_u\left(x_3\right)$ is a real function and:

$$\begin{array}{c}\hfill g_{+}^u(x_1,x_2)={\int }_{-\infty }^{+\infty }d{p}_2{b}_u\left(p_2\right)\frac{exp\left(i{p}_2{x}_2\right)}{\sqrt{2\pi }}{\left(\frac{gH}{\pi }\right)}^{\frac{1}{4}}exp[-\frac{gH}{2}{(x_1+\frac{p_2}{gH})}^2],\\ \hfill g_{-}^u(x_1,x_2)={\left[g_{+}^u(x_1,x_2)\right]}^{*}.\end{array}$$

(65)

Likewise, we obtain:

$$\begin{array}{c}\hfill v_k^{\pm }\left(\overrightarrow{x}\right)=\frac{1}{\sqrt{2}}\left(v_k^4\left(\overrightarrow{x}\right)\pm i{v}_k^5\left(\overrightarrow{x}\right)\right)\\ \hfill v_k^{\pm }\left(\overrightarrow{x}\right)=\frac{f_v\left(x_3\right)}{\sqrt{2}}\left(\begin{array}{c}1\\ \mp i\\ 0\end{array}\right)g_{\pm }^v(x_1,x_2),\end{array}$$

(66)

and

$$\begin{array}{c}\hfill g_{+}^v(x_1,x_2)={\int }_{-\infty }^{+\infty }d{p}_2{b}_v\left(p_2\right)\frac{exp\left(i{p}_2{x}_2\right)}{\sqrt{2\pi }}{\left(\frac{gH}{2\pi }\right)}^{\frac{1}{4}}exp[-\frac{gH}{4}{(x_1+\frac{p_2}{\frac{gH}{2}})}^2],\\ \hfill g_{-}^v(x_1,x_2)={\left[g_{+}^v(x_1,x_2)\right]}^{*}.\end{array}$$

(67)

Finally:

$$\begin{array}{c}\hfill w_k^{\pm }\left(\overrightarrow{x}\right)=\frac{1}{\sqrt{2}}\left(w_k^6\left(\overrightarrow{x}\right)\pm i{w}_k^7\left(\overrightarrow{x}\right)\right)\\ \hfill w_k^{\pm }\left(\overrightarrow{x}\right)=\frac{f_w\left(x_3\right)}{\sqrt{2}}\left(\begin{array}{c}1\\ \mp i\\ 0\end{array}\right)g_{\pm }^w(x_1,x_2),\end{array}$$

(68)

and

$$\begin{array}{c}\hfill g_{+}^w(x_1,x_2)={\int }_{-\infty }^{+\infty }d{p}_2{b}_w\left(p_2\right)\frac{exp\left(i{p}_2{x}_2\right)}{\sqrt{2\pi }}{\left(\frac{gH}{2\pi }\right)}^{\frac{1}{4}}exp[-\frac{gH}{4}{(x_1-\frac{p_2}{\frac{gH}{2}})}^2],\\ \hfill g_{-}^w(x_1,x_2)={\left[g_{+}^w(x_1,x_2)\right]}^{*}.\end{array}$$

(69)

One can easily check that a necessary condition for our trial configurations that could contribute to the ground-state energy density is:

$$\beta =u,v,w{\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_{1}d{x}_2{g}_{+}^{\beta }(x_1,x_2)g_{-}^{\beta }(x_1,x_2)\sim L^2$$

(70)

where $V=L^3$. Moreover, the minimum of the ground-state energy is attained for $|g_{+}^{\beta }(x_1,x_2)|=constant$ that leads to:

$$b_{\beta }\left(p_2\right)={\kappa }_{\beta }exp\left(iL{p}_2\right),\beta =u,v,w$$

(71)

for some real constants ${\kappa }_{\beta }$. Starting from Equations (61) and (62), after using Equations (64)–(69) and with some algebra, we obtain:

$$E_U=E_U^{\left(u\right)}+E_U^{\left(v\right)}+E_U^{\left(w\right)}$$

(72)

with:

$$\begin{array}{c}\hfill E_U^{\left(u\right)}=\frac{1}{2}V\frac{gH}{4{\pi }^2}{\int }_{-\infty }^{+\infty }d{p}_3\left[{\rho }_u\left(p_3\right)+\frac{p_3^2-gH}{{\rho }_u\left(p_3\right)}\right]+I_2^u{\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_3{f}_u\left(x_3\right)[-{\partial }_3^2-gH]f_u\left(x_3\right)\\ \hfill +g^2\frac{gH}{4{\pi }^2}{\int }_{-\infty }^{+\infty }d{p}_3\frac{1}{{\rho }_u\left(p_3\right)}{I}_2^u{\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_3{f}_u^2\left(x_3\right)+\frac{g^2}{2}{I}_4^u{\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_3{f}_u^4\left(x_3\right),\end{array}$$

(73)

$$\begin{array}{c}\hfill E_U^{\left(v\right)}=\frac{1}{2}V\frac{gH}{8{\pi }^2}{\int }_{-\infty }^{+\infty }d{p}_3\left[{\rho }_u\left(p_3\right)+\frac{p_3^2-\frac{gH}{2}}{{\rho }_u\left(p_3\right)}\right]+I_2^v{\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_3{f}_v\left(x_3\right)[-{\partial }_3^2-\frac{gH}{2}]f_v\left(x_3\right)\\ \hfill +g^2\frac{gH}{8{\pi }^2}{\int }_{-\infty }^{+\infty }d{p}_3\frac{1}{{\rho }_v\left(p_3\right)}{I}_2^v{\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_3{f}_v^2\left(x_3\right)+\frac{g^2}{2}{I}_4^v{\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_3{f}_v^4\left(x_3\right),\end{array}$$

(74)

$$\begin{array}{c}\hfill E_U^{\left(w\right)}=\frac{1}{2}V\frac{gH}{8{\pi }^2}{\int }_{-\infty }^{+\infty }d{p}_3\left[{\rho }_u\left(p_3\right)+\frac{p_3^2-\frac{gH}{2}}{{\rho }_w\left(p_3\right)}\right]+I_2^w{\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_3{f}_w\left(x_3\right)[-{\partial }_3^2-\frac{gH}{2}]f_w\left(x_3\right)\\ \hfill +g^2\frac{gH}{8{\pi }^2}{\int }_{-\infty }^{+\infty }d{p}_3\frac{1}{{\rho }_w\left(p_3\right)}{I}_2^w{\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_3{f}_w^2\left(x_3\right)+\frac{g^2}{2}{I}_4^w{\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_3{f}_w^4\left(x_3\right).\end{array}$$

(75)

In the previous equations, we have used the notations:

$$\beta =u,v,w{I}_2^{\beta }={\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_{1}d{x}_2{g}_{+}^{\beta }(x_1,x_2)g_{-}^{\beta }(x_1,x_2)$$

(76)

$$\beta =u,v,w{I}_4^{\beta }={\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_{1}d{x}_2{\left[g_{+}^{\beta }(x_1,x_2)g_{-}^{\beta }(x_1,x_2)\right]}^2.$$

(77)

Varying the vacuum energy functional with respect to $f_{\beta }\left(x_3\right)$ leads to the well-known kink equations [59,60,61,62]:

$$I_2^u\left[-{\partial }_3^2-gH\right]f_u\left(x_3\right)+g^2{I}_4^u{f}_u^3\left(x_3\right)=0$$

(78)

$$I_2^v\left[-{\partial }_3^2-\frac{gH}{2}\right]f_v\left(x_3\right)+g^2{I}_4^v{f}_v^3\left(x_3\right)=0$$

(79)

$$I_2^w\left[-{\partial }_3^2-\frac{gH}{2}\right]f_w\left(x_3\right)+g^2{I}_4^v{f}_w^3\left(x_3\right)=0.$$

(80)

Solving these last equations, we obtain:

$$f_u\left(x_3\right)=\sqrt{\frac{gH}{g^2}}\sqrt{\frac{I_2^u}{I_4^u}}tanh\left[\sqrt{\frac{gH}{2}}(x_3-{\overline{x}}_3)\right],$$

(81)

$$f_v\left(x_3\right)=\sqrt{\frac{gH}{2g^2}}\sqrt{\frac{I_2^v}{I_4^v}}tanh\left[\sqrt{\frac{gH}{4}}(x_3-{\overline{x}}_3)\right],$$

(82)

$$f_w\left(x_3\right)=\sqrt{\frac{gH}{2g^2}}\sqrt{\frac{I_2^w}{I_4^w}}tanh\left[\sqrt{\frac{gH}{4}}(x_3-{\overline{x}}_3)\right].$$

(83)

After that, using:

$$\beta =u,v,wL\frac{{\left(I_2^{\beta }\right)}^2}{I_4^{\beta }}=V,$$

(84)

we obtain:

$$\begin{array}{c}\hfill E_U=-V\frac{H^2}{2}+\frac{1}{2}V\frac{gH}{4{\pi }^2}{\int }_{-\infty }^{+\infty }d{p}_3\left[{\rho }_u\left(p_3\right)+\frac{p_3^2+gH}{{\rho }_u\left(p_3\right)}\right]\\ \hfill -V\frac{H^2}{8}+\frac{1}{2}V\frac{gH}{8{\pi }^2}{\int }_{-\infty }^{+\infty }d{p}_3\left[{\rho }_v\left(p_3\right)+\frac{p_3^2+\frac{gH}{2}}{{\rho }_v\left(p_3\right)}\right]\\ \hfill -V\frac{H^2}{8}+\frac{1}{2}V\frac{gH}{8{\pi }^2}{\int }_{-\infty }^{+\infty }d{p}_3\left[{\rho }_w\left(p_3\right)+\frac{p_3^2+\frac{gH}{2}}{{\rho }_w\left(p_3\right)}\right].\end{array}$$

(85)

Varying with respect to ${\rho }_{\beta }\left(p_3\right)$, we finally obtain:

$${\rho }_u\left(p_3\right)=+\sqrt{p_3^2+gH},{\rho }_v\left(p_3\right)={\rho }_w\left(p_3\right)=+\sqrt{p_3^2+\frac{gH}{2}}$$

(86)

leading to:

$$\begin{array}{c}\hfill E_U=V\{-\frac{H^2}{2}+\frac{gH}{4{\pi }^2}{\int }_{-\infty }^{+\infty }d{p}_3\sqrt{p_3^2+gH}\\ \hfill +2\times \left[-\frac{H^2}{8}+\frac{gH}{8{\pi }^2}{\int }_{-\infty }^{+\infty }d{p}_3\sqrt{p_3^2+\frac{gH}{2}}\right]\}.\end{array}$$

(87)

A few comments are in order. Firstly, Equations (81)–(83) manifest the non-analytic nature of the chromomagnetic kinks. The origin of this non-analyticity can be understood if we look at the chromomagnetic field:

$$B_i^a\left(\overrightarrow{x}\right)=\frac{1}{2}{ϵ}_{ijk}\left[{\partial }_j{A}_k^a\left(\overrightarrow{x}\right)-{\partial }_k{A}_j^a\left(\overrightarrow{x}\right)+g{f}^{abc}{A}_j^b\left(\overrightarrow{x}\right)A_k^c\left(\overrightarrow{x}\right)\right].$$

(88)

The point is that the dynamical condensation of the tachyonic modes tries to screen as much as possible the constant Abelian background field H in such a way as to eliminate the instabilities. Now, a uniform classical chromomagnetic field can be realized by the Abelian term in Equation (88) or by the non-Abelian piece if $A_i^a\sim \frac{1}{\sqrt{g}}$. Indeed, in the next section, we will show that our chromomagnetic kink solutions lead to an almost complete cancellation of the external chromomagnetic field $H{\delta }^{a3}$. On the other hand, the tachyonic modes are frozen into the lowest Landau levels. As a consequence, these modes behave like (1+1)-dimensional charged scalar fields with negative mass squared and stabilizing short-range interactions. This leads to the dynamical Bose–Einstein condensations with negative condensation energy that look like a classical energy term as explicitly displayed by Equation (87).

Let us now evaluate the ground-state energy, Equation (60), with $E_S$ given by Equation (41) and $E_U$ by Equation (87). Following I, where in Sect. VI the relevant calculations are presented in detail, after subtracting the ground-state energy of the perturbative vacuum, we obtain:

$$\Delta E\left(gH\right)=V\left\{-\frac{H^2}{4}+\frac{{\left(gH\right)}^2}{32{\pi }^2}\left[ln\left(\frac{{\Lambda }^2}{gH}\right)+const\right]\right\}$$

(89)

where $\Lambda$ is an ultraviolet cutoff and the actual value of the constant does not matter. Note that the presence of only logarithmic divergences corroborates the gauge invariance of our calculations. However, as noticed by R. P. Feynman [63], the logarithmic divergences in the ground-state energy are an inevitable consequence of the sensitivity of the variational procedure to the high frequencies. The fact that the coefficient of the logarithmic divergent term is positive strongly suggests that the stabilized ground state is not energetically favored with respect to the perturbative ground state. To better appreciate this last point, let us introduce a very high-energy scale ${\Lambda }_H$ defined by:

$$\Delta E(gH={\Lambda }_H^2)=0.$$

(90)

Combining Equation (90) with Equation (89), we have:

$$\Delta \epsilon \left(gH\right)=\frac{\Delta E\left(gH\right)}{V}=\frac{{\left(gH\right)}^2}{16{\pi }^2}ln\left(\frac{{\Lambda }_H}{\sqrt{gH}}\right),\sqrt{gH}<{\Lambda }_H.$$

(91)

The physical meaning of the high-energy scale ${\Lambda }_H$ is that our variational ground-state wavefunctional is degenerate with the perturbative vacuum at a very high scale. On the other hand, for large distances $d\gg \frac{1}{{\Lambda }_H}$, the perturbative vacuum should be replaced by our variational vacuum wavefunctional. In this way, our proposal for the QCD vacuum wavefunctional realizes at very short distances the Bjorken’s femptouniverse picture [64], while at larger distances, the perturbative vacuum should be replaced by our stabilized ground-state wavefunctional. However, there are obvious problems related to the fact that our variational wavefunctional, according to Equation (91), is not favored energetically nor does it seem to have the needed ingredients to explain the observed color and quark confinement phenomena. Anyway, these last points will be further discussed more carefully in a later section.

4. Vacuum Chromodynamics

In the previous section, we have implemented the variational procedure to overcome the one-loop instabilities. As a result, we have constructed the ground state wavefunctional that in the lowest-order approximation can be written as:

$${\mathcal{G}}_0\left[A\right]=\mathcal{N}exp\{-\frac{1}{4}\int d\overrightarrow{x}d\overrightarrow{y}[A_i^a\left(\overrightarrow{x}\right)-{\overline{A}}_i^a\left(\overrightarrow{x}\right)-U_i^a\left(\overrightarrow{x}\right)]G_{ij}^{ab}(\overrightarrow{x},\overrightarrow{y})[A_i^a\left(\overrightarrow{y}\right)-{\overline{A}}_i^a\left(\overrightarrow{y}\right)-U_i^a\left(\overrightarrow{y}\right)]\}.$$

(92)

where:

$$G_{ij}^{ab}(\overrightarrow{x},\overrightarrow{y})=\sum _{k=1}^5\sum _{N_k}2{\lambda }^{\frac{1}{2}}\left(N_k\right){\varphi }_i^{a*}(N_k;\overrightarrow{x}){\varphi }_j^b(N_k;\overrightarrow{y})+\sum _{\beta =u,v,w}\sum _{p_2,p_3}2{\rho }_{\beta }(p_2,p_3){\varphi }_{\beta i}^{a*}\left(\overrightarrow{x}\right){\varphi }_{\beta j}^b\left(\overrightarrow{y}\right)$$

(93)

with ${\rho }_{\beta }(p_2,p_3)$ given by Equation (86). In these approximations the scalar product of physical states is simply:

$$<{\mathcal{G}}_0|{\mathcal{G}}_0>=\int \mathcal{D}A{\mathcal{G}}_0^{*}\left[A\right]{\mathcal{G}}_0\left[A\right]\delta \left[D_i^{ab}\left(\overrightarrow{x}\right){\eta }_i^b\left(\overrightarrow{x}\right)\right]$$

(94)

where the Faddeev–Popov determinant has been englobed in the normalization constant. Presently, we are interested in evaluating the expectation value of the field strength tensor $F_{\mu \nu }^a\left(x\right)$ on the ground-state wavefunctional, Equation (92). Evidently, we have:

$$<{\mathcal{G}}_0|E_i^a\left(\overrightarrow{x}\right)|{\mathcal{G}}_0>=<{\mathcal{G}}_0\left|i\frac{\delta }{\delta A_i^a\left(\overrightarrow{x}\right)}\right|{\mathcal{G}}_0>=0.$$

(95)

On the other hand, it is easy to see that the chromomagnetic fields:

$$B_i^a\left(\overrightarrow{x}\right)=<{\mathcal{G}}_0\left|\frac{1}{2}{ϵ}_{ijk}[{\partial }_j{A}_k^a\left(\overrightarrow{x}\right)-{\partial }_k{A}_j^a\left(\overrightarrow{x}\right)+g{f}^{abc}{A}_j^b\left(\overrightarrow{x}\right)A_k^c\left(\overrightarrow{x}\right)]\right|{\mathcal{G}}_0>$$

(96)

have a non-zero expectation value. In fact, one obtains:

$$B_i^a\left(\overrightarrow{x}\right)=\frac{1}{2}{ϵ}_{ijk}\left\{{\partial }_j[{\overline{A}}_k^a\left(\overrightarrow{x}\right)+U_k^a\left(\overrightarrow{x}\right)]-{\partial }_k[{\overline{A}}_j^a\left(\overrightarrow{x}\right)+U_j^a\left(\overrightarrow{x}\right)]+g{f}^{abc}[{\overline{A}}_k^a\left(\overrightarrow{x}\right)+U_k^a\left(\overrightarrow{x}\right)][{\overline{A}}_k^a\left(\overrightarrow{x}\right)+U_k^a\left(\overrightarrow{x}\right)]\right\}.$$

(97)

Before addressing the concrete calculations of the ground-state chromomagnetic field, we need to better characterize the peculiar structure of the background fields generated by the dynamical condensation of the tachyonic modes. As we have shown before, the background field ${\overrightarrow{U}}^a\left(\overrightarrow{x}\right)$ is composed of three background fields ${\overrightarrow{u}}^a\left(\overrightarrow{x}\right)$, ${\overrightarrow{v}}^a\left(\overrightarrow{x}\right)$ and ${\overrightarrow{w}}^a\left(\overrightarrow{x}\right)$ corresponding to the condensation of the three different unstable modes, respectively. Since the structure of these last background fields is quite similar, for definitiveness, we shall focus on ${\overrightarrow{u}}^a\left(\overrightarrow{x}\right)$. According to the previous section, we need to consider only the background field ${\overrightarrow{u}}^{+}\left(\overrightarrow{x}\right)$, Equation (64):

$$u_k^{+}\left(\overrightarrow{x}\right)=\frac{f_u\left(x_3\right)}{\sqrt{2}}\left(\begin{array}{c}1\\ -i\\ 0\end{array}\right)g_{+}^u(x_1,x_2)$$

(98)

with:

$$g_{+}^u(x_1,x_2)={\int }_{-\infty }^{+\infty }d{p}_2{b}_u\left(p_2\right)\frac{exp\left(i{p}_2{x}_2\right)}{\sqrt{2\pi }}{\left(\frac{gH}{\pi }\right)}^{\frac{1}{4}}exp[-\frac{gH}{2}{(x_1+\frac{p_2}{gH})}^2].$$

(99)

Now, taking into account Equation (71), we can write:

$$g_{+}^u(x_1,x_2)={\int }_{-\infty }^{+\infty }d{p}_2{\kappa }_{u}exp\left(iL{p}_2\right)\frac{exp\left(i{p}_2{x}_2\right)}{\sqrt{2\pi }}{\left(\frac{gH}{\pi }\right)}^{\frac{1}{4}}exp[-\frac{gH}{2}{(x_1+\frac{p_2}{gH})}^2].$$

(100)

Evidently, we have:

$$\begin{array}{c}\hfill g_{+}^u(x_1,x_2)g_{-}^u(x_1,x_2)={\int }_{-\infty }^{+\infty }d{p}_{2}d{p}_2^{\prime }{\kappa }_u^{2}exp\left[iL(p_2-p_2^{\prime })\right]\frac{exp\left[i(p_2-p_2^{\prime })x_2\right]}{2\pi }\\ \hfill {\left(\frac{gH}{\pi }\right)}^{\frac{1}{2}}exp[-\frac{gH}{2}{(x_1+\frac{p_2}{gH})}^2]exp[-\frac{gH}{2}{(x_1+\frac{p_2^{\prime }}{gH})}^2].\end{array}$$

(101)

The function within the integrals is absolutely summable, so that by the Riemann–Lebesgue lemma in the thermodynamical limit, $L\to \infty$ survives only the term with $p_2=p_2^{\prime }$ so that we are left with:

$$g_{+}^u(x_1,x_2)g_{-}^u(x_1,x_2)={\int }_{-\infty }^{+\infty }d{p}_2\frac{{\kappa }_u^2}{2\pi }{\left(\frac{gH}{\pi }\right)}^{\frac{1}{2}}exp[-gH{(x_1+\frac{p_2}{gH})}^2]={\kappa }_u^2\frac{gH}{2\pi }.$$

(102)

Since $g_{-}^u=g_{+}^u*$, we can write:

$$g_{\pm }^u(x_1,x_2)=\left|g_{+}^u(x_1,x_2)\right|exp[\pm i{\delta }^u(x_1,x_2)]={\kappa }_u\sqrt{\frac{gH}{2\pi }}exp[\pm i{\delta }^u(x_1,x_2)].$$

(103)

Moreover, the same arguments lead to the conclusion that in the thermodynamical limit, $g_{\pm }^u(x_1,x_2)\to 0$ so that we must admit that the phase ${\delta }^u(x_1,x_2)$ is rapidly varying so that $exp[\pm i{\delta }^u(x_1,x_2)]$ averages zero, while $|g_{+}^u(x_1,x_2)|$ stays finite. This last result is not so strange for, as we have repeatedly stressed, the induced background fields are generated by the dynamical condensation of the tachyonic modes by quantum fluctuations. Nevertheless, these evanescent background fields are able to give non-zero contributions to physical observables that are not sensitive to the quantum phases ${\delta }^u$, ${\delta }^v$ and ${\delta }^w$.

Let us, now, turn to the calculation of the chromomagnetic field, Equation (97). Evidently, we have:

$$B_i^3\left(\overrightarrow{x}\right)={ϵ}_{ijk}{\partial }_j{\overline{A}}_k^a\left(\overrightarrow{x}\right)+\frac{g}{2}{ϵ}_{ijk}{f}^{3bc}{U}_j^b\left(\overrightarrow{x}\right)U_k^c\left(\overrightarrow{x}\right),$$

(104)

or

$$\begin{array}{c}{B}_i^3\left(\overrightarrow{x}\right)={\delta }_{i3}H+\frac{g}{2}{ϵ}_{ijk}{f}^{312}[u_j^1\left(\overrightarrow{x}\right)u_k^2\left(\overrightarrow{x}\right)-u_j^2\left(\overrightarrow{x}\right)u_k^1\left(\overrightarrow{x}\right)]\hfill \\ +\frac{g}{2}{ϵ}_{ijk}{f}^{345}[v_j^4\left(\overrightarrow{x}\right)v_k^5\left(\overrightarrow{x}\right)-v_j^5\left(\overrightarrow{x}\right)v_k^4\left(\overrightarrow{x}\right)]+\frac{g}{2}{ϵ}_{ijk}{f}^{367}[w_j^6\left(\overrightarrow{x}\right)w_k^7\left(\overrightarrow{x}\right)-w_j^7\left(\overrightarrow{x}\right)w_k^6\left(\overrightarrow{x}\right)].\hfill \end{array}$$

(105)

Now, a straightforward calculation shows that:

$$\frac{g}{2}{ϵ}_{ijk}{f}^{312}[u_j^1\left(\overrightarrow{x}\right)u_k^2\left(\overrightarrow{x}\right)-u_j^2\left(\overrightarrow{x}\right)u_k^1\left(\overrightarrow{x}\right)]={\delta }_{i3}ig[u_1^{+}\left(\overrightarrow{x}\right)u_2^{-}\left(\overrightarrow{x}\right)-u_1^{-}\left(\overrightarrow{x}\right)u_2^{+}\left(\overrightarrow{x}\right)],$$

(106)

that leads to:

$$\frac{g}{2}{ϵ}_{ijk}{f}^{312}[u_j^1\left(\overrightarrow{x}\right)u_k^2\left(\overrightarrow{x}\right)-u_j^2\left(\overrightarrow{x}\right)u_k^1\left(\overrightarrow{x}\right)]=-{\delta }_{i3}g{f}_u^2\left(x_3\right)g_{+}^u(x_1,x_2)g_{-}^u(x_1,x_2).$$

(107)

Further, considering that $f^{345}=-f^{367}=\frac{1}{2}$, one can check that the contributions due to ${\overrightarrow{v}}^a\left(\overrightarrow{x}\right)$ and ${\overrightarrow{w}}^a\left(\overrightarrow{x}\right)$ cancel each other out so that we are left with:

$$B_i^3\left(\overrightarrow{x}\right)={\delta }_{i3}[H-g{f}_u^2\left(x_3\right)g_{+}^u(x_1,x_2)g_{-}^u(x_1,x_2)].$$

(108)

Finally, after using Equations (102) and (81), we obtain:

$$B_i^3\left(\overrightarrow{x}\right)={\delta }_{i3}H\left\{1-{tanh}^2\left[\sqrt{\frac{gH}{2}}(x_3-{\overline{x}}_3)\right]\right\}$$

(109)

or better:

$$B_i^3\left(\overrightarrow{x}\right)={\delta }_{i3}\frac{H}{{cosh}^2\left[\sqrt{\frac{gH}{2}}(x_3-{\overline{x}}_3)\right]}.$$

(110)

These last equations clearly show that the induced background field ${\overrightarrow{u}}^a\left(\overrightarrow{x}\right)$ screens almost completely the external Abelian chromomagnetic field $H{\delta }^{a3}$ such that the resulting vacuum chromomagnetic field is localized on the kink plane $x_3={\overline{x}}_3$. Interestingly enough, the screening of the external Abelian chromomagnetic field resembles closely what happens in type II superconductors where an external magnetic field is screened into narrow flux tubes by means of the creation of Abrikosov vortices.

With similar calculations, one can evaluate the other components of the chromomagnetic field. Here, we merely display the final results:

$$B_i^1\left(\overrightarrow{x}\right)=-{\delta }_{i3}\frac{H}{2}{tanh}^2\left[\sqrt{\frac{gH}{4}}(x_3-{\overline{x}}_3)\right]exp[-\frac{gH}{2}{x}_1^2],$$

(111)

$$B_i^2\left(\overrightarrow{x}\right)=0,$$

(112)

$$B_i^4\left(\overrightarrow{x}\right)={\delta }_{i3}\frac{H}{\sqrt{3}}tanh\left[\sqrt{\frac{gH}{2}}(x_3-{\overline{x}}_3)\right]tanh\left[\sqrt{\frac{gH}{4}}(x_3-{\overline{x}}_3)\right]exp[-\frac{3}{4}gH{x}_1^2],$$

(113)

$$B_i^5\left(\overrightarrow{x}\right)=0,$$

(114)

$$B_i^6\left(\overrightarrow{x}\right)={\delta }_{i3}\frac{H}{\sqrt{3}}tanh\left[\sqrt{\frac{gH}{2}}(x_3-{\overline{x}}_3)\right]tanh\left[\sqrt{\frac{gH}{4}}(x_3-{\overline{x}}_3)\right]exp[-\frac{gH}{2}{x}_1^2],$$

(115)

$$B_i^7\left(\overrightarrow{x}\right)=0,$$

(116)

$$B_i^8\left(\overrightarrow{x}\right)=-{\delta }_{i3}\frac{\sqrt{3}}{2}H{tanh}^2\left[\sqrt{\frac{gH}{4}}(x_3-{\overline{x}}_3)\right].$$

(117)

The last point we would like to discuss in the present section is that our stabilized ground-state wavefunctional implies the presence of chromomagnetic charges according to:

$$D_i^{ab}\left(\overrightarrow{x}\right)B_i^b\left(\overrightarrow{x}\right)={\rho }_M^a\left(\overrightarrow{x}\right).$$

(118)

Combining Equation (118) with Equations (110)–(117), we obtain:

$${\rho }_M^1\left(\overrightarrow{x}\right)=-H\frac{\sqrt{gH}}{2}\frac{tanh\left[\sqrt{\frac{gH}{4}}(x_3-{\overline{x}}_3)\right]}{{cosh}^2\left[\sqrt{\frac{gH}{4}}(x_3-{\overline{x}}_3)\right]}exp[-\frac{gH}{2}{x}_1^2],$$

(119)

$${\rho }_M^3\left(\overrightarrow{x}\right)=-\sqrt{2}H\sqrt{gH}\frac{tanh\left[\sqrt{\frac{gH}{2}}(x_3-{\overline{x}}_3)\right]}{{cosh}^2\left[\sqrt{\frac{gH}{2}}(x_3-{\overline{x}}_3)\right]},$$

(120)

$${\rho }_M^4\left(\overrightarrow{x}\right)=\frac{H}{\sqrt{3}}\frac{\sqrt{gH}}{2}\left\{\frac{tanh\left[\sqrt{\frac{gH}{4}}(x_3-{\overline{x}}_3)\right]}{{cosh}^2\left[\sqrt{\frac{gH}{2}}(x_3-{\overline{x}}_3)\right]}+\frac{tanh\left[\sqrt{\frac{gH}{2}}(x_3-{\overline{x}}_3)\right]}{{cosh}^2\left[\sqrt{\frac{gH}{4}}(x_3-{\overline{x}}_3)\right]}\right\}exp[-\frac{3gH}{4}{x}_1^2],$$

(121)

$${\rho }_M^6\left(\overrightarrow{x}\right)=\frac{H}{\sqrt{3}}\frac{\sqrt{gH}}{2}\left\{\sqrt{2}\frac{tanh\left[\sqrt{\frac{gH}{4}}(x_3-{\overline{x}}_3)\right]}{{cosh}^2\left[\sqrt{\frac{gH}{2}}(x_3-{\overline{x}}_3)\right]}+\frac{tanh\left[\sqrt{\frac{gH}{2}}(x_3-{\overline{x}}_3)\right]}{{cosh}^2\left[\sqrt{\frac{gH}{4}}(x_3-{\overline{x}}_3)\right]}\right\}exp[-\frac{gH}{2}{x}_1^2],$$

(122)

$${\rho }_M^8\left(\overrightarrow{x}\right)=-\frac{\sqrt{3}}{2}H\sqrt{gH}\frac{tanh\left[\sqrt{\frac{gH}{4}}(x_3-{\overline{x}}_3)\right]}{{cosh}^2\left[\sqrt{\frac{gH}{4}}(x_3-{\overline{x}}_3)\right]},$$

(123)

$${\rho }_M^2\left(\overrightarrow{x}\right)={\rho }_M^5\left(\overrightarrow{x}\right)={\rho }_M^7\left(\overrightarrow{x}\right)=0.$$

(124)

Later on, we shall see that these chromomagnetic charges will play a fundamental role in the formation of the chromoelectric flux tube generated by static color sources.

5. The QCD Vacuum Wavefunctional

In the previous sections, we have been able to implement the stabilization of the one-loop instabilities. Accordingly, we have seen that to the lowest order, the trial wavefunctional can be written as:

$${\mathcal{G}}_0\left[\tilde{\eta }\right]=\mathcal{N}exp\left[-\frac{1}{4}\int d\overrightarrow{x}d\overrightarrow{y}{\tilde{\eta }}_i^a\left(\overrightarrow{x}\right)G_{ij}^{ab}(\overrightarrow{x},\overrightarrow{y}){\tilde{\eta }}_j^b\left(\overrightarrow{y}\right)\right]$$

(125)

where:

$${\tilde{\eta }}_i^a\left(\overrightarrow{x}\right)=A_i^a\left(\overrightarrow{x}\right)-{\overline{A}}_i^a\left(\overrightarrow{x}\right)-U_i^a\left(\overrightarrow{x}\right)$$

(126)

and $G_{ij}^{ab}(\overrightarrow{x},\overrightarrow{y})$ given by Equation (93). Moreover, the scalar product between physical states reduces to:

$$<\mathcal{G}|\mathcal{F}>=\int \mathcal{D}\tilde{\eta }{\mathcal{G}}^{*}\left[\tilde{\eta }\right]\mathcal{F}\left[\tilde{\eta }\right]$$

(127)

where the functional integrations are restricted to transverse gauge field fluctuations and the harmless Faddeev–Popov determinant has been englobed in the normalization constant. Our aim is to set up a wavefunctional for the QCD vacuum. Evidently, the trail wavefunctional Equation (125) is not good enough. Firstly, we showed in the preceding section that the chromomagnetic fields have a non-zero value on this wavefunctional. More importantly, the vacuum energy associated to ${\mathcal{G}}_0$ is greater than the perturbative vacuum energy. Since the proposal is that the states with a constant chromomagnetic field could lower the vacuum energy [35,36,37], there is a widespread conviction in the literature that, even after stabilization of the tachyonic unstable modes, these states are energetically favored. On the contrary, we have shown that a full quantum-mechanical treatment of the tachyonic modes taking into account the severe constraints due to the gauge symmetry leads to a stabilized state that increases the vacuum energy for both SU(2) and SU(3) gauge theories.

Let us look closely at the structure of the induced background field $U_i^a\left(\overrightarrow{x}\right)$. The dynamical condensation of the unstable modes leads to the non-perturbative background fields $U_i^a\left(\overrightarrow{x}\right)$ characterized by the kink-profile functions $f_u\left(x_3\right)$, $f_v\left(x_3\right)$ and $f_w\left(x_3\right)$. These last functions vanish at the kink plane $x_3={\overline{x}}_3$. Evidently, for $x_3={\overline{x}}_3$, the background field is given by the Abelian background field:

$${\overline{A}}_i^a(x_1,x_2,{\overline{x}}_3)={\delta }^{a,3}{\delta }_{i,2}{x}_{1}H.$$

(128)

Therefore, on the kink plane, we are in the same situation as in the seminal Feynman’s paper on the qualitative behavior of Yang–Mills theory in (2+1)-dimensions [27]. We, now, reproduce in SU(3) the gauge transformations used by Feynman in SU(2). For an SU(3) unitary matrix, we write:

$$\Lambda \left(\overrightarrow{x}\right)=exp[-ig{\theta }^a\left(\overrightarrow{x}\right)\frac{{\lambda }^a}{2}],$$

(129)

where ${\lambda }^a$ are the Gell-Mann matrices. We further set:

$${\theta }^a(x_1,x_2)={\theta }^a(x_1,x_2,{\overline{x}}_3),$$

(130)

and introduce:

$${\overline{A}}_i(x_1,x_2)=\frac{{\lambda }^a}{2}{\overline{A}}_i^a(x_1,x_2)=\frac{{\lambda }^3}{2}{\delta }_{i,2}{x}_{1}H.$$

(131)

Under a planar gauge transformation, we can write:

$$g{\overline{A}}_i^{\prime }(x_1,x_2)=\Lambda (x_1,x_2)g{\overline{A}}_i(x_1,x_2){\Lambda }^{-1}(x_1,x_2)-i{\partial }_i\Lambda (x_1,x_2){\Lambda }^{-1}(x_1,x_2).$$

(132)

Now, we divide the $x_3={\overline{x}}_3$ plane into $L_D\times L_D$ square domains, with $L_D\ll L$. Further, we label the domains with an integer m as follows:

$$x_1=\frac{L_D}{2\pi }\xi ,x_2=\frac{L_D}{2\pi }\eta ,$$

(133)

$$\begin{array}{c}\hfill m=00\le x_1\le L_{D}0\le \xi \le 2\pi \\ \hfill m=1L_D\le x_1\le 2L_{D}2\pi \le \xi \le 4\pi \\ \hfill ....\end{array}$$

(134)

so that we have:

$$\xi =2\pi m+\beta ,0\le \beta \le 2\pi .$$

(135)

We do not need the residual of $x_2$ since only the integer m matters here.

Writing:

$$\Lambda (x_1,x_2)={\Lambda }_1(x_1,x_2){\Lambda }_2(x_1,x_2),$$

(136)

with:

$${\Lambda }_1(x_1,x_2)=exp\{-i\frac{\eta }{2}[cos\left(\frac{\beta }{2}\right){\lambda }^3+sin\left(\frac{\beta }{2}\right){\lambda }^2]\},$$

(137)

$${\Lambda }_2(x_1,x_2)=exp\{-i\frac{{\ell }_D^2}{2\pi }\eta (m+\frac{1}{2}){\lambda }^3\},$$

(138)

with ${\ell }_D$ being the dimensionless domain linear size, i.e., $L_D={\ell }_D{a}_H$ with the magnetic length $a_H\simeq \frac{1}{\sqrt{gH}}$, it is easy to check that:

$${\Lambda }_1(x_1,x_2)=cos\left(\frac{\eta }{2}\right)-isin\left(\frac{\eta }{2}\right)[cos\left(\frac{\beta }{2}\right){\lambda }^3+sin\left(\frac{\beta }{2}\right){\lambda }^2]$$

(139)

and

$${\Lambda }_2(x_1,x_2)=cos\left[(m+\frac{1}{2})\frac{{\ell }_D^2}{2\pi }\eta \right]-i{\lambda }^{3}sin\left[(m+\frac{1}{2})\frac{{\ell }_D^2}{2\pi }\eta \right].$$

(140)

The gauge-transformed vector potential can be easily evaluated. We have:

$$g{\overline{A}}_2^{\prime }(x_1,x_2)=gH{x}_1\Lambda (x_1,x_2)\frac{{\lambda }^3}{2}{\Lambda }^{-1}(x_1,x_2)-i{\partial }_2\Lambda (x_1,x_2){\Lambda }^{-1}(x_1,x_2).$$

(141)

Now, a straightforward calculation leads to:

$$gH{x}_1\Lambda (x_1,x_2)\frac{{\lambda }^3}{2}{\Lambda }^{-1}(x_1,x_2)=\frac{L_D}{2\pi }gH(2\pi m+\beta ){\Lambda }_1(x_1,x_2)\frac{{\lambda }^3}{2}{\Lambda }_1^{-1}(x_1,x_2),$$

(142)

$$-i{\partial }_2\Lambda (x_1,x_2){\Lambda }^{-1}(x_1,x_2)=-i\frac{2\pi }{L_D}\frac{\partial }{\partial \eta }{\Lambda }_1{\Lambda }_1^{-1}-{\Lambda }_1\left[\frac{{\ell }_D^2}{L_D}(m+\frac{1}{2})\frac{{\lambda }^3}{2}\right]{\Lambda }_1^{-1}.$$

(143)

Combining Equations (142) and (143), we see that the terms depending on m cancel each other out. Thus, we are left with:

$$g{\overline{A}}_2^{\prime }(x_1,x_2)={\Lambda }_1\left\{\left[\sqrt{gH}{\ell }_D(\frac{\beta }{2\pi }+\frac{1}{2})-\frac{4\pi }{{\ell }_D}\sqrt{gH}cos\frac{\beta }{2}\right]\frac{{\lambda }^3}{2}-\frac{4\pi }{{\ell }_D}\sqrt{gH}sin\frac{\beta }{2}\frac{{\lambda }^2}{2}\right\}{\Lambda }_1^{-1}.$$

(144)

This last quantity varies periodically but remains of the order $\sqrt{gH}$ over the entire area $L^2$. Moreover, we have:

$$g{\overline{A}}_1^{\prime }(x_1,x_2)=-i{\partial }_1\Lambda (x_1,x_2){\Lambda }^{-1}(x_1,x_2).$$

(145)

After some algebra, we find:

$$g{\overline{A}}_1^{\prime }(x_1,x_2)=-\frac{2\pi }{{\ell }_D}\sqrt{gH}\left\{sin\frac{\eta }{2}\left[-sin\frac{\beta }{2}\frac{{\lambda }^3}{2}+cos\frac{\beta }{2}\frac{{\lambda }^2}{2}\right]·\left[cos\frac{\eta }{2}+isin\frac{\eta }{2}(cos\frac{\beta }{2}{\lambda }^3+sin\frac{\beta }{2}{\lambda }^2)\right]\right\}.$$

(146)

Additionally, $g{\overline{A}}_1^{\prime }(x_1,x_2)$ does not depend on m, so it is periodic over the square domains and of order $\sqrt{gH}$. Let us consider, now, the chromomagnetic field $B_i^a$. We have:

$$g{B}_3^{\prime }(x_1,x_2)=gH\Lambda (x_1,x_2)\frac{{\lambda }^3}{2}{\Lambda }^{-1}(x_1,x_2)=gH{\Lambda }_1(x_1,x_2)\frac{{\lambda }^3}{2}{\Lambda }_1^{-1}(x_1,x_2).$$

(147)

From Equation (139), we see that the gauge-transformed chromomagnetic field also does not depend on m and, therefore, it is periodic with period $L_D$. Now, Feynman pointed out that the vector potential $A_i^a(x_1,x_2)$ may vary independently in the various domains. Indeed, one must avoid insisting on correlations that are not required by the potential energy interaction terms. As discussed in Ref. [27], one can vary the vector potential $A_i^{\prime }$ in a given domain to become zero, while in all the other domains it stayed the same. It turns out that no potential energy barrier arises to prevent the given domain from behaving independently of the other domains. In our case, however, aside from the Abelian vector potential, we must also consider the non-Abelian vector potentials induced by the vacuum condensation of the tachyonic modes. In addition, we are dealt three spatial dimensions instead of the two dimensions discussed in Ref. [27]. Now, we would like to show that, indeed, there are no strong potential energy barriers that prevent the chromomagnetic domains to behave independently. To see this, let us consider the contributions of the unstable modes to the vacuum energy, Equation (72). After taking into account the kink equations, Equations (78)–(80), we rewrite Equations (72)–(75) as:

$$E_U=E_U^{\left(u\right)}+E_U^{\left(v\right)}+E_U^{\left(w\right)}$$

(148)

where:

$$\begin{array}{c}\hfill E_U^{\left(u\right)}=\frac{1}{2}V\frac{gH}{4{\pi }^2},{\int }_{-\infty }^{+\infty }d{p}_3\left[{\rho }_u\left(p_3\right)+\frac{p_3^2-gH}{{\rho }_u\left(p_3\right)}\right]-\frac{g^2}{2}{I}_4^u{\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_3{f}_u^4\left(x_3\right)\\ \hfill +g^2\frac{gH}{4{\pi }^2}{\int }_{-\infty }^{+\infty }d{p}_3\frac{1}{{\rho }_u\left(p_3\right)}{I}_2^u{\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_3{f}_u^2\left(x_3\right),\end{array}$$

(149)

$$\begin{array}{c}\hfill E_U^{\left(v\right)}=\frac{1}{2}V\frac{gH}{8{\pi }^2}{\int }_{-\infty }^{+\infty }d{p}_3\left[{\rho }_v\left(p_3\right)+\frac{p_3^2-\frac{gH}{2}}{{\rho }_v\left(p_3\right)}\right]-\frac{g^2}{2}{I}_4^v{\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_3{f}_v^4\left(x_3\right)\\ \hfill +g^2\frac{gH}{8{\pi }^2}{\int }_{-\infty }^{+\infty }d{p}_3\frac{1}{{\rho }_v\left(p_3\right)}{I}_2^v{\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_3{f}_v^2\left(x_3\right),\end{array}$$

(150)

$$\begin{array}{c}\hfill E_U^{\left(w\right)}=\frac{1}{2}V\frac{gH}{8{\pi }^2}{\int }_{-\infty }^{+\infty }d{p}_3\left[{\rho }_w\left(p_3\right)+\frac{p_3^2-\frac{gH}{2}}{{\rho }_w\left(p_3\right)}\right]-\frac{g^2}{2}{I}_4^w{\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_3{f}_w^4\left(x_3\right)\\ \hfill +g^2\frac{gH}{8{\pi }^2}{\int }_{-\infty }^{+\infty }d{p}_3\frac{1}{{\rho }_w\left(p_3\right)}{I}_2^w{\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_3{f}_w^2\left(x_3\right).\end{array}$$

(151)

Moreover, it is useful to recall that we have the following kink equations:

$$\begin{array}{c}\hfill I_2^u\left[-{\partial }_3^2-gH\right]f_u\left(x_3\right)+g^2{I}_4^u{f}_u^3\left(x_3\right)=0\\ \hfill I_2^u={\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_{1}d{x}_2{g}_{+}^u(x_1,x_2)g_{-}^u(x_1,x_2)\\ \hfill I_4^u={\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_{1}d{x}_2{\left[g_{+}^u(x_1,x_2)g_{-}^u(x_1,x_2)\right]}^2,\end{array}$$

(152)

$$\begin{array}{c}\hfill I_2^v\left[-{\partial }_3^2-\frac{gH}{2}\right]f_v\left(x_3\right)+g^2{I}_4^v{f}_v^3\left(x_3\right)=0\\ \hfill I_2^v={\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_{1}d{x}_2{g}_{+}^v(x_1,x_2)g_{-}^v(x_1,x_2)\\ \hfill I_4^v={\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_{1}d{x}_2{\left[g_{+}^v(x_1,x_2)g_{-}^v(x_1,x_2)\right]}^2,\end{array}$$

(153)

$$\begin{array}{c}\hfill I_2^w\left[-{\partial }_3^2-\frac{gH}{2}\right]f_w\left(x_3\right)+g^2{I}_4^w{f}_w^3\left(x_3\right)=0\\ \hfill I_2^w={\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_{1}d{x}_2{g}_{+}^w(x_1,x_2)g_{-}^w(x_1,x_2)\\ \hfill I_4^w={\int }_{-\frac{L}{2}}^{+\frac{L}{2}}d{x}_{1}d{x}_2{\left[g_{+}^w(x_1,x_2)g_{-}^w(x_1,x_2)\right]}^2.\end{array}$$

(154)

We said that to stabilize the one-loop instabilities the induced gauge vector potential $U_i^a\left(\overrightarrow{x}\right)$ must satisfy the constraints:

$${\int }_{-\frac{L}{2}}^{\frac{L}{2}}d{x}_3{f}^2\left(x_3\right)\sim L,{\int }_{-\frac{L}{2}}^{\frac{L}{2}}d{x}_3{f}^4\left(x_3\right)\sim L$$

(155)

together with:

$$I_2\sim L^2,I_4\sim L^2.$$

(156)

Moreover, the minimum of the vacuum energy is attained when:

$$\frac{{\left(I_2^u\right)}^2}{I_4^u}=\frac{{\left(I_2^v\right)}^2}{I_4^v}=\frac{{\left(I_2^w\right)}^2}{I_4^w}=L^2.$$

(157)

It is evident that the kink solutions of Equations (152)–(154) satisfy the above constraints. On the other hand, the most general solution of the kink equations are given by the diluted multi-kink solutions:

$$f^u\left(x_3\right)=\sqrt{\frac{gH}{g^2}\frac{I_2^u}{I_4^u}}\prod _{n=1}^{N_{kink}}sign(x_3-x_n),$$

(158)

and the analogous expressions for $f^v$ and $f^w$. In Equation (158), the hyperbolic tangent function has been approximated by the step function and $N_{kink}=\frac{L}{L_D}$. We note that the width of the kink plane is of order of the magnetic length $a_H$ such that for distances greater than the magnetic length, the kink-profile functions reduce to a constant. Since $L_D$ is the distance between kinks, the dilute approximation is assured if ${\ell }_D\gg 1$. A more stringent condition on ${\ell }_D$ comes from the fact that we must allow for unstable modes. This leads to:

$${\ell }_D\gtrsim \sqrt{2}\pi \simeq 4.4.$$

(159)

In this way, we have divided the spatial volume V into slices of thickness $L_D$. The kink planes are assumed to be at the middle of the slice. Moreover, we have seen that the kink planes can be further divided into squares of linear size $L_D$. As a consequence, the whole volume V turns out to be divided into cubic domains of volume $L_D^3$. Since we are assuming $L_D\gg a_H$, Equations (155)–(157) are still valid after replacing L with $L_D$. Therefore, the vacuum energy can be written as:

$$\Delta E\left(gH\right)\simeq N_D{V}_D\frac{{\left(gH\right)}^2}{16{\pi }^2}ln\left(\frac{{\Lambda }_H}{\sqrt{gH}}\right),$$

(160)

where:

$$V_D=L_D^3,N_D=\frac{V}{V_D}.$$

(161)

Interestingly enough, we can rewrite the vacuum functional Equation (125) as:

$${\mathcal{G}}_0\left[\tilde{\eta }\right]=\mathcal{N}\prod _{n}exp\left[-\frac{1}{4}{\int }_{D_n}d\overrightarrow{x}d\overrightarrow{y}{\tilde{\eta }}_i^a\left(\overrightarrow{x}\right)G_{ij}^{ab}(\overrightarrow{x},\overrightarrow{y}){\tilde{\eta }}_j^b\left(\overrightarrow{y}\right)\right]$$

(162)

where the integer n labels the $N_D$ domains. It follows, then, that we can look at the quantum state Equation (162) as a collection of $N_D$ cubic domains with approximately the same energy:

$$\Delta E_D\left(gH\right)\simeq V_D\frac{{\left(gH\right)}^2}{16{\pi }^2}ln\left(\frac{{\Lambda }_H}{\sqrt{gH}}\right).$$

(163)

Moreover, the calculations of the chromomagnetic fields extend to a single domain so that our state closely resembles a ferromagnetic substance 2 where, however, all the domains have the same magnetic moment oriented in the same direction. We recall that the domain chromomagnetic fields are directed along the perpendicular to the kink plane with a strength that depends on the chromomagnetic condensate $\sqrt{gH}$.

We would like to push the analogy with ferromagnetism a little further. Ferromagnetic materials are paramagnetic but show drastically different behavior since, below the Curie temperature, they show spontaneous magnetization. P. Weiss [66] was able to explain the principal aspects of ferromagnetism by postulating the existence of a molecular field and the existence of domain structure. It is now known that the origin of the molecular field lies in quantum-mechanical exchange forces. The explanation of the origin of domain structure as a natural consequence of the various contributions due to the exchange, anisotropy and magnetic energies was given by Landau and Lifshitz [67]. The direction of magnetization of a different domain needs not necessarily be parallel such that the resultant magnetization vanishes. When an external magnetic field is applied, the domains rotate to align their magnetic moment with the field direction leading to a non-zero magnetization. Two domains magnetized in different directions are separated by a transition layer, called a Bloch wall [68], that, in general, has a certain amount of energy associated with it characterized by the energy per unit area.

Returning to our wavefunctional, we have seen in Section 4 that this quantum state has a non-zero expectation value of the chromomagnetic field. On the other hand, we found that the gauge system can be thought of as made of $N_D$ cubic domains. The non-zero expectation value of the chromomagnetic field arises from the implicit assumption that all the domains are oriented in the same direction. However, following Feynman’s suggestion that one must be careful not to insist on correlations that are not required by the potential energy, we should check if, indeed, there are huge potential barriers preventing a given domain from behaving independently from the other domains. To this end, let us consider, firstly, two adjacent domains. Let us suppose, now, the direction of the chromomagnetic field in one domain is reverted. From the calculations presented in the previous section, it is easy to see that $gB\to -gB$ amounts to $g_{+}^u(x_1,x_2)\to g_{-}^u(x_1,x_2)$ for the u-kink, and the same for the v- and w-kinks. From Equations (148)–(151), it is evident that these changes do not vary the domain energy. In other words, reverting the direction of the chromomagnetic field in a given domain does not have a cost in energy. As a consequence, we can change the sign of $gB$ independently without affecting the vacuum energy. For instance, we may arrange the domain chromomagnetic field in a three-dimensional checkerboard order so that the chromomagnetic fields averaged over distances much greater than $L_D$ vanish. This could make the wavefunctional Equation (162) a better candidate for the QCD vacuum. In addition, we may rotate the chromomagnetic field in a given domain without changing the vacuum energy since Equation (163) shows that the domain energy depends only on the strength of the chromomagnetic condensate $\sqrt{gH}$. However, there is a transition layer that separates adjacent domains with chromomagnetic fields pointing in different directions where we need to smoothly connect the domain background field to the one in the adjacent domain. Evidently, this will require a certain expenditure of energy to establish a boundary layer. On the other hand, this energy will depend on $|\overrightarrow{\nabla }({\overline{A}}_i^a+U_i^a){|}^2$ and on the area of the boundary layer. Observing that the domain energy scales as $L_D^3$, while the surface energy of the boundary layer (Bloch wall) grows as $L_D^2$, we see that no potential energy barriers arise to prevent domains from behaving independently once $L_D\gg a_H$.

Before proceeding further, it is useful to pause to summarize our results. We have considered the SU(3) pure gauge theory in the presence of a constant Abelian chromomagnetic background field. We found that in the one-loop approximation, there are three different kinds of unstable modes. We performed a full quantum-mechanical variational calculation leading to the dynamical condensation of the tachyonic modes that, in turn, generated a new non-perturbative background field. Starting from the multi-kink structure of the induced background fields and following Feynman’s argumentations on the effects of the gauge symmetry on the ground-state wavefunctional, we concluded that the stabilized vacuum wavefunctional can be thought as a collection of independent chromomagnetic domains that can be rewritten more explicitly as:

$${\mathcal{G}}_0\left[A\right]=\mathcal{N}\prod _{n}exp\{-\frac{1}{4}{\int }_{D_n}d\overrightarrow{x}d\overrightarrow{y}[A_i^a\left(\overrightarrow{x}\right)-{\overline{A}}_i^a\left(\overrightarrow{x}\right)-U_i^a\left(\overrightarrow{x}\right)]G_{ij}^{ab}(\overrightarrow{x},\overrightarrow{y})[A_i^a\left(\overrightarrow{y}\right)-{\overline{A}}_i^a\left(\overrightarrow{y}\right)-U_i^a\left(\overrightarrow{y}\right)]\}.$$

(164)

In Equation (164), the background field in a given domain is intended to be directed along an arbitrary spatial direction. Moreover, due to the local gauge symmetry, we can orientate the domain background field in an arbitrary color direction. As a consequence, the functional measure is given by:

$$\mathcal{D}A=\prod _n{\left(\mathcal{D}A\right)}_n$$

(165)

where the functional integrations over the domain $D_n$ involve gauge potential vector fields transverse with respect to the domain background fields averaged over all the allowed spatial and color directions. To ensure the translational invariance of the ground-state wavefunctional, all the domains must be characterized by the same average chromomagnetic condensate that, henceforth, will be denoted by $\sqrt{g{H}_0}$. We may conclude, thus, that our ground-state wavefunctional describes the quantum vacuum as a disordered chromomagnetic condensate. Therefore, we are led to suppose that the wavefunctional Equation (164), being gauge and translational invariant and having the energy that scales with the spatial volume, should be a good candidate for the QCD vacuum, at least for large distances $\sqrt{g{H}_0}\ll {\Lambda }_H$. However, Equation (160) shows that the energy of our wavefunctional is greater with respect to the perturbative ground state. In other words, our vacuum wave functional is not energetically favored. Nevertheless, having pictured the gauge system as a collection of $N_D$ independent domains, the number of gauge field configurations accounted for by the wavefunctional Equation (164) is easily estimated as:

$$N_D!\simeq exp\{N_{D}ln{N}_D\}.$$

(166)

This allows us to introduce the configurational entropy:

$$exp\left\{S_{conf}\right\}\simeq N_D!\simeq exp\{N_{D}ln{N}_D\},$$

(167)

or:

$$S_{conf}\simeq \frac{V}{L_D^3}ln{N}_D.$$

(168)

so that the configurational entropy scales with the volume. This means that, even though our vacuum wavefunctional has greater energy with respect to the perturbative vacuum wavefunctional:

$${\mathcal{G}}_0^{pert}\left[A\right]=\mathcal{N}exp\left\{-\int d\overrightarrow{x}d\overrightarrow{y}\frac{{\overrightarrow{B}}^a\left(\overrightarrow{x}\right)·{\overrightarrow{B}}^a\left(\overrightarrow{y}\right)}{4{\pi }^2{|\overrightarrow{x}-\overrightarrow{y}|}^2}\right\},$$

(169)

the number of gauge field configurations that realize the vacuum wavefunctional is large enough to span a set of finite measures in the functional space of physical states. On the contrary, the perturbative vacuum spans a zero-measure set of gauge field configurations 3. More precise statements will be addressed later on. Therefore, the transition from the perturbative vacuum to our variational vacuum wavefunctional can be thought as an order–disorder quantum phase transition analogous to the Berezinskii–Kosterlitz–Thouless (B-K-T) phase transition [71,72,73,74,75,76]. As is well known, in the B-K-T phase transitions, the increase in the entropy due to the unbinding of topological excitations overcomes the energy barrier, leading to a decrease in the free energy F = E − TS, with T being the temperature. We can come in closer analogy with the thermodynamics of the B-K-T phase transitions by introducing the domain fugacity:

$$z_D={\left(\kappa \mu L_D\right)}^3$$

(170)

where $\mu$ is an energy scale and $\kappa$ a constant that will be specified later on. If we have $N_D$ domains, we may define the entropy as:

$$exp\left\{S_D\right\}=z_D^{N_D}=exp\{N_{D}ln{z}_D\}=exp\{\frac{V}{V_D}ln{z}_D\}.$$

(171)

We have already shown that the energy needed to create $N_D$ domains is:

$$\Delta E\left(g{H}_0\right)\simeq N_D{V}_D\frac{{\left(g{H}_0\right)}^2}{16{\pi }^2}ln\left(\frac{{\Lambda }_H}{\sqrt{g{H}_0}}\right).$$

(172)

Since we are dealing with a quantum phase transition, the temperature T is zero. To introduce the free energy, the role of the temperature is played by the energy scale $\mu$. Accordingly, we may introduce the quantum free energy:

$$F_D=\Delta E-\mu S_D$$

(173)

or

$$\frac{F_D}{N_D}\simeq V_D\frac{{\left(g{H}_0\right)}^2}{16{\pi }^2}ln\left(\frac{{\Lambda }_H}{\sqrt{g{H}_0}}\right)-3\mu ln\left(\kappa \mu L_D\right).$$

(174)

At the phase transition, the free energy vanishes and the fugacity becomes $z_D=1$. From Equation (174), we see that $z_D=1$ for $\mu ={\mu }^{*}$ where:

$$V_D\frac{{\left(g{H}_0\right)}^2}{16{\pi }^2}ln\left(\frac{{\Lambda }_H}{\sqrt{g{H}_0}}\right)\simeq 3{\mu }^{*}ln\left(\kappa {\mu }^{*}{L}_D\right).$$

(175)

Neglecting logarithmic corrections, we obtain:

$${\mu }^{*}\simeq V_D\frac{{\left(g{H}_0\right)}^2}{48{\pi }^2}\simeq \frac{{\ell }_D^3}{48{\pi }^2}\sqrt{g{H}_0},$$

(176)

and

$$\kappa \simeq \frac{48{\pi }^2}{{\ell }_D^4}.$$

(177)

From Equations (159) and (177), we infer that $\kappa \sim O\left(1\right)$, and Equation (176) can be rewritten as:

$${\mu }^{*}\simeq \frac{\sqrt{g{H}_0}}{{\ell }_D}.$$

(178)

At the quantum phase transition, there is a proliferation of domains without variation in the free energy; to add one more domain, the increase in the entropy compensates the energy variation.

To conclude the present section, our variational perturbative approach aimed at stabilizing the SU(3) pure gauge theory in the presence of an Abelian constant background field led to the conclusion that the QCD vacuum at large scales behaves like a disordered chromomagnetic condensate. Our results show the quantum phase transition from the perturbative vacuum to the confining QCD vacuum as an order–disordered transition driven by the proliferation of chromomagnetic domains. Even though these results look promising, it remains to check if the proposed QCD vacuum wavefunctional does display the known physical properties of the confining physical vacuum.

6. Color Confinement, Flux Tubes and Meissner Effects

Let $\mathcal{O}\left[A\right]$ be a generic physical observable; then, we define the vacuum expectation value as usual:

$$<\mathcal{O}\left[A\right]>=\int \mathcal{D}A{\mathcal{G}}_0^{*}\left[A\right]\mathcal{O}\left[A\right]{\mathcal{G}}_0\left[A\right],$$

(179)

where the vacuum functional is given by Equation (164) and the functional integrations are performed according to Equation (165). The normalization constant is fixed by:

$$\int \mathcal{D}A{\mathcal{G}}_0^{*}\left[A\right]{\mathcal{G}}_0\left[A\right]=1.$$

(180)

Evidently, if we consider a local colored observable ${\mathcal{O}}^{a,b,\cdots }\left[A\right]$, then:

$$<{\mathcal{O}}^{a,b,\cdots }\left[A\right]>=0$$

(181)

in accordance with Elitzur’s theorem [77]. In particular, we have:

$$<B_i^a\left(\overrightarrow{x}\right)>=<E_i^a\left(\overrightarrow{x}\right)>=0.$$

(182)

so that only colorless local observables have a non-zero expectation value on the vacuum wavefunctional ${\mathcal{G}}_0\left[A\right]$. For instance, we have that $<{\left(B_i^a\left(\overrightarrow{x}\right)\right)}^2>$ and $<{\left(E_i^a\left(\overrightarrow{x}\right)\right)}^2>$ are different from zero. Indeed, we can write:

$$\begin{array}{c}\hfill <{\left(g{B}_i^a\left(\overrightarrow{x}\right)\right)}^2>=\int \mathcal{D}A{\mathcal{G}}_0^{*}\left[A\right]{\left[g{B}_i^a\left(\overrightarrow{x}\right)\right]}^2{\mathcal{G}}_0\left[A\right]\\ \hfill =\int \mathcal{D}A{\mathcal{G}}_0^{*}\left[A\right]\left\{\frac{1}{V_D}{\int }_{D\left(\overrightarrow{x}\right)}d\overrightarrow{x}{\left(g{B}_i^a\left(\overrightarrow{x}\right)\right)}^2\right\}{\mathcal{G}}_0\left[A\right]\end{array}$$

(183)

where the spatial integration is over the volume of the domain $D\left(\overrightarrow{x}\right)$ containing $\overrightarrow{x}$. In Equation (183), we used the translational invariance of the vacuum functional. Using Equations (164) and (165), we have (aside of the normalization constant):

$$\begin{array}{c}\hfill <{\left(g{B}_i^a\left(\overrightarrow{x}\right)\right)}^2>=\int {\left[\mathcal{D}A\right]}_{D\left(\overrightarrow{x}\right)}\left\{\frac{1}{V_D}{\int }_{D\left(\overrightarrow{x}\right)}d\overrightarrow{x}{\left(g{B}_i^a\left(\overrightarrow{x}\right)\right)}^2\right\}\times \\ \hfill exp\{-\frac{1}{2}{\int }_{D\left(\overrightarrow{x}\right)}d\overrightarrow{x}d\overrightarrow{y}[A_i^a\left(\overrightarrow{x}\right)-{\overline{A}}_i^a\left(\overrightarrow{x}\right)-U_i^a\left(\overrightarrow{x}\right)]G_{ij}^{ab}(\overrightarrow{x},\overrightarrow{y})[A_i^a\left(\overrightarrow{y}\right)-{\overline{A}}_i^a\left(\overrightarrow{y}\right)-U_i^a\left(\overrightarrow{y}\right)]\}.\end{array}$$

(184)

From the results of Section 4, it is straightforward to ascertain that:

$$<{\left(g{B}_i^a\left(\overrightarrow{x}\right)\right)}^2>\simeq {\left(g{H}_0\right)}^2.$$

(185)

Analogous calculations can be performed to evaluate $<{\left(E_i^a\left(\overrightarrow{x}\right)\right)}^2>$ that, however, turns out to be negligibly small with respect to the chromomagnetic contributions. As a consequence, our vacuum wavefunctional has a non-trivial gluon condensate:

$$<\frac{\alpha }{\pi }{F}_{\mu \nu }^a\left(\overrightarrow{x}\right)F_a^{\mu \nu }\left(\overrightarrow{x}\right)>\simeq \frac{1}{2{\pi }^2}<{\left(g{B}_i^a\left(\overrightarrow{x}\right)\right)}^2>\simeq \frac{{\left(g{H}_0\right)}^2}{2{\pi }^2}.$$

(186)

Later on, we shall see that for QCD, $\sqrt{g{H}_0}\simeq 1.0$ GeV, so that we reach an estimate of the gluon condensate:

$$<\frac{\alpha }{\pi }{F}_{\mu \nu }^a{F}_a^{\mu \nu }>\simeq {\left(0.1\mathrm{GeV}\right)}^4$$

(187)

that is in reasonable agreement with phenomenological estimates (see, e.g., Table 1 in Ref. [78]) and the direct determination on the lattice [79].

The vacuum wavefunctional does not admit long-range color correlations. For instance, let us consider the two point correlation function $<g{B}_i^a\left(\overrightarrow{x}\right)g{B}_i^a\left(\overrightarrow{y}\right)>$. Evidently, for $|\overrightarrow{x}-\overrightarrow{y}|>L_D$, we have:

$$<g{B}_i^a\left(\overrightarrow{x}\right)g{B}_i^a\left(\overrightarrow{y}\right)>\simeq <g{B}_i^a\left(\overrightarrow{x}\right))><g{B}_i^a\left(\overrightarrow{y}\right)>=0.$$

(188)

In general, the lack of long-range color correlations can be easily understood. In fact, our vacuum functional is basically made of chromomagnetic domains completely decorrelated. Thereby, the quantum vacuum does not share the color coherence needed to propagate an arbitrary color disturbance over distances larger than $L_D$. Finally, the lowest excited states are gapped. Indeed, as pointed out by Feynman in Ref. [27], when a system can be considered as made of approximately independent parts, the lowest excitation energy is the excitation of one of the parts. Evidently, the lowest excitation energy of a single chromomagnetic domain is of order $\frac{1}{L_D}$, so that for the energy gap, we obtain:

$$\Delta \simeq \frac{\sqrt{g{H}_0}}{{\ell }_D}\simeq {\mu }^{*}.$$

(189)

The absence of long-range color correlations together with the presence of a finite energy gap for the low-lying excitations ensures that our vacuum wavefunctional satisfies the color confinement criterion. Moreover, from phenomenological considerations, we infer that $L_D\sim 1.0$ fm. Since we already anticipated that the chromomagnetic condensate strength is about 1.0 GeV, we are led to estimate ${\ell }_D\sim 5$, leading to a mass gap $\Delta \sim {10}^2$ MeV.

Nevertheless, this is not enough to conclude that our vacuum wavefunctional is good enough to capture the relevant physical properties to describe the large-distance dynamics of the QCD vacuum. The crucial point is that we must also be able to explain the quark confinement physics. Since we are still dealing with the pure gauge theory, the quark confinement problem amounts to us demonstrating that a static quark–antiquark pair interact via a confining linear potential:

$$V_{conf}=\sigma R$$

(190)

for distances R large enough. In Equation (190), $\sigma$ is the string tension that is related to the Regge slope [80]:

$$\sqrt{\sigma }\simeq 464\mathrm{MeV}.$$

(191)

Actually, a great deal of numerical evidence has shown that a static quark–antiquark pair interacts by means of a linear potential for distances above about 0.5 fm. Moreover, the linear potential is almost completely due to the chromoelectric fields that are longitudinal, namely oriented along the line connecting the static color sources. However, a first-principle theoretical explanation of this phenomenon is still lacking. Therefore, the current understanding of quark confinement is mainly based on models of the QCD vacuum. We intend to show that our theoretical proposal for the QCD vacuum allows us to gain a vivid picture of the formation of the chromoelectric flux tube between static color charges and, in addition, to determine the color structure and the transverse profile of the flux-tube chromoelectric fields.

The presence of static color charges modifies the Gauss’s law constraints as:

$$\left\{i{D}^{ab}\left(\overrightarrow{x}\right)\frac{\delta }{\delta {\eta }^b\left(\overrightarrow{x}\right)}-Q^a\left[\delta (\overrightarrow{x}-{\overrightarrow{x}}_Q)-\delta (\overrightarrow{x}-{\overrightarrow{x}}_{\overline{Q}})\right]\right\}\mathcal{G}\left[A\right]=0,$$

(192)

where we are assuming the presence of a static quark charge $Q^a$ at ${\overrightarrow{x}}_Q$ and a static antiquark charge ${\overline{Q}}^a$ at ${\overrightarrow{x}}_{\overline{Q}}$. We have seen that the ground-state wavefunctional ${\mathcal{G}}_0\left[A\right]$ does not allow color disturbances to propagate over large distances. On the other hand, the Gauss law imposes that the chromoelectric flux originating from the source $Q^a$ must reach the sink ${\overline{Q}}^a$. As a consequence, it is necessary to modify ${\mathcal{G}}_0\left[A\right]$ into a wavefunctional $\mathcal{G}\left[A\right]$ that, indeed, satisfies the Gauss law constraints Equation (192). Evidently, we need a wavefunctional with energy as low as possible and, at the same time, we must ensure a region around the static color charges with restored color coherence so that color disturbances are allowed to spread over large distances. The most obvious way is to create bags of perturbative vacuum (false vacuum) around the color sources. Indeed, by assuming that by quantum fluctuations a chromomagnetic domain may evaporate, one gains energy $\Delta E_D\left(g{H}_0\right)$, Equation (163), and loses configurational entropy such that, according to Equation (175), there is no appreciable variation in the vacuum free energy. Evidently, the amplitude for quantum fluctuations to tunnel into the perturbative vacuum is of order $\mathcal{A}\sim exp(-\Delta E_{D}R)\sim exp(-\sqrt{g{H}_0}R)$ with $R=|{\overrightarrow{x}}_Q-{\overrightarrow{x}}_{\overline{Q}}|$. We already said that $\sqrt{g{H}_0}\sim 1.0$ GeV, so that the tunnelling probability is sizeable for distances $R\sim a_H\sim {10}^{-1}$ fm. However, extensive numerical simulations of quenched QCD on the lattice demonstrated unequivocally the formation of the squeezed chromoelectric flux tube for distances well above $R\sim 1.0$ fm. Since for $R\gg a_H$ the tunnelling probability is vanishingly small, we need an alternative mechanism to explain the formation of the chromoelectric flux tubes around static color charges separated by large distances. As a matter of fact, an alternative way to generate long-range color coherence is to polarize the chromomagnetic domains such that the chromomagnetic fields point in the same direction.

More precisely, we must admit that in a spatial region comprising the static color charges, the chromomagnetic domains share the same kink plane with the domain chromomagnetic fields pointing in the same direction transverse to the kink plane. It should be clear that the polarization of the domains does not vary the energy of the wavefunctional, but it increases the free energy since we lost configurational entropy. To minimize the vacuum free energy, the polarization region must have the spatial volume as small as possible. Due to the symmetry of the problem, the polarization volume is a cylinder with the symmetry axis coincident with the line jointing the static color charges and with a transverse sectional area of order $A_T\lesssim L_D^2$. 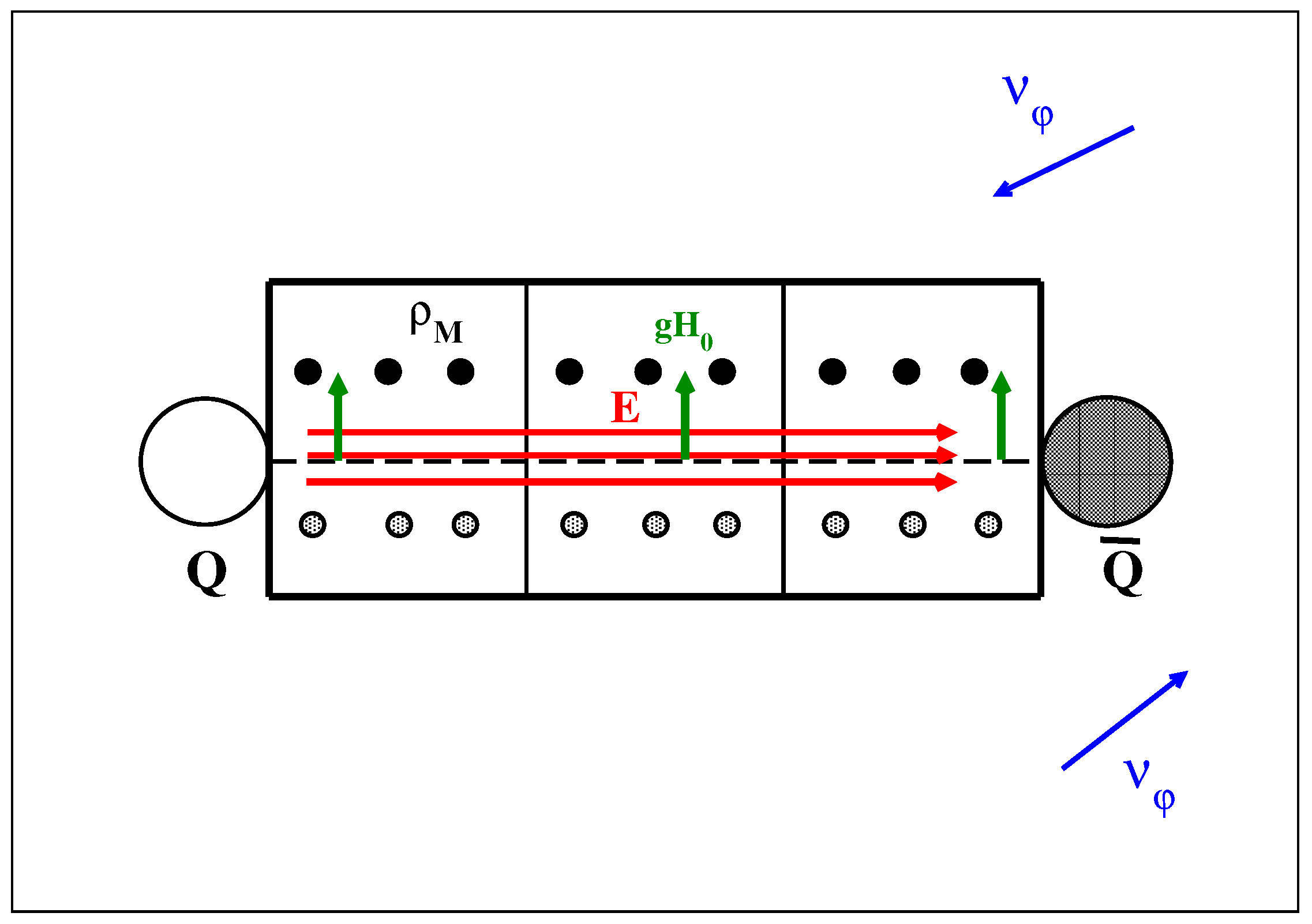The cylinder symmetry axis must lie on the common kink plane of the polarized chromomagnetic domains. This allows the polarized domains to rotate rigidly around the symmetry axis such that the increase in the vacuum free energy is reduced as much as possible. As a consequence, we are led to a modified vacuum wavefunctional as schematically illustrated in Figure 1.

We noted in Section 4 that the vacuum chromomagnetic fields lead to the presence of chromomagnetic charges whose density was given by:

$${\overrightarrow{D}}^{ab}\left(\overrightarrow{x}\right)·{\overrightarrow{B}}^b\left(\overrightarrow{x}\right)={\rho }_M^a\left(\overrightarrow{x}\right).$$

(193)

These chromomagnetic charges give rise to a chromomagnetic current density:

$${\overrightarrow{J}}_M^a\left(\overrightarrow{x}\right)={\overrightarrow{v}}_{\varphi }{\rho }_M^a\left(\overrightarrow{x}\right)$$

(194)

where ${\overrightarrow{v}}_{\varphi }$ is the rotational velocity of the polarized domains. Now, let us introduce cylindrical coordinate system $(x_{\ell },x_t,\varphi )$ where $x_{\ell }$ is the coordinate along the symmetry axis, $x_t$ the distance from the axis and $\varphi$ the azimuthal angle. Evidently:

$${\overrightarrow{v}}_{\varphi }=v_{\varphi }\widehat{\varphi },$$

(195)

so that the azimuthal chromomagnetic current will give rise to a Lorentz force that tends to squeeze the chromoelectric fields of the static color charges into a narrow structure directed along the longitudinal direction $\widehat{x_{\ell }}$. To do this, however, we need a chromomagnetic current density that is almost uniform along the flux tube. From the results in Section 4, we see that this requirement is satisfied only by the Abelian component of the chromomagnetic charge density ${\rho }_M^3\left(\overrightarrow{x}\right)$ and ${\rho }_M^8\left(\overrightarrow{x}\right)$. Evidently, we have:

$${\overrightarrow{J}}_M^3\left(\overrightarrow{x}\right)={\overrightarrow{v}}_{\varphi }{\rho }_M^3\left(\overrightarrow{x}\right),{\overrightarrow{J}}_M^8\left(\overrightarrow{x}\right)={\overrightarrow{v}}_{\varphi }{\rho }_M^8\left(\overrightarrow{x}\right),$$

(196)

with:

$$g{\rho }_M^3\left(\overrightarrow{x}\right)\simeq -\sqrt{2}{\left(g{H}_0\right)}^{\frac{3}{2}}\frac{tanh\left(\sqrt{\frac{g{H}_0}{2}}{x}_t\right)}{{cosh}^2\left(\sqrt{\frac{g{H}_0}{2}}{x}_t\right)},$$

(197)

$$g{\rho }_M^8\left(\overrightarrow{x}\right)\simeq -\frac{\sqrt{3}}{2}{\left(g{H}_0\right)}^{\frac{3}{2}}\frac{tanh\left(\sqrt{\frac{g{H}_0}{4}}{x}_t\right)}{{cosh}^2\left(\sqrt{\frac{g{H}_0}{4}}{x}_t\right)}.$$

(198)

Observing that the chromomagnetic current densities belong to the maximal Abelian SU(3) subgroup, the equations relating the chromomagnetic currents to the chromoelectric fields are given by the Ampere law (see, for instance, Refs. [81,82]):

$$-\overrightarrow{\nabla }\times {\overrightarrow{E}}^a\left(\overrightarrow{x}\right)={\overrightarrow{J}}_M^a\left(\overrightarrow{x}\right).$$

(199)

From Equations (196)–(199) we obtain:

$${\overrightarrow{E}}^a\left(\overrightarrow{x}\right)\simeq E^a\left(x_t\right){\widehat{x}}_{\ell },$$

(200)

$$E^a\left(x_t\right)\simeq {\delta }^{a3}{E}^3\left(x_t\right)+{\delta }^{a8}{E}^8\left(x_t\right)$$

(201)

with:

$$\frac{d}{d{x}_t}g{E}^3\left(x_t\right)\simeq v_{\varphi }g{\rho }_M^3\left(x_t\right),$$

(202)

$$\frac{d}{d{x}_t}g{E}^8\left(x_t\right)\simeq v_{\varphi }g{\rho }_M^8\left(x_t\right).$$

(203)

One easily obtains:

$$g{E}^3\left(x_t\right)\simeq v_{\varphi }g{H}_0\frac{1}{{cosh}^2\left(\sqrt{\frac{g{H}_0}{2}}{x}_t\right)},$$

(204)

$$g{E}^8\left(x_t\right)\simeq \frac{\sqrt{3}}{2}{v}_{\varphi }g{H}_0\frac{1}{{cosh}^2\left(\sqrt{\frac{g{H}_0}{4}}{x}_t\right)}.$$

(205)

It is worth pausing to briefly recap on the origin of the chromomagnetic charge density that plays a fundamental role in the formation and structure of the chromoelectric flux tube between far apart static color charges. From the results presented in Section 4, it should be evident that the chromomagnetic charge densities originated from the kink structures that, in turn, come from the condensation of the tachyonic unstable modes. As discussed in detail in I and in Section 2 and Section 3 of the present paper, the spin couplings of the gauge vector fields to the chromomagnetic background field generate negative mass squared terms in the lowest Landau levels. These instabilities drive the dynamical condensation of the tachyonic modes that were stabilized by the short-range repulsive interactions due to the positive quartic self-couplings of the gauge vector bosons. Albeit our calculations are based on a perturbative approach by means of a variational basis, we have already remarked that the results presented in I for the SU(2) gauge theory and for SU(3) in the present paper have been corroborated by non-perturbative lattice numerical simulations of non-Abelian gauge theories in the presence of external background fields [51,52,53,54,55].

The static quark–antiquark system is confined through the generation of the chromoelectric flux tube for which the quark and antiquark act as source and sink. Moreover, since the chromoelectric fields in the flux tube do not depend on the longitudinal coordinate $x_{\ell }$, we see that the quark and the antiquark at large separation distances are confined by a linearly rising potential, Equation (190), with string tension given by the energy per unit length stored in the flux-tube chromoelectric fields:

$$\sigma \simeq \frac{1}{2}\int d{\overrightarrow{x}}_t\left\{{\left[g{E}^3\left(x_t\right)\right]}^2+{\left[g{E}^8\left(x_t\right)\right]}^2\right\}.$$

(206)

A straightforward calculation gives:

$$\sqrt{\sigma }\simeq \sqrt{5\pi J_1}{v}_{\varphi }\sqrt{g{H}_0},$$

(207)

where:

$$J_1={\int }_0^{\infty }dz\frac{z}{{cosh}^{4}z}\simeq 0.295431.$$

(208)

We may also introduce the radius $R_T$ of the transverse section of the flux tube as:

$$R_T\simeq \frac{\int d{\overrightarrow{x}}_t\left|{\overrightarrow{x}}_t\right|\left\{{\left[g{E}^3\left(x_t\right)\right]}^2+{\left[g{E}^8\left(x_t\right)\right]}^2\right\}}{\int d{\overrightarrow{x}}_t\left\{{\left[g{E}^3\left(x_t\right)\right]}^2+{\left[g{E}^8\left(x_t\right)\right]}^2\right\}}.$$

(209)

We easily obtain:

$$R_T\simeq \frac{2\sqrt{2}+6}{5}\frac{J_2}{J_1}\frac{1}{\sqrt{g{H}_0}},$$

(210)

where:

$$J_2={\int }_0^{\infty }dz\frac{z^2}{{cosh}^{4}z}\simeq 0.214978.$$

(211)

An alternative definition of the transverse radius is given by w where:

$$w^2\simeq \frac{\int d{\overrightarrow{x}}_t{\left|{\overrightarrow{x}}_t\right|}^{2}g{E}_{\ell }\left(x_t\right)}{\int d{\overrightarrow{x}}_{t}g{E}_{\ell }\left(x_t\right)},$$

(212)

with

$$g{E}_{\ell }\left(x_t\right)=g{E}^3\left(x_t\right)+g{E}^8\left(x_t\right).$$

(213)

Performing the integrals one obtains:

$$w^2\simeq \frac{9}{4}\frac{1+2\sqrt{3}}{1+\sqrt{3}}\frac{\zeta \left(3\right)}{ln2}\frac{1}{g{H}_0}.$$

(214)

It turns out that:

$$w\simeq 2.0R_T.$$

(215)

According to Equations (204) and (205), the transverse profile of the flux-tube chromoelectric fields depends only on the strength of the chromomagnetic condensate $\sqrt{g{H}_0}$, while the azimuthal velocity fixes the chromoelectric field normalization. In principle, we can determine these two parameters by looking at observations. However, due to quark confinement we can only compare with theoretical experiments such as the non-perturbative numerical simulations of QCD on the lattice. In a series of papers [83,84,85,86,87] it was investigated by lattice Monte Carlo simulations of both SU(3) pure gauge theory and (2+1)-flavor QCD at almost the physical point some properties of the chromoelectric flux tube at zero temperature generated by a static quark–antiquark pair. More precisely, these distributions were obtained from lattice measurements of the connected correlators between a plaquette and a Wilson loop. Indeed, the connected correlator provides a lattice definition of a gauge-invariant field strength tensor $g{F}_{\mu \nu }$ generated by the static color sources. The Wilson loop connected to the plaquette generates the static quark color fields, which point in an unknown direction $n^a$ in color space. The Schwinger lines connecting the Wilson loop to the plaquette perform the parallel transport of the color direction $n^a$ from the Wilson loop to the plaquette, so that:

$$g{F}_{\mu \nu }\left(x\right)=g{F}_{\mu \nu }^a\left(x\right)·n^a.$$

(216)

Equation (216) is an inevitable consequence of the gauge invariance of the lattice operator, and its linear dependence on the color fields in the continuum limit has been explicitly tested in Ref. [83] (see Figure 3 there). Remarkably, extensive lattice simulations showed that, far from the sources, the flux tube is almost completely formed by the longitudinal chromoelectric field $g{E}_{\ell }$, which is constant along the flux tube and decreases rapidly in the transverse direction $x_t$. Introducing (here, $\beta$ is the lattice gauge coupling):

$$E_{\ell }\left(x\right)=\sqrt{\frac{\beta }{6}}g{E}_{\ell }\left(x\right),$$

(217)

the formation of the longitudinal chromoelectric field $E_{\ell }\left(x\right)$ was interpreted as the dual Meissner effect within the dual superconductor mechanism of quark confinement. Accordingly, the lattice data for the longitudinal chromoelectric field were analyzed by exploiting a variational model for the magnitude of the normalized order parameter of an isolated vortex in type II superconductors advanced in Ref. [88]. As a consequence, the transverse distribution of the chromoelectric flux tube were described according to:

$$E_{\ell }\left(x_t\right)=\frac{\phi }{2\pi }\frac{1}{\lambda {\xi }_v}\frac{K_0(\sqrt{x_t^2+{\xi }_v^2)}}{K_1\left(\frac{{\xi }_v}{\lambda }\right)},$$

(218)

where ${\xi }_v$ is a variational core-radius parameter, $\lambda$ is the penetration length and $K_n\left(x\right)$ is the modified Bessel function of order n. Moreover, the so-called Ginzburg–Landau parameter ${\kappa }_{GL}$ can be obtained by:

$${\kappa }_{GL}=\frac{\lambda }{\xi }=\sqrt{2}\frac{\lambda }{{\xi }_v}{\left[1-\frac{K_0^2\left(\frac{{\xi }_v}{\lambda }\right)}{K_1^2\left(\frac{{\xi }_v}{\lambda }\right)}\right]}^{\frac{1}{2}},$$

(219)

with $\xi$ being the coherence length.

It resulted that the phenomenological law Equation (218) allowed us to track very well the transverse profile of the longitudinal chromoelectric field giving support to the dual superconductor mechanism of quark confinement. On the other hand, our attempt to unveil from first principles the structure of the large-scale QCD vacuum led us to a completely different picture for the formation of the color flux tube generated by static sources. According to our previous discussion, the chromoelectric flux tube is mainly composed of the Abelian components $g{E}^3$ and $g{E}^8$. Therefore, we can safely assume that:

$$g{E}^a\left(x\right)·n^a\simeq g{E}^3\left(x\right)+g{E}^8\left(x\right)$$

(220)

where $g{E}^3\left(x\right)$ and $g{E}^8\left(x\right)$ are explicitly given by Equations (204) and (205) so that we have for the measured chromoelectric longitudinal field:

$$E_{\ell }\left(x_t\right)\simeq v_{\varphi }g{H}_0\left\{\frac{1}{{cosh}^2\left(\sqrt{\frac{g{H}_0}{2}}{x}_t\right)}+\frac{\sqrt{3}}{2}\frac{1}{{cosh}^2\left(\sqrt{\frac{g{H}_0}{4}}{x}_t\right)}\right\}.$$

(221)

In Equation (221), we considered that $\sqrt{\frac{\beta }{6}}\approx 1$ and that the smearing procedure needed to extract the physical information from the measured lattice connected correlator leads to an effective non-perturbative finite renormalization of the field strength tensor. As a consequence, in Equation (221), it is intended that the presence of an unknown renormalization constant, however, affects only the value of the longitudinal chromoelectric field at $x_t=0$. A remarkable consequence of Equation (221) is that the transverse profile of the longitudinal chromoelectric field depends only on the vacuum chromomagnetic condensate strength $\sqrt{g{H}_0}$. For comparison, Clem’s ansatz, Equation (218), needs two parameters $\lambda$ and ${\xi }_v$ to track the transverse profile.

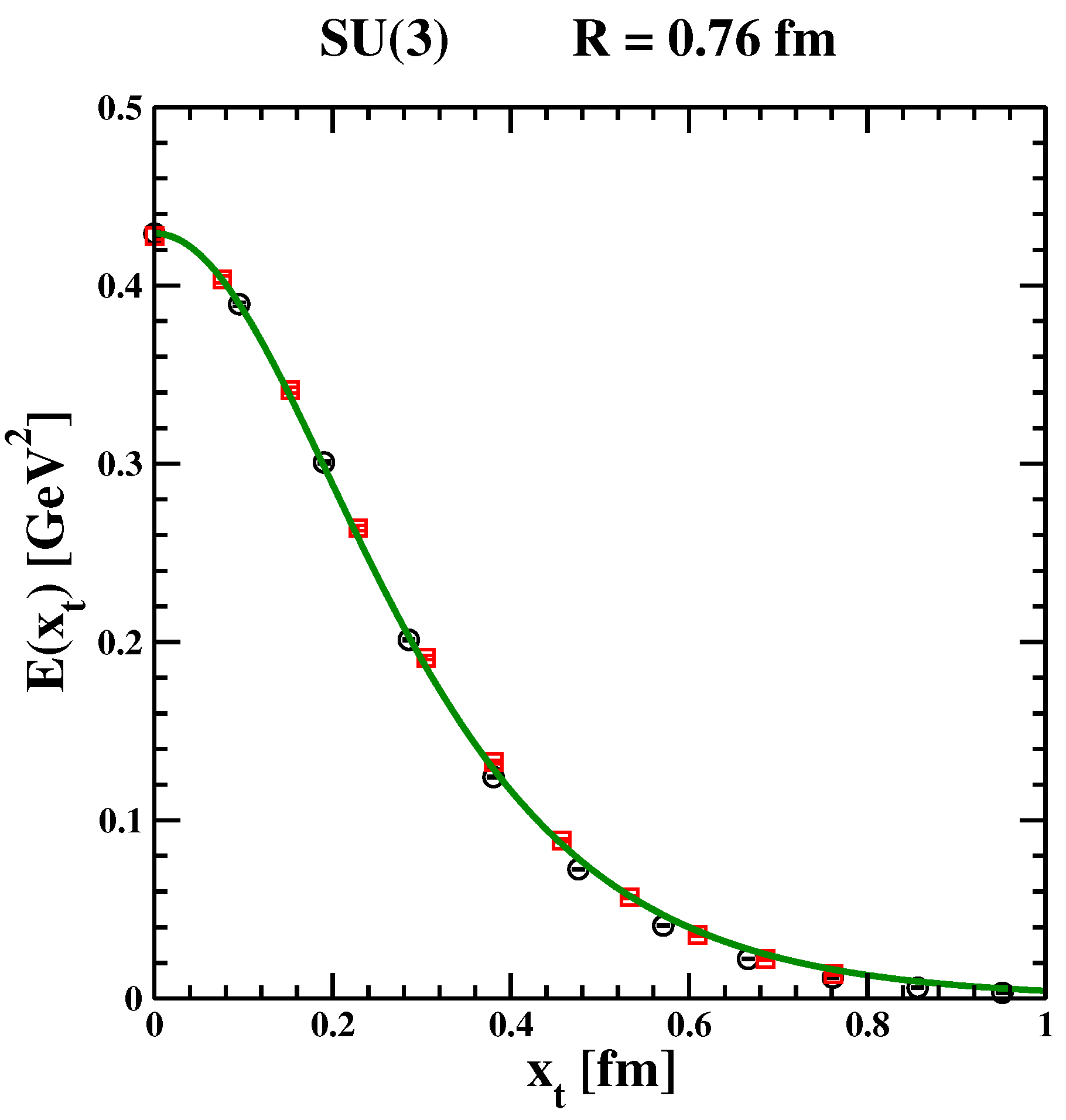
We have contrasted Equation (221) to several lattice measurements of the longitudinal chromoelectric field and, surprisingly, we found that Equation (221) is able to reproduce the transverse profiles of $E_{\ell }\left(x_t\right)$ quite well. To better appreciate this last point, in Figure 2, we display the behavior of the longitudinal chromoelectric field as a function of the transverse distance for two different values of the gauge coupling for the SU(3) pure gauge theory as reported in Figure 3, left panel, of Ref. [84]. In Ref. [84], the lattice data for $E_{\ell }\left(x_t\right)$ were nicely fitted by Clem’s ansatz, Equation (218). Likewise, we find that the transverse profile of the longitudinal chromoelectric field can be accounted for by using Equation (221) with (see Figure 2):

$$v_{\varphi }\simeq 0.21,\sqrt{g{H}_0}\simeq 1.05\mathrm{GeV}.$$

(222)

However, in Refs. [85,86], the presence of an effective Coulomb-like chromoelectric field ${\overrightarrow{E}}^C$ was shown to be associated with the static quark sources. Indeed, we have said that the formation of bubbles of a perturbative vacuum around the static color sources with a linear size of order of the chromomagnetic length is conceivable by quantum tunneling so that near the static charges there is a perturbative Coulomb chromoelectric field that, however, may penetrate at larger distances due to the restoration of color coherence along the flux tube. Therefore, the measured chromoelectric field $\overrightarrow{E}$ can be written as [85,86]:

$$\overrightarrow{E}={\overrightarrow{E}}^{NP}+{\overrightarrow{E}}^C$$

(223)

with the non-perturbative chromoelectric field ${\overrightarrow{E}}^{NP}$ being purely longitudinal. In other words, ${\overrightarrow{E}}^{NP}$ must be identified with the confining field of the QCD flux tube. Following Ref. [86], in Figure 3, left panel, we display the transverse profile of the non-perturbative chromoelectric field for the SU(3) pure gauge theory corresponding to a source distance of $R\simeq 0.85$ fm. The transverse profile is consistent with Equation (221) with (solid line in Figure 3):

$$v_{\varphi }\simeq 0.185,\sqrt{g{H}_0}\simeq 1.0\mathrm{GeV},\sqrt{\sigma }\simeq 398.5\mathrm{MeV}.$$

(224)

In Equation (224) the string tension has been evaluated by means of Equation (207). Note that the value of the string tension in Equation (224) is smaller with respect to the accepted value, Equation (191). This is to be expected for we have already noticed that there is a non-perturbative renormalization constant due to the smearing procedure that affects the measured chromoelectric field. Such a renormalization constant can be easily evaluated from the ratio of the estimate of the string tension in Equation (224) to the reference value given by Equation (191).

We saw that the connected correlators allow us to extract the gauge-invariant flux-tube field strength tensor $F_{\mu \nu }$. In Ref. [86], a stress–energy–momentum tensor with the Maxwell form was constructed from a field strength tensor $T_{\mu \nu }\left(x\right)$. In fact, in Appendix A of Ref. [86], the energy–momentum tensor $T_{\mu \nu }$ was considered as a function of the field strength tensor $F_{\mu \nu }$ characterizing the color flux tube. Assuming that the field strength tensor points in a single color direction parallel to the color direction of the static sources, it follows that the energy–momentum tensor lies in the same single color direction and, therefore, it has the Maxwell form [86]:

$$T_{\mu \nu }\left(x\right)=F_{\mu \alpha }\left(x\right)F_{\alpha \nu }\left(x\right)-\frac{1}{4}{g}_{\mu \nu }{F}_{\alpha \beta }\left(x\right)F_{\alpha \beta }\left(x\right).$$

(225)

However, we have shown that the field strength tensor is mainly composed of the Abelian color directions $a=3,8$. Nevertheless, the Abelian nature of the flux-tube field strength tensor fully justifies the Maxwell construction proposed in Ref. [86]. More recently, in Ref. [87], the evidence of a solenoidal chromomagnetic current responsible for the formation of the longitudinal chromoelectric field was presented for the first time. The chromomagnetic current density was defined by the Ampere law:

$${\overrightarrow{J}}_{mag}\left(\overrightarrow{x}\right)=\overrightarrow{\nabla }\times \overrightarrow{E}\left(\overrightarrow{x}\right)=\overrightarrow{\nabla }\times {\overrightarrow{E}}^{NP}\left(\overrightarrow{x}\right),$$

(226)

where we used $\overrightarrow{\nabla }\times {\overrightarrow{E}}^C\left(\overrightarrow{x}\right)=0$. Comparing Equation (226) with our Equation (199), we infer that:

$${\overrightarrow{J}}_{mag}\left(\overrightarrow{x}\right)=-\left[{\overrightarrow{J}}_M^3\left(\overrightarrow{x}\right)+{\overrightarrow{J}}_M^8\left(\overrightarrow{x}\right)\right]$$

(227)

with ${\overrightarrow{J}}_M^{3,8}\left(\overrightarrow{x}\right)$ given by Equations (196)–(198). In Figure 3, right panel, we report the chromomagnetic current, Equation (226), for three different values of the gauge coupling evaluated at the transverse plane at a distance $\frac{R}{4}$ from the source. The data have been reproduced from Figure 5 in Ref. [87]. Since the distance between the static sources is rather small ($R\simeq 0.511$ fm), the data seem to display some noticeable scattering, probably due to systematic effects arising from the subtraction of the Coulomb field from the measured flux-tube chromoelectric field. Nevertheless, our theoretical chromomagnetic current seems to track the lattice data reasonably well.

In our opinion, the essential Abelian nature of the chromomagnetic currents and the ensuing flux-tube chromoelectric fields are at the heart of the so-called Abelian dominance observed in several lattice simulations [8,10,16]. Indeed, the dual superconductivity scenario is realized by adopting a gauge-fixing procedure analogous to the unitary gauge where a suitable matrix-valued operator is diagonalized, leaving unfixed the maximal Abelian subgroup U(1)×U(1) whose generators belong to the Cartan subalgebra of the SU(3) gauge group. In these gauges, the given gauge theory can be thought of as an essentially Abelian gauge theory. Our previous results should make it evident that the observed Abelian dominance is not the cause, but it is a consequence of the structure of the confining quantum vacuum.

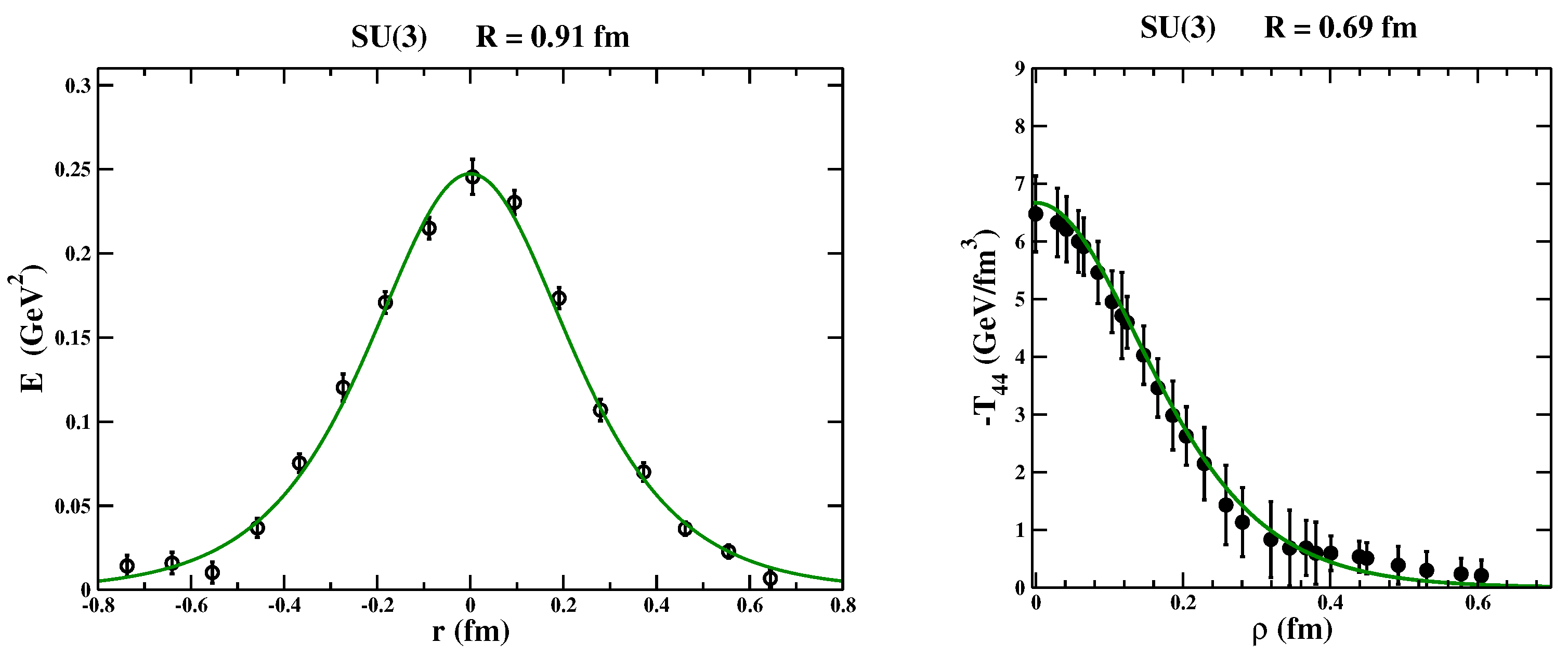
It is interesting to also check if our theoretical transverse shape of the flux-tube chromoelectric field is consistent with numerical studies in QCD with maximal Abelian gauge fixing.

As a matter of fact, in Figure 4, left panel, we report the profile of the Abelian flux-tube chromoelectric field (in physical units) in quenched QCD in the maximal Abelian gauge as displayed in Figure 15 of Ref. [89] together with our theoretical transverse profile, Equation (221), with:

$$v_{\varphi }\simeq 0.102,\sqrt{g{H}_0}\simeq 1.14\mathrm{GeV}.$$

(228)

We can see that, also in this case, our theoretical expectations are able to track the lattice data quite well.

As the last check, we focus, now, on several numerical studies of the pure gauge SU(3) theory on the structure of the static quark flux tube implemented with correlators between Wilson loops and plaquettes. In this case, in general, the lattice observables give information on the square of the flux-tube field strength tensor. For definitiveness, we have considered the quite recent studies on the spatial distribution of the stress–energy–momentum tensor around the static quark–antiquark color sources reported in Ref. [90]. The authors of Ref. [90] investigated the spatial distribution of the stress–energy–momentum tensor $T_{\mu \nu }$ around a static quark–antiquark pair in the SU(3) pure gauge theory. To smooth the gauge field configurations, the Yang–Mills gradient flow was employed (for a recent review, see, e.g., Ref. [91] and references therein). The spatial distribution of the static color source energy–momentum tensor was obtained by measuring the correlators of the conserved renormalized stress tensor [92] and a Wilson loop. It is worth mentioning that in Appendix A of Ref. [86], it was shown that the Maxwell energy–momentum tensor built from the field strength tensor characterizing the SU(3) flux tube resulted in satisfying agreements with the results presented in Ref. [90]. For a more quantitative comparison, we looked at the transverse distribution of the flux-tube energy density $\mathcal{E}\left(x\right)=-T_{44}\left(x\right)$ measured at the mid-transverse plane and displayed in Figure 3 of Ref. [90]. According to our results, we should have:

$$-T_{44}\simeq \frac{1}{2}\left\{{\left[g{E}^3\left(r\right)\right]}^2+{\left[g{E}^8\left(r\right)\right]}^2\right\}$$

(229)

where r is the transverse distance in the cylindrical coordinate system. The fit of Equation (229) to the lattice data returned (see Figure 4, right panel):

$$v_{\varphi }\simeq 0.20,\sqrt{g{H}_0}\simeq 1.10\mathrm{GeV},\sqrt{\sigma }\simeq 474\mathrm{MeV}.$$

(230)

Again, we see that the lattice data are in quite good agreement with theoretical expectations. Furthermore, we note that the estimate of the string tension in Equation (230) is in accordance with the large R behavior of the quark–antiquark force, displayed in Figure 4 of Ref. [90], as directly determined from the Wilson loops and the renormalized energy–momentum tensor as well as with the string tension reference value Equation (191), signaling that the renormalized lattice energy–momentum tensor does not need further non-perturbative renormalization since it is expected to have a smooth continuum limit [92].

To summarize, we have shown that our picture for the formation of a chromoelectric squeezed flux tube generated by a static quark–antiquark pair in the SU(3) pure gauge theory turned out to be in reasonable agreement with lattice outcomes from different collaborations. Our previous discussion leads to the following estimate for the strength of the vacuum chromomagnetic condensate in the pure gauge SU(3) theory:

$$\sqrt{g{H}_0}\simeq 1.0-1.1\mathrm{GeV}\mathrm{SU}\left(3\right).$$

(231)

From this last equation, we may estimate the flux-tube transverse radius, Equation (210), $R_T\simeq 0.2$ fm, or the width, Equation (215), $w\simeq 0.4$ fm, in agreement with several lattice determinations.

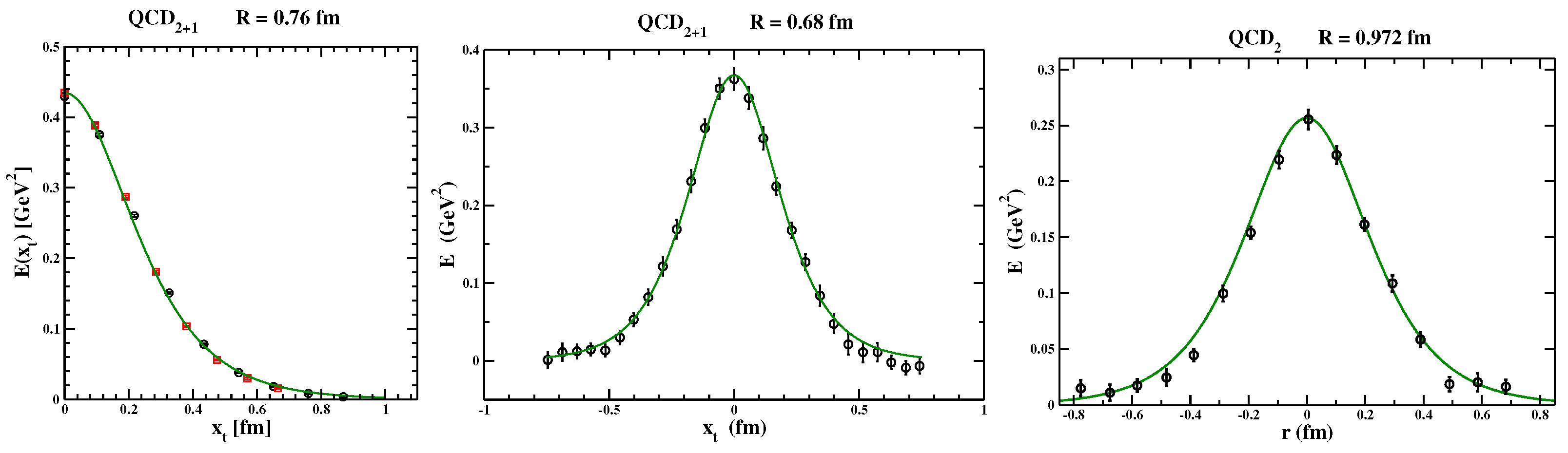
Up to now we have dealt with only the SU(3) gluon fields and completely neglected the dynamical role of the fermion fields. Although this point will be addressed in more details in the following section, it is, nevertheless, worthwhile to ascertain how dynamical quarks affect the structure of the chromoelectric fields generated by a static quark–antiquark pair. Indeed, we looked at lattice studies in full QCD on the flux-tube color fields, and in Figure 5, we present the transverse distribution of the longitudinal flux-tube chromoelectric field as obtained by three different lattice groups.

Firstly, in Figure 5, left panel, the behavior of the longitudinal chromoelectric field versus the transverse distance is displayed as obtained from two different values of the gauge coupling, $\beta =6.743$ (circles) and $\beta =6.885$ (squares), for (2+1)-flavors QCD with HISQ/Tree action [84]. The data were obtained on the line of constant physics by adjusting the gauge coupling and the bare quark masses so as to keep the strange quark mass fixed at the physical point and the light quark masses corresponding to a pion mass $m_{\pi }\simeq 160$ MeV. The data have been extracted from Figure 3, right panel, in Ref. [84]. The continuous line corresponds to Equation (221) with:

$$v_{\varphi }\simeq 0.17,\sqrt{g{H}_0}\simeq 1.17\mathrm{GeV}.$$

(232)

In Figure 5, middle panel, we report the transverse profile of the flux-tube chromoelectric field reported in Figure 14 of Ref. [93], where the flux tube properties were investigated by numerical lattice simulations for full QCD with (2+1)-flavors of stoud-improved staggered fermions with physical quark masses (pion mass $m_{\pi }\simeq 135$ MeV). In this case, we found (continuous line in Figure 5):

$$v_{\varphi }\simeq 0.108,\sqrt{g{H}_0}\simeq 1.35\mathrm{GeV}.$$

(233)

Finally, in Figure 5, right panel, we consider the transverse distribution of the flux-tube chromoelectric field for QCD in the maximal Abelian gauge with two degenerate non-perturbatively improved Wilson fermions with a rather heavy mass $m_q\simeq 100$ MeV [89]. Fitting the lattice data to our Equation (221), we obtain:

$$v_{\varphi }\simeq 0.104,\sqrt{g{H}_0}\simeq 1.15\mathrm{GeV}.$$

(234)

It is remarkable that, in accordance with common expectations, the inclusion of dynamical quarks does not substantially modify the color structure of the flux tube. The only effect seems to be a small increase in the chromomagnetic condensate strength:

$$\sqrt{g{H}_0}\simeq 1.2-1.3\mathrm{GeV}\mathrm{QCD}.$$

(235)

Our quantum vacuum functional leads us to reach a clear picture on the flux-tube physics. Indeed, the squeezing of the chromoelectric fields generated by a static quark–antiquark pair is due to chromomagnetic currents belonging to the maximal Abelian subgroup of SU(3) whose transverse distribution only depends on the strength of the vacuum chromomagnetic condensate. It is remarkable that the resulting flux-tube chromoelectric fields are obtained by solving the quite simple Ampere law, Equation (199). Evidently, the qualitative agreement of our theoretical expectations with several lattice measurements leads us to believe that we are on the right path. Undoubtedly, the knowledge of the color structure and distribution of the flux tube has several interesting phenomenological consequences. Here, we restrict ourselves to the comparison with the seminal paper by Casher, Neuberger and Nussinov [94] that lies at the basis of several high-energy physics Monte Carlo codes. In Ref. [94], quark confinement is assumed to be generated by the formation of chromoelectric flux tubes with almost uniform energy density. By employing the approximations where the chromoelectric field that develops between the quarks is assumed to be an almost classical field, the authors of Ref. [94] found that the flux-tube chromoelectric field is practically longitudinal. Moreover, to estimate the production of quark pairs in the flux tubes, it is assumed that the longitudinal chromoelectric field is Abelian:

$$g{E}^a\simeq {\delta }^{a3}g{E}^3+{\delta }^{a8}g{E}^8.$$

(236)

Using the Gauss law and:

$$\frac{1}{2}{A}_T\sum _{a=1}^8{\left(E^a\right)}^2\simeq \sigma$$

(237)

where $A_T\simeq \pi R_T^2$ is the cross-sectional area, one obtains:

$$\frac{1}{2}g{E}^3\simeq \frac{3}{2}\sigma ,g{E}^8\simeq \frac{1}{\sqrt{3}}g{E}^3.$$

(238)

Within the above framework, the quark dynamics in the flux tube may be approximately described by the Dirac equation in the presence of a classical almost uniform longitudinal chromoelectric field given by a diagonal matrix in color space [94]:

$$\left[-i\cancel{\partial }-m_{eff}-2i\sigma z\left(\begin{array}{ccc}1& & \\ & -\frac{1}{2}& \\ & & -\frac{1}{2}\end{array}\right)\right]\psi =0,$$

(239)

where $m_{eff}$ is the effective quark mass and z is our longitudinal coordinate $x_{\ell }$. After that, the dynamical process of quark pair creation may be described rather well by the well-known Schwinger mechanism [95,96].

It is remarkable that within our approach, we have confirmed the Abelian structure of the flux-tube chromoelectric fields. More precisely, the chromoelectric fields that confine the static quark–antiquark pair is longitudinal, and it is almost completely formed by the $a=3,8$ color directions. However, if we assume a uniform flux tube, instead of Equation (238), we obtain:

$$g{E}^8(x_t=0)\simeq \frac{2}{\sqrt{3}}g{E}^3(x_t=0),$$

(240)

and

$$g{E}^3(x_t=0)\simeq v_{\varphi }g{H}_0\simeq \frac{\sigma }{5\pi J_1{v}_{\varphi }}\simeq 1.08\sigma ,$$

(241)

where we used Equation (207) and assumed $v_{\varphi }\simeq 0.2$. As a consequence, we are led to the following Dirac equation:

$$\left[-i\cancel{\partial }-m_{eff}-1.08i\sigma z\left(\begin{array}{ccc}1& & \\ & -\frac{1}{3}& \\ & & -\frac{2}{3}\end{array}\right)\right]\psi =0.$$

(242)

In addition, it is interesting to note that we may go beyond the approximations adopted in Ref. [94], for we have an explicit expression for the transverse distribution of the flux-tube chromoelectric fields. In fact, the transverse profile of the chromoelectric fields allows us, in principle, to determine the transverse distribution of the quark–antiquark pairs produced by the Schwinger mechanism (for a good account, see, e.g., Ref. [97] and references therein); however such a matter goes beyond the aim of the present paper.

Let us conclude this rather lengthy section by discussing the remarkable color Meissner effect [31,32,33,34] that led us to picture the QCD vacuum like a chromomagnetic condensate. In order to investigate non-perturbatively the quantum vacuum structure in Refs. [28,29,30], by means of the so-called Schrödinger functional, a gauge-invariant effective action for gauge systems in external static background fields was introduced. In particular, it was shown that the deconfinement temperature depends on the strength of an external Abelian chromomagnetic field in both the pure SU(3) gauge theory [31,32,33] and QCD with two degenerate staggered dynamical quarks [34]. Actually, it was ascertained that the deconfinement temperature decreases when the strength of the applied field is increased and eventually goes to zero. 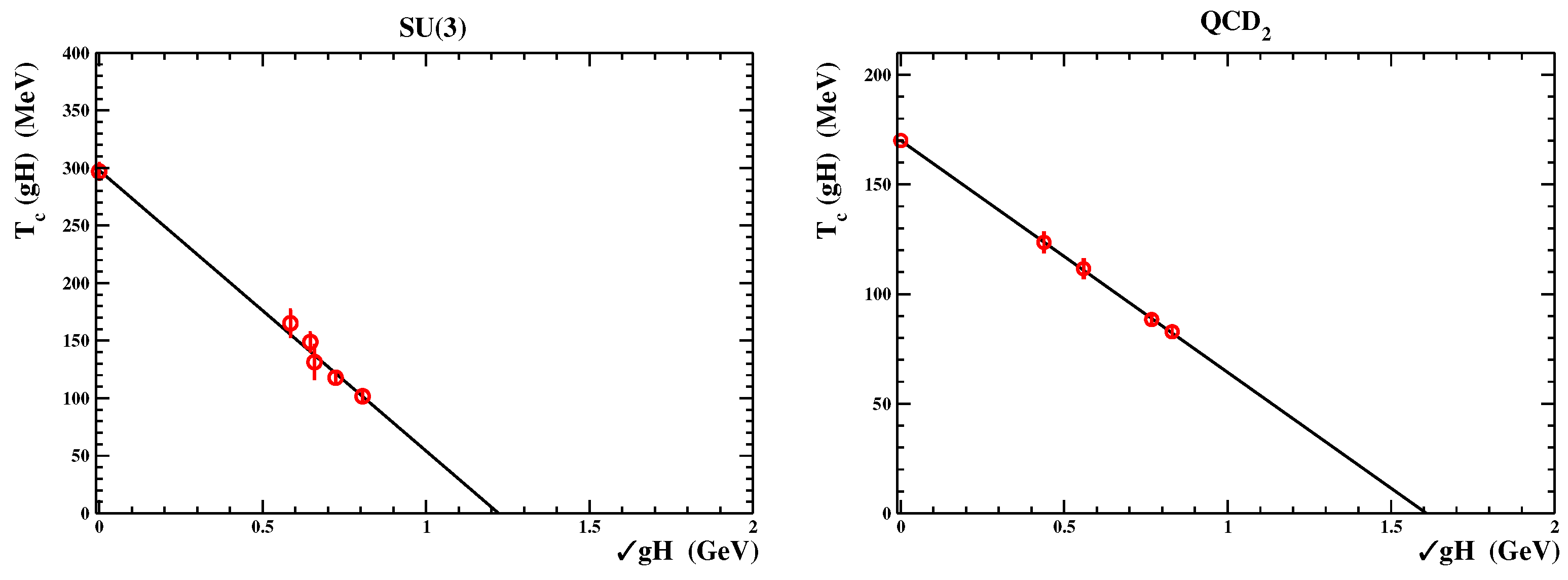Indeed, in Figure 6, we display the critical temperature of deconfinement versus the strength of the applied chromomagnetic field for SU(3) (left panel) and QCD (right panel). For the pure gauge theory, the data have been taken from Figure 4 in Ref. [32] taking into account that $T_c=300\left(7\right)$ MeV [98], while for QCD with two dynamical staggered quarks with a rather large mass (pion mass $m_{\pi }$ around 500 MeV), the data have been extracted from Figure 7 of Ref. [34] assuming $T_c\simeq 170$ MeV. From Figure 6, we infer that in both cases, the deconfinement critical temperature decreases linearly with $\sqrt{gH}$. In fact, the lattice data can be fitted to Equation (1), giving (see the continuous lines in Figure 6):

$$T_c\left(0\right)=298\left(10\right)\mathrm{MeV},\sqrt{g{H}_c}=1.22\left(4\right)\mathrm{GeV}\mathrm{SU}\left(3\right),$$

(243)

$$T_c\left(0\right)=170\left(12\right)\mathrm{MeV},\sqrt{g{H}_c}=1.61\left(14\right)\mathrm{GeV}\mathrm{QCD}.$$

(244)

From a dynamical point of view, these peculiar behaviors of the critical temperatures point to the prevalent role of the chromomagnetic length. Actually, we may now try to interpret the color Meissner effect within our picture of the confining vacuum wavefunctional. Firstly, we note that the gauge systems were probed with external fields whose strengths $\sqrt{gH}$ were smaller than $\sqrt{g{H}_0}$, Equations (231) and (235) so that it is conceivable that the main effects of the applied chromomagnetic fields are to polarize the chromomagnetic domains such that the vacuum chromomagnetic condensate tends to lie in the same direction as the external field. As a consequence, we see that the polarization effects cause an increase in the effective domain size leading to a decrease in the mass gap $\Delta \sim \frac{1}{L_D}$. Since on dimensional ground the deconfinement temperature $T_c$ is of order of the mass gap, we may explain the observed decreases in the critical temperature $T_c\left(gH\right)$. If this interpretation is correct, then at the critical strength $\sqrt{g{H}_c}\sim \sqrt{g{H}_0}$, the gauge system undergoes a quantum deconfinement phase transition. However, the deconfined phase is far from being similar to a weakly interacting gas of quarks and gluons, but it should resemble the quantum Hall liquid of the condensed matter physics. A clear indication of this would come from the measurements of the chromoelectric fields generated by a static quark–antiquark pair immersed in a uniform chromomagnetic field. Indeed, at $T=0$ and $\sqrt{gH}>\sqrt{g{H}_c}$, we lost confinement due to the absence of a mass gap and the insaturation of long-range color correlations. However, since the quantum vacuum is characterized by polarized chromomagnetic domains, we expect the formation of a squeezed flux tube with a non-zero string tension when the static-source joining line is perpendicular to the external field, $\sqrt{{\sigma }_T}\simeq \sqrt{\sigma }$. On the other hand, for a static quark–antiquark pair in the direction parallel to the external field, the formation of the flux tube should be strongly suppressed leading to $\sqrt{{\sigma }_L}\simeq 0$. Unfortunately, in the literature, there are no lattice data that could support the above scenario. However, quite recently, such an investigation was presented in Ref. [93] for full QCD with (2+1)-flavor at the physical point immersed in extremely strong magnetic fields. Actually, the influence of external magnetic background fields on QCD has attracted growing interest in recent years (see, for instance, Refs. [99,100,101,102] and references therein).

Quantum chromodynamics with background magnetic fields can be studied directly by means of non-perturbative lattice simulations. Continuum extrapolated results employing improved staggered quarks with physical masses have been used to map out the QCD phase diagram up to field strength $eB=9{\mathrm{GeV}}^2$. It turned out that the applied magnetic field increases the light quark condensate in the confined phase. This enhancement has been called magnetic catalysis. Conversely, in the transition region from the confined phase to the deconfined one, the light quark condensate seems to decrease, leading to the so-called inverse magnetic catalysis. It is important to stress that the chiral and deconfinement critical temperatures always coincide as happened in the absence of the external magnetic fields. Moreover, as a result of the non-monotonous dependence of the light quark condensate on the magnetic field strength and temperature, $T_c\left(eB\right)$ is reduced by the magnetic field.

It is widely believed that the mechanisms behind the magnetic catalysis are quite transparent, and these can be understood in terms of the dimensional reduction in the gauge system and the high degeneracy of the lowest Landau levels. Unfortunately, theoretical predictions are only in reasonable agreement with the lattice data for not too strong magnetic fields, $eB\lesssim 0.3{\mathrm{GeV}}^2$. On the contrary, we feel that there is a more mundane explanation of the magnetic catalysis, at least in the confined phase. Indeed, one must bear in mind that in the QCD confined phase, the physical states are colorless hadrons. Considering that an external magnetic field is coupled to the gauge system through the electromagnetic vector current, we may employ the old vector meson dominance idea to argue that the electromagnetic current is mainly coupled to vector mesons. Moreover, a long time ago in Ref. [103], the duality relation between quark–antiquark bound states and asymptotically free quarks was proved by using relativistic wave functions and couplings to both the vector and axial current. Within these approximations, we were able to evaluate that an external constant magnetic field contributes to the vacuum energy density and, thereby, the zero-temperature renormalized chiral condensate as usually measured in numerical lattice simulations is:

$${\Sigma }_{ud}(eB,T)=\frac{m_{ud}}{m_{\pi }^4}\left\{<\psi \overline{\psi }>(eB,T)-<\psi \overline{\psi }>(0,0)\right\}.$$

(245)

Interestingly enough, we found that our theoretical estimate was in rather good agreement with the lattice data [93,104,105] for the average chiral condensate $\frac{1}{2}[{\Sigma }_u(eB,0)+{\Sigma }_d(eB,0)]$ in the whole range of applied magnetic fields $eB\le 9{\mathrm{GeV}}^2$. Moreover, we checked that our theoretical results were able to track the behavior of $\frac{1}{2}[{\Sigma }_u(eB,0)-{\Sigma }_d(eB,0)]$ versus $eB$ quite well as reported in Ref. [104]. We have, also, evaluated the thermal corrections and found satisfying agreement with the continuum extrapolated lattice results [104] in the confined phase. On the other hand, it should be evident that to understand the inverse magnetic catalysis, it is necessary to unravel the nature of the deconfined QCD vacuum in the presence of external magnetic fields. To do this, it is mandatory to try to explain the behavior of the critical deconfinement temperature as a function of the strength of the external magnetic field.

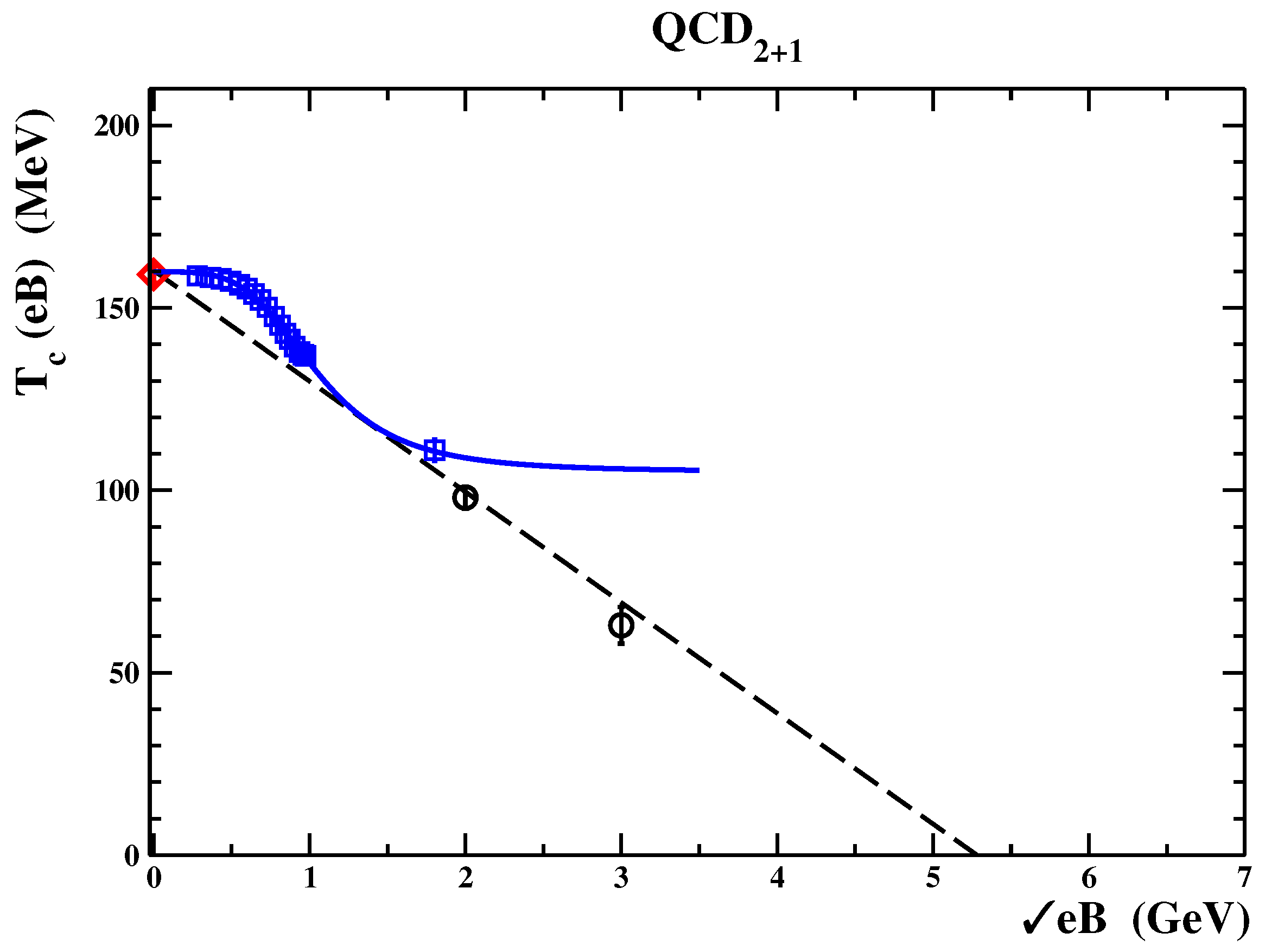
To this end, in Figure 7, we display the deconfinement temperature versus $\sqrt{eB}$. The lattice data have been taken from Figure 9, left upper panel, in Ref. [106] for $eB\lesssim 1{\mathrm{GeV}}^2$, from Ref. [105] at $eB=3.25{\mathrm{GeV}}^2$ and from Ref. [107] at $eB=4,9{\mathrm{GeV}}^2$. Looking at Figure 7, we see that the behavior of the deconfinement temperature clearly indicates the presence of two different regimes. For not too strong magnetic fields, $T_c\left(eB\right)$ smoothly decreases by increasing the strength of the applied magnetic field and it seems to saturate in the limit $eB\to \infty$. We agree with the discussion presented in Ref. [105] where this effect is ascribed to the explicit breaking of the rotational symmetry by the external magnetic field and the expected dimensional reduction in the quark sector. Indeed, from the structure of the gluon propagator in very strong magnetic fields (see Ref. [100] and references therein), one argues that the limiting effective gauge theory corresponds to an anisotropic pure gauge theory due to the enhancement of the chromo-dielectric constant. This qualitatively explains the small reduction in the deconfinement temperature and the saturation to an asymptotic value since for very strong magnetic fields, the fermions are expected to be frozen into the lowest Landau levels. Accordingly, in Ref. [105], the lattice data were fitted to the phenomenological law:

$$T_c\left(eB\right)=T_c\left(0\right)\frac{1+a_1{\left(eB\right)}^2}{1+a_2{\left(eB\right)}^2}.$$

(246)

In fact, for $eB\le 3.25{\mathrm{GeV}}^2$, the data are very well described by Equation (246) with [105]:

$$T_c\left(0\right)=160\left(2\right)\mathrm{MeV},a_1=0.54\left(2\right),a_2=0.82\left(2\right).$$

(247)

As a consistency check, we have fitted the data displayed in Figure 7 to Equation (246) and found:

$$T_c\left(0\right)=159.9\left(1.5\right)\mathrm{MeV},a_1=0.55\left(15\right),a_2=0.83\left(19\right).$$

(248)

It is reassuring to see that our fit is perfectly consistent with Equation (247), albeit with larger errors.

However, more recent studies presented in Ref. [107] found that the critical deconfinement temperatures suffer a further decrease in extremely strong magnetic fields $eB=4,9{\mathrm{GeV}}^2$ (see Figure 7). This kind of behavior cannot be explained by the screening effects for we already argued that the quarks are frozen into the lowest Landau levels. However, we may offer a plausible explanation within our picture of the QCD vacuum as a disordered chromomagnetic condensate. We rely on the one-loop calculations of the effective potential in QCD in external Abelian chromomagnetic and magnetic fields [108]. In fact, the chromomagnetic and magnetic fields are coupled to each other through the quark loops such that the vacuum energy is minimized if the external fields lie in the same direction. This means that external magnetic fields tend to polarize the chromomagnetic domains of our QCD vacuum. As a consequence, according to our previous discussion for the SU(3) pure gauge theory, we are led to expect the presence of the Meissner effect where the critical deconfinement temperature should decrease according to:

$$T_c\left(eB\right)=T_c\left(0\right)\left[1-\frac{\sqrt{eB}}{\sqrt{e{B}_c}}\right].$$

(249)

Actually, we find that the lattice data are consistent with Equation (249) for $eB\gtrsim 3{\mathrm{GeV}}^2$ (see the dashed line in Figure 7):

$$T_c\left(0\right)=160.2\left(3.7\right)\mathrm{MeV},\sqrt{e{B}_c}=5.28\left(31\right)\mathrm{GeV}.$$

(250)

It is interesting to note that Equation (249) agrees with Equation (1). However, before addressing any conclusions, it is desirable to investigate the behavior of the critical temperature versus applied chromomagnetic fields in QCD with dynamical quarks at the physical point.

A further indirect confirmation of our picture comes from the fact that at $eB=9{\mathrm{GeV}}^2$, the deconfinement transition turns into a first-order transition as in the pure gauge theory [107]. We may, now, gain further insight into the nature of the quantum vacuum by looking at the structure of the flux-tube chromoelectric fields. Remarkably, the authors of Ref. [93] investigated the transverse profile of the longitudinal chromoelectric field generated by static quark–antiquark pairs directed along the applied external magnetic field (longitudinal flux tube) as well as perpendicular to the magnetic field (transverse flux tube).

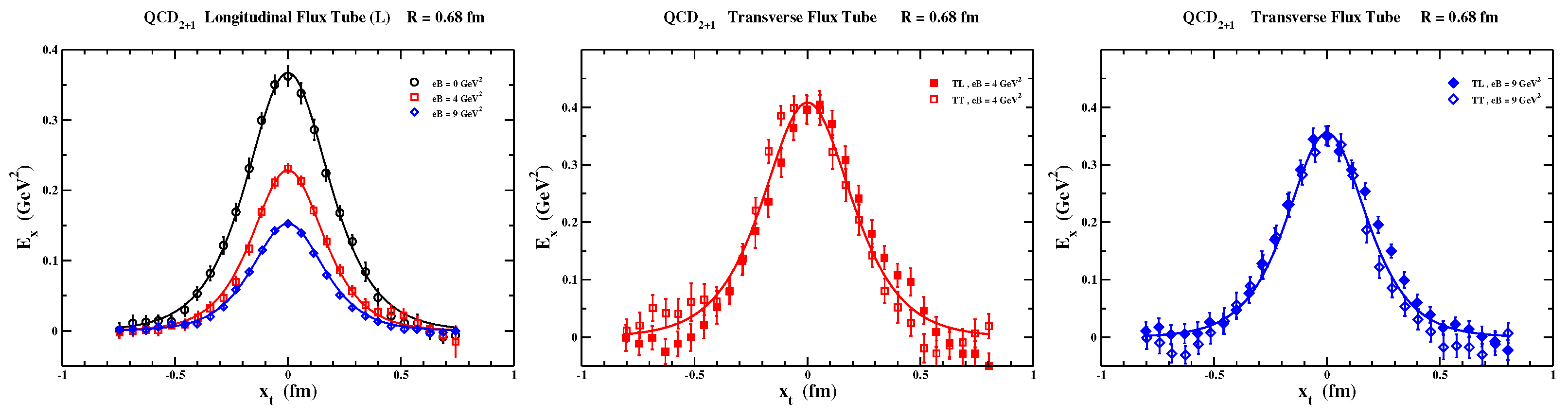
In Figure 8, we display the profile of the chromoelectric field for longitudinal and transverse flux tubes for three different values of the external magnetic field. Note that for $eB=0$, the lattice data have already been displayed in Figure 5, middle panel. From the fit to our Equation (221), we obtained:

$$\mathrm{eB}=0:v_{\varphi }\simeq 0.108,\sqrt{g{H}_0}\simeq 1.35\mathrm{GeV},\sqrt{\sigma }\simeq 314\mathrm{MeV}$$

(251)

where for the string tension, we are using Equations (207) and (208). Likewise, for the longitudinal flux tube (L), we obtain:

$$\mathrm{eB}=4{\mathrm{GeV}}^2:v_{\varphi }\simeq 0.051,\sqrt{g{H}_0}\simeq 1.55\mathrm{GeV},\sqrt{\sigma }\simeq 170\mathrm{MeV},$$

(252)

$$\mathrm{eB}=9{\mathrm{GeV}}^2:v_{\varphi }\simeq 0.034,\sqrt{g{H}_0}\simeq 1.55\mathrm{GeV},\sqrt{\sigma }\simeq 113\mathrm{MeV},$$

(253)

while for the transverse flux tubes (TT, TL) we obtain:

$$\mathrm{eB}=4{\mathrm{GeV}}^2:v_{\varphi }\simeq 0.14,\sqrt{g{H}_0}\simeq 1.25\mathrm{GeV},\sqrt{\sigma }\simeq 370\mathrm{MeV},$$

(254)

$$\mathrm{eB}=9{\mathrm{GeV}}^2:v_{\varphi }\simeq 0.10,\sqrt{g{H}_0}\simeq 1.45\mathrm{GeV},\sqrt{\sigma }\simeq 293\mathrm{MeV}.$$

(255)

The above results show quite clearly that the external magnetic field introduces strong anisotropies depending on the strength and orientation of the background field. Interestingly enough, we find that the transverse string tension does not vary appreciably, $\sqrt{{\sigma }_T}\simeq \sqrt{\sigma }$. On the contrary, the longitudinal string tension $\sqrt{{\sigma }_L}$ decreases rapidly with the increase in the strength of the magnetic field consistently with the decrease in the deconfinement critical temperature, Equation (249). More importantly, the decrease in the longitudinal string tension can be entirely ascribed to the drastic reduction in the azimuthal velocity $v_{\varphi }$, while the fitted chromomagnetic condensate $\sqrt{g{H}_0}$ seems to not vary appreciably. This means that for longitudinal flux tubes, only the chromomagnetic current responsible for the squeezing of the chromoelectric fields via the Ampere law is strongly suppressed. We see, thus, that the physical picture emerging from the behavior of a static quark–antiquark flux tube is in satisfying agreement with our scenario where the gauge system is driven in the deconfinement phase by means of polarization by the external background field of the vacuum chromomagnetic domains. Obviously, it remains an open question to see if and how our proposal to look at the thermal gauge system in the deconfined phase as a strongly correlated quantum liquid would eventually lead to the inverse magnetic catalysis.

7. Dynamical Quarks and Chiral Symmetry Breaking

Thus far, our analysis has been limited to the pure gauge sector of the theory. Now, we would like to take into account the dynamical fermion fields. Let us consider a massive quark field. In this case, in the temporal gauge, we must add to the gauge field Hamiltonian the following Dirac Hamiltonian:

$${\mathcal{H}}_D=\int d\overrightarrow{x}{\psi }^{†}\left(\overrightarrow{x}\right)\left\{\overrightarrow{\alpha }·[-i\overrightarrow{\nabla }+g{\overrightarrow{A}}^a\left(\overrightarrow{x}\right)\frac{{\lambda }^a}{2}]+\beta m\right\}\psi \left(\overrightarrow{x}\right).$$

(256)

In Equation (256), we are using the Bjorken–Drell [109] convention for the Dirac matrices. We are interested in evaluating the contributions of dynamical quarks to the vacuum energy in the lowest-order approximation. This approximation, after separating the gauge fields ${\overrightarrow{A}}^a\left(\overrightarrow{x}\right)$ into quantum fluctuations over the background field ${\overrightarrow{\overline{A}}}^a\left(\overrightarrow{x}\right)+{\overrightarrow{U}}^a\left(\overrightarrow{x}\right)$, amounts to neglecting in the Dirac Hamiltonian the contribution due to the fluctuations. Moreover, since the background fields ${\overrightarrow{U}}^a\left(\overrightarrow{x}\right)$ generated by the dynamical condensation driven by the unstable modes mainly affect the low-lying modes, in evaluating the vacuum energy, we may further simplify the Dirac Hamiltonian as:

$${\mathcal{H}}_D^{\left(0\right)}=\int d\overrightarrow{x}{\psi }^{†}\left(\overrightarrow{x}\right)\left\{\overrightarrow{\alpha }·[-i\overrightarrow{\nabla }+g{\overrightarrow{\overline{A}}}^a\left(\overrightarrow{x}\right)\frac{{\lambda }^a}{2}]+\beta m\right\}\psi \left(\overrightarrow{x}\right).$$

(257)

The role of the ${\overrightarrow{U}}^a\left(\overrightarrow{x}\right)$ background field will be discussed more fully later on. Obviously, the presence of the fermion fields modifies the Gauss constraints. Within the above approximations, for the Gauss law, we obtain:

$$D_i^{ab}\left(\overrightarrow{x}\right)\frac{\delta }{\delta {\eta }_i^b\left(\overrightarrow{x}\right)}\mathcal{S}[A,{\psi }^{†},\psi ]=-ig{\psi }^{†}\left(\overrightarrow{x}\right)\frac{{\lambda }^a}{2}\psi \left(\overrightarrow{x}\right)\mathcal{S}[A,{\psi }^{†},\psi ].$$

(258)

Following our previous variational studies in U(1) [110,111] and SU(2) [112] gauge theories in three space-time dimensions, we may solve Equation (258) by writing:

$$\mathcal{S}[\eta ,{\psi }^{†},\psi ]=\mathcal{G}\left[\eta \right]\mathcal{F}[{\psi }^{†},\psi ]exp\left\{{\Gamma }_{\psi }[\eta ,{\psi }^{†},\psi ]\right\}$$

(259)

with

$$D_i^{ab}\left(\overrightarrow{x}\right)\frac{\delta \mathcal{G}\left[\eta \right]}{\delta {\eta }_i^b\left(\overrightarrow{x}\right)}=0,$$

(260)

namely the wavefunctional $\mathcal{G}\left[\eta \right]$ depends on the transverse gauge fluctuations. It is, now, easy to see that:

$${\Gamma }_{\psi }[\eta ,{\psi }^{†},\psi ]=-ig\int d\overrightarrow{x}d\overrightarrow{y}{\psi }^{†}\left(\overrightarrow{x}\right)\frac{{\lambda }^a}{2}\psi \left(\overrightarrow{x}\right){\left[D^{-1}\right]}_j^{ab}(\overrightarrow{x},\overrightarrow{y}){\eta }_j^b\left(\overrightarrow{y}\right)$$

(261)

solves the Gauss law Equation (258). As shown in Ref. [110], it is quite easy to check that when evaluating the vacuum energy, the functional ${\Gamma }_{\psi }[\eta ,{\psi }^{†},\psi ]$ merely adds the Coulombic Hamiltonian:

$${\mathcal{H}}_C=\frac{g^2}{2}\int d\overrightarrow{x}d\overrightarrow{y}{\psi }^{†}\left(\overrightarrow{x}\right)\frac{{\lambda }^a}{2}\psi \left(\overrightarrow{x}\right){\left[D^{-2}\right]}^{ab}(\overrightarrow{x},\overrightarrow{y}){\psi }^{†}\left(\overrightarrow{y}\right)\frac{{\lambda }^b}{2}\psi \left(\overrightarrow{y}\right)$$

(262)

that in the one-loop approximation can be neglected. To determine the fermion wavefunctional $\mathcal{F}[{\psi }^{†},\psi ]$, following Refs. [110,111,112], we shall employ the holomorphic representation [113,114]. Firstly, for completeness, we show how this representation works for free massive Dirac fermions. The fermion field $\psi \left(\overrightarrow{x}\right)$ can be expanded as:

$$\psi \left(\overrightarrow{x}\right)=\sum _{\overrightarrow{p},s}\left[{\psi }_{\overrightarrow{p},s}^{(+)}\left(\overrightarrow{x}\right)a_{\overrightarrow{p},s}^{*}+{\psi }_{\overrightarrow{p},s}^{(-)}\left(\overrightarrow{x}\right)b_{\overrightarrow{p},s}^{*}\right]$$

(263)

where ${\psi }_{\overrightarrow{p},s}^{(\pm )}\left(\overrightarrow{x}\right)$ are the positive- and negative-energy solutions of the Dirac equation:

$$\left\{-i\overrightarrow{\alpha }·\overrightarrow{\nabla }+\beta m\right\}\psi \left(\overrightarrow{x}\right)=E\psi \left(\overrightarrow{x}\right).$$

(264)

In the holomorphic representation, $a_{\overrightarrow{p},s},a_{\overrightarrow{p},s}^{*},b_{\overrightarrow{p},s},b_{\overrightarrow{p},s}^{*}$ are independent Grassmann variables that act in the space of states $\mathcal{F}[a^{*},b^{*}]$ polynomials in $a_{\overrightarrow{p},s}^{*},b_{\overrightarrow{p},s}^{*}$ with the following scalar product:

$$<{\mathcal{F}}_1^{*},{\mathcal{F}}_2>=\int \prod _{\overrightarrow{p},s}d{a}_{\overrightarrow{p},s}^{*}d{a}_{\overrightarrow{p},s}exp\{-a_{\overrightarrow{p},s}^{*}{a}_{\overrightarrow{p},s}\}d{b}_{\overrightarrow{p},s}^{*}d{b}_{\overrightarrow{p},s}exp\{-b_{\overrightarrow{p},s}^{*}{b}_{\overrightarrow{p},s}\}{\mathcal{F}}_1^{*}[a^{*},b^{*}]{\mathcal{F}}_2[a^{*},b^{*}].$$

(265)

In this representation, the states, in general, can be written as:

$$\mathcal{F}[a^{*},b^{*}]=\prod _{\overrightarrow{p},s}\left[{\alpha }_{\overrightarrow{p},s}+{\beta }_{\overrightarrow{p},s}{a}_{\overrightarrow{p},s}^{*}\right]\left[{\gamma }_{\overrightarrow{p},s}+{\delta }_{\overrightarrow{p},s}{b}_{\overrightarrow{p},s}^{*}\right].$$

(266)

It is easy to check that:

$$<{\mathcal{F}}^{*},\mathcal{F}>=\prod _{\overrightarrow{p},s}\left[|{\alpha }_{\overrightarrow{p},s}{|}^2+{\left|{\beta }_{\overrightarrow{p},s}\right|}^2\right]\left[|{\gamma }_{\overrightarrow{p},s}{|}^2+{\left|{\delta }_{\overrightarrow{p},s}\right|}^2\right],$$

(267)

so that from $<{\mathcal{F}}^{*},\mathcal{F}>=1$ we obtain:

$${\alpha }_{\overrightarrow{p},s}=sin{\theta }_{\overrightarrow{p},s},{\beta }_{\overrightarrow{p},s}=cos{\theta }_{\overrightarrow{p},s},{\gamma }_{\overrightarrow{p},s}=sin{\varphi }_{\overrightarrow{p},s},{\delta }_{\overrightarrow{p},s}=cos{\varphi }_{\overrightarrow{p},s}.$$

(268)

It also straightforward to see that the ground state is given by:

$$\mathcal{F}\left[a^{*}\right]=\prod _{\overrightarrow{p},s}{a}_{\overrightarrow{p},s}^{*},$$

(269)

corresponding to ${\theta }_{\overrightarrow{p},s}=0$, ${\varphi }_{\overrightarrow{p},s}=\frac{\pi }{2}$, with vacuum energy:

$$E_0=-\frac{1}{2}\sum _{\overrightarrow{p},s}\sqrt{{\overrightarrow{p}}^2+m^2}=-V\int \frac{d\overrightarrow{p}}{{\left(2\pi \right)}^3}\sqrt{{\overrightarrow{p}}^2+m^2}.$$

(270)

Let us consider the Hamiltonian Equation (257). To determine the ground-state wavefunctional, it is enough to solve the following Dirac equation:

$$\left\{\overrightarrow{\alpha }·[-i\overrightarrow{\nabla }+g{\overrightarrow{\overline{A}}}^a\left(\overrightarrow{x}\right)\frac{{\lambda }^a}{2}]+\beta m\right\}\psi \left(\overrightarrow{x}\right)=E\psi \left(\overrightarrow{x}\right).$$

(271)

One finds that the calculation of the spectrum reduces to solving the Dirac equation for an electron in a uniform magnetic field by replacing $eH$ with $\pm \frac{gH}{2}$. Accordingly, we find the following spectrum:

$$\begin{array}{c}\hfill N_1=(\overrightarrow{p},s)E_{N_1}=\pm \sqrt{{\overrightarrow{p}}^2+m^2}\\ \hfill N_2=(p_3,p_2,n,\alpha )E_{N_2}=\pm \sqrt{p_3^2+m^2+\frac{g{H}_0}{2}(2n+1)+\alpha }n=0,1,2...,\alpha =\pm 1\\ \hfill N_3=(p_3^{\prime },p_2^{\prime },n^{\prime },{\alpha }^{\prime })E_{N_3}=\pm \sqrt{{p_3^{\prime }}^2+m^2+\frac{g{H}_0}{2}(2n^{\prime }+1)+{\alpha }^{\prime }}{n}^{\prime }=0,1,2...,{\alpha }^{\prime }=\pm 1\end{array}$$

(272)

Therefore, the vacuum wavefunctional turns out to be:

$${\mathcal{F}}_0[{\psi }^{†},\psi ]=\prod _{N_1,N_2,N_3}{a}_{N_1}^{*}{a}_{N_2}^{*}{a}_{N_3}^{*}$$

(273)

with energy:

$$E^{quark}\left(g{H}_0\right)=-V\left\{\sqrt{{\overrightarrow{p}}^2+m^2}+\frac{g{H}_0}{4{\pi }^2}{\int }_{-\infty }^{+\infty }d{p}_3\sum _{n=0}^{\infty }\sum _{\alpha =\pm 1}\sqrt{p_3^2+m^2+\frac{g{H}_0}{2}(2n+1)+\alpha }\right\}.$$

(274)

Proceeding as we did in Section 3 (see also Ref. [110], Appendix A), we may evaluate the sum over n and the integration over $p_3$. After subtracting the energy of the perturbative vacuum, we obtain:

$$\Delta E^{quark}\left(g{H}_0\right)=V\frac{g{H}_0}{8{\pi }^2}{\int }_0^{\infty }\frac{ds}{s^2}exp[-m^{2}s]\left\{coth\left(\frac{g{H}_{0}s}{2}\right)-\frac{2}{g{H}_{0}s}\right\}.$$

(275)

From Equation (275), we deduce that the main contribution comes from quarks with $m\ll \sqrt{gH}$. In this case, we find:

$$\Delta E^{quark}\left(g{H}_0\right)\simeq V{N}_f\frac{{\left(g{H}_0\right)}^2}{48{\pi }^2}\left[ln\left(\frac{{\Lambda }^2}{g{H}_0}\right)+const\right],$$

(276)

where $N_f$ is the number of almost massless flavors. As a consequence, we may still look at the vacuum wavefunctional as composed by almost independent chromomagnetic domains with energy ($N_c=3$):

$$\Delta E_D\left(g{H}_0\right)\simeq V_D(N_c+2N_f)\frac{{\left(g{H}_0\right)}^2}{48{\pi }^2}ln\left(\frac{{\Lambda }_H}{\sqrt{g{H}_0}}\right).$$

(277)

Remarkably, Equation (277) also applies to the SU(2) gauge theory ($N_c=2$). We are led, thus, to conclude that, within our approximations, the main effect of dynamical quarks is a slight increase in the vacuum energy in qualitative agreement with the discussion in the previous section. However, on the one hand it is well ascertained that confinement leads to the chiral symmetry breaking [115]; on the other hand, our proposal for the QCD vacuum wavefunctional does not give rise to a non-zero chiral condensate for massless quarks. Indeed, the Banks–Casher relation [116]

$$<\overline{\psi }\psi >=-\pi \rho \left(0\right)$$

(278)

relates the chiral condensate for massless quarks to the density of zero modes of the Dirac operator so that, for massless quarks, we need at least one zero mode localized in our chromomagnetic domains. However, for a given chromomagnetic domain, the fermion wavefunctional given by Equation (273) is built from modes corresponding to fermions in a uniform Abelian chromomagnetic field localized in the given domain. As a consequence, even for massless quarks, the low-lying modes display a mass gap of order $\frac{1}{L_D}$ and, thereby, cannot give rise to a non-zero chiral condensate. At this point, it is mandatory to take into account the background field $U_i^a\left(\overrightarrow{x}\right)$ induced by the condensation of the tachyonic modes that, as noticed before, could modify the fermion low-lying spectrum. In particular, we are interested in localized non-trivial solutions of the massless Dirac equation:

$$\overrightarrow{\alpha }·\left\{-i\overrightarrow{\nabla }+g[{\overrightarrow{\overline{A}}}^a\left(\overrightarrow{x}\right)+{\overrightarrow{U}}^a\left(\overrightarrow{x}\right)]\frac{{\lambda }^a}{2}\right\}\psi \left(\overrightarrow{x}\right)=0.$$

(279)

In the first part of the present paper, we showed that there are three different kinds of unstable modes, namely the u-modes, v-modes and w-modes. To gain insight into what is going on, for the moment, we simplify the problem by focusing on eventual zero modes due to the u-modes. In this case, we try to solve Equation (279) by writing:

$$\psi \left(\overrightarrow{x}\right)=\left(\begin{array}{c}{\psi }^{\left(1\right)}\left(\overrightarrow{x}\right)\\ {\psi }^{\left(2\right)}\left(\overrightarrow{x}\right)\\ 0\end{array}\right)$$

(280)

where ${\psi }^{\left(i\right)}\left(\overrightarrow{x}\right)$ are Dirac spinors. We further simplify the problem by assuming that:

$$\begin{array}{c}\hfill {\psi }^{\left(1\right)}\left(\overrightarrow{x}\right)=h\left(\overrightarrow{x}\right)\left(\begin{array}{c}{\chi }^{\left(2\right)}\\ {\chi }^{\left(2\right)}\end{array}\right),\\ \hfill {\psi }^{\left(2\right)}\left(\overrightarrow{x}\right)=h\left(\overrightarrow{x}\right)\left(\begin{array}{c}{\chi }^{\left(1\right)}\\ {\chi }^{\left(1\right)}\end{array}\right),\\ \hfill {\chi }^{\left(1\right)}=\left(\begin{array}{c}1\\ 0\end{array}\right),{\chi }^{\left(2\right)}=\left(\begin{array}{c}0\\ 1\end{array}\right).\end{array}$$

(281)

Inserting Equation (281) into Equation (279), we obtain:

$$-i\overrightarrow{\alpha }·\overrightarrow{\nabla }{\psi }^{\left(1\right)}\left(\overrightarrow{x}\right)+\frac{g{H}_0}{2}{x}_1{\alpha }_2{\psi }^{\left(1\right)}\left(\overrightarrow{x}\right)+g{f}^u\left(x_3\right)g_{-}^u(x_1,x_2){\psi }^{\left(1\right)}\left(\overrightarrow{x}\right)=0,$$

(282)

$$-i\overrightarrow{\alpha }·\overrightarrow{\nabla }{\psi }^{\left(2\right)}\left(\overrightarrow{x}\right)-\frac{g{H}_0}{2}{x}_1{\alpha }_2{\psi }^{\left(2\right)}\left(\overrightarrow{x}\right)+g{f}^u\left(x_3\right)g_{+}^u(x_1,x_2){\psi }^{\left(2\right)}\left(\overrightarrow{x}\right)=0.$$

(283)

Inspection of Equations (282) and (283) shows that:

$$h\left(\overrightarrow{x}\right)=\phi (x_1,x_2)\theta \left(x_3\right),$$

(284)

where the functions $\phi (x_1,x_2)$ and $\theta \left(x_3\right)$ must satisfy the following equations:

$$({\partial }_1-i{\partial }_2+\frac{g{H}_0}{2}{x}_1)\phi (x_1,x_2)=0$$

(285)

$$[i{\partial }_3+g{f}^u\left(x_3\right)g_{+}^u(x_1,x_2)]\theta \left(x_3\right)=0$$

(286)

with the constraint that $\theta \left(x_3\right)$ must be a real function. Solving Equation (285), we obtain:

$$\phi (x_1,x_2)=exp\left(i{p}_2{x}_2\right)exp\left[-\frac{g{H}_0}{4}{(x_1+\frac{p_2}{\frac{g{H}_0}{2}})}^2\right],$$

(287)

i.e., $\phi (x_1,x_2)$ belongs to the lowest Landau level wavefunctions. It is evident from Equation (287) that the zero-mode wavefunction is not localized in the chromomagnetic domain. However, due to the energy degeneracy, we may employ a suitable linear combination of the lowest Landau level wavefunctions such that the resulting wavefunction is localized in the given chromomagnetic domain. The best way to illustrate this point is to solve the Dirac equation in the symmetric gauge ${\overrightarrow{A}}_{sym}=(-\frac{1}{2}{x}_2{H}_0,\frac{1}{2}{x}_1{H}_0)$ that is related to the vector potential in the Landau gauge ${\overrightarrow{A}}_{Landau}=(-0,x_1{H}_0)$ by a gauge transformation:

$${\overrightarrow{A}}_{sym}(x_1,x_2)={\overrightarrow{A}}_{Landau}(x_1,x_2)-\overrightarrow{\nabla }\Phi (x_1,x_2),\Phi (x_1,x_2)=\frac{1}{2}{H}_0{x}_1{x}_2.$$

(288)

In our case, the relevant gauge transformation is implemented by the SU(3) matrix:

$$\Lambda \left(\overrightarrow{x}\right)=exp\left\{ig\Phi \left(\overrightarrow{x}\right)\frac{{\lambda }_3}{2}\right\}.$$

(289)

In the symmetric gauge, the eigenstates of the Dirac Hamiltonian are eigenstates of the angular momentum labeled by the integer m. In particular, the zero-mode wave functions are given by:

$${\Psi }_{0,m}(x_1,x_2)=\frac{1}{\sqrt{2^{m+1}\pi m!a_0^2}}{\left(\frac{x_1+i{x}_2}{a_0}\right)}^{m}exp\left[-\frac{(x_1^2+x_2^2)}{4a_0}\right],$$

(290)

where $a_0=\sqrt{\frac{2}{g{H}_0}}$. Using the normalized wavefunctions:

$${\phi }_{0,p_2}(x_1,x_2)={\left(\frac{g{H}_0}{2\pi }\right)}^{\frac{1}{4}}\frac{1}{\sqrt{2\pi }}exp\left(i{p}_2{x}_2\right)exp\left[-\frac{g{H}_0}{4}{(x_1+\frac{p_2}{\frac{g{H}_0}{2}})}^2\right],$$

(291)

one can show that [111]:

$$exp\left(i\frac{x_1{x}_2}{2a_0^2}\right){\Psi }_{0,m}(x_1,x_2)=\int d{p}_2{d}_m\left(p_2\right){\phi }_{0,p_2}(x_1,x_2)$$

(292)

with:

$$d_m\left(p_2\right)={\left(\frac{a_0^2}{\pi }\right)}^{\frac{1}{4}}\frac{1}{\sqrt{2^{m}m!}}exp(-a_0^2{p}_2^2)H_m\left(a_0{p}_2\right),$$

(293)

with $H_m\left(z\right)$ being Hermite polynomials. Note that the phase factor in Equation (292) is due to the gauge invariance. Since:

$$<r>=\sqrt{<x_1^2+x_2^2>}=\frac{1}{\sqrt{g{H}_0}}\sqrt{2(2m+1)},$$

(294)

we see that the condition $<r>\lesssim \frac{L_D}{2}$ requires $m=0$. As a consequence, the zero-mode wavefunction is given by:

$${\Psi }_{z-m}(x_1,x_2)={\Psi }_{0,0}(x_1,x_2)=\sqrt{\frac{g{H}_0}{4\pi }}exp\left[-\frac{g{H}_0}{8}(x_1^2+x_2^2)\right].$$

(295)

Let us consider now, Equation (286). By using the results in Section 3, we can rewrite this equation as:

$$\left[{\partial }_3-i\sqrt{g{H}_0}exp\left\{i{\delta }^u(x_1,x_2)\right\}tanh\left\{\frac{\sqrt{g{H}_0}}{2}{x}_3\right\}\right]\theta \left(x_3\right)=0$$

(296)

The formal solution of this last equation is:

$$\theta \left(x_3\right)={\left[\sec \mathrm{h}\left\{\frac{\sqrt{g{H}_0}}{2}{x}_3\right\}\right]}^{-i\sqrt{2}exp\left\{i{\delta }^u(x_1,x_2)\right\}}.$$

(297)

As discussed at length in Section 4, inside the chromomagnetic domain, the phase ${\delta }^u(x_1,x_2)$ is rapidly varying so that $exp\left\{i{\delta }^u(x_1,x_2)\right\}$ averages to zero. Therefore, we are led to conclude that

$$\theta \left(x_3\right)\simeq 1,\left|x_3\right|<\frac{L_D}{2}.$$

(298)

On the other hand, in the transition layer between two adjacent domains, the phase ${\delta }^u(x_1,x_2)$ must vary smoothly going from one domain to the adjacent domain. Since:

$$|\theta \left(x_3\right)|={\left[\sec \mathrm{h}\left\{\frac{\sqrt{g{H}_0}}{2}{x}_3\right\}\right]}^{\sqrt{2}sin\left\{{\delta }^u(x_1,x_2)\right\}},$$

(299)

we see that for $sin\left\{{\delta }^u(x_1,x_2)\right\}<0$, the zero-mode wavefunction is exponentially suppressed. In this case, we can write:

$$h_{z-m}(x_1,x_2,x_3)\simeq \frac{1}{\sqrt{L_D}}\sqrt{\frac{g{H}_0}{4\pi }}exp\left[-\frac{g{H}_0}{8}(x_1^2+x_2^2)\right],\left|x_3\right|\lesssim \frac{L_D}{2}.$$

(300)

We have also checked that even including the effects due to the induced background fields ${\overrightarrow{v}}^a\left(\overrightarrow{x}\right)$ and ${\overrightarrow{w}}^a\left(\overrightarrow{x}\right)$ does not modify the zero-mode wavefunction given by Equation (300). We may, thus, conclude that an arbitrary chromomagnetic domain could accommodate two zero modes as given by Equations (281) and (300) so that, according to the Banks–Casher relation, we have:

$$<\overline{\psi }\psi >\simeq -\frac{2\pi }{L_D^3}.$$

(301)

Note that:

$$|<\overline{\psi }{\psi >|}^{\frac{1}{3}}\sim \frac{1}{L_D}\sim {10}^2\mathrm{MeV}$$

(302)

that is of the correct order of magnitude with respect to several lattice determinations (see, e.g., Ref. [117], and references therein). Moreover, according to the general discussion in Ref. [94], the rate of change of chirality leads to an effective quark mass $m_{eff}\sim \frac{1}{L_D}\sim {10}^2$ MeV that compares reasonably well to phenomenology.

We would like to conclude the present section by discussing the intriguing results presented in Ref. [118] where it was shown that the magnitude of the chiral condensate is reduced inside the color flux tube generated by a static quark–antiquark pair. This result is interpreted as evidence of partial restoration of the chiral symmetry inside hadrons. However, our explanation for the formation of the chiral condensate leads to different conclusions. Indeed, in the previous section, we have seen that the squeezing of the color fields into a narrow flux tube is due to chromomagnetic currents almost uniform along the flux tube that, in turn, originate from the polarization of the chromomagnetic domains. As a consequence, along the flux tube, one must picture having a larger coherent chromomagnetic domain with an effective volume that increases according to $V_D\frac{R}{L_D}$, where R is the distance between the static color sources. It follows, then, that the chiral condensate is reduced by approximatively a factor $\frac{L_D}{R}$ for large enough R. This result, not only explains naturally the suppression of the chiral condensate inside the flux tube, but also seems to be in qualitative agreement with Figure 3 in Ref. [118] where the ratio of the chiral condensate at the center of the flux tube versus the separation distance R is displayed.

8. Summary and Concluding Remarks

Quantum chromodynamics is widely accepted as the fundamental theory of strong interactions. However, the confinement of quarks and gluons into hadrons, namely color singlet states, has evaded a satisfying understanding. Actually, the absence of asymptotic colored particle states leads to the time-honored confinement problem in QCD. The purpose of this paper was to gain an insight into color and quark confinement starting from first principles. The first part of this paper was devoted to extending the SU(3) gauge theory from our previous work in the pure gauge SU(2) theory in the presence of an Abelian chromomagnetic field. We demonstrated for the first time the presence in SU(3) of three different kinds of unstable modes. We set up a perturbative-variational scheme by employing gauge-invariant wavefunctionals that allowed us to minimize the ground-state energy and, at the same time, to stabilize the instabilities that affected the low-order evaluation of the vacuum energy. As in the SU(2) theory, the condensation of the tachyonic modes by quantum fluctuations lead to the dynamical generation of three different background fields with a peculiar kink structure typical of the (1+1)-dimensional charged scalar fields subject to dynamical symmetry breaking. The resulting stabilized ground-state wavefunctional turned out to be not energetically favoured with respect to the perturbative quantum vacuum. However, we have shown that the stabilized ground-state wavefunctional looked like a collection of independent domains each characterized by almost the same chromomagnetic condensate pointing in arbitrary space and color directions. Separating these chromomagnetic domains are Bloch walls that carry an energy per unit area leading to a further increase in the vacuum energy. Nevertheless, we argued that the number of gauge field configurations that realize the vacuum wavefunctional were large enough to span a set of finite volume in the functional space of physical states. After introducing the configurational entropy, we found that there was an order–disorder quantum phase transition of the Berezinskii–Kosterlitz–Thouless type at an energy scale of order $\frac{1}{L_D}$ separating the perturbative vacuum from our disordered chromomagnetic condensate quantum vacuum. It is important, at this point, to stress that our proposal for the ground-state wavefunctional should account for the QCD vacuum at large distances. On the other hand, at very small distances, our wavefunctional should be smoothly replaced by the perturbative ground state, realizing in this way the Bjorken’s femptouniverse.

In the second part of the paper, we addressed the problem of seeing if our vacuum wavefunctional could be a viable proposal for the QCD quantum vacuum. Indeed, we showed that the disordered chromomagnetic condensate vacuum displayed a non-zero gluon condensate of the right order of magnitude. In addition, we argued that our proposal for the QCD vacuum had both a finite energy gap and absence of color correlations for distances larger than $L_D$ leading to the confinement of colors. We have, also, advanced a vivid picture of the formation of the flux-tube chromoelectric fields for a static quark–antiquark pair. The squeezing of the chromoelectric fields into a narrow tube was caused by Lorentz forces generated by the chromomagnetic currents originating from the background fields induced by the dynamical condensation by quantum fluctuations of the tachyonic mode. This allowed us to determine the color structure and the transverse profile of the flux-tube chromoelectric fields that compared favorably to several non-perturbative numerical simulations in lattice QCD. Our proposal for the quantum QCD vacuum allowed us to understand the origin of the color Meissner effect observed in lattice simulations of the pure gauge SU(3) theory as well as in QCD with two massive degenerate staggered quarks. Moreover, our proposal allowed us to reach a physical explanation of the evidence of the Meissner effect from lattice simulations of QCD with (2+1)-flavors at the physical point in very strong external magnetic fields. This led us to the prevision of a new quantum phase transition in the QCD phase diagram where at the critical magnetic field, the gauge system undergoes a deconfinement transition to a quantum liquid made of quarks and gluons with strong chromomagnetic correlations. Finally, we showed that the inclusion of dynamical quarks did not modify substantially the chromomagnetic domain structure of our vacuum wavefunctional. Remarkably, we suggested that for massless quarks, the background fields dynamically generated by the condensation of the unstable modes could allow the formation of fermion zero modes localized on the chromomagnetic domains that, in turn, led to the spontaneous breaking of the chiral symmetry with an ensuing chiral condensate of the correct order of magnitude.

To conclude, the purpose of this paper has been to understand confinement from first principles. As a matter of fact, we are aware that the analysis we followed, albeit quite involved, has been useful, leading to a proof of concept that confinement can be understood. The comparison of our approach to hadron phenomenology and non-perturbative simulations of QCD on the lattice seems to suggest that we are on the right track, even though there are still many things to do and questions to answer. Nevertheless, with the present paper, we hope to stimulate further studies to reach a complete quantitative understanding of confinement in quantum chromodynamics.