The Magellanic Clouds Are Very Rare in the IllustrisTNG Simulations
Abstract
1. Introduction
2. Methods
2.1. Observations
2.2. The TNG Cosmological Simulations
2.3. Selecting Analogues to the MW
2.4. Selecting Analogues to the MCs
3. Results
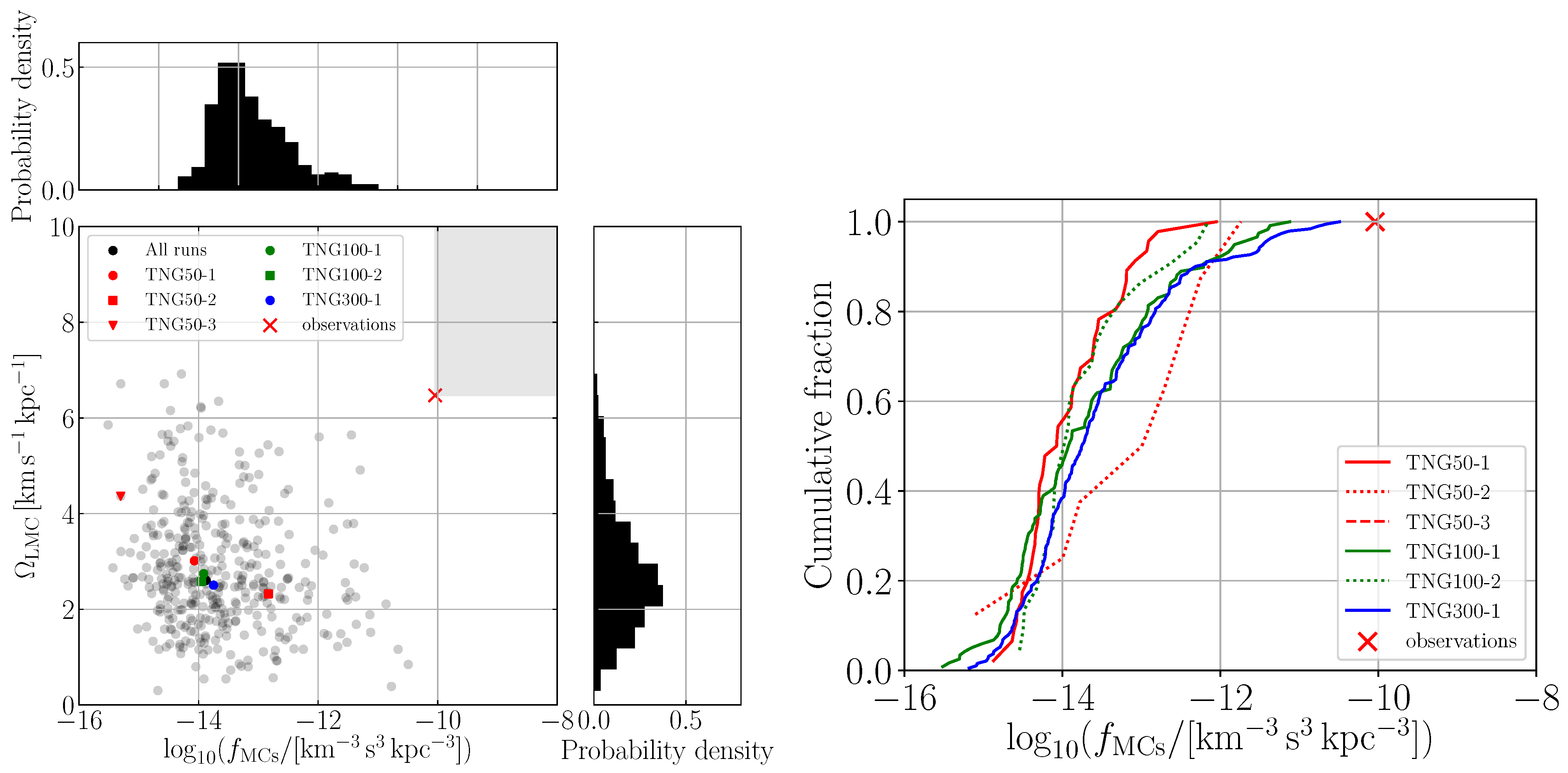
3.1. Phase-Space Density of the MCs
3.2. Tracing Back Analogues to the MCs in Light of the MS
4. Discussion
4.1. Prior Studies on the MCs in CDM
4.2. First Infall Scenario
4.3. Relating the MCs to the DoS
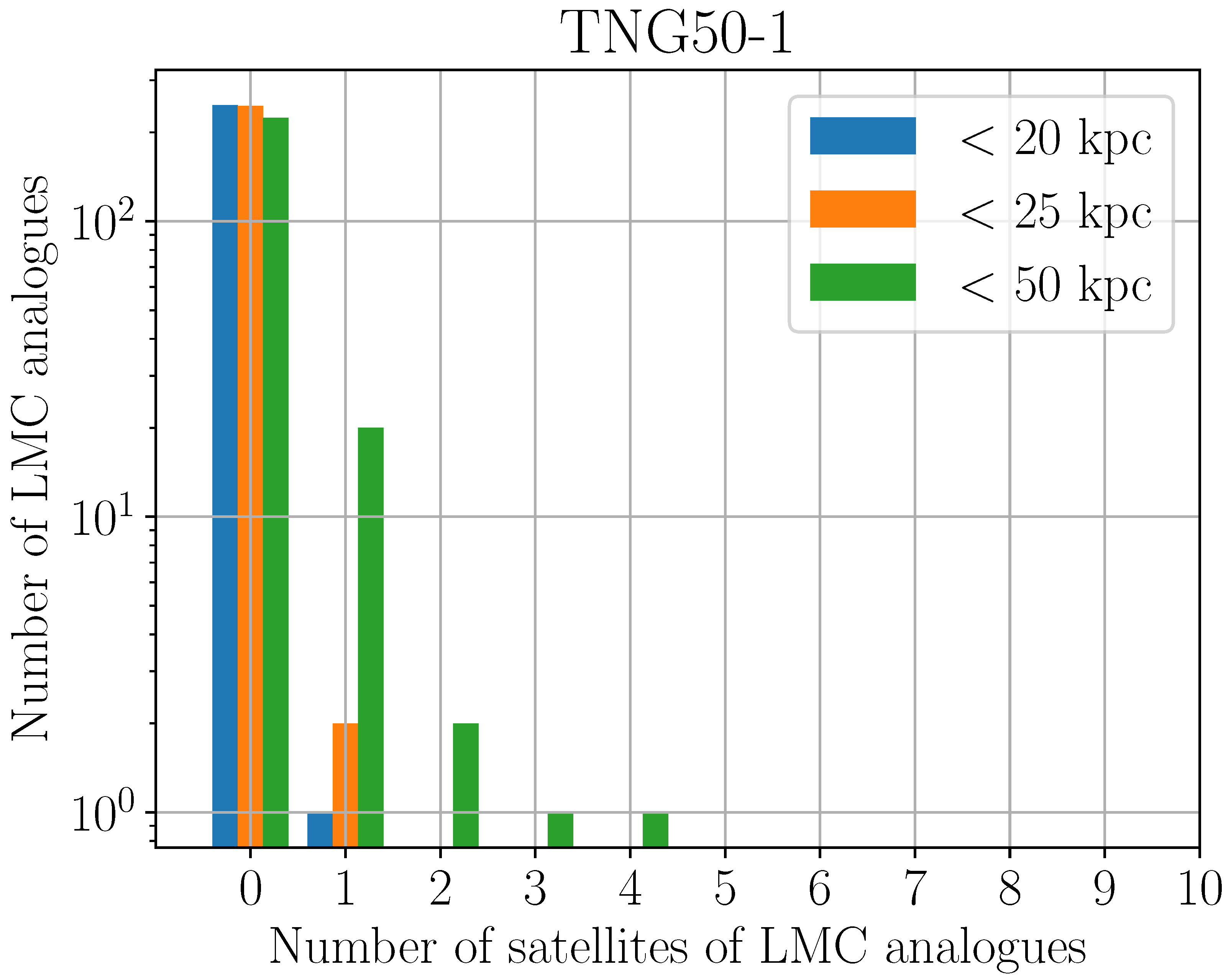
4.3.1. Satellites of the LMC
4.3.2. Alignment of the LMC with the DoS
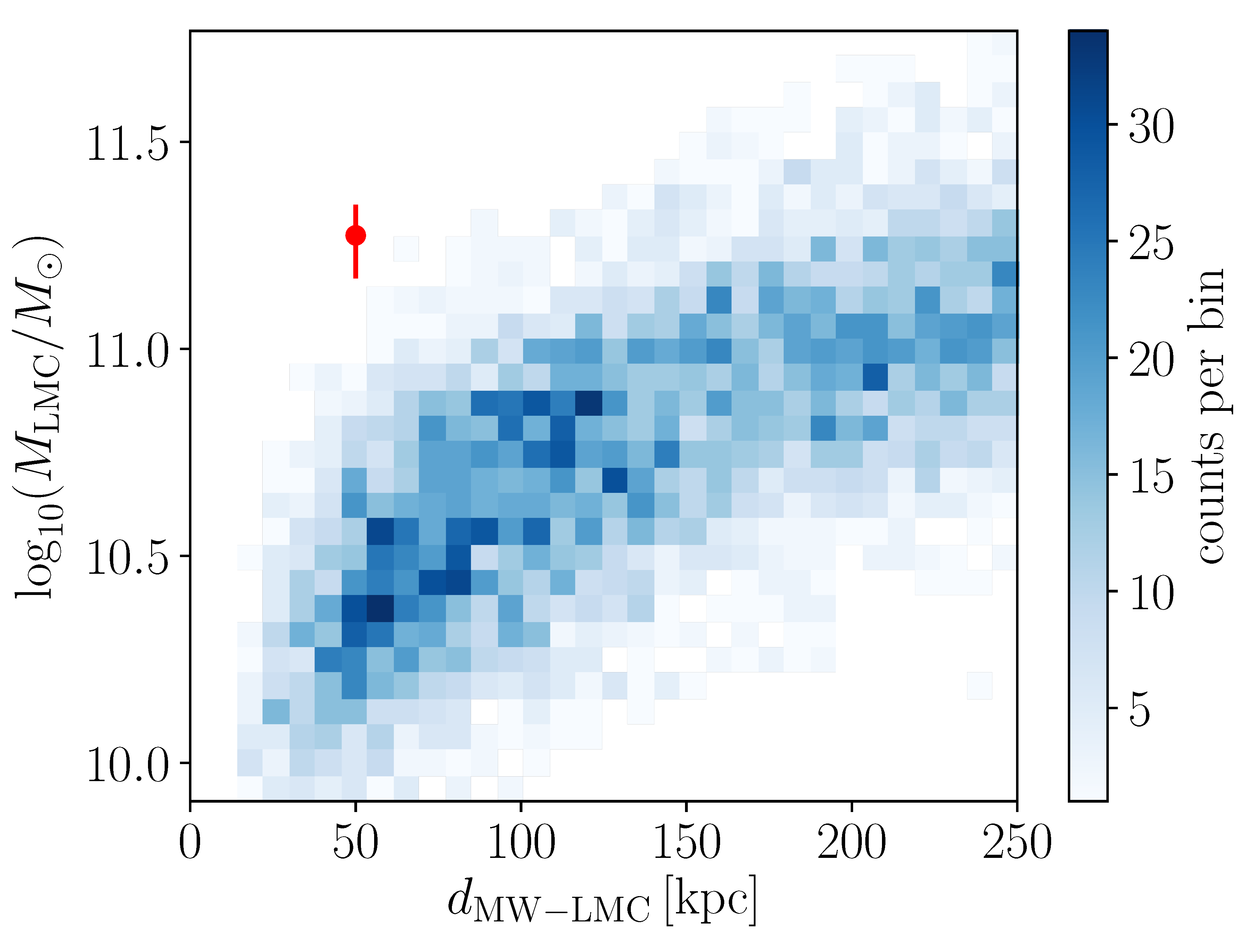
4.4. Total Mass of LMC Analogues
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
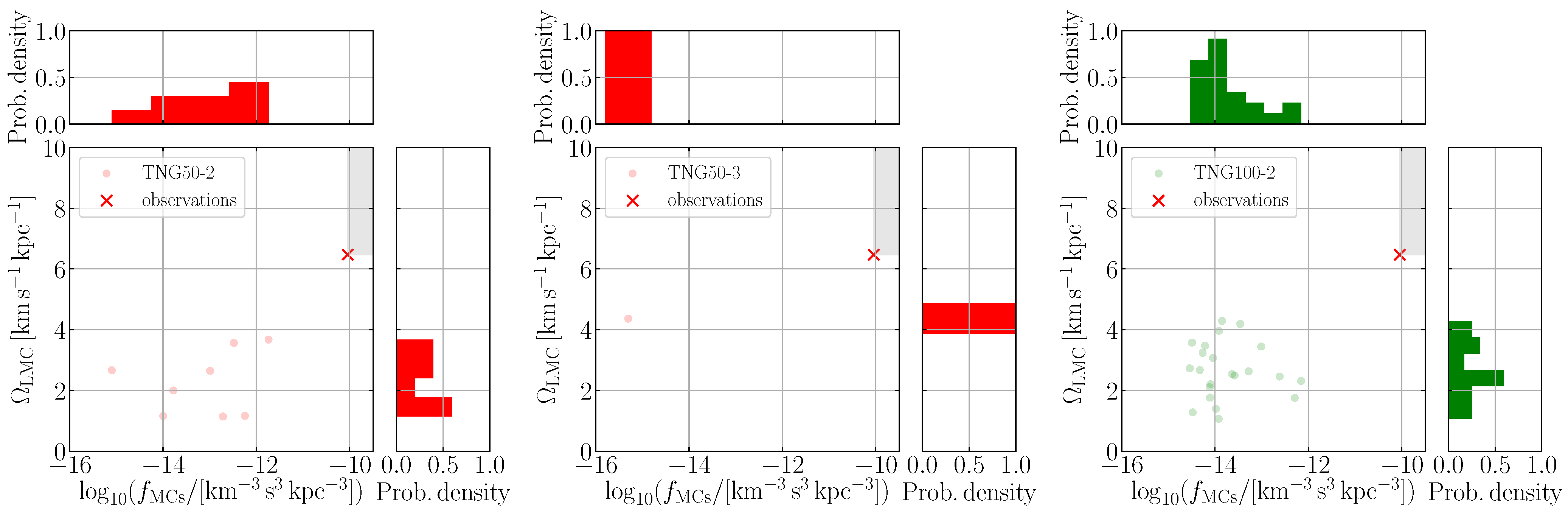
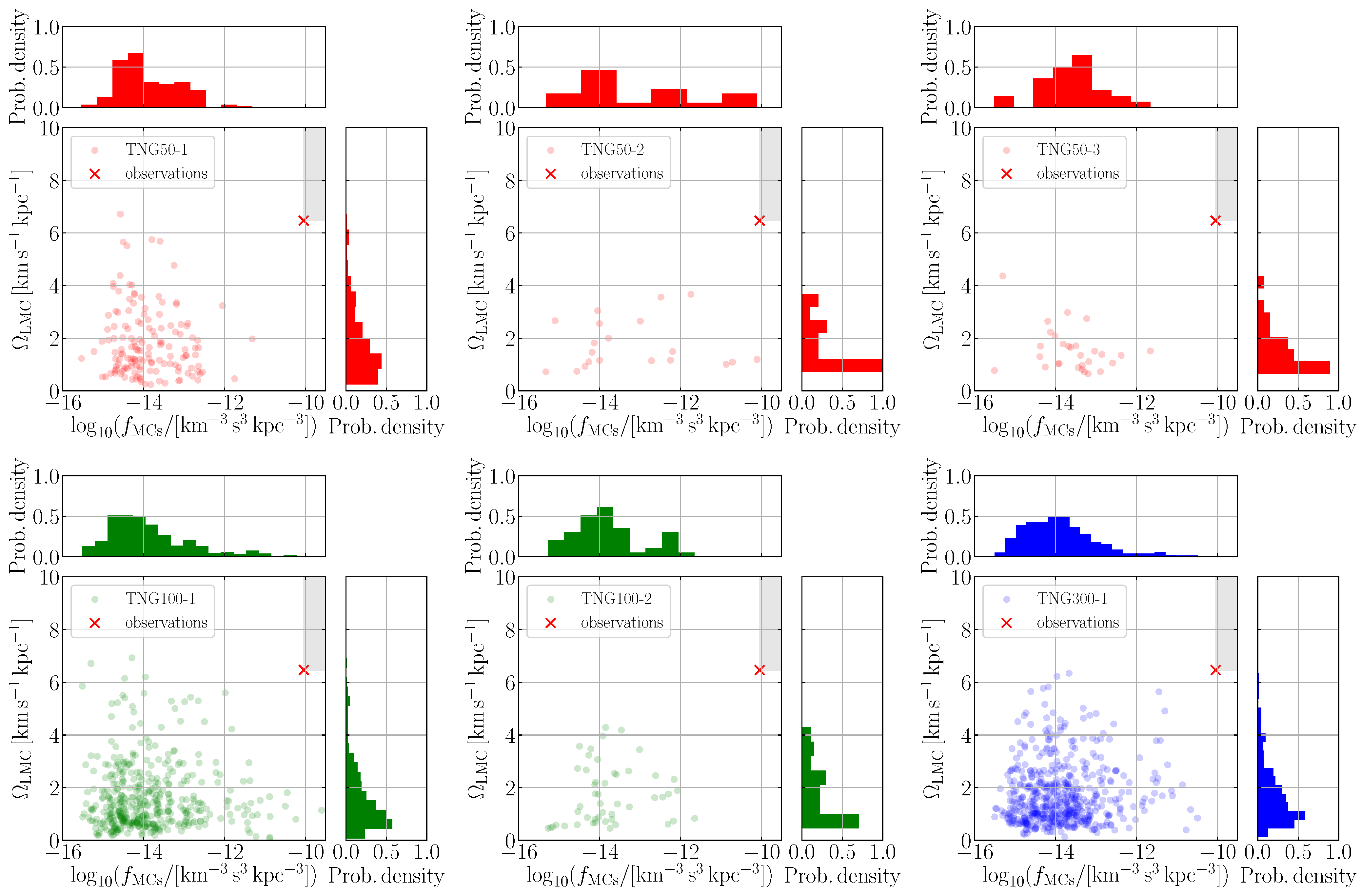
Appendix A. Effect of Resolution
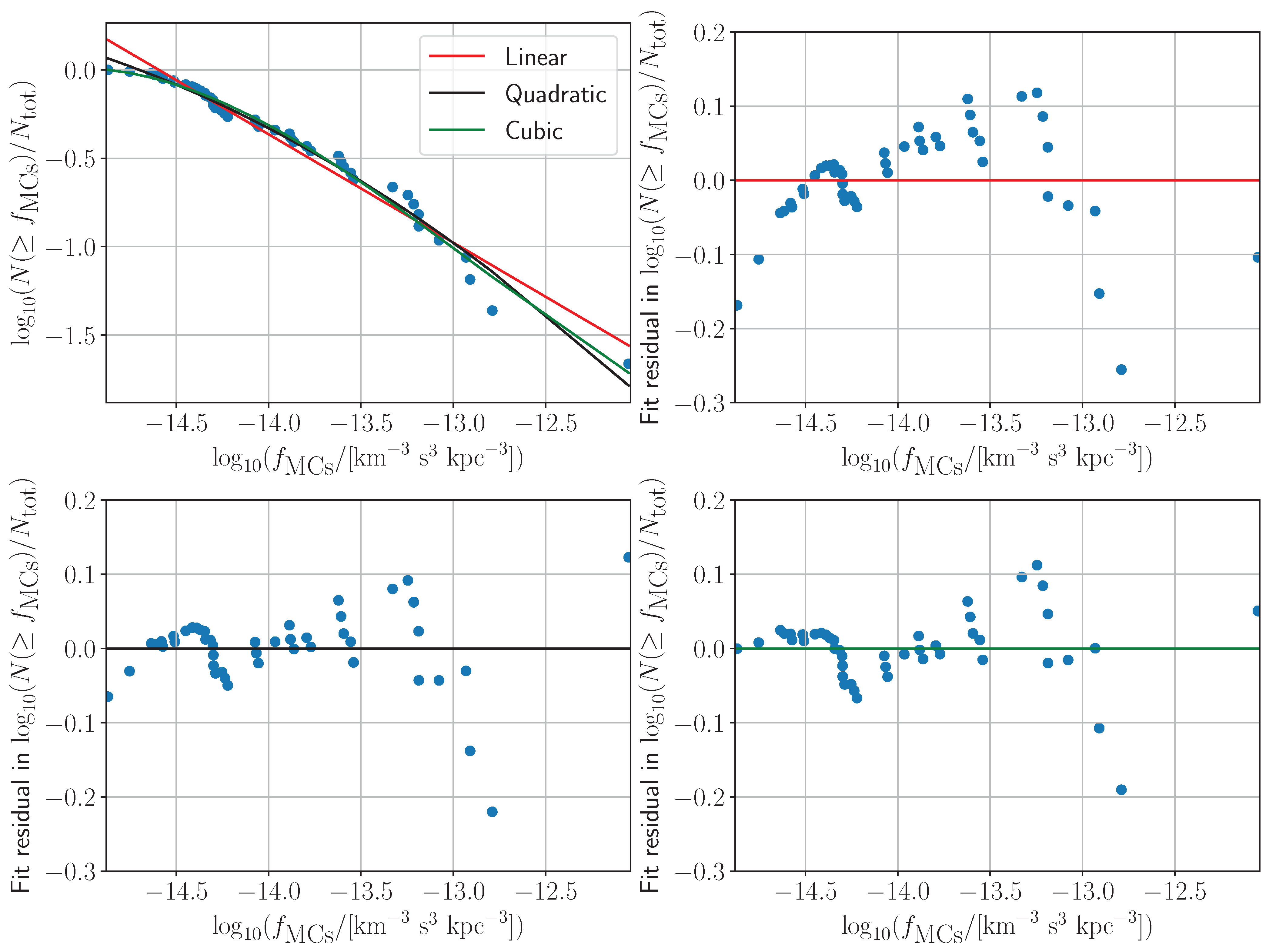
Appendix B. Comparison of Polynomial Fits to the fMCs Distribution
Appendix C. Different Selection Criteria
| 1 | Stellar particles and gas cells. |
| 2 | https://www.tng-project.org/data/docs/specifications/ (accessed on 15 March 2021). |
| 3 | https://seafile.unistra.fr/d/6b09464443da478d8926/ (accessed on 7 November 2022). |
| 4 | The corresponding range of virial radii is 168–287 kpc. |
| 5 | A description of the SubhaloFlag parameter can be found here: https://www.tng-project.org/data/docs/background/#subhaloflag (accessed on 8 March 2022). |
| 6 | |
| 7 | here refers to the total mass of all particles and cells which are bound to this subhalo as listed in the subfind subhalos catalogue (https://www.tng-project.org/data/docs/specifications/#sec2b, accessed on 23 September 2024). |
References
- Kroupa, P. Galaxies as simple dynamical systems: Observational data disfavor dark matter and stochastic star formation. Can. J. Phys. 2015, 93, 169–202. [Google Scholar] [CrossRef]
- Oehm, W.; Kroupa, P. The Relevance of Dynamical Friction for the MW/LMC/SMC Triple System. Universe 2024, 10, 143. [Google Scholar] [CrossRef]
- Massana, P.; Ruiz-Lara, T.; Noël, N.E.D.; Gallart, C.; Nidever, D.L.; Choi, Y.; Sakowska, J.D.; Besla, G.; Olsen, K.A.G.; Monelli, M.; et al. The synchronized dance of the magellanic clouds’ star formation history. Mon. Not. R. Astron. Soc. 2022, 513, L40–L45. [Google Scholar] [CrossRef]
- Kroupa, P.; Röser, S.; Bastian, U. On the motion of the Magellanic Clouds. Mon. Not. R. Astron. Soc. 1994, 266, 412–420. [Google Scholar] [CrossRef]
- Röser, S.; Bastian, U. The Final PPM Star Catalogue for Both Hemispheres. Bull. D’Inf. Cent. Donnees Stellaires 1993, 42, 11–16. [Google Scholar]
- Perryman, M.A.C.; Lindegren, L.; Kovalevsky, J.; Hog, E.; Bastian, U.; Bernacca, P.L.; Creze, M.; Donati, F.; Grenon, M.; Grewing, M.; et al. The Hipparcos Catalogue. Astron. Astrophys. 1997, 500, 501–504. [Google Scholar]
- Kroupa, P.; Bastian, U. The HIPPARCOS proper motion of the Magellanic Clouds. Nat. Astron. 1997, 2, 77–90. [Google Scholar] [CrossRef]
- Kallivayalil, N.; van der Marel, R.P.; Alcock, C.; Axelrod, T.; Cook, K.H.; Drake, A.J.; Geha, M. The Proper Motion of the Large Magellanic Cloud Using HST. Astrophys. J. 2006, 638, 772–785. [Google Scholar] [CrossRef]
- Kallivayalil, N.; van der Marel, R.P.; Alcock, C. Is the SMC Bound to the LMC? The Hubble Space Telescope Proper Motion of the SMC. Astrophys. J. 2006, 652, 1213–1229. [Google Scholar] [CrossRef]
- Kallivayalil, N.; van der Marel, R.P.; Besla, G.; Anderson, J.; Alcock, C. Third-epoch Magellanic Cloud Proper Motions. I. Hubble Space Telescope/WFC3 Data and Orbit Implications. Astrophys. J. 2013, 764, 161. [Google Scholar] [CrossRef]
- Gaia Collaboration. The Gaia mission. Astron. Astrophys. 2016, 595, A1. [Google Scholar] [CrossRef]
- Gaia Collaboration. Gaia Data Release 2. Summary of the contents and survey properties. Astron. Astrophys. 2018, 616, A1. [Google Scholar] [CrossRef]
- Gaia Collaboration. Gaia Data Release 2. Kinematics of globular clusters and dwarf galaxies around the Milky Way. Astron. Astrophys. 2018, 616, A12. [Google Scholar] [CrossRef]
- Efstathiou, G.; Sutherland, W.J.; Maddox, S.J. The cosmological constant and cold dark matter. Nature 1990, 348, 705–707. [Google Scholar] [CrossRef]
- Ostriker, J.P.; Steinhardt, P.J. The observational case for a low-density Universe with a non-zero cosmological constant. Nature 1995, 377, 600–602. [Google Scholar] [CrossRef]
- McConnachie, A.W. The Observed Properties of Dwarf Galaxies in and around the Local Group. Astron. J. 2012, 144, 4. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Kroupa, P. The Milky Way’s disc of classical satellite galaxies in light of Gaia DR2. Mon. Not. R. Astron. Soc. 2020, 491, 3042–3059. [Google Scholar] [CrossRef]
- Besla, G.; Kallivayalil, N.; Hernquist, L.; Robertson, B.; Cox, T.J.; van der Marel, R.P.; Alcock, C. Are the Magellanic Clouds on Their First Passage about the Milky Way? Astrophys. J. 2007, 668, 949–967. [Google Scholar] [CrossRef]
- Weisz, D.R.; Dolphin, A.E.; Skillman, E.D.; Holtzman, J.; Dalcanton, J.J.; Cole, A.A.; Neary, K. Comparing the ancient star formation histories of the Magellanic Clouds. Mon. Not. R. Astron. Soc. 2013, 431, 364–371. [Google Scholar] [CrossRef][Green Version]
- Mazzi, A.; Girardi, L.; Zaggia, S.; Pastorelli, G.; Rubele, S.; Bressan, A.; Cioni, M.R.L.; Clementini, G.; Cusano, F.; Rocha, J.P.; et al. The VMC survey—XLIII. The spatially resolved star formation history across the Large Magellanic Cloud. Mon. Not. R. Astron. Soc. 2021, 508, 245–266. [Google Scholar] [CrossRef]
- Nidever, D.L.; Majewski, S.R.; Butler Burton, W.; Nigra, L. The 200° Long Magellanic Stream System. Astrophys. J. 2010, 723, 1618–1631. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Pflamm-Altenburg, J.; Kroupa, P. The VPOS: A vast polar structure of satellite galaxies, globular clusters and streams around the Milky Way. Mon. Not. R. Astron. Soc. 2012, 423, 1109–1126. [Google Scholar] [CrossRef]
- D’Onghia, E.; Fox, A.J. The Magellanic Stream: Circumnavigating the Galaxy. Annu. Rev. Astron. Astrophys. 2016, 54, 363–400. [Google Scholar] [CrossRef]
- Hammer, F.; Yang, Y.B.; Flores, H.; Puech, M.; Fouquet, S. The Magellanic Stream System. I. Ram-Pressure Tails and the Relics of the Collision Between the Magellanic Clouds. Astrophys. J. 2015, 813, 110. [Google Scholar] [CrossRef]
- Busha, M.T.; Marshall, P.J.; Wechsler, R.H.; Klypin, A.; Primack, J. The Mass Distribution and Assembly of the Milky Way from the Properties of the Magellanic Clouds. Astrophys. J. 2011, 743, 40. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Besla, G.; Hernquist, L. Dynamics of the Magellanic Clouds in a Lambda cold dark matter universe. Mon. Not. R. Astron. Soc. 2011, 414, 1560–1572. [Google Scholar] [CrossRef]
- Santos-Santos, I.M.E.; Fattahi, A.; Sales, L.V.; Navarro, J.F. Magellanic satellites in ΛCDM cosmological hydrodynamical simulations of the Local Group. Mon. Not. R. Astron. Soc. 2021, 504, 4551–4567. [Google Scholar] [CrossRef]
- Pillepich, A.; Springel, V.; Nelson, D.; Genel, S.; Naiman, J.; Pakmor, R.; Hernquist, L.; Torrey, P.; Vogelsberger, M.; Weinberger, R.; et al. Simulating galaxy formation with the IllustrisTNG model. Mon. Not. R. Astron. Soc. 2018, 473, 4077–4106. [Google Scholar] [CrossRef]
- Nelson, D.; Springel, V.; Pillepich, A.; Rodriguez-Gomez, V.; Torrey, P.; Genel, S.; Vogelsberger, M.; Pakmor, R.; Marinacci, F.; Weinberger, R.; et al. The IllustrisTNG simulations: Public data release. Comput. Astrophys. Cosmol. 2019, 6, 2. [Google Scholar] [CrossRef]
- Pillepich, A.; Nelson, D.; Springel, V.; Pakmor, R.; Torrey, P.; Weinberger, R.; Vogelsberger, M.; Marinacci, F.; Genel, S.; van der Wel, A.; et al. First results from the TNG50 simulation: The evolution of stellar and gaseous discs across cosmic time. Mon. Not. R. Astron. Soc. 2019, 490, 3196–3233. [Google Scholar] [CrossRef]
- Nelson, D.; Pillepich, A.; Springel, V.; Weinberger, R.; Hernquist, L.; Pakmor, R.; Genel, S.; Torrey, P.; Vogelsberger, M.; Kauffmann, G.; et al. First results from the IllustrisTNG simulations: The galaxy colour bimodality. Mon. Not. R. Astron. Soc. 2018, 475, 624–647. [Google Scholar] [CrossRef]
- Nelson, D.; Pillepich, A.; Springel, V.; Pakmor, R.; Weinberger, R.; Genel, S.; Torrey, P.; Vogelsberger, M.; Marinacci, F.; Hernquist, L. First results from the TNG50 simulation: Galactic outflows driven by supernovae and black hole feedback. Mon. Not. R. Astron. Soc. 2019, 490, 3234–3261. [Google Scholar] [CrossRef]
- Marinacci, F.; Vogelsberger, M.; Pakmor, R.; Torrey, P.; Springel, V.; Hernquist, L.; Nelson, D.; Weinberger, R.; Pillepich, A.; Naiman, J.; et al. First results from the IllustrisTNG simulations: Radio haloes and magnetic fields. Mon. Not. R. Astron. Soc. 2018, 480, 5113–5139. [Google Scholar] [CrossRef]
- Naiman, J.P.; Pillepich, A.; Springel, V.; Ramirez-Ruiz, E.; Torrey, P.; Vogelsberger, M.; Pakmor, R.; Nelson, D.; Marinacci, F.; Hernquist, L.; et al. First results from the IllustrisTNG simulations: A tale of two elements—Chemical evolution of magnesium and europium. Mon. Not. R. Astron. Soc. 2018, 477, 1206–1224. [Google Scholar] [CrossRef]
- Springel, V.; Pakmor, R.; Pillepich, A.; Weinberger, R.; Nelson, D.; Hernquist, L.; Vogelsberger, M.; Genel, S.; Torrey, P.; Marinacci, F.; et al. First results from the IllustrisTNG simulations: Matter and galaxy clustering. Mon. Not. R. Astron. Soc. 2018, 475, 676–698. [Google Scholar] [CrossRef]
- Vogelsberger, M.; Genel, S.; Springel, V.; Torrey, P.; Sijacki, D.; Xu, D.; Snyder, G.; Bird, S.; Nelson, D.; Hernquist, L. Properties of galaxies reproduced by a hydrodynamic simulation. Nature 2014, 509, 177–182. [Google Scholar] [CrossRef]
- Nelson, D.; Pillepich, A.; Genel, S.; Vogelsberger, M.; Springel, V.; Torrey, P.; Rodriguez-Gomez, V.; Sijacki, D.; Snyder, G.F.; Griffen, B.; et al. The illustris simulation: Public data release. Astron. Comput. 2015, 13, 12–37. [Google Scholar] [CrossRef]
- Planck Collaboration XIII. Planck 2015 results. XIII. Cosmological parameters. Astron. Astrophys. 2016, 594, A13. [Google Scholar] [CrossRef]
- Springel, V.; White, S.D.M.; Tormen, G.; Kauffmann, G. Populating a cluster of galaxies—I. Results at z = 0. Mon. Not. R. Astron. Soc. 2001, 328, 726–750. [Google Scholar] [CrossRef]
- Dolag, K.; Borgani, S.; Murante, G.; Springel, V. Substructures in hydrodynamical cluster simulations. Mon. Not. R. Astron. Soc. 2009, 399, 497–514. [Google Scholar] [CrossRef]
- Rodriguez-Gomez, V.; Genel, S.; Vogelsberger, M.; Sijacki, D.; Pillepich, A.; Sales, L.V.; Torrey, P.; Snyder, G.; Nelson, D.; Springel, V.; et al. The merger rate of galaxies in the Illustris simulation: A comparison with observations and semi-empirical models. Mon. Not. R. Astron. Soc. 2015, 449, 49–64. [Google Scholar] [CrossRef]
- Banik, I.; Haslbauer, M.; Pawlowski, M.S.; Famaey, B.; Kroupa, P. On the absence of backsplash analogues to NGC 3109 in the ΛCDM framework. Mon. Not. R. Astron. Soc. 2021, 503, 6170–6186. [Google Scholar] [CrossRef]
- McMillan, P.J. The mass distribution and gravitational potential of the Milky Way. Mon. Not. R. Astron. Soc. 2017, 465, 76–94. [Google Scholar] [CrossRef]
- Posti, L.; Helmi, A. Mass and shape of the Milky Way’s dark matter halo with globular clusters from Gaia and Hubble. Astron. Astrophys. 2019, 621, A56. [Google Scholar] [CrossRef]
- Vasiliev, E.; Belokurov, V.; Erkal, D. Tango for three: Sagittarius, LMC, and the Milky Way. Mon. Not. R. Astron. Soc. 2021, 501, 2279–2304. [Google Scholar] [CrossRef]
- Kravtsov, A.; Winney, S. Effect of the Large Magellanic Cloud on the kinematics of Milky Way satellites and virial mass estimate. Open J. Astrophys. 2024, 7, 50. [Google Scholar] [CrossRef]
- Licquia, T.C.; Newman, J.A. Improved Estimates of the Milky Way’s Stellar Mass and Star Formation Rate from Hierarchical Bayesian Meta-Analysis. Astrophys. J. 2015, 806, 96. [Google Scholar] [CrossRef]
- Karachentsev, I.D.; Telikova, K.N. Stellar and dark matter density in the Local Universe. Astron. Nachrichten 2018, 339, 615–622. [Google Scholar] [CrossRef]
- Ploeckinger, S.; Sharma, K.; Schaye, J.; Crain, R.A.; Schaller, M.; Barber, C. Tidal dwarf galaxies in cosmological simulations. Mon. Not. R. Astron. Soc. 2018, 474, 580–596. [Google Scholar] [CrossRef]
- Haslbauer, M.; Dabringhausen, J.; Kroupa, P.; Javanmardi, B.; Banik, I. Galaxies lacking dark matter in the Illustris simulation. Astron. Astrophys. 2019, 626, A47. [Google Scholar] [CrossRef]
- Livio, M.; Brown, T.M. The Local Group as an Astrophysical Laboratory; Number 17 in Space Telescope Science Institute Symposium Series; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Asencio, E.; Banik, I.; Kroupa, P. A massive blow for ΛCDM—The high redshift, mass, and collision velocity of the interacting galaxy cluster El Gordo contradicts concordance cosmology. Mon. Not. R. Astron. Soc. 2021, 500, 5249–5267. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Lucchini, S.; D’Onghia, E.; Fox, A.J.; Bustard, C.; Bland-Hawthorn, J.; Zweibel, E. The Magellanic Corona as the key to the formation of the Magellanic Stream. Nature 2020, 585, 203–206. [Google Scholar] [CrossRef]
- Cullinane, L.R.; Mackey, A.D.; Da Costa, G.S.; Erkal, D.; Koposov, S.E.; Belokurov, V. The Magellanic Edges Survey—II. Formation of the LMC’s northern arm. Mon. Not. R. Astron. Soc. 2022, 510, 445–468. [Google Scholar] [CrossRef]
- Cullinane, L.R.; Mackey, A.D.; Da Costa, G.S.; Erkal, D.; Koposov, S.E.; Belokurov, V. The Magellanic Edges Survey—III. Kinematics of the disturbed LMC outskirts. Mon. Not. R. Astron. Soc. 2022, 512, 4798–4818. [Google Scholar] [CrossRef]
- Lucchini, S.; D’Onghia, E.; Fox, A.J. The Magellanic Stream at 20 kpc: A New Orbital History for the Magellanic Clouds. Astrophys. J. Lett. 2021, 921, L36. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Springel, V.; White, S.D.M.; Jenkins, A.; Lemson, G. Resolving cosmic structure formation with the Millennium-II Simulation. Mon. Not. R. Astron. Soc. 2009, 398, 1150–1164. [Google Scholar] [CrossRef]
- Klypin, A.A.; Trujillo-Gomez, S.; Primack, J. Dark Matter Halos in the Standard Cosmological Model: Results from the Bolshoi Simulation. Astrophys. J. 2011, 740, 102. [Google Scholar] [CrossRef]
- Trujillo-Gomez, S.; Klypin, A.; Primack, J.; Romanowsky, A.J. Galaxies in ΛCDM with Halo Abundance Matching: Luminosity-Velocity Relation, Baryonic Mass-Velocity Relation, Velocity Function, and Clustering. Astrophys. J. 2011, 742, 16. [Google Scholar] [CrossRef]
- Busha, M.T.; Wechsler, R.H.; Behroozi, P.S.; Gerke, B.F.; Klypin, A.A.; Primack, J.R. Statistics of Satellite Galaxies around Milky-Way-like Hosts. Astrophys. J. 2011, 743, 117. [Google Scholar] [CrossRef][Green Version]
- Liu, L.; Gerke, B.F.; Wechsler, R.H.; Behroozi, P.S.; Busha, M.T. How Common are the Magellanic Clouds? Astrophys. J. 2011, 733, 62. [Google Scholar] [CrossRef]
- SDSS Collaboration. The Sloan Digital Sky Survey: Technical Summary. Astron. J. 2000, 120, 1579–1587. [Google Scholar] [CrossRef]
- Kroupa, P.; Theis, C.; Boily, C.M. The great disk of Milky-Way satellites and cosmological sub-structures. Astron. Astrophys. 2005, 431, 517–521. [Google Scholar] [CrossRef]
- Metz, M.; Kroupa, P.; Jerjen, H. The spatial distribution of the Milky Way and Andromeda satellite galaxies. Mon. Not. R. Astron. Soc. 2007, 374, 1125–1145. [Google Scholar] [CrossRef]
- Metz, M.; Kroupa, P.; Theis, C.; Hensler, G.; Jerjen, H. Did the Milky Way Dwarf Satellites Enter The Halo as a Group? Astrophys. J. 2009, 697, 269–274. [Google Scholar] [CrossRef]
- D’Onghia, E.; Lake, G. Small Dwarf Galaxies within Larger Dwarfs: Why Some Are Luminous while Most Go Dark. Astrophys. J. Lett. 2008, 686, L61. [Google Scholar] [CrossRef]
- Li, Y.S.; Helmi, A. Infall of substructures on to a Milky Way-like dark halo. Mon. Not. R. Astron. Soc. 2008, 385, 1365–1373. [Google Scholar] [CrossRef]
- Samuel, J.; Wetzel, A.; Chapman, S.; Tollerud, E.; Hopkins, P.F.; Boylan-Kolchin, M.; Bailin, J.; Faucher-Giguère, C.A. Planes of satellites around Milky Way/M31-mass galaxies in the FIRE simulations and comparisons with the Local Group. Mon. Not. R. Astron. Soc. 2021, 504, 1379–1397. [Google Scholar] [CrossRef]
- Pawlowski, M.S. Phase-Space Correlations among Systems of Satellite Galaxies. Galaxies 2021, 9, 66. [Google Scholar] [CrossRef]
- Fattahi, A.; Navarro, J.F.; Sawala, T.; Frenk, C.S.; Oman, K.A.; Crain, R.A.; Furlong, M.; Schaller, M.; Schaye, J.; Theuns, T.; et al. The APOSTLE project: Local Group kinematic mass constraints and simulation candidate selection. Mon. Not. R. Astron. Soc. 2016, 457, 844–856. [Google Scholar] [CrossRef]
- Sawala, T.; Frenk, C.S.; Fattahi, A.; Navarro, J.F.; Bower, R.G.; Crain, R.A.; Dalla Vecchia, C.; Furlong, M.; Helly, J.C.; Jenkins, A.; et al. The APOSTLE simulations: Solutions to the Local Group’s cosmic puzzles. Mon. Not. R. Astron. Soc. 2016, 457, 1931–1943. [Google Scholar] [CrossRef]
- Garavito-Camargo, N.; Patel, E.; Besla, G.; Price-Whelan, A.M.; Gómez, F.A.; Laporte, C.F.P.; Johnston, K.V. The Clustering of Orbital Poles Induced by the LMC: Hints for the Origin of Planes of Satellites. Astrophys. J. 2021, 923, 140. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Oria, P.A.; Taibi, S.; Famaey, B.; Ibata, R. On the Effect of the Large Magellanic Cloud on the Orbital Poles of Milky Way Satellite Galaxies. Astrophys. J. 2022, 932, 70. [Google Scholar] [CrossRef]
- Correa Magnus, L.; Vasiliev, E. Measuring the Milky Way mass distribution in the presence of the LMC. Mon. Not. R. Astron. Soc. 2022, 511, 2610–2630. [Google Scholar] [CrossRef]
- Sawala, T.; Cautun, M.; Frenk, C.; Helly, J.; Jasche, J.; Jenkins, A.; Johansson, P.H.; Lavaux, G.; McAlpine, S.; Schaller, M. The Milky Way’s plane of satellites is consistent with ΛCDM. Nat. Astron. 2023, 7, 481–491. [Google Scholar] [CrossRef]
- Gaia Collaboration. Gaia Early Data Release 3. Summary of the contents and survey properties. Astron. Astrophys. 2021, 649, A1. [Google Scholar] [CrossRef]
- Gaia Collaboration. Gaia Data Release 3. Summary of the content and survey properties. Astron. Astrophys. 2023, 674, A1. [Google Scholar] [CrossRef]
- Nichols, M.; Bland-Hawthorn, J. Gas Depletion in Local Group Dwarfs on ~250 kpc Scales: Ram Pressure Stripping Assisted by Internal Heating at Early Times. Astrophys. J. 2011, 732, 17. [Google Scholar] [CrossRef]
- Klimentowski, J.; Łokas, E.L.; Knebe, A.; Gottlöber, S.; Martinez-Vaquero, L.A.; Yepes, G.; Hoffman, Y. The grouping, merging and survival of subhaloes in the simulated Local Group. Mon. Not. R. Astron. Soc. 2010, 402, 1899–1910. [Google Scholar] [CrossRef]
- Deason, A.J.; McCarthy, I.G.; Font, A.S.; Evans, N.W.; Frenk, C.S.; Belokurov, V.; Libeskind, N.I.; Crain, R.A.; Theuns, T. Mismatch and misalignment: Dark haloes and satellites of disc galaxies. Mon. Not. R. Astron. Soc. 2011, 415, 2607–2625. [Google Scholar] [CrossRef]
- Pawlowski, M.S. It’s time for some plane speaking. Nat. Astron. 2021, 5, 1185–1187. [Google Scholar] [CrossRef]
- Lovell, M.R.; Eke, V.R.; Frenk, C.S.; Jenkins, A. The link between galactic satellite orbits and subhalo accretion. Mon. Not. R. Astron. Soc. 2011, 413, 3013–3021. [Google Scholar] [CrossRef]
- Libeskind, N.I.; Knebe, A.; Hoffman, Y.; Gottlöber, S.; Yepes, G.; Steinmetz, M. The preferred direction of infalling satellite galaxies in the Local Group. Mon. Not. R. Astron. Soc. 2011, 411, 1525–1535. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Famaey, B.; Jerjen, H.; Merritt, D.; Kroupa, P.; Dabringhausen, J.; Lüghausen, F.; Forbes, D.A.; Hensler, G.; Hammer, F.; et al. Co-orbiting satellite galaxy structures are still in conflict with the distribution of primordial dwarf galaxies. Mon. Not. R. Astron. Soc. 2014, 442, 2362–2380. [Google Scholar] [CrossRef]
- Shao, S.; Cautun, M.; Frenk, C.S.; Grand, R.J.J.; Gómez, F.A.; Marinacci, F.; Simpson, C.M. The multiplicity and anisotropy of galactic satellite accretion. Mon. Not. R. Astron. Soc. 2018, 476, 1796–1810. [Google Scholar] [CrossRef]
- Ibata, R.A.; Ibata, N.G.; Lewis, G.F.; Martin, N.F.; Conn, A.; Elahi, P.; Arias, V.; Fernando, N. A Thousand Shadows of Andromeda: Rotating Planes of Satellites in the Millennium-II Cosmological Simulation. Astrophys. J. Lett. 2014, 784, L6. [Google Scholar] [CrossRef]
- Osipova, A.; Pilipenko, S.; Gottlöber, S.; Libeskind, N.I.; Newton, O.; Sorce, J.G.; Yepes, G. Hermeian haloes: Extreme objects with two interactions in the past. Phys. Dark Universe 2023, 42, 101328. [Google Scholar] [CrossRef]
- Mirabel, I.F.; Dottori, H.; Lutz, D. Genesis of a dwarf galaxy from the debris of the Antennae. Astron. Astrophys. 1992, 256, L19–L22. [Google Scholar]
- Barnes, J.E.; Hernquist, L. Formation of dwarf galaxies in tidal tails. Nature 1992, 360, 715–717. [Google Scholar] [CrossRef]
- Wetzstein, M.; Naab, T.; Burkert, A. Do dwarf galaxies form in tidal tails? Mon. Not. R. Astron. Soc. 2007, 375, 805–820. [Google Scholar] [CrossRef]
- McGaugh, S.S.; Wolf, J. Local Group Dwarf Spheroidals: Correlated Deviations from the Baryonic Tully-Fisher Relation. Astrophys. J. 2010, 722, 248–261. [Google Scholar] [CrossRef]
- McGaugh, S.; Milgrom, M. Andromeda Dwarfs in Light of Modified Newtonian Dynamics. Astrophys. J. 2013, 766, 22. [Google Scholar] [CrossRef]
- McGaugh, S.; Milgrom, M. Andromeda Dwarfs in Light of MOND. II. Testing Prior Predictions. Astrophys. J. 2013, 775, 139. [Google Scholar] [CrossRef]
- Shipp, N.; Erkal, D.; Drlica-Wagner, A.; Li, T.S.; Pace, A.B.; Koposov, S.E.; Cullinane, L.R.; Da Costa, G.S.; Ji, A.P.; Kuehn, K.; et al. Measuring the Mass of the Large Magellanic Cloud with Stellar Streams Observed by S 5. Astrophys. J. 2021, 923, 149. [Google Scholar] [CrossRef]
- Koposov, S.E.; Erkal, D.; Li, T.S.; Da Costa, G.S.; Cullinane, L.R.; Ji, A.P.; Kuehn, K.; Lewis, G.F.; Pace, A.B.; Shipp, N.; et al. S 5: Probing the Milky Way and Magellanic Clouds potentials with the 6D map of the Orphan-Chenab stream. Mon. Not. R. Astron. Soc. 2023, 521, 4936–4962. [Google Scholar] [CrossRef]
- Boylan-Kolchin, M.; Springel, V.; White, S.D.M.; Jenkins, A. There is no place like home? Statistics of Milky Way-mass dark matter haloes. Mon. Not. R. Astron. Soc. 2010, 406, 896–912. [Google Scholar] [CrossRef]
- Moster, B.P.; Naab, T.; White, S.D.M. Galactic star formation and accretion histories from matching galaxies to dark matter haloes. Mon. Not. R. Astron. Soc. 2013, 428, 3121–3138. [Google Scholar] [CrossRef]
- Dooley, G.A.; Peter, A.H.G.; Carlin, J.L.; Frebel, A.; Bechtol, K.; Willman, B. The predicted luminous satellite populations around SMC- and LMC-mass galaxies—A missing satellite problem around the LMC? Mon. Not. R. Astron. Soc. 2017, 472, 1060–1073. [Google Scholar] [CrossRef]
- Shao, S.; Cautun, M.; Deason, A.J.; Frenk, C.S.; Theuns, T. Evolution of LMC/M33-mass dwarf galaxies in the EAGLE simulation. Mon. Not. R. Astron. Soc. 2018, 479, 284–296. [Google Scholar] [CrossRef]
- Oehm, W.; Thies, I.; Kroupa, P. Constraints on the dynamical evolution of the galaxy group M81. Mon. Not. R. Astron. Soc. 2017, 467, 273–289. [Google Scholar] [CrossRef]
- Asencio, E.; Banik, I.; Mieske, S.; Venhola, A.; Kroupa, P.; Zhao, H. The distribution and morphologies of Fornax Cluster dwarf galaxies suggest they lack dark matter. Mon. Not. R. Astron. Soc. 2022, 515, 2981–3013. [Google Scholar] [CrossRef]
- Sohn, S.T.; Patel, E.; Fardal, M.A.; Besla, G.; van der Marel, R.P.; Geha, M.; Guhathakurta, P. HST Proper Motions of NGC 147 and NGC 185: Orbital Histories and Tests of a Dynamically Coherent Andromeda Satellite Plane. Astrophys. J. 2020, 901, 43. [Google Scholar] [CrossRef]
- Casetti-Dinescu, D.I.; Pawlowski, M.S.; Girard, T.M.; Kanehisa, K.J.; Petroski, A.; Martone, M.; Kozhurina-Platais, V.; Platais, I. HST Proper Motion of Andromeda III: Another Satellite Co-orbiting The M31 Satellite Plane. Astrophys. J. 2024, in press. [Google Scholar] [CrossRef]
- Pawlowski, M.S.; Müller, O.; Taibi, S.; Júlio, M.P.; Kanehisa, K.J.; Heesters, N. The satellite galaxy plane of NGC 4490 in light of ΛCDM. Sparsity of similarly extreme analogs and a possible role of satellite pairs. Astron. Astrophys. 2024, 688, A153. [Google Scholar] [CrossRef]
- Angus, G.W.; Diaferio, A.; Kroupa, P. Using dwarf satellite proper motions to determine their origin. Mon. Not. R. Astron. Soc. 2011, 416, 1401–1409. [Google Scholar] [CrossRef]
- Roshan, M.; Banik, I.; Ghafourian, N.; Thies, I.; Famaey, B.; Asencio, E.; Kroupa, P. Barred spiral galaxies in modified gravity theories. Mon. Not. R. Astron. Soc. 2021, 503, 2833–2860. [Google Scholar] [CrossRef]
- Roshan, M.; Ghafourian, N.; Kashfi, T.; Banik, I.; Haslbauer, M.; Cuomo, V.; Famaey, B.; Kroupa, P. Fast galaxy bars continue to challenge standard cosmology. Mon. Not. R. Astron. Soc. 2021, 508, 926–939. [Google Scholar] [CrossRef]
- Haslbauer, M.; Banik, I.; Kroupa, P.; Wittenburg, N.; Javanmardi, B. The High Fraction of Thin Disk Galaxies Continues to Challenge ΛCDM Cosmology. Astrophys. J. 2022, 925, 183. [Google Scholar] [CrossRef]
- Berezhiani, L.; Khoury, J. Theory of dark matter superfluidity. Phys. Rev. D 2015, 92, 103510. [Google Scholar] [CrossRef]
- Berezhiani, L.; Famaey, B.; Khoury, J. Phenomenological consequences of superfluid dark matter with baryon-phonon coupling. J. Cosmol. Astropart. Phys. 2018, 2018, 021. [Google Scholar] [CrossRef]
- Berezhiani, L.; Elder, B.; Khoury, J. Dynamical friction in superfluids. J. Cosmol. Astropart. Phys. 2019, 2019, 074. [Google Scholar] [CrossRef]
- Spergel, D.N.; Steinhardt, P.J. Observational Evidence for Self-Interacting Cold Dark Matter. Phys. Rev. Lett. 2000, 84, 3760–3763. [Google Scholar] [CrossRef] [PubMed]
- Ren, T.; Kwa, A.; Kaplinghat, M.; Yu, H.B. Reconciling the Diversity and Uniformity of Galactic Rotation Curves with Self-Interacting Dark Matter. Phys. Rev. X 2019, 9, 031020. [Google Scholar] [CrossRef]
- Lancaster, L.; Giovanetti, C.; Mocz, P.; Kahn, Y.; Lisanti, M.; Spergel, D.N. Dynamical friction in a Fuzzy Dark Matter universe. J. Cosmol. Astropart. Phys. 2020, 2020, 001. [Google Scholar] [CrossRef]
- Buehler, R.; Desjacques, V. Dynamical friction in fuzzy dark matter: Circular orbits. Phys. Rev. D 2023, 107, 023516. [Google Scholar] [CrossRef]
- Vitsos, A.; Gourgouliatos, K.N. Dynamical friction due to fuzzy dark matter on satellites described by axisymmetric logarithmic potentials. J. Cosmol. Astropart. Phys. 2023, 2023, 071. [Google Scholar] [CrossRef]
- Milgrom, M. A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 1983, 270, 365–370. [Google Scholar] [CrossRef]
- Famaey, B.; McGaugh, S.S. Modified Newtonian Dynamics (MOND): Observational Phenomenology and Relativistic Extensions. Living Rev. Relativ. 2012, 15, 10. [Google Scholar] [CrossRef]
- Banik, I.; Zhao, H. From Galactic Bars to the Hubble Tension: Weighing Up the Astrophysical Evidence for Milgromian Gravity. Symmetry 2022, 14, 1331. [Google Scholar] [CrossRef]
- Banik, I.; Zhao, H. The escape velocity curve of the Milky Way in modified Newtonian dynamics. Mon. Not. R. Astron. Soc. 2018, 473, 419–430. [Google Scholar] [CrossRef]
- Zhao, H.; Famaey, B.; Lüghausen, F.; Kroupa, P. Local Group timing in Milgromian dynamics. A past Milky Way-Andromeda encounter at z > 0.8. Astron. Astrophys. 2013, 557, L3. [Google Scholar] [CrossRef]
- Banik, I.; O’Ryan, D.; Zhao, H. Origin of the Local Group satellite planes. Mon. Not. R. Astron. Soc. 2018, 477, 4768–4791. [Google Scholar] [CrossRef]
- Banik, I.; Thies, I.; Truelove, R.; Candlish, G.; Famaey, B.; Pawlowski, M.S.; Ibata, R.; Kroupa, P. 3D hydrodynamic simulations for the formation of the Local Group satellite planes. Mon. Not. R. Astron. Soc. 2022, 513, 129–158. [Google Scholar] [CrossRef]
- Bílek, M.; Thies, I.; Kroupa, P.; Famaey, B. MOND simulation suggests an origin for some peculiarities in the Local Group. Astron. Astrophys. 2018, 614, A59. [Google Scholar] [CrossRef]
- Kroupa, P.; Jerabkova, T.; Thies, I.; Pflamm-Altenburg, J.; Famaey, B.; Boffin, H.M.J.; Dabringhausen, J.; Beccari, G.; Prusti, T.; Boily, C.; et al. Asymmetrical tidal tails of open star clusters: Stars crossing their cluster’s práh challenge Newtonian gravitation. Mon. Not. R. Astron. Soc. 2022, 517, 3613–3639. [Google Scholar] [CrossRef]
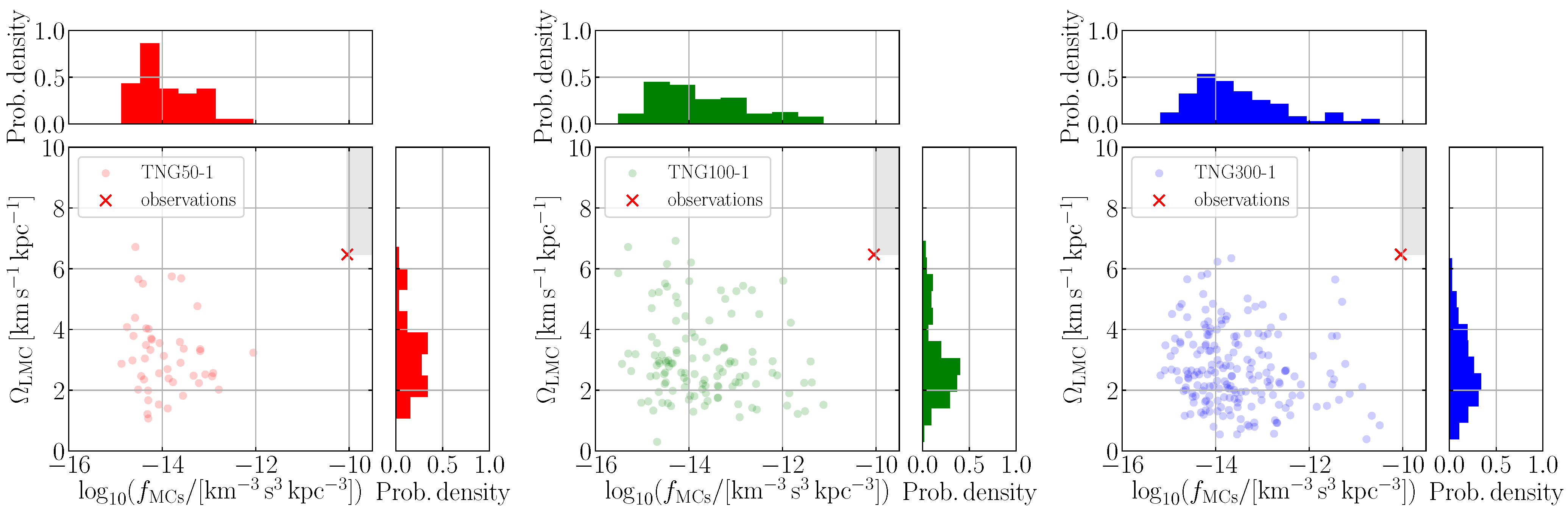
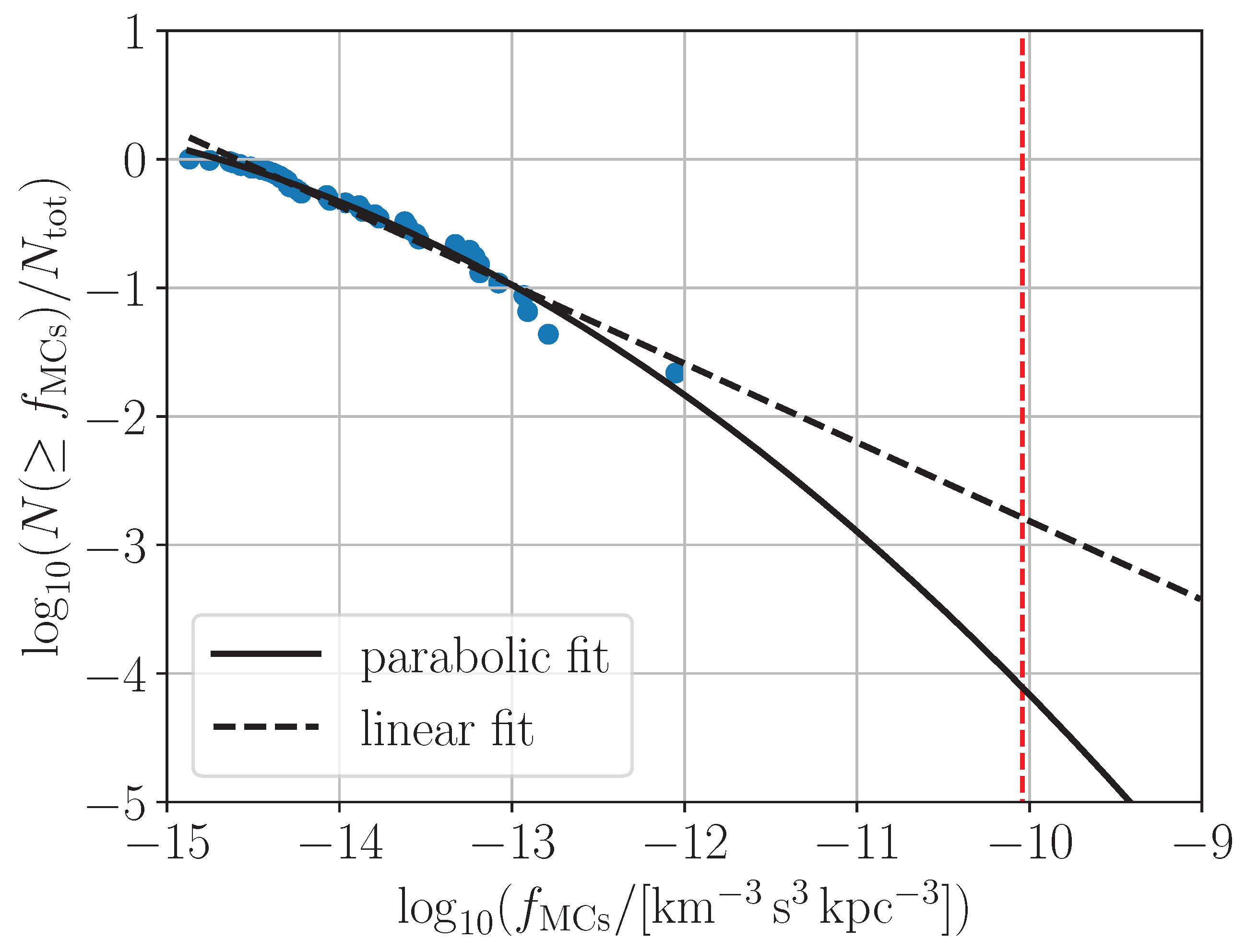
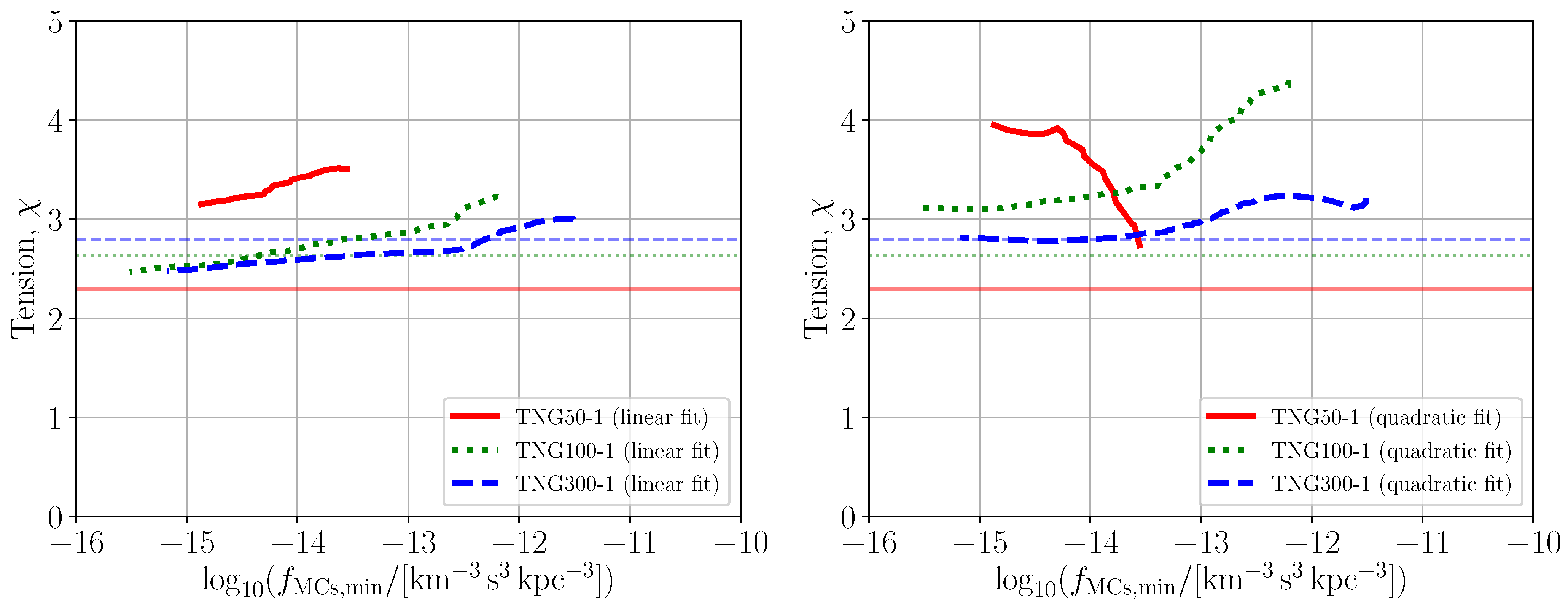
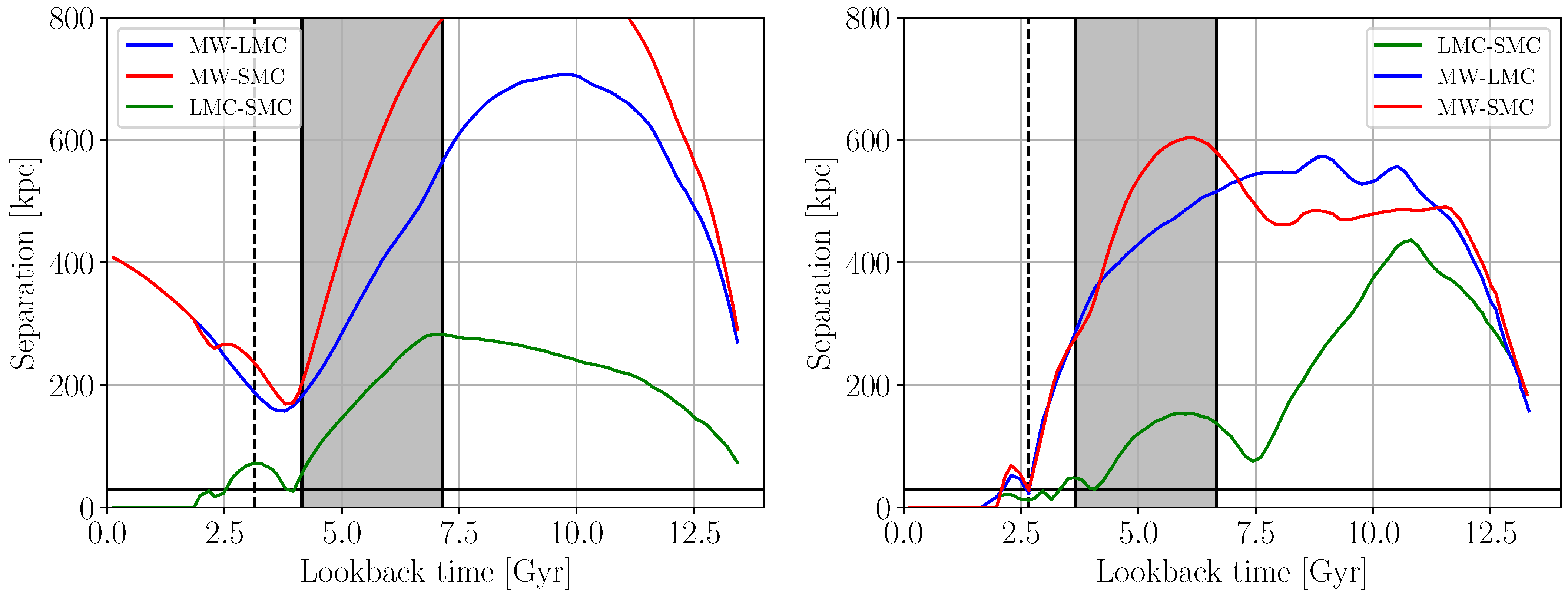

| Object | d | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| [] | [kpc] | [kpc] | [kpc] | [kpc] | [] | [] | [] | [] | [] | |
| LMC | ||||||||||
| SMC |
| Selection Criteria | Simulation | Number of Analogues | Frequency | Significance |
|---|---|---|---|---|
| Initial sample of analogues to the MW (Section 2.3) | TNG50-1: | 1547 | − | − |
| TNG100-1: | 7360 | − | − | |
| TNG300-1: | 40,075 | − | − | |
| All 3 runs: | 48,982 | − | − | |
| Initial sample of analogues to the LMC (Section 2.4) | TNG50-1: | 331 | ||
| TNG100-1: | 1414 | 1414/7360 | ||
| TNG300-1: | 3823 | 3823/40,075 | ||
| All 3 runs: | 5568 | 5568/48,982 | ||
| Initial sample of analogues to the SMC (Section 2.4) | TNG50-1: | 343 | ||
| TNG100-1: | 766 | |||
| TNG300-1: | 1148 | 1148/40,075 | ||
| All 3 runs: | 2257 | 2257/48,982 | ||
| Initial sample of analogues to the MCs (Section 2.4) | TNG50-1: | 147 | ||
| TNG100-1: | 454 | |||
| TNG300-1: | 601 | 601/40,075 | ||
| All 3 runs: | 1202 | 1202/48,982 | ||
| Initial sample of analogues to the MCs (Section 2.4) | TNG50-1: | 46 | ||
| + | TNG100-1: | 118 | ||
| TNG300-1: | 191 | 191/40,075 | ||
| All 3 runs: | 355 | 355/48,982 | ||
| Sample of analogues to the MCs with | TNG50-1: | 0 | <1/46 | >2.29 |
| (Equation (1)) | TNG100-1: | 0 | <1/118 | >2.63 |
| TNG300-1: | 0 | <1/191 | >2.79 | |
| All 3 runs: | 0 | <1/355 | >2.99 | |
| Sample of analogues to the MCs with | TNG50-1: | − | ||
| Extrapolation of distribution using a linear fit (Figure 3) | TNG100-1: | − | ||
| TNG300-1: | − | |||
| Sample of analogues to the MCs with | TNG50-1: | − | ||
| Extrapolation of distribution using a quadratic fit (Figure 3) | TNG100-1: | − | ||
| TNG300-1: | − | |||
| Sample of analogues to the MCs with | TNG50-1: | 0 | < | >2.70 |
| TNG100-1: | 0 | < | >2.97 | |
| +LMC-DoS alignment | TNG300-1: | 0 | < | >3.10 |
| All 3 runs: | 0 | < | >3.26 | |
| Sample of analogues to the MCs with | TNG50-1: | − | ||
| Extrapolation of distribution using a linear fit (Figure 3) | TNG100-1: | − | ||
| +LMC-DoS alignment | TNG300-1: | − | ||
| Sample of analogues to the MCs with | TNG50-1: | − | ||
| Extrapolation of distribution using a quadratic fit (Figure 3) | TNG100-1: | − | ||
| +LMC-DoS alignment | TNG300-1: | − |
| Parameter | Unit | Observed | System 1 | System 2 | System 3 |
|---|---|---|---|---|---|
| Simulation | − | − | TNG100-1 | TNG300-1 | TNG300-1 |
| Redshift | − | 0 | 0.26 | 0.21 | 0.20 |
| Lookback time | Gyr | 0 | |||
| − | 171 | 232 | 232 | ||
| − | 159 | 202 | 202 | ||
| − | |||||
| − | |||||
| − | |||||
| − | |||||
| 50.0 | 187.2 | 23.7 | 47.0 | ||
| 61.3 | 235.3 | 28.7 | 55.8 | ||
| 24.5 | 72.5 | 11.6 | 14.03 | ||
| 323.8 | 213.2 | 381.2 | 92.3 | ||
| 245.6 | 192.2 | 248.3 | 185.7 | ||
| 90.8 | 21.9 | 173.3 | 148.0 | ||
| 15.9 | 36.8 | 5.6 | 2.1 | ||
| 15.0 | 40.5 | 1.2 | 5.2 | ||
| (Equation (1)) | 0.91 | 2.51 | 1.22 | 1.12 | |
| (Equation (3)) | 6.48 | 1.14 | 16.09 | 1.96 | |
| − | |||||
| − |
| Problem for CDM | Frequency | Significance |
|---|---|---|
| MW satellite plane | ||
| M31 satellite plane | ||
| NGC 3109 backsplash | < | >3.96 |
| Phase-space density of MCs | ||
| Phase-space density of MCs | ||
| + MW DoS |
| Sample | Simulation | Number of Analogues | Frequency | Significance |
|---|---|---|---|---|
| Initial sample of analogues to the LMC (Section 2.4) | TNG50-1: | 54 | ||
| TNG100-1: | 163 | |||
| TNG300-1: | 354 | |||
| All runs: | 571 | |||
| Sample of analogues to the LMC with | TNG50-1: | 2 | ||
| TNG100-1: | 3 | |||
| TNG300-1: | 4 | |||
| All runs: | 9 | |||
| Sample of analogues to the LMC with | TNG50-1: | 0 | <1/5 | >1.28 |
| TNG100-1: | 0 | <1/70 | >2.45 | |
| TNG300-1: | 0 | <1/453 | >3.06 | |
| All runs: | 0 | <1/528 | >3.11 | |
| Initial sample of analogues to the LMC (Section 2.4) | All runs: | 0 | <1/5568 | >3.75 |
| & | ||||
| Initial sample of analogues to the LMC (Section 2.4) | All runs: | 0 | < | >5.09 |
| & | ||||
| +Extrapolation of distribution using quadratic fit (TNG50-1) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haslbauer, M.; Banik, I.; Kroupa, P.; Zhao, H.; Asencio, E. The Magellanic Clouds Are Very Rare in the IllustrisTNG Simulations. Universe 2024, 10, 385. https://doi.org/10.3390/universe10100385
Haslbauer M, Banik I, Kroupa P, Zhao H, Asencio E. The Magellanic Clouds Are Very Rare in the IllustrisTNG Simulations. Universe. 2024; 10(10):385. https://doi.org/10.3390/universe10100385
Chicago/Turabian StyleHaslbauer, Moritz, Indranil Banik, Pavel Kroupa, Hongsheng Zhao, and Elena Asencio. 2024. "The Magellanic Clouds Are Very Rare in the IllustrisTNG Simulations" Universe 10, no. 10: 385. https://doi.org/10.3390/universe10100385
APA StyleHaslbauer, M., Banik, I., Kroupa, P., Zhao, H., & Asencio, E. (2024). The Magellanic Clouds Are Very Rare in the IllustrisTNG Simulations. Universe, 10(10), 385. https://doi.org/10.3390/universe10100385








