Abstract
The suppression of relic gravitational waves due to their conversion into electromagnetic radiation in a cosmological magnetic field is studied. The coupled system of equations describing gravitational and electromagnetic wave propagation in an arbitrary curved space-time and in external magnetic field is derived. The subsequent elimination of photons from the beam due to their interaction with the primary plasma is taken into account. The resulting system of equations is solved numerically in the Friedman–LeMaitre–Robertson–Walker metric for the upper limit of the intergalactic magnetic field strength of 1 nGs. We conclude that the gravitational wave conversion into photons in the intergalactic magnetic field cannot significantly change the amplitude of the relic gravitational wave and their frequency spectrum.
1. Introduction
The transformation between gravitons and photons in an external magnetic field was considered in a multitude of papers starting from 1961 [1,2,3,4,5,6,7,8]. The problem acquired particular importance in connection with the possible transformation of relic gravitational waves (GW) produced at the inflationary stage [9,10,11,12] into electromagnetic waves (EMW) in primordial magnetic fields. However, in all previous works see, e.g., [8,13] the calculations have always been conducted in Minkowski space-time, though the curvature effects in the very early universe could be quite essential.
In the present work, we go beyond the flat space-time restriction and consider graviton and photon propagation in an arbitrary curved background. The propagation of gravitational waves in curved space-time was almost always considered in the Friedman–LeMaitre–Robertson–Walker metric (FLRW), see, e.g., textbooks [14,15], except for some Bianchi type metrics and our recent paper [16], where an arbitrary background metric was allowed. Here, we derive the propagation equations for the coupled system of photons and gravitons in an arbitrary background. Next, we will turn to the Friedman–LeMaitre–Robertson–Walker (FLRW) space-time, which is a good approximation of the real universe. However, deviations from FLRW could be essential and lead to interesting observable effects.
For over a century, the Friedman equations have served as a basement for the conventional cosmological model. They well describe the early universe, that is homogeneous and isotropic to a very good approximation. They are operative also in the contemporary universe on very large scales. Friedman cosmology allows for description of cosmological dark matter and what is more surprising dark energy, though the physical nature of the latter is not yet established.
The propagation of gravitational waves in curved space-time was almost always considered in FLRW metric, except for some Bianchi type metrics and our recent paper [16], where an arbitrary background metric was allowed.
Here, we derive the coupled equations of motion for metric perturbations and electromagnetic waves over an arbitrary cosmological background in the external cosmic magnetic field. The metric perturbations and EMW are treated in the first order of the perturbation theory.
We introduce the full electromagnetic field as the sum of an external classical component of the electromagnetic field and a small quantum fluctuation , which is considered as a perturbation,
The stress tensors of and are then introduced accordingly:
The full metric tensor is expanded around the metric tensor of the background space-time as
with being a small perturbation of the metric.
The properties of the metric tensor are specified by: the orthogonality condition , where is the Kronecker delta-symbol; rising and lowering of the indices of the tensors and by the background metric tensor . Note that the indices of the full and classical stress tensors of the electromagnetic fields are raised and lowered with the full metric tensor .
The corrections to the metric determinant can be found from the first-order expansion of an arbitrary non-degenerate matrix :
So we obtain:
It is assumed usually that tensor perturbations are traceless:
However, we see in what follows that the corrections to the Maxwell energy–momentum tensor are not traceless, see, e.g., Equations (69)–(115) and a nonzero trace of the gravitational field source leads to the nonzero h, so .
The initially derived equations are supposed to be valid in an arbitrary space-time metric, but ultimately we assume that the background metric has the -flat FLRW form:
where is the cosmological scale factor. The Hubble parameter is expressed through it in the usual way as . The curved metric reduces to the flat one when .
The paper is organized as follows. We start in Section 2 with a brief reminder of the equation for metric perturbations over arbitrary space-time. In Section 3, we recall the expansion of metric perturbations in terms of helicity eigenstates. After that, in Section 4 we show that the scalar and tensor modes can mix in the general case of inhomogeneous space. Further, in Section 5 we consider propagation of metric perturbation over FLRW space-time in an external magnetic field. In Section 6, the propagation of electromagnetic waves in a magnetic field is considered. In both sections, we start from the classical Maxwell and Hilbert–Einstein actions ignoring for a while the Heisenberg–Euler (HE) [17] corrections, the quantum trace anomaly and matter effects. They are taken into account step-by-step in the subsequent subsections. On the way, we discuss the definition of physical magnetic fields through the electromagnetic field tensor in cosmological background (Section 5.3) and the impact of the HE-corrections to the electromagnetic wave propagation expressed through the physical magnetic field (Section 6.2). In Section 7, we analyze the full set, of differential equations (SDE) for -coupled system, choose a reference frame, and simplify the system for the choice made. Next, in Section 8, we divide the task into two cases: and , and find out that the conversion effect is present only for the second case. In the last Section 9, we divide SDE into two independent subsystems and solve the first of them numerically. Lastly, we conclude the paper by summarizing the obtained results and formulating the prospects for future research.
2. Metric Perturbations in General Case
In [16], we obtained Equation (23) for the propagation of metric perturbations in arbitrary space-time. Let us write it for two lower indices:
where G is the gravitational constant, and is the covariant derivative, are the Riemann tensor, Ricci tensor and scalar curvature, respectively.
The equation contains additional terms that disappear in the special cases of Minkowski and FLRW spaces. These extra terms could have significant effects on the GW and EMW propagation over background metric that differs from the FLRW one.
Let us note the agreement between Equations (9) and (2.33) from the work [18], published after our work [16]. The apparent difference with our result disappears in the Lorentz calibration
In this article, the authors obtained the same equation using a double variation of the action, while we obtained it by expanding the Einstein equation to first order in perturbation.
3. Helicity Decomposition and Choice of Gauge
Now it is worth recalling the formalism of the expansion of the perturbation in terms of helicity states [19,20,21,22,23]. The generally accepted approach is that (along with the vectors and the traceless tensor ) four scalars are introduced, through which the components of the metric perturbation are expressed:
One can impose gauge conditions such that two scalars turn to zero. The so called synchronous gauge corresponds to the choice and . Under this gauge there still remains some more freedom, that may allow to simplify algebra in a specific problem. The second well-known type of gauge is the Newtonian gauge, where , , , and . The choice of this gauge better fits our task, so for the scalar sector we will use the Newtonian gauge.
In addition to the gauge in the scalar sector, the Lorentz gauge (10) is usually imposed on the entire tensor perturbation of metric. This calibration naturally arises in the case when the so-called harmonic Fock coordinates are used. It allows to obtain a simpler expression for the Ricci tensor and, as a consequence, to simplify the equation for the propagation of metric perturbations. Formerly in our paper [16], we have only used the Lorentz gauge.
4. Mixing of Metric Perturbation Modes
Note that from the expression for the trace of the Equation (9) it turns out that in the general case, for an arbitrary form of the Ricci tensor, there appears a mixing of scalar and tensor modes of metric perturbations. In general case it is impossible to separate the equations for these two sectors. Indeed, taking trace of Equation (9), we obtain the following expression
where , and from which it is clearly seen that the second term in the left hand side includes both terms from the scalar and the tensor sectors.
In addition, it is important to pay attention to the trace from the source on the right-hand side of the equation. As will be shown below for the problem of graviton conversion into photons in an external magnetic field, the trace from the correction to the EMT contains a convolution of the background electromagnetic tensor and the tensor perturbation to the metric, , which also leads to mixing between scalar and tensor modes. This result is evident, because the expansion of metric perturbations in polarizations is valid for a problem with axial symmetry: in this problem there is only one specific direction—the direction of the wave vector of the metric perturbation. If space is for some reason unisotropic (as, for example, in the case of an external magnetic field or in the presence of an anisotropic stress tensor), this symmetry disappears.
5. Metric Perturbations in Magnetic Field
5.1. Equation in the FLRW Metric
Recall that in the FLRW metric
We write the trace of the GW tensor in the following form:
where the notation was introduced:
Let us write down the system of Equation (9) for the case of the FLRW metric. To do this, we will use the expressions (15)–(18). We get
where the Latin indices are the spatial ones (vary from one to three).
For a medium where the perturbation propagates, we will consider a model of an ideal fluid. The total energy–momentum tensor in this case is determined through the full metric as follows
where is the energy density, p is the pressure, is the four-speed. Then the right side of Equation (19) can be rewritten as
where the first term in the last equality is obtained by expanding Equation (20) to the first order in perturbation at (index j varies from one to three) and the second term is responsible for the perturbation of the EMT due to the presence of an external magnetic field.
The factor before the last term on the left side of the Equation (19) is exactly
Thus, Equation (19) can be simplified:
Now, for brevity, we omit the expressions for the components of the Riemann tensor and the Christoffel symbols in the covariant derivative and write the final equations for 00, , and components separately:
where notation (18) is used, and the last equation is written in terms of mixed components, since then it looks more consistent with the equation for the 00 component.
5.2. Corrections to the Energy–Momentum Tensor (EMT)
Corrections to the EMT are due to the presence of an external electromagnetic field. We will find them in accordance with the definition of EMT of matter:
There are two contributions to the EMT perturbation: from the Maxwell action and from the Heisenberg–Euler action.
The gravity of the background magnetic field is negligible compared to the background of matter and we ignore its contribution to the EMT corrections.
5.2.1. Corrections to EMT Emerging from the Maxwell Action
The Maxwell action is written as follows:
where . Hence the energy-momentum tensor is
or for the mixed components:
Clearly this tensor is conserved and its trace is zero:
The vanishing of the EMT trace in Maxwell electrodynamics is a consequence of the conformal invariance of the Maxwell action (26). This is not so for higher order quantum corrections (trace anomaly), see Section 6.3.
The trace of the zero-order term with mixed components:
is also zero. Note that moving indices up or down in this equation is done by the background metric, e.g., and .
The zero-order term is presumably small in comparison with the total cosmological energy–momentum tensor and can be neglected in what follows.
For the first order term with mixed components we obtain:
where and . Evidently , as is expected.
5.2.2. Heisenberg–Euler (HE) Lagrangian
The second origin of EMT corrections is Heisenberg–Euler effective Lagrangian [17]. It describes quartic self-interaction of electromagnetic field and is induced by the loop of virtual electrons with four external electromagnetic legs. In the weak field limit, and low energies, much smaller than the electron mass, , the corresponding action has the form:
Here
and is the fine structure constant. At high temperatures C, , and change with T. At this stage, we omit the bar over to simplify notations. The dual Maxwell tensor is defined as
because the tensor quantity is but not just , see e.g., chapter 83 from textbook [24].
In what follows, we apply this action to photon propagation in an external magnetic field B and the weak field limit means .
We need to generalize the Heisenberg–Euler action (32) to high energies/temperatures and curved FLRW space-time. To do so, let us start from the canonical action of photons and electrons written in terms of the conformal metric:
where is the Minkowski metric tensor, and is the scale factor as a function of conformal time .
The action of photons and electrons written in terms of the inverse metric to , given by Equation (35), takes the form:
where is a generalization of the Dirac matrices for curved space-time. For FLRW metric they have the form , where are the usual Dirac matrices which anticommute as , ; is the covariant derivative for spin-(1/2) field. For the FLRW metric, it has the form .
Introducing conformally transformed spinor , we arrive to the action:
This is essentially the same action as it is in flat space-time with rescaled mass and charge: and , so formally does not change, but since we plan to go to very high temperatures, even above the electroweak phase transition, where all bare masses of charged particles vanish, we have to substitute the high temperature value of the mass, to sum over all charged particles, and to take the high temperature value of the electromagnetic coupling . So
where is the charge of the contributing to the loop particles in the electron charge units, e.g., for down or up quarks or .
The integrand in the expression for the action is a scalar with respect to the general coordinate transformation, so we can use for it the same expression as (32) in arbitrary metric.
In the early universe, the Heisenberg–Euler action at high temperatures keeps the same form as (32) with substitution of instead of :
where , , and we have returned bar over and to the metric determinant in accordance with expansion (5).
The HE action given by Equation (39) leads to the following contribution to the energy-momentum tensor:
Here, the over-bars are eliminated to simplify notation but we keep in mind that this expression will be used with the non-expanded complete quantities, see Equation (5).
An explanatory comment may be in order here, namely, the second term containing the dual Maxwell tensor, , depends upon metric only through the factor , so with the account of the integration measure the action depends on metric as instead on . Hence, this gives the contribution to from proportional to instead of the usual one proportional to .
One can see that the trace of tensor (40) is non-vanishing:
It is instructive to check conservation of the energy–momentum tensor (40), though it surely must be true, since it was obtained by the variation of a scalar function over metric. Still, at least the verification of the conservation would indicate that the calculations are correct. Let us note that the conservation condition should be fulfilled only if . Evidently, the energy–momentum tensor (40) is non-conserved for a non-constant because the dependence on temperature appears due to interaction and an exchange of energy with external system.
It would be more convenient to express the square of the dual electromagnetic tensor through F. It enters the action in the form, see Equation (34):
Expressing the product of epsilons through the Kronecker symbols and properly contracting the indices we obtain:
where . We can verify result (43) expressing the Maxwell tensor through electromagnetic fields B and E coming to the well-known relation .
The first part of the action (39), proportional to , leads to the following contribution to the energy–momentum tensor
The same contribution, up to a numerical factor, comes from the first term in Equation (43), So to find the total EMT we need to find the variation of the second term of Equation (43). Eventually, the remaining part of the energy–momentum tensor is
Bringing together Equations (44) and (45) and raising one index we obtain for the total energy–momentum tensor, originating from the Heisenberg–Euler action, the following expression:
Now, let us check the conservation of the obtained energy–momentum tensor (46) in the case of constant . We consider and separately.
where semicolons mean covariant derivatives in the background metric. The last term in this equation is zero according to the equation of motion corresponding to the Lagrangian .
The first two ones can be rewritten using the relation
Renaming some dummy indices we come to
Here, we proved EMT conservation law for those parts of the action which contain . It must be analogous for the EMT part originated from (see Equation (43)).
where we used the Maxwell equation . Considering the part inside square brackets and taking into account the equation of motion , that follows from the part of the action:
For the transition to the third term of these equalities, we used Equation (48).
The conclusion for this section is that EMT originated from the Heisenberg–Euler action with is conserved
It is noteworthy that EMT (46) is not traceless. Indeed, it is equal to
5.2.3. Corrections to EMT Emerging from the HE Action
Now making the usual perturbation expansion (5), we find the following first-order correction to the energy–momentum tensor:
This expression can be simplified, because in the absence of a background electric field and we get:
The trace of this expression is nonvanishing:
It is usually demanded in FLRW space-time that the source term for gravitational wave Equation (24) must be traceless. To this end, one may separate the traceless part out of Equation (56) subtracting out of it. However, this prescription would break the conservation of the source and, as is shown in Section 6 of paper [16], it would lead to a violation of the transversality conditions . Indeed, in [16] we used the condition to prove a compatibility of the Einstein equations in the first perturbation order with gauge fixing conditions (89).
Note that the energy–momentum tensor (40) is non-conserved for a non-constant because the dependence on the temperature appears due to interaction with external system. Thus, EMT is not formally conserved.
5.2.4. Summary
As a conclusion of this subsection, we write the result for the correction to the EMT from the Maxwell action and from the Heisenberg–Euler action, respectively:
where .
5.3. Maxwell Tensor and Cosmic Magnetic and Electric Fields
Equations (58) and (59) appear quite complicated. Further, we simplify these equations and express them in terms of physical magnetic fields. To understand the physical meaning of the different components of , , or , let us start from the geodesic equation for a charged particle in external electric and magnetic field (see, e.g., book [24]. Equation (90.7)):
where is the particle four-velocity. From this equation, it is clear that physical electric field is the Maxwell tensor with mixed components, , and physical magnetic field is expressed through the Maxwell tensor as:
or in compact form .
The first pair of Maxwell equation has the same form as in flat space-time:
If the background electric field is absent, i.e., , then
Hence remains constant in the process of cosmological expansion and correspondingly physical magnetic field behaves as:
In other words, physical magnetic field drops as , the well known result.
If an electric field is absent and the only external magnetic field is non-zero, then the dual Maxwell tensor (34) has only space-time components. The quantity is expressed through magnetic field as
In flat space-time, varying the magnetic field induces an electric field according to
In curved space-time, the analogue of this equation is Equation (62) with or Equation (63), so if the original electric field was absent, it would not be induced by a time-varying magnetic field, in the case that the time variation is created by the cosmological expansion (64).
In terms of physical magnetic field the product with indices lifted by the background metric is
5.4. Scalar and Tensor Mode Mixing in External Magnetic Field
The EMT perturbation originating from the Maxwell action is traceless, while that from the Heisenberg–Euler action has a non-zero trace. Indeed,
Now, one could naively divide the source into a traceless part and a non-zero trace part (simply subtract the trace multiplied by the background metric). To this end, let us look at Equation (68) and explicitly substitute into the right-hand side. We get
We see that the equation contains both scalar and tensor parts. Thus, it is impossible to write a separate equation for each mode. To make this even more obvious, let us fix the coordinates so that the magnetic field is directed along the x-axis. The following components of the electromagnetic field tensor will then be non-zero:
The trace from the correction to the EMT can then be rewritten taking into account the following relations:
and in Equation (70) we have
The diagonal components can be written as the sum of scalar and tensor quantities of the helicity expansion
and, substituting the helicity expansion into the complete equation, we obtain the final equation, which shows the mixing of scalars and tensor :
where .
In addition, we note that there may also be implicit mixing through the term with in the above equation, since the equation for the electromagnetic wave contains various convolutions of tensors with tensor (see below, Equation (148)).
As was noted in Section 4, the result is quite evident, since the external magnetic field gives, in addition to the GW propagation vector, another preferred direction in space. This leads to the loss of axial symmetry and to mixing of the scalar and tensor modes of metric perturbations.
6. Electromagnetic Wave Propagation in External Magnetic Field
In this section, we will derive the equation for the propagation of electromagnetic waves in curved space-time and in the presence of an external magnetic field, thereby completing the derivation of the system of differential equations (SoDE) for the metric-EMF perturbation system. We will briefly call this system , by g we mean a graviton with any possible polarization: 0, 1, 2.
6.1. Equation of Motion from the Maxwell Action
Variation in the Maxwell action from Equation (26) over leads to the equation of motion , where is the covariant derivative in the full metric . Due to antisymmetry of this equation is reduced to:
Below we assume that neither electric charge density nor electric current are present, i.e., .
The external electric field is supposed to be zero and only background magnetic field is present, so . Thus, the zero-order term, which is the equation of motion for the background magnetic field, has the form;
This is the analogue of the equation in flat space-time.
In FLRW metric the metric determinant is expanded as:
and so Equation (82) takes the form:
where we took into account that and . We also assume that and impose the transversality condition on the propagating photon modes:
which for leads to .
Thus, the first-order expansion of Equation (85) has the form:
where we introduced a new quantity to describe contributions from different additional terms such as Heisenberg–Euler corrections, matter effects, etc., to be considered below.
To derive the first-order equation for , we multiply Equation (87) by (Latin indices are always supposed to be the space ones, e.g., ) and recall that and . So, we finally obtain:
where and is the flat space Laplacian.
To proceed further, we have to fix certain gauge conditions on metric perturbations . We will follow our paper [16], where it is shown that the following conditions can be imposed in arbitrary background metric:
Since in FLRW metric the only non-zero components of the Christoffel symbols are:
the covariant derivative of is reduced to the ordinary derivative and
The terms proportional to cancel out because .
Here, we have introduced the new notation:
to be used in what follows.
6.2. Equation of Motion from the Heisenberg–Euler Action
The variation of (39) over results in the following contribution to the electromagnetic field equation:
where the first term originated from the variation of the Maxwell action (see previous subsection), while the second is the contribution from (39) and has the following form
where and .
We have shown in Section 5.3 that the free external magnetic field is not constant, but rises backward in time with the decreasing scale factor as .
Let us return to Equation (95) and make perturbative expansion according to Equation (5). We start from consideration of the first term in square brackets, which with account of the zeroth- and first-order terms takes the form
where , , and indices are shifted up or down with the background metric.
The zero-order term in this equation somewhat changes the equation of motion of the background magnetic field in FLRW metric leading to:
which is not of much importance for the evolution of . The terms proportional to the time derivatives of , C, and do not appear if and .
The first-order part of expression (96) is equal to:
The term proportional to in this expression, has the form:
where is defined in the Equations (92) and (93). The factor in the brackets in the left-hand side of the above equation coincides with the left-hand side of Equation (92), except for the last term , so it can be absorbed into Equation (92) changing the overall coefficient from 1 to .
In addition to the terms proportional to , the first two terms in Equation (98) give the following contribution of the first part of the HE action to the photon propagation equation:
So all the terms in Equation (98), except for those absorbed into Equation (92) and containing , turn into:
The contribution of the terms containing in Equation (98) can be written as
Finally, for the total we obtain
where is defined in Equation (93).
It is convenient to introduce auxiliary vector field through the equation
Physical magnetic field is related to as (because ).
To decipher the last term in Equation (103) we use the identity:
and Equation (104). So and turn into
where summation over repeated indices is performed.
The variation of the second term in the HE action, Equation (95), is equal to:
In the case that the background electric field is absent and only magnetic field is non-zero, the right-hand side of the equation above vanishes in the zeroth-perturbation order because is non-zero only for space–space components, while is non-zero for space-time components. Hence .
So using Equation (104) and contracting
we obtain from Equation (109):
where the summation over the repeated space indices is made with Kronecker delta and considers that .
So using Equations (92), (93), (103) and (109) we obtain:
and come to the almost final equation for photons
We highlight that is defined in Equation (93).
6.3. Conformal Anomaly Effect
Quantum corrections to the energy–momentum tensor of electromagnetic field in curved space-time background lead to the the well-known conformal anomaly, for a review see ref. [25], resulting in the nonzero trace of the electromagnetic energy–momentum tensor:
where is the gauge field stress tensor, is the fine structure constant and is the first coefficient of the beta-function expansion for the gauge group of rank N:
with being the number of the fermion species.
There are additional contributions into the trace proportional to the products of the Riemann, Ricci tensors, and curvature scalar which are generally nonlocal [26,27]. We will not consider them in this work.
The trace anomaly allows for photon production by the conformally flat gravitational field [28,29] in contrast to the Parker theorem [30].
The Fourier transform of the amplitude of the photon propagation in the gravitational field has pole at , where q is the four-momentum transfer to gravitational field. According to the result of paper [28] the anomalous part of the energy-momentum tensor has the form:
It is evidently conserved and has non-zero trace.
As is shown in Ref. [28], conformal anomaly (115) leads to an additional contribution to Equation (88) or, which is essentially the same, to Equation (92).
The first term here is the usual charge renormalization and the second one is the anomaly giving rise to photon production in conformally flat metric. This metric allows for the transformation to the conformal time leading to the Minkowski metric proportional to the common scale factor. The canonical Maxwell equation, without the anomalous term, transforms in this metic into the free Maxwell equation in flat space-time, while the additional anomalous term does not allow this.
6.4. Plasma Interaction Effects
Photons propagating in the primeval plasma interact with plasma particles and as a result acquire an effective mass, the so-called plasma frequency, , so the relation between photon frequency, , and momentum, k, changes as . Waves with do not propagate in plasma.
In the canonic theory, the effective action describing the plasma frequency term is usually written as
This term is proportional to the square of the small amplitude of the electromagnetic wave and seemingly should be neglected in our first order approximation. However, this is not so because to obtain the first-order equation one has to take the action in the second order in small quantities. The first-order terms are absent in the action since satisfies the equation of motion that are realised at the extreme value of action for which .
The corresponding energy–momentum tensor is
is quadratic in f and can be disregarded in our approximation. It is similar to a scalar field with small amplitude that has energy density proportional to , so its energy–momentum tensor is quadratically small but non-zero mass, is essential for propagation of waves.
All electrically charged particles contribute to plasma frequency. If the particle mass is larger than the temperature of the relativistic cosmological plasma, , the contribution to plasma frequency from such nonrelativistic charged particles is
where n is the number density of particles with charge e, . Note that the number density in this case is exponentially suppressed, [31].
On the other hand, relativistic particles, with , contribute as:
where the summation is done over all relativistic charged particles with charges . The electric charge, e, depends on temperature due to radiative corrections [32].
Plasma frequency is determined by the photon Green’s function in the limit of vanishing photon momentum. More rigorous treatment of the problem of the photon propagation in plasma demands determination of the proper Green’s function. Simple derivation of these expression including the Green’s function can be found in ref. [33]. However, in this paper we will use simplified approximation describing the plasma effects by the plasma frequency only.
We need also take into account the loss of coherence of the photons produced by gravitons. We describe this phenomenon introducing a damping term into the equation of motion for photons in the form , where we approximate as
where is the density of charged particles in plasma, is the number of charged particle species, is the relative velocity of “our” photon and the scatterer in plasma, and is the scattering cross-section.
Thus, the final equation for photons propagating in an arbitrary curved space-time background and external magnetic field in cosmic plasma accounting for photon collisions with plasma particles has the form:
7. Defining and System of Differential Equations (SoDE)
In total, we have ten equations for the components of tensor and three equations for the components of vector . In fact, only six equations for gravitational waves are linearly independent.
In the case considered here, we assume that the vector modes do not arise. The first vector in Equations (11)–(13) vanishes due to the gauge condition . The second vector is not zero because the corrections to EoM contain spacial derivative of electromagnetic potential . However, the vector modes decay as and thus they do not play an essential role in cosmology. It worth adding that an account of one more polarisation state would lead to a considerable complication of the system of equations. So, in this work we confine ourselves only to scalar and tensor modes.
Finally, let us mention that the solution for tensor does not contain pure tensor mode, but a mixture of tensor and scalar modes. Nevertheless, the solution represents them qualitatively correctly, including the behaviour of the tensor mode that we are interested in.
Assuming an absence of vector mode, we obtain two components less in the EoM. More specifically, we have two scalars, and (note that in the deal fluid model, i.e., without taking into account dissipation, ) and two polarisations of the tensor wave, that in total gives four independent equations for metric perturbations.
In the subsequent Section 7.1 and Section 7.2, the SoDE is simplified for the specific choice of the reference frame, where an external magnetic field is directed along the x-axis. Next, one of two independent subsystems is solved numerically in Section 8.
7.1. Simplification of SoDE for Metric Perturbations
To derive the system of equations for the metric perturbations, that is solved below, it remains to simplify the right-hand side of Equation (24). Let us rewrite Equations (58)–(59) for an external magnetic field that is directed along the x-axis. For individual expressions, we get:
In this section and in subsequent ones, for the sake of brevity, we will omit the signature in the correction to the EMT.
Using Equations (58) and (59) and Equations (126)–(137) we obtain the EMT components for 00 (remember that :
Similarly, we derive the expression for the component :
The expression for the components is more cumbersome:
Let us regroup the terms
It will now be useful to write down the spatial components separately. After reducing similar terms, we get
7.2. Simplification of SoDE for Electromagnetic Waves
Let us simplify the system of equations for an electromagnetic wave for the case when the external magnetic field is directed along the x-axis. For spatial components, Equation (124) was derived in general form. We assume that , so the time derivative is . Also, to begin with, let us omit the last three terms in the left-side of the equation, that considers the interaction of photons with plasma. Now, let us write the convolutions with the background tensor of the electromagnetic field in terms of field :
The last equality follows from the fact that the only non-zero component of the dual electromagnetic tensor in cases where the magnetic field is directed along the x-axis is .
So, let us write the resulting Equation (we omit the terms from the interaction with the plasma):
By analogy with the equations for gravitational waves, we write for x, y, and z components, respectively:
Similar ones can be given, taking into account that (meaning ) and that . For x components we get:
or
For y component:
or
For z component:
or
Next, we would like to show the validity of the requirement . In general, due to the homogeneity of the magnetic field (depending only on time), we arrive at the following equation for the time component:
Now we need to select a calibration. If our problem can be called magnetostatic, in such cases the Coulomb gauge is usually introduced, where we then get:
From the initial conditions of electrical neutrality, we find that this constant is equal to zero.
8. Two Examples of Gravitational Wave Directions
For any initial direction of the gravitational (tensor) wave propagation, we can decompose it into a parallel and perpendicular component relative to the external magnetic field. Note that we consider the case when an initial pure tensor plane wave propagates from vacuum into a region with a magnetic field (and, in the future, with plasma).
It is shown below that, for the scalar mode of metric perturbations is not excited, and the electromagnetic wave is not excited as well. For the perpendicular component the situation is different—the scalar mode of metric perturbations and both polarizations of the electromagnetic wave are excited. Until now, we have not taken into account dissipation and loss of coherence for photons due to their interaction with plasma. But even without taking these phenomena into account, it is already possible to detect a change in the amplitude of the initial tensor GW due to the transition to the scalar mode of metric disturbances and to an electromagnetic wave. We will consider both of these cases in more detail in the next two subsections.
8.1.
Let us write down the basic relations that allow us to simplify the system of differential equations for metric perturbations and for an electromagnetic wave (EMW):
Taking into account what was written above, we write the system of equations in terms of . From Equations (133), (134), (138)–(143) we obtain
In Equations (174)–(176), there are no terms related to the gravitational wave. Therefore, if the electromagnetic wave was not initially present, it does not arise for the case when the wave vector is parallel to the external magnetic field. Hence, we obtain that
From the remaining non-zero components of EMT Equations (171)–(173), we see that the GW configuration is preserved: it remains tensorial and no scalar modes arise.
8.2.
Similar to the previous subsection, we write down the main relations that will help to simplify the system of differential equations for perturbations of metric and for electromagnetic waves. Let us direct the wave vector along the z-axis (it is always possible to rotate the coordinate system so that ).
Taking into account what was written above, we will write the system of equations in terms of . From Equations (133), (134), (138)–(143) we obtain
In Equation (196), there are no terms associated with a gravitational wave. So, as expected, longitudinal EMW does not arise. From Equations (194) and (195), it follows that an electromagnetic wave with polarization along the x-axis is generated by the polarization of the GW, and an electromagnetic wave with polarization along the y axis—polarization of the gravitational wave. Also, from the Equations (186)–(193), we clearly see the emergence of a scalar mode from the equations for the 00 and components of the EMT (see Equation (24)).
It is important to note that the expressions for EMT in terms of are valid only at the moment of time immediately following the initial moment of GW entry into the region with a magnetic field. Further, the wave ceases to be purely tensorial, and it is impossible to assert that . To find a solution, it is necessary to express all the quantities precisely in terms of and (not in terms of ) or in terms of expansion in helicity, introducing and .
9. System Solution in the Case
Let us write out the system of equations completely, taking into account the conclusions of the previous section that components that are absent at the beginning do not arise during the conversion of tensor GW into photons and scalar perturbations of the metric.
Let us draw the reader’s attention to the fact that we write the equations in terms of the electromagnetic potential with the superscript and the gravitational wave potential with mixed indices . In this case, we use the following expansion in helicity states for perturbation of the metric
We also make the Fourier expansion in terms of momentum, and accept the law of the scale factor variation with time, corresponding to the stage of radiation dominance .
To further search for a numerical solution, it would be convenient to introduce dimensionless quantities. To do this, let us change the notation
and introduce to make the scale factor dimensionless
Due to the last change, the tensor also becomes dimensionless.
Let us assume that at the present-day Universe . This is just a choice of reference point and this choice does not influence the solution, because the constant factor in front of the scale factor function has no physical meaning. The condition is convenient in our problem to recalculate magnetic field strength using the present day magnitude. Using the scale factor dependence during matter dominance epoch we obtain for the coefficient :
where years is the age of the Universe, years is the moment when radiation and dust energy densities were equal.
We accept also that the scale factor a varies in the interval . The selected interval lies inside the radiation dominance epoch (from the hadronic to the recombination).
For the magnitude of the magnetic field in the system of equations, we take its value at the present time. There are bounds obtained from observations: Gs [34]. Therefore, let us put .
After the Fourier transform over momentum, it will be clear that the system of equations contains both imaginary and real terms. Therefore, to solve the SDE numerically, it will be necessary to decompose each of the required quantities into real and imaginary parts. For example, and so on. For brevity, we write down systems of equations without dividing into real and imaginary parts. To obtain a more universal result, it is convenient to write the system in terms of . The first independent system has the following form:
where the prime denotes the derivative with respect to the scale factor, and we introduced the attenuation of the electromagnetic wave due to its interaction with the plasma using the damping factor and the plasma frequency . Let us recall that .
All solution interval terms with the multiplier can be neglected. Therefore, the resulting system is
It can be seen that the initial conditions
give nontrivial solution.
Let us stress here that the chosen initial conditions just allow us to formulate a simple problem to solve and to obtain the effect in order of magnitude, i.e., to obtain a representative result. That is the first step of the investigation. In future works, we are going to approach step-by-step more close to the real physics conditions.
It is important to note that there are poles at in the first equation. Let us remind the reader that the effective Heisenberg–Euler action Equation (32) is correct under the assumption of a weak external electromagnetic field. In our case, that means that . This restirction is valid in the selected interval of the variation of the scale factor: . Indeed, for nGs inside the interval for the scale factor we obtain
All the values are less than the electron mass squared MeV. Using the definition (33), we can rewrite the term proportional to as:
On the other hand, we have shown that in the whole interval of solution variation. Therefore, after squaring and multiplying by , the condition remains the same
and means that the correction to the Maxwell action proportional to is sufficiently accurate for our consideration.
Another important question to be solved in future work is to what minimum value of the scale factor should the solution be expanded? The solution to this question should be sought in the theories of cosmological magnetogenesis, that study the epoch when the cosmological magnetic field was generated. We should also keep in mind that as the scale factor approaches the pole, higher order corrections will be excited [17], thereby removing any potential pole.
The second subsystem, which involves the quantities , is larger, more complex and requires solving many sub-problems. For example, the question of whether scalar metric perturbations propogate is quite nontrivial and requires careful analysis. In order to steer the article away from becoming excessively cumbersome, in this work we will concentrate on solving only the subsystem .
In order to numerically solve the system, we need to divide both parts of the equation by and to introduce two new functions to lower the order of the equation in order to make it look like: .
Two new functions and a system to be solved:
We use fifth-order implicit Runge–Kutta method, which is algebraically stable and allows solving stiff systems of differential equations, for more details see [35].
9.1. Method of Solution Validation
Before solving the system for a non-zero magnetic field strength, we must check whether the method for the SoDE solving works correctly for the case when it is absent. Equation of motion for tensor gravitational waves in the approximation , where is a conformal time, can be solved analitically. The solution has the form
where is an initial magnitude of tensor perturbation, and is a constant phase. The last two parameters are defined from the matching with the constant mode, obtained from the EoM solution in the approximation (see Section 3.2 in Ref. [15]).
In Figure 1a, the numerical and analytical solutions are presented for the two conformal time values and corresponding to them frequencies Hz satisfying the condition .
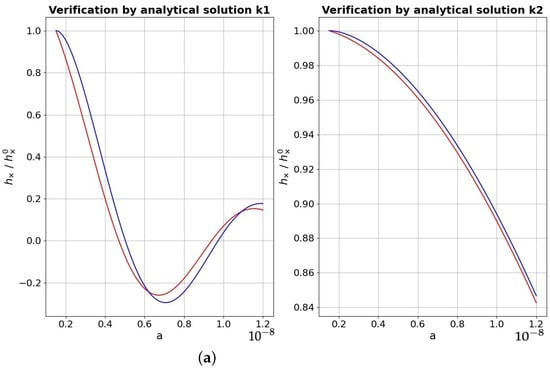
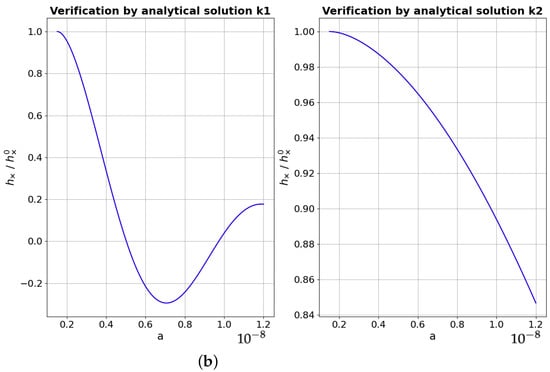
Figure 1.
Verification of the numerical solution (blue line) by the analytical solution (red line) for two frequencies (left) and (right). (a) without phases; (b) with phases.
Here, we see a significant discrepancy, but after the correct phase selections, , we obtain a coincidence with an accuracy of four orders of magnitude (Figure 1b and Figure 2). In Figure 2, an absolute difference between the numerical and the analytical solutions is presented for the two considered cases.
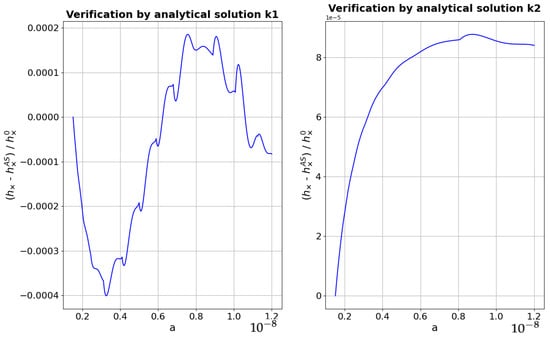
Figure 2.
Absolute difference between the numerical solution and the analytical solution for two frequencies (left) and (right).
Eventually, we can conclude that the method of numerical solution works correctly, and the results obtained for a non-zero value of magnetic field strength are reliable.
9.2. Numerical Solution Results for the System
Let us present the numerical solution results for the system of Equation (207) with the initial conditions according to the Equation (208). The code was written in Python using the solve-ivp package.
Of particular interest in the long-wave range are the wavelengths that have left their mark on the CMB. We found a solution for frequencies Hz. We use an implicit Runge–Kutta method of order five to solve the SoDE for nGs and for these frequencies. The scale factor interval is , and it lies within the radiation dominance (RD) epoch. For comparison, a solution to the system in the absence of a magnetic field was also found.
The results are as follows: by the end of the RD era, amplitude of GW with the selected frequencies is suppressed by about 0.01 percent. Thus, we can conclude that the considered effect of converting GWs into photons in a cosmological magnetic field has an extremely small effect on the amplitude of long-wavelength relic GWs.
It is instructive to say a few words about the physical reason for the suppression of the GW amplitude. In the problem we are considering, where the magnetic field is still not strong enough, the main contribution to the damping comes from the classical Maxwell action. Neglecting the loop correction in the equation of motion for the metric perturbation in Equation (207), we obtain the second term in the brackets , which works similarly to the plasma frequency for photons propagating in the plasma [36]. This term suppresses the low frequency end of the GW spectrum. Indeed, for the quantities nGs, we obtain for the boundary value of the momentum less than the above mentioned analogue of the plasma frequency for GW:
10. Discussion
In the presented work, we have derived a coupled system of equations for gravitational and electromagnetic wave propagation in an external magnetic field. Subsequently, simplification of the differential equation system was performed for the FLRW background metric and for the case of homogeneous magnetic field directed perpendicularly to the initial gravitational wave vector. Finally, we have solved the system numerically for —polarization putting nGs. The resulting estimate of the effect, without taking into account the inhomogeneity of the magnetic field, is about 0.01% suppression of the amplitude for a relic GW with a frequency of Hz at the recombination.
It is worth noting that the results are obtained under a large list of simplifying assumptions and the research demands a deeper investigation (for example, the assumption about the magnetic field homogeneity is rather crude). Despite this, the results make sense and one can conclude that the considered phenomenon of GW conversion into photons in the intergalactic magnetic field cannot significantly suppress relic gravitational wave amplitude.
Let us emphasize that this result was not obvious at the beginning of the research. The smallness of the second-order corrections to the Maxwell action does not yet infer the smallness of the relic GW suppression effect. It is also necessary to take into account the interaction of the energy generated by GW photons with the primordial plasma, as well as the fact that the conversion occurs over a long period of time during the evolution of the Universe. A crucial point is also the dependence of the cosmological magnetic field amplitude on the scale factor according to the law , which in the early stages of the evolution of the Universe could lead to a rather high magnetic field strength, and therefore to a noticeable conversion effect.
In future works, we plan to solve the second independent part of the SoDE, paying special attention to the following question: do the emerged scalar perturbations run? Subsequently, we want to expand the solution interval up to the end of the matter dominance epoch and to account for the magnetic field inhomogeneity.
It is worth stressing that the stochastic nature of the relic GW direction and the magnetic field direction should have a large impact on the magnitude of the suppression effect, and a more accurate analysis of this phenomenon is also very important. We plan to perform such an analysis in order to present quantitatively the dependence of the full relic GW spectrum suppression on the intergalactic magnetic field strength.
Future research is not only of academic interest, but can also be applied to similar problems of converting gravitational waves into photons near astrophysical sources of strong magnetic fields. Of course, the background metric must be modified to suit the specific task conditions, but the inference structure and some of the qualitative findings discussed in this manuscript will remain valid and useful. In addition, the accuracy of future measurements of CMB polarization [37] will steadily increase, and may reach values of the order of the considered effect.
Author Contributions
Conceptualization, A.D.D.; methodology, A.D.D. and L.A.P.; software, L.A.P.; validation, A.D.D., L.A.P. and V.A.B.; formal analysis, L.A.P. and V.A.B.; investigation, A.D.D. and L.A.P.; writing—original draft preparation, L.A.P.; writing—review and editing, A.D.D. and V.A.B.; visualization, L.A.P.; supervision, A.D.D.; project administration, A.D.D.; funding acquisition, A.D.D. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the RSF grant number 23-42-00066.
Data Availability Statement
No new data were created or analysed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| GW | Gravitational Wave |
| FLRW space-time | Friedman–LeMaitre–Robertson–Walker space-time |
| EMT | Energy–Momentum Tensor |
| EMW | Electromagnetic Wave |
| HE Lagrangian | Heisenberg–Euler Lagrangian |
| SoDE | System of Differential Equations |
| EoM | Equation of Motion |
References
- Gertsenshtein, M.E. Wave Resonance of Light and Gravitational Waves. Zh. Eksp. Teor. Fiz. 1961, 41, 113, Erratum in Sov. Phys. JETP 1960, 14, 84. [Google Scholar]
- Mitskevich, N.V. Physical Fields in General Relativity; Nauka: Moscow, Russia, 1970. [Google Scholar]
- Boccaletti, D.; De Sabbata, V.; Fortini, P.; Gualdi, C. Space-Time Curvature Mode Quanta. Nuovo C. 1970, 70, 129–146. [Google Scholar] [CrossRef]
- Dubrovich, V.K. Izvestiya Spetsial’noj Astrofisicheskoj Observatorii. Zel’dovich Zh. Eksp. Teor. Fiz. 1972, 65, 1311. [Google Scholar]
- Zel’dovich, Y.B. Electromagnetic and gravitational waves in a stationary magnetic field. Zh. Eksp. Teor. Fiz. 1973, 65, 1311, Erratum in Sov. Phys. JETP 1974, 38, 652. [Google Scholar]
- Fargion, D. Gravitation and Cosmology; Pleiades Publishing: New York, NY, USA, 1995; Volume 1, pp. 301–310. [Google Scholar]
- Raffelt, G.; Stodolsky, L. Mixing of the Photon with Low Mass Particles. Phys. Rev. D 1988, 37, 1237. [Google Scholar] [CrossRef] [PubMed]
- Dolgov, A.D.; Ejlli, D. Conversion of relic gravitational waves into photons in cosmological magnetic fields. J. Cosmol. Astropart. Phys. 2012, 12, 3. [Google Scholar] [CrossRef]
- Linde, A.D. Inflationary cosmology. Phys. Rep. 2000, 333, 17. [Google Scholar]
- Grishchuk, L.P. Amplification of gravitational waves in an isotropic universe. Zh. Eksp. Teor. Fiz. 1974, 67, 825, Erratum in Sov. Phys. JETP 1975, 40, 409. [Google Scholar]
- Lifshitz, E.M. On the gravitational stability of the expanding universe. Zh. Eksp. Teor. Phys. 1946, 15, 587. [Google Scholar]
- Lifshitz, E.M.; Khalatnikov, I.M. Problems of relativistic cosmology. Uspekhi Fiz. Nauk 1963, 80, 391. [Google Scholar] [CrossRef]
- Dolgov, A.D.; Ejlli, D. Resonant high energy graviton to photon conversion at post recombination epoch. Phys. Rev. D 2013, 87, 104007. [Google Scholar] [CrossRef]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; Freeman and Company: San Francisco, CA, USA, 1973. [Google Scholar]
- Gorbunov, D.S.; Rubakov, V.A. Introduction to the Theory of the Early Universe: Cosmological Perturbations and Inflationary Theory; World Scientific: Hackensack, NJ, USA, 2011. [Google Scholar]
- Arbuzova, E.V.; Dolgov, A.D.; Panasenko, L.A. On graviton propagation in curved spacetime background. J. Exp. Theor. Phys. 2022, 135, 304–311. [Google Scholar] [CrossRef]
- Heisenberg, W.; Euler, H. Folgerungen aus der Diracschen Theorie des Positrons. In Zeitschrift für Physik; Springer: Berlin/Heidelberg, Germany, 1936; Volume 98, pp. 714–732. [Google Scholar]
- Fanizza, G.; Gasperini, M.; Pavone, E.; Tedesco, L. Linearized propagation equations for metric uctuations in a general (non-vacuum) background geometry. J. Cosmol. Astropart. Phys. 2021, 7, 21. [Google Scholar] [CrossRef]
- Maggiore, M. Gravitational Waves: Theory and Experiments; Oxford University Press: Oxford, UK, 2008; Volume 1. [Google Scholar]
- Maggiore, M. Gravitational Waves: Astrophysics and Cosmology; Oxford University Press: Oxford, UK, 2018; Volume 2. [Google Scholar]
- Mukhanov, V. Physical Foundations of Cosmology; Cambridge University Press: New York, NY, USA, 2005. [Google Scholar]
- Weinberg, S. Cosmology; Oxford University Press: Oxford, UK, 2008. [Google Scholar]
- Weinberg, S. Gravitation and Cosmology: Principles and Applns of the General Theory of Relativity; Wiley: Hoboken, NJ, USA, 1972. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Pergamon Press: New York, NY, USA, 1971; Volume 2. [Google Scholar]
- Duff, M.J. Twenty Years of the Weyl Anomaly. Class. Quant. Grav. 1994, 11, 1387. [Google Scholar] [CrossRef]
- Bunch, T.S.; Davies, P.C.W. Stress Tensor and Conformal Anomalies for Massless Fields in a Robertson-Walker Universe. Proc. R. Soc. Lond. 1978, 360, 117. [Google Scholar]
- Birrell, D.N.; Davies, P.C.W. Quantum Fields in Curved Space; Cambridge University Press: Cambridge, UK, 1982. [Google Scholar]
- Dolgov, A.D. Conformal Anomaly and the Production of Massless Particles by a Conformally Flat Metric. Sov. Phys. JETP 1981, 54, 223, Erratum in Zh. Eksp. Teor. Fiz. 1981, 81, 417. [Google Scholar]
- Dolgov, A.D. Breaking of conformal invariance and electromagnetic field generation in the universe. Phys. Rev. D 1993, 48, 2499–2501. [Google Scholar] [CrossRef]
- Parker, L. Particle creation in expanding universes. Phys. Rev. Lett. 1968, 21, 562. [Google Scholar] [CrossRef]
- Pitaevskii, L.P.; Lifshitz, E.M. Physical Kinetic; International Atomic Energy Agency: Vienna, Austria, 2012; Volume 10, ch. III. [Google Scholar]
- Kraemmer, U.; Rebhan, A.K.; Schulz, H. Resummations in Hot Scalar Electrodynamics. Ann. Phys. 1995, 238, 286. [Google Scholar] [CrossRef][Green Version]
- Dolgov, A.D.; Lepidi, A.; Piccinelli, G. Electrodynamics at non-zero temperature, chemical potential, and Bose condensate. J. Cosmol. Astropart. Phys. 2008, 902, 27. [Google Scholar] [CrossRef]
- Barrow, J.D.; Ferreira, P.G.; Silk, J. Constraints on a Primordial Magnetic Field. Phys. Rev. Lett. 1997, 78, 3610. [Google Scholar] [CrossRef]
- Burrage, K.; Butcher, J.C. Stability Criteria for Implicit Runge–Kutta Methods. SIAM J. Numer. Anal. 1979, 16, 46–57. [Google Scholar] [CrossRef]
- Dolgov, A.D.; Postnov, K. Electromagnetic radiation accompanying gravitational waves. from black hole binaries. J. Cosmol. Astropart. Phys. 2017, 9, 18. [Google Scholar] [CrossRef]
- Planck Collaboration. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).