1. Introduction
Recent times have seen an overhaul of our understanding of fundamental biochemistry owing to ever-improving analytical techniques. The ability to perform high-resolution, multidimensional separations has allowed the field to move from compound-specific measurements to wide untargeted analyses that can in turn be fed to powerful statistical tools [
1]. These advances have been particularly useful for metabolomics, where the space of possible compounds ranges widely with respect to mass, size, and chemical properties. One of the go-to implementations is liquid chromatography–mass spectrometry (LC–MS). Compounds can be separated in a first dimension by LC, relying on the chemical interactions between the compounds and the column used in the separation. Afterwards, high-resolution MS is able to resolve masses up to the nuclear mass defect, unequivocally determining which atoms are present in a compound.
Steroidomics is especially affected by this [
2]. The approach targets a family of compounds appearing in diverse metabolic pathways and with different biological roles, yet possessing a high similarity in structural and chemical terms. These issues are problematic both from the MS perspective (multiple steroids share the same molecular formula rearranged with various isomeric configurations) and from the LC perspective (most chromatographic supports are unable to exhibit selectivity towards all possible spatial changes in the molecules). One could be tempted to consider MS/MS fragmentation at this point, since it provides a direct fingerprint of the structure of the compound. Unfortunately, fragmentation patterns for steroids are quite similar since the shared core structure usually leads to common unspecific fragments. In addition, in real biological samples, the quantity of certain steroids may already fall below the threshold for detection in standard MS, let alone provide an adequate number for fragmentation to observe low-quality MS/MS spectra. Hence, optimization of the chromatographic separation becomes critical and remains the main way to distinguish different candidates of biological interest. Thankfully, the retention time of different compounds is sensitive to multiple parameters and, of interest to us, the mobile phase composition gradient. By adequately tuning a gradient involving two solvents with different elution strengths, separation can be achieved for similar compounds.
Even if separation is successful enough that the LC–MS system returns a dataset of distinct experimental features, the question of identity remains. The usual procedure is to refer to a set of standards. Features in real samples measured under identical conditions as the standards can then be characterized by matching physico-chemical properties, such as their accurate mass, isotopic pattern, MS/MS spectra, and observed retention time. It is important to stress that this is not an identification, but an annotation workflow, in that one only assigns a putative identity (or quite often, a set of identities) to a certain detected feature. This distinction is because mass measurements can only determine chemical composition, and retention time can be shared within the experimental tolerance by multiple compounds, potentially not included in the reference library. A hierarchy of annotation levels is commonly used (see for instance [
3] and [
4]), including the following:
Level 4: unknown.
Exact mass.
Level 3: chemical class.
Exact mass, some additional physico-chemical properties.
Level 2: annotated metabolite.
Two orthogonal properties, from external database/in-silico calculations.
Level 1: identified metabolites.
Two orthogonal properties, reference standard, same laboratory.
In this context, it will be relevant to distinguish between the standard level 2 and a newly introduced level 2+. This is related to the dynamic retention time generation that is the keystone of DynaStI. The underlying model is extremely robust when using experimental parameters measured from standards, as will be shown in detail later in the article.
Jumping straight to level 1 can be challenging for an untargeted analysis in steroidomics. However, if the separation has been optimized, level 2 putative annotations are few per observed feature. A better approach is to study which features are statistically relevant by using some sort of multivariate analysis. With the level 2 annotations for those features in hand, one has a shortlist of candidates that can be subsequently confirmed or quantified in a targeted study.
The key clause is “if the separation has been optimized”. For every different gradient, optimized for every situation, one would naïvely need to characterize the whole library of standard compounds to retrieve the association between retention times and compound identities.
Thankfully, reverse-phase liquid chromatography (RPLC) on identical analytical columns and temperatures (i.e., stationary phase chemistry) is amenable to a certain amount of modeling, at least as far as the eluent in the separation is concerned. The linear solvent strength (LSS) model [
5] is notably able to reproduce the retention caused by an arbitrary mixture of two given components in the mobile phase by using only two experimental parameters per compound (compare with the
measurements needed for
different gradients in a naïve approach). To estimate these LSS parameters, only two retention times for each compound in the library of standards must be measured, each under two different gradient conditions. With the LSS model in hand, a database of retention times for any other gradient configuration can be dynamically generated at any time [
6,
7].
The aim of DynaStI is to implement such functionality and to wrap it in a user-friendly web interface. The basic workflow takes a list of observed features, a gradient configuration, annotation tolerances, and possibly a set of calibration compounds with known retention times. The program returns the list of annotations, together with relevant chemical information about them and references to external databases.
This article will briefly review the theoretical foundations of the prediction model. It will then describe in detail the database on which DynaStI runs, including the experimental conditions and the library of standards. The concrete web implementation is given afterwards. Finally, a real application to steroidomics will be presented to illustrate the power of the software.
4. Experimental Results
Preliminary work on dynamic annotation [
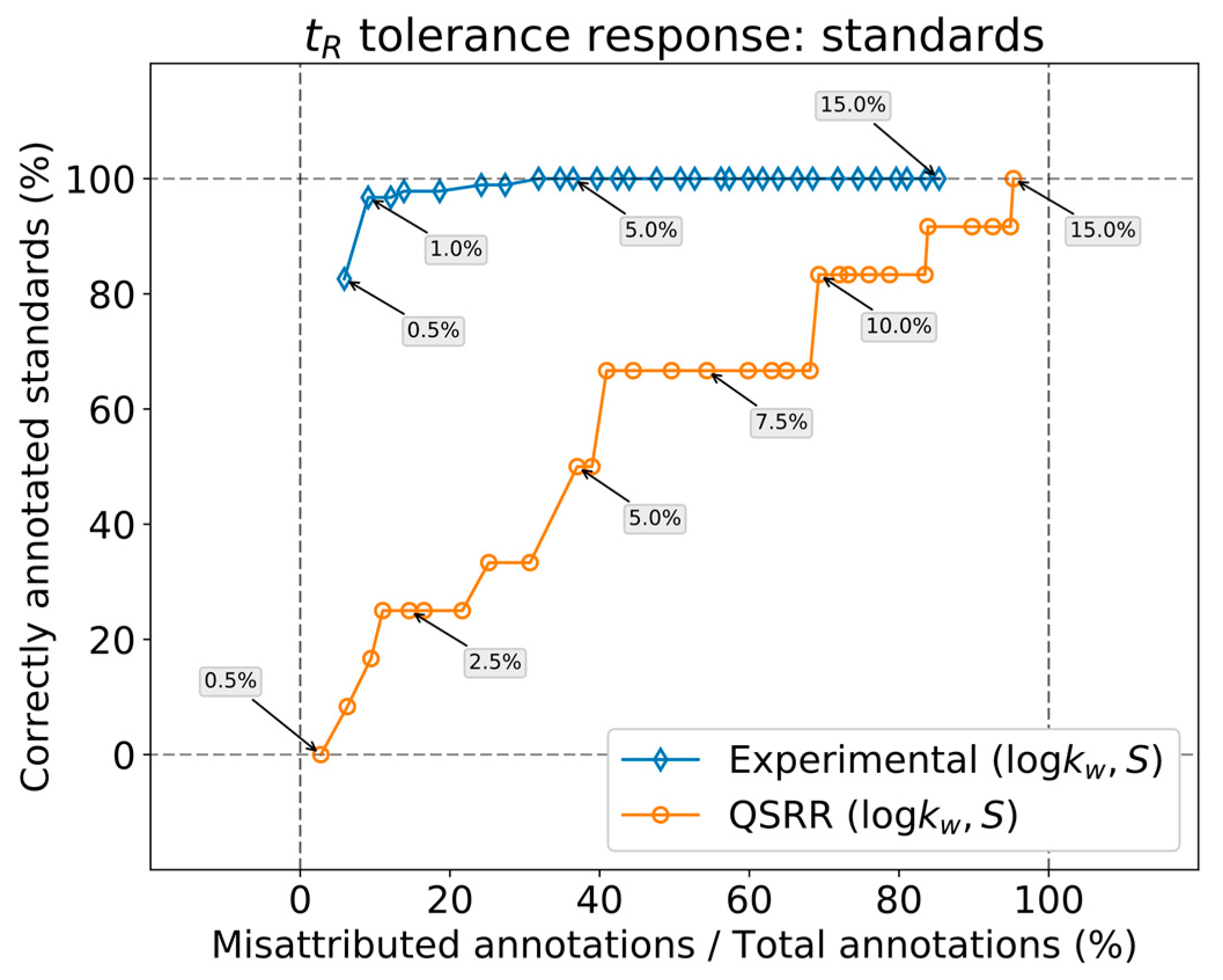
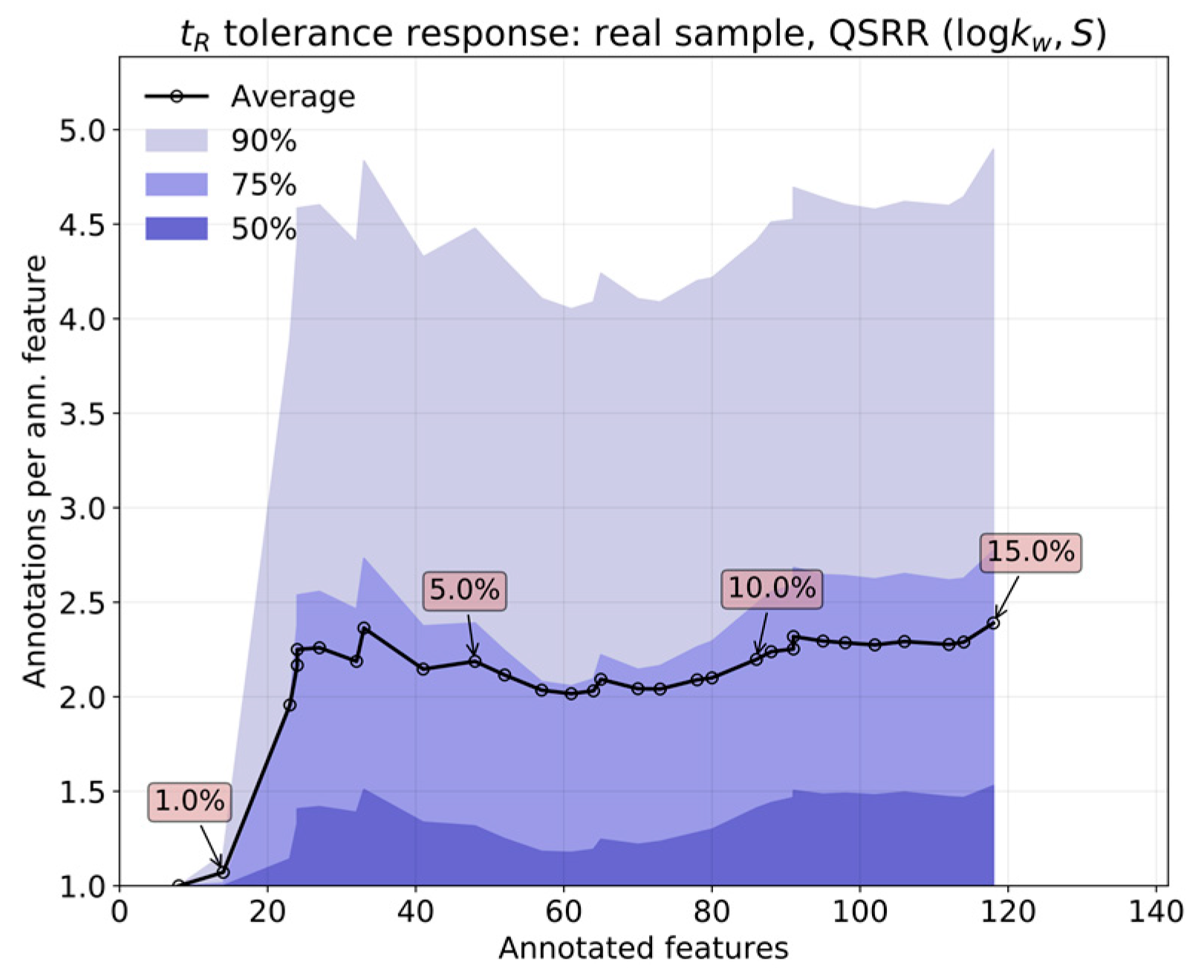
7] has demonstrated several issues, including the need for a specific study regarding the correct tolerances required for an optimal annotation with the dynamic database.
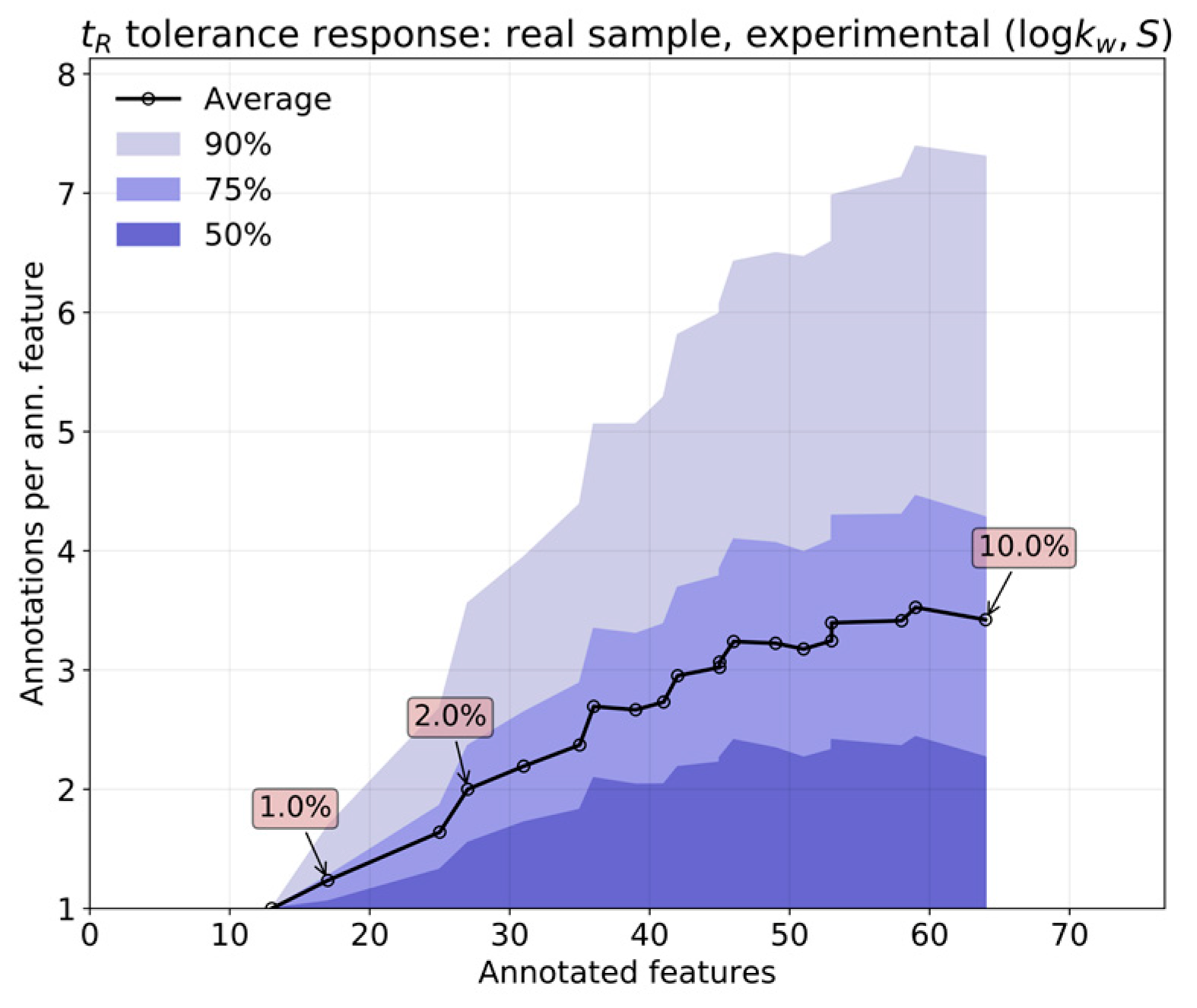
On the one hand, the error inherent to the prediction most likely outweighs that coming from measurement, owing to the high reproducibility of the chromatographic process in RPLC. This feature is, of course, superior for predictions based on in silico parameters. In contrast, real applications involve extensive sets of features. The overlap of isomers with similar interactions with the column will bloat the annotation list for any given feature, which can only be countered by limiting the tolerances as much as possible.
The relative performance of
in silico (by QSRR) relative to experimentally determined
parameters was first analyzed by comparing both predictions over a set of features obtained from known standards. The response of annotation multiplicity to tolerance was studied on both the standards and a real sample containing steroids obtained in the context of the analysis of pooled human seminal liquid samples. Such a matrix was chosen because the content of steroids of the seminal liquid has not yet been thoroughly investigated in humans [
11], and because it may provide relevant information about the steroidogenesis state for the prostate, testicle or seminal vesicle. Levels of steroids in such organs may be represented in semen as a mix of secretions originating from these glands. For instance, prostate cancer is correlated with the presence of UDP-glucuronosyltransferase 2B15, resulting in variation of 5α-dihydrotestosterone in the prostate [
12,
13]. Another example is doping abuse, which has been proven to induce impairment of steroidogenesis in testis by suppression of the luteinizing hormone signal, to induce hypogonadism and impact sperm quality (see review [
14]). The presence of endocrine disruptors such as phthalates in the environment has also been associated with a decrease in sperm quality [
15] by the possible antagonist action of phthalates with androgen receptors and enzymes, disrupting steroidogenesis. Steroidogenesis pathways are subject to environmental, pathological, and physiological influences. The monitoring of the extended steroid profile would provide a broader insight into the actual content of steroids in the semen. Hence, this application aims to demonstrate how DynaStI provides useful annotations when analyzing biological samples, as required for an eventual analysis leading to a better understanding of the underlying metabolic pathways.
4.2. Prediction Error
To assess the actual reliability of the predictions, we compared the measured retention times of the standards in the original conditions with those derived from the LSS model for a set of 70 compounds (see
Supplementary material) corresponding to the ones for which LSS parameters were available from both experimental and QSRR sources [
7]. In
Figure 1, we plot the measured/predicted retention time comparison on the left and the relative error of the predictions (w.r.t. the actual measurements) on the right, when done without the calibration. For every compound in the standards, two points are given in the left plot, one with the experimental prediction and one with the QSRR prediction. The relative errors of both are used as the coordinates in the right plot. Ideally, the retention times should fall exactly on the diagonal line, which would correspond to a perfect prediction. As indicated by the obtained slope, a systematic error was present. As previously discussed, this error is related to the determination of the parameters of the instrument’s geometry. Recall that the actual experimental system does not have 0-dimensional injection/mixing points, as the usual LSS model considers. For instance, the dwell volume is affected by capillary connections and valves and contributes a significant volume to the system.
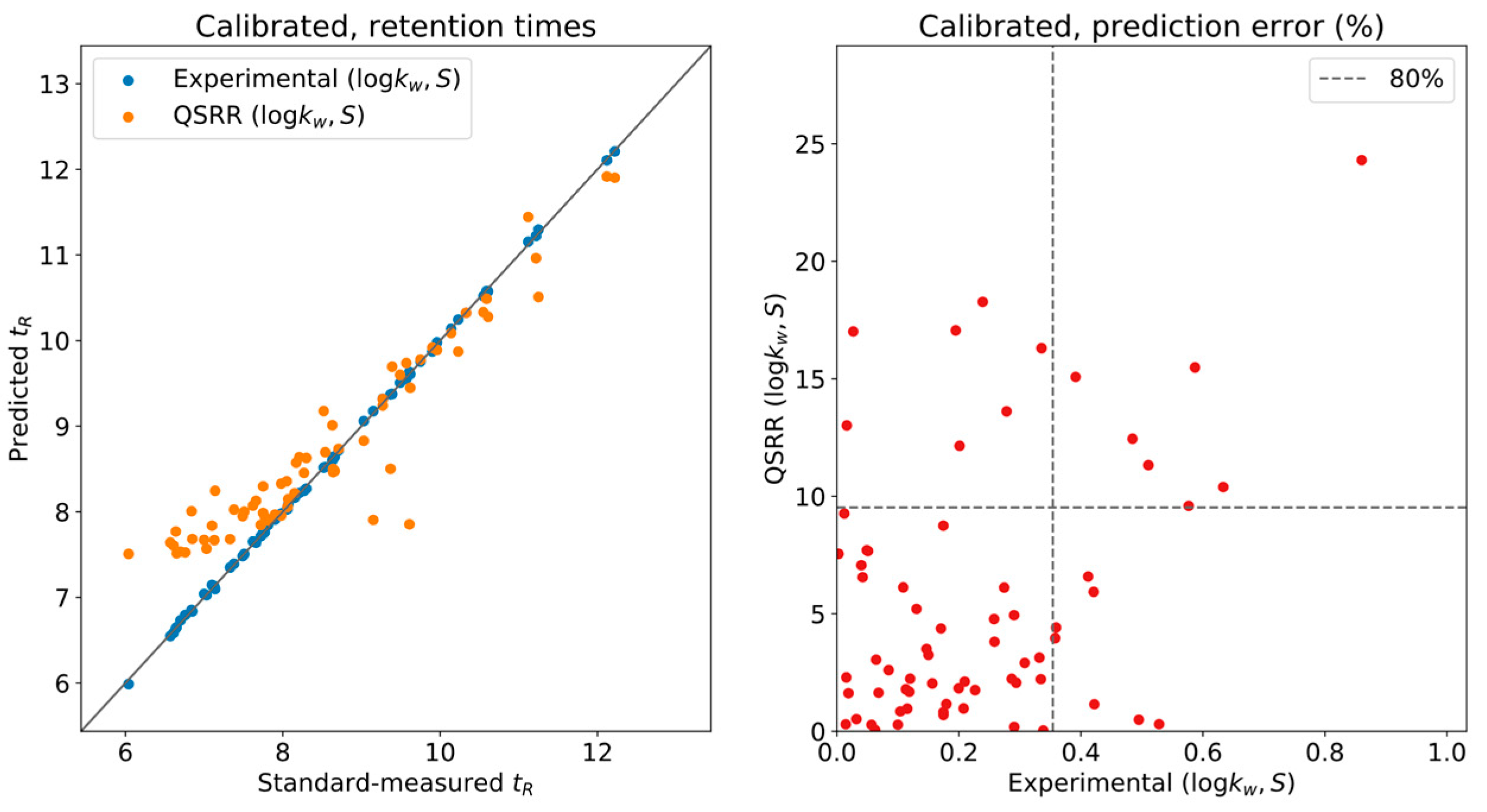
To correct for this issue, five compounds were used as calibrants for the complete database, namely, in DynaStI’s convention: androstenedione, cortisol, cortisone, testosterone and 4,5α-dihydrotestosterone. It should be noted that the experimentally predicted and QSRR-predicted times have been independently calibrated. As presented in
Figure 2, thanks to this automatic internal calibration, and as long as the
values have been experimentally measured, the LSS model provides exceptional accuracy, with
of the values having less than
deviation between measurement and prediction and none exceeding
. QSRR-predicted times show much larger deviations, up to
. However, the whole list of QSRR predictions has been calibrated using the QSRR predictions for the five selected compounds. Critically, the error in the predictions used for calibration is carried onto the calibrations themselves, and a systematic deviation is still observed at low retention times.
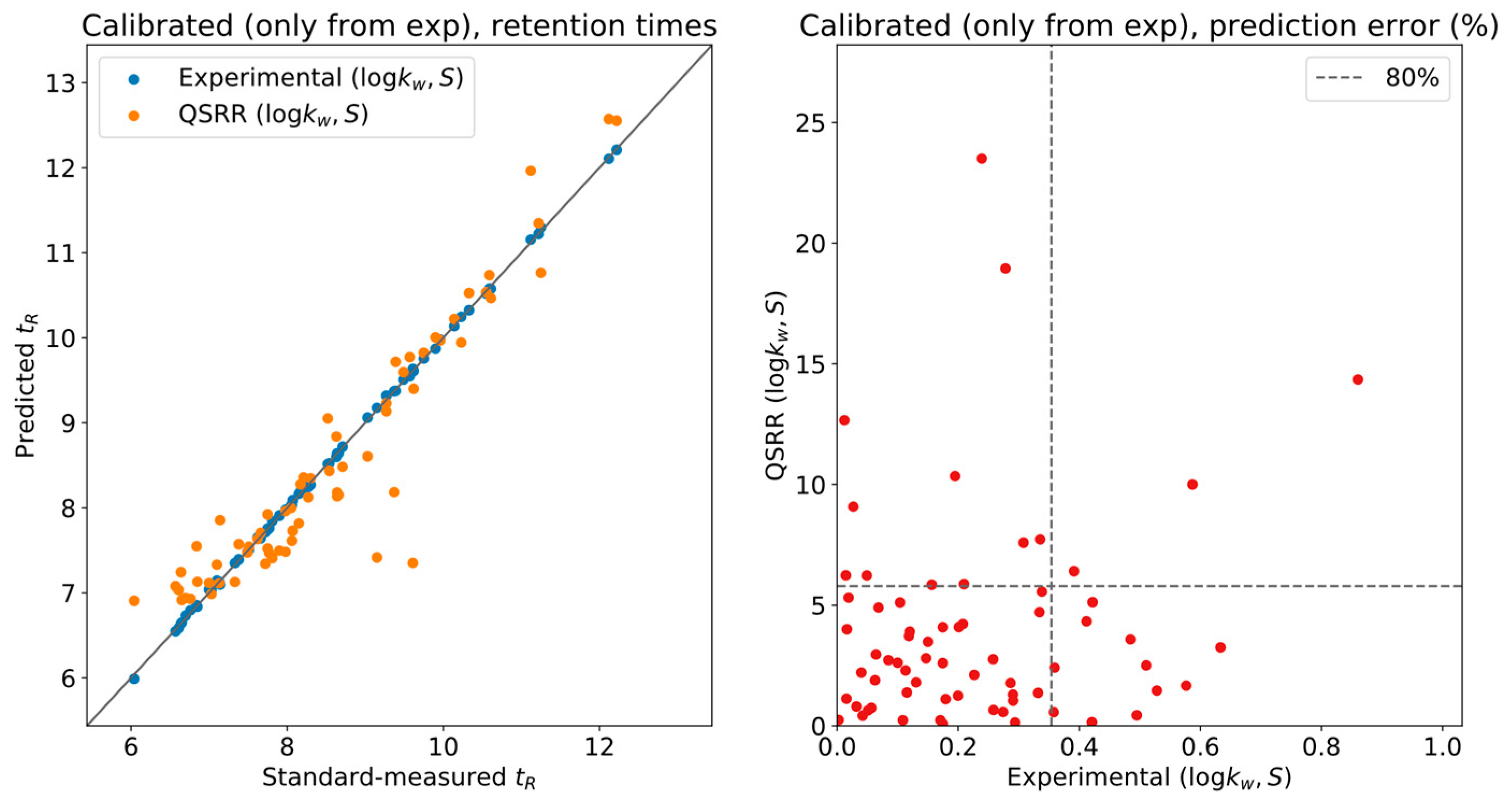
To gauge the effect of QSRR error on the calibration,
Figure 3 shows experimental and QSRR predictions, both calibrated using only the experimentally determined LSS parameters. Nearly all the systematic deviation in the QSRR predictions of
Figure 2 was corrected, and most of the compounds have less than
relative error w.r.t. the actual measurement. This is a reasonable tolerance for level two annotations, although it will provide unique results in only a limited number of situations.
In actual use of the DynaStI platform, whenever there are experimentally determined values available, they are used instead of QSRR parameter predictions. Concretely, 92 compounds are listed with experimental values, and 106 are listed with QSRR. The whole 198 metabolite database should be calibrated using any selection of compounds with experimental values of , to avoid propagating the QSRR error to the ensemble of predictions.
Author Contributions
Data curation: A.G.; Formal analysis: S.C.; Funding acquisition: S.R.; Investigation: V.G.-R., A.G.; Project administration: V.G.-R.; Resources: I.X., R.L., A.B; Software: S.C., G.M.R., F.L.; Supervision, J.B., S.R.; Writing—original draft: S.C.; Writing—review & editing, S.C., V.G.-R., A.G., J.B. and S.R.
Funding
This research was funded by the Swiss National Science Foundation through grant 31003A_166658 and by the Swiss Centre for Applied Human Toxicology through grants of the Research Programme 2017-2020 (Core Project 1: Male Reproductive Toxicology and Core Project 2: Endocrine Disruption and Steroid Hormone Action).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Boccard, J.; Veuthey, J.-L.; Rudaz, S. Knowledge discovery in metabolomics: An overview of MS data handling. J. Sep. Sci. 2010, 33, 290–304. [Google Scholar] [CrossRef] [PubMed]
- Jeanneret, F.; Tonoli, D.; Rossier, M.F.; Saugy, M.; Boccard, J.; Rudaz, S. Evaluation of steroidomics by liquid chromatography hyphenated to mass spectrometry as a powerful analytical strategy for measuring human steroid perturbations. J. Chromatogr. A 2016, 1430, 97–112. [Google Scholar] [CrossRef] [PubMed]
- Viant, M.R.; Kurland, I.J.; Jones, M.R.; Dunn, W.B. How close are we to complete annotation of metabolomes? Curr. Opin. Chem. Biol. 2017, 36, 64–69. [Google Scholar] [CrossRef] [PubMed]
- Rochat, B. Proposed confidence scale and ID score in the identification of known-unknown compounds using high resolution MS data. J. Am. Soc. Mass Spectrom. 2017, 28, 709–723. [Google Scholar] [CrossRef] [PubMed]
- Snyder, L.R.; Dolan, J.W. High-Performance Gradient Elution: The Practical Application of the Linear-Solvent-Strength Model; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Randazzo, G.M.; Tonoli, D.; Hambye, S.; Guillarme, D.; Jeanneret, F.; Nurisso, A.; Goracci, L.; Boccard, J.; Rudaz, S. Prediction of retention time in reversed-phase liquid chromatography as a tool for steroid identification. Anal. Chim. Acta 2016, 916, 8–16. [Google Scholar] [CrossRef] [PubMed]
- Randazzo, G.M.; Tonoli, D.; Strajhar, P.; Xenarios, I.; Odermatt, A.; Boccard, J.; Rudaz, S. Enhanced metabolite annotation via dynamic retention time prediction: Steroidogenesis alterations as a case study. J. Chromatogr. B 2017, 1071, 11–18. [Google Scholar] [CrossRef] [PubMed]
- Kaliszan, R. Quantitative Structure-Retention relationships. Anal. Chem. 1992, 64, 619–631. [Google Scholar] [CrossRef]
- Nord, L.I.; Fransson, D.; Jacobsson, S.P. Prediction of liquid chromatographic retention times of steroids by three-dimensional structure descriptors and partial least squares modeling. Chemometr. Intell. Lab. Syst. 1998, 44, 257–269. [Google Scholar] [CrossRef]
- Héberger, K. Quantitative structure–(chromatographic) retention relationships. J. Chromatogr. A 2007, 1158, 273–305. [Google Scholar] [CrossRef] [PubMed]
- Vitku, J.; Kolatorova, L.; Hampl, R. Occurrence and reproductive roles of hormones in seminal plasma. Basic Clin. Androl. 2017, 27, 19. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Chen, L.; Shade, K.; Lazarus, P.; Seigne, J.; Patterson, S.; Helal, M.; Pow-Sang, J. Asp85tyr Polymorphism in the Udp-Glucuronosyltransferase (Ugt) 2b15 Gene and the Risk of Prostate Cancer. J. Urol. 2004, 171, 2484–2488. [Google Scholar] [CrossRef]
- Chouinard, S.; Barbier, O.; Bélanger, A. UDP-glucuronosyltransferase 2B15 (UGT2B15) and UGT2B17 enzymes are major determinants of the androgen response in prostate cancer LNCaP cells. J. Biol. Chem. 2007, 282, 33466–33474. [Google Scholar] [CrossRef] [PubMed]
- de Souza, G.L.; Hallak, J. Anabolic steroids and male infertility: a comprehensive review. BJU Int. 2011, 108, 1860–1865. [Google Scholar] [CrossRef] [PubMed]
- Duty, S.M.; Silva, M.J.; Barr, D.B.; Brock, J.W.; Ryan, L.; Chen, Z.; Herrick, R.F.; Christiani, D.C.; Hauser, R. Phthalate Exposure and Human Semen Parameters. Epidemiology 2003, 14, 269–277. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).