Evaluation of Classifier Performance for Multiclass Phenotype Discrimination in Untargeted Metabolomics
Abstract
:1. Introduction
2. Results
2.1. Simulated Metabolomics Data
2.2. Evaluation of Classifier Performance in Simulation Studies
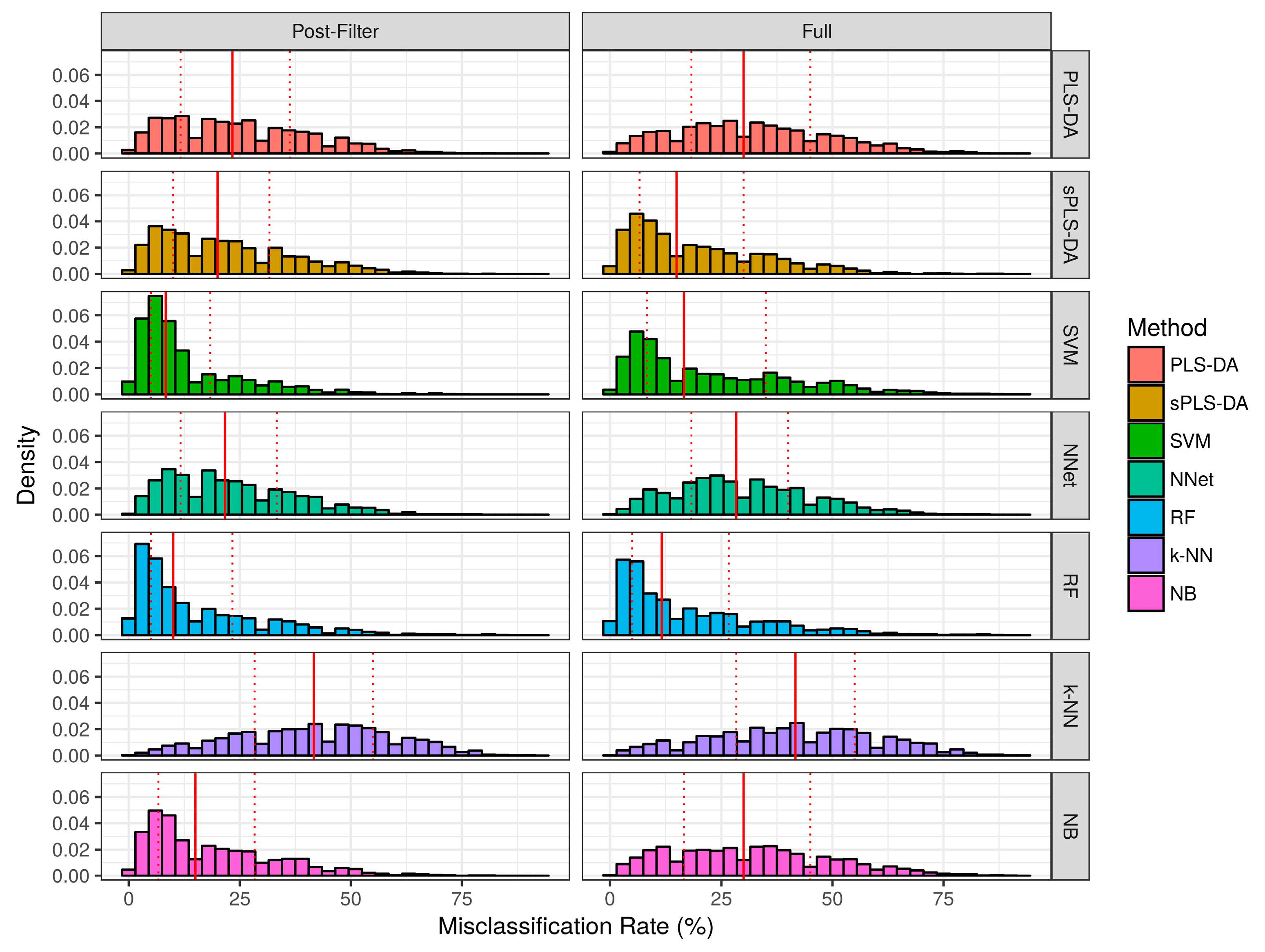
2.2.1. Aggregate Performance
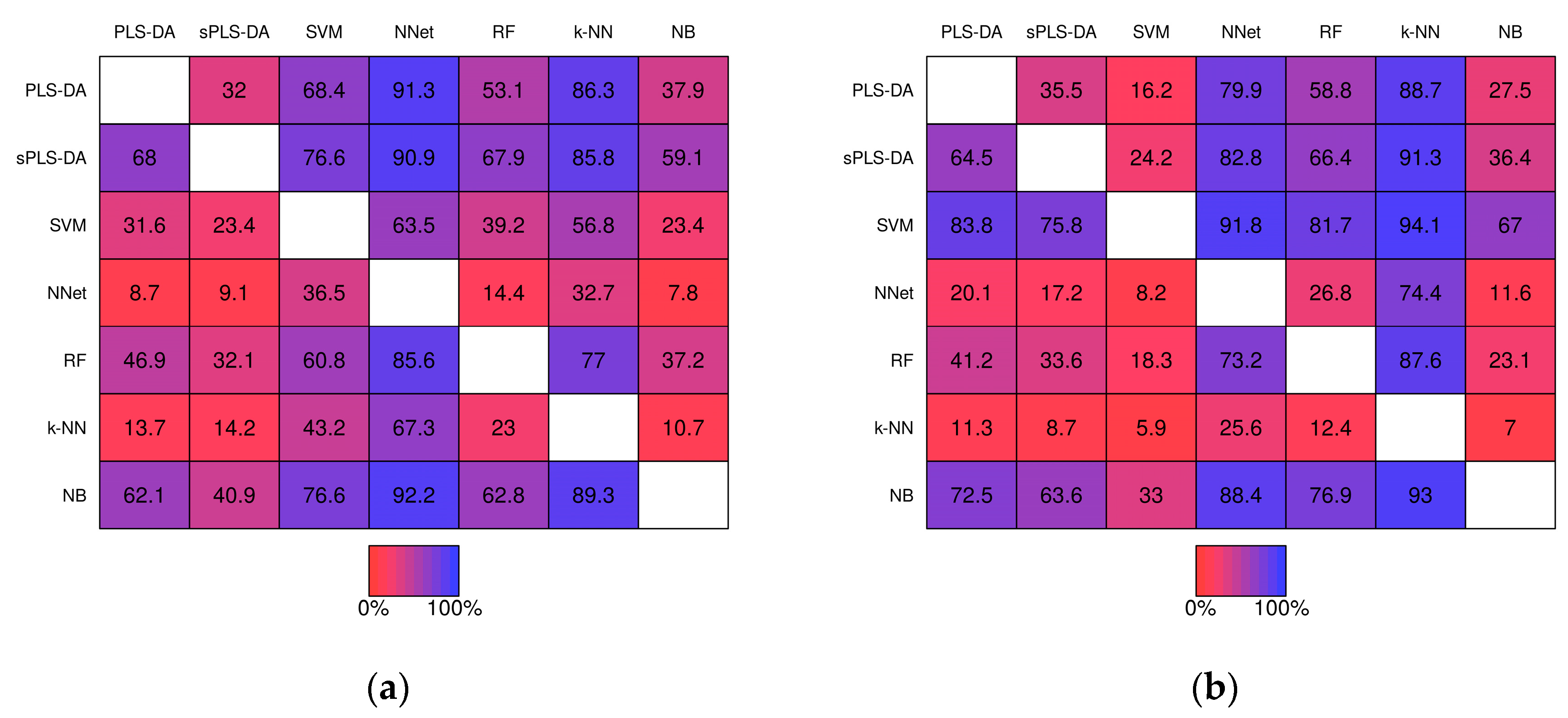
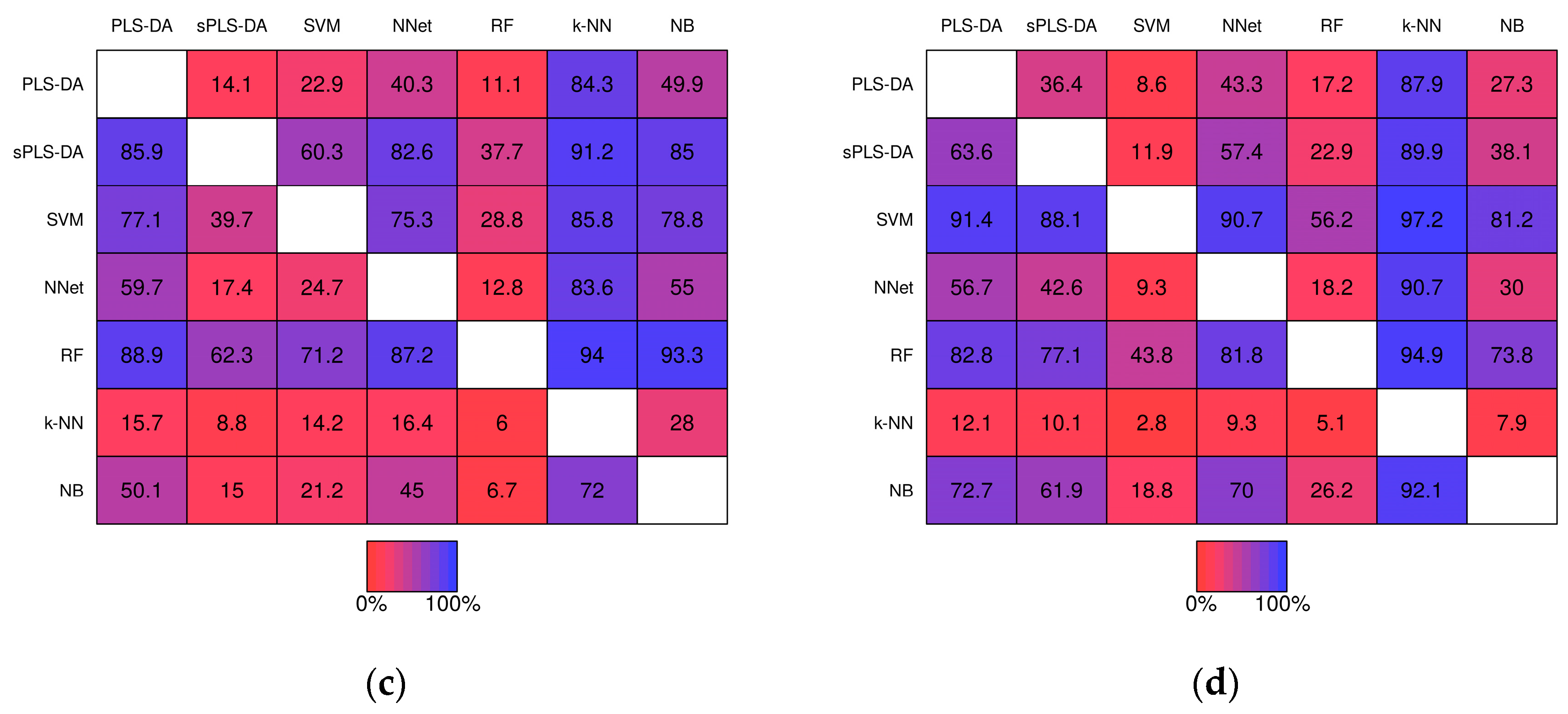
2.2.2. Pairwise Performance Comparisons within Simulation Studies
2.3. Performance over Real Datasets
3. Discussion
4. Materials and Methods
4.1. Simulated Metabolomics Data
| Algorithm 1 |
| 1: Initialize 2: For do: 3: 4: For do: 5: Generate 6: End For 7: End For 8: |
4.2. Classification Techniques
4.2.1. Partial Least Squares-Discriminant Analysis (PLS-DA)
| Algorithm 2 |
| 1: w = XT u/(uT u) 2: ‖w‖→1 3: t = Xw 4: c=YT t/(tT t) 5: ‖c‖→1 6: u=Yc. |
4.2.2. Sparse Partial Least Squares-Discriminant Analysis (sPLS-DA)
4.2.3. Support Vector Machines (SVM)
4.2.4. Neural Networks (NNet)
4.2.5. Random Forests (RF)
4.2.6. Naïve Bayes (NB)
4.2.7. k-Nearest Neighbors (k-NN)
4.3. Parameter Selection
4.4. Evaluation of Classifier Performance
4.5. Clinical Datasets
4.6. Statistical Software
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Del Prato, S.; Marchetti, P.; Bonadonna, R.C. Phasic insulin release and metabolic regulation in type 2 diabetes. Diabetes 2002, 51 (Suppl. 1), S109–S116. [Google Scholar] [CrossRef] [PubMed]
- Freeman, M.W. Lipid metabolism and coronary artery disease. In Principles of Molecular Medicine; Humana Press: New York, NY, USA, 2006; pp. 130–137. [Google Scholar]
- Ashrafian, H.; Frenneaux, M.P.; Opie, L.H. Metabolic mechanisms in heart failure. Circulation 2007, 116, 434–448. [Google Scholar] [CrossRef] [PubMed]
- Cairns, R.A.; Harris, I.S.; Mak, T.W. Regulation of cancer cell metabolism. Nat. Rev. Cancer 2011, 11, 85–95. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Liu, L.; Palacios, G.; Gao, J.; Zhang, N.; Li, G.; Lu, J.; Song, T.; Zhang, Y.; Lv, H. Plasma metabolomics reveals biomarkers of the atherosclerosis. J. Sep. Sci. 2010, 33, 2776–2783. [Google Scholar] [CrossRef] [PubMed]
- DeFilippis, A.P.; Trainor, P.J.; Hill, B.G.; Amraotkar, A.R.; Rai, S.N.; Hirsch, G.A.; Rouchka, E.C.; Bhatnagar, A. Identification of a plasma metabolomic signature of thrombotic myocardial infarction that is distinct from non-thrombotic myocardial infarction and stable coronary artery disease. PLoS ONE 2017, 12, e0175591. [Google Scholar] [CrossRef] [PubMed]
- Jung, J.Y.; Lee, H.S.; Kang, D.G.; Kim, N.S.; Cha, M.H.; Bang, O.S.; Ryu, D.H.; Hwang, G.S. 1H-NMR-based metabolomics study of cerebral infarction. Stroke 2011, 42, 1282–1288. [Google Scholar] [CrossRef] [PubMed]
- Gromski, P.S.; Muhamadali, H.; Ellis, D.I.; Xu, Y.; Correa, E.; Turner, M.L.; Goodacre, R. A tutorial review: Metabolomics and partial least squares-discriminant analysis—A marriage of convenience or a shotgun wedding. Anal. Chim. Acta 2015, 879, 10–23. [Google Scholar] [CrossRef] [PubMed]
- Frank, I.E.; Friedman, J.H. A statistical view of some chemometrics regression tools. Technometrics 1993, 35, 109. [Google Scholar] [CrossRef]
- Lê Cao, K.-A.; Martin, P.G.P.; Robert-Granié, C.; Besse, P. Sparse canonical methods for biological data integration: Application to a cross-platform study. BMC Bioinform. 2009, 10, 34. [Google Scholar] [CrossRef] [PubMed]
- Lê Cao, K.-A.; Rossouw, D.; Robert-Granié, C.; Besse, P. A sparse PLS for variable selection when integrating omics data. Stat. Appl. Genet. Mol. Biol. 2008, 7. [Google Scholar] [CrossRef] [PubMed]
- Voet, D.; Voet, J.G.; Pratt, C.W. Fundamentals of Biochemistry: Life at the Molecular Level, 4th ed.; Wiley: Hoboken, NJ, USA, 2013. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Hammer, B.; Gersmann, K. A note on the universal approximation capability of support vector machines. Neural Processing Lett. 2003, 17, 43–53. [Google Scholar] [CrossRef]
- Hornik, K. Approximation capabilities of multilayer feedforward networks. Neural Netw. 1991, 4, 251–257. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Tin Kam, H. The random subspace method for constructing decision forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Ripley, B.D. Pattern Recognition and Neural Networks; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Camacho, D.; de la Fuente, A.; Mendes, P. The origin of correlations in metabolomics data. Metabolomics 2005, 1, 53–63. [Google Scholar] [CrossRef]
- Steuer, R. Review: On the analysis and interpretation of correlations in metabolomic data. Brief. Bioinform. 2006, 7, 151–158. [Google Scholar] [CrossRef] [PubMed]
- Lewandowski, D.; Kurowicka, D.; Joe, H. Generating random correlation matrices based on vines and extended onion method. J. Multivar. Anal. 2009, 100, 1989–2001. [Google Scholar] [CrossRef]
- Brereton, R.G.; Lloyd, G.R. Partial least squares discriminant analysis: Taking the magic away. J. Chemom. 2014, 28, 213–225. [Google Scholar] [CrossRef]
- Jiang, M.; Wang, C.; Zhang, Y.; Feng, Y.; Wang, Y.; Zhu, Y. Sparse partial-least-squares discriminant analysis for different geographical origins of salvia miltiorrhizaby 1H-NMR-based metabolomics. Phytochem. Anal. 2014, 25, 50–58. [Google Scholar] [CrossRef] [PubMed]
- Gao, R.; Cheng, J.; Fan, C.; Shi, X.; Cao, Y.; Sun, B.; Ding, H.; Hu, C.; Dong, F.; Yan, X. Serum metabolomics to identify the liver disease-specific biomarkers for the progression of hepatitis to hepatocellular carcinoma. Sci. Rep. 2015, 5, 18175. [Google Scholar] [CrossRef] [PubMed]
- Guan, W.; Zhou, M.; Hampton, C.Y.; Benigno, B.B.; Walker, L.D.; Gray, A.; McDonald, J.F.; Fernández, F.M. Ovarian cancer detection from metabolomic liquid chromatography/mass spectrometry data by support vector machines. BMC Bioinform. 2009, 10, 259. [Google Scholar] [CrossRef] [PubMed]
- Brougham, D.F.; Ivanova, G.; Gottschalk, M.; Collins, D.M.; Eustace, A.J.; O’Connor, R.; Havel, J. Artificial neural networks for classification in metabolomic studies of whole cells using 1H nuclear magnetic resonance. J. Biomed. Biotechnol. 2011, 2011. [Google Scholar] [CrossRef] [PubMed]
- Gromski, P.S.; Xu, Y.; Correa, E.; Ellis, D.I.; Turner, M.L.; Goodacre, R. A comparative investigation of modern feature selection and classification approaches for the analysis of mass spectrometry data. Anal. Chim. Acta 2014, 829. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Cao, Y.; Zhang, Y.; Liu, J.; Bao, Y.; Wang, C.; Jia, W.; Zhao, A. Random forest in clinical metabolomics for phenotypic discrimination and biomarker selection. Evid.-Based Complement. Altern. Med. 2013, 2013. [Google Scholar] [CrossRef] [PubMed]
- Parthasarathy, G.; Chatterji, B.N. A class of new knn methods for low sample problems. IEEE Trans. Syst. Man Cybern. 1990, 20, 715–718. [Google Scholar] [CrossRef]
- Chun, H.; Keleş, S. Sparse partial least squares regression for simultaneous dimension reduction and variable selection. J. R. Stat. Soc. Ser. B 2010, 72, 3–25. [Google Scholar] [CrossRef] [PubMed]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Nadarajah, S. A generalized normal distribution. J. Appl. Stat. 2005, 32, 685–694. [Google Scholar] [CrossRef]
- Rosipal, R.; Trejo, L.J. Kernel partial least squares regression in reproducing kernel hilbert space. J. Mach. Learn. Res. 2001, 2, 97–123. [Google Scholar]
- Boulesteix, A.-L. PLS dimension reduction for classification with microarray data. Stat. Appl. Genet. Mol. Biol. 2004, 3, 1–30. [Google Scholar] [CrossRef] [PubMed]
- Boulesteix, A.L.; Strimmer, K. Partial least squares: A versatile tool for the analysis of high-dimensional genomic data. Brief. Bioinform. 2006, 8, 32–44. [Google Scholar] [CrossRef] [PubMed]
- Höskuldsson, A. Pls regression methods. J. Chemom. 1988, 2, 211–228. [Google Scholar] [CrossRef]
- Rosipal, R. Nonlinear partial least squares: An overview. In Chemoinformatics and Advanced Machine Learning Perspectives: Complex Computational Methods and Collaborative Technqiues; IGI Global: Hershey, PA, USA, 2011; pp. 169–189. [Google Scholar]
- Lê Cao, K.-A.; Boitard, S.; Besse, P. Sparse pls discriminant analysis: Biologically relevant feature selection and graphical displays for multiclass problems. BMC Bioinform. 2011, 12, 253. [Google Scholar] [CrossRef] [PubMed]
- Chih-Wei, H.; Chih-Jen, L. A comparison of methods for multiclass support vector machines. IEEE Trans. Neural Netw. 2002, 13, 415–425. [Google Scholar] [CrossRef] [PubMed]
- Riedmiller, R.; Braun, H. A direct adaptive method for faster backpropagation learning: The rprop algorithm. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Thygesen, K.; Alpert, J.S.; Jaffe, A.S.; Simoons, M.L.; Chaitman, B.R.; White, H.D.; Writing Group on the Joint ESC/ACCF/AHA/WHF Task Force for the Universal Definition of Myocardial Infarction; Thygesen, K.; Alpert, J.S.; White, H.D.; et al. Third universal definition of myocardial infarction. J. Am. Coll. Cardiol. 2012, 60, 1581–1598. [Google Scholar] [CrossRef] [PubMed]
- Fahrmann, J.F.; Kim, K.; DeFelice, B.C.; Taylor, S.L.; Gandara, D.R.; Yoneda, K.Y.; Cooke, D.T.; Fiehn, O.; Kelly, K.; Miyamoto, S. Investigation of metabolomic blood biomarkers for detection of adenocarcinoma lung cancer. Cancer Epidemiol. Biomark. Prev. 2015, 24, 1716–1723. [Google Scholar] [CrossRef] [PubMed]
- Yinan, Z. Metabolomic Study on a Schizophrenia and Type 2 Diabetes Susceptibility Gene nos1ap-rs12742393. 2017. Available online: http://www.metabolomicsworkbench.org/data/DRCCMetadata.php?Mode=Project&ProjectID=PR000416 (accessed on 20 June 2017).
- Filzmoser, P.; Liebmann, B.; Varmuza, K. Repeated double cross validation. J. Chemom. 2009, 23, 160–171. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2016. [Google Scholar]
- Qiu, W.; Joe, H. Clustergeneration: Random Cluster Generation (with Specified Degree of Separation), version 1.3; 2015. Available online: https://cran.r-project.org/web/packages/clusterGeneration/index.html (accessed on 20 June 2017).
- Venables, W.N.; Ripley, B.D.; Venables, W.N. Modern Applied Statistics with s, 4th ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Liaw, A.; Wiener, M. Classification and regression by randomforest. R News 2002, 2, 18–22. [Google Scholar]
- Meyer, D.; Dimitriadou, E.; Hornik, K.; Weingessel, A.; Leisch, F. E1071: Misc Functions of the Department of Statistics, Probability Theory Group. Version 1.6. 2016. Available online: https://cran.r-project.org/web/packages/e1071/index.html (accessed on 20 June 2017).
- Fritsch, S.; Guenther, F. Neuralnet: Training of Neural Networks. Version 1.33. 2016. Available online: https://cran.r-project.org/web/packages/neuralnet/index.html (accessed on 20 June 2017).
- Khun, M. Caret: Classification and Regression Training. Version 6.76. 2017. Available online: https://cran.r-project.org/web/packages/caret/index.html (accessed on 20 June 2017).
- Alfons, A. Cvtools: Cross-Validation Tools for Regression Models. Version 0.3.2. 2016. Available online: https://cran.r-project.org/web/packages/cvTools/index.html (accessed on 20 June 2017).
- Wickham, H.; Francois, R. Dplyr: A Grammar of Data Manipulation. Version 0.6.0. 2016. Available online: https://cran.r-project.org/web/packages/dplyr/index.html (accessed on 20 June 2017).
- Wickham, H. Tidyr: Easily Tidy Data with ‘Spread()’ and ‘Gather()’ Functions. Version 0.6.0. 2016. Available online: https://cran.r-project.org/web/packages/tidyr/index.html (accessed 20 June 2017).
| Method | Baseline Pre- | Baseline Post- | Realistic Pre- | Realistic Post- | ||||
|---|---|---|---|---|---|---|---|---|
| Mean ± SD | Median ± IQR | Mean ± SD | Median ± IQR | Mean ± SD | Median ± IQR | Mean ± SD | Median ± IQR | |
| PLS-DA | 15.0 ± 15.5 | 10.0 ± 28.3 | 13.1 ± 15.6 | 5.0 ± 25.0 | 32.2 ± 17.4 | 30.0 ± 26.7 | 25.0 ± 15.7 | 23.3 ± 24.6 |
| sPLS-DA | 13.1 ± 15.3 | 5.0 ± 25.0 | 12.1 ± 15.1 | 3.3 ± 23.3 | 19.7 ± 15.2 | 15.0 ± 23.3 | 22.0 ± 15.0 | 20.0 ± 21.7 |
| SVM | 23.2 ± 24.6 | 13.3 ± 41.7 | 10.4 ± 14.3 | 1.7 ± 19.6 | 22.8 ± 18.3 | 16.7 ± 26.7 | 13.3 ± 12.5 | 8.3 ± 13.3 |
| NNet | 22.0 ± 15.6 | 20.0 ± 25.0 | 15.9 ± 13.8 | 11.7 ± 21.7 | 29.9 ± 15.2 | 28.3 ± 21.7 | 23.3 ± 14.3 | 21.7 ± 21.7 |
| RF | 15.0 ± 14.8 | 10.0 ± 23.3 | 13.5 ± 14.4 | 7.5 ± 21.7 | 17.5 ± 16.0 | 11.7 ± 21.7 | 15.5 ± 15.0 | 10.0 ± 18.3 |
| k-NN | 20.2 ± 17.3 | 20.0 ± 28.3 | 21.9 ± 16.4 | 20.0 ± 25.0 | 41.3 ± 18.8 | 41.7 ± 26.7 | 41.6 ± 17.7 | 41.7 ± 26.7 |
| NB | 14.0 ± 15.3 | 8.3 ± 25.0 | 11.1 ± 14.6 | 1.8 ± 21.7 | 32.1 ± 18.2 | 30.0 ± 28.3 | 19.1 ± 14.8 | 15.0 ± 21.7 |
| Method | Baseline Pre- | Baseline Post- | Realistic Pre- | Realistic Post- | ||||
|---|---|---|---|---|---|---|---|---|
| Mean ± SD | Median ± IQR | Mean ± SD | Median ± IQR | Mean ± SD | Median ± IQR | Mean ± SD | Median ± IQR | |
| PLS-DA | 1.18 ± 0.16 | 1.17 ± 0.23 | 1.04 ± 0.18 | 0.99 ± 0.30 | 1.51 ± 0.14 | 1.51 ± 0.19 | 1.50 ± 0.16 | 1.50 ± 0.20 |
| sPLS-DA | 1.03 ± 0.18 | 0.98 ± 0.30 | 1.02 ± 0.19 | 0.96 ± 0.29 | 1.49 ± 0.16 | 1.48 ± 0.20 | 1.50 ± 0.16 | 1.49 ± 0.20 |
| SVM | 0.64 ± 0.45 | 0.70 ± 0.61 | 0.42 ± 0.40 | 0.21 ± 0.56 | 1.95 ± 0.71 | 1.83 ± 0.95 | 1.90 ± 0.61 | 1.81 ± 0.77 |
| NNet | 1.12 ± 0.20 | 1.09 ± 0.32 | 1.03 ± 0.18 | 0.97 ± 0.29 | 1.53 ± 0.17 | 1.54 ± 0.22 | 1.51 ± 0.18 | 1.52 ± 0.22 |
| RF | 0.58 ± 0.36 | 0.55 ± 0.52 | 0.55 ± 0.34 | 0.51 ± 0.50 | 6.61 ± 17.57 | 1.66 ± 0.92 | 6.37 ± 16.38 | 1.65 ± 0.92 |
| k-NN | 54.8 ± 56.4 | 44.9 ± 54.3 | 60.8 ± 52.9 | 50.6 ± 46.1 | 345.0 ± 181.6 | 326.5 ± 257.2 | 343.7 ± 171.9 | 328.9 ± 244.3 |
| NB | 3.12 ± 3.86 | 1.20 ± 5.56 | 0.94 ± 1.27 | 0.11 ± 1.85 | 129.0 ± 113.4 | 94.4 ± 119.5 | 96.9 ± 92.2 | 65.7 ± 94.3 |
| Dataset | Technique | Misclassification (%) | Cross-Entropy Loss | ||
|---|---|---|---|---|---|
| Pre- | Post- | Pre- | Post- | ||
| Adenocarcinoma | PLS-DA | 17.9 | 7.1 | 0.78 | 0.68 |
| sPLS-DA | 32.1 | 14.3 | 0.83 | 0.72 | |
| RF | 17.9 | 14.3 | 0.68 | 0.57 | |
| SVM | 21.4 | 10.7 | 0.78 | 0.53 | |
| NNet | 21.4 | 28.6 | 0.77 | 0.86 | |
| k-NN | 28.6 | 14.3 | 61.2 | 30.8 | |
| NB | 17.9 | 10.7 | 4.85 | 2.56 | |
| Acute MI | PLS-DA | 47.4 | 42.1 | 1.41 | 1.28 |
| sPLS-DA | 47.4 | 15.8 | 1.43 | 1.35 | |
| RF | 22.1 | 7.9 | 1.08 | 0.76 | |
| SVM | 55.3 | 13.2 | 1.89 | 0.65 | |
| NNet | 47.4 | 31.6 | 1.47 | 1.16 | |
| k-NN | 44.7 | 39.5 | 95.3 | 106.4 | |
| NB | 42.1 | 15.8 | 164.0 | 20.3 | |
| NOS1AP | PLS-DA | 22.9 | 6.3 | 1.14 | 0.93 |
| Variants | sPLS-DA | 2.1 | 6.3 | 0.98 | 0.93 |
| RF | 6.3 | 4.2 | 0.27 | 0.21 | |
| SVM | 12.5 | 6.3 | 0.50 | 0.26 | |
| NNet | 16.7 | 6.3 | 1.08 | 0.86 | |
| k-NN | 41.7 | 8.3 | 88.8 | 17.8 | |
| NB | 12.5 | 6.3 | 4.14 | 1.75 | |
| Technique | Parameter | Type | Value/Search Grid |
|---|---|---|---|
| PLS-DA | Number of components | Optimized | [1, 2, ..., 15] |
| Sparse PLS-DA | Number of components | Optimized | [1, 2, ..., 15] |
| Regularization () | Optimized | [0.1, ..., 0.9] by 0.1 | |
| Random Forest | Ensemble size | Fixed | 1000 |
| Random subspace size | Optimized | [5, ..., p] of length 25 | |
| SVM | Kernel | Fixed | Gaussian |
| Bandwidth () | Optimized | 10^[−5, ..., −1] of length 1000 †; 10^[−2, ..., 0] of length 1000 ‡ | |
| Neural Network | Number of hidden layers | Optimized | 1 or 2 |
| Number of hidden nodes | Optimized | [15, ..., 100] by 5 | |
| Activation function | Fixed | Logistic | |
| Learning function | Fixed | Resilient Backpropagation | |
| Error function | Fixed | Cross-entropy Loss | |
| k-NN | Number of neighbors | Optimized | [1, 2, ..., 20] |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trainor, P.J.; DeFilippis, A.P.; Rai, S.N. Evaluation of Classifier Performance for Multiclass Phenotype Discrimination in Untargeted Metabolomics. Metabolites 2017, 7, 30. https://doi.org/10.3390/metabo7020030
Trainor PJ, DeFilippis AP, Rai SN. Evaluation of Classifier Performance for Multiclass Phenotype Discrimination in Untargeted Metabolomics. Metabolites. 2017; 7(2):30. https://doi.org/10.3390/metabo7020030
Chicago/Turabian StyleTrainor, Patrick J., Andrew P. DeFilippis, and Shesh N. Rai. 2017. "Evaluation of Classifier Performance for Multiclass Phenotype Discrimination in Untargeted Metabolomics" Metabolites 7, no. 2: 30. https://doi.org/10.3390/metabo7020030
APA StyleTrainor, P. J., DeFilippis, A. P., & Rai, S. N. (2017). Evaluation of Classifier Performance for Multiclass Phenotype Discrimination in Untargeted Metabolomics. Metabolites, 7(2), 30. https://doi.org/10.3390/metabo7020030






