Influence of Missing Values Substitutes on Multivariate Analysis of Metabolomics Data
Abstract
:1. Introduction
2. Experimental Section
2.1. Materials and Methods
2.1.1. Cell Culture and Experimental Protocol
2.1.2. Methanol Metabolite Extraction
2.1.3. Metabolic Profiling Using GC-MS and Raw Data Processing
2.2. Software Tools
2.3. Data Preparation
2.4. Imputation Methods
2.4.1. Imputation of Missing Values Using k-Nearest Neighbours (kNN).
2.4.2. Missing Value Imputation Using Random Forest (RF)
2.5. Unsupervised Learning
2.5.1. Principal Components Analysis (PCA)
2.5.2. Hierarchical Cluster Analysis (HCA)
2.6. Supervised Learning
2.6.1. Linear Discriminant Analysis (LDA)
2.6.2. Partial Least Squares-Discriminant Analysis (PLS-DA)
2.7. Model Validation
3. Results and Discussion
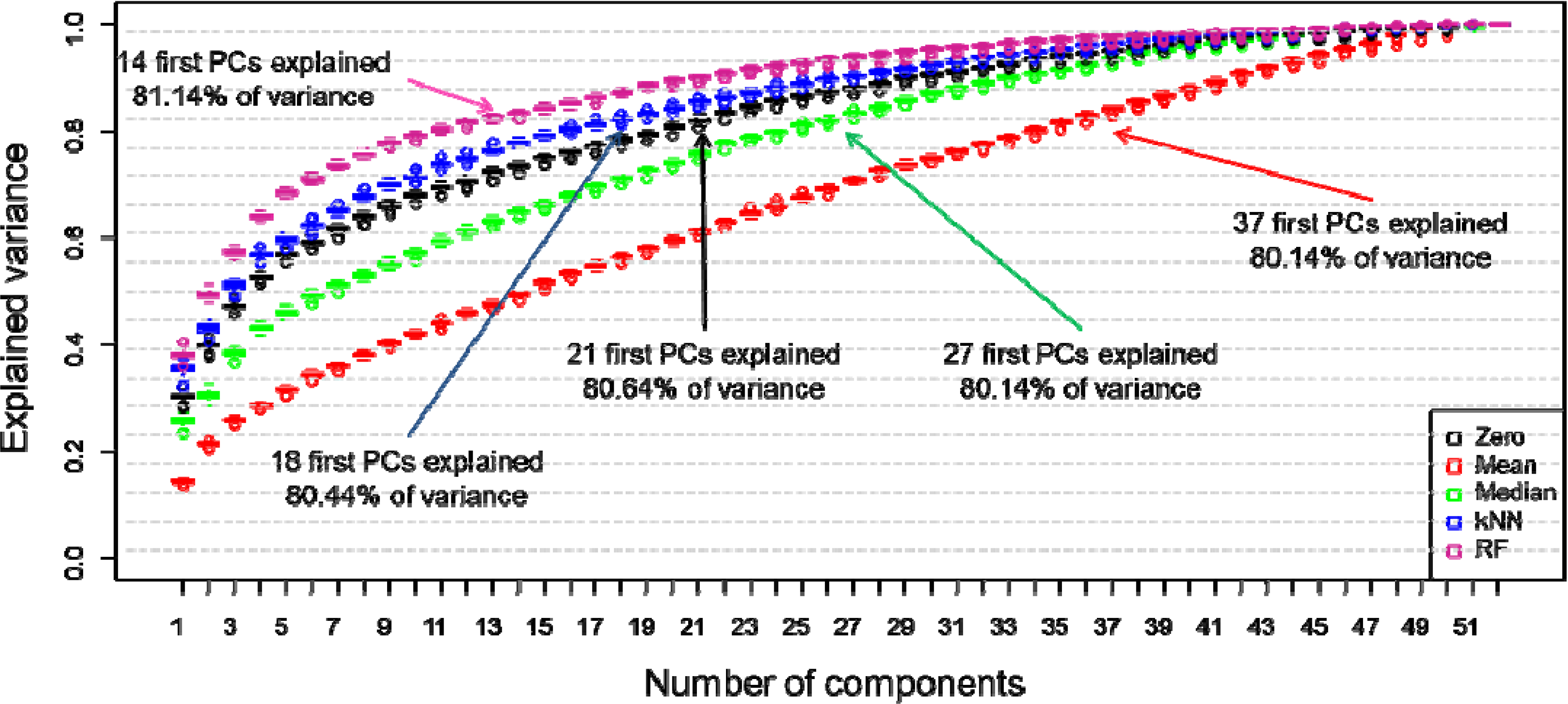
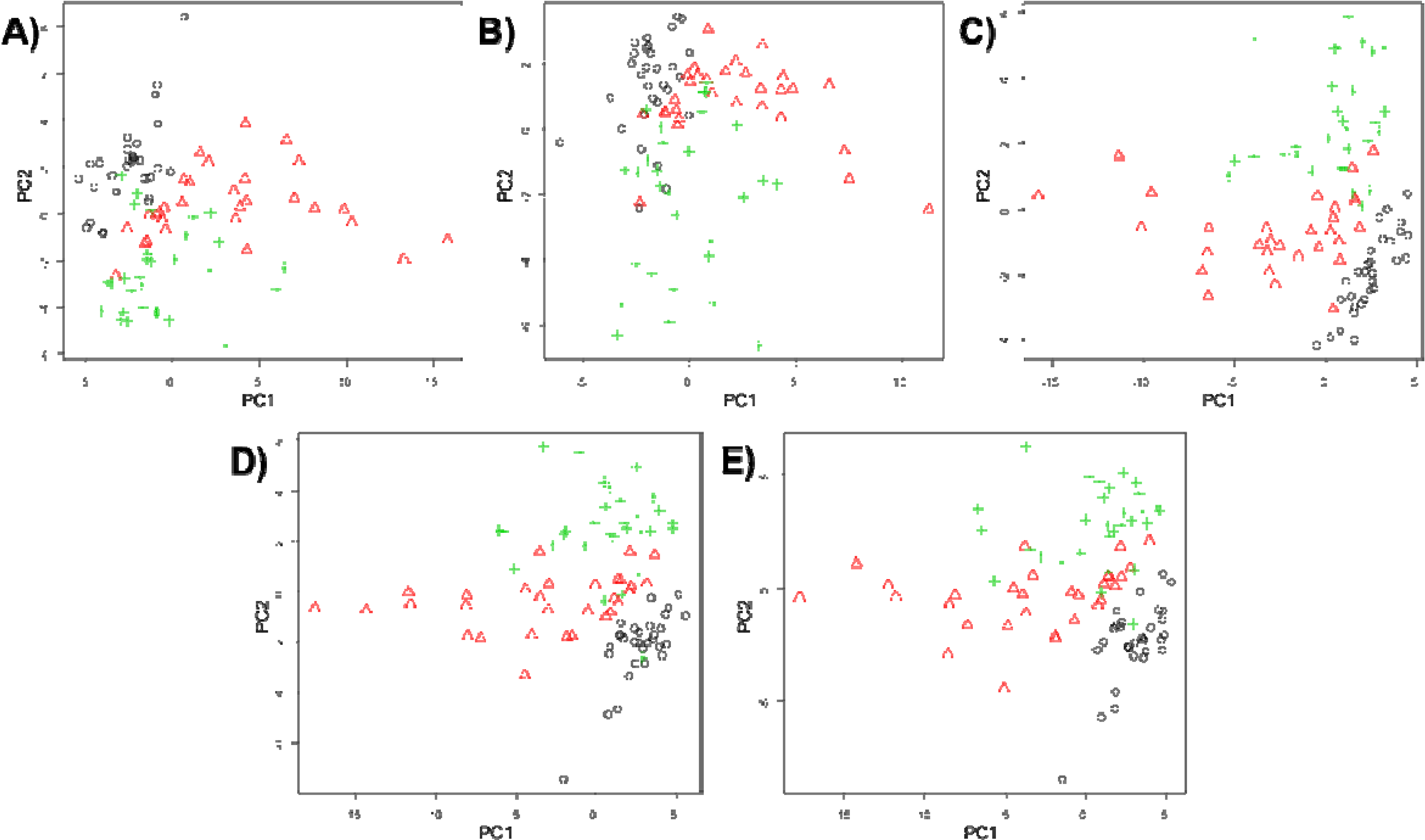
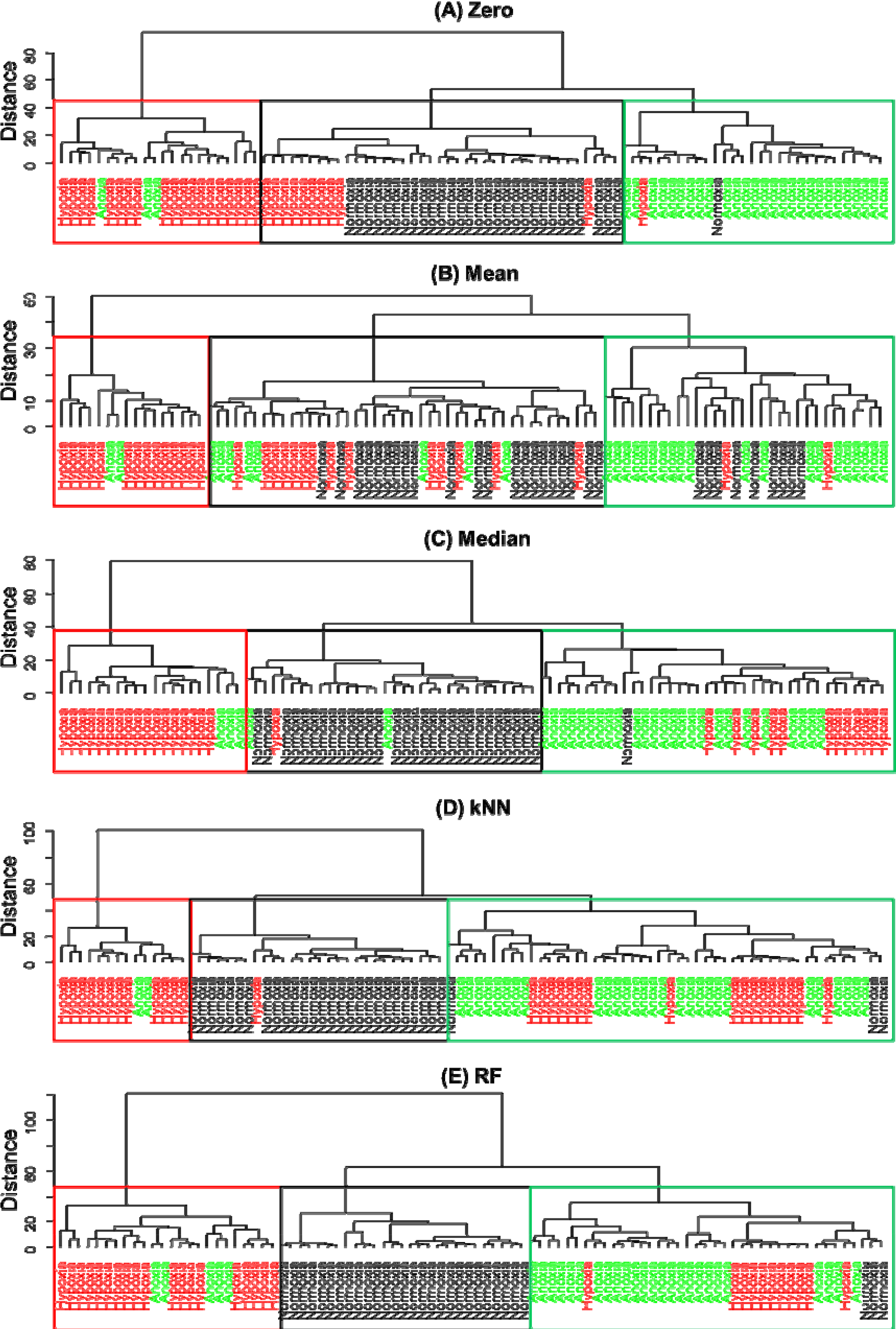
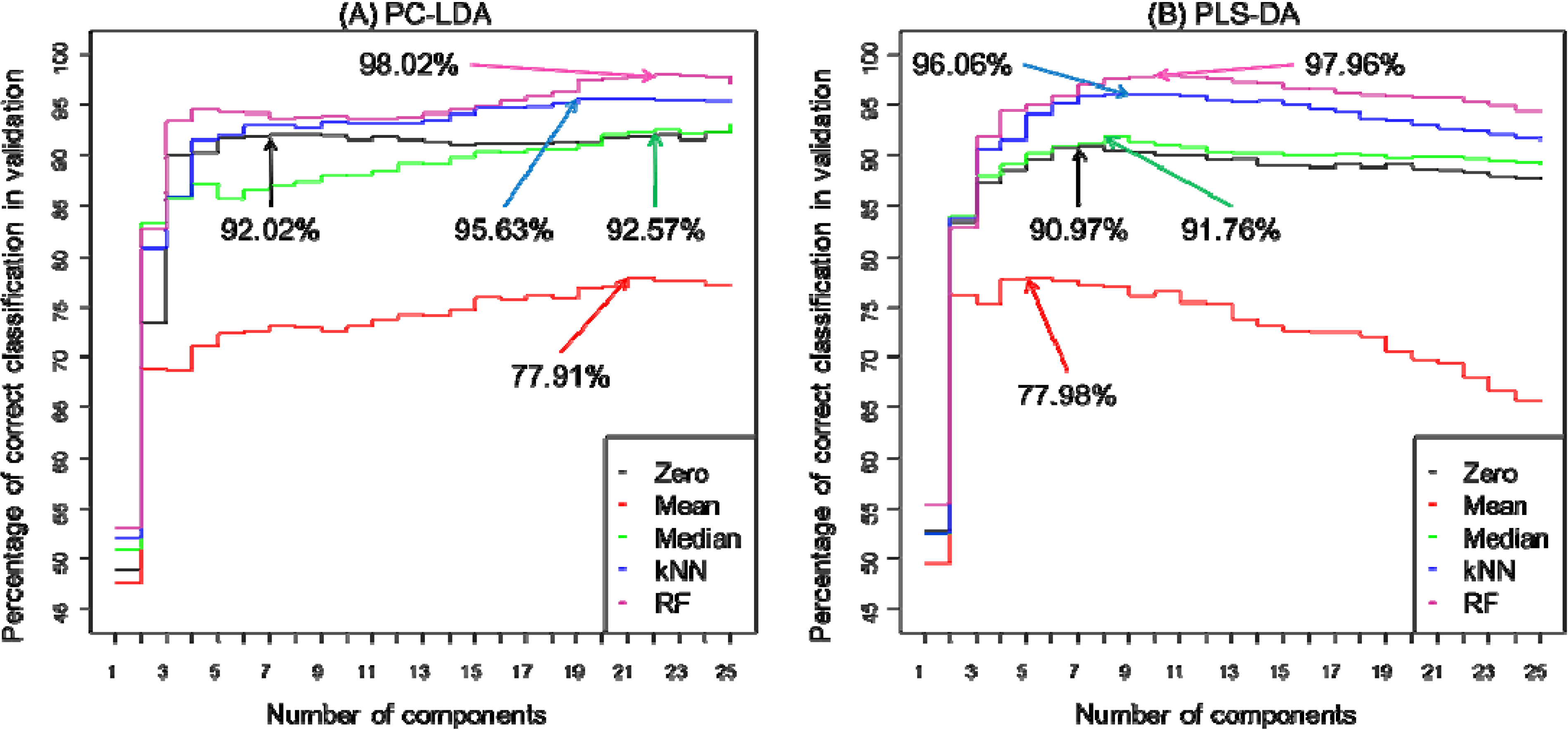
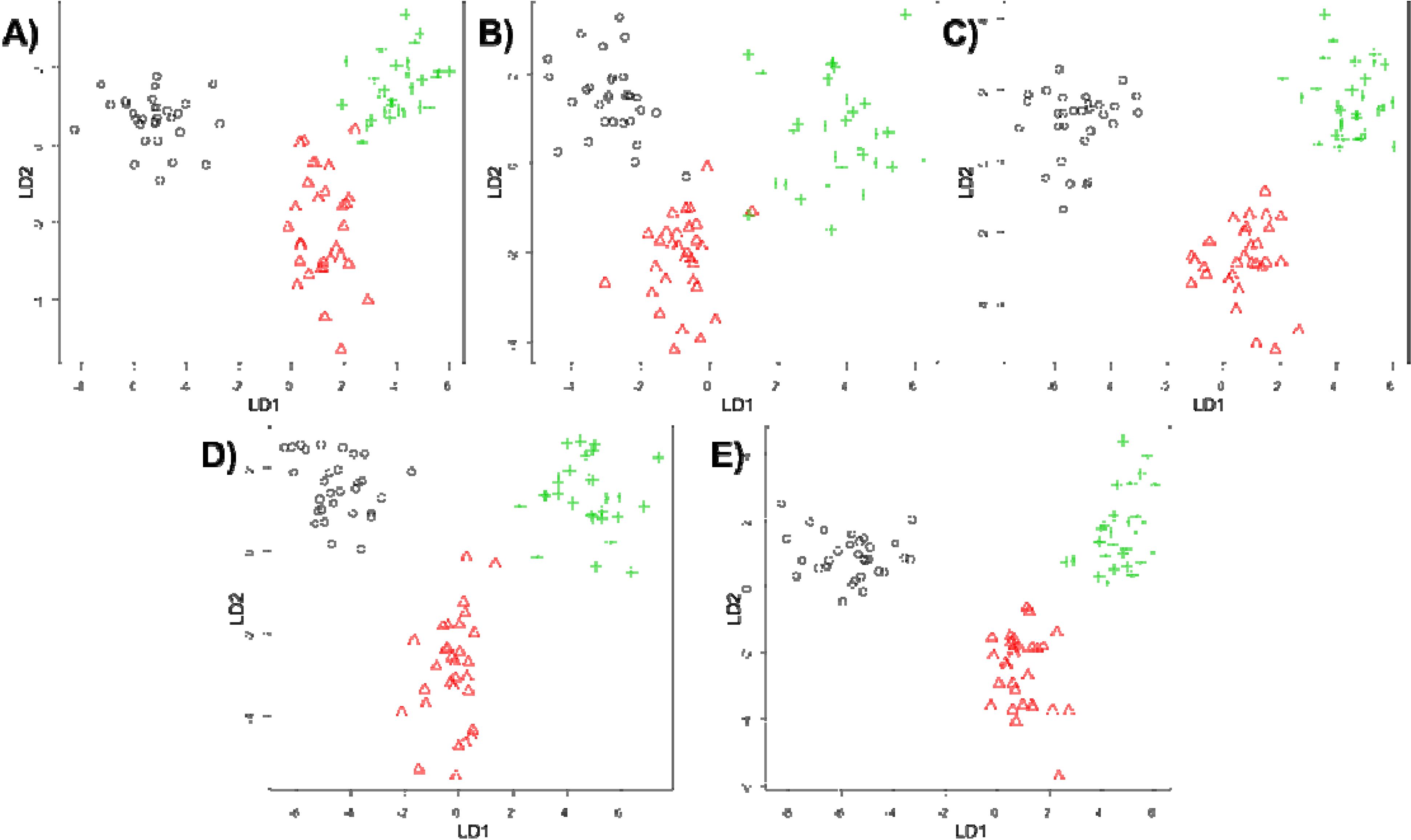
4. Conclusions
| PC-LDA | PLS-DA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Zero | Mean | Median | kNN | RF | Zero | Mean | Median | kNN | RF | |
| Classification rate (%) * | 92.02 | 77.91 | 92.57 | 95.63 | 98.02 | 90.97 | 77.98 | 91.76 | 96.06 | 97.73 |
| Number of latent variables (components) used | 7 | 21 | 22 | 19 | 22 | 7 | 6 | 8 | 9 | 10 |
| Metabolite name | Normoxia | Hypoxia | Anoxia |
|---|---|---|---|
| Glycine | –2.59 | 0.98 | 0.70 |
| Lactate | –0.25 | 0.13 | –0.35 |
| Pyruvate | 0.14 | 0.25 | 1.54 |
| Valine | 0.95 | 0.63 | 0.97 |
| Leucine | 0.27 | 0.67 | 0.92 |
| Glycerol | 0.59 | 4.03 | 1.45 |
| Isoleucine | 0.12 | 1.29 | 1.05 |
| Leucine | 1.15 | 2.07 | 1.80 |
| Malonate | –2.29 | –0.61 | –1.05 |
| Glycine | –0.55 | 0.03 | –0.09 |
| Phosphate | 1.29 | 0.78 | 1.01 |
| Threonine | –0.66 | 0.76 | 1.19 |
| Alanine | 0.84 | 0.25 | 0.96 |
| Threonine | 0.35 | 1.24 | 1.05 |
| Succinate | 0.38 | 0.84 | 0.05 |
| Benzoic acid | –0.60 | –1.06 | 4.15 |
| Threitol/erythritol | 1.07 | 1.08 | 1.58 |
| Malate | –0.09 | 0.91 | 0.45 |
| 4-hydroxyproline | –0.54 | 2.65 | 0.98 |
| Aspartate | 0.82 | 0.57 | 1.22 |
| 4-aminobutyric acid | 0.70 | 0.91 | 0.03 |
| Aspartate | –0.33 | 1.99 | –0.32 |
| 4-hydroxyproline | 0.10 | 0.00 | 0.86 |
| Xylitol | 0.99 | 1.00 | 0.68 |
| 2-hydroxyglutaric acid | 0.89 | 1.24 | 0.22 |
| 4-hydroxybenzoic acid | –0.78 | 1.26 | 1.71 |
| Methionine | 0.18 | 1.23 | 1.10 |
| Creatinine | 0.32 | 0.49 | –0.55 |
| Putrescine | 0.10 | 0.22 | 0.27 |
| Hypotaurine | –0.07 | 0.27 | –0.62 |
| Glutamate | 0.34 | 0.42 | 1.25 |
| 2-oxoglutarate | 0.32 | 0.36 | 0.56 |
| Fructose | –0.20 | 0.46 | 2.00 |
| Sorbose/fructose | 1.41 | 1.08 | 1.31 |
| Sorbitol/galactose /glucose | 1.20 | 1.08 | 0.93 |
| Sorbose/fructose | 1.55 | 1.56 | 1.34 |
| Glycerol 3-phosphate | –0.68 | 0.80 | –0.20 |
| Galactose/glucose | 2.28 | 1.33 | 1.99 |
| Galactose/glucose | 2.36 | 0.35 | 2.21 |
| Galactose/glucose | 3.01 | 1.52 | 1.97 |
| Citrate | 0.50 | 1.17 | 0.46 |
| N-acetyl aspartate | –0.90 | 0.59 | 0.78 |
| Glucose | 2.15 | 0.63 | 2.39 |
| Scyllo-inositol | 0.93 | 0.55 | 1.53 |
| Lysine | 0.46 | 0.75 | 0.94 |
| Myo-inositol | –1.65 | 0.29 | –0.09 |
| Pantothenic acid | 1.58 | 0.38 | 0.72 |
| Tyramine/tyrosine | 0.82 | 0.85 | 1.04 |
| Hexadecanoic acid | –0.86 | 1.57 | 1.57 |
| Octadecanoic acid | –2.67 | 0.97 | 2.67 |
| Myo-inositol phosphate | 0.81 | 0.84 | 2.78 |
| Lactose/maltose | 0.33 | 1.21 | 0.83 |
Supplementary Files
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fiehn, O. Combining genomics, metabolome analysis, and biochemical modelling to understand metabolic networks. Comp. Funct. Genom. 2001, 2, 155–168. [Google Scholar] [CrossRef]
- Goodacre, R.; Vaidyanathan, S.; Dunn, W.B.; Harrigan, G.G.; Kell, D.B. Metabolomics by numbers: Acquiring and understanding global metabolite data. Trends Biotechnol. 2004, 22, 245–252. [Google Scholar] [CrossRef]
- Jenkins, S.; Fischer, S.M.; Chen, L.; Sana, T.R. Global LC/MS metabolomics profiling of calcium stressed and immunosuppressant drug treated saccharomyces cerevisiae. Metabolites 2013, 3, 1102–1117. [Google Scholar] [CrossRef]
- Kassama, Y.; Xu, Y.; Dunn, W.B.; Geukens, N.; Anne, J.; Goodacre, R. Assessment of adaptive focused acoustics versus manual vortex/freeze-thaw for intracellular metabolite extraction from Streptomyces lividans producing recombinant proteins using GC-MS and multi-block principal component analysis. Analyst 2010, 135, 934–942. [Google Scholar] [CrossRef]
- Begley, P.; Francis-McIntyre, S.; Dunn, W.B.; Broadhurst, D.I.; Halsall, A.; Tseng, A.; Knowles, J.; Goodacre, R.; Kell, D.B. Development and performance of a gas chromatography-time-of-flight mass spectrometry analysis for large-scale nontargeted metabolomic studies of human serum. Anal. Chem. 2009, 81, 7038–7046. [Google Scholar] [CrossRef]
- Steuer, R.; Morgenthal, K.; Weckwerth, W.; Selbig, J. A gentle guide to the analysis of metabolomic data. Methods Mol. Biol. 2007, 358, 105–126. [Google Scholar] [CrossRef]
- Goodacre, R.; Broadhurst, D.; Smilde, A.K.; Kristal, B.S.; Baker, J.D.; Beger, R.; Bessant, C.; Connor, S.; Calmani, G.; Craig, A.; et al. Proposed minimum reporting standards for data analysis in metabolomics. Metabolomics 2007, 3, 231–241. [Google Scholar] [CrossRef]
- Hrydziuszko, O.; Viant, M.R. Missing values in mass spectrometry based metabolomics: An undervalued step in the data processing pipeline. Metabolomics 2011, 8, S161–S174. [Google Scholar]
- Xia, J.; Psychogios, N.; Young, N.; Wishart, D.S. MetaboAnalyst: A web server for metabolomic data analysis and interpretation. Nucleic Acids Res. 2009, 37, W652–W660. [Google Scholar]
- Schafer, J.L.; Graham, J.W. Missing Data: Our View of the State of the Art. Psychol. Methods 2002, 7, 147–177. [Google Scholar] [CrossRef]
- De Ligny, C.L.; Nieuwdorp, G.H.E.; Brederode, W.K.; Hammers, W.E.; Vanhouwelingen, J.C. An Application of factor analysis with missing data. Technometrics 1981, 23, 91–95. [Google Scholar] [CrossRef]
- Duran, A.L.; Yang, J.; Wang, L.J.; Sumner, L.W. Metabolomics spectral formatting, alignment and conversion tools (MSFACTs). Bioinformatics 2003, 19, 2283–2293. [Google Scholar]
- Little, R.J.A.; Rubin, D.B. Statistical Analysis with Missing Data; Wiley: New York, NY, USA, 1987. [Google Scholar]
- Shrive, F.M.; Stuart, H.; Quan, H.; Ghali, W.A. Dealing with missing data in a multi-question depression scale: A comparison of imputation methods. BMC Med. Res. Methodol. 2006, 6, 57–57. [Google Scholar] [CrossRef]
- Stacklies, W.; Redestig, H.; Scholz, M.; Walther, D.; Selbig, J. pcaMethods—A bioconductor package providing PCA methods for incomplete data. Bioinformatics 2007, 23, 1164–1167. [Google Scholar]
- Walczak, B.; Massart, D.L. Dealing with missing data: Part I. Chemom. Intell. Lab. 2001, 58, 15–27. [Google Scholar] [CrossRef]
- Walczak, B.; Massart, D.L. Dealing with missing data: Part II. Chemom. Intell. Lab. 2001, 58, 29–42. [Google Scholar]
- Steinfath, M.; Groth, D.; Lisec, J.; Selbig, J. Metabolite profile analysis: From raw data to regression and classification. Physiol. Plant. 2008, 132, 150–161. [Google Scholar] [CrossRef]
- Steuer, R. On the analysis and interpretation of correlations in metabolomic data. Brief. Bioinform. 2006, 7, 151–158. [Google Scholar] [CrossRef]
- Hair, J.F.; Black, W.C.; Babin, B.J.; Anderson, R.E. Multivariate Data Analysis, 7th ed.; Pearson: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Kotze, H.L.; Armitage, E.G.; Sharkey, K.J.; Allwood, J.W.; Dunn, W.B.; Williams, K.J.; Goodacre, R. A novel untargeted metabolomics correlation-based network analysis incorporating human metabolic reconstructions. BMC Syst. Biol. 2013, 7. [Google Scholar] [CrossRef]
- Troyanskaya, O.; Cantor, M.; Sherlock, G.; Brown, P.; Hastie, T.; Tibshirani, R.; Botstein, D.; Altman, R.B. Missing value estimation methods for DNA microarrays. Bioinformatics 2001, 17, 520–525. [Google Scholar] [CrossRef]
- Stekhoven, D.J.; Buehlmann, P. MissForest-non-parametric missing value imputation for mixed-type data. Bioinformatics 2012, 28, 112–118. [Google Scholar] [CrossRef]
- Teng, Q.; Huang, W.; Collette, T.W.; Ekman, D.R.; Tan, C. A direct cell quenching method for cell-culture based metabolomics. Metabolomics 2009, 5, 199–208. [Google Scholar] [CrossRef]
- Wedge, D.C.; Allwood, J.W.; Dunn, W.; Vaughan, A.A.; Simpson, K.; Brown, M.; Priest, L.; Blackhall, F.H.; Whetton, A.D.; Dive, C.; et al. Is serum or plasma more appropriate for intersubject comparisons in metabolomic studies? An assessment in patients with small-cell lung cancer. Anal. Chem. 2011, 83, 6689–6697. [Google Scholar] [CrossRef]
- Dunn, W.B.; Broadhurst, D.; Begley, P.; Zelena, E.; Francis-McIntyre, S.; Anderson, N.; Brown, M.; Knowles, J.D.; Halsall, A.; Haselden, J.N.; et al. Procedures for large-scale metabolic profiling of serum and plasma using gas chromatography and liquid chromatography coupled to mass spectrometry. Nat. Protoc. 2011, 6, 1060–1083. [Google Scholar] [CrossRef]
- Pope, G.A.; MacKenzie, D.A.; Defemez, M.; Aroso, M.A.M.M.; Fuller, L.J.; Mellon, F.A.; Dunn, W.B.; Brown, M.; Goodacre, R.; Kell, D.B.; et al. Metabolic footprinting as a tool for discriminating between brewing yeasts. Yeast 2007, 24, 667–679. [Google Scholar] [CrossRef]
- Kopka, J.; Schauer, N.; Krueger, S.; Birkemeyer, C.; Usadel, B.; Bergmuller, E.; Dormann, P.; Weckwerth, W.; Gibon, Y.; Stitt, M.; et al. GMD@CSB.DB: The golm metabolome database. Bioinformatics 2005, 21, 1635–1638. [Google Scholar]
- Sumner, L.W.; Amberg, A.; Barrett, D.; Beale, M.H.; Beger, R.; Daykin, C.A.; Fan, T.W.M.; Fiehn, O.; Goodacre, R.; Griffin, J.L.; et al. Proposed minimum reporting standards for chemical analysis. Metabolomics 2007, 3, 211–221. [Google Scholar] [CrossRef]
- Team, R.D.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Australia, 2008. [Google Scholar]
- Varmuza, K.; Filzmoser, P. Introduction to Multivariate Statistical Analysis in Chemometrics; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 2009; p. 321. [Google Scholar]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, 4th ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Adler, D.; Murdoch, D. rgl: 3D Visualization Device System (OpenGL), R Package Version 0.92.880; Available online: http://CRAN.R-project.org/package=rgl (accessed on 04 January 2014).
- Dejean, S.; Gonzalez, I.; Cao, K.-A.L.; Monget, P.; Coquery, J.; Yao, F.; Liquet, B.; Rohart, F. mixOmics: Omics Data Integration Project, R Package version 5.0–1; Available online: http://CRAN.R-project.org/package=mixOmics (accessed on 10 November 2013).
- Hastie, T.; Tibshirani, R.; Narasimhan, B.; Chu, G. Impute: Imputation for Microarray Data, 1.39.0. Available online: http://bioconductor.org/packages/devel/bioc/manuals/impute/man/impute.pdf2014 (accessed on 5 June 2014).
- Gentleman, R.C.; Carey, V.J.; Bates, D.M.; Bolstad, B.; Dettling, M.; Dudoit, S.; Ellis, B.; Gautier, L.; Ge, Y.C.; Gentry, J.; et al. Bioconductor: Open software development for computational biology and bioinformatics. Genome Biol. 2004, 5, R80. [Google Scholar] [CrossRef]
- Stekhoven, D.J. missForest: Nonparametric Missing Value Imputation using Random Forest, 1.4. Available online: http://cran.r-project.org/web/packages/mixOmics/index.html (accessed on 31 December 2013).
- Brereton, R.G. Consequences of sample size, variable selection, and model validation and optimisation, for predicting classification ability from analytical data. TrAC 2006, 25, 1103–1111. [Google Scholar]
- Van den Berg, R.A.; Hoefsloot, H.C.J.; Westerhuis, J.A.; Smilde, A.K.; van der Werf, M.J. Centering, scaling, and transformations: Improving the biological information content of metabolomics data. BMC Genomics 2006, 7, 142. [Google Scholar] [CrossRef]
- Bro, R.; Smilde, A.K. Centering and scaling in component analysis. J. Chemom. 2003, 17, 16–33. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Unsupervised Learning and Clustering. In Pattern Classification, 2nd ed.; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Pearson, K. On lines and planes of closest fit to systems of points in space. Philos. Mag. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 417–441. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis., 2nd ed.; Springer: New York, NY, USA, 2002. [Google Scholar]
- Burman, P. A comparative study of ordinary cross-validation, v-fold cross-validation and the repeated learning-testing methods. Biometrika 1989, 76, 503–514. [Google Scholar] [CrossRef]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. In Proceedings of the 14th International Joint Conference on Artificial Intelligence, Montreal, PQ, Canada, 1995; Morgan Kaufmann: Montreal, PQ, Canada, 1995; p. 7. [Google Scholar]
- Jain, A.K.; Duin, R.P.W.; Mao, J.C. Statistical pattern recognition: A review. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 4–37. [Google Scholar] [CrossRef]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comput. Surv. 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Everitt, B. Cluster Analysis; Heinemann Educational Books: London, UK, 1974; p. 122. [Google Scholar]
- Szekely, G.J.; Rizzo, M.L. Hierarchical clustering via joint between-within distances: Extending Ward’s minimum variance method. J. Classif. 2005, 22, 151–183. [Google Scholar]
- Ward, J.H. Hierarchical grouping to optimize an objective function. JASA 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Manly, B.F.J. Multivariate Statistical Methods: A Primer; Chapman and Hall: Boca Raton, FL, USA, 1986. [Google Scholar]
- Dixon, W.J. Biomedical Computer Programs; University of California Press: Los Angeles, CA, USA, 1975. [Google Scholar]
- Goodacre, R.; Timmins, E.M.; Burton, R.; Kaderbhai, N.; Woodward, A.M.; Kell, D.B.; Rooney, P.J. Rapid identification of urinary tract infection bacteria using hyperspectral whole-organism fingerprinting and artificial neural networks. Microbiology 1998, 144, 1157–1170. [Google Scholar] [CrossRef]
- Macfie, H.J.H.; Gutteridge, C.S.; Norris, J.R. Use of canonical variates analysis in differentiation of bacteria by pyrolysis gas-liquid chromatography. Microbiology 1978, 104, 67–74. [Google Scholar]
- Barker, M.; Rayens, W. Partial least squares for discrimination. J. Chemom. 2003, 17, 166–173. [Google Scholar] [CrossRef]
- Gromski, P.S.; Xu, Y.; Correa, E.; Ellis, D.I.; Turner, M.L.; Goodacre, R. A comparative investigation of modern feature selection and classification approaches for the analysis of mass spectrometry data. Anal. Chim. Acta 2014, 829, 1–8. [Google Scholar] [CrossRef]
- Haenlein, M.; Kaplan, A.M. A beginner’s guide to partial least squares analysis. Und. Stat. 2004, 3, 283–297. [Google Scholar]
- Wold, S.; Sjostrom, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Efron, B. 1977 rietz lecture. bootstrap methods: Another look at the Jackknife. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Efron, B.; Gong, G. A leisurely look at the bootstrap, the jackknife, and cross-validation. Am. Stat. 1983, 37, 36–48. [Google Scholar]
- Kotze, H.L. System Biology of Chemotherapy in Hypoxia Environments. The University of Manchester: Manchester, UK, 2012. [Google Scholar]
- Xu, Y.; Goodacre, R. Multiblock principal component analysis: An efficient tool for analyzing metabolomics data which contain two influential factors. Metabolomics 2012, 8, S37–S51. [Google Scholar] [CrossRef]
- Brereton, R.G.; Lloyd, G.R. Partial least squares discriminant analysis: Taking the magic away. J. Chemom. 2014, 28, 213–225. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Gromski, P.S.; Xu, Y.; Kotze, H.L.; Correa, E.; Ellis, D.I.; Armitage, E.G.; Turner, M.L.; Goodacre, R. Influence of Missing Values Substitutes on Multivariate Analysis of Metabolomics Data. Metabolites 2014, 4, 433-452. https://doi.org/10.3390/metabo4020433
Gromski PS, Xu Y, Kotze HL, Correa E, Ellis DI, Armitage EG, Turner ML, Goodacre R. Influence of Missing Values Substitutes on Multivariate Analysis of Metabolomics Data. Metabolites. 2014; 4(2):433-452. https://doi.org/10.3390/metabo4020433
Chicago/Turabian StyleGromski, Piotr S., Yun Xu, Helen L. Kotze, Elon Correa, David I. Ellis, Emily Grace Armitage, Michael L. Turner, and Royston Goodacre. 2014. "Influence of Missing Values Substitutes on Multivariate Analysis of Metabolomics Data" Metabolites 4, no. 2: 433-452. https://doi.org/10.3390/metabo4020433
APA StyleGromski, P. S., Xu, Y., Kotze, H. L., Correa, E., Ellis, D. I., Armitage, E. G., Turner, M. L., & Goodacre, R. (2014). Influence of Missing Values Substitutes on Multivariate Analysis of Metabolomics Data. Metabolites, 4(2), 433-452. https://doi.org/10.3390/metabo4020433






