Canonical Modeling of the Multi-Scale Regulation of the Heat Stress Response in Yeast
Abstract
:1. Introduction
2. Cellular Responses to Heat Stress
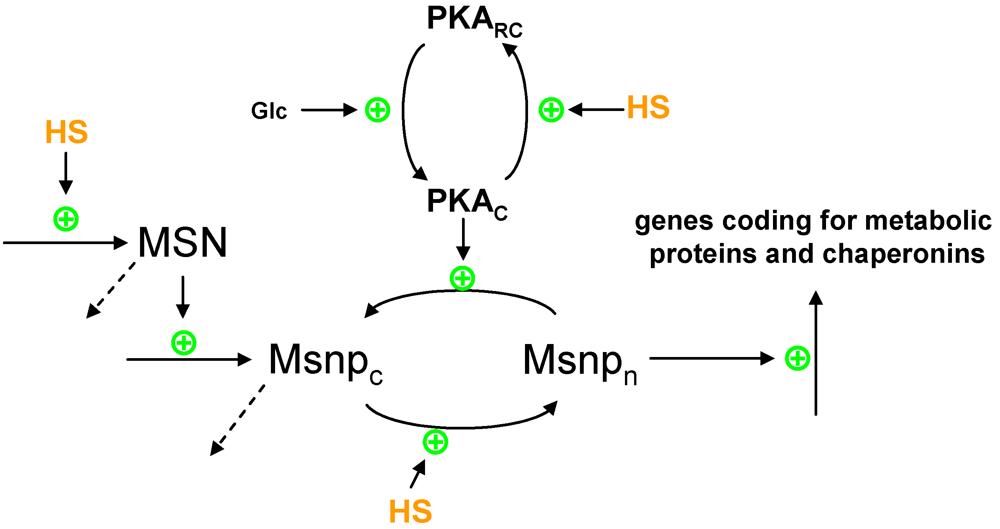
2.1. Protein Production
2.2. Protein Denaturation and Degradation
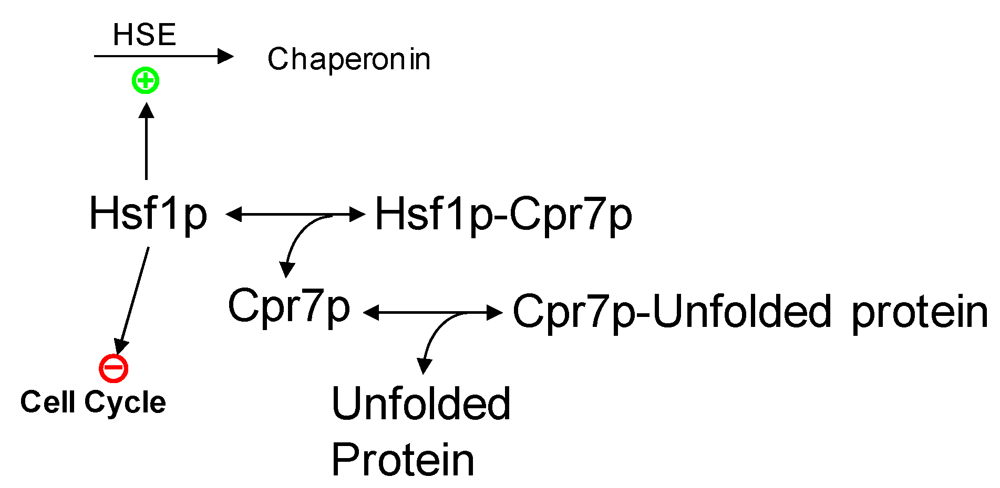
2.3. Partial Protein Unfolding
| ESR * Genes | Non-ESR* Paralogs | Function |
|---|---|---|
| HXK1 | HXK2 | Hexokinase |
| GLK1 | YDR516C | Glucokinase |
| PGM2 | PGM1 | Phosphoglucomutase |
| PFK26 | PFK27 | 2-phosphofructokinase |
| FBP26 | FBP1 | Fructose-2,6-bisphosphatase |
| GPM2 | GPM1, GPM3 | Phosphoglycerate mutase |
| GSY2 | GSY1 | Glycogen synthase |
| GLG1 | GLG2 | Glycogen initiator |
| GND2 | GND1 | 6-phosphogluconate dehydrogenase |
| GPD1 | GPD2 | Glycerol dehydrogenase |
3. Modeling Heat Stress Responses
3.1. General Considerations
3.2. Canonical Modeling
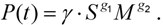
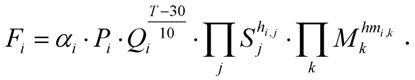
3.3. Parameterization
3.4. Modeling Gene Expression and Protein Production
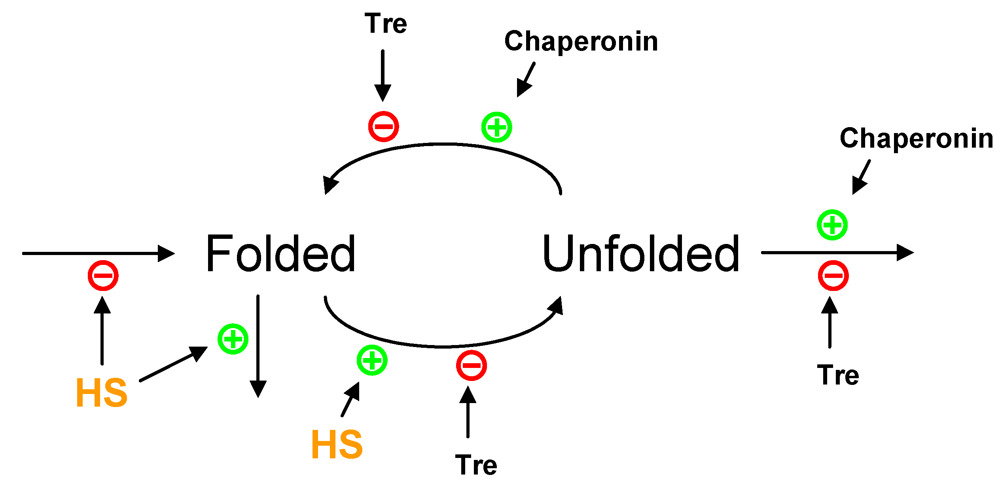
3.5. Modeling Specific Metabolic Events under Heat Stress: The Trehalose Cycle
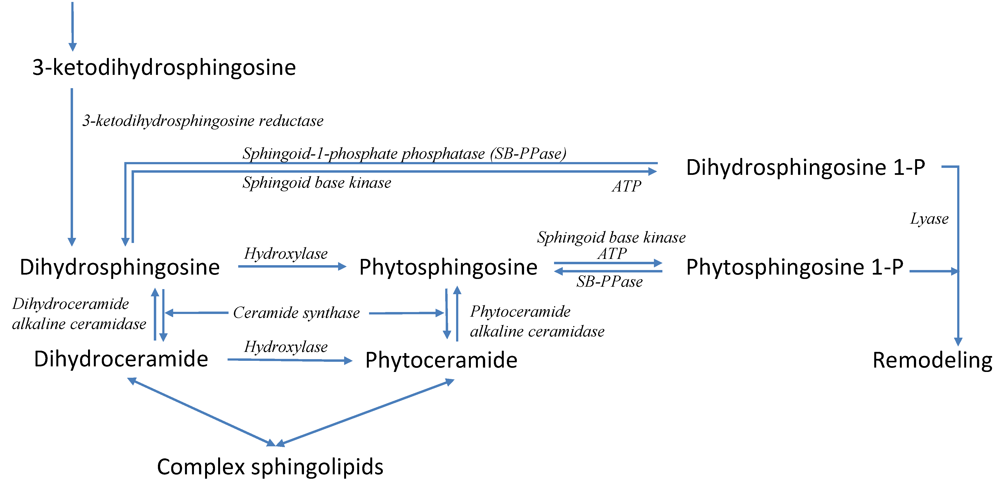
3.6. Modeling Specific Signaling Events under Heat Stress: The Role of Sphingolipids
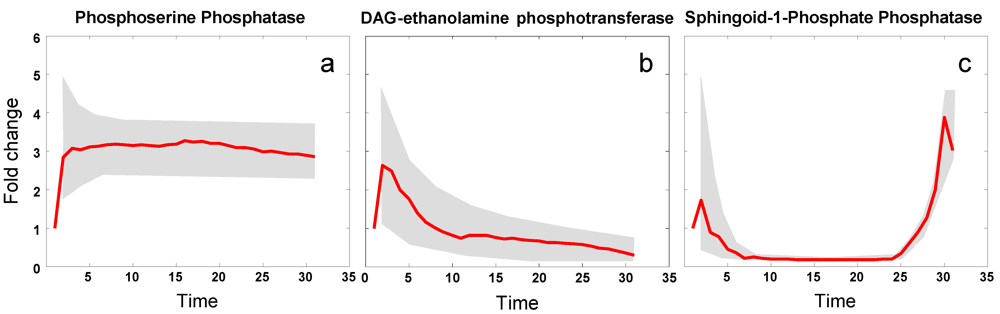
4. Conclusions

Conflicts of Interest
Acknowledgments
References
- Gasch, A.P. The Environmental Stress Response: A common yeast response to environmental stresses. In Yeast Stress Responses; Hohmann, S., Mager, P., Eds.; Springer-Verlag: Heidelberg, Germany, 2002; pp. 11–70. [Google Scholar]
- Ussery, D.W. DNA Denaturation. In Encyclopedia of Genetics; Brenner, S., H. Miller, J., Eds.; Academic Press: New York, NY, USA, 2001; pp. 550–553. [Google Scholar]
- Bruskov, V.I.; Malakhova, L.V.; Masalimov, Z.K.; Chernikov, A.V. Heat-induced formation of reactive oxygen species and 8-oxoguanine, a biomarker of damage to DNA. Nucleic Acids Res. 2002, 30, 1354–1363. [Google Scholar] [CrossRef]
- Hazel, J.R. Thermal Adaptation in biological-membranes—Is homeoviscous adaptation the explanation. Annu. Rev. Physiol. 1995, 57, 19–42. [Google Scholar] [CrossRef]
- Gasch, A.P.; Spellman, P.T.; Kao, C.M.; Carmel-Harel, O.; Eisen, M.B.; Storz, G.; Botstein, D.; Brown, P.O. Genomic expression programs in the response of yeast cells to environmental changes. Mol. Biol. Cell 2000, 11, 4241–4257. [Google Scholar]
- Warner, J.R. The economics of ribosome biosynthesis in yeast. Trends Biochem. Sci. 1999, 24, 437–440. [Google Scholar] [CrossRef]
- Castells-Roca, L.; Garcia-Martinez, J.; Moreno, J.; Herrero, E.; Belli, G.; Perez-Ortin, J.E. Heat shock response in yeast involves changes in both transcription rates and mRNA stabilities. PLoS One 2011, 6, e17272. [Google Scholar]
- Bienz, M.; Pelham, H.R. Heat shock regulatory elements function as an inducible enhancer in the Xenopus hsp70 gene and when linked to a heterologous promoter. Cell 1986, 45, 753–760. [Google Scholar] [CrossRef]
- Trott, A.; Morano, K.A. The yeast heat shock response. In Yeast Stress Responses; Hohmann, S., Mager, P., Eds.; Springer-Verlag: Heidelberg, Germany, 2002; pp. 71–119. [Google Scholar]
- Boy-Marcotte, E.; Perrot, M.; Bussereau, F.; Boucherie, H.; Jacquet, M. Msn2p and Msn4p control a large number of genes induced at the diauxic transition which are repressed by cyclic AMP in Saccharomyces cerevisiae. J. Bacteriol. 1998, 180, 1044–1052. [Google Scholar]
- Görner, W.; Durchschlag, E.; Martinez-Pastor, M.T.; Estruch, F.; Ammerer, G.; Hamilton, B.; Ruis, H.; Schuller, C. Nuclear localization of the C2H2 zinc finger protein Msn2p is regulated by stress and protein kinase A activity. Genes Dev. 1998, 12, 586–597. [Google Scholar] [CrossRef]
- Martinez-Pastor, M.T.; Marchler, G.; Schuller, C.; Marchler-Bauer, A.; Ruis, H.; Estruch, F. The Saccharomyces cerevisiae zinc finger proteins Msn2p and Msn4p are required for transcriptional induction through the stress response element (STRE). EMBO J. 1996, 15, 2227–2235. [Google Scholar]
- Schmitt, A.P.; McEntee, K. Msn2p, a zinc finger DNA-binding protein, is the transcriptional activator of the multistress response in Saccharomyces cerevisia. Proc. Natl. Acad. Sci. USA 1996, 93, 5777–5782. [Google Scholar] [CrossRef]
- Yamamoto, N.; Maeda, Y.; Ikeda, A.; Sakurai, H. Regulation of thermotolerance by stress-induced transcription factors in Saccharomyces cerevisiae. Eukaryot. Cell 2008, 7, 783–790. [Google Scholar] [CrossRef]
- Neves, M.J.; Francois, J. On the mechanism by which a heat shock induces trehalose accumulation in Saccharomyces cerevisiae. Biochem. J. 1992, 288, 859–864. [Google Scholar]
- Francois, J.; Villanueva, M.E.; Hers, H.G. The control of glycogen metabolism in yeast. 1. Interconversion in vivo of glycogen synthase and glycogen phosphorylase induced by glucose, a nitrogen source or uncouplers. Eur. J. Biochem. 1988, 174, 551–559. [Google Scholar] [CrossRef]
- Gonze, D.; Jacquet, M.; Goldbeter, A. Stochastic modelling of nucleocytoplasmic oscillations of the transcription factor Msn2 in yeast. J. R. Soc. Interface 2008, 5 Suppl 1, S95–109. [Google Scholar]
- Jenkins, G.M.; Richards, A.; Wahl, T.; Mao, C.; Obeid, L.; Hannun, Y. Involvement of yeast sphingolipids in the heat stress response of Saccharomyces cerevisiae. J. Biol. Chem. 1997, 272, 32566–32572. [Google Scholar]
- Hannun, Y.A.; Obeid, L.M. Principles of bioactive lipid signalling: Lessons from sphingolipids. Nat. Rev. Mol. Cell Biol. 2008, 9, 139–150. [Google Scholar] [CrossRef]
- Cowart, L.A.; Shotwell, M.; Worley, M.L.; Richards, A.J.; Montefusco, D.J.; Hannun, Y.A.; Lu, X. Revealing a signaling role of phytosphingosine-1-phosphate in yeast. Mol. Syst. Biol. 2010, 6, 349. [Google Scholar]
- Voit, E.O. Computational Analysis of Biochemical Systems. A Practical Guide for Biochemists and Molecular Biologists; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Goel, G.; Chou, I.C.; Voit, E.O. Biological systems modeling and analysis: a biomolecular technique of the twenty-first century. J. Biomol. Tech. 2006, 17, 252–269. [Google Scholar]
- Savageau, M.A. Enzyme kinetics in vitro and in vivo: Michaelis-Menten revisited. In Principles of Medical Biology; Bittar, E.E., Ed.; JAI Press Inc.: Greenwich, CT, USA, 1995. [Google Scholar]
- Torres, N.V.; Voit, E.O. Pathway Analysis and Optimization in Metabolic Engineering; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Voit, E.O. Modelling metabolic networks using power-laws and S-systems. Essays Biochem. 2008, 45, 29–40. [Google Scholar] [CrossRef]
- Savageau, M. Biochemical Systems Analysis. A Study of Function and Design in Molecular Biology; Addison-Wesley: Reading, MA, USA, 1976. [Google Scholar]
- Voit, E.O. Canonical Nonlinear Modeling. S-System Approach to Understanding Complexity; Van Nostrand Reinhold: NY, USA, 1991; p xi+365 pp. [Google Scholar]
- Fonseca, L.L.; Sanchez, C.; Santos, H.; Voit, E.O. Complex coordination of multi-scale cellular responses to environmental stress. Mol. Biosyst. 2011, 7, 731–741. [Google Scholar] [CrossRef]
- Voit, E.O. Parameter Estimation. In Computational Analysis of Biochemical Systems. A Practical Guide for Biochemists and Molecular Biologists; Cambridge University Press: Cambridge, UK, 2000; pp. 143–192. [Google Scholar]
- Chou, I.C.; Voit, E.O. Recent developments in parameter estimation and structure identification of biochemical and genomic systems. Math. Biosci. 2009, 219, 57–83. [Google Scholar]
- Stanford Database. Available online: http://genome-www.stanford.edu/yeast_stress/ (Accessed on 8 February 2012).
- Causton, H.C.; Ren, B.; Koh, S.S.; Harbison, C.T.; Kanin, E.; Jennings, E.G.; Lee, T.I.; True, H.L.; Lander, E.S.; Young, R.A. Remodeling of yeast genome expression in response to environmental changes. Mol. Biol. Cell 2001, 12, 323–337. [Google Scholar]
- Eisen, M.B.; Spellman, P.T.; Brown, P.O.; Botstein, D. Cluster analysis and display of genome-wide expression patterns. Proc. Natl. Acad. Sci. USA 1998, 95, 14863–14868. [Google Scholar]
- Arava, Y.; Wang, Y.; Storey, J.D.; Liu, C.L.; Brown, P.O.; Herschlag, D. Genome-wide analysis of mRNA translation profiles in Saccharomyces cerevisiae. Proc. Natl. Acad. Sci. USA 2003, 100, 3889–3894. [Google Scholar]
- Beyer, A.; Hollunder, J.; Nasheuer, H.P.; Wilhelm, T. Post-transcriptional expression regulation in the yeast Saccharomyces cerevisiae on a genomic scale. Mol. Cell Proteomics 2004, 3, 1083–1092. [Google Scholar]
- Holstege, F.C.; Jennings, E.G.; Wyrick, J.J.; Lee, T.I.; Hengartner, C.J.; Green, M.R.; Golub, T.R.; Lander, E.S.; Young, R.A. Dissecting the regulatory circuitry of a eukaryotic genome. Cell 1998, 95, 717–728. [Google Scholar]
- Belle, A.; Tanay, A.; Bitincka, L.; Shamir, R.; O'Shea, E.K. Quantification of protein half-lives in the budding yeast proteome. Proc. Natl. Acad. Sci. USA 2006, 103, 13004–13009. [Google Scholar]
- Ghaemmaghami, S.; Huh, W.K.; Bower, K.; Howson, R.W.; Belle, A.; Dephoure, N.; O'Shea, E.K.; Weissman, J.S. Global analysis of protein expression in yeast. Nature 2003, 425, 737–741. [Google Scholar]
- Nagaraj, N.; Kulak, N.A.; Cox, J.; Neuhaus, N.; Mayr, K.; Hoerning, O.; Vorm, O.; Mann, M. Systems-wide perturbation analysis with near complete coverage of the yeast proteome by single-shot UHPLC runs on a bench-top Orbitrap. Mol. Cell. Proteomics 2011. mcp.M111.013722. [Google Scholar]
- van Eunen, K.; Bouwman, J.; Daran-Lapujade, P.; Postmus, J.; Canelas, A.B.; Mensonides, F.I.; Orij, R.; Tuzun, I.; van den Brink, J.; Smits, G.J.; et al. Measuring enzyme activities under standardized in vivo-like conditions for systems biology. FEBS J. 2010, 277, 749–760. [Google Scholar]
- Rieger, T.R.; Morimoto, R.I.; Hatzimanikatis, V. Mathematical modeling of the eukaryotic heat-shock response: dynamics of the hsp70 promoter. Biophys. J. 2005, 88, 1646–1658. [Google Scholar]
- Singh, G.P.; Dash, D. Intrinsic disorder in yeast transcriptional regulatory network. Proteins 2007, 68, 602–605. [Google Scholar]
- Singer, M.A.; Lindquist, S. Thermotolerance in Saccharomyces cerevisiae: The Yin and Yang of trehalose. Trends Biotechnol. 1998, 16, 460–468. [Google Scholar]
- Voit, E.O. Biochemical and genomic regulation of the trehalose cycle in yeast: review of observations and canonical model analysis. J. Theor. Biol. 2003, 223, 55–78. [Google Scholar]
- Guillen-Gosalbez, G.; Sorribas, A. Identifying quantitative operation principles in metabolic pathways: a systematic method for searching feasible enzyme activity patterns leading to cellular adaptive responses. BMC Bioinformatics 2009, 10, 386. [Google Scholar]
- Vilaprinyo, E.; Alves, R.; Sorribas, A. Use of physiological constraints to identify quantitative design principles for gene expression in yeast adaptation to heat shock. BMC Bioinformatics 2006, 7, 184. [Google Scholar]
- Vilaprinyo, E.; Alves, R.; Sorribas, A. Minimization of biosynthetic costs in adaptive gene expression responses of yeast to environmental changes. PLoS Comput. Biol. 2010, 6, e1000674. [Google Scholar]
- Voit, E.O.; Radivoyevitch, T. Biochemical systems analysis of genome-wide expression data. Bioinformatics 2000, 16, 1023–1037. [Google Scholar]
- El-Samad, H.; Prajna, S.; Papachristodoulou, A.; Khammash, M.; Doyle, J.C. Model validation and robust stability analysis of the bacterial heat shock response using SOSTOOLS. In Proceedings of the 42nd IEEE Conference on Decision and Control; 2003; 4, pp. 3766–3771. [Google Scholar]
- Havenith, G. Individualized model of human thermoregulation for the simulation of heat stress response. J. Appl. Physiol. 2001, 90, 1943–1954. [Google Scholar]
- Kurata, H.; El-Samad, H.; Iwasaki, R.; Ohtake, H.; Doyle, J.C.; Grigorova, I.; Gross, C.A.; Khammash, M. Module-based analysis of robustness tradeoffs in the heat shock response system. PLoS Comput. Biol. 2006, 2, e59. [Google Scholar]
- Sorribas, A.; Pozo, C.; Vilaprinyo, E.; Guillen-Gosalbez, G.; Jimenez, L.; Alves, R. Optimization and evolution in metabolic pathways: global optimization techniques in Generalized Mass Action models. J. Biotechnol. 2010, 149, 141–153. [Google Scholar]
- Dickson, R.C.; Nagiec, E.E.; Skrzypek, M.; Tillman, P.; Wells, G.B.; Lester, R.L. Sphingolipids are potential heat stress signals in Saccharomyces. J. Biol. Chem. 1997, 272, 30196–30200. [Google Scholar]
- Meier, K.D.; Deloche, O.; Kajiwara, K.; Funato, K.; Riezman, H. Sphingoid base is required for translation initiation during heat dtress in Saccharomyces cerevisiae. Mol. Biol. Cell 2006, 17, 1164–1175. [Google Scholar]
- Alvarez-Vasquez, F.; Riezman, H.; Voit, E.O.; Hannun, Y.A. Mathematical modeling and validation of the ergosterol pathway in Saccharomyces cerevisiae. PLoS One 2011. in Press.. [Google Scholar]
- Alvarez-Vasquez, F.; Sims, K.J.; Cowart, L.A.; Okamoto, Y.; Voit, E.O.; Hannun, Y.A. Simulation and validation of modelled sphingolipid metabolism in Saccharomyces cerevisiae. Nature 2005, 433, 425–430. [Google Scholar]
- Alvarez-Vasquez, F.; Sims, K.J.; Hannun, Y.A.; Voit, E.O. Integration of kinetic information on yeast sphingolipid metabolism in dynamical pathway models. J. Theor. Biol. 2004, 226, 265–291. [Google Scholar]
- Sims, K.J.; Alvarez-Vasquez, F.; Voit, E.O.; Hannun, Y.A. A guide to biochemical systems modeling of sphingolipids for the biochemist. Meth. Enzym. 2007, 432, 319–350. [Google Scholar]
- Curto, R.; Sorribas, A.; Cascante, M. Comparative characterization of the fermentation pathway of Saccharomyces cerevisiae using biochemical systems theory and metabolic control analysis: model definition and nomenclature. Math. Biosci. 1995, 130, 25–50. [Google Scholar]
- Qi, Z.; Miller, G.W.; Voit, E.O. A mathematical model of presynaptic dopamine homeostasis: implications for schizophrenia. Pharmacopsychiatry 2008, 41 (Suppl. 1), S89–S98. [Google Scholar]
- Qi, Z.; Miller, G.W.; Voit, E.O. Computational analysis of determinants of dopamine (DA) dysfunction in DA nerve terminals. Synapse (New York, N.Y.) 2009, 63, 1133–1142. [Google Scholar]
- Marin-Sanguino, A.; Gupta, S.K.; Voit, E.O.; Vera, J. Biochemical pathway modeling tools for drug target detection in cancer and other complex diseases. Meth. Enzym. 2010, 487, 321–372. [Google Scholar]
- Curto, R.; Voit, E.O.; Cascante, M. Analysis of abnormalities in purine metabolism leading to gout and to neurological dysfunctions in man. Biochem. J. 1998, 329, 477–487. [Google Scholar]
- Garcia, J.; Shea, J.; Alvarez-Vasquez, F.; Qureshi, A.; Luberto, C.; Voit, E.O.; Del Poeta, M. Mathematical modeling of pathogenicity of Cryptococcus neoformans. Mol. Syst. Biol. 2008, 4, 183. [Google Scholar]
- Voit, E.O.; Qi, Z.; Kikuchi, S. Mesoscopic models of biomedical systems as intermediates between disease simulators and tools for discovering design principles: Dopamine-related diseases as case study. Pharmacopsychiatry 2012. in press.
© 2012 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Fonseca, L.L.; Chen, P.-W.; Voit, E.O. Canonical Modeling of the Multi-Scale Regulation of the Heat Stress Response in Yeast. Metabolites 2012, 2, 221-241. https://doi.org/10.3390/metabo2010221
Fonseca LL, Chen P-W, Voit EO. Canonical Modeling of the Multi-Scale Regulation of the Heat Stress Response in Yeast. Metabolites. 2012; 2(1):221-241. https://doi.org/10.3390/metabo2010221
Chicago/Turabian StyleFonseca, Luis L., Po-Wei Chen, and Eberhard O. Voit. 2012. "Canonical Modeling of the Multi-Scale Regulation of the Heat Stress Response in Yeast" Metabolites 2, no. 1: 221-241. https://doi.org/10.3390/metabo2010221
APA StyleFonseca, L. L., Chen, P.-W., & Voit, E. O. (2012). Canonical Modeling of the Multi-Scale Regulation of the Heat Stress Response in Yeast. Metabolites, 2(1), 221-241. https://doi.org/10.3390/metabo2010221





