Feature Ranking and Screening for Class-Imbalanced Metabolomics Data Based on Rank Aggregation Coupled with Re-Balance
Abstract
1. Introduction
- Under-sampling removes some of the data points from the majority class to alleviate the harms of imbalanced distribution. Random under-sampling (RUS) is a simple but effective way to randomly remove part of the majority class.
- Hybrid-sampling is a combination of over-sampling and under-sampling.
2. Results
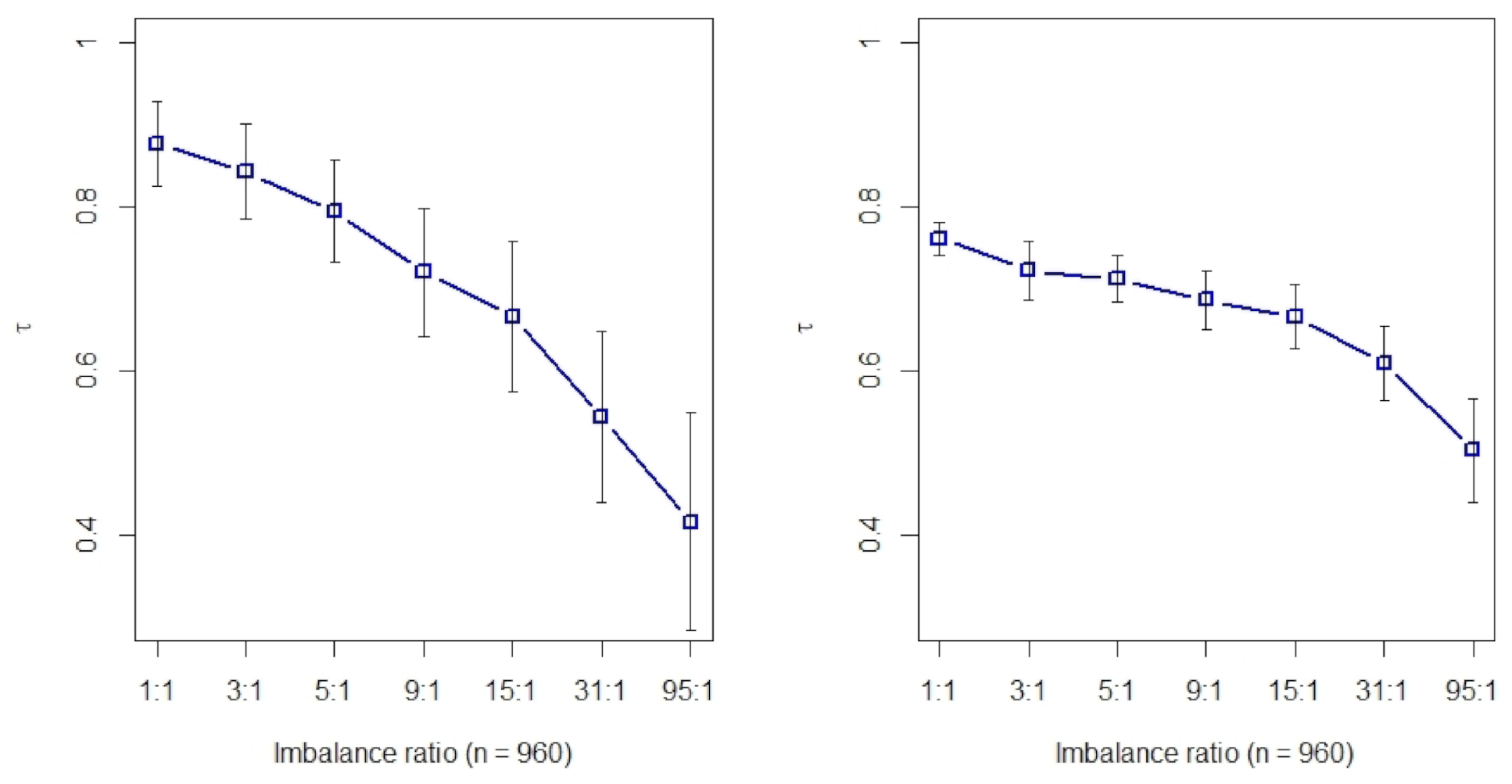
2.1. Kendall’s Rank Correlation of Eight Filtering Methods on Class-Imbalanced Data
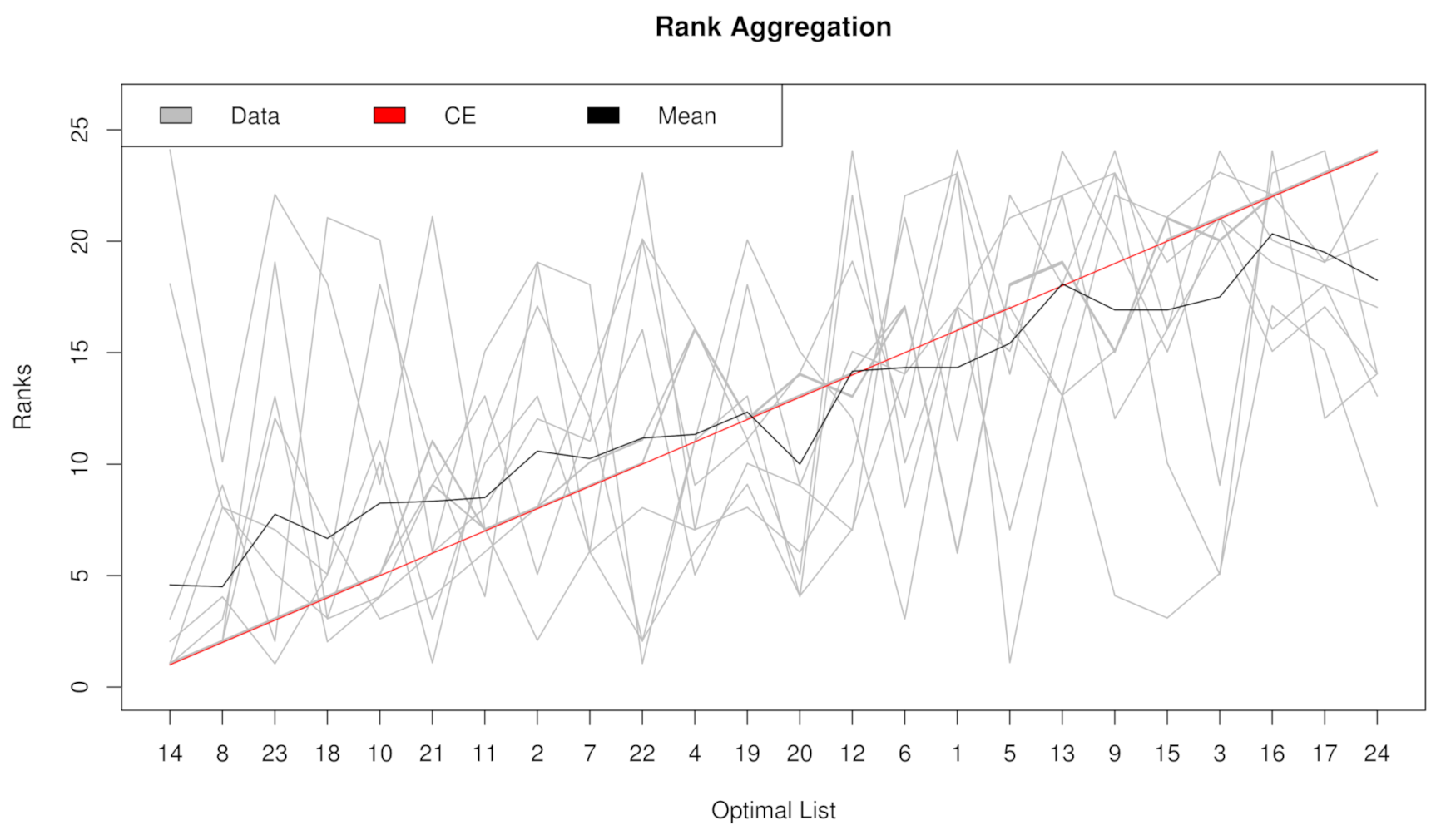
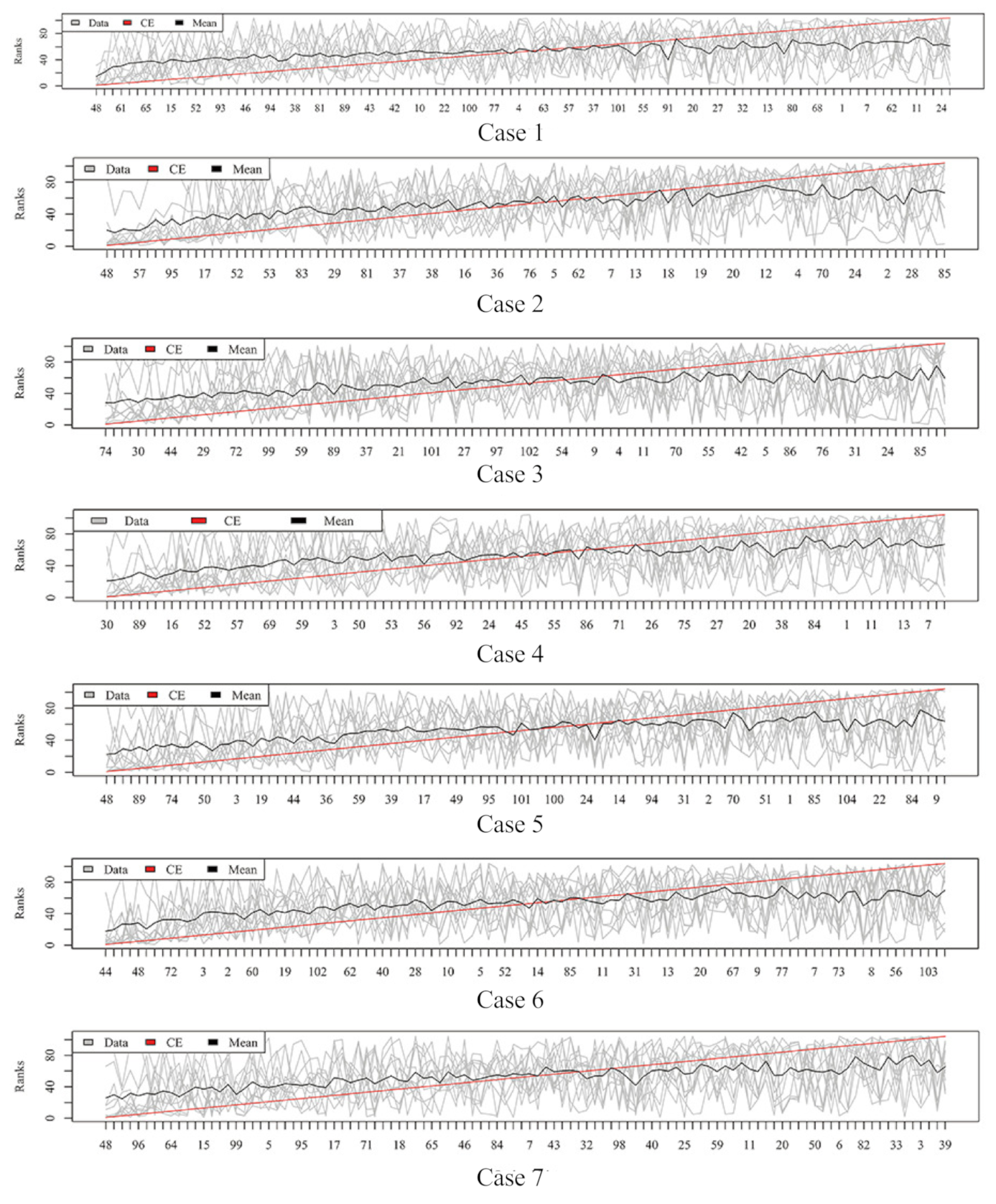
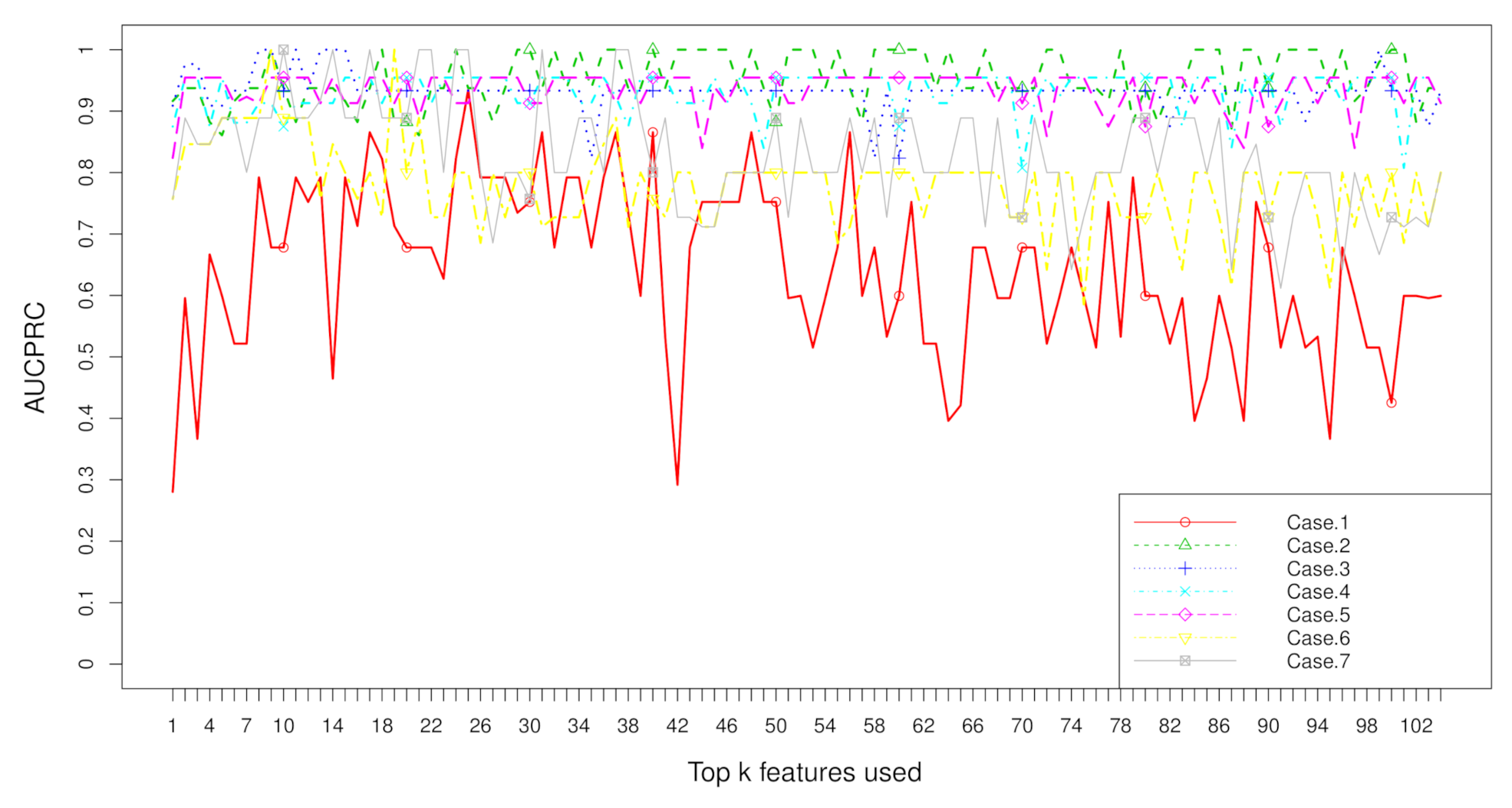
2.2. Rank Aggregation(RA) on Original Balanced Data
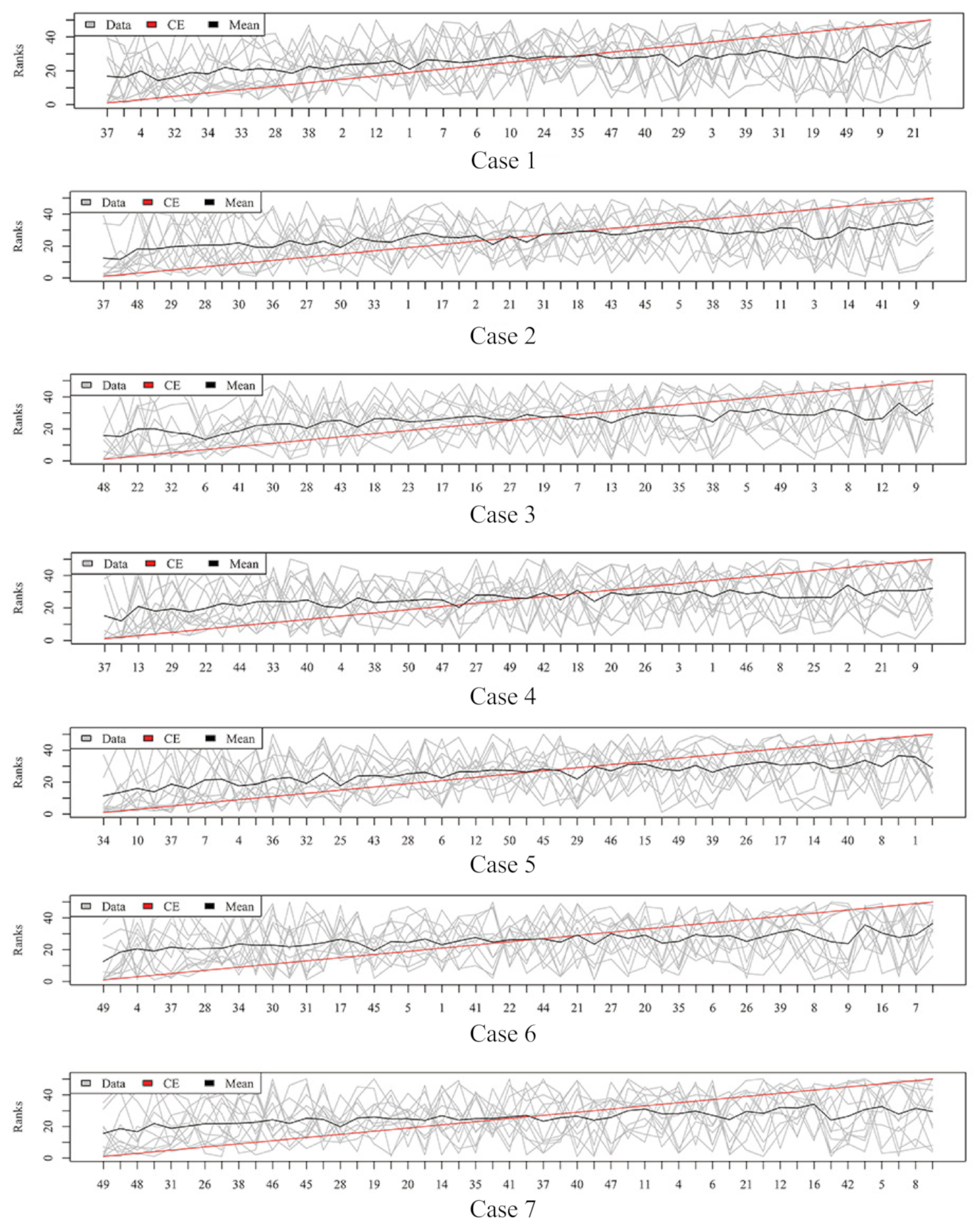
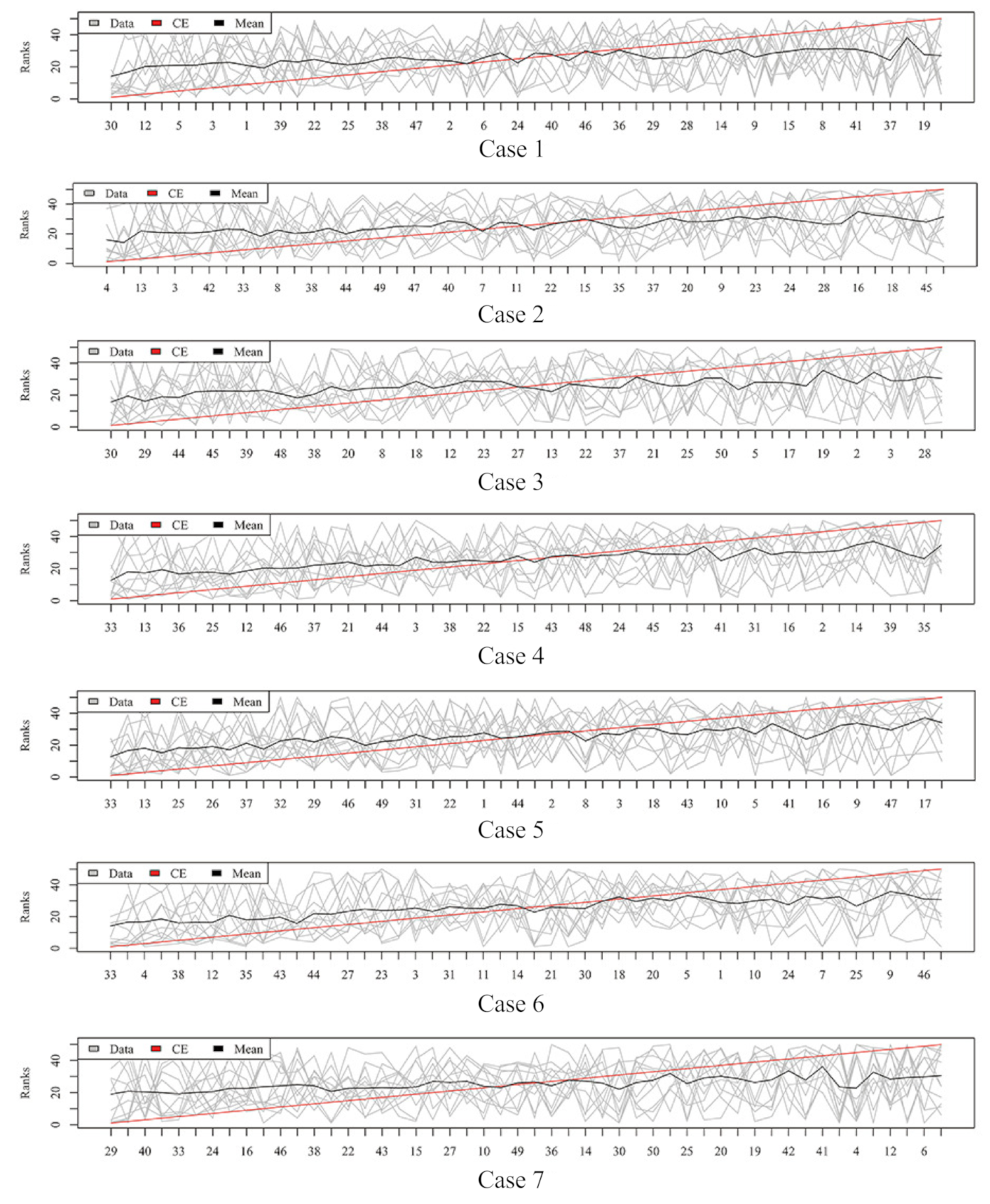
2.3. Rank Aggregation with Re-Balance (RAR) on Imbalanced Data
3. Discussion
4. Materials and Methods
4.1. Notations
| D | a dataset with two classes and |
| the minority (positive) class | |
| the majority (negative) class | |
| n | the size of the total instances in D |
| p | the number of the features in D |
| the size of , | |
| the number of samples in D | |
| the jth feature, | |
| the ith instance, | |
| the expectation of jth feature in , ; | |
| the variance of jth feature in , ; | |
| the sample mean of jth feature in , ; | |
| the sample variance of jth feature in , ; |
4.2. Eight Filtering Methods
4.2.1. t Test
4.2.2. Fisher Score
4.2.3. Hellinger Distance
4.2.4. Relief and ReliefF
4.2.5. Information Gain (IG)
4.2.6. Gini Index
4.2.7. R-Value
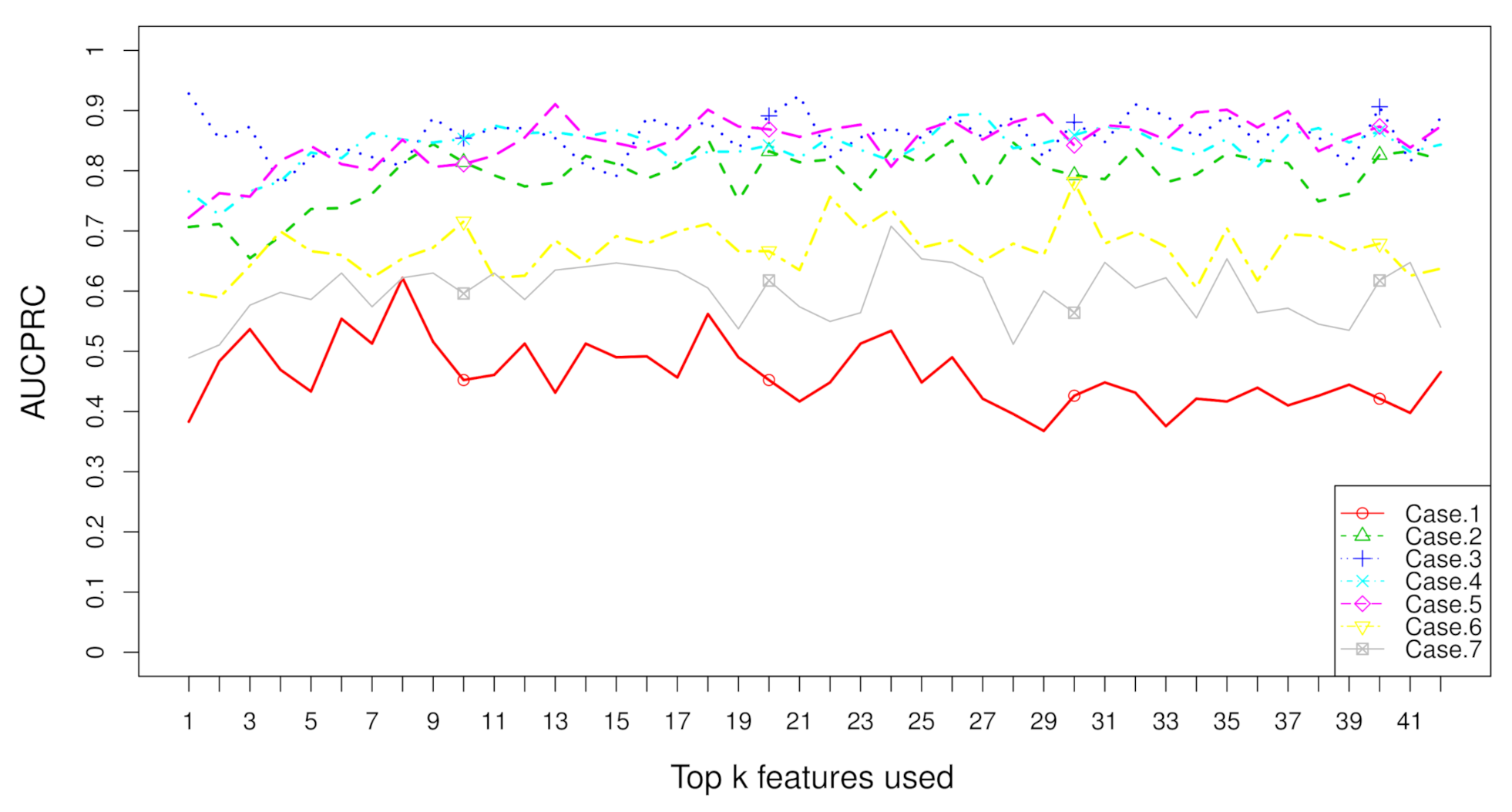
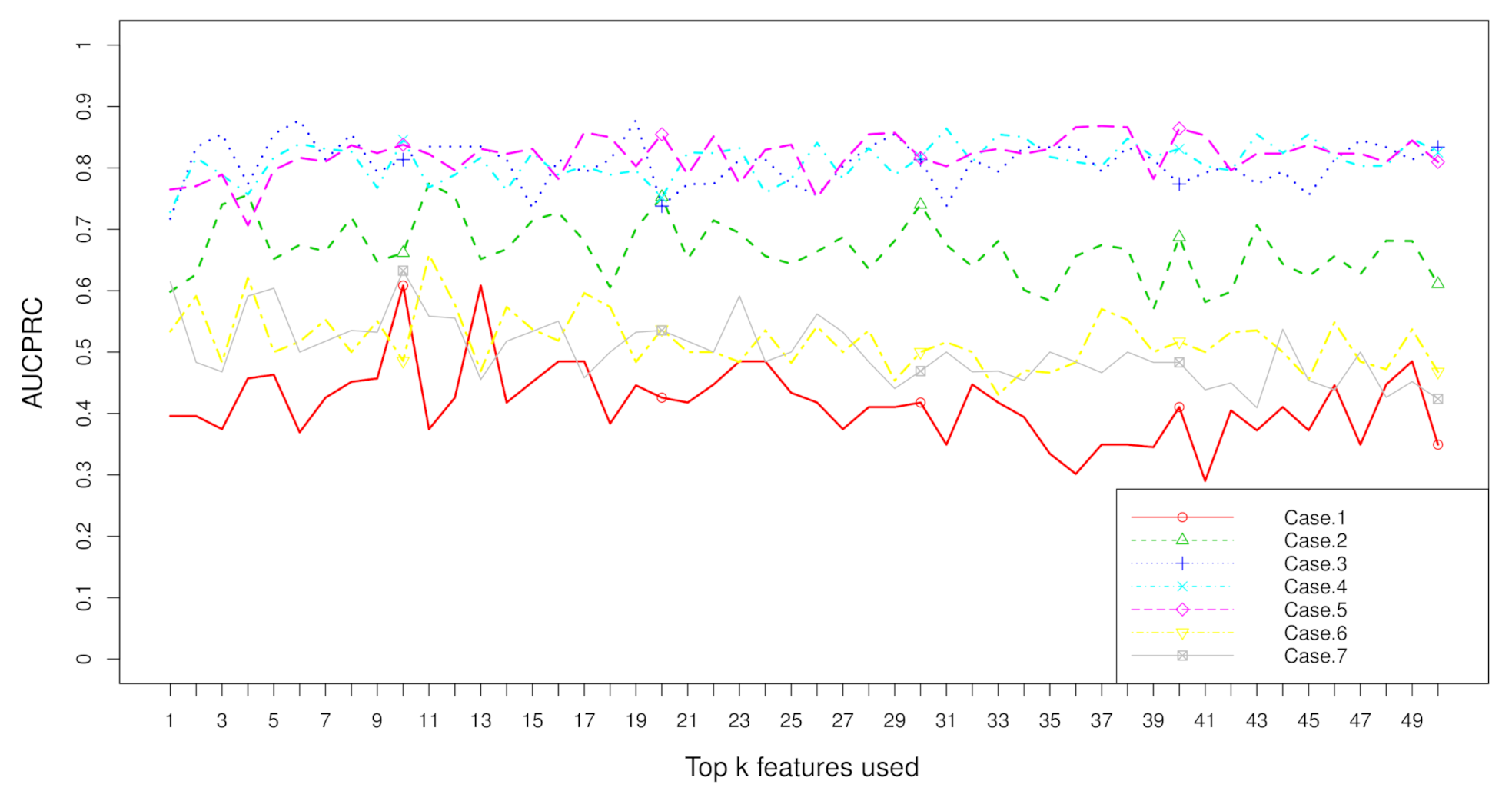
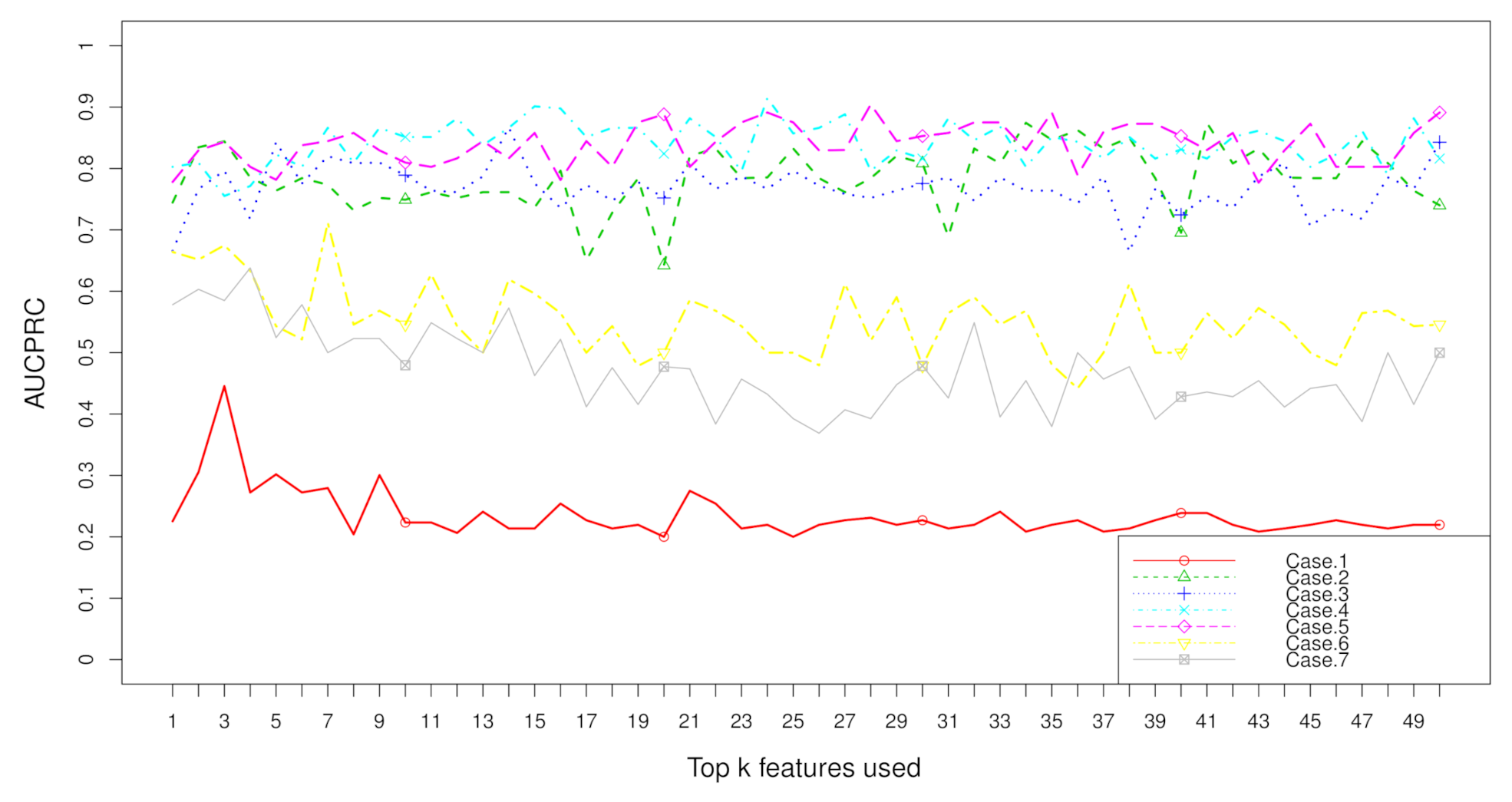
4.3. Four Evaluation Metrics
4.3.1. Geometric Mean and F-Measure
4.3.2. and
4.4. Kendall’S Rank Correlation
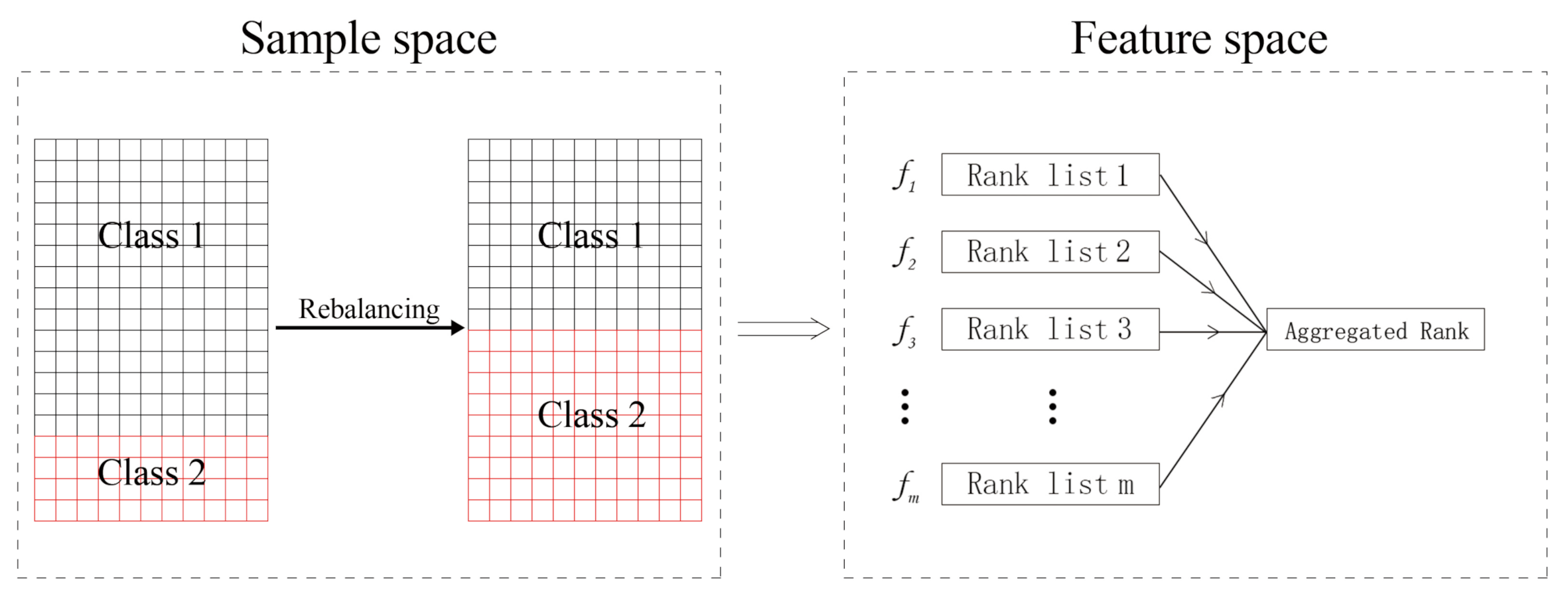
4.5. Rank Aggregation with Re-Balance for Class-Imbalanced Data
4.5.1. Rank Aggregation
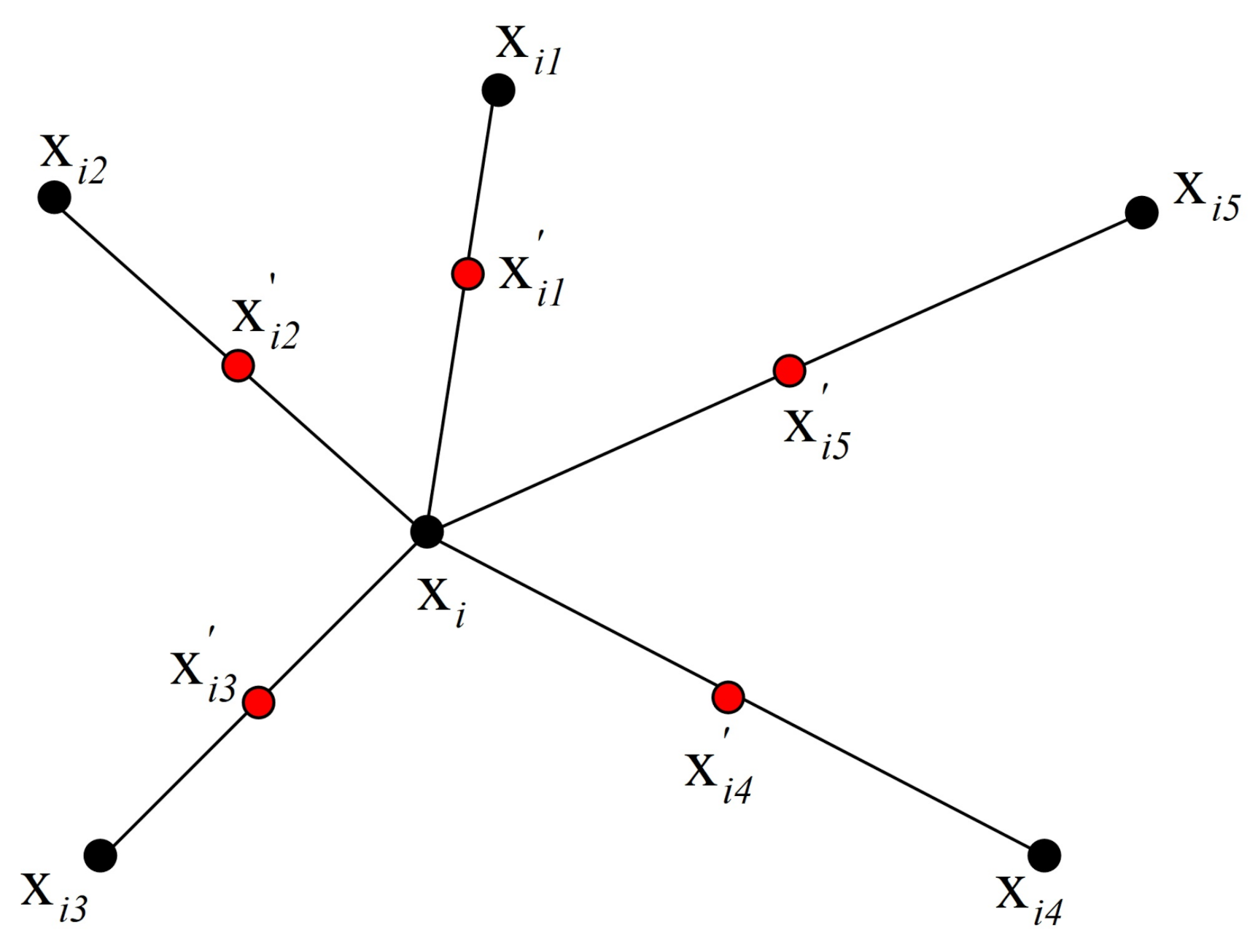
4.5.2. Strategies to Generate New Samples
Randomly Sampling
SMOTE
Smoothed Bootstrap
- step
- 1: choose with probability ;
- step
- 2: choose in the original daa set such that with probability ;
- step
- 3: sample from a probability distribution , which is centered at and depends on the smoothing matrix .
4.6. Experiment and Assessing Metrics
- : no re-sampling: the original datasets are directly utilized to perform rank aggregation. Denoted case 1 by “RA” because there is no re-sampling in it.
- : hybrid-sampling A: some instances of the majority class are randomly eliminated, and new synthetic minority examples are generated by SMOTE. The size of the remaining majority is equal to the size of the (original plus new generated) minority class.
- : hybrid-sampling B: A new synthetic dataset is generated according to the smoothed bootstrap re-sampling technique. The sizes of the majority and minority classes are approximately equal.
- : over-sampling A: new minority class instances are randomly duplicated according to the original minority group.
- : over-sampling B: new synthetic minority examples are generated on the basis of the smoothed bootstrap re-sampling technique.
- : under-sampling A: some instances from the majority class are randomly removed so that the size of the remaining majority class is equal to the size of the minority.
- : under-sampling B: new synthetic majority examples are generated according to the smoothed bootstrap re-sampling technique.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brodley, C.; Friedl, M. Identifying mislabeled training data. J. Artif. Intell. Res. 1999, 11, 131–167. [Google Scholar] [CrossRef]
- Chawla, N. Data mining for imbalanced datasets: An overview. In Data Mining and Knowledge Discovery Handbook; Springer: Berlin/Heidelberg, Germany, 2009; pp. 875–886. [Google Scholar]
- Krawczyk, B. Learning from imbalanced data: Open challenges and future directions. Prog. Artif. Intell. 2016, 5, 221–232. [Google Scholar] [CrossRef]
- Cordón, I.; García, S.; Fernández, A.; Herrera, F. Imbalance: Oversampling algorithms for imbalanced classification in R. Knowl. Based Syst. 2018, 161, 329–341. [Google Scholar] [CrossRef]
- Chawla, N.; Bowyer, K.; Hall, L.; Kegelmeyer, W. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Lunardon, N.; Menardi, G.; Torelli, N. ROSE: A Package for Binary Imbalanced Learning. R J. 2014, 6, 79–89. [Google Scholar] [CrossRef]
- Hulse, J.V.; Khoshgoftaar, T.; Napolitano, A.; Wald, R. Feature selection with high-dimensional imbalanced data. In Proceedings of the 2009 IEEE International Conference on Data Mining Workshops, Miami, FL, USA, 6 December 2009; pp. 507–514. [Google Scholar]
- Guyon, I.; Elisseeff, A. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Saeys, Y.; Inza, I.; Larrañaga, P. A review of feature selection techniques in bioinformatics. Bioinformatics 2007, 23, 2507–2517. [Google Scholar] [CrossRef]
- Yun, Y.H.; Li, H.D.; Deng, B.C.; Cao, D.S. An overview of variable selection methods in multivariate analysis of near-infrared spectra. TrAC Trends Anal. Chem. 2019, 113, 102–115. [Google Scholar] [CrossRef]
- Su, X.; Khoshgoftaar, T. A survey of collaborative filtering techniques. Adv. Artif. Intell. 2009, 2009, 421425. [Google Scholar] [CrossRef]
- Ambjørn, J.; Janik, R.; Kristjansen, C. Wrapping interactions and a new source of corrections to the spin-chain/string duality. Nucl. Phys. B 2006, 736, 288–301. [Google Scholar] [CrossRef]
- Higman, G.; Neumann, B.; Neuman, H. Embedding theorems for groups. J. Lond. Math. Soc. 1949, 1, 247–254. [Google Scholar] [CrossRef]
- Guo, H.; Li, Y.; Shang, J.; Gu, M.; Huang, Y.; Gong, B. Learning from class-imbalanced data: Review of methods and applications. Expert Syst. Appl. 2017, 73, 220–239. [Google Scholar]
- Gu, Q.; Li, Z.; Han, J. Generalized fisher score for feature selection. arXiv 2012, arXiv:1202.3725. [Google Scholar]
- Yin, L.; Ge, Y.; Xiao, K.; Wang, X.; Quan, X. Feature selection for high-dimensional imbalanced data. Neurocomputing 2013, 105, 3–11. [Google Scholar] [CrossRef]
- Spolaôr, N.; Cherman, E.; Monard, M.; Lee, H. ReliefF for multi-label feature selection. In Proceedings of the 2013 Brazilian Conference on Intelligent Systems, Fortaleza, Brazil, 19–24 October 2013; pp. 6–11. [Google Scholar]
- Kira, K.; Rendell, L. The feature selection problem: Traditional methods and a new algorithm. Aaai 1992, 2, 129–134. [Google Scholar]
- Lee, C.; Lee, G. Information gain and divergence-based feature selection for machine learning-based text categorization. Inf. Process. Manag. 2006, 42, 155–165. [Google Scholar] [CrossRef]
- Lerman, R.; Yitzhaki, S. A note on the calculation and interpretation of the Gini index. Econ. Lett. 1984, 15, 363–368. [Google Scholar] [CrossRef]
- Lobo, J.; Jiménez-Valverde, A.; Real, R. AUC: A misleading measure of the performance of predictive distribution models. Glob. Ecol. Biogeogr. 2008, 17, 145–151. [Google Scholar] [CrossRef]
- Boyd, K.; Eng, K.; Page, C. Area under the precision-recall curve: Point estimates and confidence intervals. In Joint European Conference on Machine Learning and Knowledge Discovery in Databases; Springer: Berlin/Heidelberg, Germany, 2013; pp. 451–466. [Google Scholar]
- Altidor, W.; Khoshgoftaar, T.; Napolitano, A. Wrapper-based feature ranking for software engineering metrics. In Proceedings of the 2009 International Conference on Machine Learning and Applications, Miami, FL, USA, 13–15 December 2009; pp. 241–246. [Google Scholar]
- Pillai, I.; Fumera, G.; Roli, F. F-measure optimisation in multi-label classifiers. In Proceedings of the 21st International Conference on Pattern Recognition (ICPR2012), Tsukuba, Japan, 11–15 November 2012; pp. 2424–2427. [Google Scholar]
- Lee, J.; Batnyam, N.; Oh, S. RFS: Efficient feature selection method based on R-value. Comput. Biol. Med. 2013, 43, 91–99. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.; Ali, S.I.; Kim, D.; Hur, T.; Bang, J.; Lee, S.; Kang, B.H.; Hussain, M.; Zhou, F. UEFS: An efficient and comprehensive ensemble-based feature selection methodology to select informative features. PLoS ONE 2018, 13, e0202705. [Google Scholar] [CrossRef] [PubMed]
- Hoque, N.; Singh, M.; Bhattacharyya, D.K. EFS-MI: An ensemble feature selection method for classification. Complex Intell. Syst. 2018, 4, 105–118. [Google Scholar] [CrossRef]
- Yang, P.; Liu, W.; Zhou, B.B.; Chawla, S.; Zomaya, A.Y. Ensemble-Based Wrapper Methods for Feature Selection and Class Imbalance Learning; Springer: Berlin/Heidelberg, Germany, 2013; pp. 544–555. [Google Scholar]
- Lin, X.; Yang, F.; Zhou, L.; Yin, P.; Kong, H.; Xing, W.; Lu, X.; Jia, L.; Wang, Q.; Xu, G. A support vector machine-recursive feature elimination feature selection method based on artificial contrast variables and mutual information. J. Chromatogr. B 2012, 910, 149–155. [Google Scholar] [CrossRef] [PubMed]
- Fu, G.H.; Wu, Y.J.; Zong, M.J.; Yi, L.Z. Feature selection and classification by minimizing overlap degree for class-imbalanced data in metabolomics. Chemom. Intell. Lab. Syst. 2020, 196, 103906. [Google Scholar] [CrossRef]
- Sen, P. Estimates of the regression coefficient based on Kendall’s tau. J. Am. Stat. Assoc. 1968, 63, 1379–1389. [Google Scholar] [CrossRef]
- Fu, G.H.; Xu, F.; Zhang, B.Y.; Yi, L.Z. Stable variable selection of class-imbalanced data with precision-recall criterion. Chemom. Intell. Lab. Syst. 2017, 171, 241–250. [Google Scholar] [CrossRef]
- Takaya, S.; Marc, R.; Guy, B. The Precision-Recall Plot Is More Informative than the ROC Plot When Evaluating Binary Classifiers on Imbalanced Datasets. PLoS ONE 2015, 10, e0118432. [Google Scholar]
- Yun, Y.H.; Deng, B.C.; Cao, D.S.; Wang, W.T.; Liang, Y.Z. Variable importance analysis based on rank aggregation with applications in metabolomics for biomarker discovery. Anal. Chim. Acta 2016, 911, 27–34. [Google Scholar] [CrossRef]
- Weston, J.; Mukherjee, S.; Chapelle, O. Feature selection for SVMs. In Proceedings of the Advances in Neural information Processing Systems, Vancouver, BC, Canada, 3–8 December 2001; pp. 668–674. [Google Scholar]
- Kailath, T. The Divergence and Bhattacharyya Distance Measures in Signal Selection. IEEE Trans. Commun. Technol. 1967, 15, 52–60. [Google Scholar] [CrossRef]
- Fu, G.H.; Wu, Y.J.; Zong, M.J.; Pan, J. Hellinger distance-based stable sparse feature selection for high-dimensional class-imbalanced data. BMC Bioinform. 2020, 21, 121. [Google Scholar] [CrossRef]
- Robnik-Šikonja, M.; Kononenko, I. Theoretical and Empirical Analysis of ReliefF and RReliefF. Mach. Learn. 2003, 53, 23–69. [Google Scholar] [CrossRef]
- Kononenko, I. Estimating attributes: Analysis and extensions of RELIEF. In European Conference on Machine Learning; Springer: Berlin/Heidelberg, Germany, 1994; pp. 171–182. [Google Scholar]
- Yang, Y.; Pedersen, J. A comparative study on feature selection in text categorization. Icml 1997, 97, 35. [Google Scholar]
- Shang, W.; Huang, H.; Zhu, H.; Lin, Y.; Qu, Y.; Wang, Z. A novel feature selection algorithm for text categorization. Expert Syst. Appl. 2007, 33, 1–5. [Google Scholar] [CrossRef]
- Borsos, Z.; Lemnaru, C.; Potolea, R. Dealing with overlap and imbalance: A new metric and approach. Pattern Anal. Appl. 2018, 21, 381–395. [Google Scholar] [CrossRef]
- Oh, S. A new dataset evaluation method based on category overlap. Comput. Biol. Med. 2011, 41, 115–122. [Google Scholar] [CrossRef]
- Provost, F.; Fawcett, T. Robust classification for imprecise environments. Mach. Learn. 2001, 42, 203–231. [Google Scholar] [CrossRef]
- Davis, J.; Goadrich, M. The relationship between Precision-Recall and ROC curves. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006; pp. 233–240. [Google Scholar]
- Fu, G.H.; Yi, L.Z.; Pan, J. Tuning model parameters in class-imbalanced learning with precision-recall curve. Biom. J. 2019, 61, 652–664. [Google Scholar] [CrossRef]
- Kendall, M.G. A New Measure of Rank Correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Shieh, G. A weighted Kendall’s tau statistic. Stat. Probab. Lett. 1998, 39, 17–24. [Google Scholar] [CrossRef]
- Pihur, V. Statistical Methods for High-Dimensional Genomics Data Analysis; University of Louisville: Louisville, KY, USA, 2009. [Google Scholar]
- Pihur, V.; Datta, S.; Datta, S. RankAggreg, an R package for weighted rank aggregation. BMC Bioinform. 2009, 10, 62. [Google Scholar] [CrossRef]
- Pihur, V.; Datta, S.; Datta, S. Weighted rank aggregation of cluster validation measures: A Monte Carlo cross-entropy approach. Bioinformatics 2007, 23, 1607–1615. [Google Scholar] [CrossRef]
- Pihur, V.; Datta, S.; Datta, S. Finding common genes in multiple cancer types through meta–analysis of microarray experiments: A rank aggregation approach. Genomics 2008, 92, 400–403. [Google Scholar] [CrossRef] [PubMed]
- Menardi, G.; Torelli, N. Training and assessing classification rules with imbalanced data. Data Min. Knowl. Discov. 2014, 28, 92–122. [Google Scholar] [CrossRef]
- Fu, G.H.; Yi, L.Z.; Pan, J. LASSO-based false-positive selection for class-imbalanced data in metabolomics. J. Chemom. 2019, 33. [Google Scholar] [CrossRef]
- Fu, G.H.; Zhang, B.Y.; Kou, H.D.; Yi, L.Z. Stable biomarker screening and classification by subsampling-based sparse regularization coupled with support vector machines in metabolomics. Chemom. Intell. Lab. Syst. 2017, 160, 22–31. [Google Scholar] [CrossRef]
- Ma, S.S.; Zhang, B.Y.; Chen, L.; Zhang, X.J.; Ren, D.B.; Yi, L.Z. Discrimination of Acori Tatarinowii Rhizoma from two habitats based on GC-MS fingerprinting and LASSO-PLS-DA. J. Cent. South Univ. 2018, 25, 1063–1075. [Google Scholar] [CrossRef]
- Fernández, A.; García, S.; Galar, M.; Prati, R.C.; Krawczyk, B.; Herrera, F. Dimensionality Reduction for Imbalanced Learning. In Learning from Imbalanced Data Sets; Springer: Cham, Switzerland, 2018; pp. 227–251. [Google Scholar] [CrossRef]

| Dataset | Resampling | No. | RA | RAR | t Test | Fisher | Hellinger | Relief | ReliefF | IG | Gini | R-Value |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NPC | Case 1 | 7 | 1.00 | − | 0.87 | 0.97 | 0.95 | 0.95 | 0.95 | 0.95 | 1.00 | 0.92 |
| TBI | Case 1 | 6 | 0.96 | − | 0.41 | 0.68 | 0.68 | 0.70 | 0.88 | 0.72 | 0.58 | 0.63 |
| Case 2 | 11 | − | 1.00 | 0.84 | 0.88 | 0.95 | 0.90 | 0.94 | 0.86 | 0.90 | 0.90 | |
| Case 3 | 1 | − | 1.00 | 0.95 | 0.84 | 0.95 | 0.90 | 0.80 | 0.95 | 0.90 | 1.00 | |
| Case 4 | 10 | − | 1.00 | 0.96 | 1.00 | 0.89 | 0.93 | 0.97 | 0.93 | 0.85 | 1.00 | |
| Case 5 | 7 | − | 1.00 | 0.93 | 0.90 | 0.97 | 0.97 | 0.93 | 0.97 | 0.86 | 0.93 | |
| Case 6 | 12 | − | 1.00 | 0.75 | 0.83 | 0.82 | 0.83 | 0.91 | 0.85 | 0.71 | 1.00 | |
| Case 7 | 29 | − | 1.00 | 0.71 | 0.70 | 0.65 | 0.82 | 0.85 | 0.78 | 0.71 | 0.71 | |
| CHD2-1 | Case 1 | 10 | 0.87 | − | 0.67 | 0.71 | 0.87 | 0.00 | 0.77 | 0.77 | 0.47 | 0.87 |
| Case 2 | 11 | − | 0.94 | 0.85 | 0.85 | 1.00 | 0.87 | 0.93 | 0.94 | 0.85 | 0.91 | |
| Case 3 | 6 | − | 1.00 | 0.86 | 1.00 | 1.00 | 1.00 | 0.93 | 1.00 | 0.93 | 1.00 | |
| Case 4 | 31 | − | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.95 | 1.00 | |
| Case 5 | 37 | − | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Case 6 | 11 | − | 0.87 | 0.61 | 0.75 | 0.87 | 0.87 | 0.89 | 0.87 | 0.50 | 0.87 | |
| Case 7 | 10 | − | 0.87 | 0.61 | 0.71 | 0.87 | 0.87 | 0.87 | 0.87 | 0.71 | 0.71 | |
| CHD2-2 | Case 1 | 3 | 0.58 | − | 0.48 | 0.58 | 0.48 | 0.58 | 0.55 | 0.68 | 0.00 | 0.73 |
| Case 2 | 34 | − | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Case 3 | 14 | − | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Case 4 | 24 | − | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Case 5 | 28 | − | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Case 6 | 7 | − | 1.00 | 1.00 | 0.82 | 0.82 | 1.00 | 0.82 | 0.82 | 0.47 | 0.82 | |
| Case 7 | 4 | − | 0.86 | 0.82 | 1.00 | 0.82 | 1.00 | 0.61 | 1.00 | 0.00 | 0.75 | |
| ATR | Case 1 | 25 | 1.00 | − | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.50 | 1.00 |
| Case 2 | 9 | − | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Case 3 | 8 | − | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Case 4 | 2 | − | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.89 | 1.00 | |
| Case 5 | 2 | − | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.80 | 1.00 | |
| Case 6 | 9 | − | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.71 | 1.00 | |
| Case 7 | 10 | − | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| Dataset | Resampling | NO. | RA | RAR | t Test | Fisher | Hellinger | Relief | ReliefF | IG | Gini | R-Value |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NPC | Case 1 | 8 | 1.00 | − | 0.88 | 0.95 | 0.95 | 0.97 | 1.00 | 0.95 | 0.95 | 0.92 |
| TBI | Case 1 | 11 | 0.93 | − | 0.82 | 0.86 | 0.87 | 0.90 | 0.90 | 0.88 | 0.83 | 0.88 |
| Case 2 | 13 | − | 1.00 | 0.84 | 0.90 | 0.94 | 0.95 | 0.94 | 0.84 | 0.87 | 0.86 | |
| Case 3 | 1 | − | 1.00 | 0.87 | 0.87 | 1.00 | 1.00 | 0.96 | 0.95 | 0.83 | 1.00 | |
| Case 4 | 7 | − | 1.00 | 0.91 | 0.97 | 0.93 | 0.97 | 0.90 | 0.93 | 0.89 | 1.00 | |
| Case 5 | 10 | − | 1.00 | 0.87 | 0.93 | 0.93 | 0.93 | 0.93 | 0.97 | 0.88 | 0.93 | |
| Case 6 | 19 | − | 1.00 | 0.73 | 0.80 | 0.86 | 0.86 | 0.77 | 0.80 | 0.71 | 0.91 | |
| Case 7 | 11 | − | 1.00 | 0.83 | 0.92 | 0.80 | 0.86 | 0.86 | 0.75 | 0.50 | 0.86 | |
| CHD2-1 | Case 1 | 10 | 0.88 | − | 0.87 | 0.88 | 0.87 | 0.87 | 0.87 | 0.87 | 0.83 | 0.87 |
| Case 2 | 11 | − | 0.94 | 0.94 | 0.71 | 0.93 | 0.89 | 0.93 | 0.88 | 0.67 | 0.89 | |
| Case 3 | 6 | − | 1.00 | 0.89 | 1.00 | 1.00 | 1.00 | 0.93 | 0.94 | 0.94 | 0.92 | |
| Case 4 | 31 | − | 1.00 | 0.95 | 0.95 | 0.96 | 0.90 | 0.96 | 0.90 | 0.86 | 0.95 | |
| Case 5 | 37 | − | 1.00 | 1.00 | 0.91 | 0.95 | 0.95 | 1.00 | 0.95 | 0.86 | 0.95 | |
| Case 6 | 11 | − | 0.89 | 0.50 | 0.75 | 0.73 | 0.89 | 1.00 | 0.83 | 0.55 | 0.67 | |
| Case 7 | 10 | − | 0.86 | 0.73 | 0.57 | 0.80 | 0.75 | 0.86 | 0.67 | 0.55 | 0.57 | |
| CHD2-2 | Case 1 | 3 | 0.91 | − | 0.87 | 0.86 | 0.95 | 0.87 | 0.91 | 0.90 | 0.87 | 0.91 |
| Case 2 | 34 | − | 1.00 | 1.00 | 1.00 | 0.88 | 0.92 | 0.93 | 1.00 | 0.88 | 0.93 | |
| Case 3 | 14 | − | 1.00 | 1.00 | 0.92 | 0.86 | 0.92 | 1.00 | 0.93 | 0.86 | 0.93 | |
| Case 4 | 24 | − | 1.00 | 0.90 | 0.91 | 0.95 | 0.95 | 0.95 | 1.00 | 0.95 | 0.95 | |
| Case 5 | 28 | − | 1.00 | 0.95 | 0.95 | 0.95 | 0.95 | 1.00 | 0.96 | 0.95 | 1.00 | |
| Case 6 | 7 | − | 0.86 | 0.57 | 0.80 | 0.80 | 0.75 | 0.86 | 0.86 | 0.50 | 0.86 | |
| Case 7 | 4 | − | 0.86 | 0.80 | 0.75 | 0.57 | 0.86 | 0.86 | 0.86 | 0.50 | 0.67 | |
| ATR | Case 1 | 25 | 1.00 | − | 1.00 | 0.89 | 1.00 | 1.00 | 1.00 | 1.00 | 0.89 | 1.00 |
| Case 2 | 9 | − | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Case 3 | 8 | − | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Case 4 | 2 | − | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.89 | 1.00 | |
| Case 5 | 2 | − | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | |
| Case 6 | 9 | − | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.67 | 1.00 | |
| Case 7 | 10 | − | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 0.67 | 1.00 |
| Dataset | Resampling | NO. | RA | RAR | t Test | Fisher | Hellinger | Relief | ReliefF | IG | Gini | R-Value |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NPC | Case 1 | 16 | 0.96 | − | 0.90 | 0.91 | 0.94 | 0.93 | 0.96 | 0.93 | 0.93 | 0.95 |
| TBI | Case 1 | 3 | 0.70 | − | 0.48 | 0.61 | 0.52 | 0.61 | 0.65 | 0.58 | 0.49 | 0.67 |
| Case 2 | 11 | − | 0.89 | 0.80 | 0.81 | 0.78 | 0.82 | 0.87 | 0.79 | 0.72 | 0.83 | |
| Case 3 | 1 | − | 0.95 | 0.83 | 0.74 | 0.94 | 0.85 | 0.83 | 0.85 | 0.76 | 0.95 | |
| Case 4 | 28 | − | 0.91 | 0.85 | 0.86 | 0.87 | 0.88 | 0.86 | 0.86 | 0.84 | 0.89 | |
| Case 5 | 26 | − | 0.93 | 0.91 | 0.92 | 0.90 | 0.90 | 0.92 | 0.90 | 0.88 | 0.90 | |
| Case 6 | 22 | − | 0.77 | 0.65 | 0.68 | 0.69 | 0.73 | 0.74 | 0.73 | 0.50 | 0.71 | |
| Case 7 | 25 | − | 0.71 | 0.63 | 0.56 | 0.68 | 0.53 | 0.61 | 0.61 | 0.35 | 0.66 | |
| CHD2-1 | Case 1 | 10 | 0.60 | − | 0.48 | 0.51 | 0.61 | 0.50 | 0.59 | 0.60 | 0.45 | 0.59 |
| Case 2 | 11 | − | 0.76 | 0.66 | 0.60 | 0.75 | 0.77 | 0.73 | 0.72 | 0.61 | 0.73 | |
| Case 3 | 6 | − | 0.92 | 0.85 | 0.81 | 0.92 | 0.90 | 0.81 | 0.88 | 0.80 | 0.79 | |
| Case 4 | 31 | − | 0.86 | 0.81 | 0.79 | 0.86 | 0.87 | 0.82 | 0.84 | 0.75 | 0.84 | |
| Case 5 | 37 | − | 0.87 | 0.85 | 0.84 | 0.86 | 0.86 | 0.81 | 0.86 | 0.90 | 0.82 | |
| Case 6 | 11 | − | 0.64 | 0.57 | 0.45 | 0.50 | 0.57 | 0.57 | 0.64 | 0.36 | 0.62 | |
| Case 7 | 10 | − | 0.60 | 0.52 | 0.55 | 0.52 | 0.48 | 0.52 | 0.60 | 0.36 | 0.52 | |
| CHD2-2 | Case 1 | 3 | 0.60 | − | 0.52 | 0.49 | 0.54 | 0.50 | 0.52 | 0.55 | 0.39 | 0.57 |
| Case 2 | 34 | − | 0.86 | 0.79 | 0.84 | 0.88 | 0.73 | 0.80 | 0.80 | 0.70 | 0.79 | |
| Case 3 | 14 | − | 0.90 | 0.85 | 0.84 | 0.82 | 0.90 | 0.68 | 0.88 | 0.81 | 0.84 | |
| Case 4 | 24 | − | 0.93 | 0.88 | 0.88 | 0.88 | 0.90 | 0.86 | 0.91 | 0.87 | 0.93 | |
| Case 5 | 28 | − | 0.91 | 0.88 | 0.90 | 0.88 | 0.85 | 0.91 | 0.89 | 0.89 | 0.90 | |
| Case 6 | 7 | − | 0.63 | 0.53 | 0.56 | 0.66 | 0.59 | 0.44 | 0.56 | 0.28 | 0.59 | |
| Case 7 | 4 | − | 0.66 | 0.56 | 0.63 | 0.50 | 0.66 | 0.66 | 0.63 | 0.22 | 0.56 | |
| ATR | Case 1 | 25 | 0.88 | 0.98 | − | 0.51 | 0.85 | 0.85 | 0.76 | 0.85 | 0.50 | 0.76 |
| Case 2 | 9 | − | 0.96 | 0.79 | 0.86 | 0.96 | 0.96 | 0.93 | 0.96 | 0.75 | 0.93 | |
| Case 3 | 8 | − | 0.97 | 1.00 | 0.90 | 0.97 | 0.90 | 0.97 | 0.97 | 0.80 | 0.93 | |
| Case 4 | 2 | − | 0.98 | 0.93 | 0.83 | 0.88 | 0.98 | 0.95 | 0.98 | 0.81 | 0.95 | |
| Case 5 | 2 | − | 0.98 | 0.81 | 0.86 | 0.76 | 0.93 | 0.93 | 0.95 | 0.71 | 0.88 | |
| Case 6 | 9 | − | 0.94 | 0.81 | 0.75 | 0.88 | 0.94 | 0.88 | 0.81 | 0.19 | 0.81 | |
| Case 7 | 10 | − | 0.94 | 0.81 | 0.63 | 0.69 | 0.63 | 0.94 | 0.88 | 0.19 | 0.75 |
| Dataset | Resampling | NO. | RA | RAR | t Test | Fisher | Hellinger | Relief | ReliefF | IG | Gini | R-Value |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NPC | Case 1 | 15 | 0.96 | − | 0.87 | 0.90 | 0.91 | 0.92 | 0.96 | 0.92 | 0.91 | 0.91 |
| TBI | Case 1 | 8 | 0.62 | − | 0.27 | 0.58 | 0.40 | 0.47 | 0.56 | 0.47 | 0.26 | 0.46 |
| Case 2 | 18 | − | 0.85 | 0.79 | 0.81 | 0.78 | 0.86 | 0.84 | 0.81 | 0.65 | 0.75 | |
| Case 3 | 1 | − | 0.93 | 0.77 | 0.60 | 0.91 | 0.85 | 0.74 | 0.85 | 0.74 | 0.89 | |
| Case 4 | 27 | − | 0.89 | 0.84 | 0.81 | 0.83 | 0.85 | 0.86 | 0.83 | 0.81 | 0.85 | |
| Case 5 | 13 | − | 0.91 | 0.81 | 0.82 | 0.81 | 0.82 | 0.90 | 0.86 | 0.79 | 0.81 | |
| Case 6 | 30 | − | 0.78 | 0.61 | 0.69 | 0.64 | 0.62 | 0.66 | 0.67 | 0.50 | 0.70 | |
| Case 7 | 24 | − | 0.71 | 0.65 | 0.54 | 0.64 | 0.59 | 0.57 | 0.62 | 0.41 | 0.58 | |
| CHD2-1 | Case 1 | 10 | 0.61 | − | 0.33 | 0.30 | 0.52 | 0.28 | 0.45 | 0.43 | 0.23 | 0.45 |
| Case 2 | 11 | − | 0.77 | 0.56 | 0.58 | 0.69 | 0.65 | 0.64 | 0.68 | 0.55 | 0.65 | |
| Case 3 | 6 | − | 0.88 | 0.79 | 0.88 | 0.81 | 0.77 | 0.81 | 0.86 | 0.79 | 0.86 | |
| Case 4 | 31 | − | 0.86 | 0.81 | 0.80 | 0.80 | 0.82 | 0.83 | 0.85 | 0.73 | 0.80 | |
| Case 5 | 37 | − | 0.87 | 0.81 | 0.75 | 0.84 | 0.85 | 0.82 | 0.84 | 0.78 | 0.82 | |
| Case 6 | 11 | − | 0.66 | 0.46 | 0.45 | 0.48 | 0.65 | 0.53 | 0.55 | 0.40 | 0.50 | |
| Case 7 | 10 | − | 0.63 | 0.44 | 0.53 | 0.52 | 0.55 | 0.56 | 0.56 | 0.40 | 0.48 | |
| CHD2-2 | Case 1 | 3 | 0.45 | − | 0.22 | 0.33 | 0.27 | 0.32 | 0.31 | 0.27 | 0.21 | 0.26 |
| Case 2 | 34 | − | 0.87 | 0.68 | 0.78 | 0.76 | 0.82 | 0.85 | 0.86 | 0.73 | 0.80 | |
| Case 3 | 14 | − | 0.87 | 0.81 | 0.74 | 0.81 | 0.86 | 0.76 | 0.83 | 0.79 | 0.78 | |
| Case 4 | 24 | − | 0.91 | 0.84 | 0.90 | 0.87 | 0.85 | 0.85 | 0.87 | 0.85 | 0.81 | |
| Case 5 | 28 | − | 0.90 | 0.86 | 0.88 | 0.80 | 0.88 | 0.86 | 0.89 | 0.79 | 0.79 | |
| Case 6 | 7 | − | 0.71 | 0.42 | 0.62 | 0.64 | 0.66 | 0.45 | 0.57 | 0.35 | 0.63 | |
| Case 7 | 4 | − | 0.64 | 0.64 | 0.57 | 0.50 | 0.63 | 0.55 | 0.66 | 0.40 | 0.60 | |
| ATR | Case 1 | 25 | 0.93 | − | 0.75 | 0.52 | 0.52 | 0.82 | 0.82 | 0.82 | 0.25 | 0.60 |
| Case 2 | 9 | − | 1.00 | 0.81 | 0.88 | 0.92 | 0.94 | 0.94 | 0.94 | 0.68 | 0.88 | |
| Case 3 | 8 | − | 1.00 | 1.00 | 0.78 | 1.00 | 0.88 | 0.93 | 1.00 | 0.82 | 0.88 | |
| Case 4 | 2 | − | 0.95 | 0.84 | 0.79 | 0.91 | 0.91 | 0.88 | 0.91 | 0.70 | 0.91 | |
| Case 5 | 2 | − | 0.95 | 0.79 | 0.78 | 0.78 | 0.88 | 0.90 | 0.95 | 0.61 | 0.88 | |
| Case 6 | 9 | − | 1.00 | 0.89 | 0.69 | 0.85 | 0.89 | 0.76 | 0.85 | 0.36 | 0.80 | |
| Case 7 | 10 | − | 1.00 | 0.61 | 0.54 | 0.64 | 0.54 | 0.80 | 0.89 | 0.37 | 0.80 |
| Datasets | Attributes | Instances | Majority | Minority | Ratio |
|---|---|---|---|---|---|
| NPC | 24 | 200 | 100 | 100 | 1.00 |
| TBI | 42 | 104 | 73 | 31 | 2.35 |
| CHD2-1 | 50 | 72 | 51 | 21 | 2.43 |
| CHD2-2 | 50 | 67 | 51 | 16 | 3.19 |
| ATR | 104 | 29 | 21 | 8 | 2.63 |
| Methods | Re-Sampling Process | Algorithm Process | ||||
|---|---|---|---|---|---|---|
| Under-Sampling | Over-Sampling | Hybrid | SMOTE | Random | Smoothed Bootstrap | |
| Case 2 | Yes | Yes | ||||
| Case 3 | Yes | Yes | ||||
| Case 4 | Yes | Yes | ||||
| Case 5 | Yes | Yes | ||||
| Case 6 | Yes | Yes | ||||
| Case 7 | Yes | Yes | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, G.-H.; Wang, J.-B.; Zong, M.-J.; Yi, L.-Z. Feature Ranking and Screening for Class-Imbalanced Metabolomics Data Based on Rank Aggregation Coupled with Re-Balance. Metabolites 2021, 11, 389. https://doi.org/10.3390/metabo11060389
Fu G-H, Wang J-B, Zong M-J, Yi L-Z. Feature Ranking and Screening for Class-Imbalanced Metabolomics Data Based on Rank Aggregation Coupled with Re-Balance. Metabolites. 2021; 11(6):389. https://doi.org/10.3390/metabo11060389
Chicago/Turabian StyleFu, Guang-Hui, Jia-Bao Wang, Min-Jie Zong, and Lun-Zhao Yi. 2021. "Feature Ranking and Screening for Class-Imbalanced Metabolomics Data Based on Rank Aggregation Coupled with Re-Balance" Metabolites 11, no. 6: 389. https://doi.org/10.3390/metabo11060389
APA StyleFu, G.-H., Wang, J.-B., Zong, M.-J., & Yi, L.-Z. (2021). Feature Ranking and Screening for Class-Imbalanced Metabolomics Data Based on Rank Aggregation Coupled with Re-Balance. Metabolites, 11(6), 389. https://doi.org/10.3390/metabo11060389






