Model Balancing: A Search for In-Vivo Kinetic Constants and Consistent Metabolic States
Abstract
:1. Introduction
2. Materials and Methods
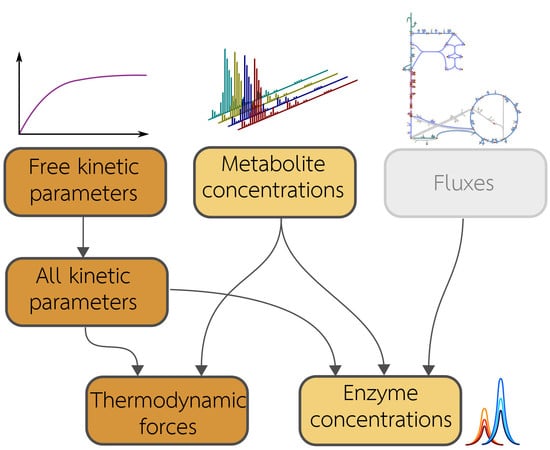
2.1. Metabolic Model and Statistical Estimation Model
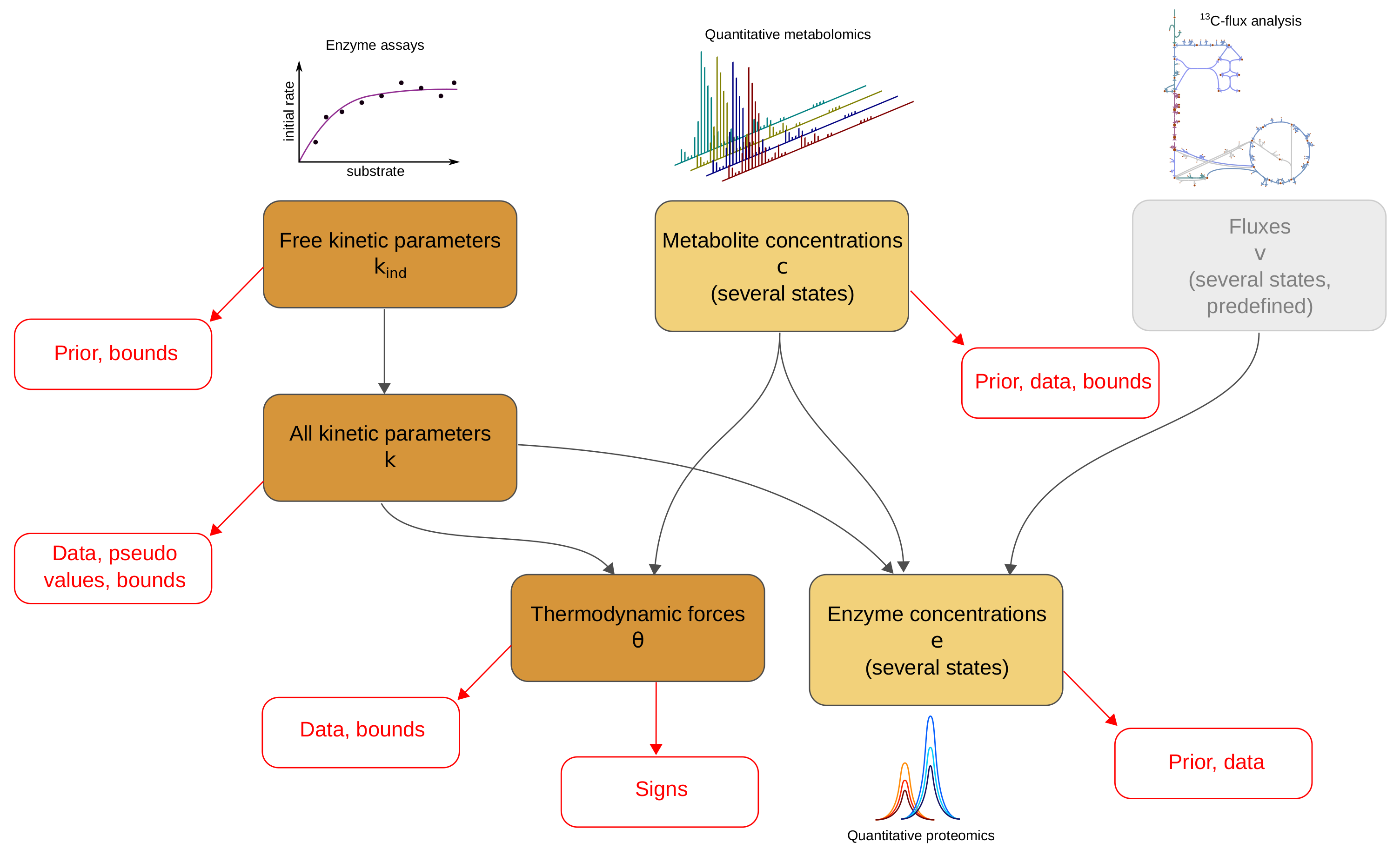
2.2. Model Balancing
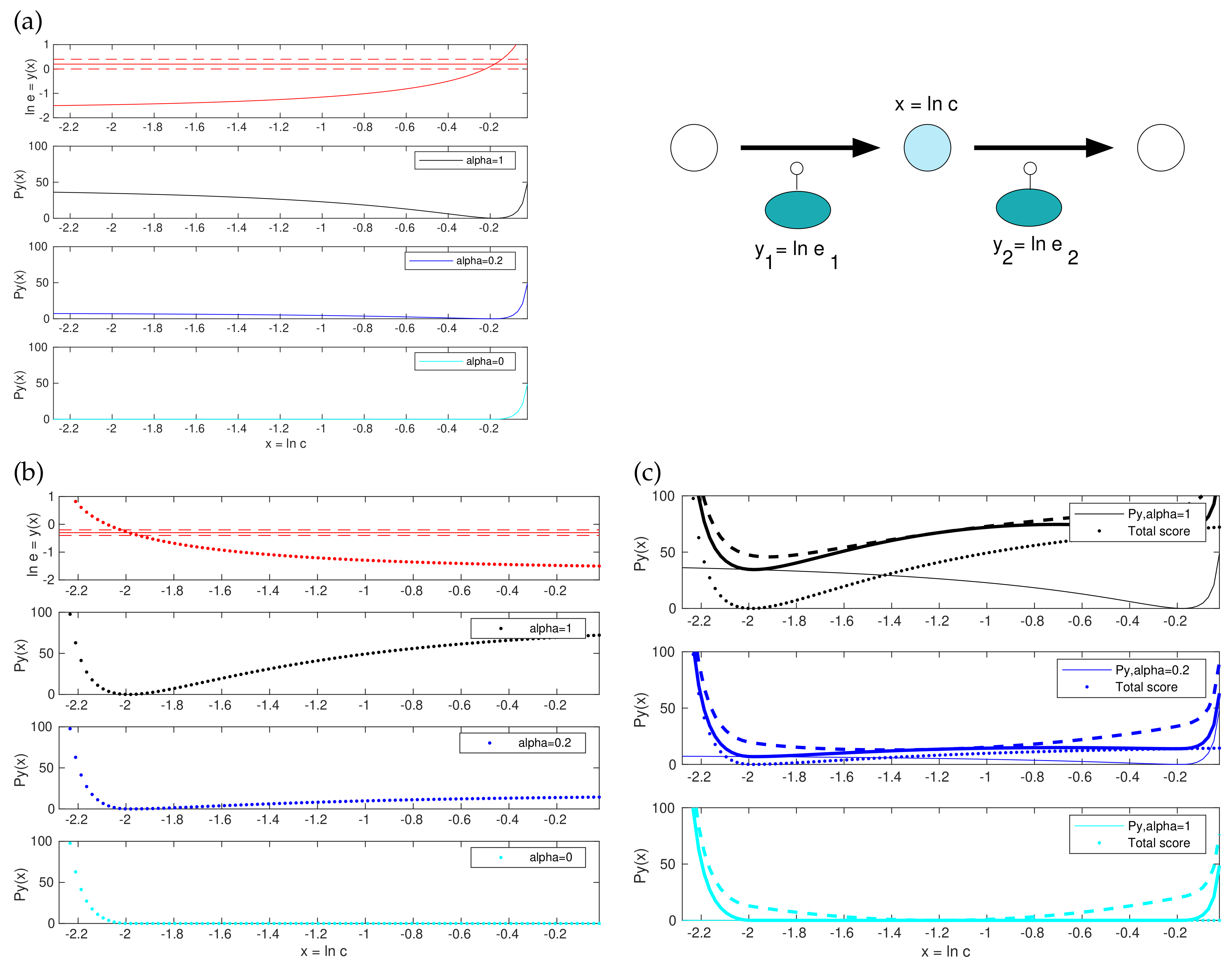
2.3. A Convex Version of the Score Functions
2.4. Details and Variants of Model Balancing
3. Results
3.1. Model Balancing
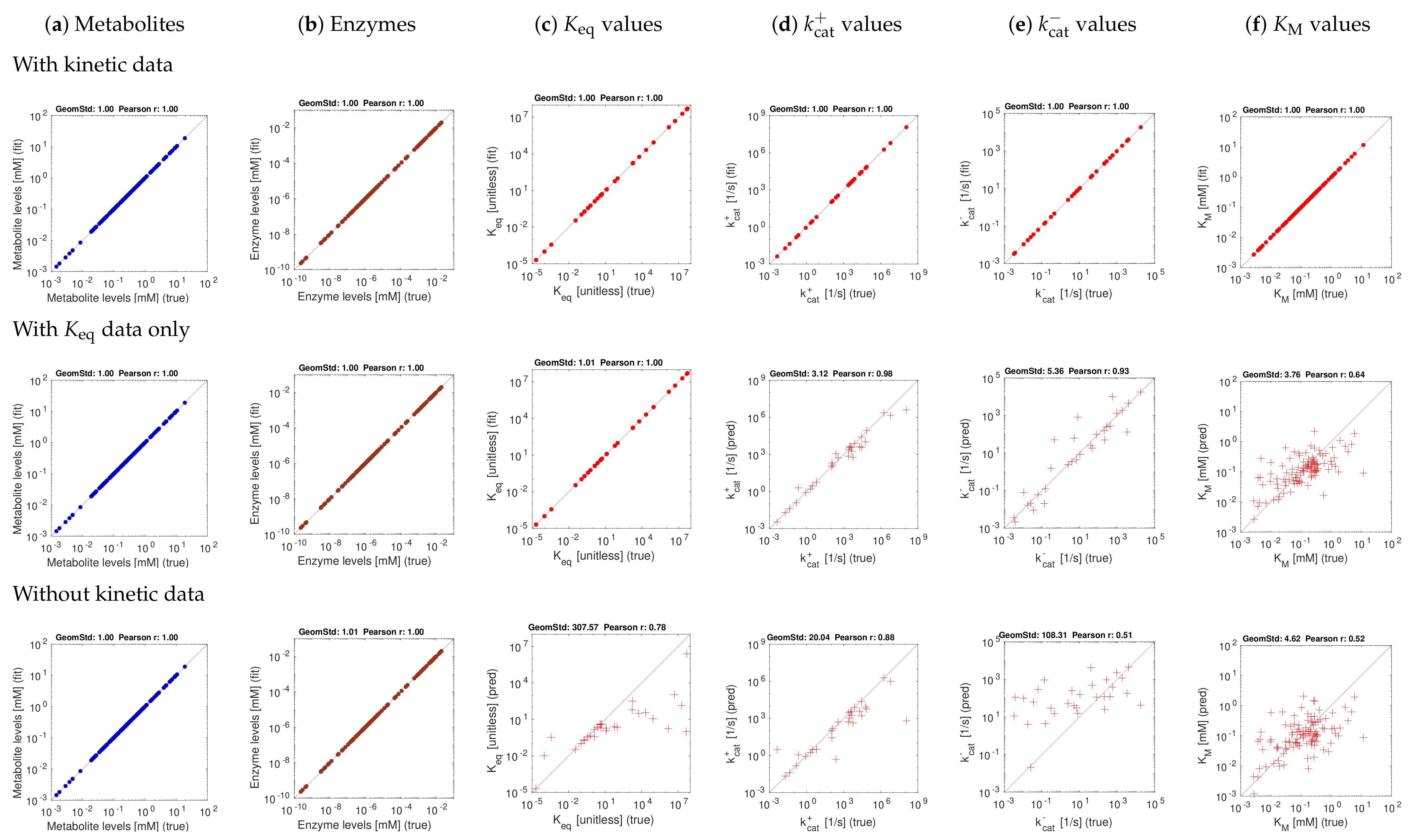
3.2. Tests with Artificial Data
3.3. Model Fitting with Experimentally Measured Data
4. Discussion
4.1. Model Balancing in Relation to Other Methods
- Parameter balancing. Parameter balancing determines consistent kinetic constants from kinetic and thermodynamic data. Unlike model balancing, it does not use rate laws or flux data. All multiplicative constants (such as Michaelis–Menten constants or catalytic constants) are described by log-values, which leads to a linear regression problem. The equilibrium constants are parameterised directly by standard chemical potentials rather than independent variables that can be adjusted if needed [24]. With Gaussian priors and measurement errors (in log-scale), likelihood and posterior terms are quadratic and convex. Parameter balancing can handle either kinetic and thermodynamic constants (“kinetic parameter balancing”), metabolite concentrations and thermodynamic forces (“state balancing”), or kinetic constants and metabolic states (“state/parameter balancing”). With known signs of thermodynamic forces, defined by the flux directions, parameter balancing can predict thermodynamically feasible kinetic constants and metabolite concentrations. While its optimisation takes place on the same set as in model balancing, it does not consider rate laws and cannot be used to fit kinetic constants to flux data. As a post-processing step, balanced kinetic constants can be adjusted to rate laws and flux data, but this works only for a single metabolic state so, unlike in model balancing, data from multiple states cannot be combined.
- Enzyme cost minimisation. Enzyme cost minimisation (ECM) [43] predicts optimal enzyme and metabolite concentrations in kinetic models with given parameter values. ECM determines metabolite and enzyme concentrations that realise predefined fluxes at a minimal cost, for instance, at a minimal total enzyme and metabolite concentration. The optimisation is carried out in (log-)metabolite space. In contrast to parameter balancing, ECM assumes given kinetic constants and optimises a biological cost rather than a goodness of fit. With given rate laws, the cost function (a weighted sum of enzyme and metabolite concentrations) is convex in log-metabolite space.
4.2. Model Balancing in Practice
- Inferring missing data types If fluxes and two of the data types are given, the third type can be estimated. For example, we may estimate in-vivo kinetic constants from metabolite concentrations and enzyme concentrations; we may estimate metabolite concentrations from enzyme concentrations and enzyme kinetics; or we may estimate enzyme concentrations from metabolite concentrations and enzyme kinetics. If the data were complete and precise, the third type of variables could be directly computed, and model balancing would not be necessary. But when data are uncertain and incomplete, model balancing allows us to infer the missing data while completing and adjusting the others.
- Adjusting omics data to obtain complete, consistent metabolic states Given a model with known kinetic constants, we can translate metabolite and enzyme data into complete, consistent metabolic states. Again, fluxes must be given and thermodynamically realisable with the assumed equilibrium constants and metabolite bounds. We can even estimate metabolic states without any enzyme or metabolite data: in this case, model balancing predicts plausible states with the given fluxes, relying on priors for enzyme or metabolite concentrations.
- Imposing thermodynamic constraints and bounds on data To build consistent metabolic models, we may collect data for kinetic and state variables and apply model balancing. The resulting kinetic constants and state variables satisfy the rate laws, agree with physical and physiological constraints, and resemble data and prior values. Above we used this to construct a physically and biologically plausible model of E. coli central metabolism. Posterior sampling (as in [16]) might be used to assess uncertainties in model parameters.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ECM | Enzyme Cost Minimisation |
| FBA | Flux Balance Analysis |
References
- Liebermeister, W.; Klipp, E. Bringing metabolic networks to life: Convenience rate law and thermodynamic constraints. Theor. Biol. Med. Mod. 2006, 3, 41. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jamshidi, N.; Palsson, B. Formulating genome-scale kinetic models in the post-genome era. Mol. Syst. Biol. 2008, 4, 171. [Google Scholar] [CrossRef] [PubMed]
- Yizhak, K.; Benyamini, T.; Liebermeister, W.; Ruppin, E.; Shlomi, T. Integrating quantitative proteomics and metabolomics with a genome-scale metabolic network model. Bioinformatics 2010, 26, i255–i260. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Soh, K.; Miskovic, L.; Hatzimanikatis, V. From network models to network responses: Integration of thermodynamic and kinetic properties of yeast genome-scale metabolic networks. FEMS Yeast Res. 2012, 12, 129–143. [Google Scholar] [CrossRef] [Green Version]
- Stanford, N.; Lubitz, T.; Smallbone, K.; Klipp, E.; Mendes, P.; Liebermeister, W. Systematic construction of kinetic models from genome-scale metabolic networks. PLoS ONE 2013, 8, e79195. [Google Scholar]
- Liebermeister, W.; Uhlendorf, J.; Klipp, E. Modular rate laws for enzymatic reactions: Thermodynamics, elasticities, and implementation. Bioinformatics 2010, 26, 1528–1534. [Google Scholar] [CrossRef]
- Büchel, F.; Rodriguez, N.; Swainston, N.; Wrzodek, C.; Czauderna, T.; Keller, R.; Mittag, F.; Schubert, M.; Glont, M.; Golebiewski, M.; et al. Path2Models: Large-scale generation of computational models from biochemical pathway maps. BMC Syst. Biol. 2013, 7, 116. [Google Scholar] [CrossRef] [Green Version]
- Du, B.; Zielinski, D.; Kavvas, E.; Dräger, A.; Tan, J.; Zhang, Z.; Ruggiero, K.; Arzumanyan, G.; Palsson, B. Evaluation of rate law approximations in bottom-up kinetic models of metabolism. BMC Syst. Biol. 2016, 10, 40. [Google Scholar] [CrossRef] [Green Version]
- Teusink, B.; Passarge, J.; Reijenga, C.; Esgalhado, E.; van der Weijden, C.; Schepper, M.; Walsh, M.; Bakker, B.; van Dam, K.; Westerhoff, H.; et al. Can yeast glycolysis be understood in terms of in vitro kinetics of the constituent enzymes? Testing biochemistry. Eur. J. Biochem. 2000, 267, 5313–5329. [Google Scholar] [CrossRef]
- Smallbone, K.; Messiha, H.L.; Carroll, K.M.; Winder, C.L.; Malys, N.; Dunn, W.B.; Murabito, E.; Swainston, N.; Dada, J.O.; Khan, F.; et al. A model of yeast glycolysis based on a consistent kinetic characterisation of all its enzymes. FEBS Lett. 2013, 587, 2832–2841. [Google Scholar] [CrossRef]
- Schomburg, I.; Chang, A.; Ebeling, C.; Gremse, M.; Heldt, C.; Huhn, G.; Schomburg, D. BRENDA, the enzyme database: Updates and major new developments. Nucleic Acids Res. 2004, 32, D431–D433. [Google Scholar] [CrossRef] [Green Version]
- Bar-Even, A.; Noor, E.; Savir, Y.; Liebermeister, W.; Davidi, D.; Tawfik, D.; Milo, R. The moderately efficient enzyme: Evolutionary and physicochemical trends shaping enzyme parameters. Biochemistry 2011, 21, 4402–4410. [Google Scholar] [CrossRef]
- Heckmann, D.; Lloyd, C.; Mih, N.; Ha, Y.; Zielinski, D.; Haiman, Z.; Desouki, A.A.; Lercher, M.; Palsson, B. Machine learning applied to enzyme turnover numbers reveals protein structural correlates and improves metabolic models. Nat. Commun. 2018, 9, 5252. [Google Scholar] [CrossRef] [Green Version]
- Heijnen, J.J.; Verheijen, P.J.T. Parameter identification of in vivo kinetic models: Limitations and challenges. Biotechnol. J. 2013, 8, 768–775. [Google Scholar] [CrossRef]
- Davidi, D.; Noor, E.; Liebermeister, W.; Bar-Even, A.; Flamholz, A.; Tummler, K.; Barenholz, U.; Goldenfeld, M.; Shlomi, T.; Milo, R. Global characterization of in vivo enzyme catalytic rates and their correspondence to in vitro kcat measurements. Proc. Natl. Aacd. Sci. USA 2016, 113, 3401–3406. [Google Scholar] [CrossRef] [Green Version]
- Hackett, S.; Zanotelli, V.; Xu, W.; Goya, J.; Park, J.; Perlman, D.; Gibney, P.; Botstein, D.; Storey, J.; Rabinowitz, J. Systems-level analysis of mechanisms regulating yeast metabolic flux. Science 2016, 354, aaf2786. [Google Scholar] [CrossRef] [Green Version]
- Ashyraliyev, M.; Fomekong-Nanfack, Y.; Kaandorp, J.; Blom, J. Systems biology: Parameter estimation for biochemical models. FEBS J. 2009, 276, 886–902. [Google Scholar] [CrossRef] [Green Version]
- Villaverde, A.; Froehlich, F.; Weindl, D.; Hasenauer, J.; Banga, J. Benchmarking optimization methods for parameter estimation in large kinetic models. Bioinformatics 2018, 35, 830–838. [Google Scholar] [CrossRef]
- Srinivasan, S.; Cluett, W.; Mahadevan, R. A scalable method for parameter identification in kinetic models of metabolism using steady state data. Bioinformatics 2019, 35, btz445. [Google Scholar] [CrossRef]
- Liebermeister, W.; Klipp, E. Bringing metabolic networks to life: Integration of kinetic, metabolic, and proteomic data. Theor. Biol. Med. Mod. 2006, 3, 42. [Google Scholar] [CrossRef] [Green Version]
- Lubitz, T.; Schulz, M.; Klipp, E.; Liebermeister, W. Parameter balancing for kinetic models of cell metabolism. J. Phys. Chem. B 2010, 114, 16298–16303. [Google Scholar] [CrossRef]
- Saa, P.; Nielsen, L. A General Framework for Thermodynamically Consistent Parameterization and Efficient Sampling of Enzymatic Reactions. PLoS Comput. Biol. 2015, 11, e1004195. [Google Scholar] [CrossRef] [Green Version]
- Mason, J.; Covert, M. An energetic reformulation of kinetic rate laws enables scalable parameter estimation for biochemical networks. J. Theor. Biol. 2019, 461, 145–156. [Google Scholar] [CrossRef]
- Lubitz, T.; Liebermeister, W. Parameter balancing: Consistent parameter sets for kinetic metabolic models. Bioinformatics 2019, 35, 3857–3858. [Google Scholar] [CrossRef]
- Khodayari, A.; Maranas, C. A genome-scale Escherichia coli kinetic metabolic model k-ecoli457 satisfying flux data for multiple mutant strains. Nat. Commun. 2016, 7, 13806. [Google Scholar] [CrossRef]
- Smith, R.; van Rosmalen, R.; dos Santos, V.M.; Fleck, C. DMPy: A Python package for automated mathematical model construction of large-scale metabolic systems. BMC Syst. Biol. 2018, 12, 72. [Google Scholar] [CrossRef]
- Foster, C.; Gopalakrishnan, S.; Antoniewicz, M.; Maranas, C. From Escherichia coli mutant 13C labeling data to a core kinetic model: A kinetic model parameterization pipeline. PLoS Comput. Biol. 2019, 15, e1007319. [Google Scholar] [CrossRef]
- Wang, L.; Birol, I.; Hatzimanikatis, V. Metabolic Control Analysis under Uncertainty: Framework Development and Case Studies. Biophys. J. 2004, 87, 3750–3763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, L.; Hatzimanikatis, V. Metabolic engineering under uncertainty. I: Framework development. Metab. Eng. 2006, 8, 133–141. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Hatzimanikatis, V. Metabolic engineering under uncertainty. II: Analysis of yeast metabolism. Metab. Eng. 2006, 8, 142–159. [Google Scholar] [CrossRef] [PubMed]
- Tran, L.; Rizk, M.; Liao, J. Ensemble Modeling of Metabolic Networks. Biophys. J. 2008, 95, 5606–5617. [Google Scholar] [CrossRef] [Green Version]
- Tan, Y.; Rivera, J.; Contador, C.; Asenjo, J.; Liao, J. Reducing the allowable kinetic space by constructing ensemble of dynamic models with the same steady-state flux. Metab. Eng. 2011, 13, 60–75. [Google Scholar] [CrossRef]
- Christodoulou, D.; Link, H.; Fuhrer, T.; Kochanowski, K.; Gerosa, L.; Sauer, U. Reserve Flux Capacity in the Pentose Phosphate Pathway Enables Escherichia coli’s Rapid Response to Oxidative Stress. Cell Syst. 2018, 6, 569–578. [Google Scholar] [CrossRef] [Green Version]
- Steuer, R.; Gross, T.; Selbig, J.; Blasius, B. Structural kinetic modeling of metabolic networks. Proc. Natl. Acad. Sci. USA 2006, 103, 11868–11873. [Google Scholar] [CrossRef] [Green Version]
- Heckmann, D.; Campeau, A.; Lloyd, C.; Phaneuf, P.; Hefner, Y.; Carrillo-Terrazas, M.; Feist, A.; Gonzalez, D.; Palsson, B. Kinetic profiling of metabolic specialists demonstrates stability and consistency of in vivo enzyme turnover numbers. Proc. Natl. Acad. Sci. USA 2020, 117, 23182. [Google Scholar] [CrossRef]
- Küken, A.; Gennermann, K.; Nikoloski, Z. Characterization of maximal enzyme catalytic rates in central metabolism of Arabidopsis thaliana. Plant J. 2020, 103, 2168–2177. [Google Scholar] [CrossRef]
- Liebermeister, W. Elasticity sampling links thermodynamics to metabolic control. arXiv 2013, arXiv:1309.0267. [Google Scholar]
- Bruck, J.; Liebermeister, W.; Klipp, E. Exploring the effect of variable enzyme concentrations in a kinetic model of yeast glycolysis. In Proceedings of the 8th Annual International Workshop on Bioinformatics and Systems Biology (IBSB 2008), Zeuthen Lake, Berlin, Germany, 9–11 June 2008; Volume 20. [Google Scholar]
- Liebermeister, W. Predicting physiological concentrations of metabolites from their molecular structure. J. Comp. Biol. 2005, 12, 1307–1315. [Google Scholar] [CrossRef] [Green Version]
- Bar-Even, A.; Noor, E.; Flamholz, A.; Buescher, J.; Milo, R. Hydrophobicity and charge shape cellular metabolite concentrations. PLoS Comput. Biol. 2011, 7, e1002166. [Google Scholar] [CrossRef]
- Tepper, N.; Noor, E.; Amador-Noguez, D.; Haraldsdóttir, H.; Milo, R.; Rabinowitz, J.; Liebermeister, W.; Shlomi, T. Steady-state metabolite concentrations reflect a balance between maximizing enzyme efficiency and minimizing total metabolite load. PLoS ONE 2013, 8, e75370. [Google Scholar]
- Flamholz, A.; Noor, E.; Bar-Even, A.; Liebermeister, W.; Milo, R. Glycolytic strategy as a trade-off between energy yield and protein cost. Proc. Natl. Acad. Sci. USA 2013, 110, 10039–10044. [Google Scholar] [CrossRef] [Green Version]
- Noor, E.; Flamholz, A.; Bar-Even, A.; Davidi, D.; Milo, R.; Liebermeister, W. The protein cost of metabolic fluxes: Prediction from enzymatic rate laws and cost minimization. PLoS Comput. Biol. 2016, 12, e1005167. [Google Scholar] [CrossRef]
- Noor, E.; Flamholz, A.; Liebermeister, W.; Bar-Even, A.; Milo, R. A note on the kinetics of enzyme action: A decomposition that highlights thermodynamic effects. FEBS Lett. 2013, 587, 2772–2777. [Google Scholar] [CrossRef] [Green Version]
- Gelman, A.; Carlin, J.B.; Stern, H.S.; Rubin, D. Bayesian Data Analysis; Chapman & Hall: New York, NY, USA, 1997. [Google Scholar]
- Grant, M.; Boyd, S.; Ye, Y. Global Optimization: From Theory to Implementation. Chapter Disciplined Convex Programming; Springer: New York, NY, USA, 2006. [Google Scholar]
- Tsigkinopoulou, A.; Hawari, A.; Uttley, M.; Breitling, R. Defining informative priors for ensemble modeling in systems biology. Nat. Protoc. 2018, 13, 2643. [Google Scholar] [CrossRef]
- Model Balancing. Available online: https://model-balancing.readthedocs.io (accessed on 15 September 2021).
- Novo Nordisk Foundation Center for Biosustainability. Maud Package. 2019. Available online: https://maud-metabolic-models.readthedocs.io (accessed on 20 October 2021).
- Gollub, M.; Kaltenbach, H.M.; Stelling, J. Probabilistic Thermodynamic Analysis of Metabolic Networks. Bioinformatics 2021, 37, 2938–2945. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liebermeister, W.; Noor, E. Model Balancing: A Search for In-Vivo Kinetic Constants and Consistent Metabolic States. Metabolites 2021, 11, 749. https://doi.org/10.3390/metabo11110749
Liebermeister W, Noor E. Model Balancing: A Search for In-Vivo Kinetic Constants and Consistent Metabolic States. Metabolites. 2021; 11(11):749. https://doi.org/10.3390/metabo11110749
Chicago/Turabian StyleLiebermeister, Wolfram, and Elad Noor. 2021. "Model Balancing: A Search for In-Vivo Kinetic Constants and Consistent Metabolic States" Metabolites 11, no. 11: 749. https://doi.org/10.3390/metabo11110749
APA StyleLiebermeister, W., & Noor, E. (2021). Model Balancing: A Search for In-Vivo Kinetic Constants and Consistent Metabolic States. Metabolites, 11(11), 749. https://doi.org/10.3390/metabo11110749