Application of Multiblock Analysis on Small Metabolomic Multi-Tissue Dataset
Abstract
1. Introduction
2. Results
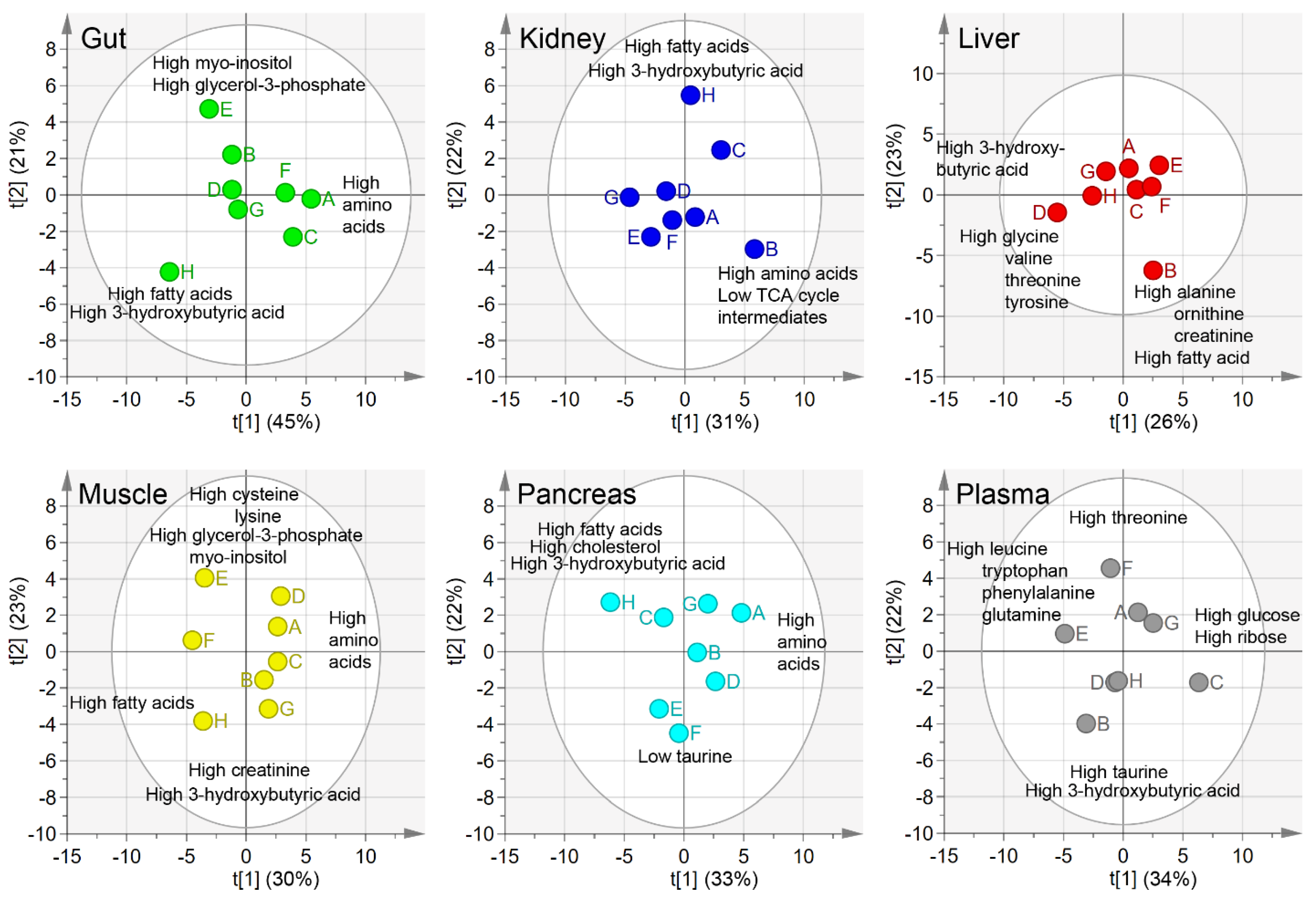
2.1. Principal Component Analysis, PCA
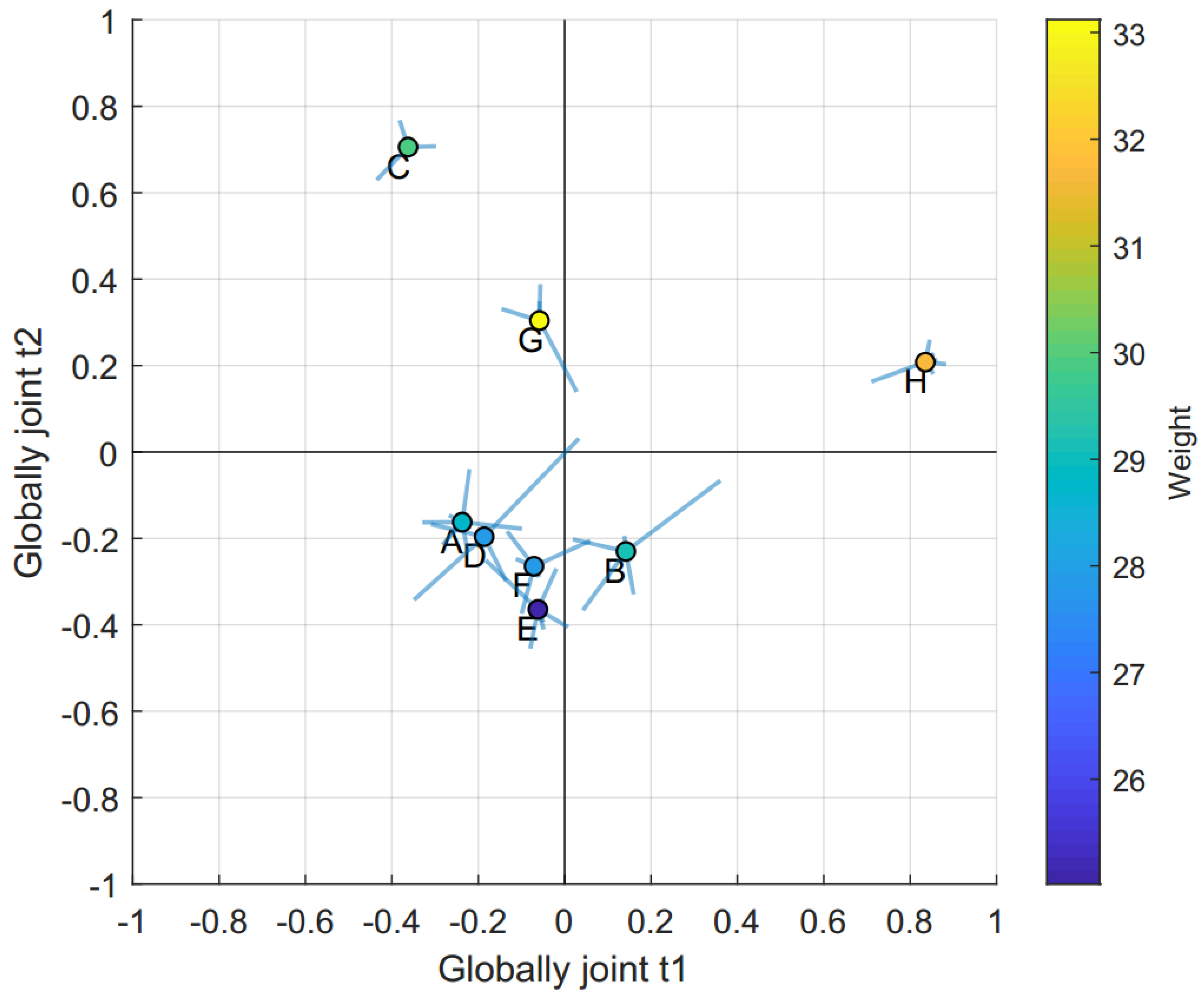
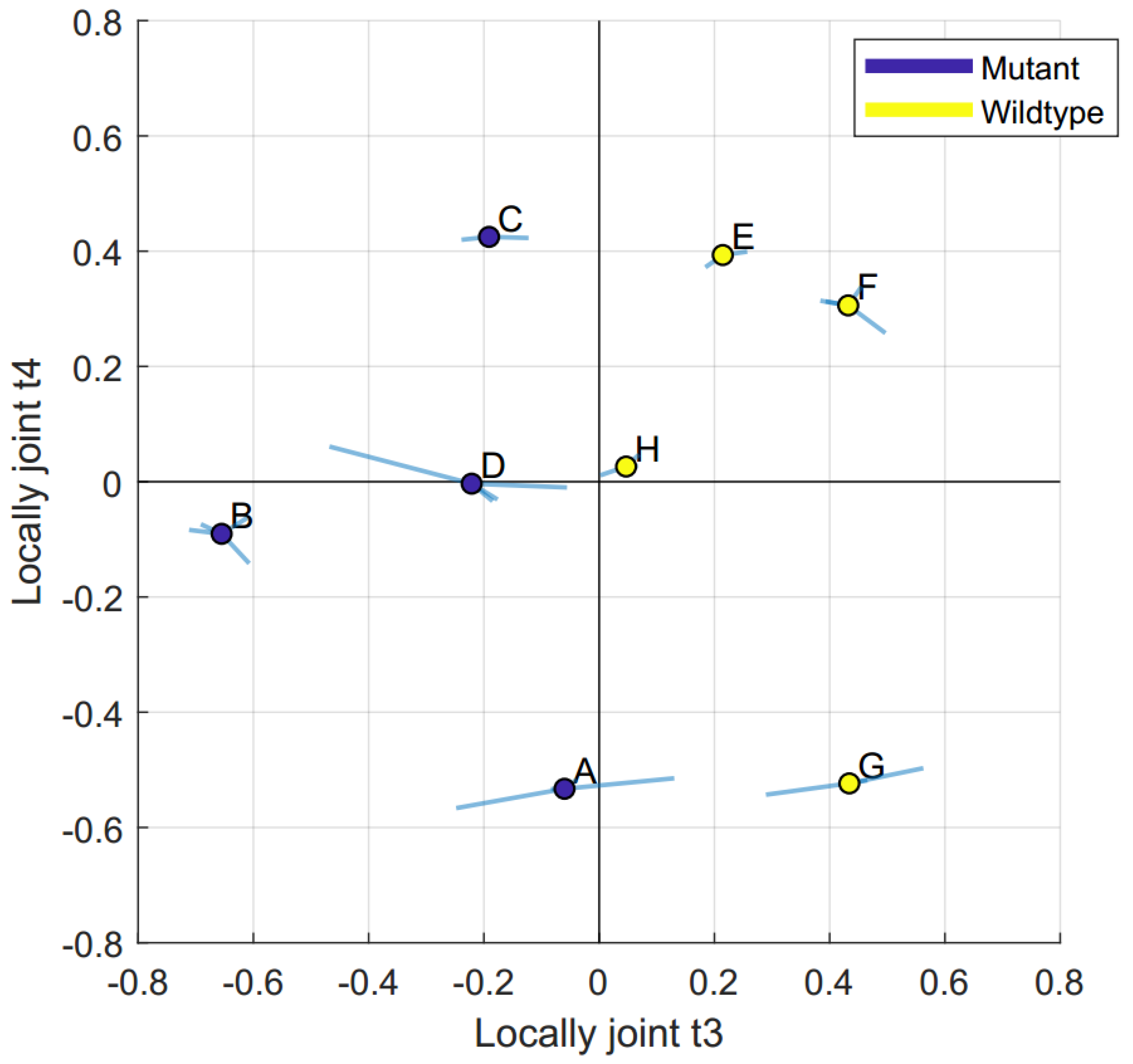
2.2. Data Integration—JUMBA
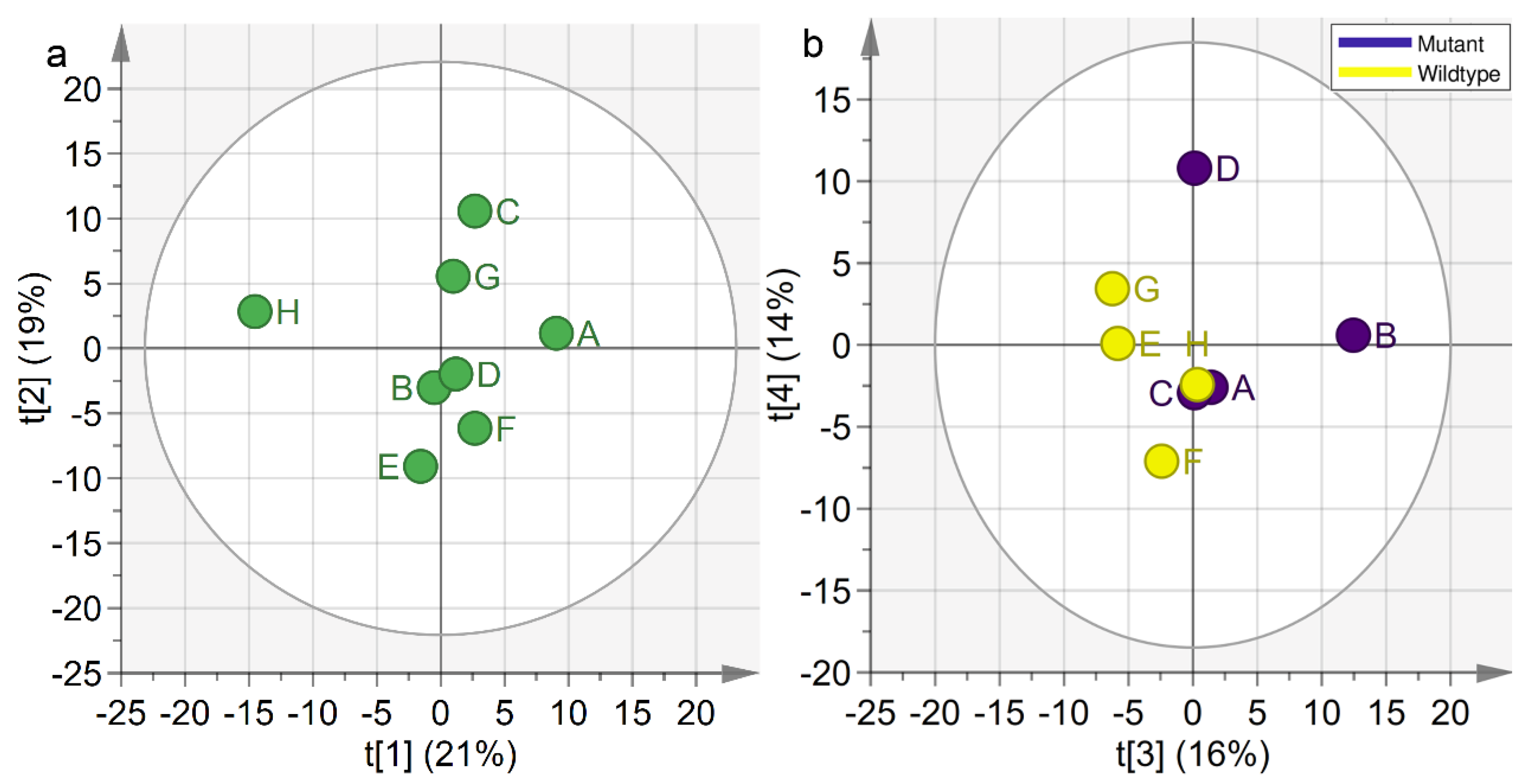
2.3. Concatenated PCA
2.4. Metabolite Concentrations
3. Discussion
4. Materials and Methods
4.1. Samples
4.2. Metabolic Profiling
4.3. Data Analysis
4.4. Software
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lahat, D.; Adali, T.; Jutten, C. Multimodal Data Fusion: An Overview of Methods, Challenges, and Prospects. Proc. IEEE 2015, 103, 1449–1477. [Google Scholar] [CrossRef]
- Hasin, Y.; Seldin, M.; Lusis, A. Multi-omics approaches to disease. Genome Biol. 2017, 18, 83. [Google Scholar] [CrossRef] [PubMed]
- Huang, S.; Chaudhary, K.; Garmire, L.X. More Is Better: Recent Progress in Multi-Omics Data Integration Methods. Front. Genet. 2017, 8, 84. [Google Scholar] [CrossRef] [PubMed]
- Parkhomenko, E.; Tritchler, D.; Beyene, J. Sparse canonical correlation analysis with application to genomic data integration. Stat. Appl. Genet. Mol. Biol. 2009, 8, 1. [Google Scholar] [CrossRef] [PubMed]
- Wold, S.; Johansson, E.; Cocchi, M. PLS—Partial least squares projections to latent structures. In 3D QSAR in Drug Design: Theory, Methods and Applications; Kubinyi, H., Ed.; ESCOM: Leiden, The Netherlands, 1993; pp. 523–550. [Google Scholar]
- Wold, S.; Kettaneh, N.; Tjessem, K. Hierarchical multiblock PLS and PC models for easier model interpretation and as an alternative to variable selection. J. Chemom. 1996, 10, 463–482. [Google Scholar] [CrossRef]
- Löfstedt, T.; Trygg, J. OnPLS—A novel multiblock method for the modelling of predictive and orthogonal variation. J. Chemom. 2011, 25, 441–455. [Google Scholar] [CrossRef]
- Löfstedt, T.; Hoffman, D.; Trygg, J. Global, local and unique decompositions in OnPLS for multiblock data analysis. Anal. Chim. Acta 2013, 791, 13–24. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. Philos. Mag. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Comon, P. Independent component analysis, A new concept? Signal Process. 1994, 36, 287–314. [Google Scholar] [CrossRef]
- Wang, H.Q.; Zheng, C.H.; Zhao, X.M. JNMFMA: A joint non-negative matrix factorization meta-analysis of transcriptomics data. Bioinformatics 2015, 31, 572–580. [Google Scholar] [CrossRef]
- Lock, E.F.; Hoadley, K.A.; Marron, J.S.; Nobel, A.B. Joint and individual variation explained (JIVE) for integrated analysis of multiple data types. Ann. Appl. Stat. 2013, 7, 523–542. [Google Scholar] [CrossRef]
- Van Deun, K.; Van Mechelen, I.; Thorrez, L.; Schouteden, M.; De Moor, B.; van der Werf, M.J.; De Lathauwer, L.; Smilde, A.K.; Kiers, H.A. DISCO-SCA and Properly Applied GSVD as Swinging Methods to Find Common and Distinctive Processes. PLoS ONE 2012, 7, e37840. [Google Scholar] [CrossRef] [PubMed]
- Smilde, A.K.; Måge, I.; Næs, T.; Hankemeier, T.; Lips, M.A.; Kiers, H.A.L.; Acar, E.; Bro, R. Common and distinct components in data fusion. J. Chemom. 2017, 31, e2900. [Google Scholar] [CrossRef]
- Zhiwen, Y.; Hau-San, W. (Eds.) GCA: A Real-time Grid-based Clustering Algorithm for Large Data Set. In Proceedings of the IEEE 18th International Conference on Pattern Recognition (ICPR’06), Hong Kong, China, 2 August 2006. [Google Scholar] [CrossRef]
- Menichelli, E.; Almøy, T.; Tomic, O.; Olsen, N.V.; Næs, T. SO-PLS as an exploratory tool for path modelling. Food Qual. Prefer. 2014, 36, 122–134. [Google Scholar] [CrossRef]
- Måge, I.; Menichelli, E.; Næs, T. Preference mapping by PO-PLS: Separating common and unique information in several data blocks. Food Qual. Prefer. 2012, 24, 8–16. [Google Scholar] [CrossRef]
- Lock, E.F.; Dunson, D.B. Bayesian consensus clustering. Bioinformatics 2013, 29, 2610–2616. [Google Scholar] [CrossRef] [PubMed]
- Ray, P.; Zheng, L.; Lucas, J.; Carin, L. Bayesian joint analysis of heterogeneous genomics data. Bioinformatics 2014, 30, 1370–1376. [Google Scholar] [CrossRef]
- Smith, A.; Wakefield, J. The hierarchical Bayesian approach to population pharmacokinetic modelling. Int. J. Biomed. Comput. 1994, 36, 35–42. [Google Scholar] [CrossRef]
- Kirk, P.; Griffin, J.E.; Savage, R.S.; Ghahramani, Z.; Wild, D.L. Bayesian correlated clustering to integrate multiple datasets. Bioinformatics 2012, 28, 3290–3297. [Google Scholar] [CrossRef]
- Van der Kloet, F.M.; Sebastián-León, P.; Conesa, A.; Smilde, A.K.; Westerhuis, J.A. Separating common from distinctive variation. BMC Bioinformatics 2016, 17, S195. [Google Scholar] [CrossRef][Green Version]
- Goodacre, R.; Vaidyanathan, S.; Dunn, W.B.; Harrigan, G.G.; Kell, D.B. Metabolomics by numbers: Acquiring and understanding global metabolite data. Trends Biotechnol. 2004, 22, 245–252. [Google Scholar] [CrossRef] [PubMed]
- Torell, F.; Bennett, K.; Cereghini, S.; Rannar, S.; Lundstedt-Enkel, K.; Moritz, T.; Haumaitre, C.; Trygg, J.; Lundstedt, T. Multi-Organ Contribution to the Metabolic Plasma Profile Using Hierarchical Modelling. PLoS ONE 2015, 10, e0129260. [Google Scholar] [CrossRef] [PubMed]
- Torell, F.; Bennett, K.; Cereghini, S.; Fabre, M.; Rannar, S.; Lundstedt-Enkel, K.; Moritz, T.; Haumaitre, C.; Trygg, J.; Lundstedt, T. Metabolic Profiling of Multiorgan Samples: Evaluation of MODY5/RCAD Mutant Mice. J. Proteome Res. 2018, 17, 2293–2306. [Google Scholar] [CrossRef]
- Srivastava, V.; Obudulu, O.; Bygdell, J.; Lofstedt, T.; Ryden, P.; Nilsson, R.; Ahnlund, M.; Johansson, A.; Jonsson, P.; Freyhult, E.; et al. OnPLS integration of transcriptomic, proteomic and metabolomic data shows multi-level oxidative stress responses in the cambium of transgenic hipI-superoxide dismutase Populus plants. BMC Genom. 2013, 14, 893. [Google Scholar] [CrossRef] [PubMed]
- Obudulu, O.; Mahler, N.; Skotare, T.; Bygdell, J.; Abreu, I.N.; Ahnlund, M.; Gandla, M.L.; Petterle, A.; Moritz, T.; Hvidsten, T.R. A multi-omics approach reveals function of Secretory Carrier-Associated Membrane Proteins in wood formation of Populus trees. BMC Genom. 2018, 19, 11. [Google Scholar] [CrossRef]
- Skotare, T.; Sjögren, R.; Surowiec, I.; Nilsson, D.; Trygg, J. Visualization of descriptive multiblock analysis. J. Chemom. 2018, 34, e3071. [Google Scholar] [CrossRef]
- Surowiec, I.; Skotare, T.; Sjögren, R.; Gouveia-Figueira, S.; Orikiiriza, J.; Bergström, S.; Normark, J.; Trygg, J. Joint and unique multiblock analysis of biological data—Multiomics malaria study. Faraday Discuss 2019, 218, 268–283. [Google Scholar] [CrossRef] [PubMed]
- Skotare, T.; Nilsson, D.; Xiong, S.; Geladi, P.; Trygg, J. Joint and Unique Multiblock Analysis for Integration and Calibration Transfer of NIR Instruments. Anal. Chem. 2019, 91, 3516–3524. [Google Scholar] [CrossRef]
- Westerhuis, J.A.; van det Kloet, F.; Smilde, A.K. Data Fusion in Metabolomics. In Metabolomics: Practical Guide to Design and Analysis, 1st ed.; Wehrens, R., Salek, R., Eds.; Chapman and Hall/CRC: Boka Raton, FL, USA, 2019; pp. 157–176. [Google Scholar]
- Jain, S.K.; Kannan, K.; Lim, G. Ketosis (acetoacetate) can generate oxygen radicals and cause increased lipid peroxidation and growth inhibition in human endothelial cells. Free Radic. Biol. Med. 1998, 25, 1083–1088. [Google Scholar] [CrossRef]
- Laffel, L. Ketone bodies: A review of physiology, pathophysiology and application of monitoring to diabetes. Diabetes Metab. Res. Rev. 1999, 15, 412–426. [Google Scholar] [CrossRef]
- Zammit, V. Regulation of ketone body metabolism: A cellular perspective. Diabetes Rev. 1994, 2, 132–155. [Google Scholar]
- Ayala, J.E.; Samuel, V.T.; Morton, G.J.; Obici, S.; Croniger, C.M.; Shulman, G.I.; Wasserman, D.H.; McGuinness, O.P. Standard operating procedures for describing and performing metabolic tests of glucose homeostasis in mice. Dis. Models Mech. 2010, 3, 525–534. [Google Scholar] [CrossRef] [PubMed]
- McGuinness, O.P.; Ayala, J.E.; Laughlin, M.R.; Wasserman, D.H. NIH experiment in centralized mouse phenotyping: The Vanderbilt experience and recommendations for evaluating glucose homeostasis in the mouse. Am. J. Physiol. Endocrinol. Metab. 2009, 297, E849–E855. [Google Scholar] [CrossRef] [PubMed]
- Horikawa, Y.; Iwasaki, N.; Hara, M.; Furuta, H.; Hinokio, Y.; Cockburn, B.N.; Lindner, T.; Yamagata, K.; Ogata, M.; Tomonaga, O.; et al. Mutation in hepatocyte nuclear factor-1 beta gene (TCF2) associated with MODY. Nat. Genet. 1997, 17, 84–85. [Google Scholar] [CrossRef]
- Bingham, C.; Hattersley, A.T. Renal cysts and diabetes syndrome resulting from mutations in hepatocyte nuclear factor-1beta. Nephrol. Dial. Transpl. 2004, 19, 2703–2708. [Google Scholar] [CrossRef] [PubMed]
- De Vas, M.G.; Kopp, J.L.; Heliot, C.; Sander, M.; Cereghini, S.; Haumaitre, C. Hnf1b controls pancreas morphogenesis and the generation of Ngn3+ endocrine progenitors. Development 2015, 142, 871–882. [Google Scholar] [CrossRef] [PubMed]
- Emmett, M. Acetaminophen toxicity and 5-oxoproline (pyroglutamic acid): A tale of two cycles, one an ATP-depleting futile cycle and the other a useful cycle. Clin. J. Am. Soc. Nephrol. 2014, 9, 191–200. [Google Scholar] [CrossRef]
- Clendenen, N.; Nunns, G.R.; Moore, E.E.; Gonzalez, E.; Chapman, M.; Reisz, J.A.; Peltz, E.; Fragoso, M.; Nemkov, T.; Wither, M.J.; et al. Selective organ ischaemia/reperfusion identifies liver as the key driver of the post-injury plasma metabolome derangements. Blood Transfus. 2019, 17, 347–356. [Google Scholar] [CrossRef]
- Westerhuis, J.A.; Kourti, T.; MacGregor, J.F. Analysis of multiblock and hierarchical PCA and PLS models. J. Chemom. 1998, 12, 301–321. [Google Scholar] [CrossRef]
- Jonsson, P.; Johansson, A.I.; Gullberg, J.; Trygg, J.; Grung, B.; Marklund, S.; Sjöström, M.; Antti, H.; Moritz, T. High-throughput data analysis for detecting and identifying differences between samples in GC/MS-based metabolomic analyses. Anal. Chem. 2005, 77, 5635–5642. [Google Scholar] [CrossRef]
- Jiye, A.; Trygg, J.; Gullberg, J.; Johansson, A.I.; Jonsson, P.; Antti, H.; Marklund, S.L.; Moritz, T. Extraction and GC/MS analysis of the human blood plasma metabolome. Anal. Chem. 2005, 77, 8086–8094. [Google Scholar] [CrossRef]
- Jackson, J.E. A User’s Guide to Principal Components; John Wiley: New York, NY, USA, 1991. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal component analysis. Chemom. Intell. Lab. 1987, 2, 37–52. [Google Scholar] [CrossRef]
| Component | Gut | Kidney | Liver | Muscle | Pancreas | Plasma |
|---|---|---|---|---|---|---|
| Globally joint t1 | 37% | 14% | 17% | 23% | 25% | 12% |
| Globally joint t2 | 19% | 19% | 14% | 18% | 19% | 29% |
| Locally joint t3 | 28% | 17% | 18% | 8% | 18% | |
| Locally joint t4 | 11% | 15% | 24% | 11% | ||
| Locally joint t5 | 19% | 21% | 11% | 7% | ||
| Locally joint t6 | 25% | 7% | 16% | |||
| Locally joint t7 | 11% | 7% | ||||
| Residual | 19% | 20% | 8% | 26% | 6% | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torell, F.; Skotare, T.; Trygg, J. Application of Multiblock Analysis on Small Metabolomic Multi-Tissue Dataset. Metabolites 2020, 10, 295. https://doi.org/10.3390/metabo10070295
Torell F, Skotare T, Trygg J. Application of Multiblock Analysis on Small Metabolomic Multi-Tissue Dataset. Metabolites. 2020; 10(7):295. https://doi.org/10.3390/metabo10070295
Chicago/Turabian StyleTorell, Frida, Tomas Skotare, and Johan Trygg. 2020. "Application of Multiblock Analysis on Small Metabolomic Multi-Tissue Dataset" Metabolites 10, no. 7: 295. https://doi.org/10.3390/metabo10070295
APA StyleTorell, F., Skotare, T., & Trygg, J. (2020). Application of Multiblock Analysis on Small Metabolomic Multi-Tissue Dataset. Metabolites, 10(7), 295. https://doi.org/10.3390/metabo10070295





