Simple Equations Pertaining to the Particle Number and Surface Area of Metallic, Polymeric, Lipidic and Vesicular Nanocarriers
Abstract
1. Introduction
2. Particle Number Determination
2.1. Quantification of Number of Metallic Particles
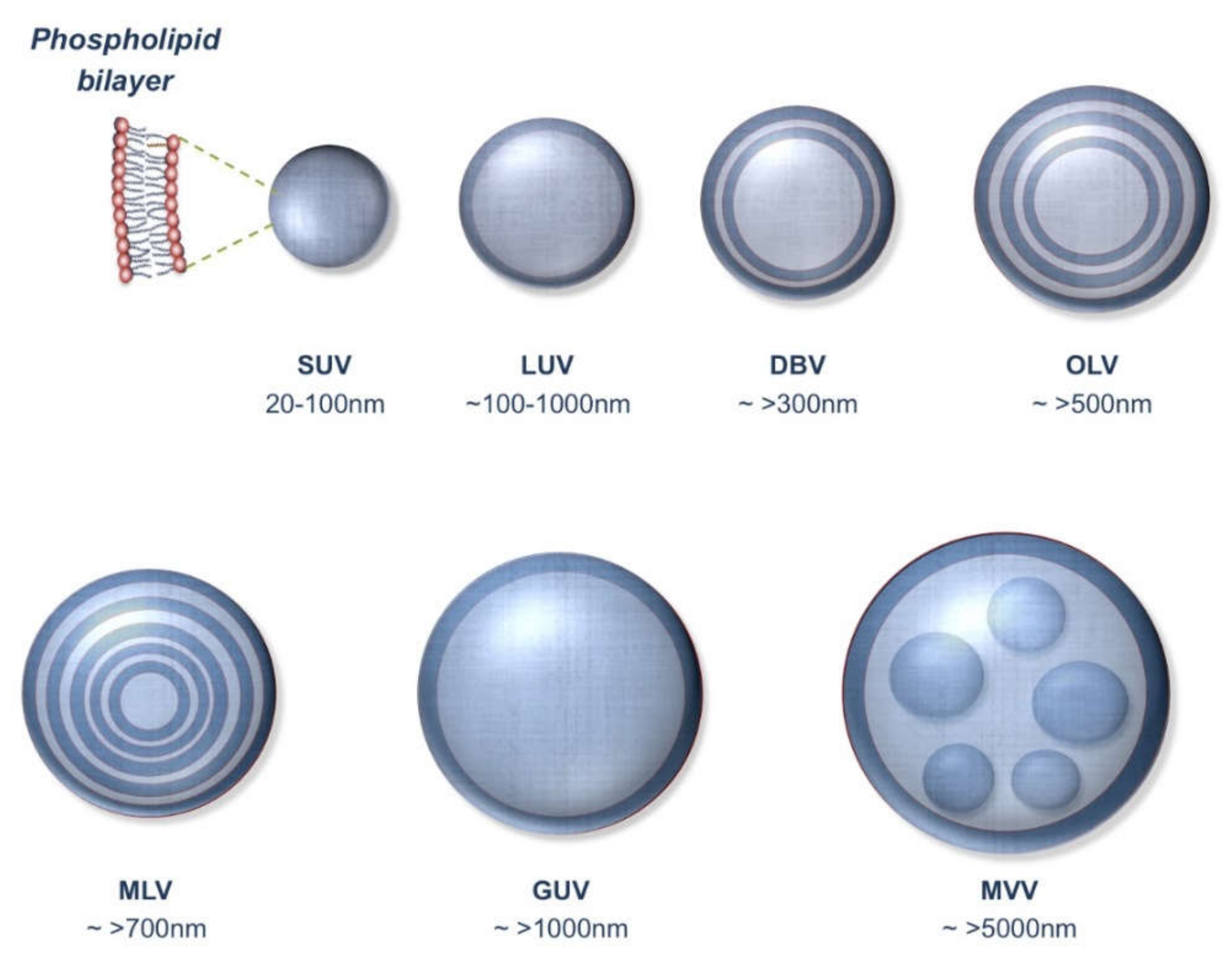
2.2. Particle Number of Vesicular Carriers
~ 588,989,868 vesicles/ml
2.3. Particle Number of Polymeric Carriers
3. Surface Area Determination
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Yang, J.; Wu, S.H.; Herman, C.J. Combinational Liposome Compositions for Cancer Therapy. U.S. Patent 16/279,977, 8 May 2019. [Google Scholar]
- Hanif, M.; Khan, H.U.; Afzal, S.; Majeed, A.; Iqbal, N.; Afzal, K.; Andleeb, M.; Rauf, A.; Farooq, A. Formulation, characterization and optimization of nebivolol-loaded sustained release lipospheres. Trop. J. Pharm. Res. 2019, 18, 223. [Google Scholar] [CrossRef]
- Mozafari, M.R.; Johnson, C.; Hatziantoniou, S.; Demetzos, C. Nanoliposomes and Their Applications in Food Nanotechnology. J. Liposome Res. 2008, 18, 309–327. [Google Scholar] [CrossRef] [PubMed]
- Hashemnejad, S.M.; Badruddoza, A.Z.M.; Zarket, B.; Castaneda, C.R.; Doyle, P.S. Thermoresponsive nanoemulsion-based gel synthesized through a low-energy process. Nat. Commun. 2019, 10, 2749. [Google Scholar] [CrossRef]
- Riva, A.; Ronchi, M.; Petrangolini, G.; Bosisio, S.; Allegrini, P. Improved Oral Absorption of Quercetin from Quercetin Phytosome®, a New Delivery System Based on Food Grade Lecithin. Eur. J. Drug Metab. Pharmacokinet. 2019, 44, 169–177. [Google Scholar] [CrossRef] [PubMed]
- Nokhodchi, A.; Jelvehgari, M.; Siahi, M.R.; Mozafari, M.R. Factors affecting the morphology of benzoyl peroxide microsponges. Micron 2007, 38, 834–840. [Google Scholar] [CrossRef]
- Asnani, G.P.; Bahekar, J.; Kokare, C.R. Development of novel pH–responsive dual crosslinked hydrogel beads based on Portulaca oleracea polysaccharide-alginate-borax for colon specific delivery of 5-fluorouracil. J. Drug Deliv. Sci. Technol. 2018, 48, 200–208. [Google Scholar] [CrossRef]
- Asnani, G.P.; Kokare, C.R. In vitro and in vivo evaluation of colon cancer targeted epichlorohydrin crosslinked Portulaca-alginate beads. Biomol. Concepts 2018, 9, 190–199. [Google Scholar] [CrossRef]
- Moku, G.; Layek, B.; Trautman, L.; Putnam, S.; Panyam, J.; Prabha, S. Improving Payload Capacity and Anti-Tumor Efficacy of Mesenchymal Stem Cells Using TAT Peptide Functionalized Polymeric Nanoparticles. Cancers 2019, 11, 491. [Google Scholar] [CrossRef]
- Sharifi, I.; Parizi, M.H.; Farajzadeh, S.; Pardakhty, A.; Parizi, M.D.; Sharifi, H.; Keyhani, A.; Mostafavi, M.; Bamorovat, M.; Khosravi, A.; et al. Tioxolone niosomes exert antileishmanial effects on Leishmania tropica by promoting promastigote apoptosis and immunomodulation. Asian Pac. J. Trop. Med. 2019, 12, 365. [Google Scholar] [CrossRef]
- Mozafari, M.; Javanmard, R.; Raji, M. Tocosome: Novel drug delivery system containing phospholipids and tocopheryl phosphates. Int. J. Pharm. 2017, 528, 381–382. [Google Scholar] [CrossRef]
- Zarrabi, A.; Alipoor Amro Abadi, M.; Khorasani, S.; Mohammadabadi, M.; Jamshidi, A.; Torkaman, S.; Taghavi, E.; Mozafari, M.R.; Rasti, B. Nanoliposomes and tocosomes as multifunctional nanocarriers for the encapsulation of nutraceutical and dietary molecules. Molecules 2020, 25, 638. [Google Scholar] [CrossRef]
- Mozafari, M.R.; Reed, C.J.; Rostron, C.; Kocum, C.; Piskin, E. Formation and characterisation of non-toxic anionic liposomes for delivery of therapeutic agents to the pulmonary airways. Cell. Mol. Biol. Lett. 2002, 7, 243–244. [Google Scholar]
- ElMeshad, A.N.; Mortazavi, S.M.; Mozafari, M.R. Formulation and characterization of nanoliposomal 5-fluorouracil for cancer nanotherapy. J. Liposome Res. 2013, 24, 1–9. [Google Scholar] [CrossRef]
- Epstein, H.; Afergan, E.; Moise, T.; Richter, Y.; Rudich, Y.; Golomb, G. Number-concentration of nanoparticles in liposomal and polymeric multiparticulate preparations: Empirical and calculation methods. Biomaterials 2006, 27, 651–659. [Google Scholar] [CrossRef] [PubMed]
- Danaei, M.; Dehghankhold, M.; Ataei, S.; Davarani, F.H.; Javanmard, R.; Dokhani, A.; Khorasani, S.; Mozafari, M.R. Impact of Particle Size and Polydispersity Index on the Clinical Applications of Lipidic Nanocarrier Systems. Pharmaceutics 2018, 10, 57. [Google Scholar] [CrossRef] [PubMed]
- Danaei, M.; Kalantari, M.; Raji, M.; Fekri, H.S.; Saber, R.; Asnani, G.; Mortazavi, S.; Mozafari, M.; Rasti, B.; Taheriazam, A. Probing nanoliposomes using single particle analytical techniques: Effect of excipients, solvents, phase transition and zeta potential. Heliyon 2018, 4, e01088. [Google Scholar] [CrossRef]
- Jurkiewicz, P.; Okruszek, A.; Hof, M.; Langner, M. Associating oligonucleotides with positively charged liposomes. Cell. Mol. Biol. Lett. 2003, 8, 77–84. [Google Scholar] [PubMed]
- Saveyn, H.; De Baets, B.; Thas, O.; Hole, P.; Smith, J.; Van der Meeren, P. Accurate particle size distribution determination by nanoparticle tracking analysis based on 2-D Brownian dynamics simulation. J. Colloid Interface Sci. 2010, 352, 593–600. [Google Scholar] [CrossRef]
- Filipe, V.; Hawe, A.; Jiskoot, W. Critical Evaluation of Nanoparticle Tracking Analysis (NTA) by NanoSight for the Measurement of Nanoparticles and Protein Aggregates. Pharm. Res. 2010, 27, 796–810. [Google Scholar] [CrossRef] [PubMed]
- Ribeiro, L.N.D.M.; Couto, V.M.; Fraceto, L.F.; De Paula, E. Use of nanoparticle concentration as a tool to understand the structural properties of colloids. Sci. Rep. 2018, 8, 1–8. [Google Scholar] [CrossRef]
- Mody, V.V.; Siwale, R.; Singh, A.K.; Mody, H.R. Introduction to metallic nanoparticles. J. Pharm. Bioallied Sci. 2010, 2, 282–289. [Google Scholar] [CrossRef]
- Hinterwirth, H.; Wiedmer, S.K.; Moilanen, M.; Lehner, A.; Allmaier, G.; Waitz, T.; Lindner, W.; Lämmerhofer, M. Comparative method evaluation for size and size-distribution analysis of gold nanoparticles. J. Sep. Sci. 2013, 36, 2952–2961. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Atwater, M.; Wang, J.; Huo, Q. Extinction coefficient of gold nanoparticles with different sizes and different capping ligands. Colloids Surf. B Biointerfaces 2007, 58, 3–7. [Google Scholar] [CrossRef] [PubMed]
- Rajakumar, G.; Gomathi, T.; Rahuman, A.A.; Thiruvengadam, M.; Mydhili, G.; Kim, S.-H.; Lee, T.-J.; Chung, I.-M. Biosynthesis and Biomedical Applications of Gold Nanoparticles Using Eclipta prostrata Leaf Extract. Appl. Sci. 2016, 6, 222. [Google Scholar] [CrossRef]
- Mucic, R.C.; Storhoff, J.J.; Mirkin, C.A.; Letsinger, R.L. DNA-Directed Synthesis of Binary Nanoparticle Network Materials. J. Am. Chem. Soc. 1998, 120, 12674–12675. [Google Scholar] [CrossRef]
- Zhang, H.; Hussain, I.; Brust, M.; Cooper, A.I. Emulsion-Templated Gold Beads Using Gold Nanoparticles as Building Blocks. Adv. Mater. 2004, 16, 27–30. [Google Scholar] [CrossRef]
- Cantarutti, C.; Raj, G.; Fogolari, F.; Giorgetti, S.; Corazza, A.; Bellotti, V.; Esposito, G. Interference of cit-rate-stabilized gold nanoparticles with β2-microglobulin oligomeric association. Chem. Commun. 2018, 54, 5422–5425. [Google Scholar] [CrossRef]
- Zhang, R.; Pan, D.; Cai, X.; Yang, X.; Senpan, A.; Allen, J.S.; Lanza, G.M.; Wang, L.V. ανβ3-targeted Copper Nanoparticles Incorporating an Sn 2 Lipase-Labile Fumagillin Prodrug for Photoacoustic Neovascular Imaging and Treatment. Theranostics 2015, 5, 124–133. [Google Scholar] [CrossRef]
- Ahamed, M.; AlSalhi, M.S.; Siddiqui, M. Silver nanoparticle applications and human health. Clin. Chim. Acta 2010, 411, 1841–1848. [Google Scholar] [CrossRef]
- Amoabediny, G.; Haghiralsadat, F.; Naderinezhad, S.; Helder, M.N.; Akhoundi Kharanaghi, E.; Mohammadnejad Arough, J.; Zandieh-Doulabi, B. Overview of preparation methods of polymeric and lipid-based (niosome, solid lipid, lip-osome) nanoparticles: A comprehensive review. Int. J. Polym. Mater. Polym. Biomater. 2018, 67, 383–400. [Google Scholar] [CrossRef]
- Mozafari, M.R. Nanoliposomes: Preparation and analysis. In Liposomes; Humana Press: Totowa, NJ, USA, 2010; pp. 29–50. [Google Scholar]
- Maherani, B.; Arab-Tehrany, E.; Mozafari, M.R.; Gaiani, C.; Linder, M. Liposomes: A Review of Manufacturing Techniques and Targeting Strategies. Curr. Nanosci. 2011, 7, 436–452. [Google Scholar] [CrossRef]
- Aveling, E.; Zhou, J.; Lim, Y.F.; Mozafari, M.R. Targeting lipidic nanocarriers: Current strategies and problems. Pharmakeftiki 2006, 19, 101–109. [Google Scholar]
- Israelachvili, J.N.; Mitchell, D. A model for the packing of lipids in bilayer membranes. Biochim. Biophys. Acta (BBA) Biomembr. 1975, 389, 13–19. [Google Scholar] [CrossRef]
- Edholm, O.; Nagle, J.F. Areas of Molecules in Membranes Consisting of Mixtures. Biophys. J. 2005, 89, 1827–1832. [Google Scholar] [CrossRef] [PubMed]
- Sapay, N.; Bennett, W.F.D.; Tieleman, D.P. Thermodynamics of flip-flop and desorption for a systematic series of phosphatidylcholine lipids. Soft Matter 2009, 5, 3295–3302. [Google Scholar] [CrossRef]
- Pidgeon, C.; Hunt, C.A.; Huntx, C. Calculating Number and Surface Area of Liposomes in Any Suspension. J. Pharm. Sci. 1981, 70, 173–176. [Google Scholar] [CrossRef]
- Lee, H.; Kwak, D.B.; Kim, S.C.; Pui, D.Y. Characterization of colloidal nanoparticles in mixtures with poly-disperse and multimodal size distributions using a particle tracking analysis and electrospray-scanning mobility particle sizer. Powder Technol. 2019, 355, 18–25. [Google Scholar] [CrossRef]
- Park, J.; Kwak, M.; Song, N.W.; Kim, J. Effect of colloidal nanoparticle concentration on sizing analysis with an electrospray scanning mobility particle sizer. Appl. Nanosci. 2019, 10, 329–336. [Google Scholar] [CrossRef]
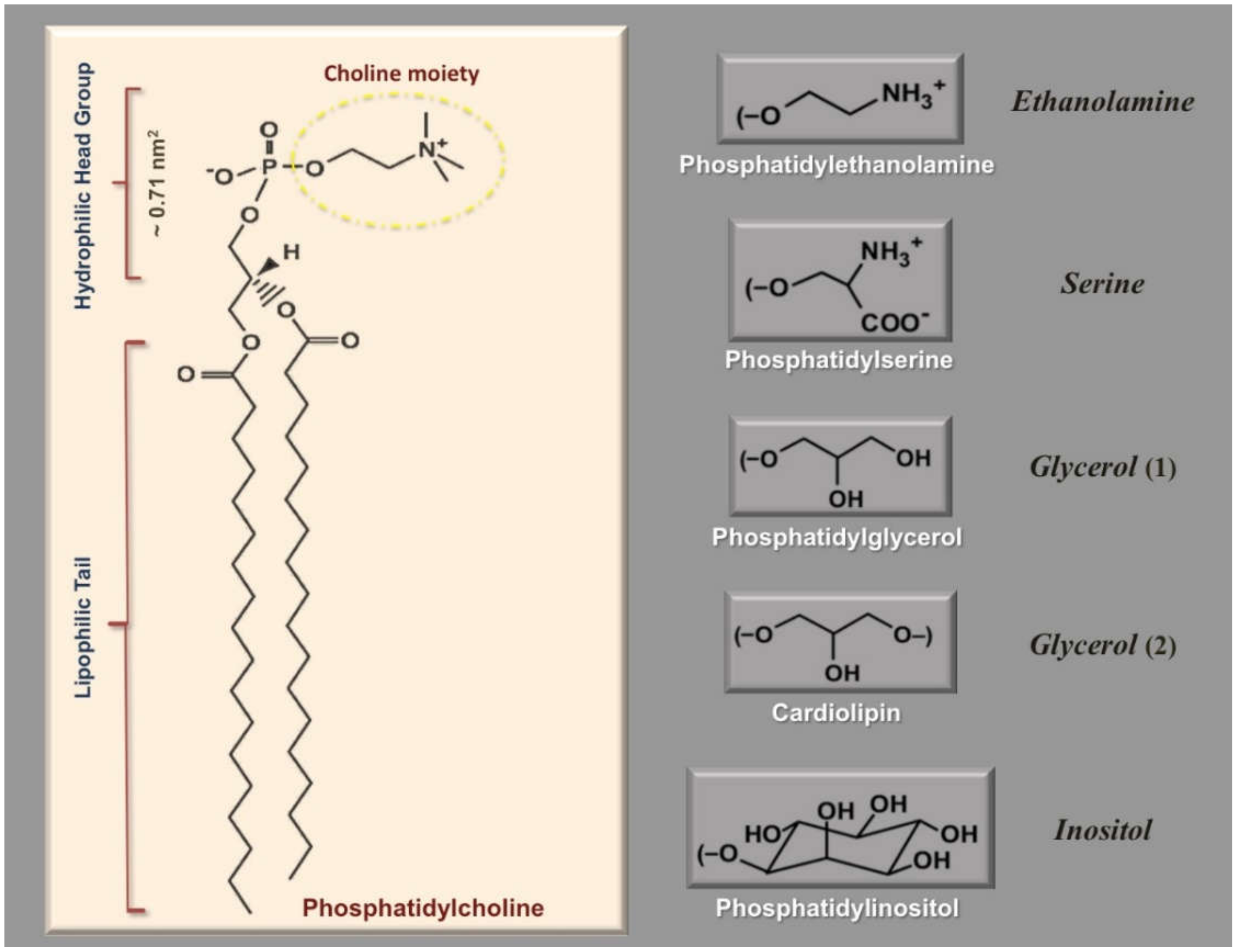

| Category | Examples | Description | |
|---|---|---|---|
| 1 | Lipidic systems | Liposome | Bilayer phospholipid vesicles |
| Liposphere | Phospholipid monolayer with a solid fat core | ||
| Nanoliposome | Nanometric liposome | ||
| Nanoemulsion | Nanometric oil/water emulsions | ||
| Phytosome | Herbal extracts & natural phospholipid mix | ||
| 2 | Polymeric carriers | Microsponges | Carrier system composed of porous microspheres |
| Hydrogel beads | Polymeric carriers which swell in water | ||
| Polymeric nanoparticles | Nanometric particulate dispersions or solid particles used as bioactive carriers | ||
| 3 | Surfactant-based | Niosome | Non-ionic surfactant vesicles |
| 4 | Tocopherol-based | Tocosome | Bilayer vesicles composed of tocopheryl derivatives & phospholipids |
| 5 | Metallic particles | Gold particles | |
| Copper particles | Colloidal metallic substrates employed as drug delivery systems | ||
| Silver particles |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mozafari, M.R.; Mazaheri, E.; Dormiani, K. Simple Equations Pertaining to the Particle Number and Surface Area of Metallic, Polymeric, Lipidic and Vesicular Nanocarriers. Sci. Pharm. 2021, 89, 15. https://doi.org/10.3390/scipharm89020015
Mozafari MR, Mazaheri E, Dormiani K. Simple Equations Pertaining to the Particle Number and Surface Area of Metallic, Polymeric, Lipidic and Vesicular Nanocarriers. Scientia Pharmaceutica. 2021; 89(2):15. https://doi.org/10.3390/scipharm89020015
Chicago/Turabian StyleMozafari, M. R., E. Mazaheri, and K. Dormiani. 2021. "Simple Equations Pertaining to the Particle Number and Surface Area of Metallic, Polymeric, Lipidic and Vesicular Nanocarriers" Scientia Pharmaceutica 89, no. 2: 15. https://doi.org/10.3390/scipharm89020015
APA StyleMozafari, M. R., Mazaheri, E., & Dormiani, K. (2021). Simple Equations Pertaining to the Particle Number and Surface Area of Metallic, Polymeric, Lipidic and Vesicular Nanocarriers. Scientia Pharmaceutica, 89(2), 15. https://doi.org/10.3390/scipharm89020015









