The Impact of COVID-19 on the Dynamic Topology and Network Flow of World Stock Markets
Abstract
:1. Introduction
2. Literature Review
3. Methodology
- : specify no correlation among the two stock indices.
- : specify perfect correlation among two stock indices.
- : specify negative or inverse correlation among two stock indices.
Network Topology Properties
4. Data
5. Findings
5.1. Dynamic Correlation Coefficients
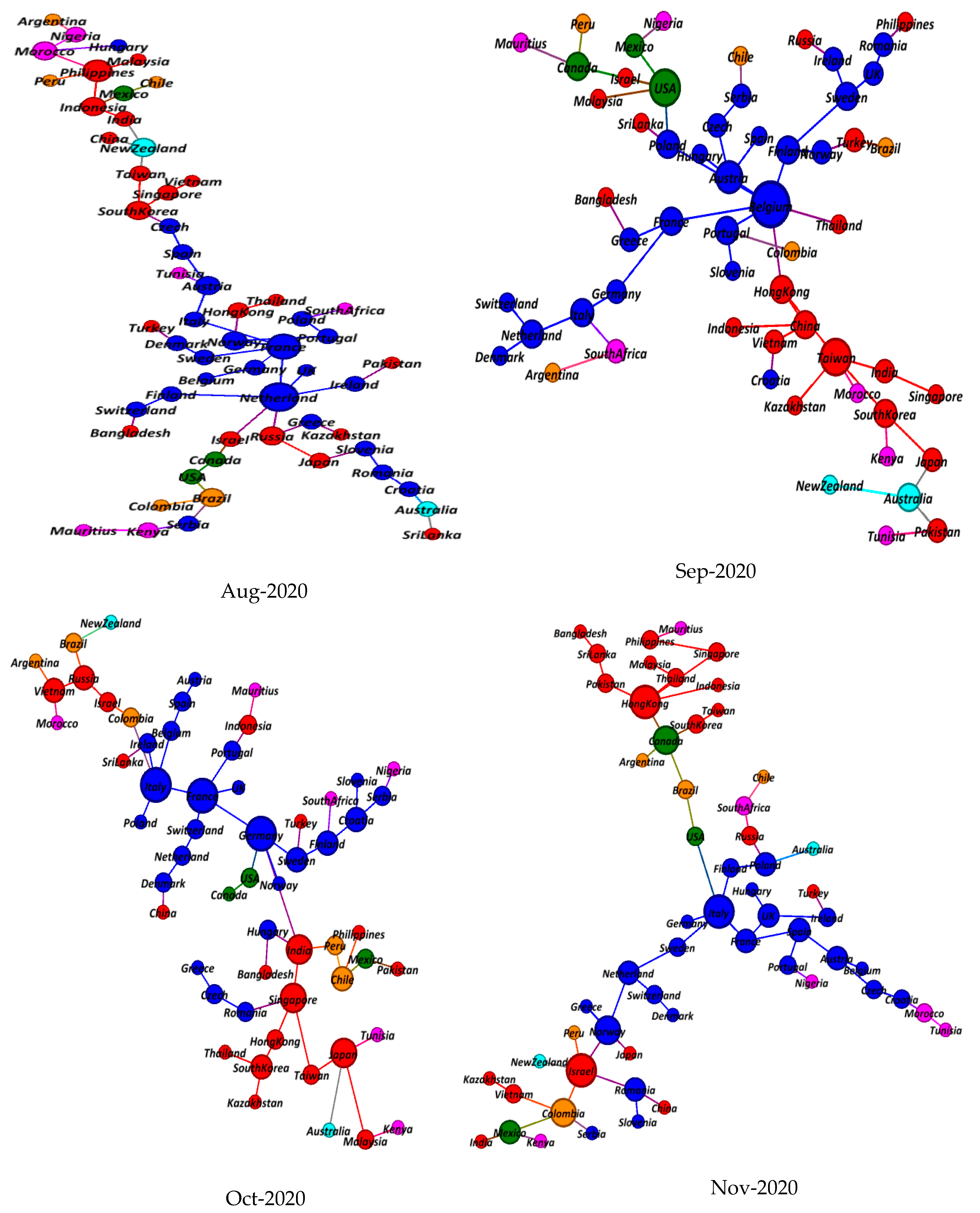
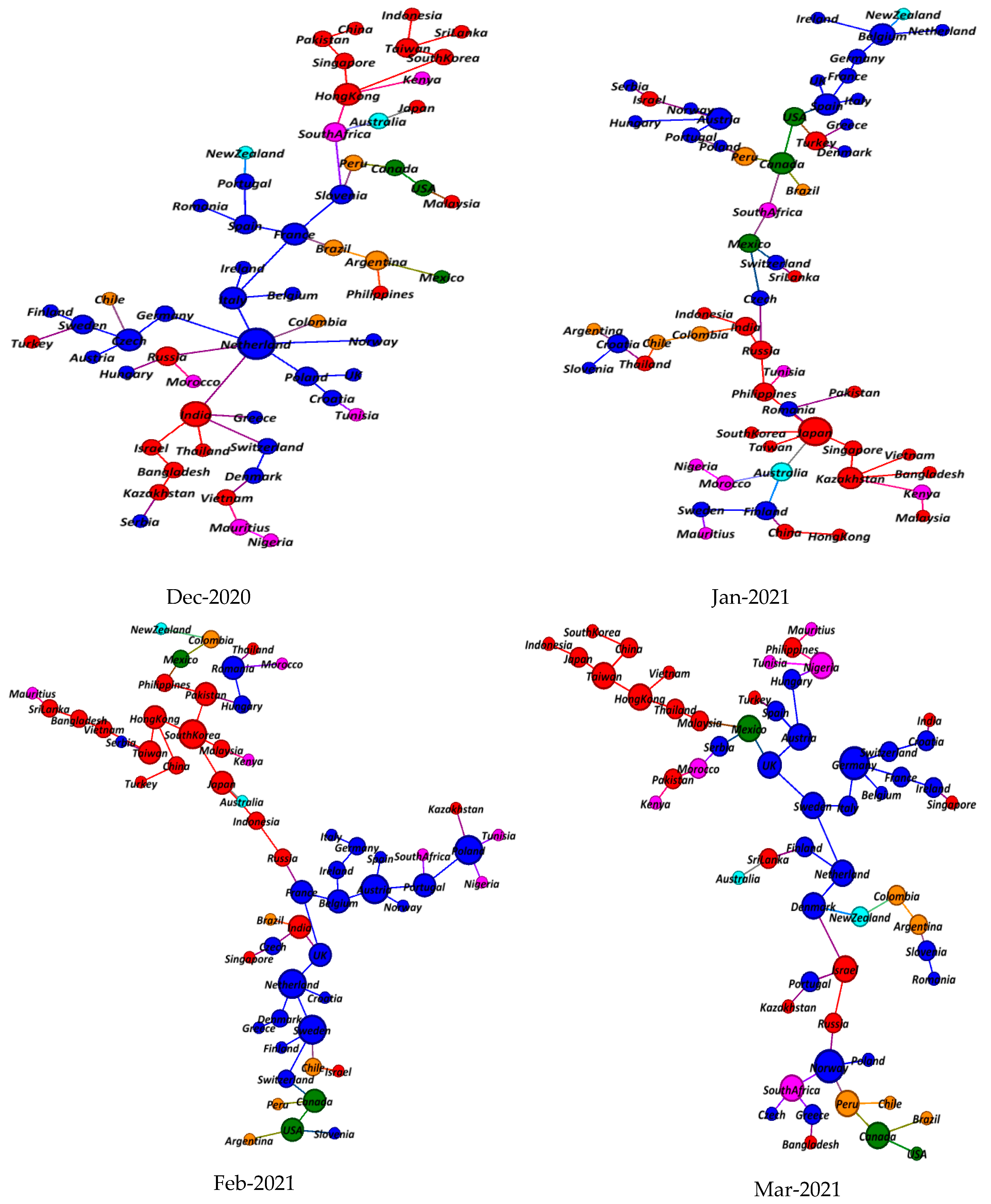
5.2. Minimum Spanning Tree Results
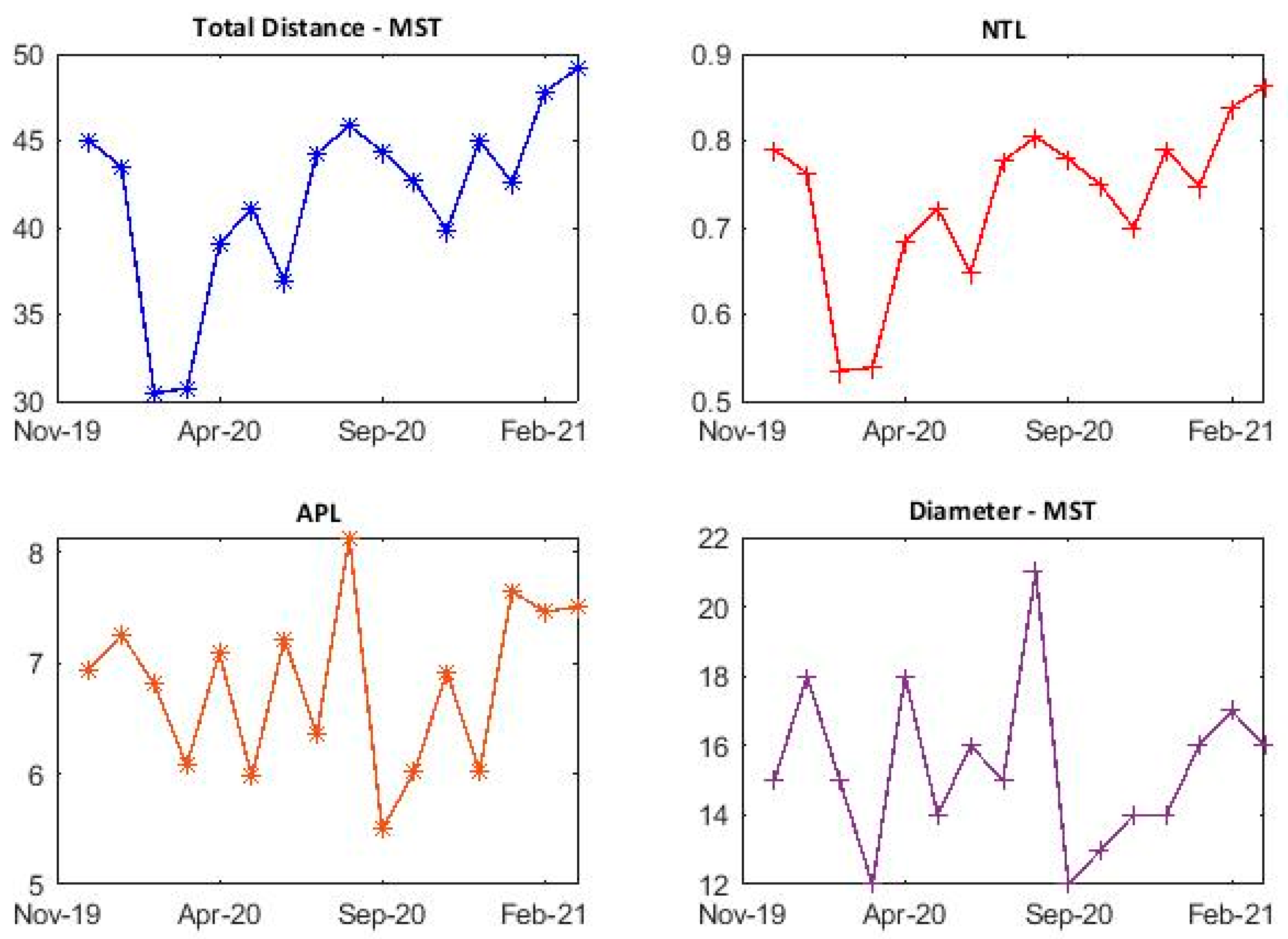
5.3. Topological Evolution Properties of MSTs
5.3.1. Centrality Analysis
5.3.2. Analysis of Dynamic Normalized Tree Length, Average Path Length and Diameter
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| S. No | Country | Stock Index | Continent | Color in MST | Reporting Date of 1st COVID-19 Confirmed Case |
|---|---|---|---|---|---|
| 1 | USA | Dow Jones Industrial Average | North America | Green | 22 January 2020 |
| 2 | Netherland | AEX | Europe | Blue | 27 February 2020 |
| 3 | Austria | Austrian Traded Index | Europe | Blue | 25 February 2020 |
| 4 | Belgium | BEL 20 | Europe | Blue | 4 February 2020 |
| 5 | Brazil | IBOVESPA | South America | Orange | 26 February 2020 |
| 6 | France | CAC 40 | Europe | Blue | 24 January 2020 |
| 7 | Germany | DAX PERFORMANCE-INDEX | Europe | Blue | 27 January 2020 |
| 8 | Canada | S&P/TSX Composite index | North America | Green | 26 January 2020 |
| 9 | Hong Kong | Hang Seng Index | Asia | Red | 22 January 2020 |
| 10 | Spain | IBEX 35 | Europe | Blue | 1 February 2020 |
| 11 | Ireland | ISEQ 20 | Europe | Blue | 29 February 2020 |
| 12 | Indonesia | Jakarta Composite Index | Asia | Red | 2 March 2020 |
| 13 | South Korea | KOSPI | Asia | Red | 22 January 2020 |
| 14 | Argentina | MERVAL | South America | Orange | 3 March 2020 |
| 15 | Mexico | IPC MEXICO | North America | Green | 28 February 2020 |
| 16 | Japan | Nikkei 225 | Asia | Red | 22 January 2020 |
| 17 | Sweden | OMX Stockholm 30 Index | Europe | Blue | 31 January 2020 |
| 18 | Switzerland | SMI | Europe | Blue | 25 February 2020 |
| 19 | Taiwan | TSEC weighted index | Asia | Red | 21 January 2020 |
| 20 | China | SSE Composite Index | Asia | Red | 31 December 2019 |
| 21 | Australia | S&P/ASX 200 | Oceania | Cyan | 26 January 2020 |
| 22 | Greece | Athens General Composite | Europe | Blue | 26 February 2020 |
| 23 | Serbia | BELEX15 | Europe | Blue | 6 March 2020 |
| 24 | Romania | BET | Europe | Blue | 26 February 2020 |
| 25 | Turkey | BIST 100 | Asia | Red | 11 March 2020 |
| 26 | Slovenia | Blue-Chip SBITOP | Europe | Blue | 5 March 2020 |
| 27 | Hungary | Budapest SE | Europe | Blue | 4 March 2020 |
| 28 | Colombia | COLCAP | South America | Orange | 6 March 2020 |
| 29 | Croatia | CROBEX | Europe | Blue | 25 February 2020 |
| 30 | Sri Lanka | CSE All-Share | Asia | Red | 27 January 2020 |
| 31 | Bangladesh | Dhaka Stock Exchange Broad | Asia | Red | 8 March 2020 |
| 32 | Malaysia | FTSE Bursa Malaysia KLCI | Asia | Red | 25 January 2020 |
| 33 | Italy | FTSE MIB | Europe | Blue | 31 January 2020 |
| 34 | UK | FTSE 100 | Europe | Blue | 31 January 2020 |
| 35 | Chile | S&P CLX IPSA | South America | Orange | 3 March 2020 |
| 36 | South Africa | JSE Top 40 | Africa | Magenta | 5 March 2020 |
| 37 | Kazakhstan | KASE | Asia | Red | 13 March 2020 |
| 38 | Kenya | Kenya NSE 20 | Africa | Magenta | 13 March 2020 |
| 39 | Pakistan | KSE 100 | Asia | Red | 26 February 2020 |
| 40 | Russia | MOEX | Asia | Red | 31 January 2020 |
| 41 | Morocco | Moroccan All Shares (MASI) | Africa | Magenta | 2 March 2020 |
| 42 | Nigeria | NSE 30 | Africa | Magenta | 28 February 2020 |
| 43 | Norway | OSE Benchmark | Europe | Blue | 26 February 2020 |
| 44 | Philippines | PSEi Composite | Asia | Red | 30 January 2020 |
| 45 | Portugal | PSI 20 | Europe | Blue | 2 March 2020 |
| 46 | Czech Republic | PX | Europe | Blue | 1 March 2020 |
| 47 | India | S&P BSE Sensex | Asia | Red | 30 January 2020 |
| 48 | Peru | S&P Lima General | South America | Orange | 6 March 2020 |
| 49 | Mauritius | SEMDEX | Africa | Magenta | 18 March 2020 |
| 50 | Thailand | SET Index | Asia | Red | 22 January 2020 |
| 51 | Singapore | STI Index | Asia | Red | 23 January 2020 |
| 52 | Israel | TA 35 | Asia | Red | 21 February 2020 |
| 53 | Tunisia | TUNINDEX | Africa | Magenta | 2 March 2020 |
| 54 | Vietnam | VN 30 | Asia | Red | 23 January 2020 |
| 55 | Poland | WIG 30 | Europe | Blue | 4 March 2020 |
| 56 | Finland | OMX Helsinki 25 | Europe | Blue | 29 January 2020 |
| 57 | Denmark | OMX Copenhagen 20 | Europe | Blue | 27 February 2020 |
| 58 | New Zealand | NZX 50 | Oceania | Cyan | 28 February 2020 |
References
- Goodell, J.W. COVID-19 and finance: Agendas for future research. Financ. Res. Lett. 2020, 35, 101512. [Google Scholar] [CrossRef] [PubMed]
- Nicola, M.; Alsafi, Z.; Sohrabi, C.; Kerwan, A.; Al-Jabir, A.; Iosifidis, C.; Agha, M.; Agha, R. The Socio-Economic Implications of the Coronavirus and COVID-19 Pandemic: A Review. Int. J. Surg. 2020, 78, 185–193. [Google Scholar] [CrossRef]
- Baker, S.R.; Bloom, N.; Davis, S.J.; Kost, K.J.; Sammon, M.C.; Viratyosin, T. The unprecedented stock market impact of COVID-19. Natl. Bur. Econ. Res. 2020. [Google Scholar] [CrossRef]
- Bahrini, R.; Filfilan, A. Impact of the novel coronavirus on stock market returns: Evidence from GCC countries. Quant. Financ. Econ. 2020, 4, 640–652. [Google Scholar] [CrossRef]
- Bora, D.; Basistha, D. The outbreak of COVID-19 pandemic and its impact on stock market volatility: Evidence from a worst-affected economy. J. Public Aff. 2021, e2623. [Google Scholar] [CrossRef] [PubMed]
- He, P.; Sun, Y.; Zhang, Y.; Li, T. COVID–19’s Impact on Stock Prices Across Different Sectors—An Event Study Based on the Chinese Stock Market. Emerg. Mark. Financ. Trade 2020, 56, 2198–2212. [Google Scholar] [CrossRef]
- Liu, H.; Manzoor, A.; Wang, C.; Zhang, L.; Manzoor, Z. The COVID-19 Outbreak and Affected Countries Stock Markets Response. Int. J. Environ. Res. Public Health 2020, 17, 2800. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ozkan, O. Impact of COVID-19 on stock market efficiency: Evidence from developed countries. Res. Int. Bus. Financ. 2021, 58, 101445. [Google Scholar] [CrossRef]
- Baker, S.R.; Bloom, N.; Davis, S.J.; Terry, S.J. Covid-Induced Economic Uncertainty. Natl. Bur. Econ. Res. 2020. [Google Scholar] [CrossRef]
- Umar, Z.; Gubareva, M. A time–frequency analysis of the impact of the Covid-19 induced panic on the volatility of currency and cryptocurrency markets. J. Behav. Exp. Financ. 2020, 28, 100404. [Google Scholar] [CrossRef]
- Corbet, S.; Hou, Y.; Hu, Y.; Larkin, C.; Oxley, L. Any port in a storm: Cryptocurrency safe-havens during the COVID-19 pandemic. Econ. Lett. 2020, 194, 109377. [Google Scholar] [CrossRef]
- Baker, S.R.; Bloom, N.; Davis, S.J.; Kost, K.; Sammon, M.; Viratyosin, T. The Unprecedented Stock Market Reaction to COVID-19. Rev. Asset Pricing Stud. 2020, 10, 742–758. [Google Scholar] [CrossRef]
- Fakhfekh, M.; Jeribi, A.; Ben Salem, M. Volatility dynamics of the Tunisian stock market before and during the COVID-19 outbreak: Evidence from the GARCH family models. Int. J. Financ. Econ. 2021, 1–14. [Google Scholar] [CrossRef]
- Salisu, A.A.; Ebuh, G.U.; Usman, N. Revisiting oil-stock nexus during COVID-19 pandemic: Some preliminary results. Int. Rev. Econ. Financ. 2020, 69, 280–294. [Google Scholar] [CrossRef]
- Sun, Y.; Wu, M.; Zeng, X.; Peng, Z. The impact of COVID-19 on the Chinese stock market: Sentimental or substantial? Financ. Res. Lett. 2021, 38, 101838. [Google Scholar] [CrossRef]
- Mazur, M.; Dang, M.; Vega, M. COVID-19 and the march 2020 stock market crash. Evidence from S&P1500. Financ. Res. Lett. 2021, 38, 101690. [Google Scholar]
- Gunay, S.; Bakry, W.; Al-Mohamad, S. The Australian Stock Market’s Reaction to the First Wave of the COVID-19 Pandemic and Black Summer Bushfires: A Sectoral Analysis. J. Risk Financ. Manag. 2021, 14, 175. [Google Scholar] [CrossRef]
- Izzeldin, M.; Muradoğlu, Y.G.; Pappas, V.; Sivaprasad, S. The impact of Covid-19 on G7 stock markets volatility: Evidence from a ST-HAR model. Int. Rev. Financ. Anal. 2021, 74, 101671. [Google Scholar] [CrossRef]
- So, M.K.P.; Chu, A.M.Y.; Chan, T.W.C. Impacts of the COVID-19 pandemic on financial market connectedness. Financ. Res. Lett. 2021, 38, 101864. [Google Scholar] [CrossRef]
- Lai, Y.; Hu, Y. A study of systemic risk of global stock markets under COVID-19 based on complex financial networks. Phys. A Stat. Mech. Its Appl. 2021, 566, 125613. [Google Scholar] [CrossRef]
- Lyócsa, Š.; Výrost, T.; Baumöhl, E. Stock market networks: The dynamic conditional correlation approach. Phys. A Stat. Mech. Its Appl. 2012, 391, 4147–4158. [Google Scholar] [CrossRef]
- Sensoy, A.; Tabak, B.M. Dynamic spanning trees in stock market networks: The case of Asia-Pacific. Phys. A Stat. Mech. Its Appl. 2014, 414, 387–402. [Google Scholar] [CrossRef]
- Song, D.M.; Tumminello, M.; Zhou, W.-X.; Mantegna, R.N. Evolution of worldwide stock markets, correlation structure, and correlation-based graphs. Phys. Rev. E 2011, 84, 026108. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brida, J.G.; Risso, W.A. Hierarchical structure of the German stock market. Expert Syst. Appl. 2010, 37, 3846–3852. [Google Scholar] [CrossRef]
- Coelho, R.; Hutzler, S.; Repetowicz, P.; Richmond, P. Sector analysis for a FTSE portfolio of stocks. Phys. A Stat. Mech. Its Appl. 2007, 373, 615–626. [Google Scholar] [CrossRef] [Green Version]
- Memon, B.A.; Yao, H. Correlation structure networks of stock market during terrorism: Evidence from Pakistan. Data Sci. Financ. Econ. 2021, 1, 117–140. [Google Scholar] [CrossRef]
- Tabak, B.M.; Serra, T.R.; Cajueiro, D.O. Topological properties of stock market networks: The case of Brazil. Phys. A Stat. Mech. Its Appl. 2010, 389, 3240–3249. [Google Scholar] [CrossRef]
- Zhuang, R.; Hu, B.; Ye, Z. Minimal spanning tree for Shanghai-Shenzhen 300 Stock Index. In Proceedings of the 2008 IEEE Congress on Evolutionary Computation, IEEE World Congress on Computational Intelligence, Hong Kong, China, 1–6 June 2008; pp. 1417–1424. [Google Scholar]
- Yao, H.; Lu, Y.; Memon, B.A. Impact of US-China Trade War on the Network Topology Structure of Chinese Stock Market. J. Asian Bus. Strategy 2019, 9, 235–250. [Google Scholar] [CrossRef]
- Nguyen, Q.; Nguyen, N.K.K.; Nguyen, L.H.N. Dynamic topology and allometric scaling behavior on the Vietnamese stock market. Phys. A Stat. Mech. Its Appl. 2019, 514, 235–243. [Google Scholar] [CrossRef]
- Birch, J.; Pantelous, A.A.; Soramäki, K. Analysis of Correlation Based Networks Representing DAX 30 Stock Price Returns. Comput. Econ. 2016, 47, 501–525. [Google Scholar] [CrossRef] [Green Version]
- Kantar, E.; Keskin, M.; Deviren, B. Analysis of the effects of the global financial crisis on the Turkish economy, using hierarchical methods. Phys. A Stat. Mech. Its Appl. 2012, 391, 2342–2352. [Google Scholar] [CrossRef]
- Coletti, P.; Murgia, M. The network of the Italian stock market during the 2008–2011 financial crises. Algorithmic Financ. 2016, 5, 111–137. [Google Scholar] [CrossRef] [Green Version]
- Memon, B.A.; Yao, H. Structural Change and Dynamics of Pakistan Stock Market during Crisis: A Complex Network Perspective. Entropy 2019, 21, 248. [Google Scholar] [CrossRef] [Green Version]
- Memon, B.A.; Yao, H.; Tahir, R. General election effect on the network topology of Pakistan’s stock market: Network-based study of a political event. Financ. Innov. 2020, 6, 2. [Google Scholar] [CrossRef] [Green Version]
- Yin, K.; Liu, Z.; Liu, P. Trend analysis of global stock market linkage based on a dynamic conditional correlation network. J. Bus. Econ. Manag. 2017, 18, 779–800. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.; Deo, N. Correlation and network analysis of global financial indices. Phys. Rev. E 2012, 86, 026101. [Google Scholar] [CrossRef] [Green Version]
- Setiawan, K. On the Dynamic of Stock Market Integration: A Minimum Spanning Tree Analysis. Int. J. Econ. Policy Stud. 2011, 6, 43–68. [Google Scholar] [CrossRef]
- Wang, G.-J.; Xie, C.; Stanley, H.E. Correlation Structure and Evolution of World Stock Markets: Evidence from Pearson and Partial Correlation-Based Networks. Comput. Econ. 2018, 51, 607–635. [Google Scholar] [CrossRef]
- Li, B.; Pi, D. Analysis of global stock index data during crisis period via complex network approach. PLoS ONE 2018, 13, e0200600. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Zheng, Y.; Guo, K.; Jin, Z.; Huang, Z. The Evolution Characteristics of Systemic Risk in China’s Stock Market Based on a Dynamic Complex Network. Entropy 2020, 22, 614. [Google Scholar] [CrossRef]
- Liu, L.; Cao, Z.; Liu, X.; Shi, L.; Cheng, S.; Liu, G. Oil security revisited: An assessment based on complex network analysis. Energy 2020, 194, 116793. [Google Scholar] [CrossRef]
- Drożdż, S.; Kwapień, J.; Oświęcimka, P.; Stanisz, T.; Wątorek, M. Complexity in Economic and Social Systems: Cryptocurrency Market at around COVID-19. Entropy 2020, 22, 1043. [Google Scholar] [CrossRef] [PubMed]
- Guo, H.; Zhao, X.; Yu, H.; Zhang, X. Analysis of global stock markets’ connections with emphasis on the impact of COVID-19. Phys. A Stat. Mech. Its Appl. 2021, 569, 125774. [Google Scholar] [CrossRef]
- Mantegna, R.N. Hierarchical structure in financial markets. Eur. Phys. J. B-Condens. Matter Complex Syst. 1999, 11, 193–197. [Google Scholar] [CrossRef] [Green Version]
- Kruskal, J.B. On the Shortest Spanning Subtree of a Graph and the Traveling Salesman Problem. Proc. Am. Math. Soc. 1956, 7, 48–50. [Google Scholar] [CrossRef]
- Huang, C.; Zhao, X.; Su, R.; Yang, X.; Yang, X. Dynamic network topology and market performance: A case of the Chinese stock market. Int. J. Financ. Econ. 2020, 1–17. [Google Scholar] [CrossRef]
- Memon, B.A.; Yao, H.; Aslam, F.; Tahir, R. Network Analysis of Pakistan stock market during the turbulence of Economic Crisis, Business. Manag. Educ. 2019, 17, 269–285. [Google Scholar]
- Jia, X.; An, H.; Sun, X.; Huang, X.; Wang, L. Evolution of world crude oil market integration and diversification: A wavelet-based complex network perspective. Appl. Energy 2017, 185, 1788–1798. [Google Scholar] [CrossRef]
- Onnela, J.P.; Chakraborti, A.; Kaski, K.; Kertész, J. Dynamic asset trees and Black Monday. Phys. A Stat. Mech. Its Appl. 2003, 324, 247–252. [Google Scholar] [CrossRef] [Green Version]
- Onnela, J.P.; Chakraborti, A.; Kaski, K.; Kertsz, J.; Kanto, A. Asset Trees and Asset Graphs in Financial Markets. Phys. Scr. 2003, T106, 48. [Google Scholar] [CrossRef]
- Yao, H.; Memon, B.A. Network topology of FTSE 100 Index companies: From the perspective of Brexit. Phys. A Stat. Mech. Its Appl. 2019, 523, 1248–1262. [Google Scholar] [CrossRef]
- Marsden, P.V. Network Centrality, Measures of. In International Encyclopedia of the Social & Behavioral Sciences, 2nd ed.; Wright, J.D., Ed.; Elsevier: Oxford, UK, 2015; pp. 532–539. [Google Scholar]
- Golbeck, J. Chapter 3-Network Structure and Measures. In Analyzing the Social Web; Golbeck, J., Ed.; Morgan Kaufmann: Boston, MA, USA, 2013; pp. 25–44. [Google Scholar]
- Brandes, U. A faster algorithm for betweenness centrality. J. Math. Sociol. 2001, 25, 163–177. [Google Scholar] [CrossRef]
- Abuzayed, B.; Bouri, E.; Al-Fayoumi, N.; Jalkh, N. Systemic risk spillover across global and country stock markets during the COVID-19 pandemic. Econ. Anal. Policy 2021, 71, 180–197. [Google Scholar] [CrossRef]
- Mokni, K.; Mansouri, F. Conditional dependence between international stock markets: A long memory GARCH-copula model approach. J. Multinatl. Financ. Manag. 2017, 42–43, 116–131. [Google Scholar] [CrossRef]
- Baig, A.S.; Butt, H.A.; Haroon, O.; Rizvi, S.A.R. Deaths, panic, lockdowns and US equity markets: The case of COVID-19 pandemic. Financ. Res. Lett. 2021, 38, 101701. [Google Scholar] [CrossRef]
- Hong, H.; Bian, Z.; Lee, C.-C. COVID-19 and instability of stock market performance: Evidence from the U.S. Financ. Innov. 2021, 7, 12. [Google Scholar] [CrossRef]
- Plerou, V.; Gopikrishnan, P.; Nunes Amaral, L.A.; Meyer, M.; Stanley, H.E. Scaling of the distribution of price fluctuations of individual companies. Phys. Review. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1999, 60, 6519–6529. [Google Scholar] [CrossRef] [Green Version]
- He, J.; Deem, M.W. Structure and response in the world trade network. Phys. Rev. Lett. 2010, 105, 198701. [Google Scholar] [CrossRef] [Green Version]
- Al-Awadhi, A.M.; Alsaifi, K.; Al-Awadhi, A.; Alhammadi, S. Death and contagious infectious diseases: Impact of the COVID-19 virus on stock market returns. J. Behav. Exp. Financ. 2020, 27, 100326. [Google Scholar] [CrossRef] [PubMed]
- O’Donnell, N.; Shannon, D.; Sheehan, B. Immune or at-risk? Stock markets and the significance of the COVID-19 pandemic. J. Behav. Exp. Financ. 2021, 30, 100477. [Google Scholar] [CrossRef]
- Sansa, N.A. The Impact of the COVID-19 on the Financial Markets: Evidence from China and USA. Electron. Res. J. Soc. Sci. Humanit. 2020, 2, 29–39. [Google Scholar] [CrossRef]




| Degree | Frequency of Node Degree | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dec-19 | Jan-20 | Feb-20 | Mar-20 | Apr-20 | May-20 | Jun-20 | Jul-20 | Aug-20 | Sep-20 | Oct-20 | Nov-20 | Dec-20 | Jan-21 | Feb-21 | Mar-21 | |
| 1 | 24 | 28 | 23 | 30 | 22 | 26 | 25 | 23 | 19 | 27 | 24 | 25 | 26 | 26 | 24 | 19 |
| 2 | 20 | 15 | 20 | 9 | 23 | 18 | 21 | 22 | 28 | 15 | 21 | 19 | 18 | 16 | 17 | 24 |
| 3 | 8 | 8 | 9 | 11 | 9 | 8 | 7 | 9 | 8 | 12 | 7 | 8 | 8 | 10 | 12 | 13 |
| 4 | 4 | 3 | 6 | 7 | 1 | 4 | 2 | 2 | 1 | 1 | 3 | 3 | 4 | 5 | 5 | 2 |
| 5 | 2 | 4 | 0 | 1 | 3 | 1 | 1 | 1 | 1 | 2 | 3 | 3 | 1 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Memon, B.A.; Yao, H. The Impact of COVID-19 on the Dynamic Topology and Network Flow of World Stock Markets. J. Open Innov. Technol. Mark. Complex. 2021, 7, 241. https://doi.org/10.3390/joitmc7040241
Memon BA, Yao H. The Impact of COVID-19 on the Dynamic Topology and Network Flow of World Stock Markets. Journal of Open Innovation: Technology, Market, and Complexity. 2021; 7(4):241. https://doi.org/10.3390/joitmc7040241
Chicago/Turabian StyleMemon, Bilal Ahmed, and Hongxing Yao. 2021. "The Impact of COVID-19 on the Dynamic Topology and Network Flow of World Stock Markets" Journal of Open Innovation: Technology, Market, and Complexity 7, no. 4: 241. https://doi.org/10.3390/joitmc7040241
APA StyleMemon, B. A., & Yao, H. (2021). The Impact of COVID-19 on the Dynamic Topology and Network Flow of World Stock Markets. Journal of Open Innovation: Technology, Market, and Complexity, 7(4), 241. https://doi.org/10.3390/joitmc7040241





