Combining Parcel Lockers with Staffed Collection and Delivery Points: An Optimization Case Study Using Real Parcel Delivery Data (London, UK)
Abstract
:1. Introduction
- (1)
- The paper differentiates from previous research publications as it uses real parcel delivery data collected for every day over one year as opposed to probabilistic scenarios.
- (2)
- The paper evaluates the variability and inhomogeneity of parcel deliveries over one year. This is especially relevant for researchers who are doing stochastic optimization.
- (3)
- The paper also differs from previous studies as it compares modular lockers (i.e., lockers adjusted once per month depending on the demand) with combining fixed lockers and staffed CDPs. Modular lockers have been proposed as a solution to the inhomogeneous demand [25,26]. Combining fixed lockers with staffed CDPs enables advantage to be taken of the low cost per parcel for lockers and low investment costs of staffed CDPs. It is assumed that parcels are placed in fixed lockers and undeliverable parcels due to insufficient locker space are placed in staffed CDPs. Both are at the same place.
- (4)
- The paper applies the decision support method to determine the optimal number of parcels being delivered to a parcel locker, while the remaining parcels are delivered to a staffed CDP if the number of lockers is insufficient. Given that parcel lockers and staffed CDPs require financial investments at different time points (e.g., high initial investment for parcel lockers and low investment for staffed CDPs), the decision support method considers the net present value (NPV) of the investment. The decision support method can be applied to any delivery trip data set, like the one used in this study.
2. Literature
3. Materials and Methods
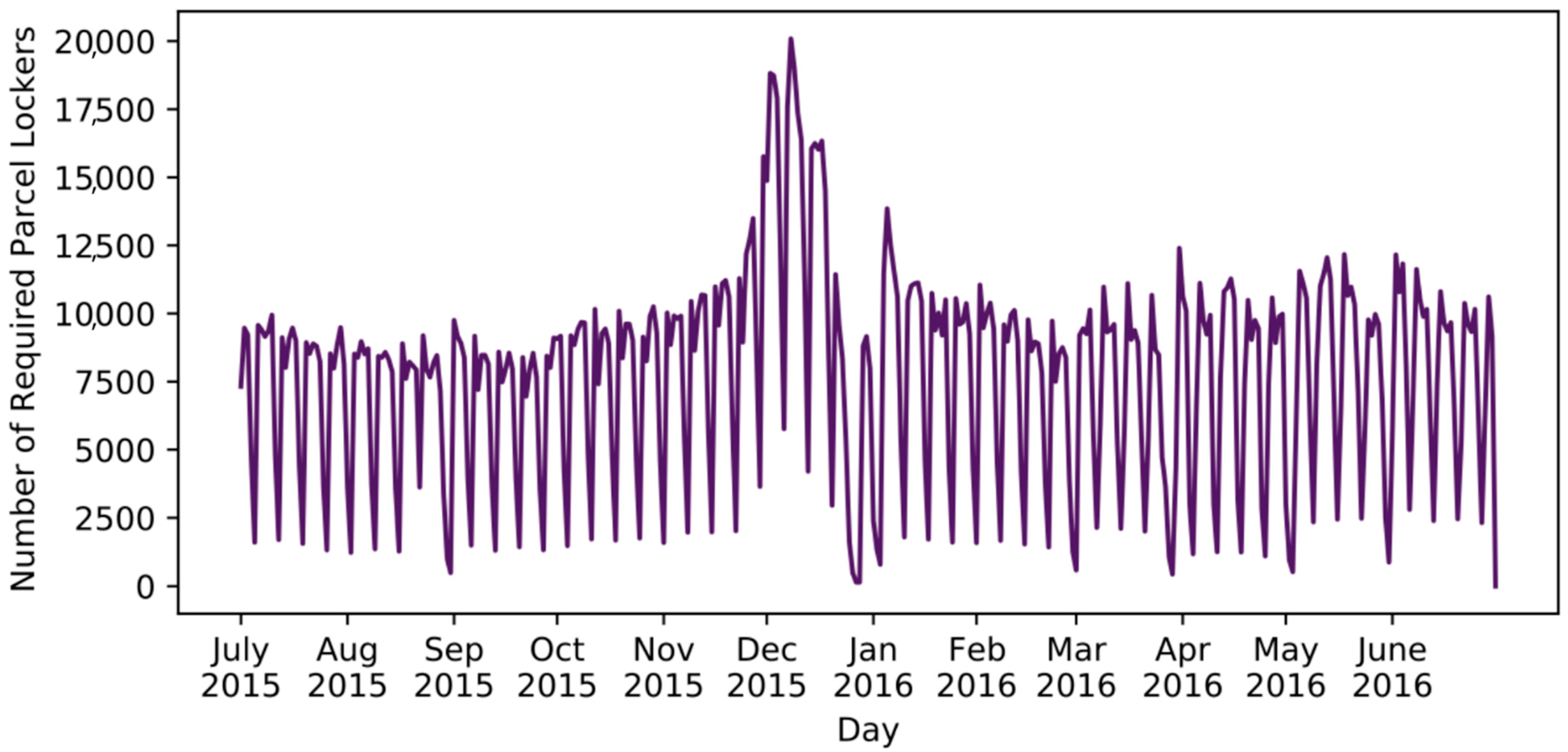
3.1. Dataset
- : Number of parcels delivered to or already in a specific CDP on day d
- : Number of successful parcel deliveries on day d
- : Number of pickups by a delivery driver on the following day (i.e., parcels returned by customer)
- : Number of parcels not picked up by customers on the previous day.
3.2. NPV/Investment
- : Cost per locker in today’s value
- : Initial investment to set up one parcel locker
- : Initial investment to set up one computer at a CDP
- : Number of lockers per computer
- : Yearly operating cost (e.g., land rent, maintenance, and driver training) per locker
- : Number of years
- : Year.
- : Cost to send one parcel to a staffed CDP in today’s monetary value
- : Cost to send one parcel to a staffed CDP
- : Number of years considered in the study
- : Increase in the fees paid to staffed CDP (0%)
- : Year.
3.3. Optimized Number of Lockers at Each Staffed CDP
- : Cost per locker in today’s value
- : Cost to send one parcel to a staffed CDP in today’s monetary value
- : Number of parcels sent to a staffed CDP per year
- : Number of days in a year
- : Number of CDPs
- : Number of parcels delivered to or are already in a specific CDP on day d
- : Number of lockers at a specific CDP
- : Cost per locker in today’s value
- : Cost to send one parcel to a staffed CDP in today’s monetary value
- : Number of parcels sent to a staffed CDP per year
- : Number of days in a year
- : Number of CDPs
- : Number of parcels delivered to or are already in a specific CDP on day d
- : Number of lockers at a specific CDP.
4. Results
4.1. Number of Locker Spaces Required per Day
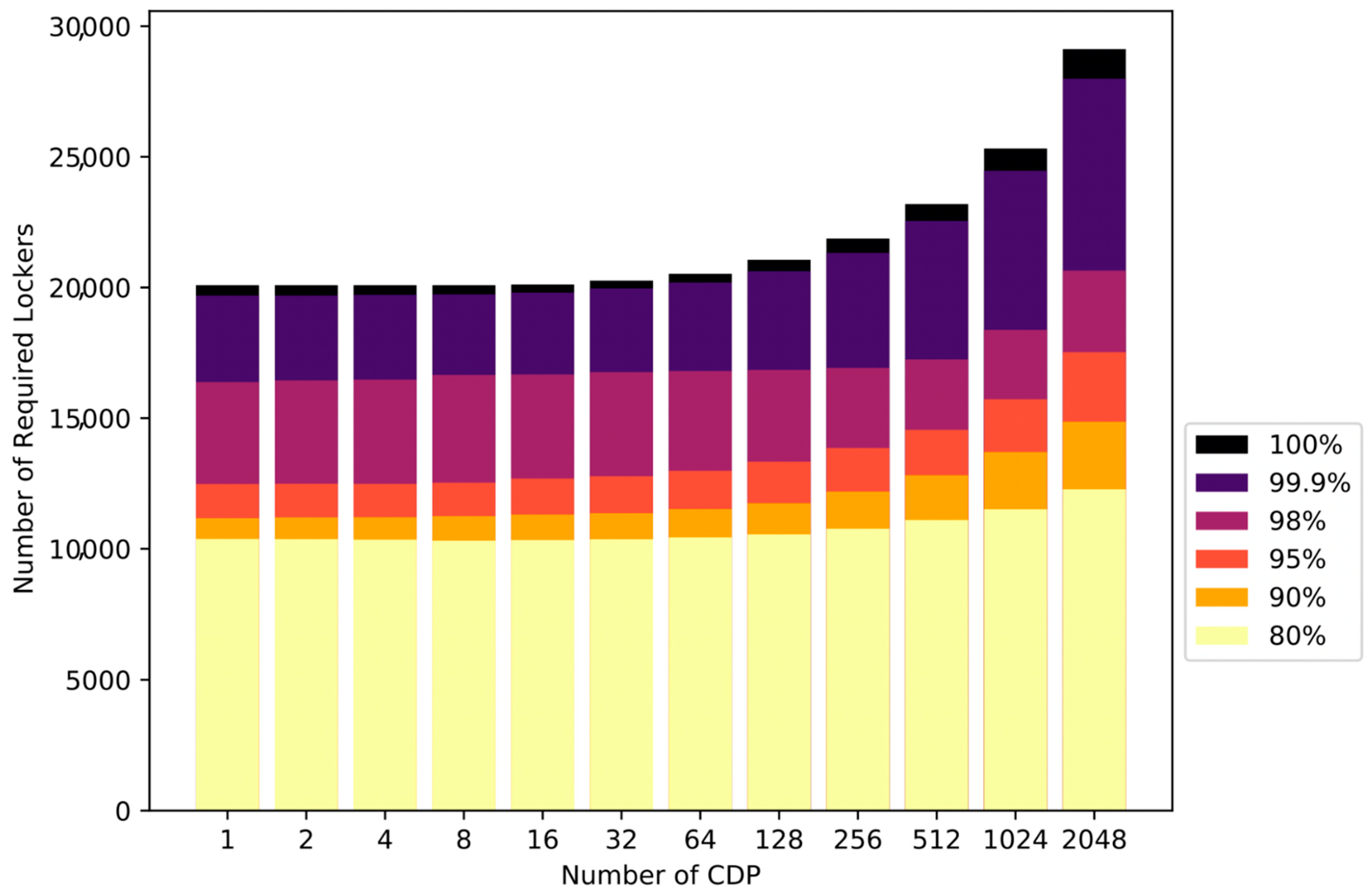
4.2. Total Number of Locker Spaces
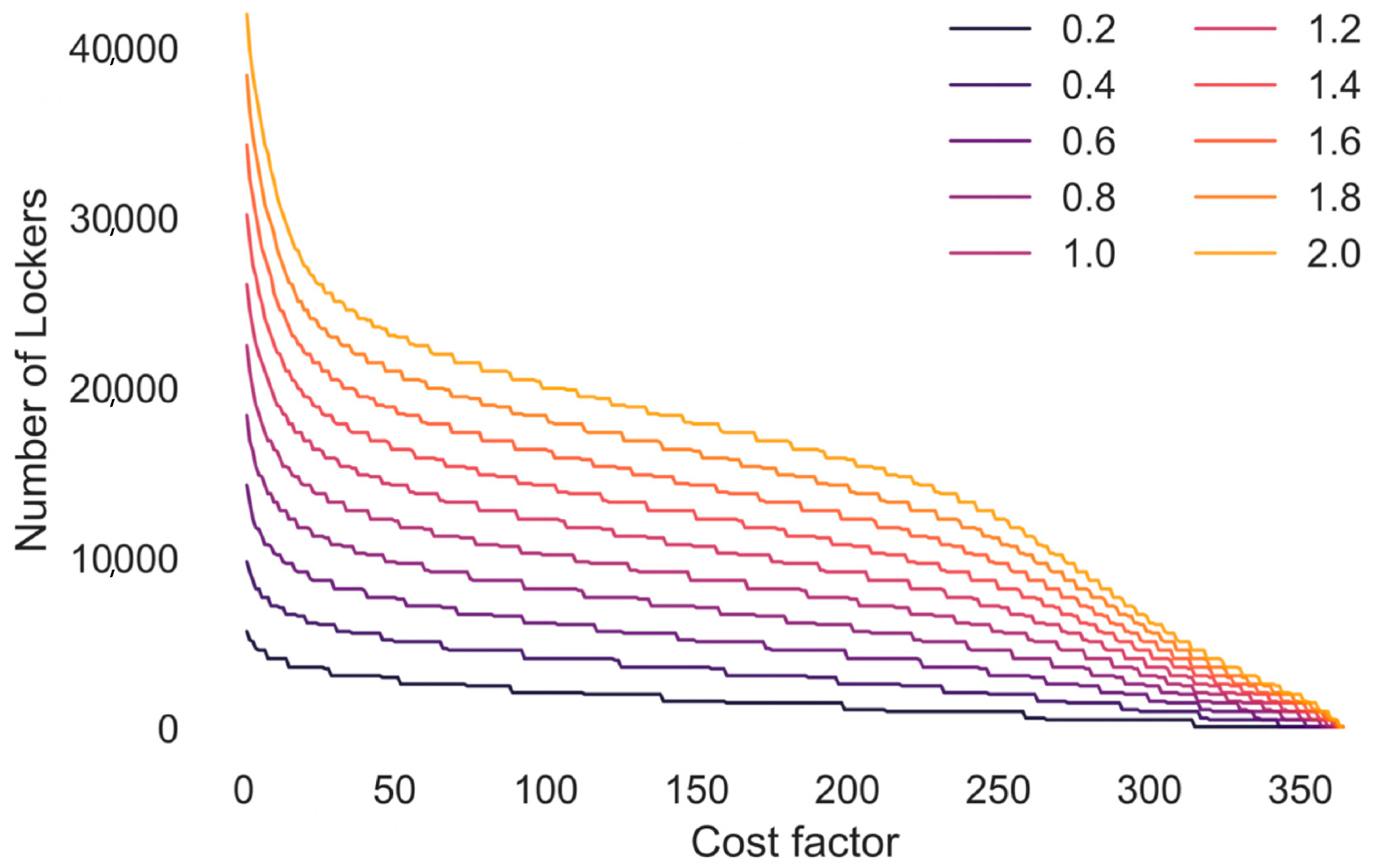
4.3. Optimal Number of Lockers
4.4. Example Calculation
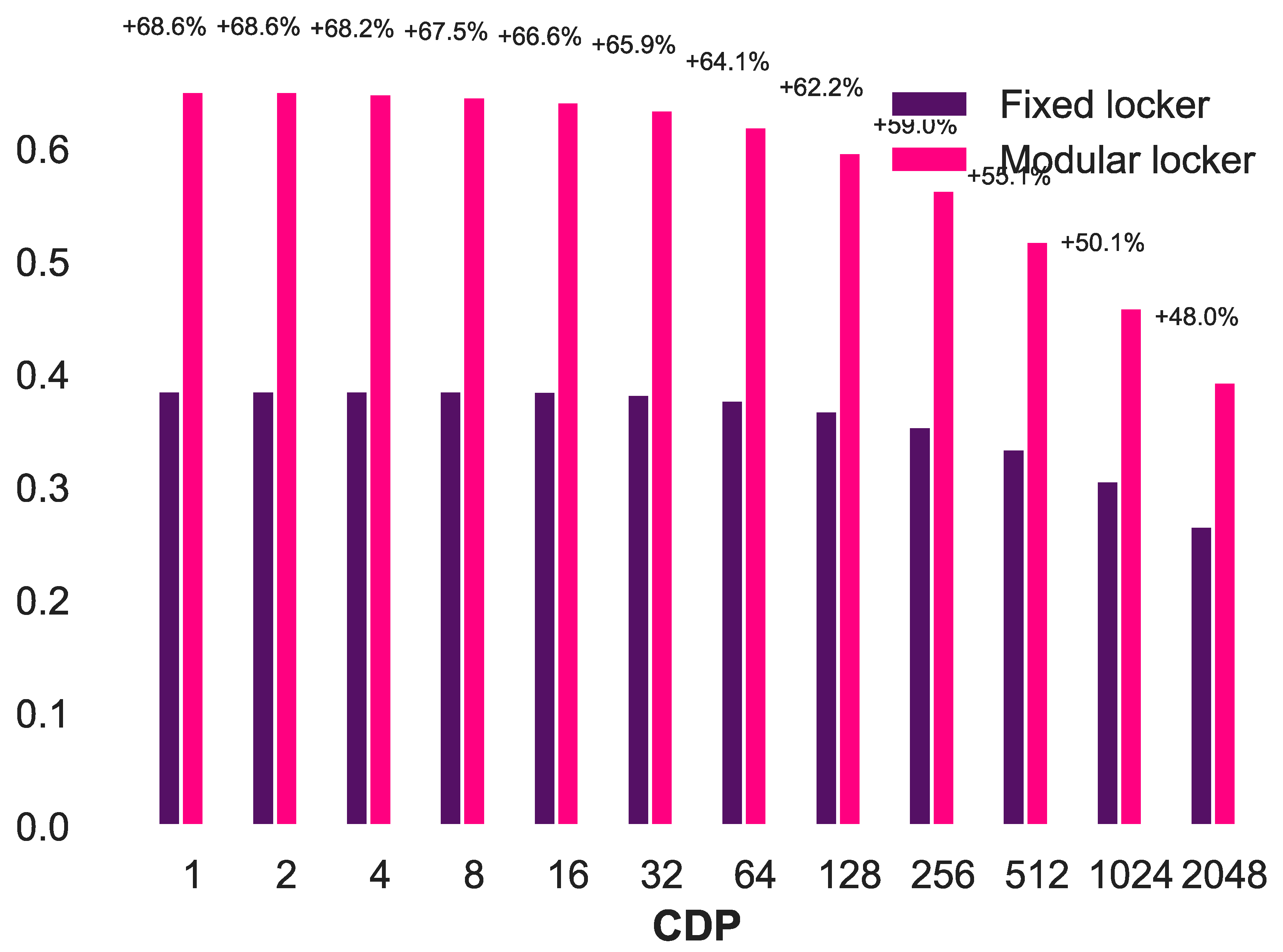
4.5. Modular Lockers vs. Fixed Lockers
5. Suggestions for Future Work and Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saad, S.M.; Bahadori, R. Sustainability evaluation of last mile food delivery: Pickup point using lockers versus home delivery. In Proceedings of the International Food Operations and Processing Simulation Workshop (FoodOPS 2018), Budapest, Hungary, 17–19 September 2018; pp. 37–42. [Google Scholar]
- Carotenuto, P.; Gastaldi, M.; Giordani, S.; Rossi, R.; Rabachin, A.; Salvatore, A. Comparison of various urban distribution systems supporting e-commerce. Point-to-point vs collection-point-based deliveries. Transp. Res. Procedia 2018, 30, 188–196. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Q.; Susilo, Y.O. Assessing the impacts of collection-delivery points to individual’s activity-travel patterns: A greener last mile alternative? Transp. Res. Part E Logist. Transp. Rev. 2019, 121, 84–99. [Google Scholar] [CrossRef]
- Weiss, C.; Onnen-Weber, U. The challenge of sustainable last mile distribution of CEP services in small towns. Transp. Res. Procedia 2019, 39, 597–604. [Google Scholar] [CrossRef]
- Ulmer, M.W.; Streng, S. Same-Day delivery with pickup stations and autonomous vehicles. Comput. Oper. Res. 2019, 108, 1–19. [Google Scholar] [CrossRef]
- Yuen, K.F.; Wang, X.; Ng, L.T.W.; Wong, Y.D. An investigation of customers’ intention to use self-collection services for last-mile delivery. Transp. Policy 2018, 66, 1–8. [Google Scholar] [CrossRef]
- Iwan, S.; Kijewska, K.; Lemke, J. Analysis of Parcel Lockers’ Efficiency as the Last Mile Delivery Solution—The Results of the Research in Poland. Transp. Res. Procedia 2016, 12, 644–655. [Google Scholar] [CrossRef] [Green Version]
- Lemke, J.; Iwan, S.; Korczak, J. Usability of the Parcel Lockers from the Customer Perspective—The Research in Polish Cities. Transp. Res. Procedia 2016, 16, 272–287. [Google Scholar] [CrossRef] [Green Version]
- de Oliveira, L.K.; Morganti, E.; Dablanc, L.; de Oliveira, R.L.M. Analysis of the potential demand of automated delivery stations for e-commerce deliveries in Belo Horizonte, Brazil. Res. Transp. Econ. 2017, 65, 34–43. [Google Scholar] [CrossRef] [Green Version]
- Kedia, A.; Kusumastuti, D.; Nicholson, A. Acceptability of collection and delivery points from consumers’ perspective: A qualitative case study of Christchurch city. Case Stud. Transp. Policy 2017, 5, 587–595. [Google Scholar] [CrossRef]
- Morganti, E.; Seidel, S.; Blanquart, C.; Dablanc, L.; Lenz, B. The Impact of E-commerce on Final Deliveries: Alternative Parcel Delivery Services in France and Germany. Transp. Res. Procedia 2014, 4, 178–190. [Google Scholar] [CrossRef] [Green Version]
- Wu, H.; Shao, D.; Ng, W.S. Locating self-collection points for last-mile logistics using public transport data. In Advances in Knowledge Discovery and Data Mining. PAKDD 2015; Cao, T., Lim, E.P., Zhou, Z.H., Ho, T.B., Cheung, D., Motoda, H., Eds.; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2015; Volume 9077, pp. 498–510. [Google Scholar] [CrossRef]
- Faugère, L.; Montreuil, B. Hyperconnected Pickup & Delivery Locker Networks. In Proceedings of the 4th International Physical Internet Conference, Graz, Austria, 4–6 July 2017; Volume 6, pp. 1–14. [Google Scholar]
- Yuen, K.F.; Wang, X.; Ma, F.; Wong, Y.D. The determinants of customers’ intention to use smart lockers for last-mile deliveries. J. Retail. Consum. Serv. 2019, 49, 316–326. [Google Scholar] [CrossRef]
- Lachapelle, U.; Burke, M.; Brotherton, A.; Leung, A. Parcel locker systems in a car dominant city: Location, characterisation and potential impacts on city planning and consumer travel access. J. Transp. Geogr. 2018, 71, 1–14. [Google Scholar] [CrossRef]
- Zenezini, G.; Lagorio, A.; Pinto, R.; de Marco, A.; Golini, R. The Collection-And-Delivery Points Implementation Process from the Courier, Express and Parcel Operator’s Perspective. IFAC-PapersOnLine 2018, 51, 594–599. [Google Scholar] [CrossRef]
- Edwards, J.; McKinnon, A.; Cherrett, T.; McLeod, F.; Song, L. The impact of failed home deliveries on carbon emissions: Are collection/delivery points environmentally-friendly alternatives? In Proceedings of the 14th Annual Logistics Research Network Conference, Cardiff, UK, 9–11 November 2009; p. M117. [Google Scholar]
- Moroz, M.; Polkowski, Z. The Last Mile Issue and Urban Logistics: Choosing Parcel Machines in the Context of the Ecological Attitudes of the Y Generation Consumers Purchasing Online. Transp. Res. Procedia 2016, 16, 378–393. [Google Scholar] [CrossRef] [Green Version]
- Punakivi, M.; Tanskanen, K. Increasing the cost efficiency of e-fulfilment using shared reception boxes. Int. J. Retail Distrib. Manag. 2002, 30, 498–507. [Google Scholar] [CrossRef] [Green Version]
- Song, L.; Cherrett, T.; McLeod, F.; Guan, W. Addressing the last mile problem: Transport impacts of collection and delivery points. Transp. Res. Rec. 2009, 2097, 9–18. [Google Scholar] [CrossRef] [Green Version]
- Jiang, L.; Chang, H.; Zhao, S.; Dong, J.; Lu, W. A Travelling Salesman Problem with Carbon Emission Reduction in the Last Mile Delivery. IEEE Access 2019, 7, 61620–61627. [Google Scholar] [CrossRef]
- Faugere, L.; Montreuil, B. Hyperconnected City Logistics: Smart Lockers Terminals & Last Mile Delivery Networks. In Proceedings of the 3rd International Physical Internet Conference, Atlanta, GA, USA, 29 June–1 July 2016; Volume 29. [Google Scholar]
- Vakulenko, Y.; Hellström, D.; Hjort, K. What’s in the parcel locker? Exploring customer value in e-commerce last mile delivery. J. Bus. Res. 2018, 88, 421–427. [Google Scholar] [CrossRef]
- Orenstein, I.; Raviv, T.; Sadan, E. Flexible parcel delivery to automated parcel lockers: Models, solution methods and analysis. EURO J. Transp. Logist. 2019, 8, 683–711. [Google Scholar] [CrossRef]
- Faugère, L.; Montreuil, B. Smart locker bank design optimization for urban omnichannel logistics: Assessing monolithic vs. modular configurations. Comput. Ind. Eng. 2020, 139, 105544. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Deloof, W.; Hadjidimitriou, S.; Vernet, G.; Schoenewolf, W. CityLog—Sustainability and efficiency of city logistics: The M-BBX (Modular BentoBox System). In Proceedings of the 2011 IEEE Forum on Integrated and Sustainable Transportation Systems, Vienna, Austria, 29 June–1 July 2011; pp. 132–135. [Google Scholar]
- Lin, Y.H.; Wang, Y.; He, D.; Lee, L.H. Last-mile delivery: Optimal locker location under multinomial logit choice model. Transp. Res. Part E Logist. Transp. Rev. 2020, 142, 102059. [Google Scholar] [CrossRef]
- Janjevic, M.; Winkenbach, M.; Merchán, D. Integrating collection-and-delivery points in the strategic design of urban last-mile e-commerce distribution networks. Transp. Res. Part E Logist. Transp. Rev. 2019, 131, 37–67. [Google Scholar] [CrossRef]
- Morganti, E.; Dablanc, L.; Fortin, F. Final deliveries for online shopping: The deployment of pickup point networks in urban and suburban areas. Res. Transp. Bus. Manag. 2014, 11, 23–31. [Google Scholar] [CrossRef] [Green Version]
- Nocera, S.; Pungillo, G.; Bruzzone, F. How to evaluate and plan the freight-passengers first-last mile. Transp. Policy 2020. [Google Scholar] [CrossRef]
- Schwerdfeger, S.; Boysen, N. Optimizing the changing locations of mobile parcel lockers in last-mile distribution. Eur. J. Oper. Res. 2020, 285, 1077–1094. [Google Scholar] [CrossRef]
- Li, J.; Ensafian, H.; Bell, M.G.H.; Geers, D.G. Deploying autonomous mobile lockers in a two-echelon parcel operation. Transp. Res. Part C Emerg. Technol. 2021, 128, 103155. [Google Scholar] [CrossRef]
- Greater London Authority (GLA). Key Performance Indicators of Freight Delivery Performance with Electric vans in Central London—London Datastore. 2017. Available online: https://data.london.gov.uk/dataset/key-performance-indicators-of-demonstrator-freight-delivery-performance-with-electric-vans-in-central-london (accessed on 18 February 2019).
- London Stock Exchange Plc. FTSE Index Records and Daily Closing Values. 2020. Available online: https://www.londonstockexchange.com/statistics/ftse/ftse.htm (accessed on 23 February 2020).
- Haldane, A.; Haskel, J.; Saunders, M.; Tenreyro, S.; Vlieghe, G. BoE Inflation Report August 2019; Bank of England: London, UK, 2019. [Google Scholar]
- Cross River Partnership. Click. Collect. Clean Air. Available online: https://clickcollect.london/ (accessed on 2 February 2020).
- Waskom, M.; Botvinnik, O.; Hobson, P.; Cole, J.B.; Halchenko, Y.; Hoyer, S.; Miles, A.; Augspurger, T.; Yarkoni, T.; Megies, T.; et al. Seaborn: V0.5.0 (November 2014). Zenodo 2014. [Google Scholar] [CrossRef]
- Gatta, V.; Marcucci, E.; Nigro, M.; Patella, S.M.; Serafini, S. Public transport-based crowdshipping for sustainable city logistics: Assessing economic and environmental impacts. Sustainability 2018, 11, 145. [Google Scholar] [CrossRef] [Green Version]
- Didenko, N.; Skripnuk, D.; Kikkas, K.; Kalinina, O.; Kosinski, E. The impact of digital transformation on the micrologistic system, and the open innovation in logistics. J. Open Innov. Technol. Mark. Complex. 2021, 7, 115. [Google Scholar] [CrossRef]
- Barykin, S.Y.; Kapustina, I.V.; Sergeev, S.M.; Yadykin, V.K. Algorithmic foundations of economic and mathematical modeling of network logistics processes. J. Open Innov. Technol. Mark. Complex. 2020, 6, 189. [Google Scholar] [CrossRef]
- Bıyık, C.; Abareshi, A.; Paz, A.; Ruiz, R.A.; Battarra, R.; Rogers, C.D.; Lizarraga, C. Smart mobility adoption: A review of the literature. J. Open Innov. Technol. Mark. Complex. 2021, 7, 146. [Google Scholar] [CrossRef]
- Solarte-Montufar, J.G.; Zartha-Sossa, J.W.; Osorio-Mora, O. Open Innovation in the Agri-Food Sector: Perspectives from a Systematic Literature Review and a Structured Survey in MSMEs. J. Open Innov. Technol. Mark. Complex. 2021, 7, 161. [Google Scholar] [CrossRef]







| Modular Locker | Fixed Locker & Staffed CDP | |
|---|---|---|
| Number of lockers | High demand season | Medium demand season |
| Land rent at CDP | More or similar to medium demand depending on season | Medium demand season |
| Locker storage space | During low demand season | N/A |
| Transport of lockers | E.g., monthly adjustments | N/A |
| Fee for staffed CDP | N/A | Ca. £0.50 per parcel [18] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schnieder, M.; Hinde, C.; West, A. Combining Parcel Lockers with Staffed Collection and Delivery Points: An Optimization Case Study Using Real Parcel Delivery Data (London, UK). J. Open Innov. Technol. Mark. Complex. 2021, 7, 183. https://doi.org/10.3390/joitmc7030183
Schnieder M, Hinde C, West A. Combining Parcel Lockers with Staffed Collection and Delivery Points: An Optimization Case Study Using Real Parcel Delivery Data (London, UK). Journal of Open Innovation: Technology, Market, and Complexity. 2021; 7(3):183. https://doi.org/10.3390/joitmc7030183
Chicago/Turabian StyleSchnieder, Maren, Chris Hinde, and Andrew West. 2021. "Combining Parcel Lockers with Staffed Collection and Delivery Points: An Optimization Case Study Using Real Parcel Delivery Data (London, UK)" Journal of Open Innovation: Technology, Market, and Complexity 7, no. 3: 183. https://doi.org/10.3390/joitmc7030183
APA StyleSchnieder, M., Hinde, C., & West, A. (2021). Combining Parcel Lockers with Staffed Collection and Delivery Points: An Optimization Case Study Using Real Parcel Delivery Data (London, UK). Journal of Open Innovation: Technology, Market, and Complexity, 7(3), 183. https://doi.org/10.3390/joitmc7030183





