A Forecasting Model for Economic Growth and CO2 Emission Based on Industry 4.0 Political Policy under the Government Power: Adapting a Second-Order Autoregressive-SEM
Abstract
1. Introduction
2. Literature Review
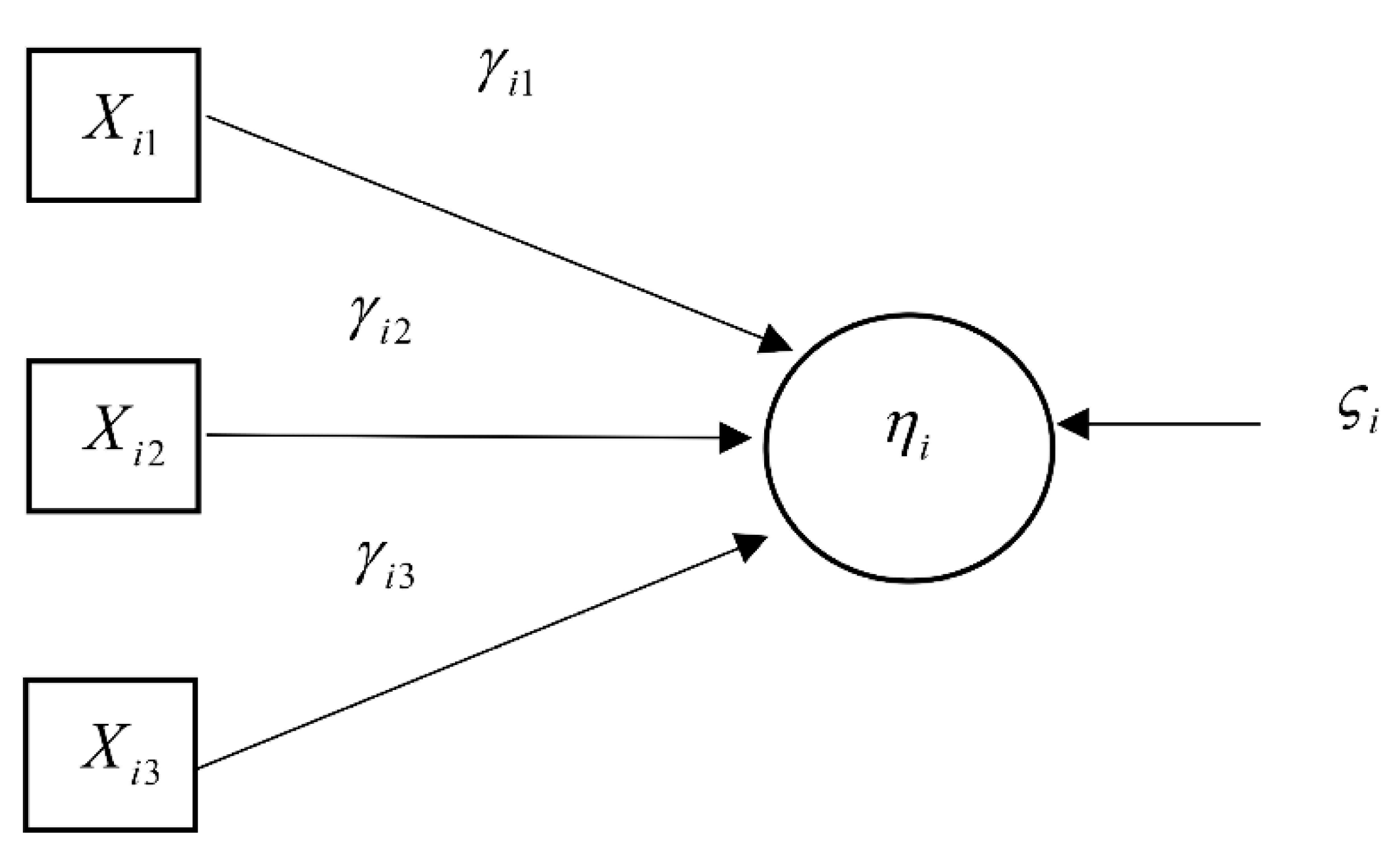
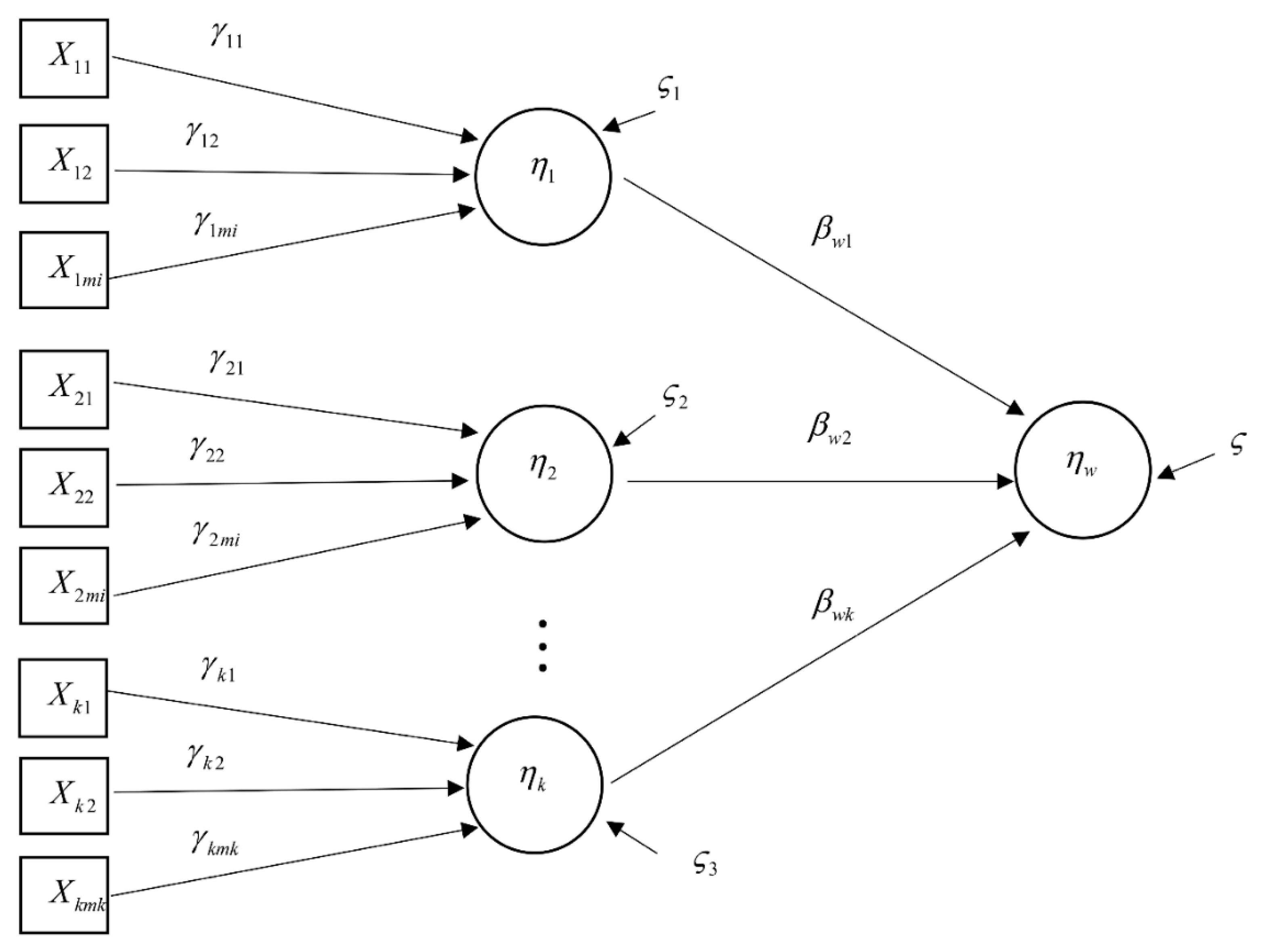
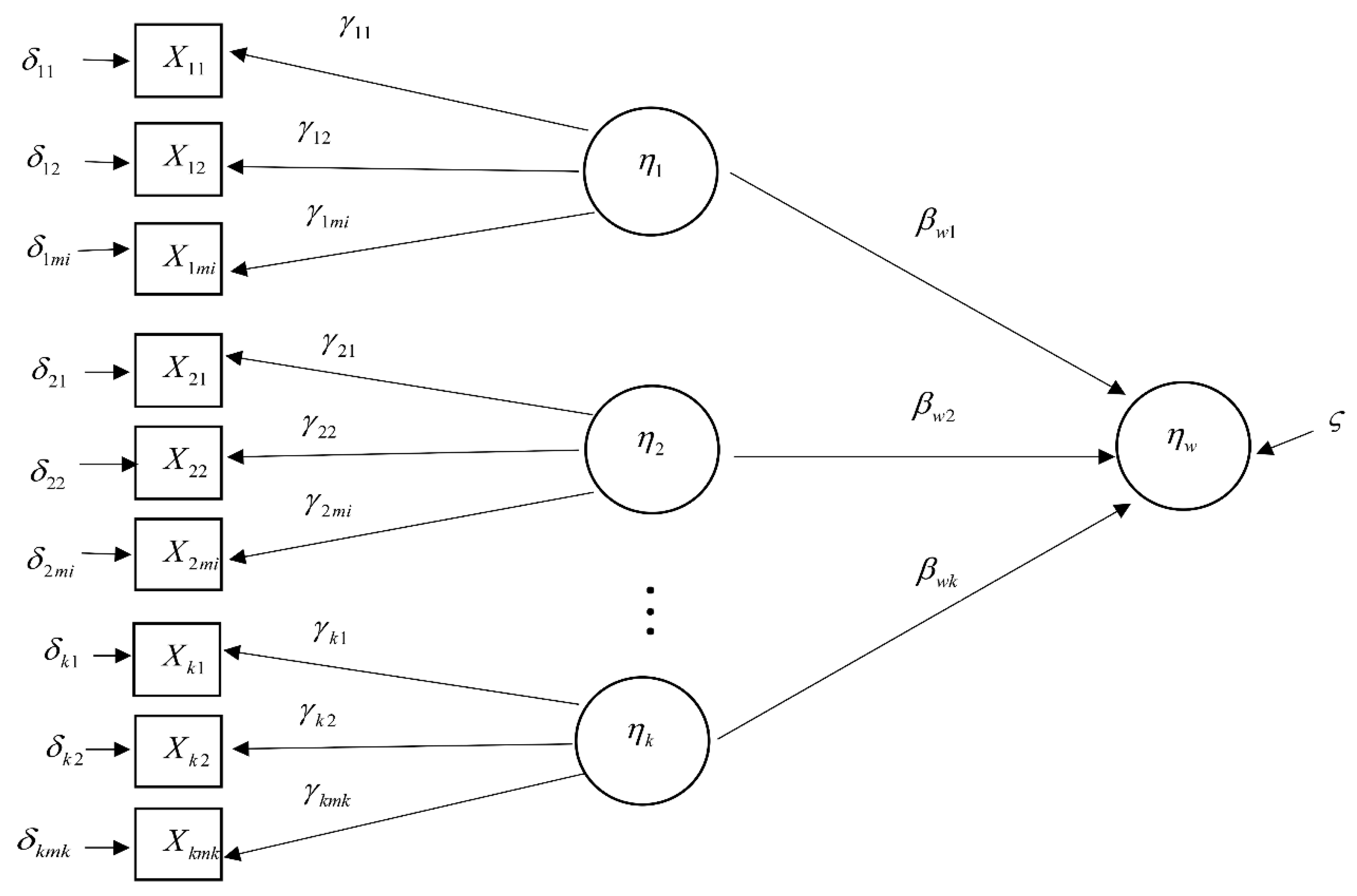
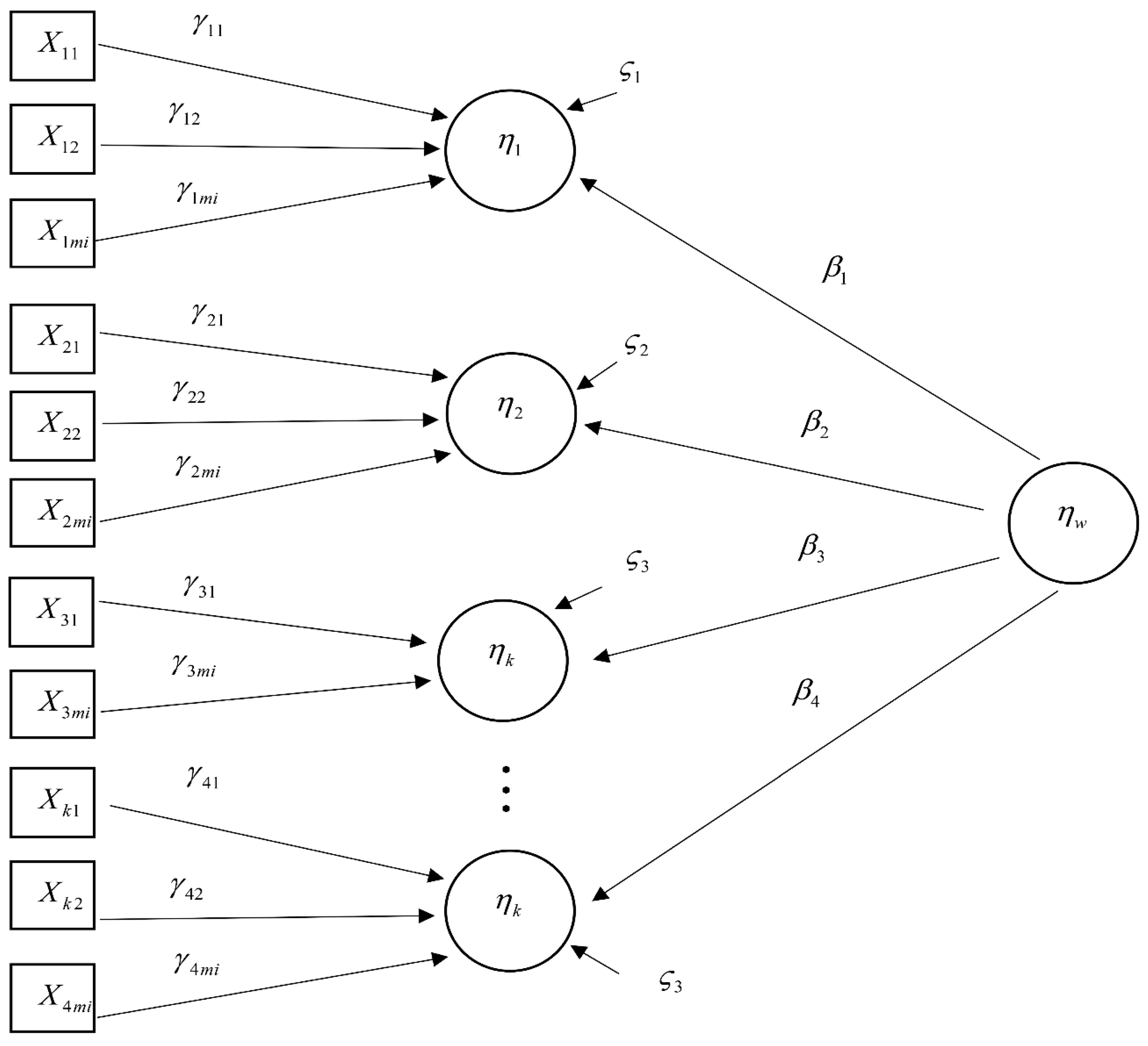
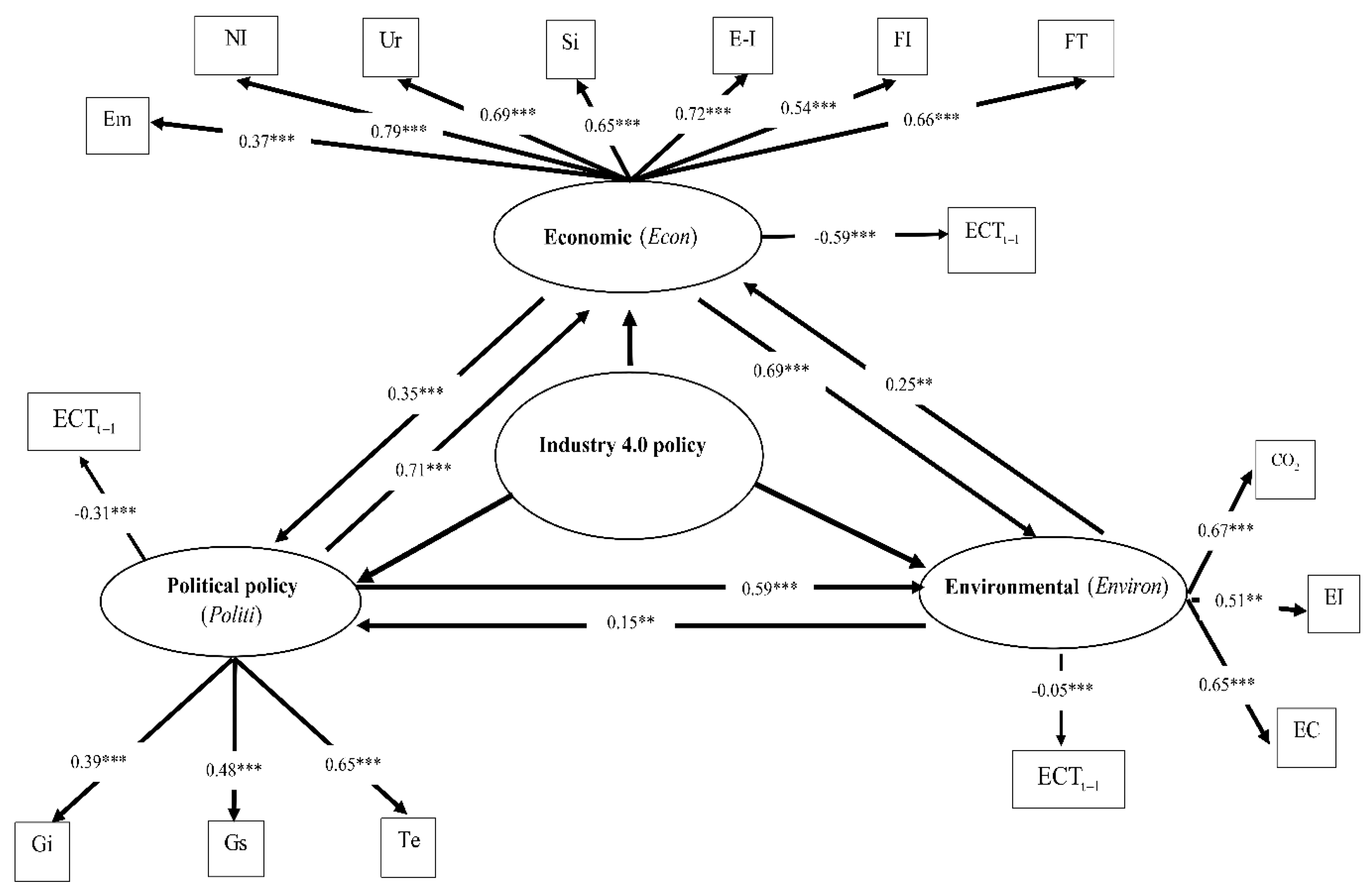
- Select variables for use in constructing the second order autoregressive-SEM, in which objectives have been specified by the government in the national strategy. The latent variables are political policy , the economy , and the environment , while the observed variables are national income , urbanization rate , industrial structure , net exports , foreign investment , foreign tourism , employment , government investment , government subsidy , technology investment , energy consumption , energy intensity , and carbon dioxide emission . The reason of considering the observed variables is to formulate a national objective of Thailand in terms of political policy , which emphasizes three main indicators: government investment , government subsidy , and technology investment . The indicators in economy are inclusive of national income , urbanization rate , industrial structure , net exports , foreign investment , foreign tourism , and employment , while the indicators in environment are energy consumption , energy intensity , and carbon dioxide emissions .
- Ensure all observed variables to be stationary at the first difference level, based on the concept of the augmented Dickey–Fuller [51].
- Forecast GNP and CO2 emission by deploying the second order autoregressive-SEM for the years 2020 to 2035, as shown in the following diagram.
3. Materials and Methods
3.1. Stationary
3.1.1. Sequence : Autoregressive Model
3.1.2. Stationary Test of Time Series
3.2. Second Order Autoregressive—SEM
- (1)
- Indicators come from different sources—that is, from specific points of different domains that are non-interchangeable—and, if some indicators are partially cut in the same way as the prior case of reflective indicator, the nature of the construct will vary and the meaning will not conform exactly to theory; there may also be a lack of construct validity.
- (2)
- Indicators may not be correlated, or some correlation may be positive or negative.
- (3)
- Indicators will not have error term which is in equation , will be the error of and not , which means the formative measurement model has no measurement error.
- (4)
- Each value of equation of formative measurement model will not be estimated in the form of a simple straight-line regression equation since it will be under-identified. It should be estimated by multiple regression equation only.
High rank model
3.3. Measurement of the Forecasting Performance
4. Empirical Analysis
4.1. Screening Influencing Factors for Model Input
4.2. Analysis of Co-Integration
4.3. Formation of Analysis Modeling with the Second Order Autoregressive-SEM
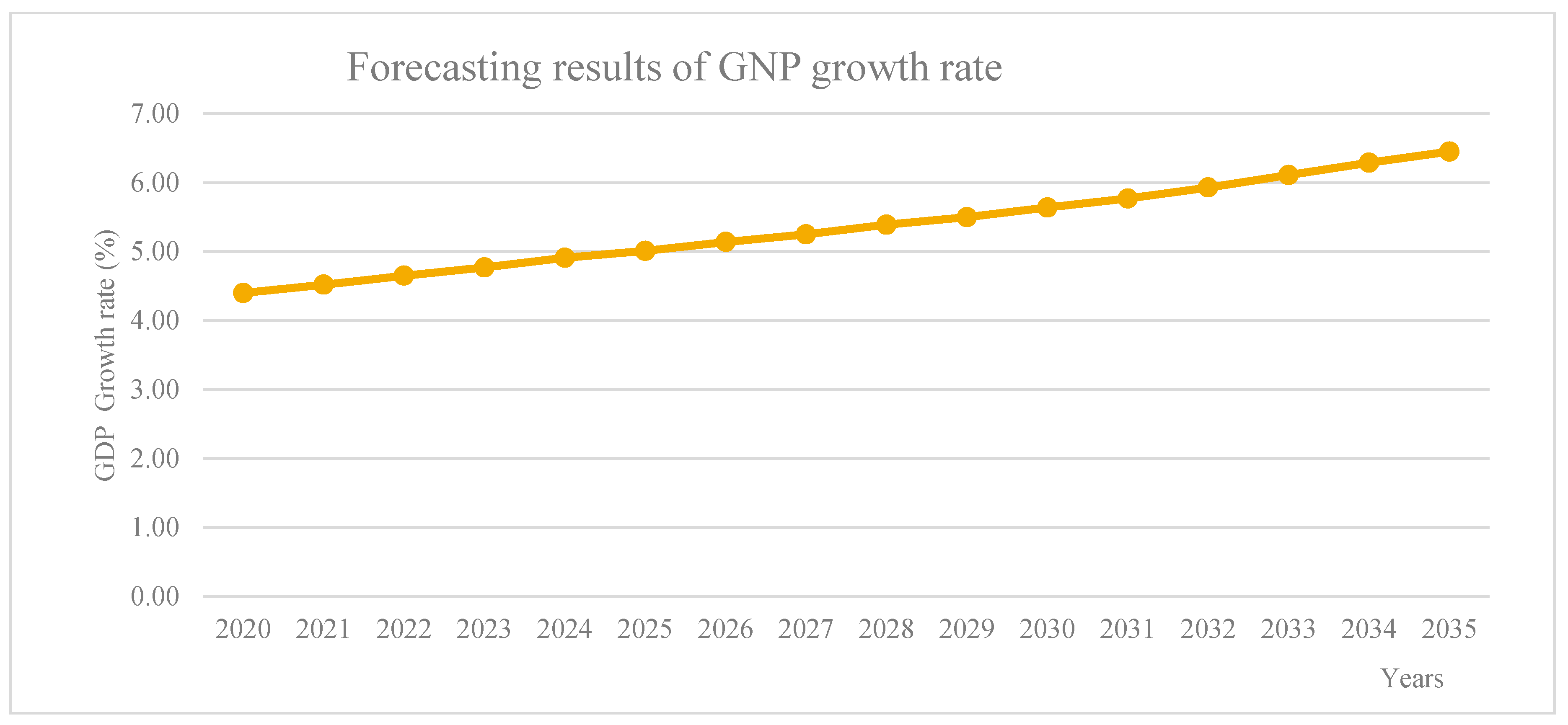
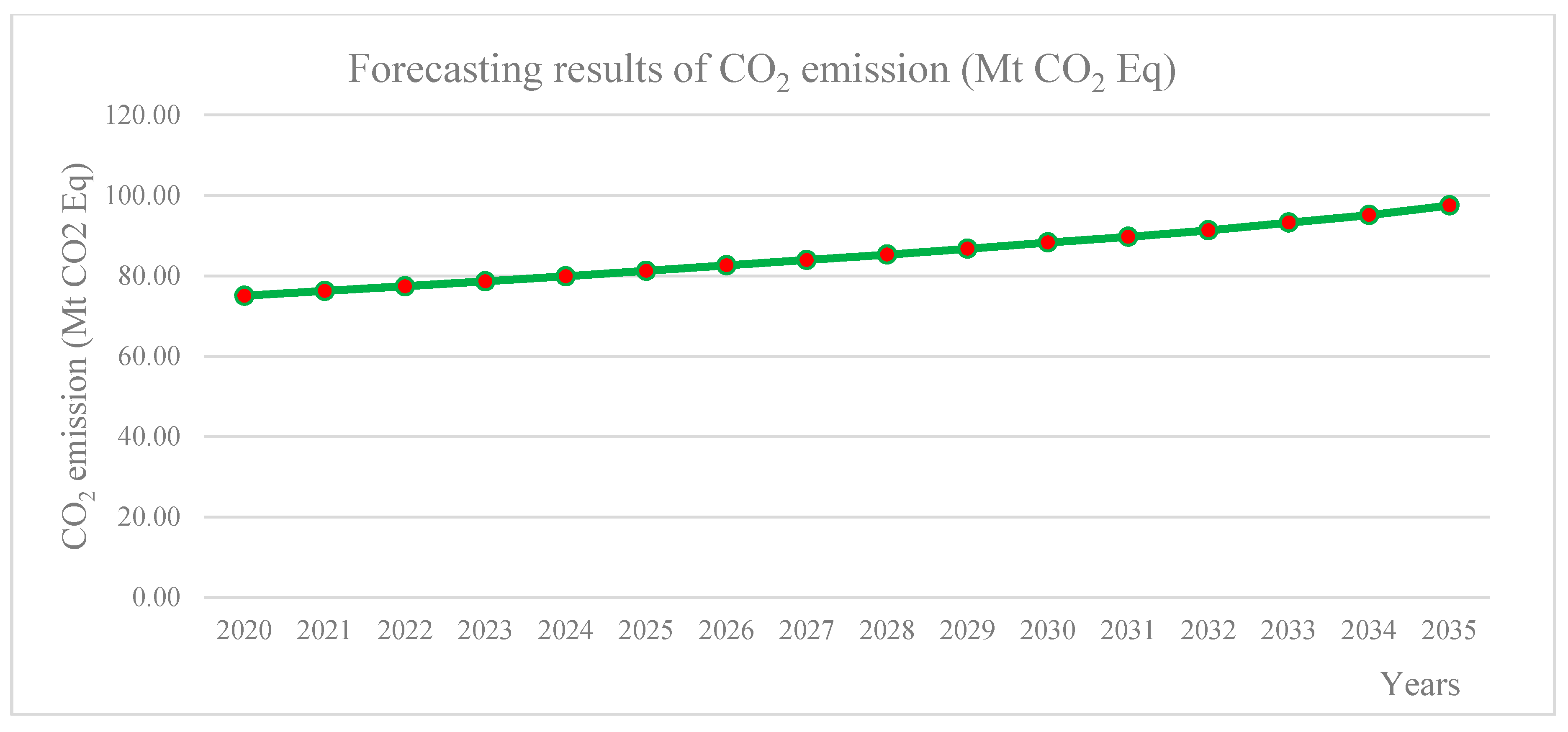
4.4. A Forecasting Model on the Changes of GNP and CO2 Emission Based on the Second Order Autoregressive-SEM
5. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Office of the National Economic and Social Development Board (NESDB). Available online: http://www.nesdb.go.th/nesdb_en/more_news.php?cid=154&filename=index (accessed on 15 June 2019).
- National Statistic Office Ministry of Information and Communication Technology. Available online: http://web.nso.go.th/index.htm (accessed on 20 June 2019).
- Sutthichaimethee, P.; Dockthaisong, B. A Relationship of Causal Factors in the Economic, Social, and Environmental Aspects Affecting the Implementation of Sustainability Policy in Thailand: Enriching the Path Analysis Based on a GMM Model. Resources 2018, 7, 87. [Google Scholar] [CrossRef]
- Sutthichaimethee, P.; Kubaha, K. The Efficiency of Long-Term Forecasting Model on Final Energy Consumption in Thailand’s Petroleum Industries Sector: Enriching the LT-ARIMAXS Model under a Sustainability Policy. Energies 2018, 11, 2063. [Google Scholar] [CrossRef]
- Office of Natural Resources and Environmental Policy and Planning. Available online: http://www.onep.go.th (accessed on 15 June 2019).
- Department of Alternative Energy Development and Efficiency. Available online: http://www.dede.go.th/ewtadmin/ewt/dede_web/ewt_news.php?nid=47140 (accessed on 15 June 2019).
- Sutthichaimethee, P.; Ariyasajjakorn, D. Forecast of Carbon Dioxide Emissions from Energy Consumption in Industry Sectors in Thailand. Environ. Clim. Technol. 2018, 22, 107–117. [Google Scholar] [CrossRef]
- Thailand Greenhouse Gas Management Organization (Public Organization). Available online: http://www.tgo.or.th/2015/thai/content.php?s1=7&s2=16&sub3=sub3 (accessed on 16 June 2019).
- Savaresi, A. The Paris Agreement: An Early Assessment. Environ. Policy Law 2016, 46, 14–18. [Google Scholar]
- Laina, E. Sustainable Development in Operation. Environ. Policy Law 2016, 46, 47–49. [Google Scholar]
- Krapp, R. Sustainable Development in the Second Committee. Environ. Policy Law 2016, 46, 10–13. [Google Scholar]
- Uddin, M.K. Climate Change and Global Environmental Politics: North-South Divide. Environ. Policy Law 2017, 47, 106–114. [Google Scholar] [CrossRef]
- Moore, P.; Pereira, E.S.; Duggin, G. Developing Environmental Law for All Citizens. Environ. Policy Law 2015, 45, 88–98. [Google Scholar]
- Savaresi, A. Developments in Environmental Law. Environ. Policy Law 2012, 42, 365–369. [Google Scholar]
- Mid-term Review. Global Progress in Environmental Law. Environ. Policy Law 2016, 46, 23–27. [Google Scholar]
- Oh, H.M.; Shin, H.Y. A Study on the Relationship between Analysts Cash Flow Forecasts Issuance and Accounting Information. Evidence from Korea. Sustainability 2019, 11, 3399. [Google Scholar] [CrossRef]
- He, X.; Yin, C. The Impact of Strategic Deviance on Analysts’ Earnings Forecasts: Evidence from China. Nankai Business Review International. Available online: https://www.emerald.com/insight/search?q=Xiqiong+He+Changping+Yin&showAll=true (accessed on 10 June 2019).
- Dong, G.H.; Zhang, P.; Sun, B.; Zhang, L.; Chen, X.; Ma, N.; Yu, F.; Guo, H.; Huang, H.; Lee, Y.L.; et al. Long-Term Exposure to Ambient Air Pollution and Respiratory Disease Mortality in Shenyang, China: A 12-Year Population-Based Retrospective Cohort Study. Respiration 2012, 84, 360–368. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.; Ren, W. Application of a Hybrid Model Based on Echo State Network and Improved Particle Swarm Optimization in PM2.5 Concentration Forecasting: A Case Study of Beijing, China. Sustainability 2019, 11, 3096. [Google Scholar] [CrossRef]
- Xu, X.; Ren, W. Prediction of Air Pollution Concentration Based on mRMR and Echo State Network. Appl. Sci. 2019, 9, 1811. [Google Scholar] [CrossRef]
- Tsui, W.H.K.; Balli, H.O.; Gilbey, A.; Gow, H. Forecasting of Hong Kong airport’s passenger throughput. Tour. Manag. 2014, 42, 62–76. [Google Scholar] [CrossRef]
- Mahajan, S.; Chen, L.J.; Tsai, T.C. Short-Term PM2.5 Forecasting Using Exponential Smoothing Method: A Comparative Analysis. Sensors 2018, 18, 3223. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, L.; Liu, S.; Wang, G. Multi-Step Wind Speed Forecasting Based On Ensemble Empirical Mode Decomposition, Long Short Term Memory Network and Error Correction Strategy. Energies 2019, 12, 1822. [Google Scholar] [CrossRef]
- Wu, Q.; Lin, H. Short-Term Wind Speed Forecasting Based on Hybrid Variational Mode Decomposition and Least Squares Support Vector Machine Optimized by Bat Algorithm Model. Sustainability 2019, 11, 652. [Google Scholar] [CrossRef]
- Methaprayoon, K.; Lee, W.-J.; Rasmiddatta, S.; Liao, J.R.; Ross, R.J. Multistage Artificial Neural Network Short-Term Load Forecasting Engine With Front-End Weather Forecast. IEEE Trans. Ind. Appl. 2007, 43, 1410–1416. [Google Scholar] [CrossRef]
- Fan, S.; Hyndman, R.J. Density Forecasting Electricity Demand in Australian National Electricity Market. In Proceedings of the IEEE Power & Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–4. [Google Scholar]
- Ramos, P.; Oliveira, J.M. A Procedure for Identification of Appropriate State Space and ARIMA Models Based on Time-Series Cross-Validation. Algorithms 2016, 9, 76. [Google Scholar] [CrossRef]
- Shi, J.; Ding, Z.; Lee, W.J.; Yang, Y.; Liu, Y.; Zhang, M. Hybrid Forecasting Model for Very-Short Term Wind Power Forecasting Based on Grey Relational Analysis and Wind Speed Distribution Features. IEEE Trans. Smart Grid 2014, 5, 521–526. [Google Scholar] [CrossRef]
- Chen, K.S.; Lin, K.P.; Yan, J.X.; Hsieh, W.L. Renewable Power Output Forecasting Using Least-Squares Support Vector Regression and Google Data. Sustainability 2019, 11, 3009. [Google Scholar] [CrossRef]
- Lu, P.; Ye, L.; Sun, B.; Zhang, C.; Zhao, Y.; Teng, J. A New Hybrid Prediction Method of Ultra-Short-Term Wind Power Forecasting Based on EEMD-PE and LSSVM Optimized by the GSA. Energies 2018, 11, 697. [Google Scholar] [CrossRef]
- Guan, W.; Chung, K.; Cheung, K.W.; Sun, X.; Luh, P.B.; Michel, L.D.; Corbo, S. Advanced Load Forecast with Hierarchical Forecasting Capability. In Proceedings of the IEEE Power & Energy Society General Meeting, Vancouver, BC, Canada, 21–25 July 2013. [Google Scholar]
- Xie, J.; Hong, T.; Stroud, J. Long-Term Retail Energy Forecasting with Consideration of Residential Customer Attrition. IEEE Trans. Smart Grid 2015, 6, 2245–2252. [Google Scholar] [CrossRef]
- Sun, S.; Wei, L.; Xu, J.; Jin, Z. A New Wind Speed Forecasting Modeling Strategy Using Two-Stage Decomposition, Feature Selection and DAWNN. Energies 2019, 12, 334. [Google Scholar] [CrossRef]
- Bobinaite, V.; Juozapaviciene, A.; Konstantinaviciute, I. Assessment of Causality Relationship between Renewable Energy Consumption and Economic Growth in Lithuania. Eng. Econ. 2011, 22, 510–518. [Google Scholar] [CrossRef]
- Soava, G.; Mehedintu, A.; Sterpu, M.; Raduteanu, M. Impact of Renewable Energy Consumption on Economic Growth: Evidence from European Union Countries. Technol. Econ. Dev. Econ. 2018, 24, 914–932. [Google Scholar] [CrossRef]
- Inglesi-Lotz, R. The impact of renewable energy consumption to economic growth: A panel data application. Energy Econ. 2016, 53, 58–63. [Google Scholar] [CrossRef]
- Pao, H.T.; Fu, H.C. Renewable energy, non-renewable energy and economic growth in Brazil. Renew. Sustain. Energy Rev. 2013, 25, 381–392. [Google Scholar] [CrossRef]
- Rafiq, S.; Salim, R. The linkage between energy consumption and income in six emerging economies of Asia an empirical analysis. Int. J. Emerg. Mark. 2011, 6, 50–73. [Google Scholar] [CrossRef]
- Chontanawat, J.; Hunt, L.C.; Pierse, R. Does energy consumption cause economic growth? Evidence from a systematic study of over 100 countries. J. Policy Model. 2008, 30, 209–220. [Google Scholar] [CrossRef]
- Sterpu, M.; Soava, G.; Mehedintu, A. Impact of Economic Growth and Energy Consumption on Greenhouse Gas Emissions: Testing Environmental Curves Hypotheses on EU Countries. Sustainability 2018, 10, 3327. [Google Scholar] [CrossRef]
- Jiang, F.; Yang, X.; Li, S. Comparison of Forecasting India’s Energy Demand Using an MGM, ARIMA Model, MGM-ARIMA Model, and BP Neural Network Model. Sustainability 2018, 10, 2225. [Google Scholar] [CrossRef]
- Wang, L.; Zhan, L.; Li, R. Prediction of the Energy Demand Trend in Middle Africa—A Comparison of MGM, MECM, ARIMA and BP Models. Sustainability 2019, 11, 2436. [Google Scholar] [CrossRef]
- Ma, M.; Su, M.; Li, S.; Jiang, F.; Li, R. Predicting Coal Consumption in South Africa Based on Linear (Metabolic Grey Model), Nonlinear (Non-Linear Grey Model), and Combined (Metabolic Grey Model-Autoregressive Integrated Moving Average Model) Models. Sustainability 2018, 10, 2552. [Google Scholar] [CrossRef]
- Boyd, G.; Na, D.; Li, Z.; Snowling, S.; Zhang, Q.; Zhou, P. Influent Forecasting for Wastewater Treatment Plants in North America. Sustainability 2019, 11, 1764. [Google Scholar] [CrossRef]
- Al-Douri, Y.K.; Hamodi, H.; Lundberg, J. Time Series Forecasting Using a Two-Level Multi-Objective Genetic Algorithm: A Case Study of Maintenance Cost Data for Tunnel Fans. Algorithms 2018, 11, 123. [Google Scholar] [CrossRef]
- Alsharif, M.H.; Younes, M.K.; Kim, J. Time Series ARIMA Model for Prediction of Daily and Monthly Average Global Solar Radiation: The Case Study of Seoul, South Korea. Symmetry 2019, 11, 240. [Google Scholar] [CrossRef]
- Liu, Q.; Shen, Y.; Wu, L.; Li, J.; Zhuang, L.; Wang, S. A hybrid FCW-EMD and KF-BA-SVM based model for short-term load forecasting. CSEE J. Power Energy Syst. 2018, 4, 226–237. [Google Scholar] [CrossRef]
- Lee, C.W.; Lin, B.Y. Application of Hybrid Quantum Tabu Search with Support Vector Regression (SVR) for Load Forecasting. Energies 2016, 9, 873. [Google Scholar] [CrossRef]
- Cai, G.; Wang, W.; Lu, J. A Novel Hybrid Short Term Load Forecasting Model Considering the Error of Numerical Weather Prediction. Energies 2016, 9, 994. [Google Scholar] [CrossRef]
- Liu, B.; Nowotarski, J.; Hong, T.; Weron, R. Probabilistic Load Forecasting via Quantile Regression Averaging on Sister Forecasts. IEEE Trans. Smart Grid 2017, 8, 730–737. [Google Scholar] [CrossRef]
- Dickey, D.A.; Fuller, W.A. Likelihood ratio statistics for autoregressive time series with a unit root. Econometrica 1981, 49, 1057–1072. [Google Scholar] [CrossRef]
- Johansen, S.; Juselius, K. Maximum likelihood estimation and inference on cointegration with applications to the demand for money. Oxf. Bull. Econ. Stat. 1990, 52, 169–210. [Google Scholar] [CrossRef]
- Johansen, S. Likelihood-Based Inference in Cointegrated Vector Autoregressive Models; Oxford University Press (OUP): New York, NY, USA, 1995. [Google Scholar]
- MacKinnon, J. Critical Values for Cointegration Test in Long-Run Economic Relationships; Engle, R., Granger, C., Eds.; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Sutthichaimethee, P. Forecasting Economic, Social and Environmental Growth in the Sanitary and Service Sector Based on Thailand’s Sustainable Development Policy. J. Ecol. Eng. 2018, 19, 205–210. [Google Scholar] [CrossRef]
- Sutthichaimethee, P.; Kubaha, K. A Relational Analysis Model of the Causal Factors Influencing CO2 in Thailand’s Industrial Sector under a Sustainability Policy Adapting the VARIMAX-ECM Model. Energies 2018, 11, 1704. [Google Scholar] [CrossRef]
- Enders, W. Applied Econometrics Time Series; Wiley Series in Probability and Statistics; University of Alabama: Tuscaloosa, AL, USA, 2010. [Google Scholar]
- Harvey, A.C. Forecasting, Structural Time Series Models and the Kalman Filter; Cambridge University Press: Cambridge, UK, 1989. [Google Scholar]
- Sutthichaimethee, P.; Ariyasajjakorn, D. The Revised Input-Output Table to Determine Total Energy Content and Total Greenhouse Gas Emission Factors in Thailand. J. Ecol. Eng. 2017, 18, 166–170. [Google Scholar] [CrossRef]
- Sutthichaimethee, P. Varimax Model to Forecast the Emission of Carbon Dioxide from Energy Consumption in Rubber and Petroleum Industries Sectors in Thailand. J. Ecol. Eng. 2017, 18, 112–117. [Google Scholar] [CrossRef][Green Version]
- Sutthichaimethee, P.; Ariyasajjakorn, D. Forecasting Model of Ghg Emission in Manufacturing Sectors of Thailand. J. Ecol. Eng. 2017, 18, 18–24. [Google Scholar] [CrossRef][Green Version]
- Sutthichaimethee, P. Modeling Environmental Impact of Machinery Sectors to Promote Sustainable Development of Thailand. J. Ecol. Eng. 2016, 17, 18–25. [Google Scholar] [CrossRef]
- Sutthichaimethee, P.; Sawangdee, Y. Model of Environmental Problems Priority Arising from the use of Environmental and Natural Resources in Machinery Sectors of Thailand. Environ. Clim. Technol. 2016, 17, 18–29. [Google Scholar] [CrossRef]

| Stationary at First Difference I (1) | MacKinnon Critical Value | ||
|---|---|---|---|
| Variables | Tau test | 1% | 5% |
| −5.75 *** | −4.05 | −3.25 | |
| −5.02 *** | −4.05 | −3.25 | |
| −5.11 *** | −4.05 | −3.25 | |
| −4.99 *** | −4.05 | −3.25 | |
| −4.35 *** | −4.05 | −3.25 | |
| −4.71 *** | −4.05 | −3.25 | |
| −4.69 *** | −4.05 | −3.25 | |
| −4.25 *** | −4.05 | −3.25 | |
| −4.31 *** | −4.05 | −3.25 | |
| −5.55 *** | −4.05 | −3.25 | |
| −5.45 *** | −4.05 | −3.25 | |
| −4.65 *** | −4.05 | −3.25 | |
| −5.81 *** | −4.05 | −3.25 | |
| Variables | Co-Integration Value | MacKinnon Critical Value | ||
|---|---|---|---|---|
| , , , , , , , , , ,, , | Trace statistic test | Max-Eigen statistic test | 1% | 5% |
| 205.05 *** | 102.11 *** | 15.25 | 10.05 | |
| Dependent Variables | Type of Effect | Independent Variables | |||
|---|---|---|---|---|---|
| Political policy | DE | - | 0.35 *** | 0.15 ** | −0.31 *** |
| IE | - | 0.12 *** | 0.04 ** | - | |
| Economy | DE | 0.71 *** | - | 0.25 ** | −0.59 *** |
| IE | 0.15 *** | - | 0.01 ** | - | |
| Environment | DE | 0.59 *** | 0.69 *** | - | −0.05 *** |
| IE | 0.02 *** | 0.35 *** | - | - | |
| Forecasting Model | MAPE (%) | RMSE (%) |
|---|---|---|
| ML model | 22.25 | 20.59 |
| BP model | 15.22 | 15.65 |
| ANN model | 12.05 | 13.11 |
| gray model | 9.25 | 10.59 |
| ARIMA model | 4.94 | 6.88 |
| Second Order Autoregressive-SEM | 1.02 | 1.51 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sutthichaimethee, P.; Chatchorfa, A.; Suyaprom, S. A Forecasting Model for Economic Growth and CO2 Emission Based on Industry 4.0 Political Policy under the Government Power: Adapting a Second-Order Autoregressive-SEM. J. Open Innov. Technol. Mark. Complex. 2019, 5, 69. https://doi.org/10.3390/joitmc5030069
Sutthichaimethee P, Chatchorfa A, Suyaprom S. A Forecasting Model for Economic Growth and CO2 Emission Based on Industry 4.0 Political Policy under the Government Power: Adapting a Second-Order Autoregressive-SEM. Journal of Open Innovation: Technology, Market, and Complexity. 2019; 5(3):69. https://doi.org/10.3390/joitmc5030069
Chicago/Turabian StyleSutthichaimethee, Pruethsan, Apinyar Chatchorfa, and Surapol Suyaprom. 2019. "A Forecasting Model for Economic Growth and CO2 Emission Based on Industry 4.0 Political Policy under the Government Power: Adapting a Second-Order Autoregressive-SEM" Journal of Open Innovation: Technology, Market, and Complexity 5, no. 3: 69. https://doi.org/10.3390/joitmc5030069
APA StyleSutthichaimethee, P., Chatchorfa, A., & Suyaprom, S. (2019). A Forecasting Model for Economic Growth and CO2 Emission Based on Industry 4.0 Political Policy under the Government Power: Adapting a Second-Order Autoregressive-SEM. Journal of Open Innovation: Technology, Market, and Complexity, 5(3), 69. https://doi.org/10.3390/joitmc5030069





