Efficiency Analysis of East Asian Zinc Smelters and the Effects of Capacity and Bonus Zinc on Efficiency
Abstract
:1. Introduction
2. Literature Review
3. Method
3.1. DEA Models
3.2. Date Collection and Variable Selection
4. Results
4.1. Efficiency Analysis
4.2. Causal Analysis
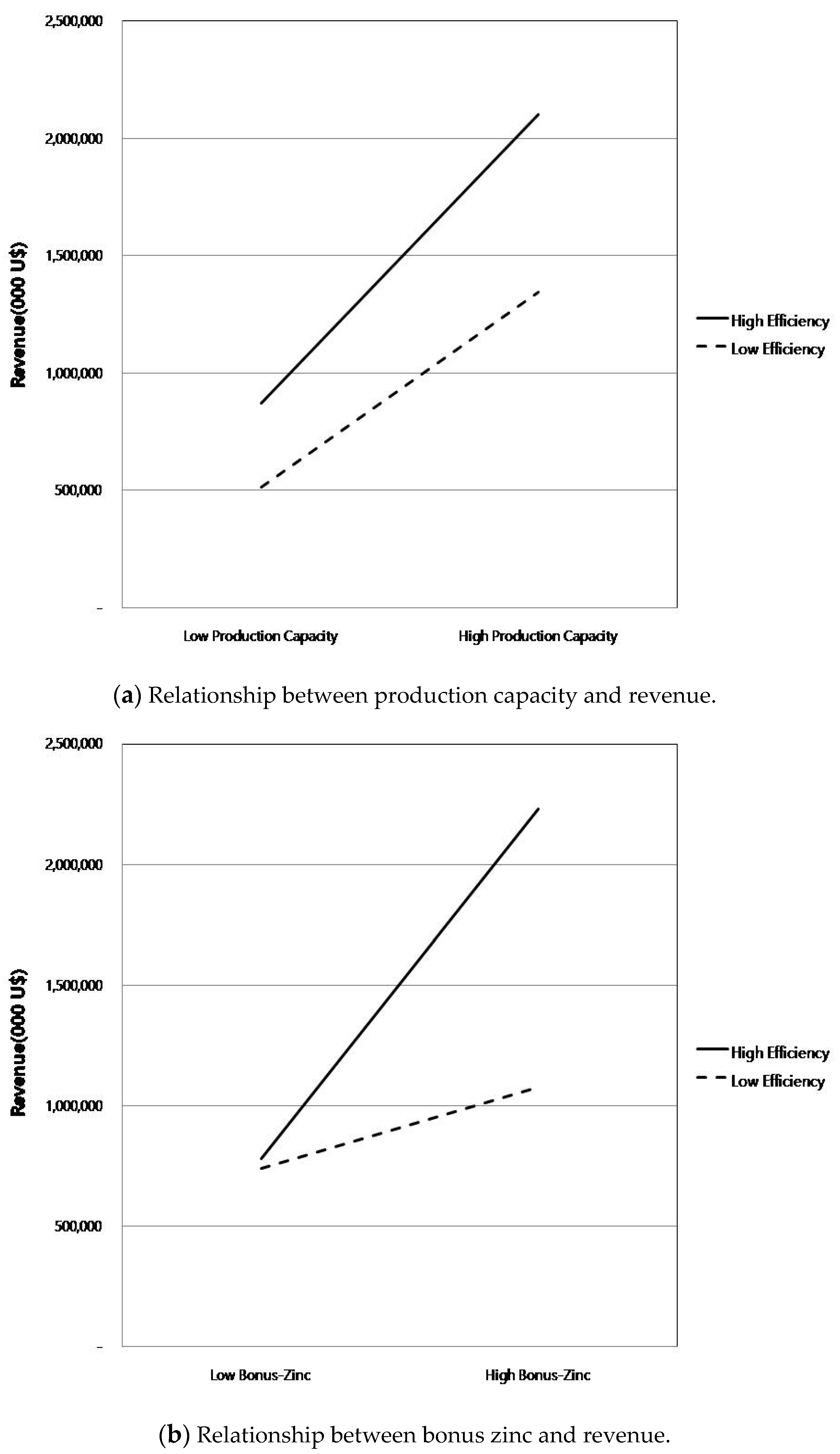
4.3. Performance Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kim, D.H. 2016 Industry Risk Rating—Nonferrous Metal. Available online: http://www.nicerating.com/common/pdfViewer.do?docId=1L5TH2jcsqQ (accessed on 16 November 2018).
- Ko, K.; Kim, D.C. The Analyses of the Operational Efficiency and Efficiency Factors of Retail Stores Using DEA Model. Korean Manag. Sci. Rev. 2014, 31, 135–150. [Google Scholar] [CrossRef] [Green Version]
- Park, J.S.; Yoo, I.S. A Study on Factors Affecting the Management Efficiencyof Korean Pharmaceutical Firms Listed in the KRX- Using DEA and Tobit Model. Prod. Rev. 2013, 27, 137–165. [Google Scholar]
- Park, B.S.; Lee, Y.K.; Kim, Y.S. Efficiency Evaluation of General Hospitals using DEA. J. Korea Contents Assoc. 2009, 9, 299–312. [Google Scholar] [CrossRef] [Green Version]
- Ju, H.J.; Kim, D.C. Efficiency Analysis of Regional SW Growth SupportingProjects Executing Agencies Using DEA. J. Korean Prod. Oper. Manag. Soc. 2014, 25, 443–463. [Google Scholar]
- Shin, C. An Analysis on the Efficiency and Productivity Changes of the National University Hospitals in the Republic of Korea. Korean Soc. Secur. Stud. 2006, 22, 49–78. [Google Scholar]
- Yoon, M.K.; Kim, J.K. The efficiency analysis of Korea stock market Listed Top-200 Manufacturing Firms-Using the DEA Technic. Korean Corp. Manag. Rev. 2006, 23, 79–97. [Google Scholar]
- Yum, D.K.; Shin, H.D. Relative Efficiency of Research and Development Business Foundations through Data Envelopment Analysis. Korean J. Public Adm. 2013, 51, 293–319. [Google Scholar]
- Lee, S.; Han, H.N. A Comparative Study on the Estimation Technical Efficiency for Public Libraries in Korea: Stochastic Production Frontier Analysis and Data Envelopment Analysis. J. Cult. Policy 2011, 25, 193–215. [Google Scholar]
- Sohn, M.; Choi, M. Association between Efficiency and Quality of Health Care in South Korea Long-term Care Hospitals: Using the Data Envelopment Analysis and Matrix Analysis. J. Korean Acad. Nurs. 2014, 44, 418–427. [Google Scholar] [CrossRef]
- Shao, L.; He, Y.; Feng, C.; Zhang, S. An empirical analysis of total-factor productivity in 30 sub-sub-sectors of China’s nonferrous metal industry. Resour. Policy 2016, 50, 264–269. [Google Scholar] [CrossRef]
- Shao, Y.; Wang, S. Productivity growth and environmental efficiency of the nonferrous metals industry: An empirical study of China. J. Clean. Prod. 2016, 137, 1663–1667. [Google Scholar] [CrossRef]
- Wei, P.; Tang, H.; Chen, Y.; Chen, X.H. Measuring technical efficiency of Chinese nonferrous metals enterprises on a background of industry consolidation. Trans. Nonferr. Metals Soc. China 2013, 23, 2797–2806. [Google Scholar] [CrossRef]
- Farrell, M.J. The Measurement of Productivity Efficiency. J. R. Stat. Soc. Ser. A (General) 1957, 120, 253–290. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some models for estimating technical and scale inefficiencies in Data Envelopment Analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Tone, K. A slack-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Hwang, B.Y.; Jun, H.J.; Chang, M.H.; Kim, D.C. A case study on the improvement of institution of high-risk high return R&D in Korea. JOItmC 2017, 3, 19. [Google Scholar]
- Yun, J. How do we conquer the growth limits of capitalism? Schumpeterian dynamics of open innovation? JOItmC 2015, 1, 17. [Google Scholar] [CrossRef]
- Park, E.S.; Kim, B.R.; Park, S.H.; Kim, D.C. Analysis of the Effects of the Home EnergyManagement System from an Open Innovation Perspective. JOItmC 2018, 4, 31. [Google Scholar] [CrossRef]
| Area | 2012 | 2013 | 2014 | 2015 |
|---|---|---|---|---|
| Africa | 170 | 139 | 134 | 83 |
| Asia | 7141 | 7626 | 8022 | 8637 |
| Europe | 2094 | 2113 | 2215 | 2224 |
| South America | 599 | 653 | 619 | 635 |
| Middle East | 103 | 103 | 103 | 103 |
| North America | 1231 | 1230 | 1106 | 1186 |
| Oceania | 498 | 499 | 484 | 489 |
| Russia | 617 | 572 | 599 | 570 |
| Total | 12,454 | 12,935 | 13,281 | 13,927 |
| Classification | Input | Output | ||||
|---|---|---|---|---|---|---|
| Labor Cost | Utility Cost | Maintenance Cost | Material Cost | Revenue | Production Volume | |
| 1000 US$ | 1000 US$ | 1000 US$ | 1000 US$ | 1000 US$ | kt | |
| Max | 39,735 | 177,917 | 77,431 | 519,682 | 730,805 | 548 |
| Min | 210 | 343 | 115 | 1282 | 903 | 1 |
| Mean | 11,781 | 42,290 | 17,433 | 151,654 | 112,401 | 120 |
| Standard Deviation | 7534 | 41,541 | 15,553 | 135,587 | 125,435 | 113 |
| DMU | Countries | CRS | VRS | Scale | Cause of Inefficiency | SBM | |
|---|---|---|---|---|---|---|---|
| TE | PTE | SE(TE/PTE) | PTE | SE | |||
| 1 | China | 0.639 | 0.888 | 0.719 | ● | 0.145 | |
| 2 | China | 0.533 | 0.853 | 0.624 | ● | 0.283 | |
| 3 | China | 0.494 | 0.787 | 0.628 | ● | 0.131 | |
| 4 | China | 0.982 | 1.000 | 0.982 | ● | 1.000 | |
| 5 | China | 0.638 | 0.835 | 0.764 | ● | 0.540 | |
| 6 | China | 0.600 | 0.847 | 0.708 | ● | 0.529 | |
| 7 | China | 0.589 | 1.000 | 0.589 | ● | 1.000 | |
| 8 | China | 0.397 | 0.817 | 0.486 | ● | 0.245 | |
| 9 | China | 0.558 | 0.918 | 0.607 | ● | 0.171 | |
| 10 | China | 0.468 | 0.825 | 0.567 | ● | 0.286 | |
| 11 | China | 0.547 | 0.829 | 0.660 | ● | 0.095 | |
| 12 | China | 0.546 | 0.810 | 0.674 | ● | 0.154 | |
| 13 | China | 0.469 | 0.875 | 0.536 | ● | 0.004 | |
| 14 | China | 1.000 | 1.000 | 1.000 | 1.000 | ||
| 15 | China | 0.413 | 0.769 | 0.537 | ● | 0.118 | |
| 16 | China | 0.809 | 1.000 | 0.809 | ● | 1.000 | |
| 17 | China | 0.356 | 0.732 | 0.486 | ● | 0.121 | |
| 18 | China | 0.681 | 0.867 | 0.786 | ● | 0.181 | |
| 19 | China | 0.248 | 0.636 | 0.390 | ● | 0.028 | |
| 20 | China | 0.331 | 0.787 | 0.420 | ● | 0.079 | |
| 21 | China | 0.519 | 0.966 | 0.536 | ● | 0.328 | |
| 22 | China | 0.872 | 1.000 | 0.872 | ● | 1.000 | |
| 23 | China | 0.824 | 1.000 | 0.824 | ● | 1.000 | |
| 24 | China | 0.467 | 0.970 | 0.481 | ● | 0.346 | |
| 25 | China | 0.617 | 1.000 | 0.617 | ● | 1.000 | |
| 26 | China | 0.455 | 0.786 | 0.579 | ● | 0.174 | |
| 27 | China | 0.290 | 0.710 | 0.409 | ● | 0.043 | |
| 28 | China | 0.448 | 0.768 | 0.583 | ● | 0.140 | |
| 29 | China | 0.345 | 0.793 | 0.435 | ● | 0.205 | |
| 30 | China | 0.476 | 0.894 | 0.532 | ● | 0.057 | |
| 31 | China | 0.827 | 1.000 | 0.827 | ● | 1.000 | |
| 32 | China | 1.000 | 1.000 | 1.000 | 1.000 | ||
| 33 | China | 0.507 | 0.769 | 0.658 | ● | 0.042 | |
| 34 | China | 0.623 | 1.000 | 0.623 | ● | 1.000 | |
| 35 | China | 0.603 | 0.760 | 0.793 | ● | 0.476 | |
| 36 | Japan | 0.579 | 0.797 | 0.726 | ● | 0.207 | |
| 37 | Japan | 0.696 | 0.832 | 0.837 | ● | 0.209 | |
| 38 | Japan | 0.369 | 0.720 | 0.512 | ● | 0.096 | |
| 39 | Japan | 0.649 | 0.909 | 0.713 | ● | 0.261 | |
| 40 | Japan | 0.908 | 1.000 | 0.908 | ● | 1.000 | |
| 41 | Japan | 0.737 | 1.000 | 0.737 | ● | 1.000 | |
| 42 | Korea | 1.000 | 1.000 | 1.000 | 1.000 | ||
| 43 | Korea | 0.892 | 1.000 | 0.892 | ● | 1.000 | |
| Average | 0.605 | 0.878 | 0.689 | PTE | 2 | 0.458 | |
| Efficient DMUs | 3 | 14 | 3 | SE | 38 | 14 | |
| DMU | Countries | BCC | Reference DMU(λ) | Frequency of References |
|---|---|---|---|---|
| Efficiency | ||||
| 1 | China | 0.888 | D4(0.186), D14(0.366), D32(0.408), D41(0.131) D42(0316) | |
| 2 | China | 0.853 | D4(0.306), D14(0.023), D32(0.069), D41(0.323), D42(0.346) | |
| 3 | China | 0.787 | D4(0.202), D32(0.414), D41(0.032), D42(0.518) | |
| 4 | China | 1.000 | 13 | |
| 5 | China | 0.835 | D7(0.141), D22(0.005), D31(0.134), D40(0494), D42(0.225) | |
| 6 | China | 0.847 | D31(0.391), D32(0.108), D40(0.418), D41(0.076), D43(0.114) | |
| 7 | China | 1.000 | 8 | |
| 8 | China | 0.817 | D7(0.249), D40(0.302), D41(0.132), D42(0.316) | |
| 9 | China | 0.918 | D14(0.079), D22(0.066), D41(0.519), D42(0.334) | |
| 10 | China | 0.825 | D4(0.104), D7(0.219), D34(0.129), D41(0.152), D42(0.525) | |
| 11 | China | 0.829 | D4(0.239), D14(0.256), D42(0.504) | |
| 12 | China | 0.810 | D4(0.651), D14(0.348) | |
| 13 | China | 0.875 | D14(0.077), D22(0.397), D41(0.525) | |
| 14 | China | 1.000 | 19 | |
| 15 | China | 0.769 | D14(0.132), D22(0.057), D41(0.366), D42(0.445) | |
| 16 | China | 1.000 | ||
| 17 | China | 0.732 | D4(0.115), D14(0.138), D41(0.280), D42(0.467) | |
| 18 | China | 0.867 | D4(0.032), D14(0.475), D42(0.493) | |
| 19 | China | 0.636 | D14(0.376), D22(0.229), D41(0.395) | |
| 20 | China | 0.787 | D7(0.158), D40(0.488), D41(0.178), D42(0.174) | |
| 21 | China | 0.966 | D7(0.430), D34(0.267), D42(0.302) | |
| 22 | China | 1.000 | 10 | |
| 23 | China | 1.000 | ||
| 24 | China | 0.970 | D7(0.528), D34(0.384), D42(0.087) | |
| 25 | China | 1.000 | ||
| 26 | China | 0.786 | D4(0.209), D14(0.006), D42(0.784) | |
| 27 | China | 0.710 | D7(0.219), D14(0.077), D22(0.295), D41(0.345), D42(0.282) | |
| 28 | China | 0.768 | D4(0.126), D14(0.198), D41(0.176), D42(0.498) | |
| 29 | China | 0.793 | D4(0.016), D14(0.015), D41(0.792), D42(0.176) | |
| 30 | China | 0.894 | D7(0.019), D40(0.226), D41(0.617), D42(0.136) | |
| 31 | China | 1.000 | 2 | |
| 32 | China | 1.000 | ||
| 33 | China | 0.769 | D4(0.548), D14(0.452) | |
| 34 | China | 1.000 | 2 | |
| 35 | China | 0.760 | D14(0.025), D22(0.059), D41(0.221), D42(0.694) | |
| 36 | Japan | 0.797 | D14(0.335), D22(0.117), D41(0.355), D42(0.192) | |
| 37 | Japan | 0.832 | D14(0.353), D22(0.481), D42(0.166) | |
| 38 | Japan | 0.720 | D14(0.303), D22(0.060), D41(0.636) | |
| 39 | Japan | 0.909 | D4(0.262), D14(0.036), D41(0.317), D42(0.383) | |
| 40 | Japan | 1.000 | 5 | |
| 41 | Japan | 1.000 | 20 | |
| 42 | Korea | 1.000 | 23 | |
| 43 | Korea | 1.000 | 1 |
| Classification | Coefficient | Standard Deviation | z value | Pr (>|z|) |
|---|---|---|---|---|
| Intercept | 0.2425 | 0.0786 | 3.0830 | 0.002049 ** |
| Capacity | 0.0007 | 0.0002 | 3.0400 | 0.002368 ** |
| Bonus Zn | 0.0216 | 0.0057 | 3.7710 | 0.000163 *** |
| Adg. R2 | 0.1656 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, H.S.; Kim, D. Efficiency Analysis of East Asian Zinc Smelters and the Effects of Capacity and Bonus Zinc on Efficiency. J. Open Innov. Technol. Mark. Complex. 2019, 5, 4. https://doi.org/10.3390/joitmc5010004
Park HS, Kim D. Efficiency Analysis of East Asian Zinc Smelters and the Effects of Capacity and Bonus Zinc on Efficiency. Journal of Open Innovation: Technology, Market, and Complexity. 2019; 5(1):4. https://doi.org/10.3390/joitmc5010004
Chicago/Turabian StylePark, Ha Sung, and Daecheol Kim. 2019. "Efficiency Analysis of East Asian Zinc Smelters and the Effects of Capacity and Bonus Zinc on Efficiency" Journal of Open Innovation: Technology, Market, and Complexity 5, no. 1: 4. https://doi.org/10.3390/joitmc5010004
APA StylePark, H. S., & Kim, D. (2019). Efficiency Analysis of East Asian Zinc Smelters and the Effects of Capacity and Bonus Zinc on Efficiency. Journal of Open Innovation: Technology, Market, and Complexity, 5(1), 4. https://doi.org/10.3390/joitmc5010004





