First-Principles Investigation of Electronic and Related Properties of Cubic Magnesium Silicide (Mg2Si)
Abstract
1. Introduction and Motivation
2. Computational Method
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Scouler, W.J. Optical Properties of Mg2Si, Mg2Ge, and Mg2Sn from 0.6 to 11.0 eV at 77 °K. Phys. Rev. 1969, 178, 1353–1357. [Google Scholar] [CrossRef]
- Borisenko, V.E. Semi-conducting Silicides. Springer Series in Material Science; Springer: New York, NY, USA, 2000. [Google Scholar] [CrossRef]
- Morris, R.G.; Redin, R.D.; Danielson, G.C. Semiconducting Properties ofMg2Si Single Crystals. Phys. Rev. 1957, 1957, 1909–1915. [Google Scholar] [CrossRef]
- Zaitsev, V.K.; Fedorov, M.I.; Gurieva, E.A.; Eremin, I.S.; Konstantinov, P.P.; Samunin, A.Y.; Vedernikov, M.V. Highly effectiveMg2Si1−xSnxthermoelectrics. Phys. Rev. B 2006, 74, 045207. [Google Scholar] [CrossRef]
- Stella, A.; Brothers, A.D.; Hopkins, R.H.; Lynch, D.W. Pressure Coefficient of the Band Gap in Mg2Si, Mg2Ge, and Mg2Sn. Phys. Status Solidi (b) 1967, 23, 697–702. [Google Scholar] [CrossRef]
- Satyala, N.; Vashaee, D. Modeling of Thermoelectric Properties of Magnesium Silicide (Mg2Si). J. Electron. Mater. 2012, 41, 1785–1791. [Google Scholar] [CrossRef]
- Kato, T.; Sago, Y.; Fujiwara, H. Optoelectronic properties of Mg2Si semiconducting layers with high absorption coefficients. J. Appl. Phys. 2011, 110, 063723. [Google Scholar] [CrossRef]
- Buchenauer, C.J.; Cardona, M. Raman Scattering in Mg2Si, Mg2Ge, and Mg2Sn. Phys. Rev. B 1971, 3, 2504–2507. [Google Scholar] [CrossRef]
- Vazquez, F.; Forman, R.A.; Cardona, M. Electroreflectance Measurements on Mg2Si, Mg2Ge, and Mg2Sn. Phys. Rev. 1968, 176, 905–908. [Google Scholar] [CrossRef]
- Sobolev, V.V. Reflectivity spectra and energy band structure of Mg2X crystals. Phys. Status Solidi (b) 1972, 209, K209–K214. [Google Scholar] [CrossRef]
- Tejeda, J.; Cardona, M. Valence bands of theMg2X (X = Si, Ge, Sn ssemiconducting compounds. Phys. Rev. B 1976, 14, 2559–2568. [Google Scholar] [CrossRef]
- McWilliams, D.; Lynch, D.W. Infrared Reflectivities of Magnesium Silicide, Germanide, and Stannide. Phys. Rev. 1963, 130, 2248–2252. [Google Scholar] [CrossRef]
- Panke, D.; Wölfel, E. Die Verteilung der Valenzelektronen im Mg2Si. Z. Für Krist.-Cryst. Mater. 1969, 129, 28. [Google Scholar] [CrossRef]
- Heller, M.; Danielson, G. Seebeck effect in Mg2Si single crystals. J. Phys. Chem. Solids 1962, 23, 601–610. [Google Scholar] [CrossRef]
- Busch, G.; Winkler, U. Elektrische Eigenschaften Der Intermetallischen Verbindungen Mg2Si, Mg2Ge, Mg2Sn Und Mg2Pb. Physica 1954, 20, 1067–1072. [Google Scholar] [CrossRef]
- Koenig, P.; Lynch, D.W.; Danielson, G.C. Infrared absorption in magnesium silicide and magnesium germanide. J. Phys. Chem. Solids 1961, 20, 122–126. [Google Scholar] [CrossRef]
- Pandit, P.; Sanyal, S.P. First principles study of electronic, elastic and lattice dynamical properties of Mg2X (X = Si, Ge and Sn) compounds. Indian J. Pure Appl. Phys. 2011, 49, 692–697. [Google Scholar]
- Corkill, J.L.; Cohen, M.L. Structural, bonding, and electronic properties of IIA-IV antifluorite compounds. Phys. Rev. B 1993, 48, 17138–17144. [Google Scholar] [CrossRef]
- Boulet, P.; Verstraete, M.; Crocombette, J.-P.; Briki, M.; Record, M.-C. Electronic properties of the Mg2Si thermoelectric material investigated by linear-response density-functional theory. Comput. Mater. Sci. 2011, 50, 847–851. [Google Scholar] [CrossRef]
- Imai, Y.; Watanabe, A.; Mukaida, M. Electronic structures of semiconducting alkaline-earth metal silicides. J. Alloy. Compd. 2003, 358, 257–263. [Google Scholar] [CrossRef]
- Arnaud, B.; Alouani, M. Electron-hole excitations inMg2SiandMg2Gecompounds. Phys. Rev. B 2001, 64, 0332021–0332024. [Google Scholar] [CrossRef]
- Mars, K.; Ihou-Mouko, H.; Pont, G.; Tobola, J.; Scherrer, H. Thermoelectric Properties and Electronic Structure of Bi- and Ag-Doped Mg2Si1−x Ge x Compounds. J. Electron. Mater. 2009, 38, 1360–1364. [Google Scholar] [CrossRef]
- Au-Yang, M.Y.; Cohen, M.L. Electronic Structure and Optical Properties of Mg2Si, Mg2Ge, and Mg2Sn. Phys. Rev. 1969, 178, 1358–1364. [Google Scholar] [CrossRef]
- Aymerich, F.; Mula, G. Pseudopotential band structures of Mg2Si, Mg2Ge, Mg2Sn, and of the solid solution Mg2(Ge, Sn). Phys. Status Solidi (b) 1970, 42, 697–704. [Google Scholar] [CrossRef]
- Balout, H.; Boulet, P.; Record, M.-C. Electronic and transport properties of Mg2Si under isotropic strains. Intermetallics 2014, 50, 8–13. [Google Scholar] [CrossRef]
- Krivosheeva, A.V.; Kholod, A.N.; Shaposhnikov, V.L.; Krivosheev, A.E.; Borisenko, V.E. Band structure of Mg2Si and Mg2Ge semiconducting compounds with a strained crystal lattice. Semiconductors 2002, 36, 496–500. [Google Scholar] [CrossRef]
- Fan, W.H.; Chen, R.X.; De Han, P.; Meng, Q.S. First-Principle Study of Electronic Structures of Y-Doped Mg2Si. Mater. Sci. Forum 2011, 689, 102–107. [Google Scholar]
- Chen, Q.; Xie, Q. First-principles calculations on the electronic structure and optical properties of Mg2Si epitaxial on Si (111). Phys. Procedia 2011, 11, 134–137. [Google Scholar] [CrossRef]
- Ryu, B.; Park, S.; Choi, E.-A.; de Boor, J.; Ziolkowski, P.; Chung, J.; Park, S.D. Hybrid-Functional and Quasi-Particle Calculations of Band Structures of Mg2Si, Mg2Ge, and Mg2Sn. J. Korean Phys. Soc. 2019, 75, 144–152. [Google Scholar] [CrossRef]
- Feibelman, P.J.; Appelbaum, J.A.; Hamann, D.R. Electronic structure of a Ti (0001) film. Phys. Rev. B 1979, 20, 1433–1443. [Google Scholar] [CrossRef]
- Harmon, B.N.; Weber, W.; Hamann, D.R. Total-energy calculations for Si with a first-principles linear-combination-of-atomic-orbitals method. Phys. Rev. B 1982, 25, 1109–1115. [Google Scholar] [CrossRef]
- Franklin, L.; Ekuma, C.; Zhao, G.; Bagayoko, D. Density functional theory description of electronic properties of wurtzite zinc oxide. J. Phys. Chem. Solids 2013, 74, 729–736. [Google Scholar] [CrossRef]
- Bagayoko, D.; Franklin, L.; Zhao, G.L. Predictions of electronic, structural, and elastic properties of cubic InN. J. Appl. Phys. 2004, 96, 4297–4301. [Google Scholar] [CrossRef]
- Bagayoko, D.; Zhao, G.L.; Fan, J.D.; Wang, J.T. Ab initio calculations of the electronic structure and optical properties of ferroelectric tetragonal. J. Phys. Condens. Matter 1998, 10, 5645–5655. [Google Scholar] [CrossRef]
- Ekuma, C.; Franklin, L.; Zhao, G.L.; Wang, J.T.; Bagayoko, D. Local density approximation description of electronic properties of wurtzite cadmium sulfide (w-CdS). Can. J. Phys. 2011, 89, 319–324. [Google Scholar] [CrossRef]
- Ayirizia, B.A.; Malozovsky, Y.; Franklin, L.; Bhandari, U.; Bagayoko, D. Ab-Initio Self-Consistent Density Functional Theory Description of Rock-Salt Magnesium Selenide (MgSe). Mater. Sci. Appl. 2020, 11, 401–414. [Google Scholar] [CrossRef]
- Bagayoko, D. Understanding the Relativistic Generalization of Density Functional Theory (DFT) and Completing It in Practice. J. Mod. Phys. 2016, 07, 911–919. [Google Scholar] [CrossRef]
- Bagayoko, D. Understanding density functional theory (DFT) and completing it in practice. AIP Adv. 2014, 4, 127104. [Google Scholar] [CrossRef]
- Bagayoko, D. Comprendre La Théorie De La Fonctionnelle De La Densité Et La Completer Dans La Pratique. In Proceedings of the Malian Symposium of Applied Sciences (MSAS), Bamako, Mali, 3–8 August 2014; pp. 251–258. [Google Scholar]
- Ceperley, D.M.; Alder, B.J. Ground State of the Electron Gas by a Stochastic Method. Phys. Rev. Lett. 1980, 45, 566–569. [Google Scholar] [CrossRef]
- Vosko, N.M.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Diakite, Y.I.; Malozovsky, Y.; Bamba, C.O.; Franklin, L.; Bagayoko, D. First Principle Calculation of Accurate Electronic and Related Properties of Zinc Blende Indium Arsenide (zb-InAs). Materials 2022, 15, 3690. [Google Scholar] [CrossRef]
- Ayirizia, B.A.; Brumfield, J.S.; Malozovsky, Y.; Bagayoko, D. Ground State Properties of the Wide Band Gap Semiconductor Beryllium Sulfide (BeS). Materials 2021, 14, 6128. [Google Scholar] [CrossRef] [PubMed]
- Hao, J.; Zou, B.; Zhu, P.; Gao, C.; Li, Y.; Liu, D.; Wang, K.; Lei, W.; Cui, Q.; Zou, G. In situ X-ray observation of phase transitions in Mg2Si under high pressure. Solid State Commun. 2009, 149, 689–692. [Google Scholar] [CrossRef]



| Measurement Method | Band Gap (eV) |
|---|---|
| Resistivity and Hall effect Measurement | 0.78 a indirect |
| Polycrystalline sample | 0.77 b indirect |
| Reflectance measurement samples cleaved from boules | 0.65 c indirect |
| Hall coefficient measurement for Mg2Si single crystal | 0.80 d indirect |
| Computational Method | Potentials | Band gap, Eg (eV) |
|---|---|---|
| Empirical pseudopotential | LDA | 0.118 h (indirect) |
| Projector augmented plane wave (PAW) | LDA | 0.12 i (indirect) |
| Crystal potential of muffin tin | LDA | 0.2 j (indirect) |
| Pseudopotential description | LDA | 0.277 k (indirect) |
| Empirical pseudopotential method | LDA | 0.53 l (indirect) |
| Empirical pseudopotential | LDA | 0.49 m (indirect) |
| Plane wave pseudopotential | GGA | 0.256 n (indirect) |
| Norm-conserving pseudopotential | GGA | 0.21 o (indirect) |
| Linear augmented plane wave | GGA | 0,19 p (indirect) |
| Plane wave pseudopotential | GGA | 0.42 q (indirect) |
| Norm-conserving pseudopotential | GGA | 0.21 r (indirect) |
| Pseudopotential approach | GGA | 0.27 s (direct) |
| Pseudopotential method | GGA | 0.2261 t (indirect) |
| Projector augmented plane wave (PAW) | GW | 0.65 u (indirect) |
| Hybrid-functional and quasi-particle GW | DFT-PBE, GW | 0.817 v (indirect) |
| 2.685 v (direct) |
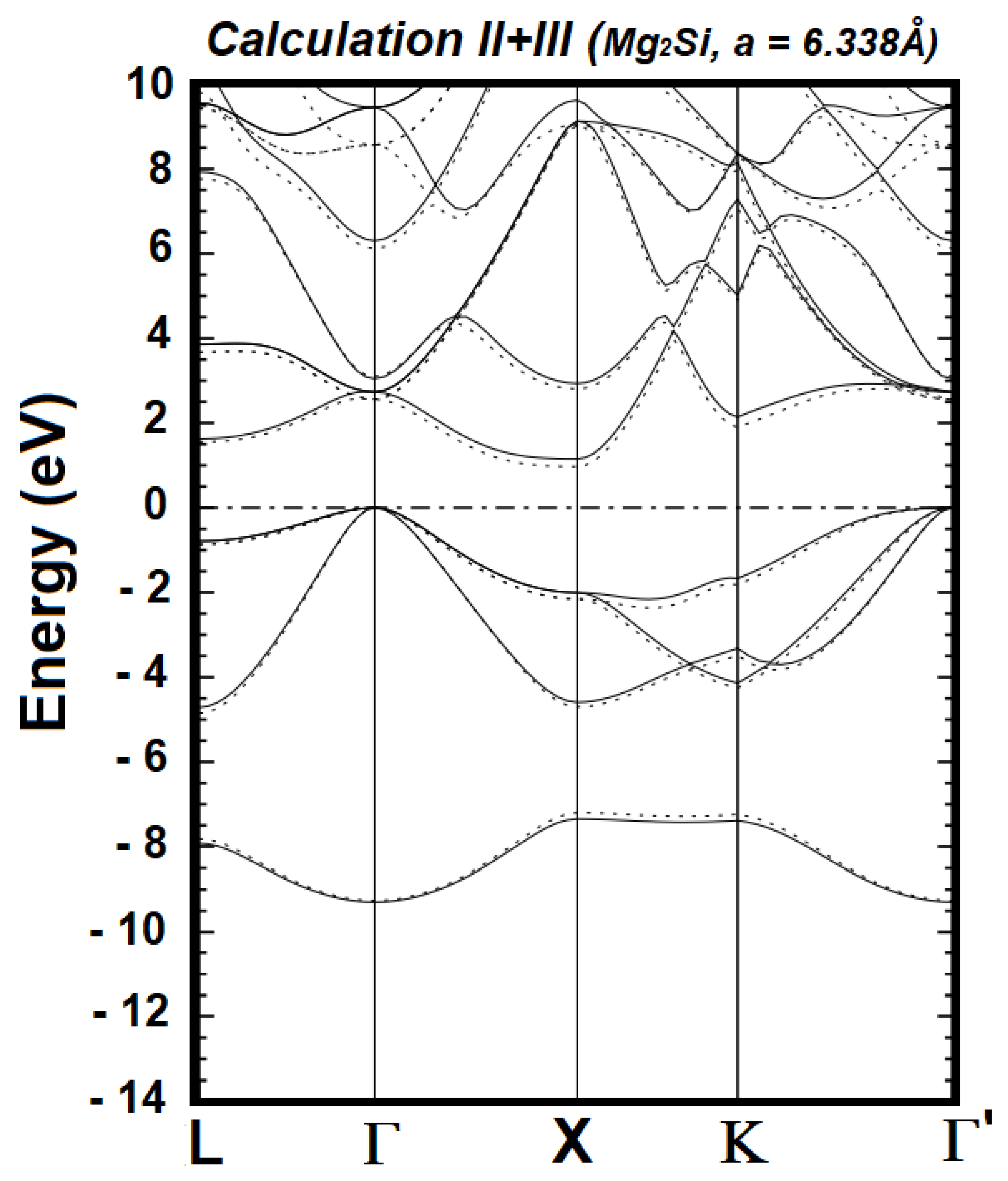
| Cal. No. | Orbitals for the Valence States of Mg1+ | Orbitals for the Valence States of Si2- | No. of Wave Functions | Band Gap (Γ–X) in eV | Band Gap (Γ–L) in eV |
|---|---|---|---|---|---|
| I | 2s2 2p6 3s1 | 2s2 2p6 3s2 3p4 | 36 | 0.3448 | 1.4000 |
| II | 2s2 2p6 3s1 3p0 | 2s2 2p6 3s2 3p4 | 48 | 1.1532 | 1.6275 |
| III | 2s2 2p6 3s1 3p0 | 2s2 2p6 3s2 3p4 4p0 | 54 | 0.9717 | 1.5560 |
| IV | 2s2 2p6 3s1 3p0 4p0 | 2s2 2p6 3s2 3p4 4p0 | 66 | 0.9949 | 1.5639 |
| V | 2s2 2p6 3s1 3p0 4p0 | 2s2 2p6 3s2 3p4 4p0 4s0 | 68 | 0.9434 | 1.5317 |
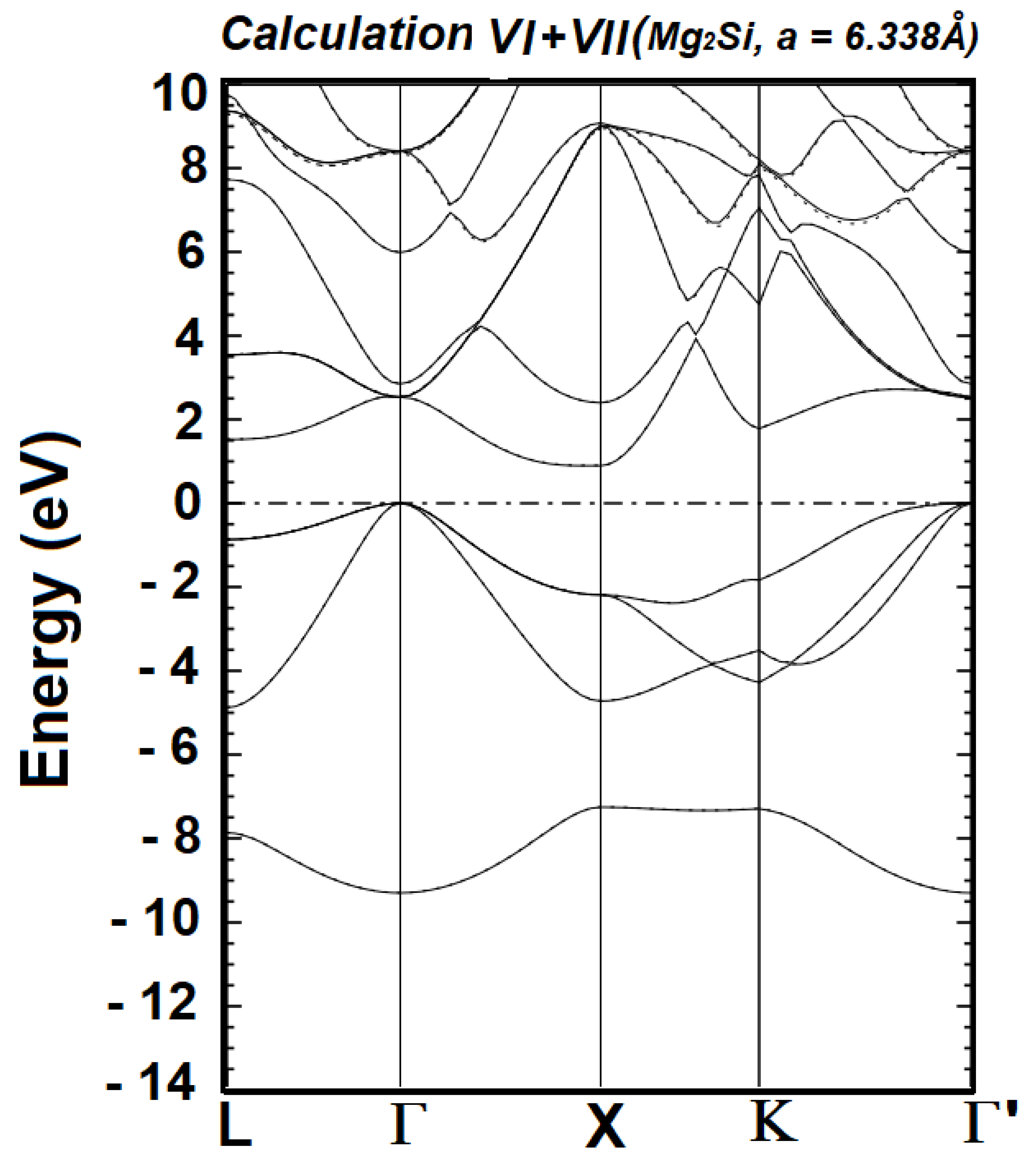
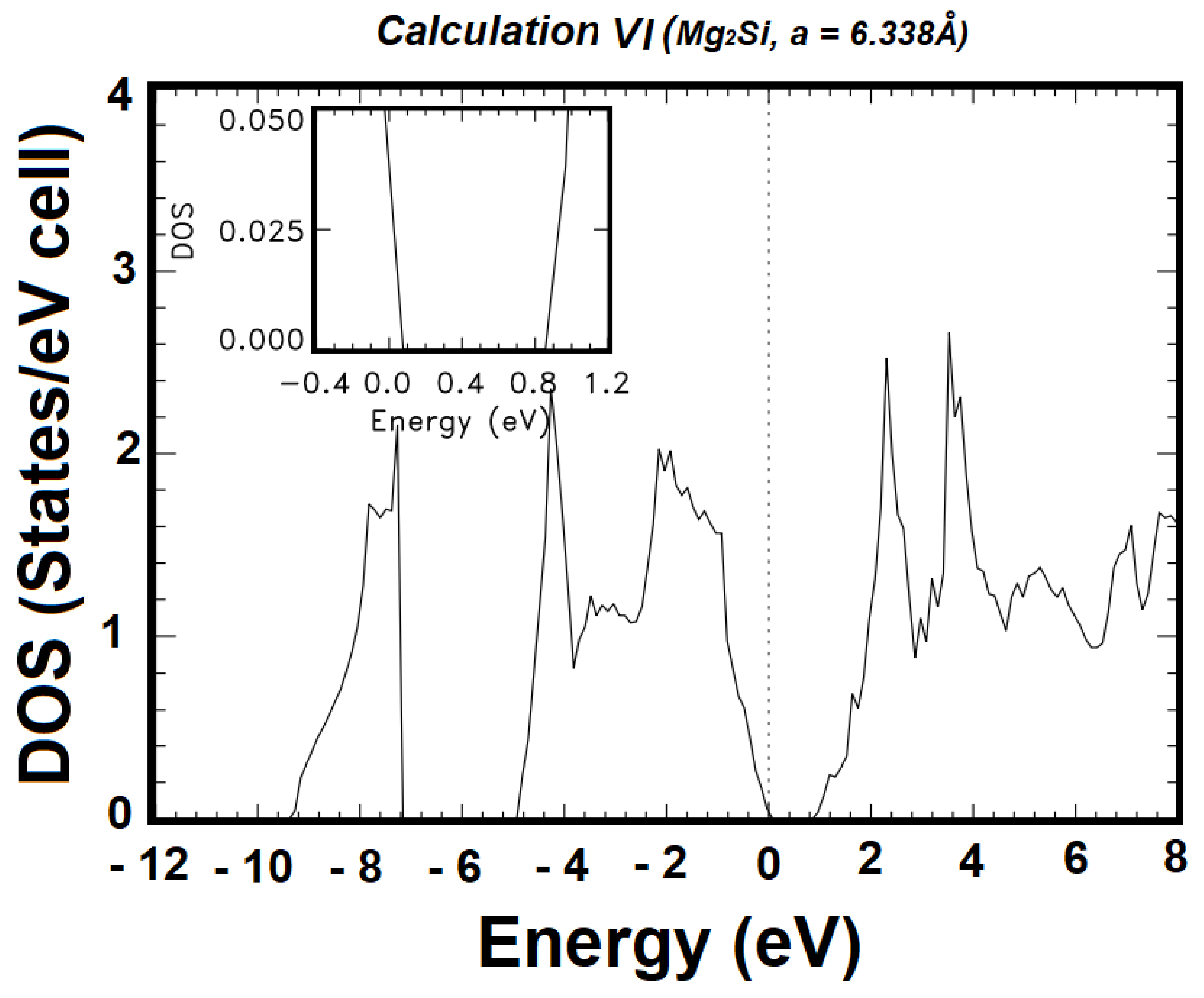
| VI | 2s22p63s13p04p04s0 | 2s22p63s23p44p04s0 | 72 | 0.8961 | 1.5219 |
| VII | 2s2 2p6 3s1 3p0 4p0 4s0 | 2s2 2p6 3s2 3p4 4p0 4s0 5p0 | 78 | 0.9040 | 1.5285 |
| VIII | 2s2 2p6 3s1 3p0 4p0 4s0 5p0 | 2s2 2p6 3s2 3p4 4p0 4s0 5p0 | 90 | 0.9048 | 1.5271 |
| L Point | Γ Point | X Point | K Point |
|---|---|---|---|
| 10.784 | 8.411 | 13.207 | 12.670 |
| 9.766 | 8.411 | 10.214 | 11.536 |
| 9.367 | 8.411 | 10.214 | 8.206 |
| 9.367 | 5.986 | 9.075 | 8.101 |
| 7.731 | 2.849 | 9.009 | 7.831 |
| 3.540 | 2.533 | 9.009 | 7.057 |
| 3.540 | 2.533 | 2.399 | 4.754 |
| 1.522 | 2.533 | 0.896 | 1.782 |
| −0.866 | 0.000 | −2.188 | −1.834 |
| −0.866 | 0.000 | −2.188 | −3.511 |
| −4.879 | 0.000 | −4.722 | −4.278 |
| −7.866 | −9.295 | −7.256 | −7.292 |
| Types and Directions of Effective Masses | Values of Effective Masses (mo) |
|---|---|
| me(Γ-L)111 | 0.418 |
| me(Γ-X)100 | 0.211 |
| me(Γ-K)110 | 0.247 |
| me(X-Γ) Longitudinal | 19.707 |
| me(X-W) Transverse | 0.171 |
| me(X-K) Transverse | 0.176 |
| me(L-Γ) Longitudinal | 3.420 |
| me(L-K) Transverse | 0.161 |
| me(L-W) Transverse | 0.173 |
| mhh1(Γ-L)111 | 0.838 |
| mhh1(Γ-X)100 | 0.288 |
| mhh1(Γ-K)110 | 0.516 |
| mhh2(Γ-K)110 | 0.327 |
| mlh(Γ-L)111 | 0.106 |
| mlh (Γ-X)100 | 0.183 |
| mlh (Γ-K)110 | 0.141 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dioum, A.; Diakité, Y.I.; Malozovsky, Y.; Ayirizia, B.A.; Beye, A.C.; Bagayoko, D. First-Principles Investigation of Electronic and Related Properties of Cubic Magnesium Silicide (Mg2Si). Computation 2023, 11, 40. https://doi.org/10.3390/computation11020040
Dioum A, Diakité YI, Malozovsky Y, Ayirizia BA, Beye AC, Bagayoko D. First-Principles Investigation of Electronic and Related Properties of Cubic Magnesium Silicide (Mg2Si). Computation. 2023; 11(2):40. https://doi.org/10.3390/computation11020040
Chicago/Turabian StyleDioum, Allé, Yacouba I. Diakité, Yuiry Malozovsky, Blaise Awola Ayirizia, Aboubaker Chedikh Beye, and Diola Bagayoko. 2023. "First-Principles Investigation of Electronic and Related Properties of Cubic Magnesium Silicide (Mg2Si)" Computation 11, no. 2: 40. https://doi.org/10.3390/computation11020040
APA StyleDioum, A., Diakité, Y. I., Malozovsky, Y., Ayirizia, B. A., Beye, A. C., & Bagayoko, D. (2023). First-Principles Investigation of Electronic and Related Properties of Cubic Magnesium Silicide (Mg2Si). Computation, 11(2), 40. https://doi.org/10.3390/computation11020040







