Abstract
Composite moulds constitute an attractive alternative to classical metallic moulds when used for components fabricated by processes such as Resin Transfer Moulding (RTM). However, there are many factors that have to be accounted for if a correct design of the moulds is sought after. In this paper, the Finite Element Method (FEM) is used to help in the design of the mould. To do so, a thermo-electrical simulation has been performed through MSC-Marc in the preheating phase in order to ensure that the mould is able to be heated, through the Joule’s effect, according to the thermal cycle specified under operating conditions. Mean temperatures of 120 °C and 100 °C are predicted for the lower and upper semi-mould parts, respectively. Additionally, a thermo-electrical-mechanical calculation has been completed with MSC-Marc to calculate the tensile state along the system during the preheating stage. For the filling phase, the filling process itself has been simulated through RTM-Worx. Both the uniform- and non-uniform temperature distribution approaches have been used to assess the resulting effect. It has been found that this piece of software cannot model the temperature dependency of the resin and a numerical trick must have been applied in the second case to overcome it. Results have been found to be very dependent on the approach, the filling time being 73% greater when modelling a non-uniform temperature distribution. The correct behaviour of the mould during the filling stage, as a consequence of the filling pressure, has been also proved with a specific mechanical analysis conducted with MSC-Marc. Finally, the thermo-elastic response of the mould during the curing stage has been numerically assessed. This analysis has been made through MSC-Marc, paying special attention to the curing of the resin and the exothermic reaction that takes place. For the sake of accuracy, a user subroutine to include specific curing laws has been used. Material properties employed are also described in detail following a modified version of the Scott model, with curing properties extracted from experiments. All these detailed calculations have been the cornerstone to designing the composite mould and have also unveiled some capabilities that were missed in the commercial codes employed. Future versions of these commercial codes will have to deal with these weak points but, as a whole, the Finite Element Method is shown to be an appropriate tool for helping in the design of composite moulds.
1. Introduction
To this day, metals (mainly steel and aluminium alloys) are the most reasonable option for the fabrication of tools and moulds, as they meet the basic requirements of mass production processes [1]. However, metals as tooling materials present a number of serious disadvantages such as much higher coefficients of thermal expansion (CTE) than the materials of the produced parts, raw material consumption, and high costs for machining [2].
Despite of having a much shorter useful life than metal tools and entailing more problems related to micro-cracking and porosity, composite tooling offers many advantages as it is a lightweight, less costly solution that has lower thermal inertia and is relatively easy to produce. They offer potentially decreased fabrication time, easy repair/maintenance, lower CTE mismatches, tailored thermal and structural properties, and reduced health and safety risks as well.
Consequently, it seems appropriate to develop innovative, robust and easy to heat composite moulds (both closed and open), through addressing all those issues that currently prevent composite tooling from being a viable alternative for the industrial production of plastic and composite parts across a wide range of manufacturing routes.
Resin Transfer Moulding (RTM) is one of the manufacturing processes that can be studied through the Finite Element Method (FEM) [3,4,5,6,7,8]. It involves not only the RTM process itself, but also the design of the mould and its behaviour from a thermal, electrical, mechanical, filling, and curing point of view. During a typical RTM process (see Figure 1), four steps can be distinguished: (1) Preheating of the mould until it reaches an adequate temperature, (2) Filling through resin injection, (3) Curing of the resin, and (4) Cooling of the mould.
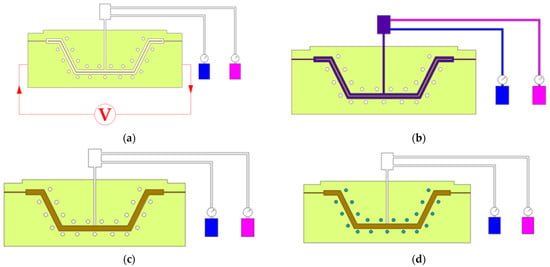
Figure 1.
Different stages of a typical RTM process: (a) preheating of the mould, (b) resin filling, (c) curing stage, and (d) cooling down phase.
In reference [3], Zade et al. simulated the RTM and cure process of a wing flap composite part through the commercial FEM code ANSYS. They paid special attention to the material properties of the resin, obtained through Differential Scanning Calorimetry (DSC). They also simulated the filling process with different number of injection and vent points. However, they did not simulate the preheating phase of the process and assumed a uniform initial temperature of 120 °C in the mould, which heavily conditioned their filling results. In reference [4], Joo et al. concentrated their simulation efforts on the mechanical strength obtained for an automotive composite front bumper assemble. The composite part was obtained by High Pressure Resin Transfer Moulding Process and shows good agreement when comparing FEM results obtained with LS-DYNA and the experimental results. Reference [5] shows the work performed by Simacek et al. They used the LIMS FEM software to simulate a Compression RTM process. Their geometry was a real 3-D B-pillar, but they recognized that some simplifications had to be accepted if an affordable numerical calculation was to be performed. Once again, preheating was not simulated and initial temperatures for the process were taken based on previous experience. Reference [6] shows the RTM process simulation of another car component, a cab front, performed with the commercial software PAM-RTM by Kuppusamy et al. They simulated the air entrapment that can happen in such a process and simulated the filling for different mould temperatures. In reference [7], Xiong et al. incorporated the idea of multiobjective optimization for the design of lightweight car components. Finally, in reference [8], Mal et al. investigated the RTM process of thin components and the effect of mechanical dispersion on the general heat transfer.
These references show the importance of simulation by FEM in the context of industrial processes, such as RTM and others. In fact, computational simulation via the Finite Element Method brings advantages compared to experimental and/or analytical studies, such as faster results and lower cost. The objective of this paper is to show that the Finite Element Method is an adequate tool to ensure an appropriate design of a composite mould and to shorten development costs and times. Consequently, many design decisions can be taken now based on simulation results, which will be confirmed afterwards by appropriate experimentation.
2. Methodology
FEM calculations can be a guide and a suitability check of a mould design in the context of an RTM process [9]. In this paper, different aspects that were taken into account to ensure a proper mould design will be shown.
As the mould was expected to be heated by means of the direct resistance method, the preheating was modelled through a thermo-electric analysis to determine the temperature distribution of the mould due to the Joule’s effect. After that, a mechanical analysis was planned to account for the thermal stresses generated by the heating. However, a thermo-electrical-mechanical analysis was carried out to obtain the mechanical response of the mould because of the thermal expansion: the entire coupled analysis could be easily performed with the simulation code used, MSC-Marc [10].
Based on the theoretical thermal cycle, the filling of the mould was modelled assuming isothermal conditions with a commercial software, RTM-Worx [11]. Additionally, using the temperature contour on the cavity determined in the preheating stage, the filling process simulation was repeated assuming a non-isothermal temperature distribution. In both cases, the pressure profile and the filling time were obtained to compare the effect of the approach selected. Following, a structural analysis was conducted to assess the mechanical behaviour of the mould due to the internal pressure.
Regarding the curing of the resin [12,13,14,15], a thermal analysis was completed considering the exothermal reaction that took place. Finally, a thermo-mechanical analysis was conducted to determine the dimensional stability of the mould and the stress state due to the resulting transient temperature profile. The cooling down of the mould was not studied.
As it can be deduced from this short description, several FEM analyses have been performed in a certain order, making some simplifications. Some other possibilities and coupled analyses have been disregarded and considered not needed, as the complexity would have been excessive and the software employed presented some limitations, which will be explained later in the paper. Figure 2 summarizes the FEM calculations performed.
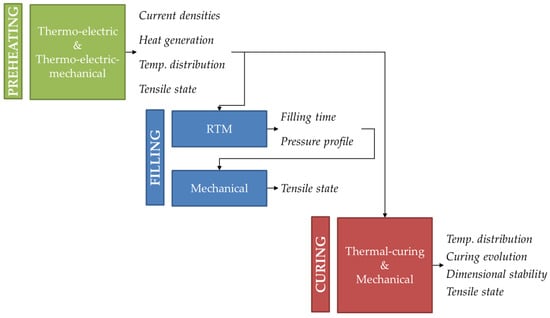
Figure 2.
Software framework for the mould design.
3. Mould Design
A composite mould with a resistive heater system was developed to be used in the simulation and fabrication activities. As shown in Figure 3, the mould was made up of two mica layers, two semi-moulds of composite, a gasket and the resistive heater system. Mica layers were used for thermal insulation purposes.
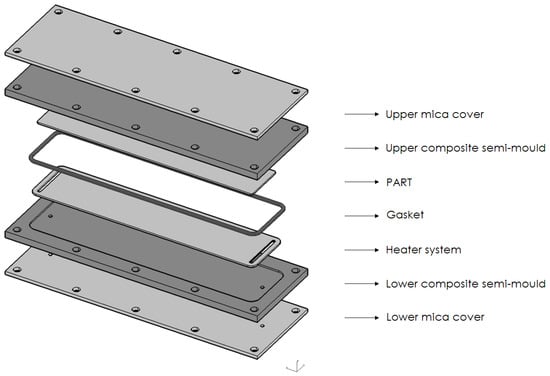
Figure 3.
Components of the mould and views of the resulting assembly.
Regarding the heater system concept, a resistive material with needed electrical connections inside and an external housing of fibreglass (to avoid electrical leaks) was considered. Main dimensions of the mould analysed are presented in Figure 4.
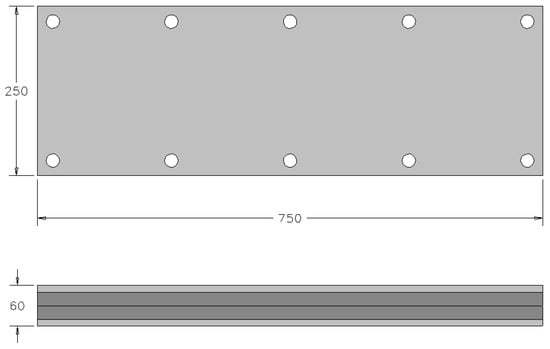
Figure 4.
Main dimensions of the mould (in mm).
Table 1 collects the physical, electrical, thermal, mechanical, and viscosity properties of the materials involved in the RTM process. A composite made of high conductivity fibres was used for both semi-moulds. For the composite to be manufactured, properties from the AS43K fibres and the RTM6 resin were considered. Rubber, mica, and fibreglass were also used. Table 1 also shows that several properties of the sample have not been considered (NC) as its mechanical influence (which is small) can be neglected.

Table 1.
Material properties.
The heat power that is produced during the curing process follows Equation (1):
where Pc represents the generated power (W), dα/dt is the curing rate (s−1), Vf is the fibre volume fraction (no units), ρr is the resin density(kg/m3), Hr is the resin cure reaction heat (J/kg), and VT is the total volume (m3).
The resin curing degree α, no units, can be calculated according to Equation (2):
Finally, the curing rate follows a modified version of the Scott model [16]:
where
Values of the coefficients and Hr are collected in Table 2. These values come from previous experiments performed in a previous project, not reported in the open literature.

Table 2.
Coefficients values of the curing rate equation.
4. Results and Discussion
4.1. Preheating
In an RTM process, the temperature of the cavity is the control variable that must be imposed. This thermal cycle depends on the resin and is the key parameter that defines the evolution of the filling and the curing of the resin and, consequently, the resulting part quality. The thermal cycle considered in this case is presented in Figure 5.
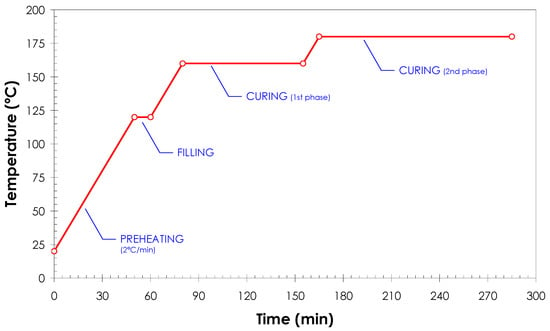
Figure 5.
Thermal cycle considered for RTM6.
In the real RTM process considered here, in which the mould was heated by Joule’s effect, the set temperatures depended on the electric potential applied. In this context, it was necessary to calculate the electric potential time evolution that produced a cavity temperature evolution as close as possible to the one shown in Figure 5. To do so, temperatures were applied as thermal loads in the heater plates in a preliminary heat transfer calculation. As a result, the heat power (W) was obtained and the electric potential needed to produce this electric power was also calculated. The electric potential calculation was obtained from the electric power, considering the electrical resistance of the heaters. Figure 6 shows the evolution of the electric power and the electric potential needed to obtain the temperature evolution of Figure 5.
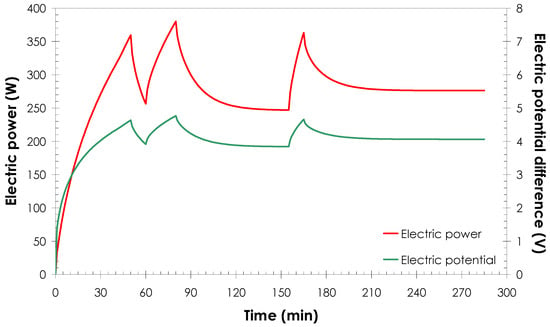
Figure 6.
Evolutions of electric power and voltage difference needed to reach the required temperatures.
Once the electrical voltages were determined, a thermo-electric analysis was carried out to numerically confirm that the thermal cycle was actually followed. After that, the structural response caused by the thermal dilatations was studied through a thermo-electrical-mechanical analysis.
A finite element mesh (Figure 7) formed by 39,280 hexahedral element and 44,384 nodes was built. Marc Element number 7 (8 nodes linear hexahedral element) was used for mechanical calculations, while Marc Element number 43 (8 nodes linear hexahedral element) was used for thermal, thermal–mechanical, thermal–electric, and cure thermal–mechanical calculations. Due to the existing symmetry on the geometry, materials, and loads, just half of the entire mould was modelled.
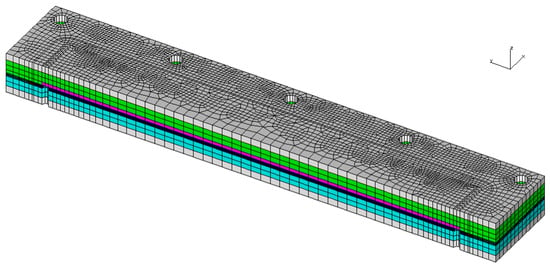
Figure 7.
Finite element mesh used (half model).
The electric voltage load applied was already obtained from the preliminary calculation, shown in Figure 6. Regarding thermal boundary conditions, a natural convection of 5 W/(m2K) and a radiation to environment condition were defined in the outer surfaces. An ambient temperature of 20 °C was considered and a value of 20 °C was defined as initial thermal condition.
Additionally, some mechanical constraints were applied for the thermo-electrical–mechanical analysis. That way, null displacements were defined in the X direction at the symmetry plane, in the Y direction at the centre of the mould, and in the Z direction at the mould base.
Results show that a time-dependent electric current was produced due to the imposed voltage difference. At the end of the preheating process (time = 50 min), the value of the current density was about 1.3 × 106 A/m2 and it was nearly uniform in the whole heater. It was observed also that the electric current was almost zero at the outer surfaces, which indicates that the fibreglass insulates the heater well enough and, consequently, there will be no risk of electrocution.
The temperature distribution obtained after the preheating can be seen in Figure 8, and it shows that the maximum temperatures were reached in the resistive heater. The heat generated here was then transferred to the adjoining components. Due to the thermal insulations of mica, the temperature of the outer surfaces was not so high and the temperature in the centre was higher.

Figure 8.
Temperatures (°C) distribution at the end of the preheating.
The temperature of the cavity was close to the target temperature 120 °C. In fact, average cavity temperature was 120 °C in the lower part and 100 °C in the upper part. However, the distribution was not uniform and higher (up to 134 °C in the lower semi-mould and 106 °C in the upper one) and lower values (up to 92 °C in the lower semi-mould and 91 °C in the upper one) could be found. This temperature distribution has influence in the filling phase of the RTM process. Evolutions of the maximum and minimum temperatures of the cavity were close to the set temperature and indicated that the heating rate was nearly linear. This evolution can be seen in Figure 9.
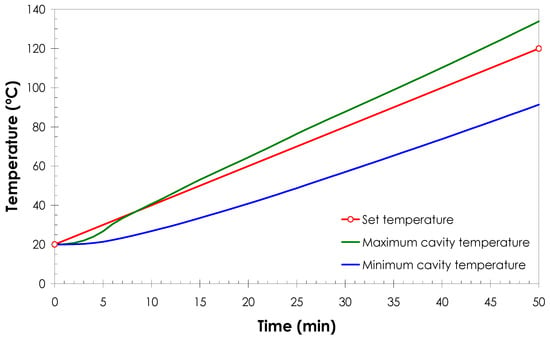
Figure 9.
Evolutions of the maximum and minimum temperatures of the cavity.
Looking at the mechanical behaviour predicted by this preheating calculation, Table 3 summarizes the most significant results.

Table 3.
Maximum von Mises stresses and displacements.
Results show that the CTE mismatch between the composite and the mica was relevant, and stresses generated were quite high. The highest values were found near the holes due to stress concentrations. Out of them, maximum stresses were significantly lower (about 70 MPa). This CTE mismatch could be easily avoided by replacing the mica layers by alternative insulation systems (e.g., flexible rockwool blankets).
4.2. Filling of the Mould
Once a suitable cavity temperature was achieved, the resin, previously preheated at 80 °C, was injected from one or more gates. Vacuum of 1 to 3 bar was applied to enable a proper resin flow through dry fibres up to fill the cavity completely.
The filling process was simulated in order to calculate the filling time and the pressure profile in the cavity. It was observed that the cavity temperature distribution influenced both the filling time and the pressure profile. This was a result that was not foreseen before the simulated works started. The simulation code used was RTM-Worx.
The mechanical response of the mould due to the internal pressure was also determined using MSC-Marc.
4.2.1. RTM Process Simulation Considering a Constant Mould Temperature of 120 °C
As a first step, the RTM-Worx software was used to simulate the filling of the mould at a uniform temperature of 120 °C, the ideal situation. A two-dimensional mesh of linear triangular elements was used and can be seen in Figure 10.
Figure 10.
Mesh used in the RTM process simulation.
Regarding the injection strategy, a central vacuum of 2 bar with two injection gates was considered. Figure 11 shows the filling time for the different parts of the mould. A total time of 325 was needed to completely fill the mould. The filling speed is high at the beginning, but the pressure gradient decreases as the resin flows and, therefore, the speed goes down.

Figure 11.
Filling time isothermal process.
4.2.2. RTM Process Simulation Considering Non-Constant Mould Temperatures
The thermo-electric analysis of Section 3 predicted a heterogeneous distribution of temperatures along the mould. This distribution had an important effect in the viscosity of the filling resin, thus the filling time of the process changes. However, the available software RTM-Worx had only isothermal capabilities and, consequently, viscosity is defined as a constant.
To bypass this limitation of the simulation software, different values of the permeability were defined for different areas of the mould while considering a single viscosity. Some partitions were made to that end in the model according to the isothermal lines from the preheating analysis and different permeability values were defined. It is noteworthy that the real ratio between permeability and viscosity was kept for this analysis and, consequently, the resin flow can be simulated in a realistic manner. This can be seen in Figure 12 and in Table 4, where mean values of temperatures have been used, as well as their corresponding simulated material properties values.
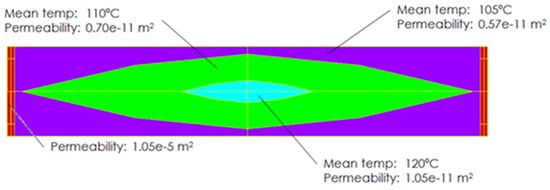
Figure 12.
Permeability values contour.

Table 4.
Temperature-dependent real and simulation values for viscosity and permeability.
The results show that the thermal effect is very relevant, and that 561 s (73% more) were needed to fill the cavity, see Figure 13. It was also observed that higher temperatures provoked a slower resin flow in the borders than in the centre. A higher filling speed at the beginning that went down as the resin flowed was observed in this case as well.
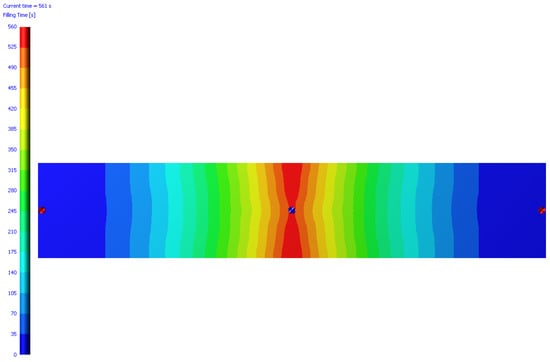
Figure 13.
Filling time non-isothermal process.
Finally, to complete the study of the filling stage of the process, a mechanical analysis was performed, where the load was the filling contour pressure obtained from RTM-Worx. As expected, this was not a critical step, as resulting stresses were low, and displacements were small.
4.3. Curing of the Component
The resin curing process analysis performed is presented in this section. As shown in Figure 5, RTM6 is usually cured in two phases. Both thermal and mechanical responses of the mould were studied again through MSC-Marc simulation code. The finite element model used is presented in Figure 7. A user subroutine was used to include the curing laws previously presented in Section 3.
Although it was desired to define an electric potential difference at the resistive heater according to the values determined in Section 4, it was found that results related to curing cannot be obtained in MSC-Marc if electric loads were applied. Therefore, the heat (that changes with time) caused due to Joule’s effect was applied as an internal heat generation. Heat coming from the curing process has also been considered for the thermal analysis.
Regarding thermal boundary conditions, a natural convection of 5 W/(m2K) and a radiation to environment condition were defined in the outer surfaces. An ambient temperature of 20 °C was considered. Temperatures at the end of the preheating analysis were used as initial conditions for the thermal curing analysis. However, some problems were encountered when a user subroutine was used at the same time that an initial temperature had non-uniform distribution. Thus, consequently, the whole RTM process was finally modelled and, consequently, a value of 20 °C was established as initial temperature.
The temperature distribution obtained at the end of the RTM process, see Figure 14, showed that the maximum temperatures were reached in the resistive heater. The heat generated here was then transferred to the adjoining components. Due to the thermal insulations of mica, the temperature of the outer surfaces was not so high and the temperature in the centre was the highest.
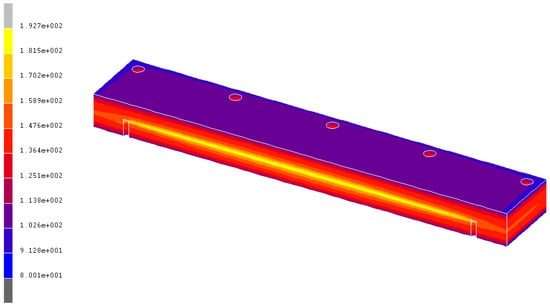
Figure 14.
Temperature (°C) distribution at the end of the RTM process.
Regarding the cavity, the evolutions of the maximum and minimum temperatures calculated are presented in Figure 15. It can be observed that values close to the set temperature have been obtained.
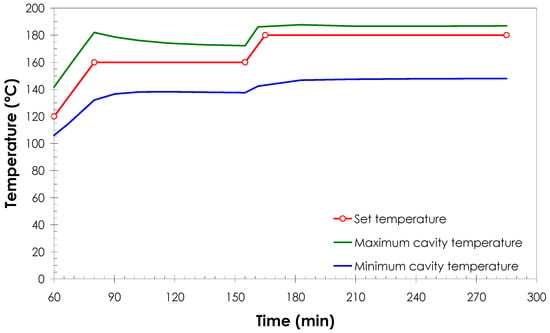
Figure 15.
Evolutions of the maximum and minimum temperatures of the cavity.
Regarding the curing process, it was observed that the resin was cured faster in the centre of the sample because higher temperatures were reached. It was also observed that, according to the simulation, the resin did not cure completely at the end of the process.
Finally, the mechanical stresses and displacements that were produced because of the transient temperature distribution are summarized in Table 5.

Table 5.
Stresses and displacements at different locations.
Results show that the CTE mismatch between the composite and the mica was relevant and generated stresses were quite high. Highest values were found near the holes due to stress concentrations. Out of them, maximum stresses were significantly lower (values about 140 MPa). Simulation results suggest that this CTE mismatch could be avoided by replacing the mica layers by alternative insulation systems (e.g., flexible rockwool blankets).
5. Conclusions
The simulations presented in this paper have helped to make an adequate design of a composite mould, with heating capabilities through an electric system. Some important points are now highlighted:
- A suitable dielectric material, such as fibreglass, around the resistive heater is needed to minimize electric current to the outer surfaces and to, consequently, avoid the risk of electrocution.
- Appropriate thermal insulation is recommended to minimize heat flows to the adjoining components and, therefore, to reduce the electric energy consumption.
- The temperature distribution reached in the cavity is not uniform (temperature uniformity was desired in the cavity), meaning heating alternatives should be found. A solution could be devised with heaters with variable electric resistances in different zones, but this is a point to be further investigated.
- Due to the temperature dependency of the resin properties, the expected temperature distribution should be considered when the injection strategy of a mould is studied. That way, zones of highest temperatures should be filled at the end of the process if a faster filling is desired.
- Materials of similar CTE’s should be used when possible in order to minimize the stresses and displacements generated. Such parameters could be critical in cases of large CTE mismatches.
- Neither the stresses nor the displacements caused due to the internal pressure from the filling process are expected to be critical with the present design.
It is interesting to note also that some limitations have been found in the commercial simulation codes employed. These codes are extremely good but, when a particular case or situation has to be modelled, it is easy that some small detail does not exactly fit the general code, meaning workarounds must be used. New versions of the programs usually solve the limitations previously mentioned and better general codes are available.
Some limitations encountered are now listed:
- Significant differences in resulting temperatures of up to 10% were found in the preheating stage depending on the analysis type conducted (thermo-electric or thermo-electric–mechanical). Several trials were made and it was concluded that such differences were not generated because of the deformations, but due to the internal formulation used by each analysis. An additional thermal analysis demonstrated that the results from the thermo-electric analysis are more accurate.
- Curing parameters cannot be obtained when electric loads are applied. Therefore, it is concluded that a common heat transfer analysis (assuming the Joule’s effect through an internal heat generation) is required.
Regarding the RTM simulation itself, some limitations were also found:
- Only two-dimensional analyses can be performed. However, this may not be critical as thin samples are usually manufactured by RTM.
- Since just linear triangular elements can be used, different meshes have been built in RTM-Worx and, therefore, problems to exchange data/results with MSC-Marc have been found.
- Only isothermal conditions can be considered. Thus, the viscosity of the resin is defined as a constant and, consequently, thermal effects cannot be analysed directly. However, a simple way to take into account the resin temperature dependency by defining different permeability values in the model through real permeability/viscosity ratios has been found.
Future improvements and research directions for this type of simulation are mainly foreseen in two fields: a better integration of all the software needed (electrical, joule effect, filling, curing, mechanical…) and a better on-line measurement of the real temperatures of the semi-moulds, which will permit better filling strategies.
Author Contributions
Conceptualization, I.G. and H.V.; methodology, I.G. and H.V.; software, H.V.; validation, I.G., U.O. and H.V.; investigation, I.G. and H.V.; resources, I.G.; data curation, H.V.; writing—original draft preparation, H.V.; writing—review and editing, I.G., H.V. and U.O.; visualization, H.V.; supervision, I.G.; project administration, I.G.; funding acquisition, I.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was developed under the European Seventh Framework Program, Theme 4, NMP—Nanosciences, Nanotechnologies, Materials and new Production Technologies, Project COEUS-TITAN [Grant Agreement no. CP-TP 246256-2].
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to consortium agreement restrictions.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Trollman, H.; Trollman, F. A Sustainability Assessment of Smart Innovations for Mass Production, Mass Customization and Direct Digital Manufacturing. In Mass Production Processes; Akdogan, A., Vanli, A.S., Eds.; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef]
- Matvienko, O.; Daneyko, O.; Kovalevskaya, T.; Khrustalyov, A.; Zhukov, I.; Vorozhtsov, A. Investigation of Stresses Induced Due to the Mismatch of the Coefficients of Thermal Expansion of the Matrix and the Strengthening Particle in Aluminum-Based Composites. Metals 2021, 11, 279. [Google Scholar] [CrossRef]
- Zade, A.; Neogi, S.; Kuppusamy, R.R.P. Design of effective injection strategy and operable cure window for an aircraft wing flap composite part using neat resin characterization and multi-physics process simulation. Polym. Compos. 2022, 43, 3426. [Google Scholar] [CrossRef]
- Joo, S.J.; Yu, M.H.; Seock Kim, W.; Lee, J.W.; Kim, H.S. Design and manufacture of automotive composite front bumper assemble component considering interfacial bond characteristics between over-molded chopped glass fiber polypropylene and continuous glass fiber polypropylene composite. Compos. Struct. 2020, 236, 111849. [Google Scholar] [CrossRef]
- Simacek, P.; Advani, S.G.; Iobst, S.A. Modeling Flow in Compression Resin Transfer Molding for Manufacturing of Complex Lightweight High-Performance Automotive Parts. J. Compos. Mater. 2008, 42, 2523–2545. [Google Scholar] [CrossRef]
- Kuppusamy, R.R.P.; Neogi, S. Simulation of air entrapment and resin curing during manufacturing of composite cab front by resin transfer moulding process. Arch. Metall. Mater. 2017, 62, 1839–1844. [Google Scholar] [CrossRef]
- Xiong, F.; Wang, D.; Ma, Z.; Chen, S.; Lv, T.; Lu, F. Structure-material integrated multi-objective lightweight design of the front end structure of automobile body. Struct. Multidiscip. Optim. 2018, 57, 829–847. [Google Scholar] [CrossRef]
- Mal, O.; Couniot, A.; Dupret, F. Non isothermal simulation of the resin transfer moulding press. Compos. Part A Appl. Sci. Manuf. 1998, 29, 189–198. [Google Scholar] [CrossRef]
- Garmendia, I.; Vallejo, H.; Iriarte, A.; Anglada, E. Direct Resistive Heating Simulation Tool for the Repair of Aerospace Structures through Composite Patches. Math. Probl. Eng. 2018, 2018, 4136795. [Google Scholar] [CrossRef]
- Volume A: Theory and User Information; Msc-Marc 2008R1; Msc Software: Newport Beach, CA, USA, 2008.
- RTM-Worxs v2.8, Users Documentation. Available online: https://www.polyworx.com/doc/ (accessed on 8 December 2022).
- Yi, S.; Hilton, H.H.; Ahmad, M.F. A finite element approach for cure simulation of thermosetting matrix composites. Comput. Struct. 1997, 64, 383–388. [Google Scholar] [CrossRef]
- Kim, J.; Moon, T.J.; Howell, J.R. Cure Kinetic Model, Heat of Reaction, and Glass Transition Temperature of AS4/3501-6 Graphite–Epoxy Prepregs. J. Compos. Mater. 2002, 36, 2479–2498. [Google Scholar] [CrossRef]
- Rider, A.N.; Wang, C.H.; Cao, J. Internal resistance heating for homogeneous curing of adhesively bonded repairs. Int. J. Adhes. Adhes. 2011, 31, 168–176. [Google Scholar] [CrossRef]
- Maguire, J.M.; Sharp, N.D.; Pipes, R.B.; Bradaigh, C.M. Advanced process simulations for thick-section epoxy powder composite structures. Compos. Part A 2022, 161, 107073. [Google Scholar] [CrossRef]
- Kenny, J.M.; Maffezzoli, A.M.; Nicolais, L.; Mazzola, M. A model for the thermal and chemorheological behavior of thermoset processing: II) Unsaturated polyester based composites. Compos. Sci. Technol. 1990, 38, 339–358. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).