Author Contributions
W.T.: Conceptualization, Methodology, Validation, Investigation, Resources, Supervision, Project Administration, Visualization, Writing—review and editing; L.P.: Software, Formal analysis, Data curation, Writing—original draft preparation, Visualization; C.T., W.N.: Software, Methodology, Visualization. All authors have read and agreed to the published version of the manuscript.
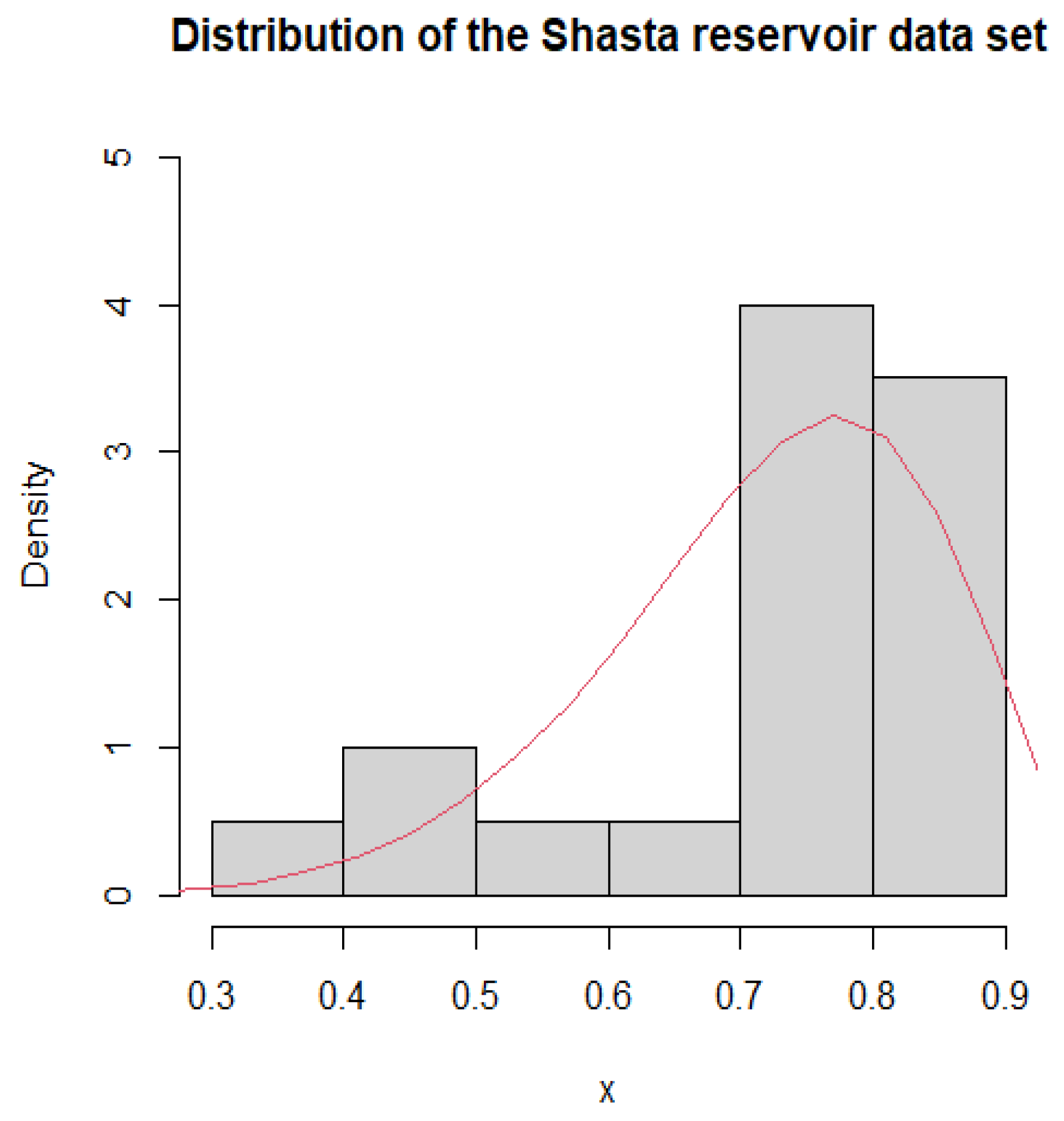
Figure 1.
Histogram and PDF fitting of Shasta reservoir dataset.
Figure 1.
Histogram and PDF fitting of Shasta reservoir dataset.
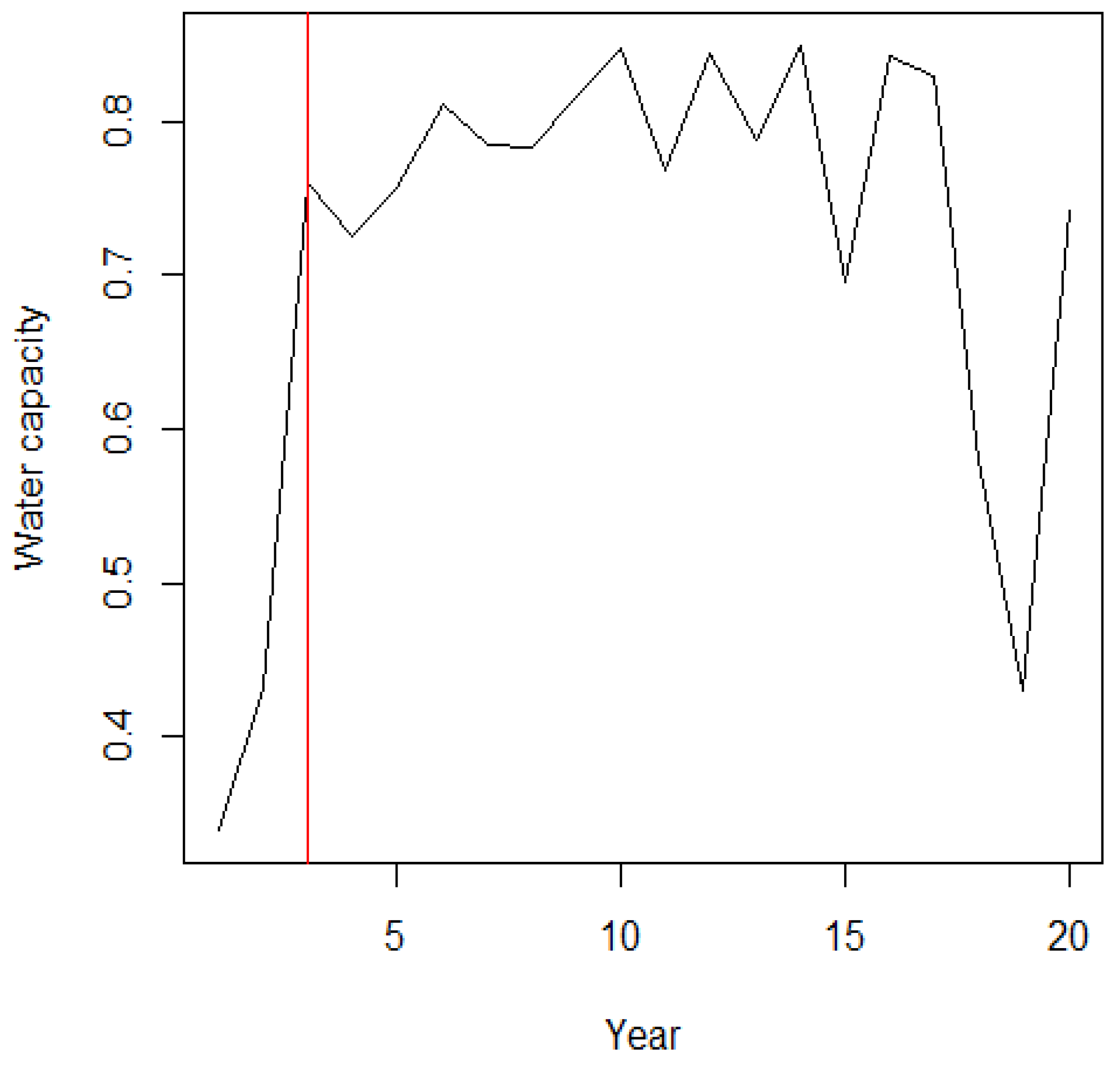
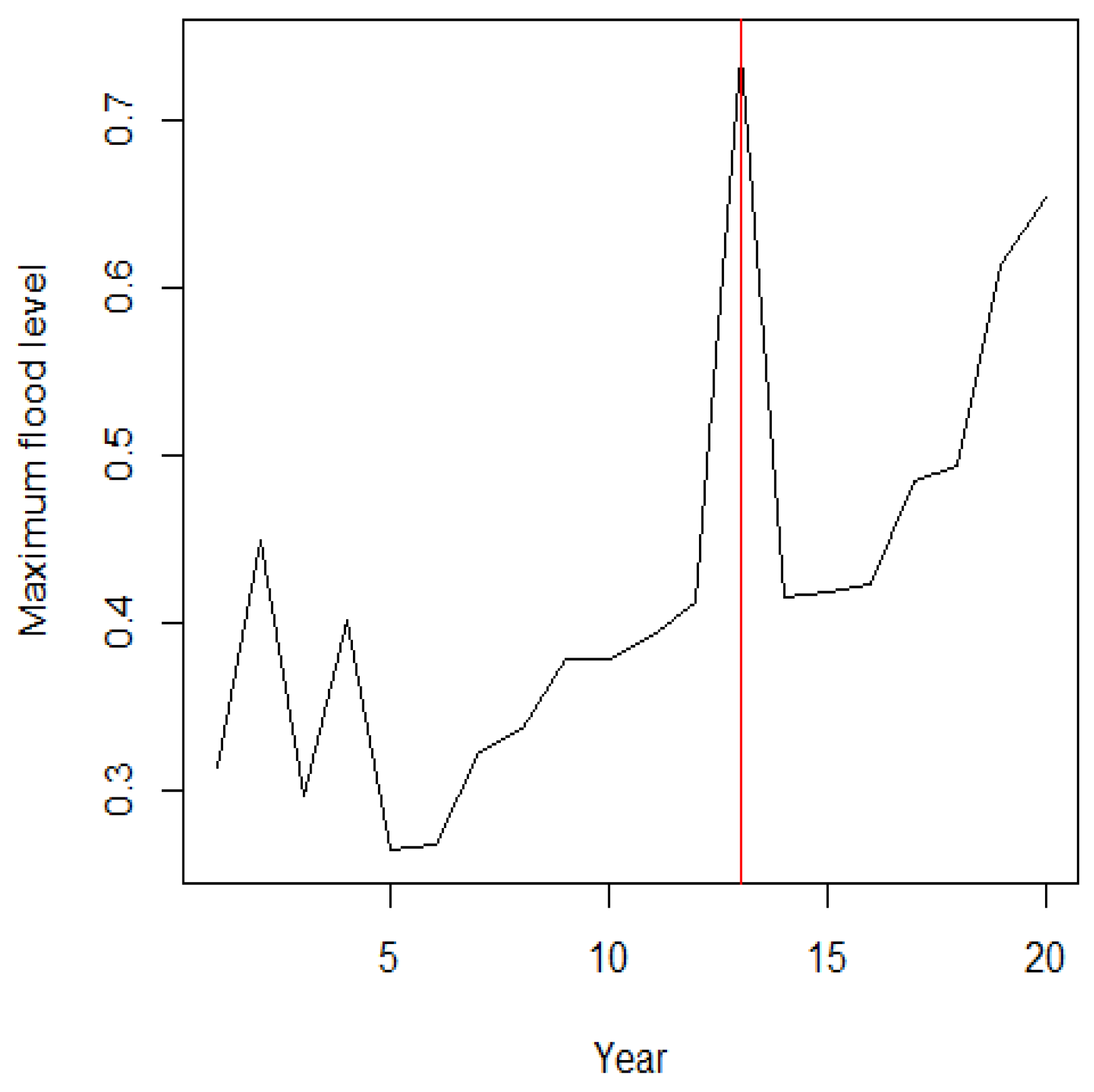
Figure 2.
The Shasta reservoir dataset and position of change point.
Figure 2.
The Shasta reservoir dataset and position of change point.
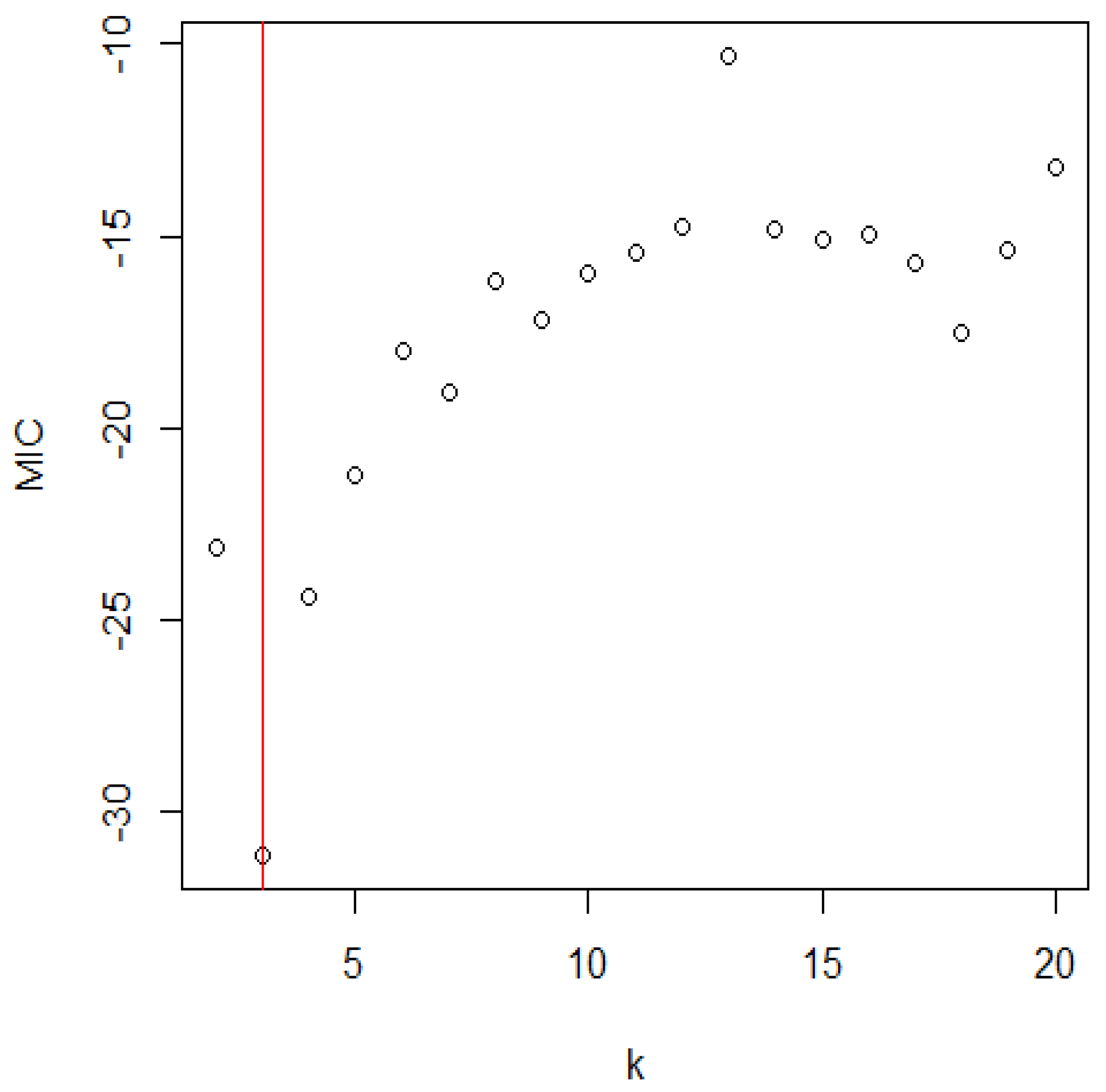
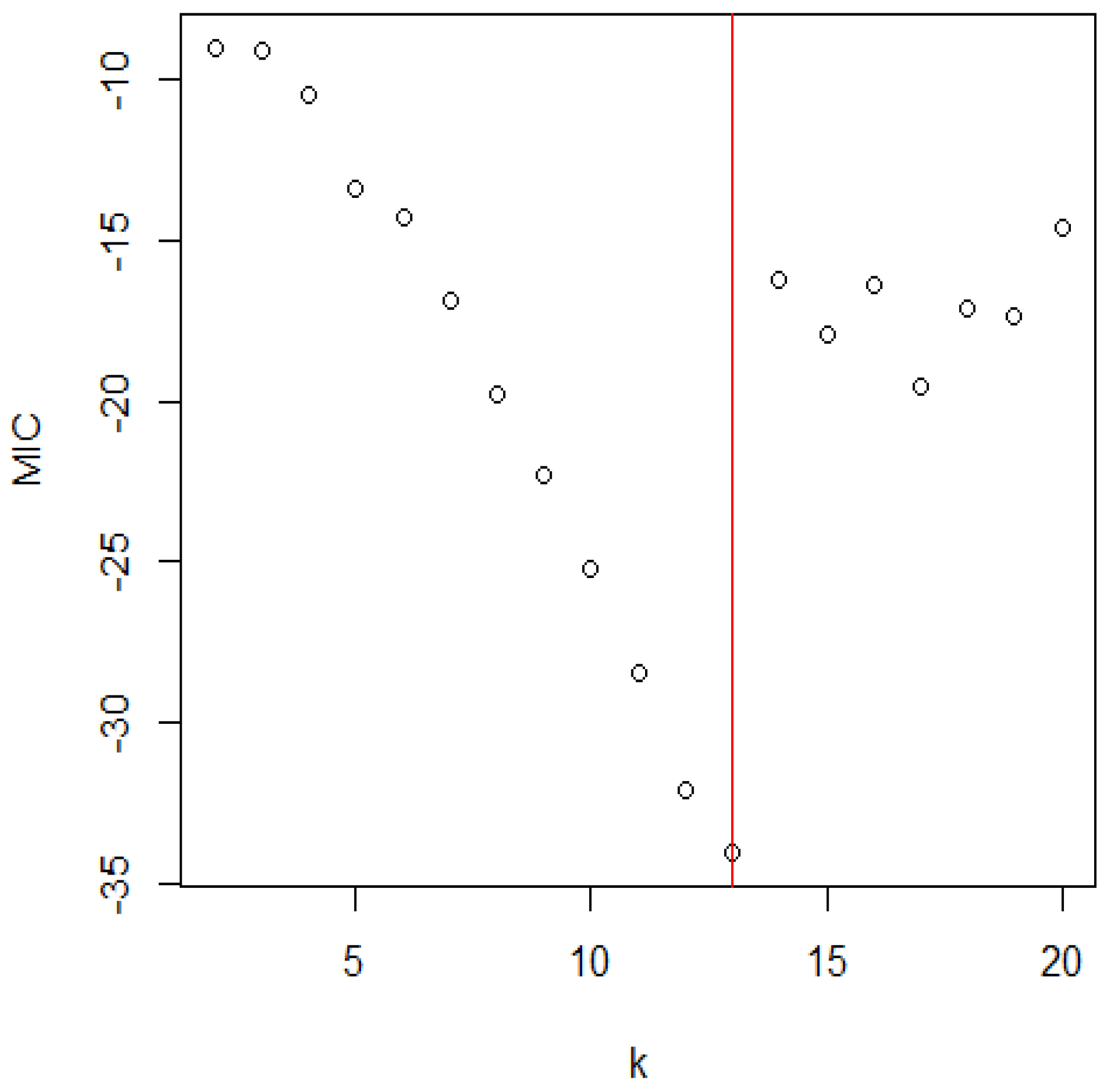
Figure 3.
The distribution of MIC for the Shasta reservoir.
Figure 3.
The distribution of MIC for the Shasta reservoir.
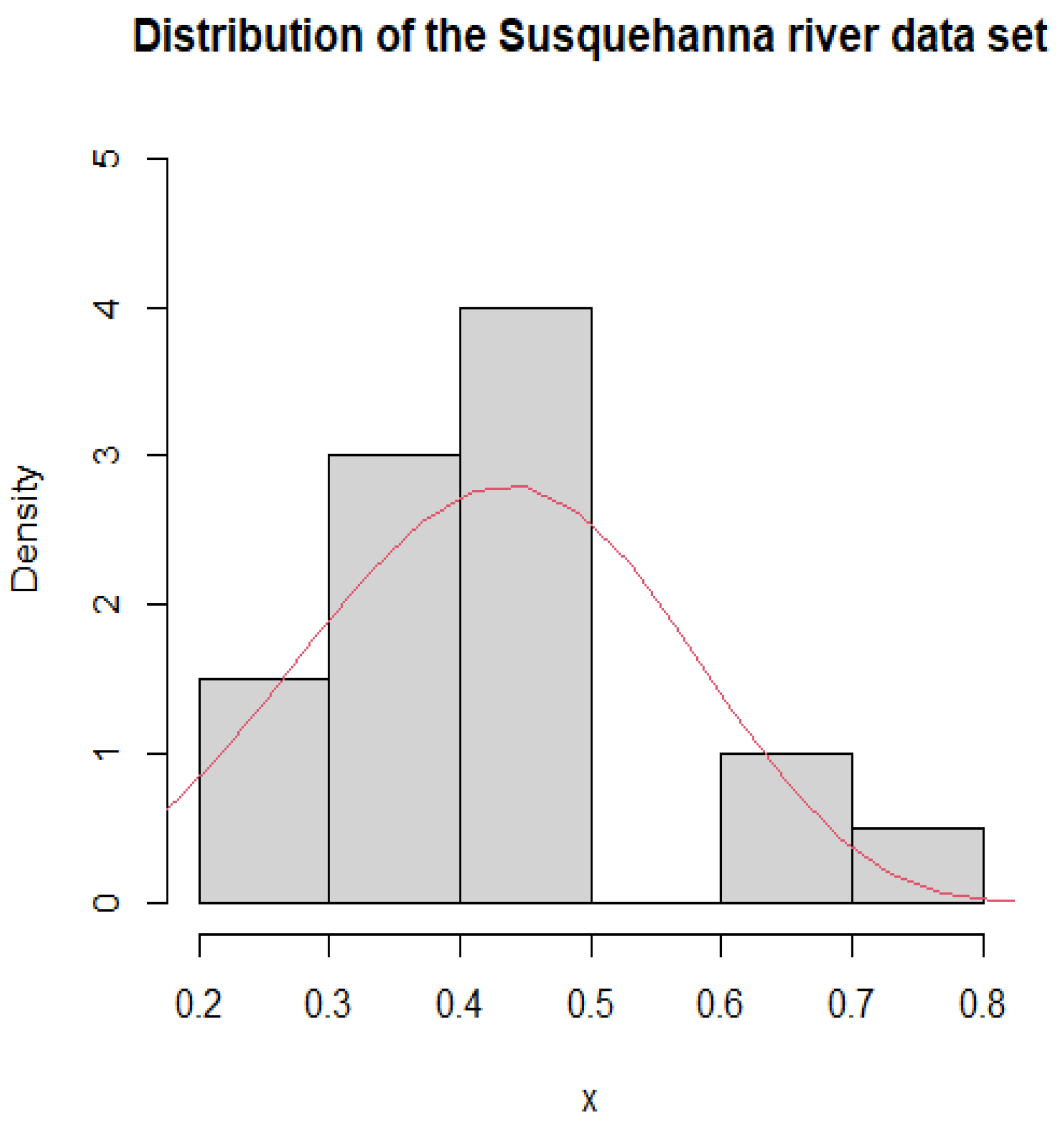
Figure 4.
Histogram and PDF fitting of Susquehanna river dataset.
Figure 4.
Histogram and PDF fitting of Susquehanna river dataset.
Figure 5.
The Susquehanna river dataset and position of change point.
Figure 5.
The Susquehanna river dataset and position of change point.
Figure 6.
The distribution of MIC for the Susquehanna river.
Figure 6.
The distribution of MIC for the Susquehanna river.
Figure 7.
Histogram and PDF fitting of 1.5 cm glass fibre strengths dataset.
Figure 7.
Histogram and PDF fitting of 1.5 cm glass fibre strengths dataset.
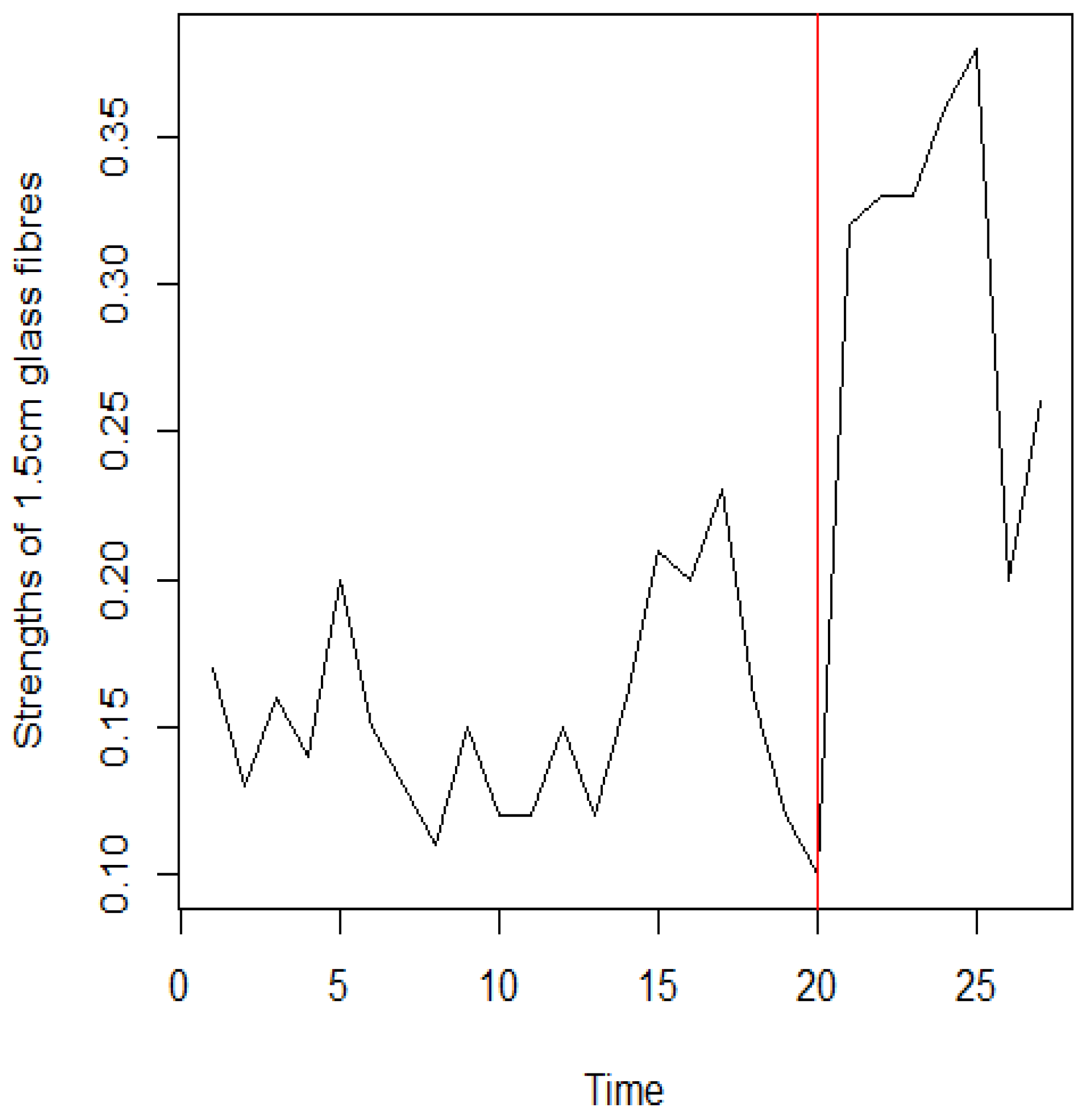
Figure 8.
The strengths of 1.5cm glass fibres dataset and position of change point.
Figure 8.
The strengths of 1.5cm glass fibres dataset and position of change point.
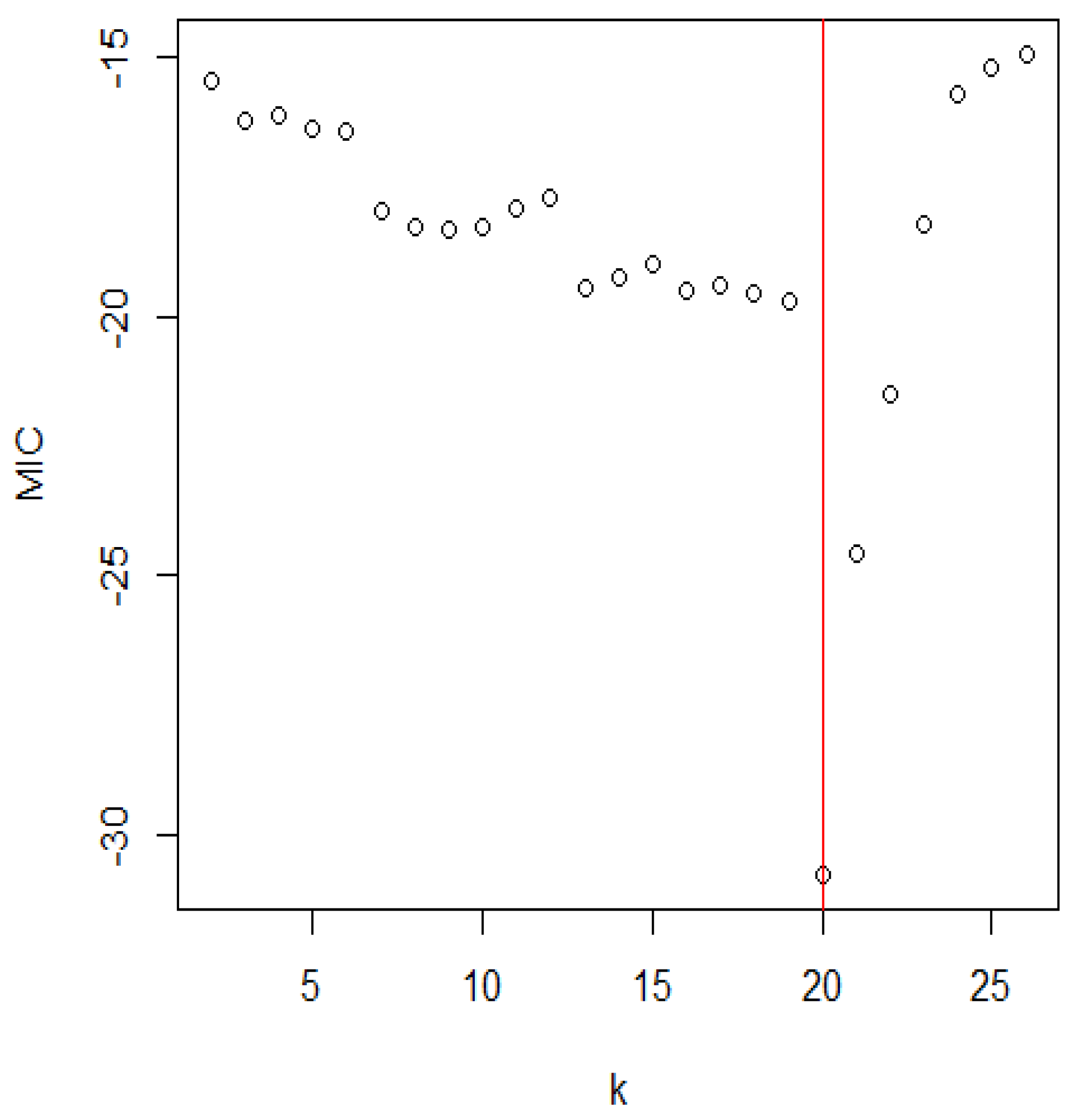
Figure 9.
The distribution of the MIC for the strengths of 1.5 cm glass fibres.
Figure 9.
The distribution of the MIC for the strengths of 1.5 cm glass fibres.
Table 1.
Approximate critical values of LRT with different values of and n.
Table 1.
Approximate critical values of LRT with different values of and n.
| n | | | | n | | | |
|---|
| 15 | 27.9478 | 12.6744 | 8.8511 | 90 | 21.3668 | 13.6862 | 10.8365 |
| 20 | 21.6147 | 12.6386 | 9.4401 | 100 | 21.3745 | 13.7889 | 10.9661 |
| 35 | 21.4807 | 12.8847 | 9.7842 | 110 | 21.3845 | 12.6386 | 11.0768 |
| 40 | 21.4207 | 13.0768 | 10.0440 | 120 | 21.3957 | 13.9551 | 11.1734 |
| 50 | 21.3725 | 13.3602 | 10.4182 | 140 | 21.4191 | 14.0856 | 11.3344 |
| 60 | 21.3889 | 13.2315 | 10.2496 | 160 | 21.4050 | 14.0108 | 11.2422 |
| 70 | 21.3679 | 13.4170 | 10.4920 | 180 | 21.4238 | 14.1086 | 11.3626 |
| 80 | 21.3633 | 13.5646 | 10.6819 | 200 | 21.4425 | 14.1922 | 11.4649 |
Table 2.
Approximate critical values of SIC with different values of and n.
Table 2.
Approximate critical values of SIC with different values of and n.
| n | | | | n | | | |
|---|
| 15 | 21.1982 | 10.6171 | 6.7932 | 70 | 16.8038 | 8.0819 | 4.8147 |
| 20 | 20.1949 | 10.1444 | 6.4766 | 80 | 16.4902 | 7.8592 | 4.6200 |
| 25 | 19.5007 | 9.7790 | 6.2091 | 90 | 16.2178 | 7.6623 | 4.4463 |
| 30 | 18.9726 | 9.4804 | 5.9793 | 100 | 15.9772 | 7.4857 | 4.2894 |
| 35 | 18.5476 | 9.2275 | 5.7782 | 150 | 15.0740 | 6.8020 | 3.6737 |
| 40 | 18.1927 | 9.0080 | 5.5997 | 200 | 14.4507 | 6.3133 | 3.2268 |
| 50 | 17.6222 | 8.6400 | 5.2932 | 250 | 13.9751 | 5.9321 | 2.8751 |
| 60 | 17.1733 | 8.3381 | 5.0362 | 300 | 13.5907 | 5.6193 | 2.5847 |
Table 3.
Approximate critical values for MIC under different parameters.
Table 3.
Approximate critical values for MIC under different parameters.
| n | | | | | | | | |
|---|
| 15 | | 16.0214 | 12.1440 | 9.9910 | | 12.7805 | 8.4131 | 6.6169 |
| 20 | | 13.5348 | 9.4129 | 7.7097 | | 9.1797 | 4.8304 | 3.0177 |
| 30 | | 12.5291 | 9.3880 | 7.2124 | | 14.6126 | 9.0067 | 6.5348 |
| 40 | | 12.4641 | 9.4281 | 7.4635 | | 13.3377 | 8.6004 | 5.0923 |
| 50 | | 11.6223 | 7.6873 | 6.0628 | | 12.0217 | 7.2745 | 5.1606 |
| 55 | | 15.2560 | 12.1560 | 10.1627 | | 16.4481 | 13.0652 | 11.7789 |
| 60 | | 19.7908 | 13.6454 | 11.8123 | | 16.1109 | 12.2783 | 10.4150 |
| 80 | | 17.7720 | 13.5650 | 11.3690 | | 16.7704 | 12.3216 | 10.3872 |
| 100 | | 17.4697 | 12.9035 | 10.9909 | | 10.0437 | 6.7711 | 4.1757 |
| 150 | | 18.0801 | 13.0013 | 11.0911 | | 15.0437 | 11.7711 | 10.1757 |
| 200 | | 16.2452 | 12.5573 | 10.6762 | | 15.5848 | 11.9499 | 10.0195 |
Table 4.
Approximate critical values for MIC under parameters.
Table 4.
Approximate critical values for MIC under parameters.
| n | | | | |
|---|
| 15 | | 19.4604 | 12.9669 | 10.3656 |
| 20 | | 18.4070 | 13.0958 | 10.5379 |
| 30 | | 21.8363 | 16.0958 | 14.8520 |
| 40 | | 17.5919 | 13.9549 | 11.5930 |
| 50 | | 17.2003 | 10.8230 | 8.3099 |
| 55 | | 18.2946 | 13.9232 | 11.8138 |
| 60 | | 17.9610 | 13.1129 | 11.1608 |
| 80 | | 16.4356 | 12.1177 | 10.8341 |
| 100 | | 11.3732 | 7.0083 | 6.4604 |
| 150 | | 15.2264 | 11.8086 | 9.2993 |
| 200 | | 15.6294 | 12.1649 | 10.5434 |
Table 5.
Powers of the LRT, SIC, and MIC procedures at , .
Table 5.
Powers of the LRT, SIC, and MIC procedures at , .
| | | | | |
|---|
| k | Model | | (4, 2.5) | (0.2, 0.5) | (2, 2) | (4, 0.5) |
|---|
| 0.01 | 5 | LRT | (4, 0.5) | 0.116 | 0.037 | 0.146 | 0.000 |
| | | SIC | (4, 0.5) | 0.048 | 0.015 | 0.075 | 0.000 |
| | | MIC | (4, 0.5) | 0.483 | 0.594 | 0.610 | 0.016 |
| | 10 | LRT | (4, 0.5) | 0.107 | 0.248 | 0.187 | 0.001 |
| | | SIC | (4, 0.5) | 0.024 | 0.076 | 0.086 | 0.000 |
| | | MIC | (4, 0.5) | 0.567 | 0.809 | 0.707 | 0.018 |
| | 15 | LRT | (4, 0.5) | 0.036 | 0.225 | 0.079 | 0.004 |
| | | SIC | (4, 0.5) | 0.008 | 0.159 | 0.018 | 0.000 |
| | | MIC | (4, 0.5) | 0.592 | 0.804 | 0.583 | 0.015 |
| 0.05 | 5 | LRT | (4, 0.5) | 0.520 | 0.471 | 0.641 | 0.027 |
| | | SIC | (4, 0.5) | 0.342 | 0.235 | 0.434 | 0.012 |
| | | MIC | (4, 0.5) | 0.734 | 0.773 | 0.857 | 0.033 |
| | 10 | LRT | (4, 0.5) | 0.601 | 0.846 | 0.780 | 0.029 |
| | | SIC | (4, 0.5) | 0.337 | 0.615 | 0.551 | 0.026 |
| | | MIC | (4, 0.5) | 0.838 | 0.968 | 0.930 | 0.037 |
| | 15 | LRT | (4, 0.5) | 0.326 | 0.815 | 0.542 | 0.025 |
| | | SIC | (4, 0.5) | 0.148 | 0.665 | 0.275 | 0.013 |
| | | MIC | (4, 0.5) | 0.656 | 0.932 | 0.804 | 0.029 |
| 0.1 | 5 | LRT | (4, 0.5) | 0.726 | 0.782 | 0.831 | 0.049 |
| | | SIC | (4, 0.5) | 0.558 | 0.510 | 0.673 | 0.030 |
| | | MIC | (4, 0.5) | 0.853 | 0.928 | 0.912 | 0.065 |
| | 10 | LRT | (4, 0.5) | 0.813 | 0.962 | 0.923 | 0.051 |
| | | SIC | (4, 0.5) | 0.583 | 0.840 | 0.794 | 0.037 |
| | | MIC | (4, 0.5) | 0.912 | 0.988 | 0.975 | 0.065 |
| | 15 | LRT | (4, 0.5) | 0.610 | 0.893 | 0.778 | 0.030 |
| | | SIC | (4, 0.5) | 0.354 | 0.835 | 0.549 | 0.017 |
| | | MIC | (4, 0.5) | 0.782 | 0.970 | 0.908 | 0.037 |
Table 6.
Powers of the LRT, SIC, and MIC procedures at , .
Table 6.
Powers of the LRT, SIC, and MIC procedures at , .
| | | | | |
|---|
| k | Model | | (4, 2.5) | (0.2, 0.5) | (2, 2) | (4, 0.5) |
|---|
| 0.01 | 15 | LRT | (4, 0.5) | 0.795 | 0.869 | 0.930 | 0.000 |
| | | SIC | (4, 0.5) | 0.617 | 0.672 | 0.837 | 0.000 |
| | | MIC | (4, 0.5) | 0.979 | 0.998 | 0.998 | 0.002 |
| | 25 | LRT | (4, 0.5) | 0.828 | 0.995 | 0.955 | 0.001 |
| | | SIC | (4, 0.5) | 0.639 | 0.960 | 0.904 | 0.000 |
| | | MIC | (4, 0.5) | 0.996 | 1.000 | 1.000 | 0.006 |
| | 35 | LRT | (4, 0.5) | 0.530 | 0.988 | 0.977 | 0.002 |
| | | SIC | (4, 0.5) | 0.300 | 0.976 | 0.718 | 0.000 |
| | | MIC | (4, 0.5) | 0.964 | 0.999 | 0.994 | 0.002 |
| 0.05 | 15 | LRT | (4, 0.5) | 0.963 | 0.996 | 0.998 | 0.012 |
| | | SIC | (4, 0.5) | 0.930 | 0.983 | 0.983 | 0.006 |
| | | MIC | (4, 0.5) | 0.996 | 1.000 | 1.000 | 0.014 |
| | 25 | LRT | (4, 0.5) | 0.986 | 1.000 | 0.999 | 0.022 |
| | | SIC | (4, 0.5) | 0.955 | 0.998 | 0.995 | 0.004 |
| | | MIC | (4, 0.5) | 1.000 | 1.000 | 1.000 | 0.034 |
| | 35 | LRT | (4, 0.5) | 0.936 | 0.999 | 0.996 | 0.010 |
| | | SIC | (4, 0.5) | 0.810 | 0.997 | 0.978 | 0.009 |
| | | MIC | (4, 0.5) | 0.998 | 1.000 | 1.000 | 0.011 |
| 0.1 | 15 | LRT | (4, 0.5) | 0.991 | 1.000 | 0.999 | 0.026 |
| | | SIC | (4, 0.5) | 0.974 | 0.996 | 0.993 | 0.024 |
| | | MIC | (4, 0.5) | 0.999 | 1.000 | 1.000 | 0.032 |
| | 25 | LRT | (4, 0.5) | 0.997 | 1.000 | 1.000 | 0.029 |
| | | SIC | (4, 0.5) | 0.992 | 1.000 | 0.999 | 0.029 |
| | | MIC | (4, 0.5) | 1.000 | 1.000 | 1.000 | 0.034 |
| | 35 | LRT | (4, 0.5) | 0.989 | 0.999 | 0.999 | 0.017 |
| | | SIC | (4, 0.5) | 0.931 | 0.998 | 0.996 | 0.011 |
| | | MIC | (4, 0.5) | 1.000 | 1.000 | 1.000 | 0.028 |
Table 7.
Powers of the LRT, SIC, and MIC procedures at , .
Table 7.
Powers of the LRT, SIC, and MIC procedures at , .
| | | | | |
|---|
| k | Model | | (4, 2.5) | (0.2, 0.5) | (2, 2) | (4, 0.5) |
|---|
| 0.01 | 25 | LRT | (4, 0.5) | 0.995 | 1.000 | 0.998 | 0.002 |
| | | SIC | (4, 0.5) | 0.989 | 1.000 | 0.997 | 0.001 |
| | | MIC | (4, 0.5) | 0.999 | 1.000 | 1.000 | 0.008 |
| | 50 | LRT | (4, 0.5) | 1.000 | 1.000 | 1.000 | 0.000 |
| | | SIC | (4, 0.5) | 0.998 | 1.000 | 1.000 | 0.000 |
| | | MIC | (4, 0.5) | 1.000 | 1.000 | 1.000 | 0.005 |
| | 75 | LRT | (4, 0.5) | 0.972 | 1.000 | 1.000 | 0.002 |
| | | SIC | (4, 0.5) | 0.913 | 1.000 | 0.996 | 0.000 |
| | | MIC | (4, 0.5) | 0.991 | 1.000 | 1.000 | 0.006 |
| 0.05 | 25 | LRT | (4, 0.5) | 1.000 | 1.000 | 1.000 | 0.033 |
| | | SIC | (4, 0.5) | 0.999 | 1.000 | 1.000 | 0.006 |
| | | MIC | (4, 0.5) | 1.000 | 1.000 | 1.000 | 0.046 |
| | 50 | LRT | (4, 0.5) | 1.000 | 1.000 | 1.000 | 0.023 |
| | | SIC | (4, 0.5) | 1.000 | 1.000 | 1.000 | 0.012 |
| | | MIC | (4, 0.5) | 1.000 | 1.000 | 1.000 | 0.051 |
| | 75 | LRT | (4, 0.5) | 0.999 | 1.000 | 1.000 | 0.034 |
| | | SIC | (4, 0.5) | 0.999 | 1.000 | 1.000 | 0.010 |
| | | MIC | (4, 0.5) | 0.999 | 1.000 | 1.000 | 0.042 |
| 0.1 | 25 | LRT | (4, 0.5) | 1.000 | 1.000 | 1.000 | 0.075 |
| | | SIC | (4, 0.5) | 1.000 | 1.000 | 1.000 | 0.033 |
| | | MIC | (4, 0.5) | 1.000 | 1.000 | 1.000 | 0.093 |
| | 50 | LRT | (4, 0.5) | 1.000 | 1.000 | 1.000 | 0.072 |
| | | SIC | (4, 0.5) | 1.000 | 1.000 | 1.000 | 0.040 |
| | | MIC | (4, 0.5) | 1.000 | 1.000 | 1.000 | 0.099 |
| | 75 | LRT | (4, 0.5) | 1.000 | 1.000 | 1.000 | 0.094 |
| | | SIC | (4, 0.5) | 1.000 | 1.000 | 1.000 | 0.039 |
| | | MIC | (4, 0.5) | 1.000 | 1.000 | 1.000 | 0.096 |
Table 8.
Powers of the LRT, SIC, and MIC procedures at , .
Table 8.
Powers of the LRT, SIC, and MIC procedures at , .
| | | | | |
|---|
| k | Model | | (0.5, 1.5) | (1.2, 3.5) | (0.8, 2.5) | (0.5, 3.5) |
|---|
| 0.01 | 5 | LRT | (0.5, 3.5) | 0.165 | 0.388 | 0.208 | 0.001 |
| | | SIC | (0.5, 3.5) | 0.105 | 0.271 | 0.162 | 0.000 |
| | | MIC | (0.5, 3.5) | 0.423 | 0.680 | 0.495 | 0.003 |
| | 10 | LRT | (0.5, 3.5) | 0.246 | 0.493 | 0.327 | 0.001 |
| | | SIC | (0.5, 3.5) | 0.162 | 0.320 | 0.218 | 0.000 |
| | | MIC | (0.5, 3.5) | 0.514 | 0.812 | 0.570 | 0.006 |
| | 15 | LRT | (0.5, 3.5) | 0.201 | 0.268 | 0.254 | 0.001 |
| | | SIC | (0.5, 3.5) | 0.111 | 0.151 | 0.159 | 0.000 |
| | | MIC | (0.5, 3.5) | 0.450 | 0.677 | 0.477 | 0.002 |
| 0.05 | 5 | LRT | (0.5, 3.5) | 0.446 | 0.694 | 0.518 | 0.028 |
| | | SIC | (0.5, 3.5) | 0.334 | 0.586 | 0.411 | 0.004 |
| | | MIC | (0.5, 3.5) | 0.879 | 0.953 | 0.892 | 0.036 |
| | 10 | LRT | (0.5, 3.5) | 0.543 | 0.794 | 0.616 | 0.045 |
| | | SIC | (0.5, 3.5) | 0.394 | 0.736 | 0.469 | 0.017 |
| | | MIC | (0.5, 3.5) | 0.903 | 0.987 | 0.923 | 0.059 |
| | 15 | LRT | (0.5, 3.5) | 0.476 | 0.599 | 0,517 | 0.024 |
| | | SIC | (0.5, 3.5) | 0.300 | 0.542 | 0.377 | 0.006 |
| | | MIC | (0.5, 3.5) | 0.866 | 0.959 | 0.898 | 0.039 |
| 0.1 | 5 | LRT | (0.5, 3.5) | 0.763 | 0.875 | 0.833 | 0.043 |
| | | SIC | (0.5, 3.5) | 0.581 | 0.761 | 0.643 | 0.031 |
| | | MIC | (0.5, 3.5) | 0.989 | 0.999 | 0.997 | 0.056 |
| | 10 | LRT | (0.5, 3.5) | 0.823 | 0.928 | 0.889 | 0.054 |
| | | SIC | (0.5, 3.5) | 0.628 | 0.875 | 0.713 | 0.048 |
| | | MIC | (0.5, 3.5) | 0.999 | 1.000 | 0.998 | 0.078 |
| | 15 | LRT | (0.5, 3.5) | 0.781 | 0.885 | 0.814 | 0.049 |
| | | SIC | (0.5, 3.5) | 0.526 | 0.747 | 0.638 | 0.034 |
| | | MIC | (0.5, 3.5) | 0.992 | 0.998 | 0.998 | 0.061 |
Table 9.
Powers of the LRT, SIC, and MIC procedures at , .
Table 9.
Powers of the LRT, SIC, and MIC procedures at , .
| | | | | |
|---|
| k | Model | | (0.5, 1.5) | (1.2, 3.5) | (0.8, 2.5) | (0.5, 3.5) |
|---|
| 0.01 | 15 | LRT | (0.5, 3.5) | 0.543 | 0.889 | 0.735 | 0.001 |
| | | SIC | (0.5, 3.5) | 0.326 | 0.750 | 0.551 | 0.000 |
| | | MIC | (0.5, 3.5) | 0.790 | 0.987 | 0.820 | 0.010 |
| | 25 | LRT | (0.5, 3.5) | 0.639 | 0.932 | 0.825 | 0.004 |
| | | SIC | (0.5, 3.5) | 0.426 | 0.841 | 0.624 | 0.001 |
| | | MIC | (0.5, 3.5) | 0.897 | 0.995 | 0.901 | 0.015 |
| | 35 | LRT | (0.5, 3.5) | 0.588 | 0.805 | 0.744 | 0.000 |
| | | SIC | (0.5, 3.5) | 0.365 | 0.648 | 0.547 | 0.000 |
| | | MIC | (0.5, 3.5) | 0.832 | 0.981 | 0.827 | 0.007 |
| 0.05 | 15 | LRT | (0.5, 3.5) | 0.724 | 0.975 | 0.844 | 0.029 |
| | | SIC | (0.5, 3.5) | 0.608 | 0.929 | 0.810 | 0.010 |
| | | MIC | (0.5, 3.5) | 0.929 | 0.999 | 0.965 | 0.033 |
| | 25 | LRT | (0.5, 3.5) | 0.803 | 0.989 | 0.906 | 0.033 |
| | | SIC | (0.5, 3.5) | 0.742 | 0.956 | 0.858 | 0.010 |
| | | MIC | (0.5, 3.5) | 0.954 | 1.000 | 0.988 | 0.048 |
| | 35 | LRT | (0.5, 3.5) | 0.732 | 0.966 | 0,850 | 0.034 |
| | | SIC | (0.5, 3.5) | 0.635 | 0.886 | 0.789 | 0.012 |
| | | MIC | (0.5, 3.5) | 0.926 | 0.999 | 0.971 | 0.048 |
| 0.1 | 15 | LRT | (0.5, 3.5) | 0.922 | 0.994 | 0.968 | 0.070 |
| | | SIC | (0.5, 3.5) | 0.720 | 0.969 | 0.817 | 0.031 |
| | | MIC | (0.5, 3.5) | 0.992 | 1.000 | 0.997 | 0.085 |
| | 25 | LRT | (0.5, 3.5) | 0.950 | 1.000 | 0.980 | 0.079 |
| | | SIC | (0.5, 3.5) | 0.823 | 0.986 | 0.916 | 0.033 |
| | | MIC | (0.5, 3.5) | 0.999 | 1.000 | 1.000 | 0.095 |
| | 35 | LRT | (0.5, 3.5) | 0.908 | 0.996 | 0.950 | 0.077 |
| | | SIC | (0.5, 3.5) | 0.749 | 0.952 | 0.868 | 0.035 |
| | | MIC | (0.5, 3.5) | 0.988 | 1.000 | 0.999 | 0.090 |
Table 10.
Powers of the LRT, SIC, and MIC procedures at , .
Table 10.
Powers of the LRT, SIC, and MIC procedures at , .
| | | | | |
|---|
| k | Model | | (0.5, 1.5) | (1.2, 3.5) | (0.8, 2.5) | (0.5, 3.5) |
|---|
| 0.01 | 25 | LRT | (0.5, 3.5) | 0.773 | 0.974 | 0.821 | 0.002 |
| | | SIC | (0.5, 3.5) | 0.618 | 0.932 | 0.693 | 0.001 |
| | | MIC | (0.5, 3.5) | 0.890 | 1.000 | 0.945 | 0.011 |
| | 50 | LRT | (0.5, 3.5) | 0.840 | 0.996 | 0.854 | 0.007 |
| | | SIC | (0.5, 3.5) | 0.759 | 0.984 | 0.763 | 0.001 |
| | | MIC | (0.5, 3.5) | 0.981 | 1.000 | 0.993 | 0.019 |
| | 75 | LRT | (0.5, 3.5) | 0.835 | 0.948 | 0.839 | 0.002 |
| | | SIC | (0.5, 3.5) | 0.625 | 0.908 | 0.638 | 0.000 |
| | | MIC | (0.5, 3.5) | 0.919 | 1.000 | 0.949 | 0.007 |
| 0.05 | 25 | LRT | (0.5, 3.5) | 0.809 | 0.997 | 0.880 | 0.032 |
| | | SIC | (0.5, 3.5) | 0.673 | 0.993 | 0.857 | 0.007 |
| | | MIC | (0.5, 3.5) | 0.939 | 1.000 | 0.994 | 0.060 |
| | 50 | LRT | (0.5, 3.5) | 0.895 | 1.000 | 0.957 | 0.038 |
| | | SIC | (0.5, 3.5) | 0.780 | 1.000 | 0.911 | 0.012 |
| | | MIC | (0.5, 3.5) | 0.992 | 1.000 | 0.998 | 0.074 |
| | 75 | LRT | (0.5, 3.5) | 0.819 | 0.996 | 0,870 | 0.025 |
| | | SIC | (0.5, 3.5) | 0.674 | 0.996 | 0.813 | 0.007 |
| | | MIC | (0.5, 3.5) | 0.955 | 1.000 | 0.992 | 0.039 |
| 0.1 | 25 | LRT | (0.5, 3.5) | 0.943 | 1.000 | 0.989 | 0.076 |
| | | SIC | (0.5, 3.5) | 0.833 | 0.996 | 0.900 | 0.037 |
| | | MIC | (0.5, 3.5) | 0.997 | 1.000 | 1.000 | 0.087 |
| | 50 | LRT | (0.5, 3.5) | 0.987 | 1.000 | 0.995 | 0.080 |
| | | SIC | (0.5, 3.5) | 0.890 | 1.000 | 0.963 | 0.029 |
| | | MIC | (0.5, 3.5) | 0.999 | 1.000 | 1.000 | 0.090 |
| | 75 | LRT | (0.5, 3.5) | 0.945 | 1.000 | 0.992 | 0.064 |
| | | SIC | (0.5, 3.5) | 0.847 | 1.000 | 0.895 | 0.034 |
| | | MIC | (0.5, 3.5) | 0.992 | 1.000 | 1.000 | 0.082 |
Table 11.
Powers of the LRT, SIC, and MIC procedures at , .
Table 11.
Powers of the LRT, SIC, and MIC procedures at , .
| | | | | |
|---|
| k | Model | | (5, 3.5) | (0.5, 2) | (1.5, 4.5) | (5, 2) |
|---|
| 0.01 | 5 | LRT | (5, 2) | 0.274 | 0.263 | 0.295 | 0.000 |
| | | SIC | (5, 2) | 0.099 | 0.114 | 0.118 | 0.000 |
| | | MIC | (5, 2) | 0.483 | 0.600 | 0.513 | 0.007 |
| | 10 | LRT | (5, 2) | 0.381 | 0.494 | 0.333 | 0.002 |
| | | SIC | (5, 2) | 0.144 | 0.218 | 0.119 | 0.000 |
| | | MIC | (5, 2) | 0.686 | 0.749 | 0.808 | 0.007 |
| | 15 | LRT | (5, 2) | 0.186 | 0.358 | 0.152 | 0.001 |
| | | SIC | (5, 2) | 0.069 | 0.144 | 0.036 | 0.000 |
| | | MIC | (5, 2) | 0.445 | 0.617 | 0.611 | 0.005 |
| 0.05 | 5 | LRT | (5, 2) | 0.670 | 0.796 | 0.848 | 0.013 |
| | | SIC | (5, 2) | 0.514 | 0.599 | 0.635 | 0.004 |
| | | MIC | (5, 2) | 0.749 | 0.926 | 0.870 | 0.050 |
| | 10 | LRT | (5, 2) | 0.828 | 0.887 | 0.963 | 0.038 |
| | | SIC | (5, 2) | 0.648 | 0.684 | 0.864 | 0.006 |
| | | MIC | (5, 2) | 0.885 | 0.974 | 0.968 | 0.063 |
| | 15 | LRT | (5, 2) | 0.659 | 0.694 | 0,818 | 0.043 |
| | | SIC | (5, 2) | 0.319 | 0.358 | 0.731 | 0.005 |
| | | MIC | (5, 2) | 0.750 | 0.954 | 0.804 | 0.059 |
| 0.1 | 5 | LRT | (5, 2) | 0.743 | 0.922 | 0.884 | 0.053 |
| | | SIC | (5, 2) | 0.629 | 0.784 | 0.861 | 0.049 |
| | | MIC | (5, 2) | 0.823 | 0.983 | 0.957 | 0.074 |
| | 10 | LRT | (5, 2) | 0.782 | 0.975 | 0.894 | 0.062 |
| | | SIC | (5, 2) | 0.635 | 0.888 | 0.881 | 0.051 |
| | | MIC | (5, 2) | 0.857 | 0.998 | 0.996 | 0.080 |
| | 15 | LRT | (5, 2) | 0.623 | 0.871 | 0.883 | 0.049 |
| | | SIC | (5, 2) | 0.569 | 0.658 | 0.820 | 0.043 |
| | | MIC | (5, 2) | 0.835 | 0.996 | 0.968 | 0.080 |
Table 12.
Powers of the LRT, SIC, and MIC procedures at , .
Table 12.
Powers of the LRT, SIC, and MIC procedures at , .
| | | | | |
|---|
| k | Model | | (5, 3.5) | (0.5, 2) | (1.5, 4.5) | (5, 2) |
|---|
| 0.01 | 15 | LRT | (5, 2) | 0.512 | 0.886 | 0.999 | 0.001 |
| | | SIC | (5, 2) | 0.403 | 0.719 | 0.998 | 0.001 |
| | | MIC | (5, 2) | 0.600 | 1.000 | 1.000 | 0.004 |
| | 25 | LRT | (5, 2) | 0.519 | 0.954 | 1.000 | 0.002 |
| | | SIC | (5, 2) | 0.415 | 0.761 | 1.000 | 0.001 |
| | | MIC | (5, 2) | 0.649 | 1.000 | 1.000 | 0.013 |
| | 35 | LRT | (5, 2) | 0.507 | 0.932 | 1.000 | 0.000 |
| | | SIC | (5, 2) | 0.404 | 0.754 | 0.998 | 0.000 |
| | | MIC | (5, 2) | 0.612 | 1.000 | 1.000 | 0.005 |
| 0.05 | 15 | LRT | (5, 2) | 0.832 | 0.997 | 1.000 | 0.028 |
| | | SIC | (5, 2) | 0.668 | 0.842 | 1.000 | 0.008 |
| | | MIC | (5, 2) | 0.834 | 1.000 | 1.000 | 0.035 |
| | 25 | LRT | (5, 2) | 0.894 | 0.999 | 1.000 | 0.036 |
| | | SIC | (5, 2) | 0.670 | 0.853 | 1.000 | 0.011 |
| | | MIC | (5, 2) | 0.866 | 1.000 | 1.000 | 0.048 |
| | 35 | LRT | (5, 2) | 0.814 | 0.878 | 1.000 | 0.017 |
| | | SIC | (5, 2) | 0.655 | 0.796 | 1.000 | 0.008 |
| | | MIC | (5, 2) | 0.848 | 1.000 | 1.000 | 0.027 |
| 0.1 | 15 | LRT | (5, 2) | 0.909 | 1.000 | 1.000 | 0.064 |
| | | SIC | (5, 2) | 0.777 | 0.998 | 1.000 | 0.028 |
| | | MIC | (5, 2) | 0.948 | 1.000 | 1.000 | 0.078 |
| | 25 | LRT | (5, 2) | 0.923 | 1.000 | 1.000 | 0.069 |
| | | SIC | (5, 2) | 0.796 | 0.999 | 1.000 | 0.038 |
| | | MIC | (5, 2) | 0.962 | 1.000 | 1.000 | 0.083 |
| | 35 | LRT | (5, 2) | 0.881 | 1.000 | 1.000 | 0.050 |
| | | SIC | (5, 2) | 0.737 | 0.979 | 1.000 | 0.031 |
| | | MIC | (5, 2) | 0.958 | 1.000 | 1.000 | 0.081 |
Table 13.
Powers of the LRT, SIC, and MIC procedures at , .
Table 13.
Powers of the LRT, SIC, and MIC procedures at , .
| | | | | |
|---|
| k | Model | | (5, 3.5) | (0.5, 2) | (1.5, 4.5) | (5, 2) |
|---|
| 0.01 | 25 | LRT | (5, 2) | 0.755 | 0.917 | 1.000 | 0.002 |
| | | SIC | (5, 2) | 0.628 | 0.767 | 1.000 | 0.000 |
| | | MIC | (5, 2) | 0.799 | 1.000 | 1.000 | 0.009 |
| | 50 | LRT | (5, 2) | 0.869 | 0.993 | 1.000 | 0.003 |
| | | SIC | (5, 2) | 0.722 | 0.869 | 1.000 | 0.001 |
| | | MIC | (5, 2) | 0.890 | 1.000 | 1.000 | 0.013 |
| | 75 | LRT | (5, 2) | 0.832 | 0.962 | 1.000 | 0.002 |
| | | SIC | (5, 2) | 0.710 | 0.814 | 1.000 | 0.001 |
| | | MIC | (5, 2) | 0.765 | 1.000 | 1.000 | 0.010 |
| 0.05 | 25 | LRT | (5, 2) | 0.894 | 0.999 | 1.000 | 0.035 |
| | | SIC | (5, 2) | 0.775 | 0.860 | 1.000 | 0.008 |
| | | MIC | (5, 2) | 0.937 | 1.000 | 1.000 | 0.061 |
| | 50 | LRT | (5, 2) | 0.945 | 0.949 | 1.000 | 0.039 |
| | | SIC | (5, 2) | 0.804 | 0.921 | 1.000 | 0.009 |
| | | MIC | (5, 2) | 0.979 | 1.000 | 1.000 | 0.071 |
| | 75 | LRT | (5, 2) | 0.848 | 0.973 | 1.000 | 0.025 |
| | | SIC | (5, 2) | 0.716 | 0.885 | 1.000 | 0.009 |
| | | MIC | (5, 2) | 0.940 | 1.000 | 1.000 | 0.067 |
| 0.1 | 25 | LRT | (5, 2) | 0.979 | 1.000 | 1.000 | 0.065 |
| | | SIC | (5, 2) | 0.898 | 0.998 | 1.000 | 0.028 |
| | | MIC | (5, 2) | 0.989 | 1.000 | 1.000 | 0.086 |
| | 50 | LRT | (5, 2) | 0.984 | 1.000 | 1.000 | 0.081 |
| | | SIC | (5, 2) | 0.918 | 1.000 | 1.000 | 0.037 |
| | | MIC | (5, 2) | 0.997 | 1.000 | 1.000 | 0.091 |
| | 75 | LRT | (5, 2) | 0.943 | 1.000 | 1.000 | 0.075 |
| | | SIC | (5, 2) | 0.852 | 0.999 | 1.000 | 0.030 |
| | | MIC | (5, 2) | 0.992 | 1.000 | 1.000 | 0.087 |
Table 14.
The MLEs and the goodness-of-fit statistics for the Shasta reservoir dataset.
Table 14.
The MLEs and the goodness-of-fit statistics for the Shasta reservoir dataset.
| Model | n | | | K–S (pval) |
|---|
| 20 | 6.060 | 4.083 | 0.221 (0.245) |
Table 15.
The MLEs and the goodness-of-fit statistics for Susquehanna river dataset.
Table 15.
The MLEs and the goodness-of-fit statistics for Susquehanna river dataset.
| Model | n | | | K–S (pval) |
|---|
| 20 | 3.353 | 11.658 | 0.213 (0.284) |
Table 16.
The MLEs and the goodness-of-fit statistics for 1.5cm glass fibre strengths dataset.
Table 16.
The MLEs and the goodness-of-fit statistics for 1.5cm glass fibre strengths dataset.
| Model | n | | | K–S (pval) |
|---|
| 27 | 1.383 | 6.461 | 0.240 (0.074) |