Early Detection for Dengue Using Local Indicator of Spatial Association (LISA) Analysis
Abstract
:1. Introduction
2. Materials and Methods
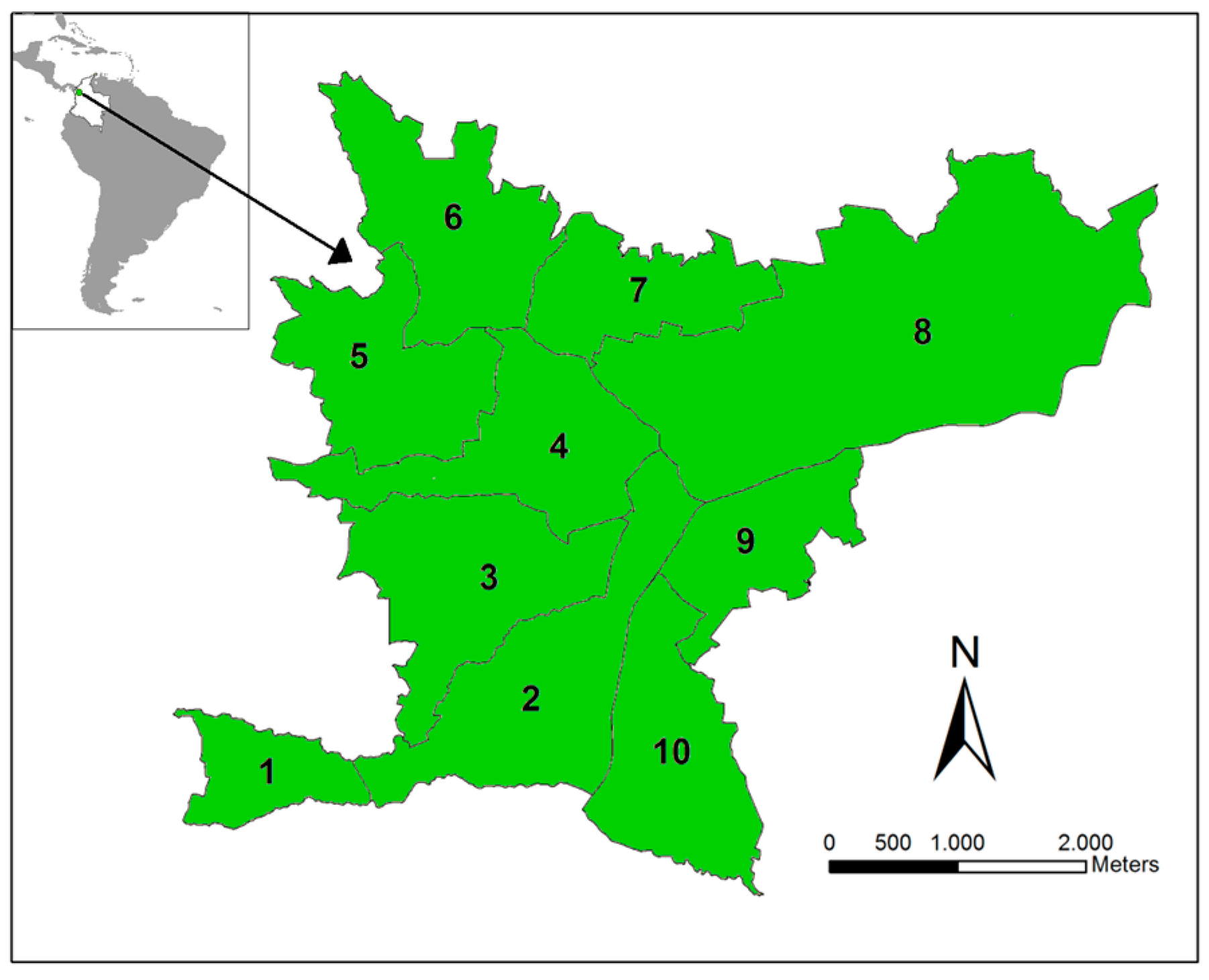
2.1. Study Site
2.2. Epidemiological Data
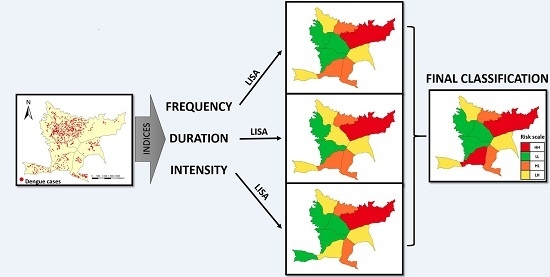
2.3. Temporal Indices to Measure Dengue Risk
2.3.1. Literature Indices
2.3.2. Modified Indices
2.4. Risk Classification
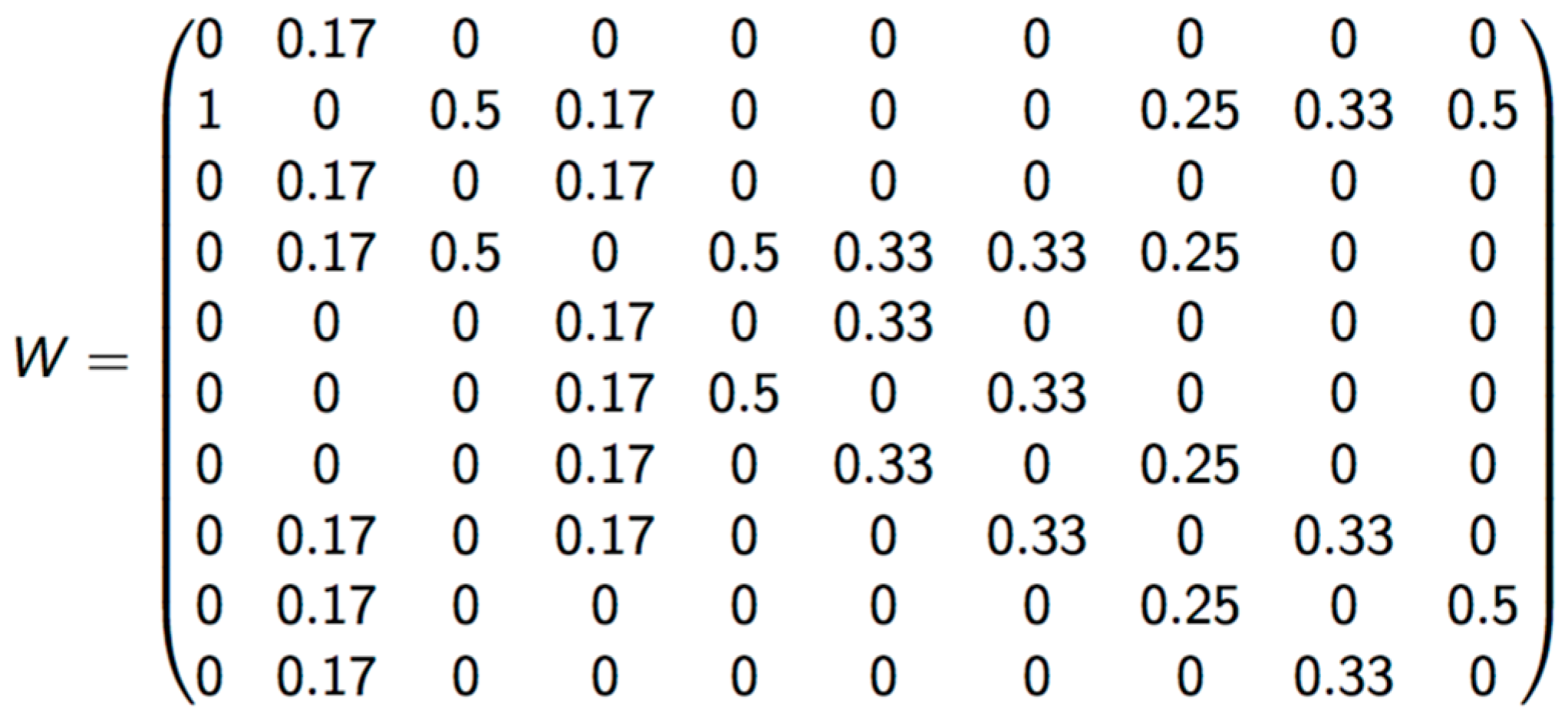
2.4.1. LISA
2.4.2. Chen’s Classification
2.4.3. Scenarios to Validate the Modified Indices
3. Results
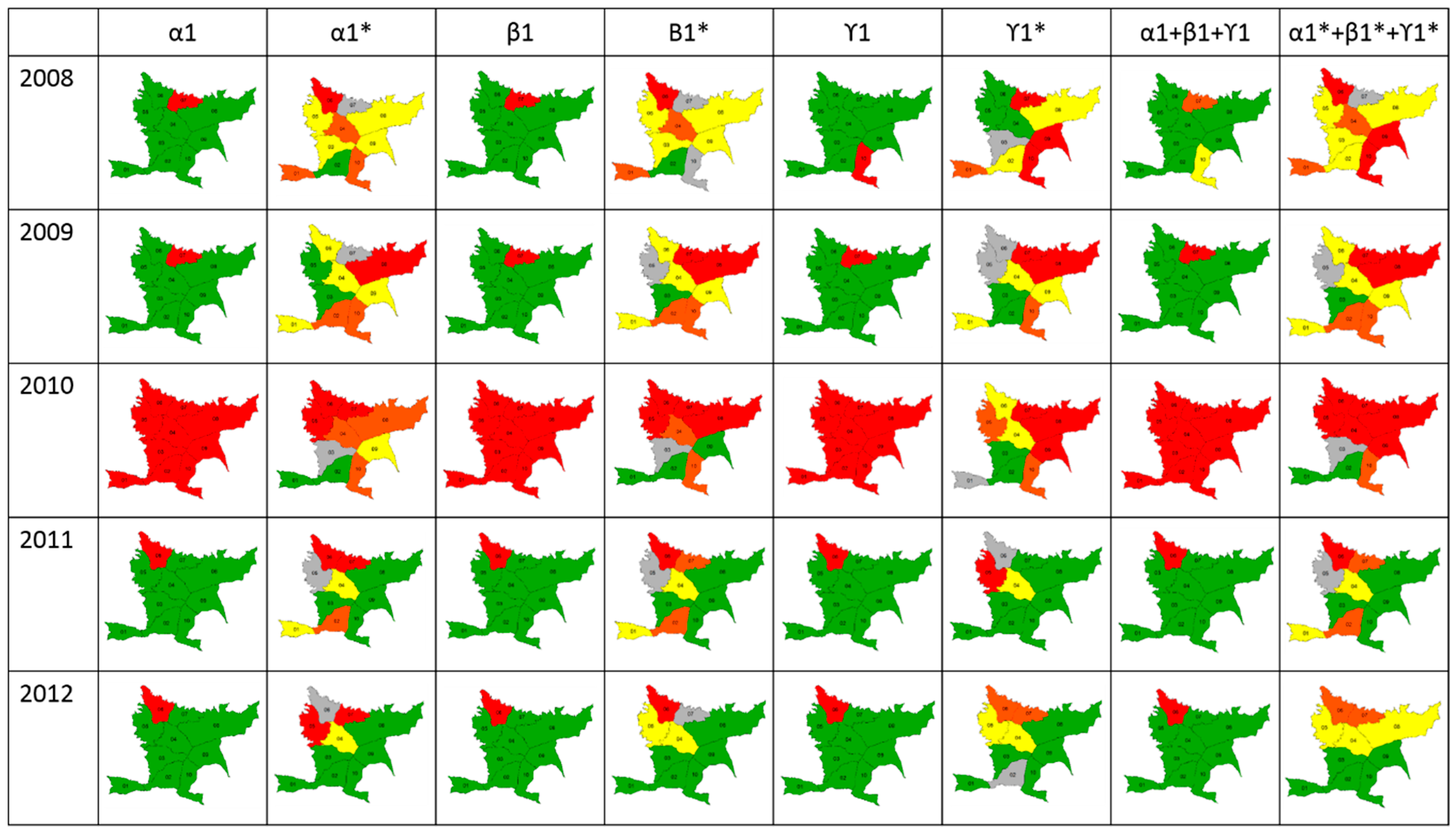
3.1. Temporal Indices for Early Detection of Dengue
3.2. Risk Classification
3.3. Index Validation
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dengue: Guidelines for diagnosis, treatment, prevention and control. Available online: http://www.who.int/tdr/publications/documents/dengue-diagnosis.pdf (accessed on 7 October 2015).
- Descripción de la situación epidemiologica actual del dengue en las Américas. Available online: http://www.paho.org/hq/index.php?option=com_content&view=article&id=4494%3A2010-descripcion-situacion-epidemiologica-actual-dengue-americas&catid=1221%3Adengue-statistics-maps&Itemid=41505&lang=es (accessed on 7 October 2015).
- Castañeda-Orjuela, C.; Díaz, H.; Alvis-Guzman, N.; Olarte, A.; Rodriguez, H.; Camargo, G.; de la Hoz-Restrepo, F. Burden of disease and economic impact of dengue and severe dengue in Colombia, 2011. Value Health Reg. Issues 2012, 1, 123–128. [Google Scholar] [CrossRef]
- Padilla, J.C.; Rojas, D.P.; Sáenz-Gómez, R. Dengue en Colombia: Epidemiología de la reemergencia a la hiperendemia. Rev. Salud Bosque 2015, 5, 81–83. [Google Scholar]
- Castañeda, O.; Segura, O.; Ramírez, A.N. Knowledge, attitudes and community practice during an outbreak of dengue in a town in Colombia, 2010. Rev. Salud Pública 2011, 13, 514–527. [Google Scholar] [PubMed]
- Chadee, D.D. Dengue cases and Aedes aegypti indices in Trinidad, West Indies. Acta Trop. 2009, 112, 174–180. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, L.; Cortinas, J.; Pelaez, O.; Gutierrez, H.; Concepción, D.; van der Stuyft, P. Breteau Index threshold levels indicating risk for dengue transmission in areas with low Aedes infestation. Trop. Med. Int. Health 2010, 15, 173–175. [Google Scholar] [CrossRef] [PubMed]
- Pham, H.V.; Doan, H.T.M.; Phan, T.T.T.; Minh, N.N.T. Ecological factors associated with dengue fever in a central highlands province, Vietnam. BMC Infect. Dis. 2011, 11, 172. [Google Scholar] [CrossRef] [PubMed]
- Rubio-Palis, Y.; Pérez-Ybarra, L.M.; Infante-Ruíz, M.; Comach, G.; Urdaneta-Márquez, L. Influence of climatic variables on dengue cases and abundance of Aedes aegypti (Diptera: Culicidae) in Maracay, Venezuela. Bol. Malariol. Salud Ambient. 2011, 51, 145–157. [Google Scholar]
- Focks, D.A. A Review of Entomological Sampling Methods and Indicators for Dengue Vectors; TDR/IDE/Den/03.1; World Health Organization: Geneva, Switzerland, 2003. [Google Scholar]
- Arboleda, S.; Jaramillo-O., N.; Peterson, A.T. Spatial and temporal dynamics of Aedes aegypti larval sites in Bello, Colombia. J. Vector Ecol. 2012, 37, 37–48. [Google Scholar] [CrossRef] [PubMed]
- Bowman, L.R.; Runge-Ranzinger, S.; McCall, P.J. Assessing the relationship between vector indices and dengue transmission: A systematic review of the evidence. PLoS Negl. Trop. Dis. 2014, 8, e2848. [Google Scholar] [CrossRef] [PubMed]
- Focks, D.A.; Barrera, R. Dengue Transmission Dynamics: Assessment And Implications For Control. In Proceedings of the Scientific Working Group meeting on Dengue Research; World Health Organization: Geneva, Switzerland, 2006. [Google Scholar]
- Wen, T.H.; Lin, N.H.; Lin, C.H.; King, C.C.; Su, M.D. Spatial mapping of temporal risk characteristics to improve environmental health risk identification: A case study of a dengue epidemic in Taiwan. Sci. Total Environ. 2006, 367, 631–640. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.Q.; Meng, Y.J.; Li, Y.; Qi, X.P. Frequency, duration and intensity of dengue fever epidemic risk in townships in Pearl River Delta and Yunnan in China, 2013. Biomed. Environ. Sci. 2015, 28, 388–395. [Google Scholar] [PubMed]
- Sistema Nacional de Vigilancia en Salud Pública (SIVIGILA) from 2008 to 2012. Available online: http://www.ins.gov.co/lineas-de-accion/Subdireccion-Vigilancia/sivigila/Paginas/vigilancia-rutinaria.aspx (accessed on 28 March 2016).
- Google Earth. Available online: https://www.google.com/earth/ (accessed on 28 March 2016).
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The Monte Carlo method. J. Am. Stat. Assoc. 2012, 11, 335–341. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2008. [Google Scholar]
- Castrillón, J.C.; Carlos, J.; Urcuqui, S. Dengue in Colombia: Ten years of database records. Rev. Chil. Infectol. 2015, 32, 22–29. [Google Scholar]
- Cassab, A.; Morales, V.; Mattar, S. Climatic factors and cases of dengue in Monteria, Colombia: 2003–2008. Rev. Salud Publica 2011, 13, 115–128. [Google Scholar] [CrossRef] [PubMed]
- Reiner, R.C.; Perkins, T.A.; Barker, C.M.; Niu, T.; Chaves, L.F.; Ellis, A.M.; George, D.B.; le Menach, A.; Pulliam, J.R.C.; Bisanzio, D.; et al. A systematic review of mathematical models of mosquito-borne pathogen transmission: 1970–2010. J. R. Soc. Interface 2013, 10, 20120921. [Google Scholar] [CrossRef] [PubMed]
- Eastin, M.; Delmelle, E.; Casas, I.; Wexler, J.; Self, C. Intra-and interseasonal autoregressive prediction of dengue outbreaks using local weather and regional climate for a tropical environment in Colombia. Am. J. Trop. Med. Hyg. 2014, 91, 598–610. [Google Scholar] [CrossRef] [PubMed]
- Hagenlocher, M.; Delmelle, E.; Casas, I.; Kienberger, S. Assessing socioeconomic vulnerability to dengue fever in Cali, Colombia: statistical vs expert-based modeling. Int. J. Health Geogr. 2013, 12, 36. [Google Scholar] [CrossRef] [PubMed]
- Stewart-Ibarra, A.M.; Muñoz, Á.G.; Ryan, S.J.; Ayala, E.B.; Borbor-Cordova, M.J.; Finkelstein, J.L.; Mejía, R.; Ordoñez, T.; Recalde-Coronel, G.C.; Rivero, K. Spatiotemporal clustering, climate periodicity, and social-ecological risk factors for dengue during an outbreak in Machala, Ecuador, in 2010. BMC Infect. Dis. 2014, 14, 610. [Google Scholar] [CrossRef] [PubMed]

| α1 | β1 | ϒ1 (×2) | Punctuation |
|---|---|---|---|
| L | L | L | 4 |
| H | L | L | 5 |
| L | H | L | 5 |
| L | L | H | 6 * |
| H | H | L | 6 * |
| H | L | H | 7 * |
| L | H | H | 7 * |
| H | H | H | 8 * |
| Hypothetical Scenarios | Zone | EW | EVmax | Risk Classification |
|---|---|---|---|---|
| A1 | 1 | 45 | 40 | High |
| 2 | 40 | 40 | Moderate | |
| 3 | 45 | 40 | High | |
| 4 | 46 | 40 | Very high | |
| B1 | 1 | 50 | 25 | Very high |
| 2 | 30 | 25 | Moderate | |
| 3 | 40 | 25 | High | |
| 4 | 50 | 25 | Very high | |
| 5 | 30 | 25 | Moderate | |
| 6 | 30 | 25 | Low | |
| 7 | 50 | 25 | Very high | |
| 8 | 30 | 25 | Moderate | |
| 9 | 30 | 25 | Low | |
| A2 | 1 | 30 | 48 | High |
| 2 | 40 | 28 | Very high | |
| 3 | 50 | 25 | High | |
| 4 | 30 | 20 | Moderate | |
| B2 | 1 | 50 | 10 | Moderate |
| 2 | 40 | 40 | Very high | |
| 3 | 40 | 40 | High | |
| 4 | 50 | 48 | High | |
| 5 | 30 | 28 | Moderate | |
| 6 | 30 | 25 | Low | |
| 7 | 50 | 25 | Very high | |
| 8 | 30 | 25 | Moderate | |
| 9 | 30 | 25 | Low |
| α & α1 | β | β1 | ϒ | ϒ1 | |
|---|---|---|---|---|---|
| 2008 | 0.92 ** | 0.08 | 0.90 ** | 0.20 | 0.32 |
| 2009 | 0.85 ** | 0.61 ** | 0.85 ** | −0.06 | 0.81 ** |
| 2010 | 0.64 ** | 0.46 * | 0.74 ** | 0.37 * | 0.53 * |
| 2011 | 0.88 ** | 0.46 * | 0.93 ** | −0.11 | 0.91 ** |
| 2012 | 0.97 ** | 0.91 * | 0.99 ** | 0.18 | 0.88 ** |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parra-Amaya, M.E.; Puerta-Yepes, M.E.; Lizarralde-Bejarano, D.P.; Arboleda-Sánchez, S. Early Detection for Dengue Using Local Indicator of Spatial Association (LISA) Analysis. Diseases 2016, 4, 16. https://doi.org/10.3390/diseases4020016
Parra-Amaya ME, Puerta-Yepes ME, Lizarralde-Bejarano DP, Arboleda-Sánchez S. Early Detection for Dengue Using Local Indicator of Spatial Association (LISA) Analysis. Diseases. 2016; 4(2):16. https://doi.org/10.3390/diseases4020016
Chicago/Turabian StyleParra-Amaya, Mayra Elizabeth, María Eugenia Puerta-Yepes, Diana Paola Lizarralde-Bejarano, and Sair Arboleda-Sánchez. 2016. "Early Detection for Dengue Using Local Indicator of Spatial Association (LISA) Analysis" Diseases 4, no. 2: 16. https://doi.org/10.3390/diseases4020016
APA StyleParra-Amaya, M. E., Puerta-Yepes, M. E., Lizarralde-Bejarano, D. P., & Arboleda-Sánchez, S. (2016). Early Detection for Dengue Using Local Indicator of Spatial Association (LISA) Analysis. Diseases, 4(2), 16. https://doi.org/10.3390/diseases4020016