A Neural Network Decomposition Algorithm for Mapping on Crossbar-Based Computing Systems

Abstract

Crossbar-based neuromorphic computing to accelerate neural networks is a popular alternative to conventional von Neumann computing systems. It is also referred as processing-in-memory and in-situ analog computing. The crossbars have a fixed number of synapses per neuron and it is necessary to decompose neurons to map networks onto the crossbars. This paper proposes the k-spare decomposition algorithm that can trade off the predictive performance against the neuron usage during the mapping. The proposed algorithm performs a two-level hierarchical decomposition. In the first global decomposition, it decomposes the neural network such that each crossbar has k spare neurons. These neurons are used to improve the accuracy of the partially mapped network in the subsequent local decomposition. Our experimental results using modern convolutional neural networks show that the proposed method can improve the accuracy substantially within about 10% extra neurons.

1. Introduction

Deep learning has demonstrated astonishing performance in various fields such as computer vision, natural language processing, games, etc., over the past several years [1,2,3], and there is no doubt that deep models will play a critical role in the machine intelligence in the future. The deep models require massive amounts of computation and a large memory [4], so they are difficult to deploy in embedded systems where computational resources and energy are tightly constrained [5]. In order to address this challenge, much research effort is devoted to develop domain-specific computing systems to deep learning using ASICs and FPGAs [6,7]. Most of these systems are built upon the von Neumann architecture where instructions, implicit or explicit, and data are stored in memories separated from processors. This approach is practical but more radical changes may be necessary to cope with rapidly increasing demand on computing power in deep learning [8].

Another approach starts from the idea that we can create more powerful computers by learning from the most advanced, existing intelligent system, our brain [9]. While some neuromorphic systems still use von Neumann architectures, many neuromorphic systems tailor even the fundamental architecture for drastic improvements in computing power and energy efficiency, resulting in non-von Neumann systems. In the non-von Neumann neuromorphic systems, each weight in a neural network is stationary within a processing element for the entire testing of the neural network [10,11]. In neuromorphic systems, processing elements, each with its own local memory, are arranged in two different ways. The first type of neuromorphic systems arranges neuron-like processing elements in a grid and each of them stores a fixed number of weights. This type is referred as the matrix-based neuromorphic system [12]. The second type of neuromorphic systems implement synapse-like processing elements at each crosspoint in a crossbar. This type is referred as the crossbar-based neuromorphic system [13,14]. This is also considered a processing-in-memory (PIM) architecture [15]. Resistive devices like memristors are usually used as the synaptic elements.

Given a trained neural network with high precision weights, the weights should be quantized because neuromorphic systems usually employ low-precision synapses to integrate a large number of synapses onto a chip [16]. This process incurs quantization error, leading to accuracy loss. Quantization-aware training is also possible to reduce this loss, but post-training quantization is often needed or preferred because it doesn’t require time-consuming training and the full-size dataset, which is often unavailable for various reasons such as privacy and proprietary [17].

In the weight stationary neuromorphic systems, units in neural networks cannot be often mapped ono-to-one into the neurons in the hardware because the neurons have a fixed, small number p of synapses. Thus, given a trained network, a unit with more than p connections should be assigned to and evaluated with more than one hardware neuron, and this can be considered that the unit is decomposed into multiple units. There are many ways to perform this decomposition for a given unit. Due to the per-neuron dynamic fixed-point, this decomposition affects the accuracy loss during weight quantization. Moreover, it is possible to minimize the accuracy loss further if we are allowed to use extra hardware resources. In [12], the authors formulate this problem into a dual objective optimization problem and propose two heuristics, the sorting-based algorithm (SBA) and the packing-based algorithm (PBA). The SBA finds a good partitioning in terms of the accuracy loss without use of extra neurons, whereas the PBA reduces the accuracy loss further at a marginal use of extra neurons. However, the previous work targets at the matrix-based neuromorphic systems, which is not the mainstream neuromorphic architecture at the moment. For the crossbar-based neuromorphic systems, this optimization problem becomes more difficult due to the constraints from crossbars. In this case, each neuron cannot be decomposed independently any more as in the previous work. In this paper, we first address the neural network decomposition problem for mapping onto the crossbar-based neuromorphic systems and propose a novel decomposition algorithm.

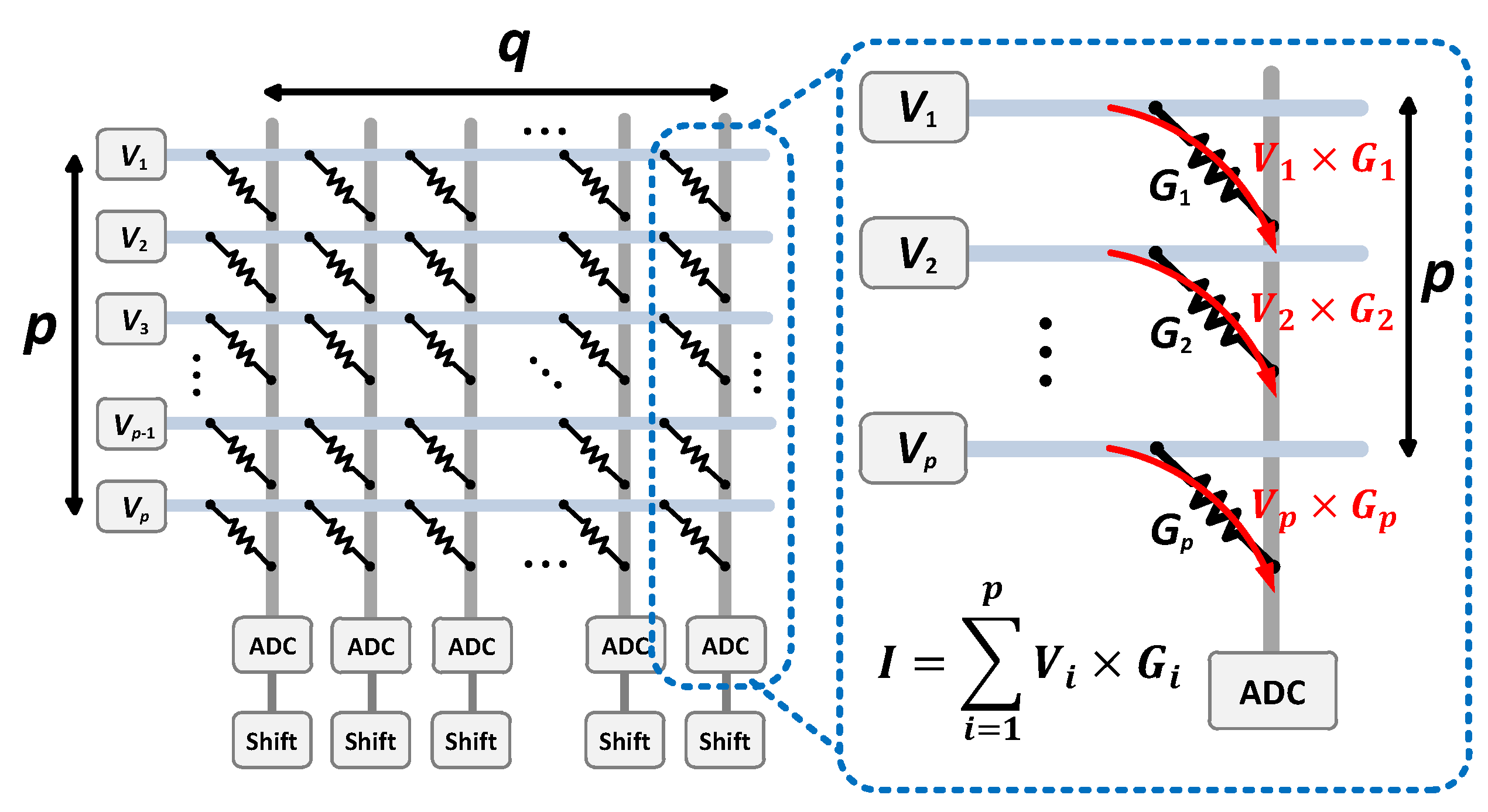
2. Problem Formulation

Our algorithm primarily targets at RRAM-based computing systems such as PRIME [13]. Figure 1 illustrates our hardware model of RRAM-based computing systems. In the RRAM core, each cell consists of a single programmable resistor. Let us consider a bitline in the core. If voltages $V_1,\cdots ,V_p$ are applied to each wordline simultanesously as shown in Figure 1, the current from the i-th wordline to the bitline becomes $V_i\times G_i$ where $G_i$ is the conduction of the ith resistor, and the bitline current becomes the sum of the currents flowing from each wordline by Kirchoff’s Law. In this analog way, each bitline can compute a dot-product value and the crossbar array can perform matrix-vector multiplication, which is the key primitive in machine learning workloads. Our model assumes a programmable shifter for each column so the dot-product values can be shifted in parallel. Most of recent RRAM-based computing systems are equipped with shifters right below the RRAM core [13,14,18]. Some RRAM-based systems simply use the fixed-point representation for weights, but considering a huge performance gap and a small hardware cost difference between the dynamic fixed-point and the fixed-point [19], it is more suitable to adopt the dynamic-fixed point as in PRIME. In the dynamic fixed-point representation, a group of numbers shares a scaling factor as in the fixed-point format, but the scaling factor is dynamically determined depending on the numbers in the group as in the floating-point format. When the group size is 1, or each number has one scaling factor, the dynamic fixed-point is reduced to a floating-point format. We assume that the scaling factor is a power of 2, and the exponent values are programmed to the shifters.

Figure 2 shows a mapping example. Each unit with four connections is decomposed into two units with two connections to be mapped on 2 × 3 crossbars. The outputs of the two decomposed neurons are added by a neuron with weights of 1 but this type of neurons are not considered in this paper because they are very few in any practical size of crossbars. The red dotted part is mapped into a single crossbar. Unlike the typical per-layer dynamic fixed-point, the target system allows a scaling factor per (decomposed) neuron, reducing quantization error. If we use the minimum number of neurons, 2, the quantization error in the mean square sense becomes 0.0003. On the other hand, if we use one extra neuron, it is reduced to 0.0001 taking advantage of one extra scaling factor. This motivates us to develop a mapping algorithm that uses hardware neurons wisely to reduce the accuracy loss induced by quantization error.

Now we formally define our problem. The two parts of bipartite graph are denoted by U and V. The set of edges is denoted by E. The set of nodes of a tree is denoted by O. The set of nodes at the ith level is denoted by $O^{\left(i\right)}$. A layer of a neural network is represented by a bipartite graph G where $U\left(G\right)$ and $V\left(G\right)$ are associated with the inputs and the outputs of the layer, respectively. A decomposition of a graph G is a family $\mathcal{F}$ of edge-disjoint subgraphs of G such that $E\left(G\right)={\bigcup }_{F\in \mathcal{F}}E\left(F\right)$.

The subgraphs in decomposition can be decomposed further so decompositions can be hierarchical. A hierarchical decomposition of a graph G is represented by a tree $\mathcal{T}$ where a node $s\in O\left(\mathcal{T}\right)$ is associated with a subgraph $G_s$ of G. If the set of the children of a node $s\in O\left(\mathcal{T}\right)$ is $\{t_1,\cdots ,t_n\}$, $\{G_{t_1},\cdots ,G_{t_n}\}$ is a decomposition of $G_s$. We will consider two-level hierarchical decompositions only. We call the first-level decomposition the global decomposition, and the second-level decomposition the local decomposition. The set of all possible 2-level decompositions is denoted by $\mathcal{U}$.

A graph G is $p\times q$ mappable if $\left|U\right(G\left)\right|\le p$ and $\left|V\right(G\left)\right|\le q$. A mappable decomposition of a graph G is a 2-level decomposition of G such that all subgraphs at the first level are $p\times q$ mappable and all the subgraphs at the second level are $p\times 1$ mappable. The set of all mappable decompositions is denoted by ${\mathcal{U}}^{(p,q)}$. When we map the layer per a mappable decomposition $\mathcal{T}$, the weights are quantized using a dynamic fixed-point quantizer Q. The quantizer is applied on a leaf node basis, and the weights associated with a leaf node are quantized together. If $\theta$ is the weight parameters of the layer, the quantized parameters are denoted by ${\tilde{\theta }}_{Q,\mathcal{T}}$. Then, the neural network decomposition problem is formulated as a dual-objective combinatorial optimization problem

$$\underset{\mathcal{T}\in {\mathcal{U}}^{(p,q)}}{min}(J\left(\theta \right)-J\left({\tilde{\theta }}_{Q,\mathcal{T}}\right),|O^{\left(1\right)}\left(\mathcal{T}\right)\left|\right),$$

(1)

where J is the loss function. Considering the enormous solution space, it seems to be intractable to solve this problem optimally and we propose heuristics for this problem.

3. Decomposition Algorithms

3.1. Vanilla Decomposition Algorithm (VDA)

This algorithm simply ignores the accuracy objective and just minimizes the crossbar usage. It first partitions vertices in $U\left(G\right)$ into groups of size p, called input groups and vertices in $V\left(G\right)$ into groups of size q, called output groups. Then, we have $\lceil \left|U\right(G\left)\right|/p\rceil$ input groups and $\lceil \left|V\right(G\left)\right|/q\rceil$ output groups. Let $\mathcal{T}$ be the resulting decomposition of VDA. The global decomposition of VDA can be constructed so that a pair of one input group and one output group corresponds to a mappable subgraph at the first level whose edge set contains all the edges between the two groups. Then, the local decomposition is constructed so that for all $s\in O^{\left(1\right)}\left(\mathcal{T}\right)$, the edges of each vertex in $V\left(G_s\right)$ becomes a partition at the second level. For any grouping, it guarantees

$$|O^{\left(1\right)}\left(\mathcal{T}\right)|=\lceil |U\left(G\right)|/p\rceil \times \lceil |V\left(G\right)|/q\rceil .$$

(2)

Let $N=\left|U\right(G\left)\right|,M=\left|V\right(G\left)\right|$. If N and M are divisible by p and q, respectively, we have

$$\frac{N!M!}{(N/p)!{(p!)}^{(N/p)}(M/q)!{(q!)}^{M/q}},$$

(3)

ways of grouping. Depending on grouping, the predictive performance varies, but VDA aims to minimize the resource utilization only. Thus, to create the input (output) groups, we simply group the first p (q) vertices into the first groups, and the next p (q) vertices into the next group until all vertices are grouped. Figure 3 illustrates VDA when $p=3$ and $q=3$.

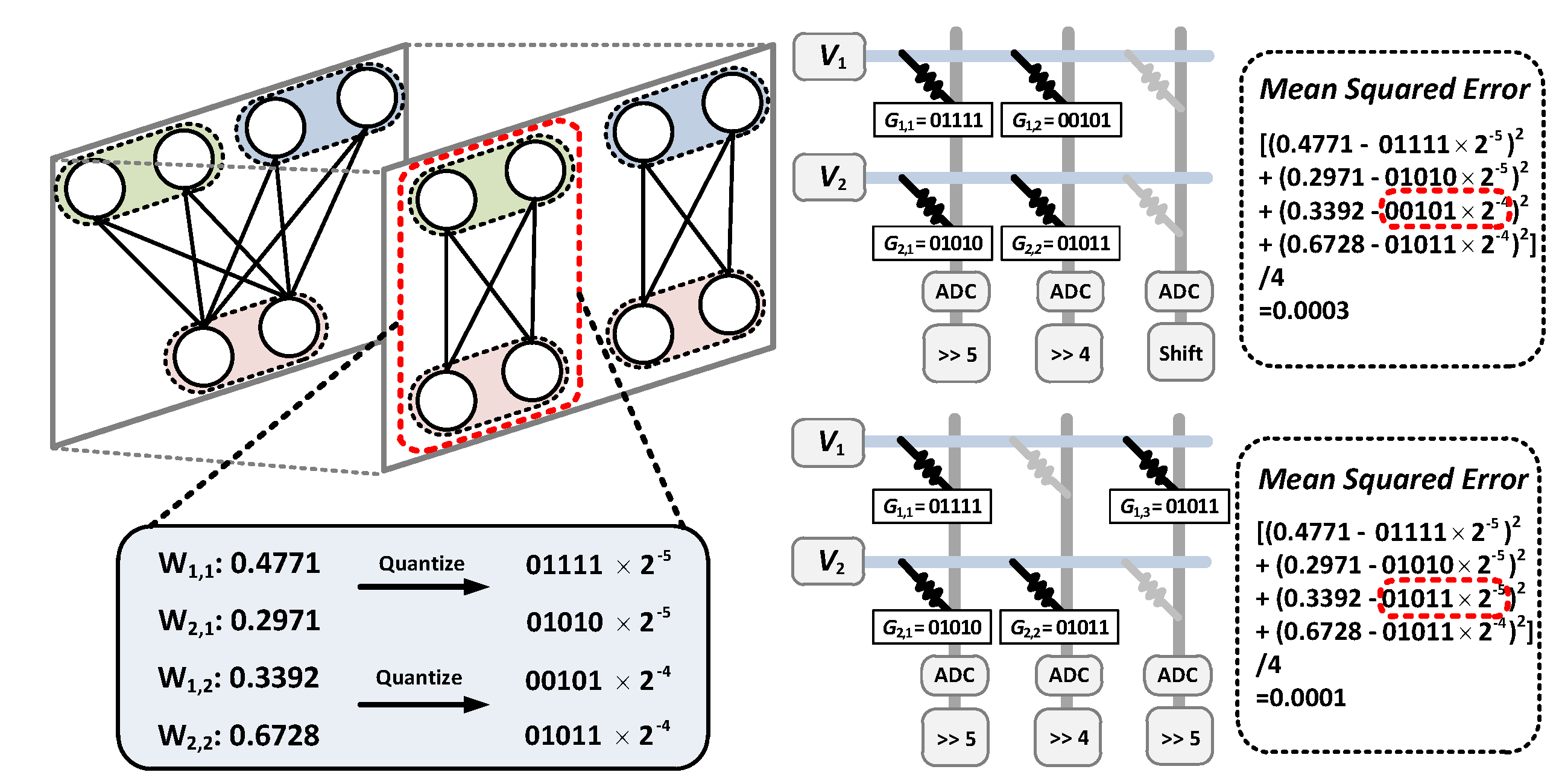
3.2. k-Spare Decomposition Algorithm (k-SDA)

3.2.1. Global Decomposition

Our proposed k-SDA employs the same global decomposition procedure as that of VDA but we partition vertices in $V\left(G\right)$ into groups of size $q-k$ instead of q. Thus, when we map each subgraph of the global decomposition into a $p\times q$ crossbar and k neurons remain unmapped and unused. These kspare neurons will be used in the subsequent local decomposition procedure. Figure 4 illustrates k-SDA when $k=1$.

3.2.2. Local Decomposition

There are various methods to obtain a local decomposition of a subgraph in the global decomposition. We describe them in the next section.

4. Local Decomposition Methods

Let $\mathcal{T}$ be the decomposition of k-SDA. After the global decomposition, for each $s\in O^{\left(1\right)}\left(\mathcal{T}\right)$, a local decomposition method is applied to $G_s$ independently. It selects some important vertices in $V\left(G_s\right)$ and unlike VDA, the edges of each of the selected vertices are partitioned into two or more groups. In VDA, the vertices in $V\left(G_s\right)$ are mapped to the neurons in a crossbar one to one. If some vertices in $V\left(G_s\right)$ are mapped to two or more neurons, the quantization error can be reduced. To utilize the k spare neurons effectively, we need to select most salient vertices in the sense that reducing quantization error of those vertices will have the most effect on the training loss.

4.1. Candidate Selection

To select the salient vertices, we rank vertices in $V\left(G_s\right)$ using a score metric S. We consider a vertex $v\in V\left(G_s\right)$. Let ${\mathbf{w}}^{\left(v\right)}\in {\mathbb{R}}^n$ be the weights associated with v. The ith element of a vector is denoted by the subscript. The dynamic fixed-point quantizer Q is ${\mathbb{R}}^n\to {\mathbb{R}}^n$. A vertex with a negligible quantization error will have negligible effect on the training loss. Thus, we can use the mean square quantization error (MSEQ) as a score metric. We can write the MSQE by

$$S_{MSQE}\left(v\right):=\sum _{i=1}^n{({\mathbf{w}}_i^{\left(v\right)}-Q{\left({\mathbf{w}}^{\left(v\right)}\right)}_i)}^2,$$

(4)

However, the training loss has different sensitivities to each vertex, they should be taken into account. Usually, this is done by considering $E[dJ/y_v]$. However, when the training is done, $E[dJ/d{y}_v]\approx 0$, so we use the second-order derivative as in Optimal Brain Damage (OBD) [20]. Let $y_v$ denote the activation of a vertex v when ${\mathbf{w}}^{\left(v\right)}$ is used. Moreover, let ${\tilde{y}}_v$ be the activation of v when $Q\left({\mathbf{w}}^{\left(v\right)}\right)$ is used. Then, similar to OBD,

$$S_{DL}\left(v\right):=E\left[\frac{{\partial }^{2}J}{\partial y_v^2}{(y_v-{\tilde{y}}_v)}^2\right],$$

(5)

Moreover, after the training is done, the Fisher information is an approximation to the second-order derivative so we can use the Fisher information [21], which is easier to compute because the standard backprop for stochastic gradient descent (SGD) can do it. Thus we can write

$$S_{DL}\left(v\right)\approx E\left[{\left(\frac{\partial J}{\partial y_v}\right)}^2{(y_v-{\tilde{y}}_v)}^2\right].$$

(6)

These score metrics enable us to select a given number of neurons to be decomposed. At last, we introduce ways to fill up the spare neurons with the selection method.

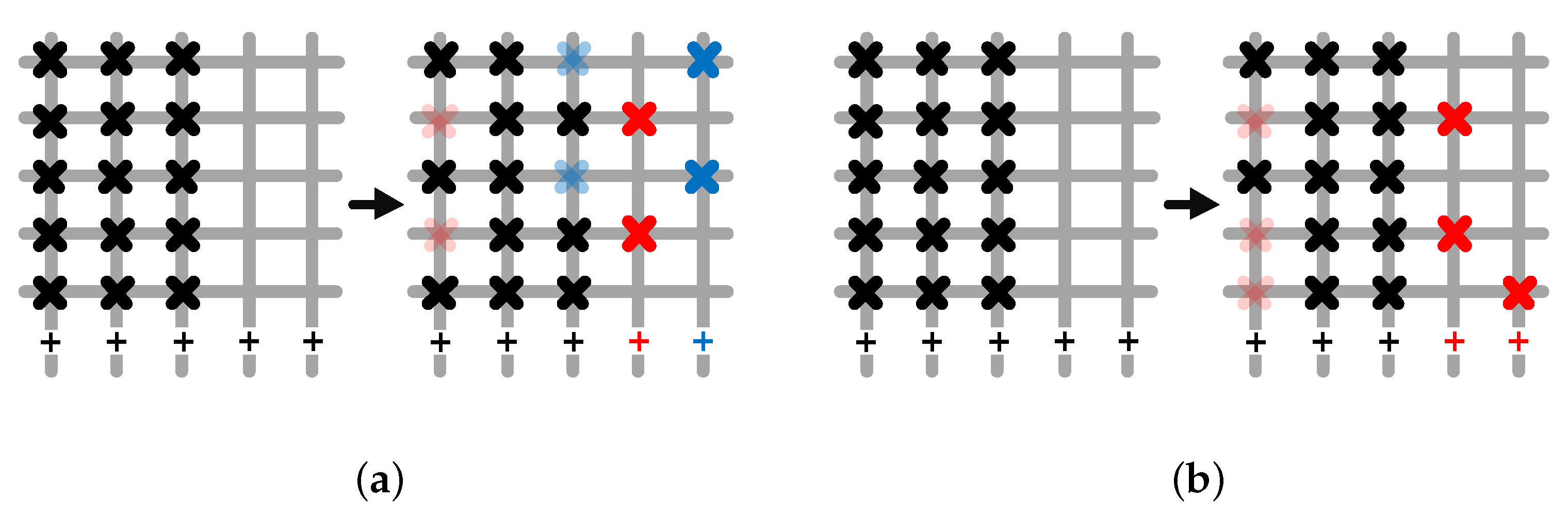
4.2. k Split-in-Two (KS2)

In this scheme, k salient vertices in $V\left(G_s\right)$ is selected. Then, the edges of each vertex are partitioned into two groups. This process is performed independently for each vertex and this problem was explored well in our previous work [12], where the packing-based algorithm (PBA) and the sorting-based algorithm (SBA) were proposed. For the partitioning, we can use either one of them.

4.3. One Split-in-$k+1$ (1SK)

This heuristic selects the most salient single vertex in $G_s$ for each $s\in O^{\left(1\right)}\left(\mathcal{T}\right)$. Then its edges are split into $k+1$ partitions. For the split, we again use PBA or SBA. This algorithm would work best if there is one vertex in $V\left(G_s\right)$ from which the most accuracy loss comes.

Figure 5 illustrates how KS2 and 1SK fill up the spare neurons in a $5\times 5$ crossbar with two extra neurons. KS2 selects two neurons because there are two sparse neurons. Each selected neuron is decomposed into two. 1SK select the first neuron and split it into three ways, filling up the two spare neurons only from the first neuron.

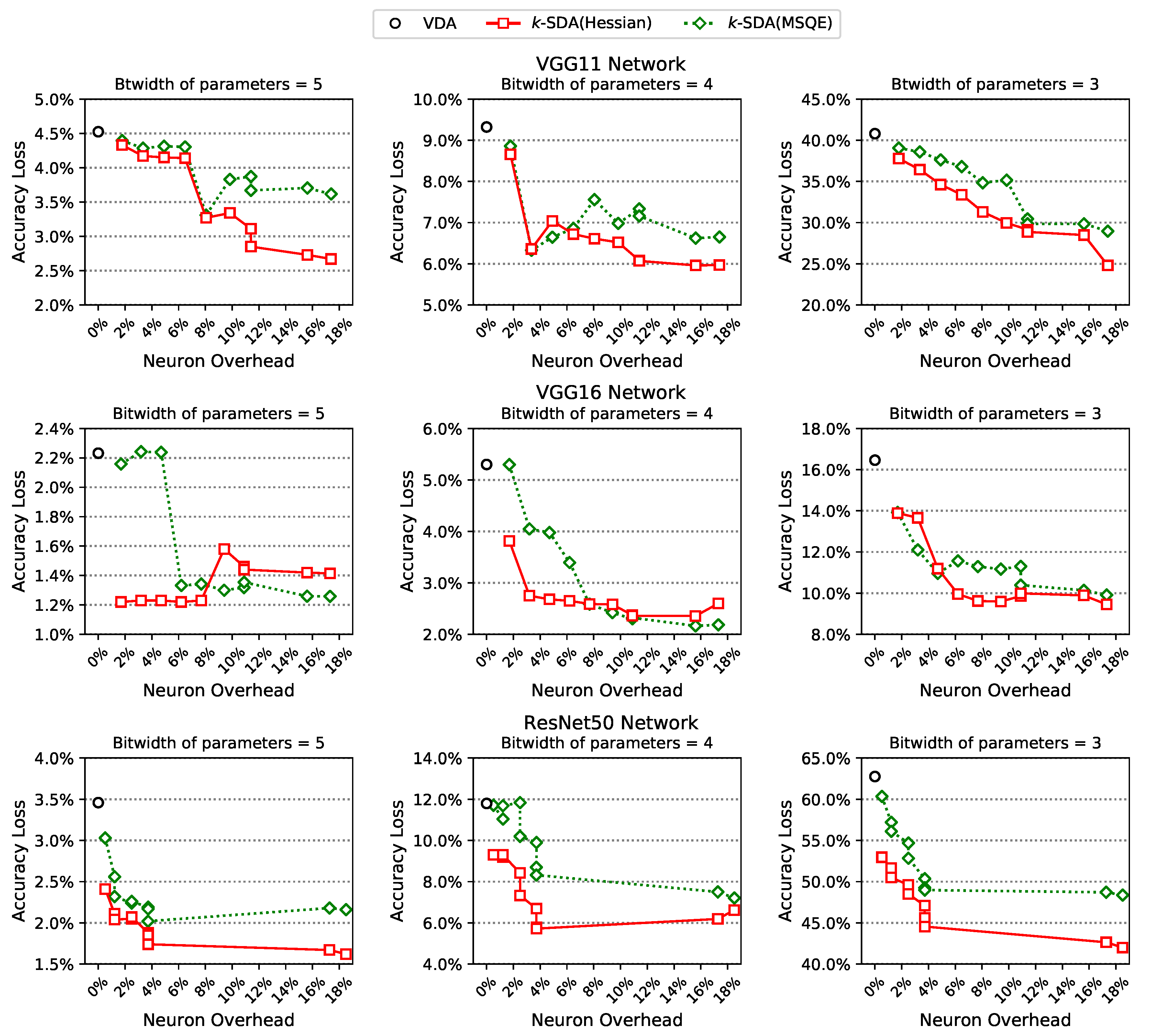
5. Experimental Results

We have implemented the proposed decomposition algorithm using PyTorch [22]. We have used six convolutional neural networks, VGG11, VGG13, VGG16 [2], ResNet18, ResNet50 [23] and Mobilenet_v2 [24], and ILSVRC2012 dataset. Their original accuracies for the dataset are 69.02%, 69.93%, 71.59%, 69.79%, 76.15% and 71.88% respectively. The original networks are mapped onto $p\times q$ crossbars (i.e., a crossbar has q neurons, each with p synapses). We use the per-neuron dynamic fixed-point format to represent weights (i.e., each neuron has a scaling factor that is shared across the weights of the neuron). The synapses in the crossbars can store m-bit weights. The scaling factor is set to $2^{-m+2-E}$, where E is a non-negative integer determined dynamically and $-m+2$ is the exponent bias. We assume that each neuron has a e-bit storage for E. Thus, the range of E becomes $\langle 0,2^e-1\rangle$. For all experiments, we use $p=72$, $q=72$ and $e=3$ unless stated otherwise.

We use two metrics to evaluate the algorithms. The first one is the ’accuracy loss’, which is defined as the original accuracy minus the accuracy of the mapped network. The second one is the ’neuron overhead’, which is defined as the ratio of the extra neurons used to the minimum required neurons.

We have several options to choose in designing our k-sparse decomposition algorithm (k-SDA). The chosen options are validated empirically. Figure 6 compares the two local decomposition methods for k-SDA. For the candidate selection, we use the mean square quantization error (MSQE). Note that we use the sorting-based algorithm of [12] to decompose a neuron into two. The KS2 clearly outperforms 1SK. This results seem to come from that decomposing a neuron into two provides enough reduction in the quantization error. Thus, we choose KS2 as our default local decomposition method.

Figure 7 compares our k-SDA(Hessian), k-SDA(MSQE) to the baseline, VDA. VDA always uses the minimum required neurons and has zero neuron overhead, but it does not provide a knob to control the trade-off. Our two k-SDA reduce the accuracy loss significantly at a reasonable cost of extra neurons. Among them, k-SDA(Hessian) takes the sensitivity of the quantization error to the accuracy into account and can select better candidates to decompose. Besides, it provides the knob to trade off the neuron usage against the accuracy. For the rest of the experiments, we use Hessian for the candidate selection and KS2(SBA) for the local decomposition.

Table 1. Accuracy loss and neuron overhead of VGG11, VGG13, VGG16, ResNet18, ResNet50 and Mobilenet_v2 for neural network decomposition algorithms.

Network	m	VDA		k-SDA
				k = 1		k = 3		k = 5		k = 8
		AccLoss	NeuOvr	AccLoss	NeuOvr	AccLoss	NeuOvr	AccLoss	NeuOvr	AccLoss	NeuOvr
VGG11	3	40.8%	0.00%	37.78%	1.78%	34.62%	4.91%	31.65%	8.05%	28.87%	11.40%
	4	9.32%		8.66%		7.04%		6.60%		6.07%
	5	4.52%		4.33%		4.14%		3.26%		2.85%
	6	0.61%		0.58%		0.51%		0.47%		0.42%
VGG13	3	23.54%	0.00%	21.65%	1.78%	15.93%	4.91%	13.72%	8.05%	13.44%	11.38%
	4	11.36%		10.30%		9.84%		8.01%		8.52%
	5	1.05%		0.94%		0.75%		0.83%		0.63%
	6	0.03%		0.19%		0.17%		0.19%		0.18%
VGG16	3	18.46%	0.00%	13.89%	1.70%	11.19%	4.70%	9.62%	7.69%	9.99%	10.89%
	4	5.30%		3.82%		2.67%		2.58%		2.35%
	5	2.23%		1.22%		1.22%		1.22%		1.44%
	6	0.04%		0.00%		0.01%		−0.03%		−0.05%
ResNet18	3	66%	0.00%	60.04%	0.31%	57.62%	0.31%	56.73%	0.31%	56.72%	0.63%
	4	25.17%		17.07%		16.34%		14.75%		14.05%
	5	6.15%		4.24%		4.08%		3.6%		3.7%
	6	1.12%		0.83%		0.54%		0.53%		0.53%
ResNet50	3	62.27%	0.00%	52.97%	0.52%	50.5%	1.22%	48.5%	2.5%	44.55%	3.72%
	4	11.8%		9.31%		9.3%		7.33%		5.72%
	5	3.46%		2.41%		2.04%		2.07%		1.74%
	6	1.69%		1.01%		0.61%		0.55%		0.45%
Mobilenet	3	71.78%	0.00%	71.75%	3.92%	71.77%	3.92%	71.76%	5.77%	71.75%	7.73%
	4	70.51%		69.76%		69.3%		68.42%		68.62%
	5	36.93%		28.34%		26.82%		21.74%		23.27%
	6	8.24%		6.66%		6.18%		8.52%		8%

summarizes the results of VDA and our k-SDA. For k-SDA, we use $k=1,3,5,8$. When the synapse resolution is low, our proposed method provides higher accuracy improvements, which suggests that we can potentially lower the synapse resolution counting on the proposed technique. As is widely known, Mobilenet is very sensitive to quantization error because of the reduced number of parameters, requiring a high synapse resolution. However, the enhancement by the proposed method is consistent across the various networks.

6. Conclusions

We have proposed a neural network decomposition algorithm to map neural networks to crossbar-based neuromorphic computing systems. It minimizes the accuracy loss incurred at the quantization during mapping at a small cost of extra neurons. Traditionally, increasing the synapse resolution has been the only way to prevent this accuracy loss in the post-training mapping, but the proposed algorithm has added a new dimension to control the accuracy–resource trade-off. We believe that this algorithm can also be extended to any weight-stationary neural net accelerators, which may be our future work.