ST-TrafficNet: A Spatial-Temporal Deep Learning Network for Traffic Forecasting
Abstract
:1. Introduction
- We propose attentive diffusion convolution to uncover unseen spatial dependencies from traffic graph signals automatically and further present the multi-diffusion convolution block to harvest spatial features in various manners. Extensive experiments demonstrate the ability of our MDC to improve the results when the graph structure is false or unknown.
- We construct a novel deep learning hybrid network, the ST-TrafficNet, for spatial-temporal traffic forecasting. The holistic ST-TrafficNet is effective and efficient to capture spatial-temporal features with cascading spatial-temporal layers by adopting residual connections. The core idea of the spatial-temporal layer is to enable our proposed MDC block to tackle spatial dependencies of traffic graph signals with high-dimension temporal features extracted by stacked LSTM block.
- We evaluate ST-TrafficNet on two benchmark datasets and compare it with various baseline methods for traffic forecasting. The experiments show that our proposed method achieves state-of-the-art results in terms of three widely used criteria.
2. Related Works
3. Preliminary
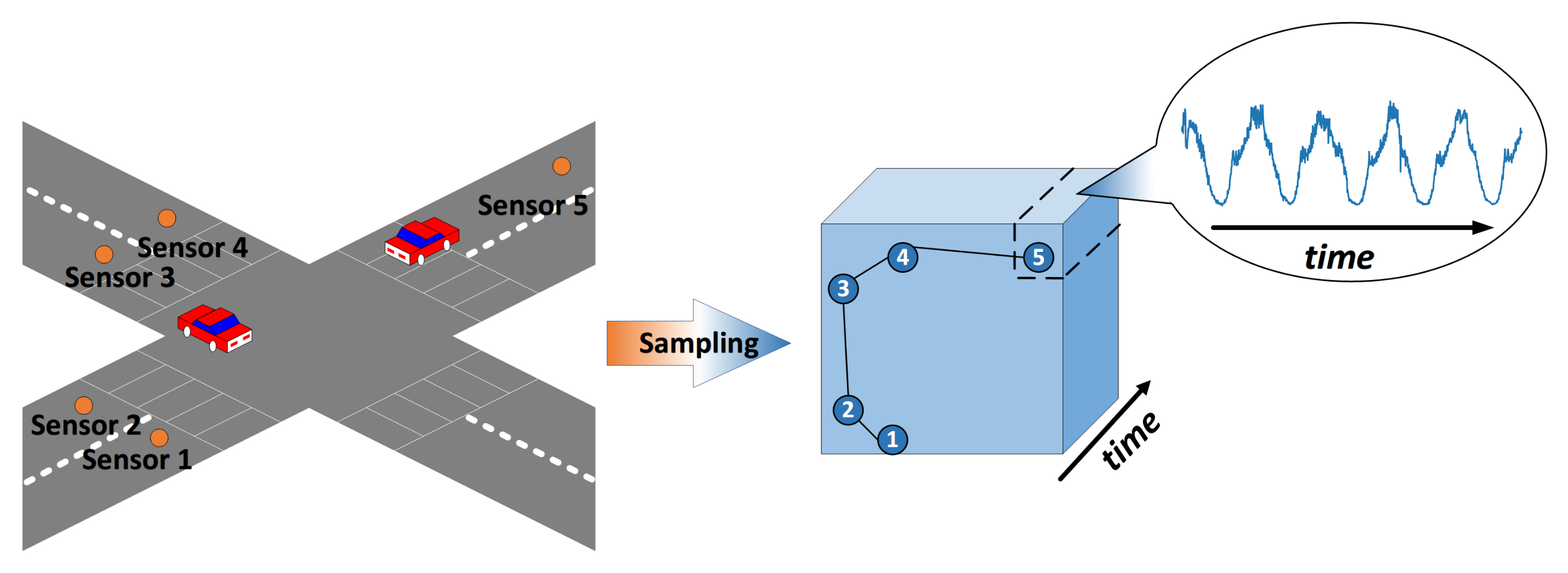
3.1. Traffic Forecasting Modeling
3.2. Graph Diffusion Convolution
3.3. Graph Attention Mechanism
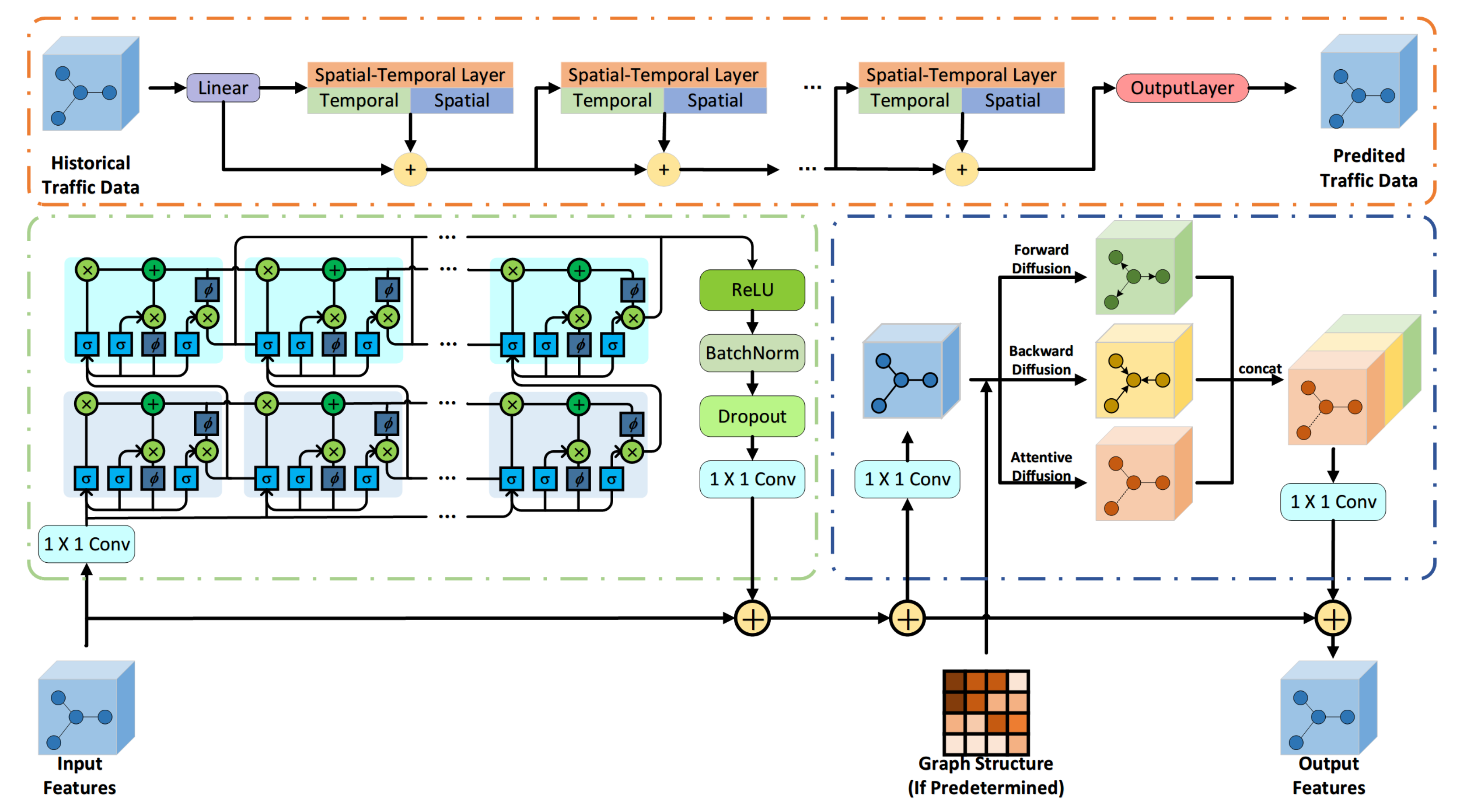
4. Methodology
4.1. Spatial Aware Multi-Diffusion Convolution Block
4.2. Temporal Aware Stacked LSTM Block
4.3. Framework of Spatial-temporal Deep Leaning Network
5. Experiments and Discussion
5.1. Data Preparation
5.2. Baseline Methods
5.3. Experimental Setup and Evaluation Criteria
5.4. Performance Comparison
5.5. Efficacy of Multi-Diffusion Convolution Block
5.6. Influence of Missing and Incorrect Graph Structure Knowledge
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Di Febbraro, A.; Giglio, D.; Sacco, N. A deterministic and stochastic Petri net model for traffic-responsive signaling control in urban areas. IEEE Trans. Intell. Transp. Syst. 2015, 17, 510–524. [Google Scholar] [CrossRef]
- Boriboonsomsin, K.; Barth, M.J.; Zhu, W.; Vu, A. Eco-routing navigation system based on multisource historical and real-time traffic information. IEEE Trans. Intell. Transp. Syst. 2012, 13, 1694–1704. [Google Scholar] [CrossRef]
- Veres, M.; Moussa, M. Deep learning for intelligent transportation systems: A survey of emerging trends. IEEE Trans. Intell. Transp. Syst. 2019, 21, 3152–3168. [Google Scholar] [CrossRef]
- Zambrano-Martinez, J.L.; Calafate, C.T.; Soler, D.; Cano, J.C.; Manzoni, P. Modeling and characterization of traffic flows in urban environments. Sensors 2018, 18, 2020. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zheng, Y.; Qi, D. Deep spatio-temporal residual networks for citywide crowd flows prediction. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 23 June 2017. [Google Scholar]
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Seo, Y.; Defferrard, M.; Vandergheynst, P.; Bresson, X. Structured sequence modeling with graph convolutional recurrent networks. In Proceedings of the International Conference on Neural Information Processing, Siem Reap, Cambodia, 13–16 December 2018; pp. 362–373. [Google Scholar]
- Yao, H.; Tang, X.; Wei, H.; Zheng, G.; Li, Z. Revisiting spatial-temporal similarity: A deep learning framework for traffic prediction. In Proceedings of the AAAI Conference on Artificial Intelligence, Honolulu, HI, USA, 27 January–1 February 2019; Volume 33, pp. 5668–5675. [Google Scholar]
- Zhang, J.; Shi, X.; Xie, J.; Ma, H.; King, I.; Yeung, D.Y. GaAN: Gated Attention Networks for Learning on Large and Spatiotemporal Graphs. arXiv 2018, arXiv:1803.07294. [Google Scholar]
- Du, X.; Zhang, H.; Van Nguyen, H.; Han, Z. Stacked LSTM deep learning model for traffic prediction in vehicle-to-vehicle communication. In Proceedings of the 2017 IEEE 86th Vehicular Technology Conference (VTC-Fall), Toronto, ON, Canada, 24–27 September 2017; pp. 1–5. [Google Scholar]
- Zhou, T.; Han, G.; Xu, X.; Han, C.; Huang, Y.; Qin, J. A learning-based multimodel integrated framework for Dynamic traffic flow forecasting. Neural Process. Lett. 2019, 43, 407–430. [Google Scholar] [CrossRef]
- Li, X.; Pan, G.; Wu, Z.; Qi, G.; Li, S.; Zhang, D.; Zhang, W.; Wang, Z. Prediction of urban human mobility using large-scale taxi traces and its applications. Front. Comput. Sci. 2012, 6, 111–121. [Google Scholar]
- Guo, J.; Huang, W.; Williams, B.M. Adaptive Kalman filter approach for stochastic short-term traffic flow rate prediction and uncertainty quantification. Transp. Res. Part C Emerg. Technol. 2014, 43, 50–64. [Google Scholar] [CrossRef]
- Zhou, T.; Jiang, D.; Lin, Z.; Han, G.; Xu, X.; Qin, J. Hybrid dual Kalman filtering model for short-term traffic flow forecasting. IET Intell. Transp. Syst. 2019, 13, 1023–1032. [Google Scholar] [CrossRef]
- Cai, L.; Zhang, Z.; Yang, J.; Yu, Y.; Zhou, T.; Qin, J. A noise-immune Kalman filter for short-term traffic flow forecasting. Phys. A Stat. Mech. Appl. 2019, 536, 122601. [Google Scholar] [CrossRef]
- Zhang, S.; Song, Y.; Jiang, D.; Zhou, T.; Qin, J. Noise-identified Kalman filter for short-term traffic flow forecasting. In Proceedings of the 2019 15th International Conference on Mobile Ad-Hoc and Sensor Networks (MSN), Shenzhen, China, 11–13 December 2019; pp. 462–466. [Google Scholar]
- Moreira-Matias, L.; Gama, J.; Ferreira, M.; Mendes-Moreira, J.; Damas, L. Predicting taxi–passenger demand using streaming data. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1393–1402. [Google Scholar] [CrossRef] [Green Version]
- Tan, M.C.; Wong, S.C.; Xu, J.M.; Guan, Z.R.; Zhang, P. An aggregation approach to short-term traffic flow prediction. IEEE Trans. Intell. Transp. Syst. 2009, 10, 60–69. [Google Scholar]
- Castro-Neto, M.; Jeong, Y.S.; Jeong, M.K.; Han, L.D. Online-SVR for short-term traffic flow prediction under typical and atypical traffic conditions. Expert Syst. Appl. 2009, 36, 6164–6173. [Google Scholar] [CrossRef]
- Cai, L.; Chen, Q.; Cai, W.; Xu, X.; Zhou, T.; Qin, J. SVRGSA: A hybrid learning based model for short-term traffic flow forecasting. IET Intell. Transp. Syst. 2019, 13, 1348–1355. [Google Scholar] [CrossRef]
- Cai, W.; Yang, J.; Yu, Y.; Song, Y.; Zhou, T.; Qin, J. PSO-ELM: A hybrid learning model for short-term traffic flow forecasting. IEEE Access 2020, 8, 6505–6514. [Google Scholar] [CrossRef]
- Chang, H.; Lee, Y.; Yoon, B.; Baek, S. Dynamic near-term traffic flow prediction: System-oriented approach based on past experiences. IET Intell. Transp. Syst. 2012, 6, 292–305. [Google Scholar] [CrossRef]
- Cai, L.; Yu, Y.; Zhang, S.; Song, Y.; Xiong, Z.; Zhou, T. A Sample-rebalanced Outlier-rejected k-nearest Neighbour Regression Model for Short-Term Traffic Flow Forecasting. IEEE Access 2020, 8, 22686–22696. [Google Scholar] [CrossRef]
- Huang, W.; Song, G.; Hong, H.; Xie, K. Deep architecture for traffic flow prediction: Deep belief networks with multitask learning. IEEE Trans. Intell. Transp. Syst. 2014, 15, 2191–2201. [Google Scholar] [CrossRef]
- Lv, Y.; Duan, Y.; Kang, W.; Li, Z.; Wang, F.Y. Traffic flow prediction with big data: A deep learning approach. IEEE Trans. Intell. Transp. Syst. 2014, 16, 865–873. [Google Scholar] [CrossRef]
- Zhou, T.; Han, G.; Xu, X.; Lin, Z.; Han, C.; Huang, Y.; Qin, J. δ-agree AdaBoost stacked autoencoder for short-term traffic flow forecasting. Neurocomputing 2017, 247, 31–38. [Google Scholar] [CrossRef]
- Mackenzie, J.; Roddick, J.F.; Zito, R. An evaluation of HTM and LSTM for short-term arterial traffic flow prediction. IEEE Trans. Intell. Transp. Syst. 2018, 20, 1847–1857. [Google Scholar] [CrossRef]
- Yang, B.; Sun, S.; Li, J.; Lin, X.; Tian, Y. Traffic flow prediction using LSTM with feature enhancement. Neurocomputing 2019, 332, 320–327. [Google Scholar] [CrossRef]
- Cai, L.; Lei, M.; Zhang, S.; Yu, Y.; Zhou, T.; Qin, J. A noise-immune LSTM network for short-term traffic flow forecasting. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 023135. [Google Scholar] [CrossRef]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and deep locally connected networks on graphs. In Proceedings of the 2nd International Conference on Learning Representations, ICLR 2014, Banff, AB, Canada, 14–16 April 2014. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. In Proceedings of the NIPS 2014 Workshop on Deep Learning, Montreal, QB, Canada, 8–13 December 2014. [Google Scholar]
- Li, G.; Muller, M.; Thabet, A.; Ghanem, B. Deepgcns: Can gcns go as deep as cnns? In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 9267–9276. [Google Scholar]
- Teng, S.H. Scalable algorithms for data and network analysis. Found. Trends Theor. Comput. Sci. 2016, 12, 1–274. [Google Scholar] [CrossRef]
- Veličković, P.; Cucurull, G.; Casanova, A.; Romero, A.; Liò, P.; Bengio, Y. Graph Attention Networks. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Shen, T.; Zhou, T.; Long, G.; Jiang, J.; Pan, S.; Zhang, C. Disan: Directional self-attention network for rnn/cnn-free language understanding. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Li, X.; Bai, L.; Ge, Z.; Lin, Z.; Yang, X.; Zhou, T. Early Diagnosis of Neuropsychiatric Systemic Lupus Erythematosus by Deep Learning Enhanced Magnetic Resonance Spectroscopy. J. Med. Imaging Health Inform. In press.
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Lin, F.; Feng, X.; Chen, Y. A Hybrid Deep Learning Model With Attention-Based Conv-LSTM Networks for Short-Term Traffic Flow Prediction. IEEE Trans. Intell. Transp. Syst. 2020. Early Access. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Earn. Res. 2014, 15, 1929–1958. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Zhang, C. Graph WaveNet for deep spatial-temporal graph modeling. In Proceedings of the International Joint Conference on Artificial Intelligence 2019, Macao, China, 10–16 August 2019; pp. 1907–1913. [Google Scholar]
- Yu, B.; Yin, H.; Zhu, Z. ST-UNet: A Spatio-Temporal U-Network for Graph-structured Time Series Modeling. arXiv 2019, arXiv:1903.05631. [Google Scholar]
- Li, J.; Perrine, K.; Walton, C.M. Identifying Faulty Loop Detectors Through Kinematic Wave Based Traffic State Reconstruction from Transit Probe Data. In Proceedings of the Transportation Research Board 96th Annual Meeting, Washington, DC, USA, 8–12 January 2017; p. 17-04843. [Google Scholar]
- Shuman, D.I.; Narang, S.K.; Frossard, P.; Ortega, A.; Vandergheynst, P. The emerging field of signal processing on graphs: Extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Process. Mag. 2013, 30, 83–98. [Google Scholar] [CrossRef] [Green Version]
- Van den Oord, A.; Dieleman, S.; Zen, H.; Simonyan, K.; Vinyals, O.; Graves, A.; Kalchbrenner, N.; Senior, A.; Kavukcuoglu, K. WaveNet: A Generative Model for Raw Audio. In Proceedings of the 9th ISCA Speech Synthesis Workshop, Sunnyvale, CA, USA, 13–15 September 2016; p. 125. [Google Scholar]
- Yu, B.; Yin, H.; Zhu, Z. Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting. In Proceedings of the International Joint Conference on Artificial Intelligence(IJCAI), Stockholm, Sweden, 13–19 July 2018; pp. 3634–3640. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Smith, B.L.; Williams, B.M.; Oswald, R.K. Comparison of parametric and nonparametric models for traffic flow forecasting. Transp. Res. Part C Emerg. Technol. 2002, 10, 303–321. [Google Scholar] [CrossRef]





| METR-LA Dataset | 15 min | 30 min | 60 min | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAPE | MAE | RMSE | MAPE | MAE | RMSE | MAPE | |
| (Vehs) | (Vehs) | (%) | (Vehs) | (Vehs) | (%) | (Vehs) | (Vehs) | (%) | |
| HA | 4.16 | 7.80 | 13.00 | 4.16 | 7.80 | 13.00 | 4.16 | 7.80 | 13.00 |
| ARIMA | 3.99 | 8.21 | 9.60 | 5.15 | 10.45 | 12.70 | 6.90 | 13.23 | 17.40 |
| LSVR | 2.97 | 5.89 | 7.68 | 3.64 | 7.35 | 9.90 | 4.67 | 9.13 | 13.63 |
| FNN | 3.99 | 7.94 | 9.91 | 4.23 | 8.17 | 12.92 | 4.49 | 8.69 | 14.01 |
| FC-LSTM | 3.44 | 6.30 | 9.60 | 3.77 | 7.23 | 10.90 | 4.37 | 8.69 | 13.20 |
| WaveNet | 2.99 | 5.89 | 8.04 | 3.59 | 7.28 | 10.25 | 4.45 | 8.93 | 13.62 |
| STGCN | 2.88 | 5.74 | 7.62 | 3.47 | 7.24 | 9.57 | 4.59 | 9.40 | 12.70 |
| DCRNN | 2.77 | 5.38 | 7.30 | 3.15 | 6.45 | 8.80 | 3.60 | 7.60 | 10.50 |
| ST-UNet | 2.83 | 5.17 | 7.03 | 3.22 | 6.36 | 8.63 | 3.65 | 7.40 | 10.00 |
| GWaveNet | 2.70 | 5.15 | 6.92 | 3.09 | 6.22 | 8.37 | 3.55 | 7.37 | 10.01 |
| ST-TrafficNet | 2.56 | 5.06 | 6.82 | 2.89 | 6.17 | 8.35 | 3.46 | 7.29 | 9.89 |
| PEMS-BAY Dataset | 15 min | 30 min | 60 min | ||||||
|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAPE | MAE | RMSE | MAPE | MAE | RMSE | MAPE | |
| (Vehs) | (Vehs) | (%) | (Vehs) | (Vehs) | (%) | (Vehs) | (Vehs) | (%) | |
| HA | 2.88 | 5.59 | 6.80 | 2.88 | 5.59 | 6.80 | 2.88 | 5.59 | 6.80 |
| ARIMA | 1.62 | 3.30 | 3.50 | 2.33 | 4.76 | 5.40 | 3.38 | 6.50 | 8.30 |
| LSVR | 1.42 | 3.45 | 3.31 | 2.13 | 4.37 | 5.28 | 2.34 | 4.28 | 5.55 |
| FNN | 1.59 | 3.42 | 3.53 | 2.11 | 4.42 | 5.16 | 3.18 | 6.24 | 8.12 |
| FC-LSTM | 2.05 | 4.19 | 4.80 | 2.20 | 4.55 | 5.20 | 2.37 | 4.96 | 5.70 |
| WaveNet | 1.39 | 3.01 | 2.91 | 1.83 | 4.21 | 4.16 | 2.35 | 5.43 | 5.87 |
| STGCN | 1.36 | 2.96 | 2.90 | 1.81 | 4.27 | 4.17 | 2.49 | 5.69 | 5.79 |
| DCRNN | 1.38 | 2.95 | 2.90 | 1.74 | 3.97 | 3.90 | 2.37 | 4.94 | 5.30 |
| ST-UNet | 1.38 | 2.83 | 2.79 | 1.72 | 3.82 | 3.75 | 1.97 | 4.63 | 4.83 |
| GWaveNet | 1.31 | 2.74 | 2.73 | 1.63 | 3.70 | 3.67 | 1.98 | 4.65 | 4.92% |
| ST-TrafficNet | 1.26 | 2.72 | 2.68 | 1.58 | 3.57 | 3.59 | 1.93 | 4.61 | 4.88 |
| Data-Set | Model | 15 min | 30 min | 60 min | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAPE | MAE | RMSE | MAPE | MAE | RMSE | MAPE | ||
| (Vehs) | (Vehs) | (%) | (Vehs) | (Vehs) | (%) | (Vehs) | (Vehs) | (%) | ||
| T(Temporal only) | 3.36 | 6.27 | 9.61 | 3.75 | 7.21 | 10.92 | 4.34 | 8.65 | 13.21 | |
| METR- | (Attentive only) | 2.81 | 5.32 | 7.36 | 3.12 | 6.46 | 8.56 | 3.69 | 7.48 | 10.42 |
| LA | (without Attentive) | 2.68 | 5.19 | 7.01 | 2.95 | 6.31 | 8.48 | 3.57 | 7.36 | 10.01 |
| (proposed model) | 2.56 | 5.06 | 6.82 | 2.89 | 6.17 | 8.35 | 3.46 | 7.29 | 9.89 | |
| T(Temporal only) | 2.02 | 4.14 | 4.78 | 2.20 | 4.54 | 5.19 | 2.34 | 4.94 | 5.70 | |
| PEMS- | (Attentive only) | 1.41 | 2.86 | 2.79 | 1.74 | 3.80 | 3.91 | 2.13 | 4.78 | 5.17 |
| BAY | (without Attentive) | 1.33 | 2.74 | 2.75 | 1.66 | 3.68 | 3.73 | 2.01 | 4.69 | 5.00 |
| (proposed model) | 1.26 | 2.72 | 2.68 | 1.58 | 3.57 | 3.59 | 1.93 | 4.61 | 4.88 |
| Model | Computational Time | |
|---|---|---|
| Train (Seconds/Epoch) | Predict (Seconds) | |
| ARIMA | - | 0.94 |
| ST-TrafficNet | 83.74 | 3.52 |
| Disturbance | ST-TrafficNet | ST-TrafficNet | |
|---|---|---|---|
| () | () | ||
| original | 1.33 | 1.26 | |
| noise | 5% | 1.37 | 1.26 |
| 10% | 1.44 | 1.29 | |
| original | 1.33 | 1.26 | |
| missing | 50% | 1.57 | 1.29 |
| 100% | 2.02 | 1.41 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, H.; Huang, D.; Song, Y.; Jiang, D.; Zhou, T.; Qin, J. ST-TrafficNet: A Spatial-Temporal Deep Learning Network for Traffic Forecasting. Electronics 2020, 9, 1474. https://doi.org/10.3390/electronics9091474
Lu H, Huang D, Song Y, Jiang D, Zhou T, Qin J. ST-TrafficNet: A Spatial-Temporal Deep Learning Network for Traffic Forecasting. Electronics. 2020; 9(9):1474. https://doi.org/10.3390/electronics9091474
Chicago/Turabian StyleLu, Huakang, Dongmin Huang, Youyi Song, Dazhi Jiang, Teng Zhou, and Jing Qin. 2020. "ST-TrafficNet: A Spatial-Temporal Deep Learning Network for Traffic Forecasting" Electronics 9, no. 9: 1474. https://doi.org/10.3390/electronics9091474
APA StyleLu, H., Huang, D., Song, Y., Jiang, D., Zhou, T., & Qin, J. (2020). ST-TrafficNet: A Spatial-Temporal Deep Learning Network for Traffic Forecasting. Electronics, 9(9), 1474. https://doi.org/10.3390/electronics9091474








